The Risk Function of Breast and Ovarian Cancers in the Avrami–Dobrzyński Cellular Phase-Transition Model
Abstract
1. Introduction
2. Results
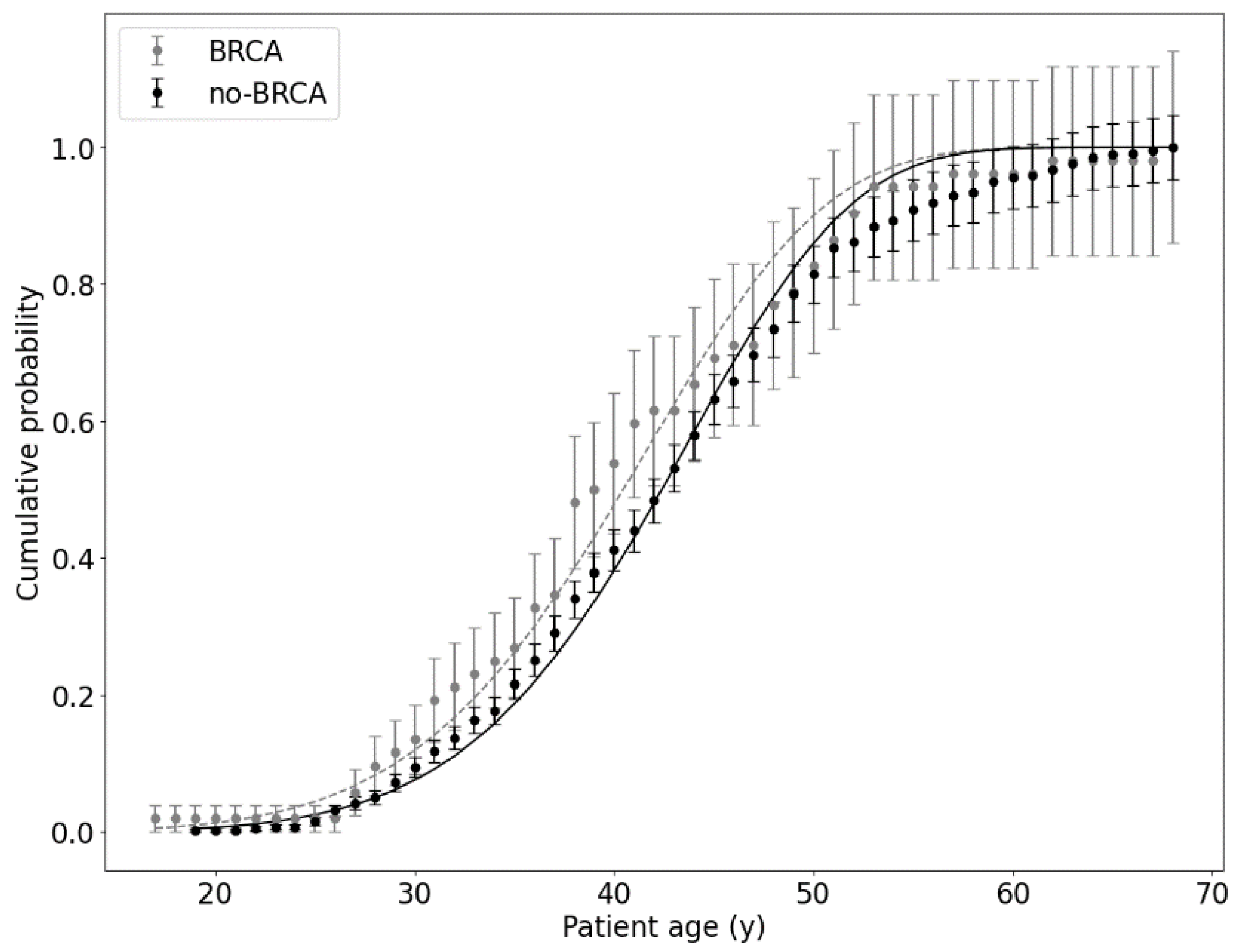
2.1. Patients Tested for BRCA1/BRCA2
2.2. Results for Cancer Patients without Genetic Tests
| No. of the Dataset | No. of Patients | Cancer Type | α Parameter (y−1) | k Parameter | Description |
|---|---|---|---|---|---|
| 1 | 459 | Breast, ovary, or both | (3.6 ± 1.6) 10−11 | 6.32 ± 0.12 | Patients without BRCA1/BRCA2 (no-BRCA group); see Figure 1 |
| 52 | (5.0 ± 6.0) 10−10 | 5.69 ± 0.33 | Patients with BRCA1/BRCA2 (BRCA group); see Figure 1 | ||
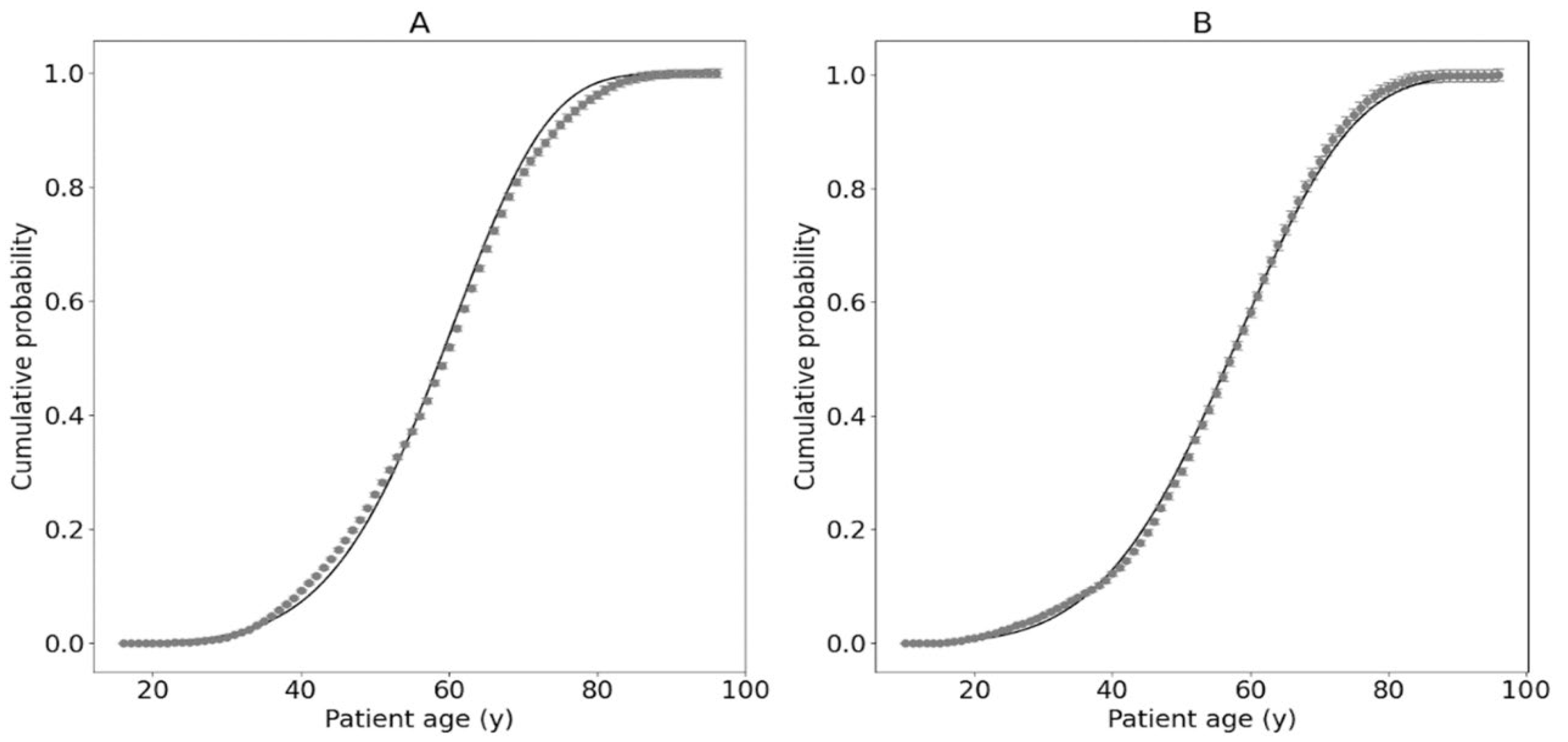
| 2 | 20,802 | Breast | (4.16 ± 0.21) 10−11 | 5.775 ± 0.013 | Patients diagnosed with breast cancer (C50 group); see Figure 3 |
| 3 | 9106 | Ovary | (6.58 ± 0.43) 10−9 | 4.570 ± 0.016 | Patients diagnosed with ovarian cancer (C56 group); see Figure 3 |
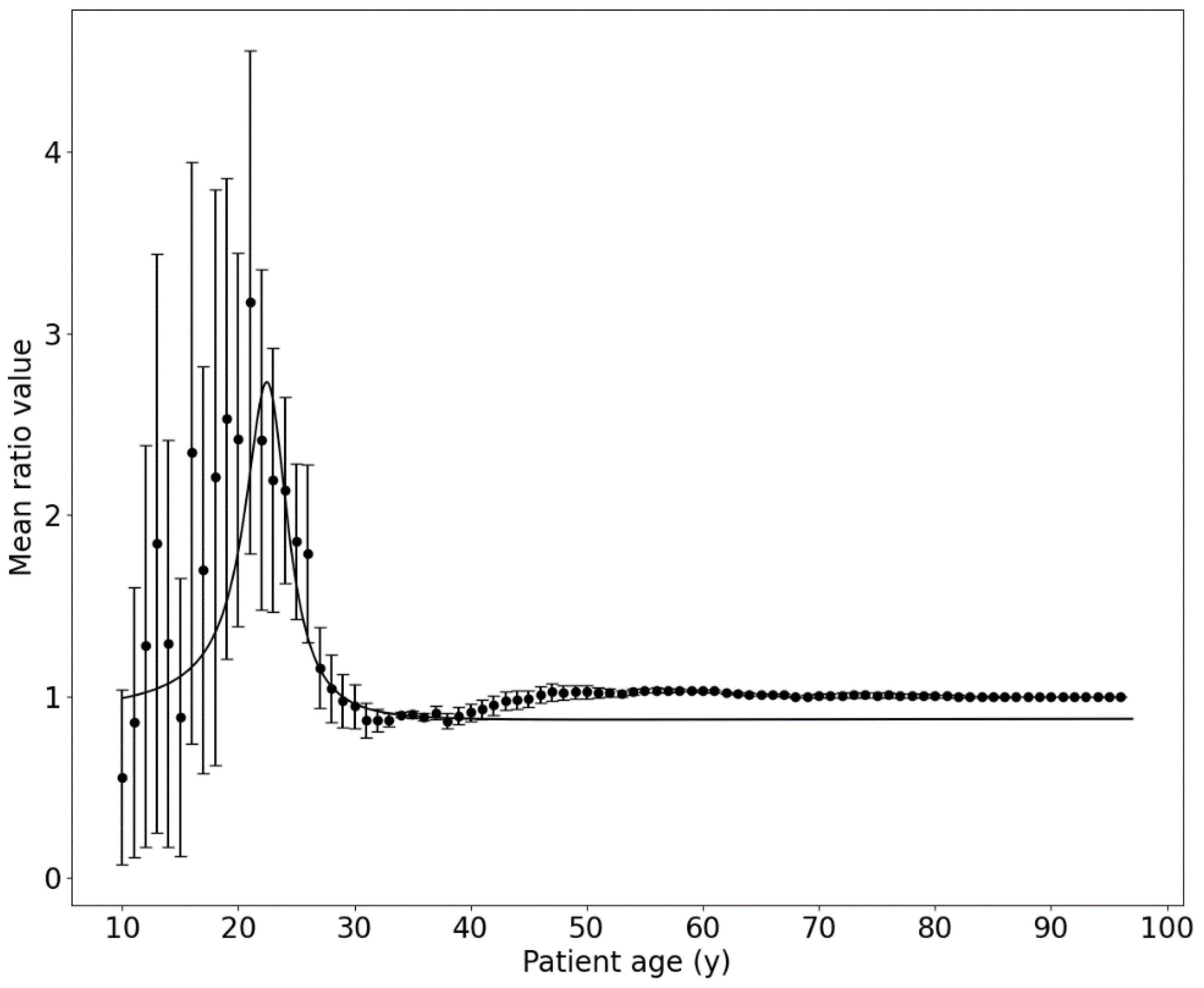
2.3. Protection Curve
2.4. Fractality
3. Discussion
- The geometric structure of DNA represents a fractal character; indeed, the DNA globule has many limited fractal elements, such as self-similarity and limited scale-free or power-law distribution of some DNA elements [25,26,27,28]. However, the process in which this fractality is functioning during cancer transformation is still unknown, especially from a dynamic point of view.
- DNA creates a complex multidimensional protein and metabolic network [29,30,31]; the proposed dimensionality problem should not be thought of as a spatial dimension related to the geometry of the DNA globule but rather the effective dimension of the network of protein interactions that are encoded by DNA. If we draw all proteins in the cell into a large network and connect all the nodes of proteins participating in the same processes (they have high affinity, regulate each other, etc.), we will obtain a network with a complicated topology. Such a complex network of connections can be associated with a dimension characterising the structure of this network (e.g., how many proteins are connected by one edge, how many by two edges, three, etc., and how it grows with the number of edges), not the space in which we draw it. In that way, the number of neighbours acts as a mathematical concept of dimension, and this feature does not have to be limited to 3D but can reach any number.
4. Materials and Methods
4.1. Clinical Data Collection
4.2. Statistical Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ATM | Ataxia–telangiectasia mutated |
| BOC | Breast and ovarian cancer |
| BRCA | Breast Cancer gene |
| CDH1 | Cadherin1 |
| CHEK2 | Checkpoint kinase 2 |
| DNA | Deoxyribonucleic acid |
| ICD | International Classification of Diseases |
| JMAK | Johnson–Mehl–Avrami–Kolmogorov |
| MSCI | Maria Skłodowska-Curie National Research Institute of Oncology |
| MSD | MedStream Designer |
| NBN | Nijmegen breakage syndrome (nibrin) |
| PALB2 | Partner and localizer of BRCA2 |
| PTEN | Phosphatase and tensin homolog |
| TP53 | Tumor protein p53 |
| XRCC2 | X-ray repair cross-complementating 2 |
References
- O’Donovan, P.J.; Livingston, D.M. BRCA1 and BRCA2: Breast/Ovarian Cancer Susceptibility Gene Products and Participants in DNA Double-Strand Break Repair. Carcinogenesis 2010, 31, 961–967. [Google Scholar] [CrossRef] [PubMed]
- Hanley, G.E.; McAlpine, J.N.; Cheifetz, R.; Schrader, K.A.; McCullum, M.; Huntsman, D. Selected Medical Interventions in Women with a Deleterious BRCA Mutation: A Population-Based Study in British Columbia. Curr. Oncol. 2019, 26, e17–e23. [Google Scholar] [CrossRef]
- Andreassen, P.R.; Seo, J.; Wiek, C.; Hanenberg, H. Understanding BRCA2 Function as a Tumor Suppressor Based on Domain-Specific Activities in DNA Damage Responses. Genes 2021, 12, 1034. [Google Scholar] [CrossRef] [PubMed]
- Bogdanova, N.V.; Antonenkova, N.N.; Rogov, Y.I.; Karstens, J.H.; Hillemanns, P.; Dörk, T. High Frequency and Allele-Specific Differences of BRCA1 Founder Mutations in Breast Cancer and Ovarian Cancer Patients from Belarus. Clin. Genet. 2010, 78, 364–372. [Google Scholar] [CrossRef] [PubMed]
- Plakhins, G.; Irmejs, A.; Gardovskis, A.; Subatniece, S.; Rozite, S.; Bitina, M.; Keire, G.; Purkalne, G.; Teibe, U.; Trofimovics, G.; et al. Genotype-Phenotype Correlations among BRCA1 4153delA and 5382insC Mutation Carriers from Latvia. BMC Med. Genet. 2011, 12, 147. [Google Scholar] [CrossRef] [PubMed]
- Solano, A.R.; Mele, P.G.; Jalil, F.S.; Liria, N.C.; Podesta, E.J.; Gutiérrez, L.G. Study of the Genetic Variants in BRCA1/2 and Non-BRCA Genes in a Population-Based Cohort of 2155 Breast/Ovary Cancer Patients, Including 443 Triple-Negative Breast Cancer Patients, in Argentina. Cancers 2021, 13, 2711. [Google Scholar] [CrossRef]
- Tung, N.; Lin, N.U.; Kidd, J.; Allen, B.A.; Singh, N.; Wenstrup, R.J.; Hartman, A.-R.; Winer, E.P.; Garber, J.E. Frequency of Germline Mutations in 25 Cancer Susceptibility Genes in a Sequential Series of Patients with Breast Cancer. J. Clin. Oncol. 2016, 34, 1460–1468. [Google Scholar] [CrossRef]
- Cybulski, C.; Kluźniak, W.; Huzarski, T.; Wokołorczyk, D.; Kashyap, A.; Rusak, B.; Stempa, K.; Gronwald, J.; Szymiczek, A.; Bagherzadeh, M.; et al. The Spectrum of Mutations Predisposing to Familial Breast Cancer in Poland. Int. J. Cancer 2019, 145, 3311–3320. [Google Scholar] [CrossRef]
- Szczerba, E.; Kamińska, K.; Mierzwa, T.; Misiek, M.; Kowalewski, J.; Lewandowska, M.A. BRCA1/2 Mutation Detection in the Tumor Tissue from Selected Polish Patients with Breast Cancer Using Next Generation Sequencing. Genes 2021, 12, 519. [Google Scholar] [CrossRef]
- Manganaro, L.; Bianco, S.; Bironzo, P.; Cipollini, F.; Colombi, D.; Corà, D.; Corti, G.; Doronzo, G.; Errico, L.; Falco, P.; et al. Consensus Clustering Methodology to Improve Molecular Stratification of Non-Small Cell Lung Cancer. Sci. Rep. 2023, 13, 7759. [Google Scholar] [CrossRef]
- Koh, D.-M.; Papanikolaou, N.; Bick, U.; Illing, R.; Kahn, C.E.; Kalpathi-Cramer, J.; Matos, C.; Martí-Bonmatí, L.; Miles, A.; Mun, S.K.; et al. Artificial Intelligence and Machine Learning in Cancer Imaging. Commun. Med. 2022, 2, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Shi, H.; Wang, H. Machine Learning and AI in Cancer Prognosis, Prediction, and Treatment Selection: A Critical Approach. J. Multidiscip. Healthc. 2023, 16, 1779–1791. [Google Scholar] [CrossRef] [PubMed]
- Dobrzyński, L.; Fornalski, K.W.; Socol, Y.; Reszczyńska, J.M. Modeling of Irradiated Cell Transformation: Dose- and Time-Dependent Effects. Radiat. Res. 2016, 186, 396–406. [Google Scholar] [CrossRef] [PubMed]
- Fornalski, K.W.; Dobrzyński, L. Modeling of Single Cell Cancer Transformation Using Phase Transition Theory: Application of the Avrami Equation. Radiat. Environ. Biophys. 2022, 61, 169–175. [Google Scholar] [CrossRef] [PubMed]
- Avrami, M. Kinetics of Phase Change. I General Theory. J. Chem. Phys. 2004, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change. II Transformation-Time Relations for Random Distribution of Nuclei. J. Chem. Phys. 2004, 8, 212–224. [Google Scholar] [CrossRef]
- Avrami, M. Granulation, Phase Change, and Microstructure Kinetics of Phase Change. III. J. Chem. Phys. 2004, 9, 177–184. [Google Scholar] [CrossRef]
- Shirzad, K.; Viney, C. A Critical Review on Applications of the Avrami Equation beyond Materials Science. J. R. Soc. Interface 2023, 20, 20230242. [Google Scholar] [CrossRef]
- Davies, P.C.; Demetrius, L.; Tuszynski, J.A. Cancer as a Dynamical Phase Transition. Theor. Biol. Med. Model. 2011, 8, 30. [Google Scholar] [CrossRef]
- Tsuchiya, M.; Giuliani, A.; Hashimoto, M.; Erenpreisa, J.; Yoshikawa, K. Emergent Self-Organized Criticality in Gene Expression Dynamics: Temporal Development of Global Phase Transition Revealed in a Cancer Cell Line. PLoS ONE 2015, 10, e0128565. [Google Scholar] [CrossRef]
- Ashley, D.J. The Two “Hit” and Multiple “Hit” Theories of Carcinogenesis. Br. J. Cancer 1969, 23, 313–328. [Google Scholar] [CrossRef] [PubMed]
- Anandakrishnan, R.; Varghese, R.T.; Kinney, N.A.; Garner, H.R. Estimating the Number of Genetic Mutations (Hits) Required for Carcinogenesis Based on the Distribution of Somatic Mutations. PLoS Comput. Biol. 2019, 15, e1006881. [Google Scholar] [CrossRef] [PubMed]
- Moore, L.; Cagan, A.; Coorens, T.H.; Neville, M.D.; Sanghvi, R.; Sanders, M.A.; Oliver, T.R.; Leongamornlert, D.; Ellis, P.; Noorani, A.; et al. The Mutational Landscape of Human Somatic and Germline Cells. Nature 2021, 597, 381–386. [Google Scholar] [CrossRef] [PubMed]
- Cagan, A.; Baez-Ortega, A.; Brzozowska, N.; Abascal, F.; Coorens, T.H.; Sanders, M.A.; Lawson, A.R.; Harvey, L.M.; Bhosle, S.; Jones, D.; et al. Somatic Mutation Rates Scale with Lifespan across Mammals. Nature 2022, 604, 517–524. [Google Scholar] [CrossRef] [PubMed]
- Grosberg, A.; Rabin, Y.; Havlin, S.; Neer, A. Crumpled Globule Model of the Three-Dimensional Structure of DNA. EPL 1993, 23, 373. [Google Scholar] [CrossRef]
- Cattani, C. Fractals and Hidden Symmetries in DNA. Math. Probl. Eng. 2010, 2010, e507056. [Google Scholar] [CrossRef]
- Mirny, L.A. The Fractal Globule as a Model of Chromatin Architecture in the Cell. Chromosome Res. 2011, 19, 37–51. [Google Scholar] [CrossRef]
- Lazniewski, M.; Dawson, W.K.; Rusek, A.M.; Plewczynski, D. One Protein to Rule Them All: The Role of CCCTC-Binding Factor in Shaping Human Genome in Health and Disease. Semin. Cell Dev. Biol. 2019, 90, 114–127. [Google Scholar] [CrossRef]
- Song, C.; Havlin, S.; Makse, H.A. Self-Similarity of Complex Networks. Nature 2005, 433, 392–395. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Hu, Y.; Di, Z. Accuracy of the Ball-Covering Approach for Fractal Dimensions of Complex Networks and a Rank-Driven Algorithm. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008, 78, 046109. [Google Scholar] [CrossRef]
- Fronczak, A.; Fronczak, P.; Samsel, M.; Makulski, K.; Łepek, M.; Mrowinski, M.J. Scaling Theory of Fractal Complex Networks: Bridging Local Self-Similarity and Global Scale-Invariance. arXiv 2023, arXiv:2306.13751. [Google Scholar]
- Mitkowski, P.J. Mathematical Structures of Ergodicity and Chaos in Population Dynamics; Studies in Systems, Decision and Control; Springer International Publishing: Cham, Switzerland, 2021; Volume 312, ISBN 978-3-030-57677-6. [Google Scholar]
- Beatty, G.L.; Gladney, W.L. Immune Escape Mechanisms as a Guide for Cancer Immunotherapy. Clin. Cancer Res. 2015, 21, 687–692. [Google Scholar] [CrossRef] [PubMed]
- Simon, A.K.; Hollander, G.A.; McMichael, A. Evolution of the Immune System in Humans from Infancy to Old Age. Proc. Biol. Sci. 2015, 282, 20143085. [Google Scholar] [CrossRef] [PubMed]
- Mold, J.E.; Réu, P.; Olin, A.; Bernard, S.; Michaëlsson, J.; Rane, S.; Yates, A.; Khosravi, A.; Salehpour, M.; Possnert, G.; et al. Cell Generation Dynamics Underlying Naive T-Cell Homeostasis in Adult Humans. PLoS Biol. 2019, 17, e3000383. [Google Scholar] [CrossRef]
- Cunha, L.L.; Perazzio, S.F.; Azzi, J.; Cravedi, P.; Riella, L.V. Remodeling of the Immune Response with Aging: Immunosenescence and Its Potential Impact on COVID-19 Immune Response. Front. Immunol. 2020, 11, 1748. [Google Scholar] [CrossRef] [PubMed]
- Yoshimura, A.; Imoto, I.; Iwata, H. Functions of Breast Cancer Predisposition Genes: Implications for Clinical Management. Int. J. Mol. Sci. 2022, 23, 7481. [Google Scholar] [CrossRef]
- Thorat, M.A.; Balasubramanian, R. Breast Cancer Prevention in High-Risk Women. Best. Pract. Res. Clin. Obstet. Gynaecol. 2020, 65, 18–31. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.H.; Anders, C.K.; Litton, J.K.; Ruddy, K.J.; Bleyer, A. Breast Cancer in Adolescents and Young Adults. Pediatr. Blood Cancer 2018, 65, e27397. [Google Scholar] [CrossRef]
- Kluska, A.; Balabas, A.; Paziewska, A.; Kulecka, M.; Nowakowska, D.; Mikula, M.; Ostrowski, J. New Recurrent BRCA1/2 Mutations in Polish Patients with Familial Breast/Ovarian Cancer Detected by next Generation Sequencing. BMC Med. Genom. 2015, 8, 19. [Google Scholar] [CrossRef]
- Ranganathan, A. The Levenberg-Marquardt Algorithm. Tutoral LM Algorithm 2004, 11, 101–110. [Google Scholar]
- Lourakis, M.I. A Brief Description of the Levenberg-Marquardt Algorithm Implemented by Levmar. Found. Res. Technol. 2005, 4, 1–6. [Google Scholar]
- Moré, J.J. The Levenberg-Marquardt Algorithm: Implementation and Theory. In Numerical Analysis; Watson, G.A., Ed.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1978; Volume 630, pp. 105–116. ISBN 978-3-540-08538-6. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zawadzka, A.; Brzozowska, B.; Matyjanka, A.; Mikula, M.; Reszczyńska, J.; Tartas, A.; Fornalski, K.W. The Risk Function of Breast and Ovarian Cancers in the Avrami–Dobrzyński Cellular Phase-Transition Model. Int. J. Mol. Sci. 2024, 25, 1352. https://doi.org/10.3390/ijms25021352
Zawadzka A, Brzozowska B, Matyjanka A, Mikula M, Reszczyńska J, Tartas A, Fornalski KW. The Risk Function of Breast and Ovarian Cancers in the Avrami–Dobrzyński Cellular Phase-Transition Model. International Journal of Molecular Sciences. 2024; 25(2):1352. https://doi.org/10.3390/ijms25021352
Chicago/Turabian StyleZawadzka, Anna, Beata Brzozowska, Anna Matyjanka, Michał Mikula, Joanna Reszczyńska, Adrianna Tartas, and Krzysztof W. Fornalski. 2024. "The Risk Function of Breast and Ovarian Cancers in the Avrami–Dobrzyński Cellular Phase-Transition Model" International Journal of Molecular Sciences 25, no. 2: 1352. https://doi.org/10.3390/ijms25021352
APA StyleZawadzka, A., Brzozowska, B., Matyjanka, A., Mikula, M., Reszczyńska, J., Tartas, A., & Fornalski, K. W. (2024). The Risk Function of Breast and Ovarian Cancers in the Avrami–Dobrzyński Cellular Phase-Transition Model. International Journal of Molecular Sciences, 25(2), 1352. https://doi.org/10.3390/ijms25021352







