Structural Characterization and Physicochemical Properties of Functionally Porous Proton-Exchange Membrane Based on PVDF-SPA Graft Copolymers
Abstract
1. Introduction
2. Results and Discussion
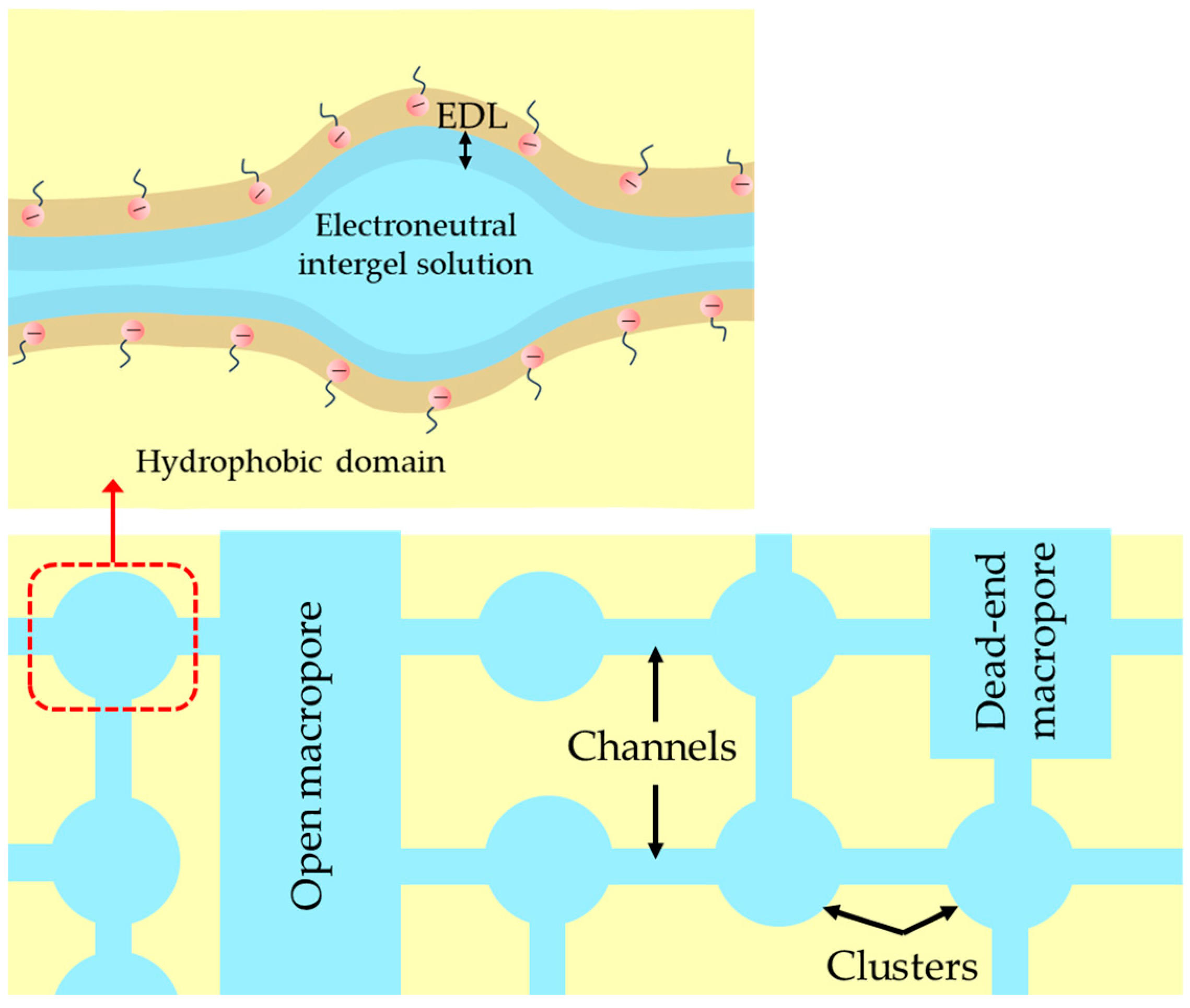
2.1. Structural Characteristics of the Membranes under Study
2.2. Structural Characteristics of the Membranes Used for Comparison
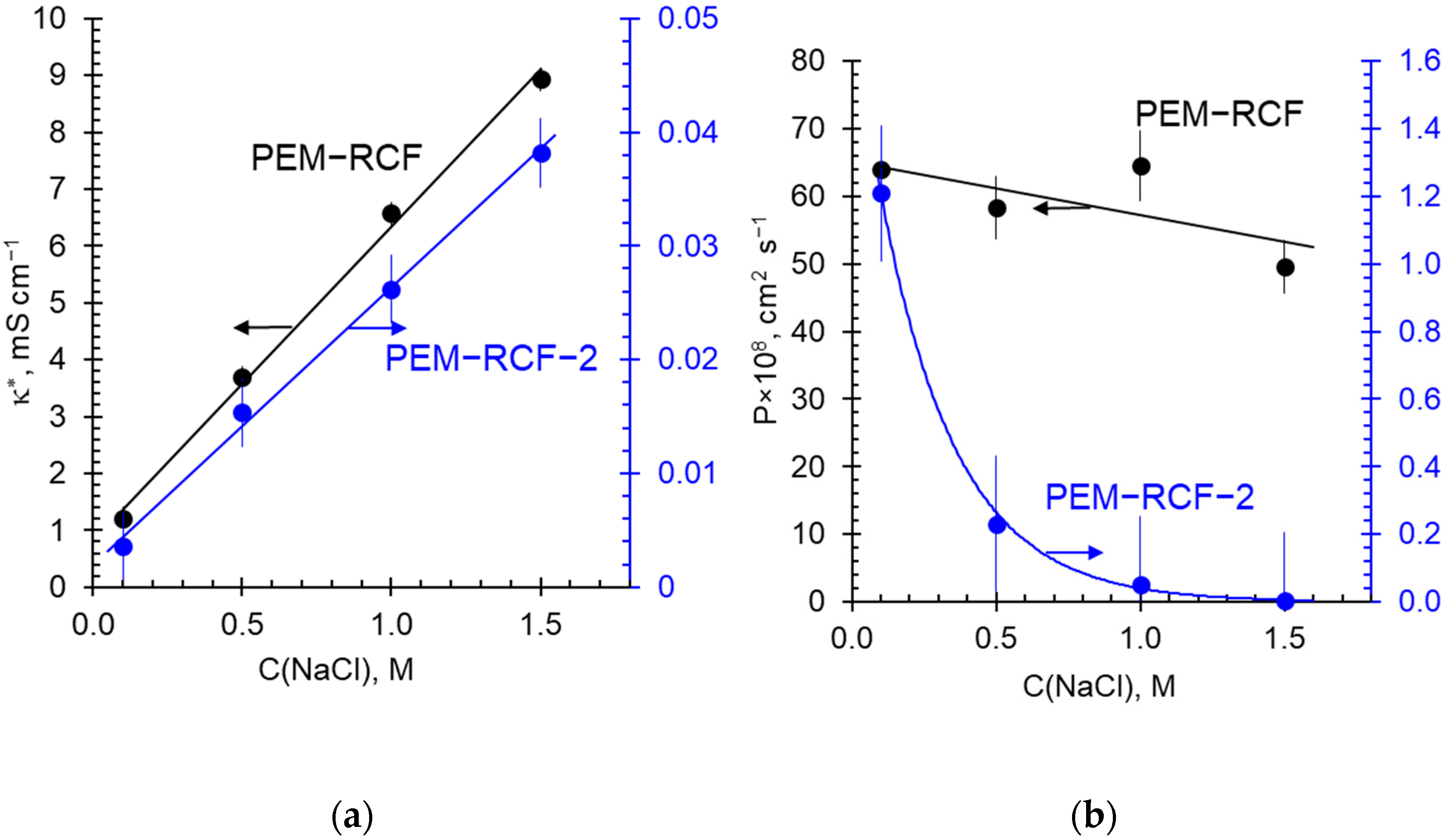
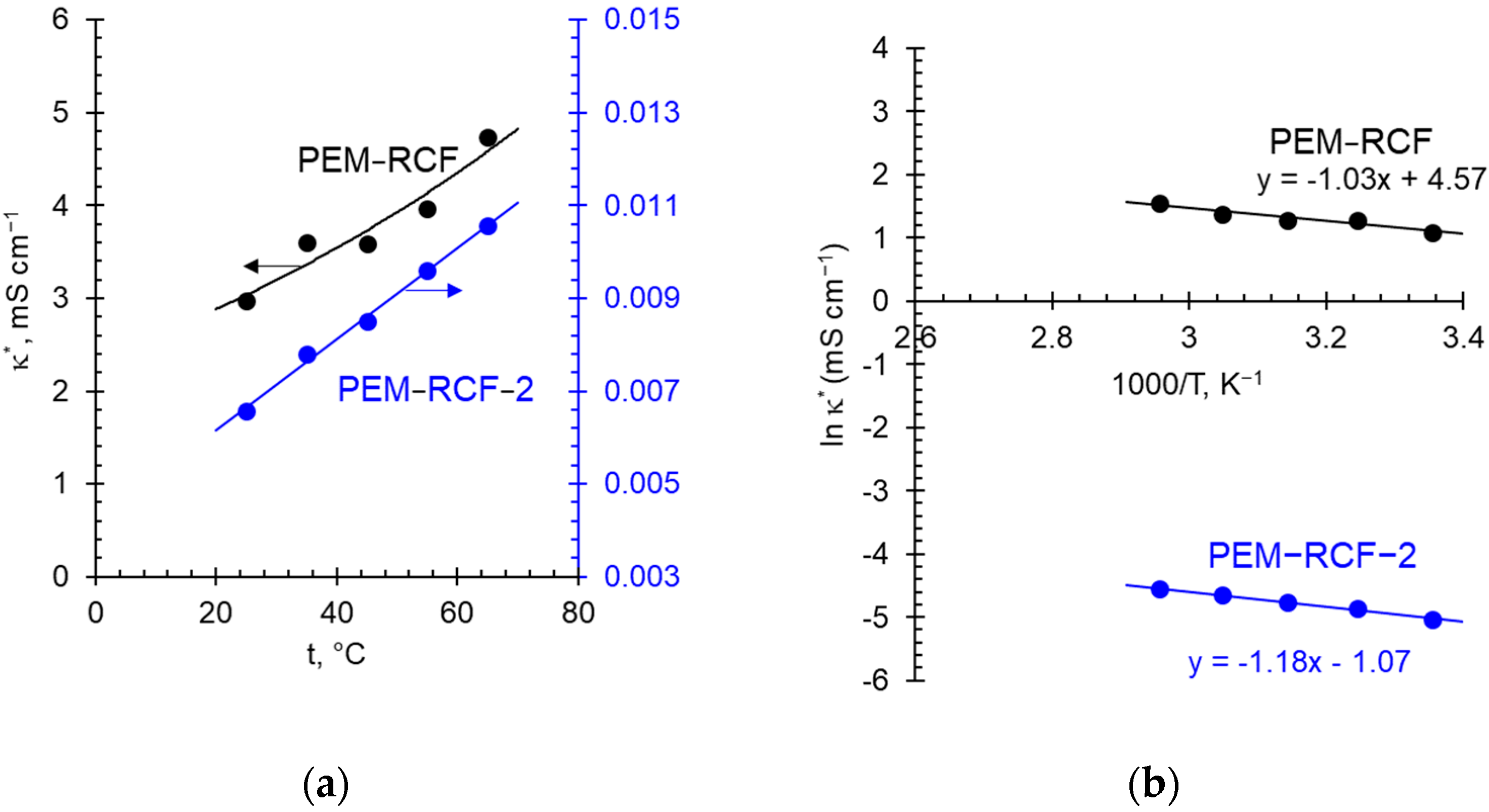
2.3. Transport Characteristics
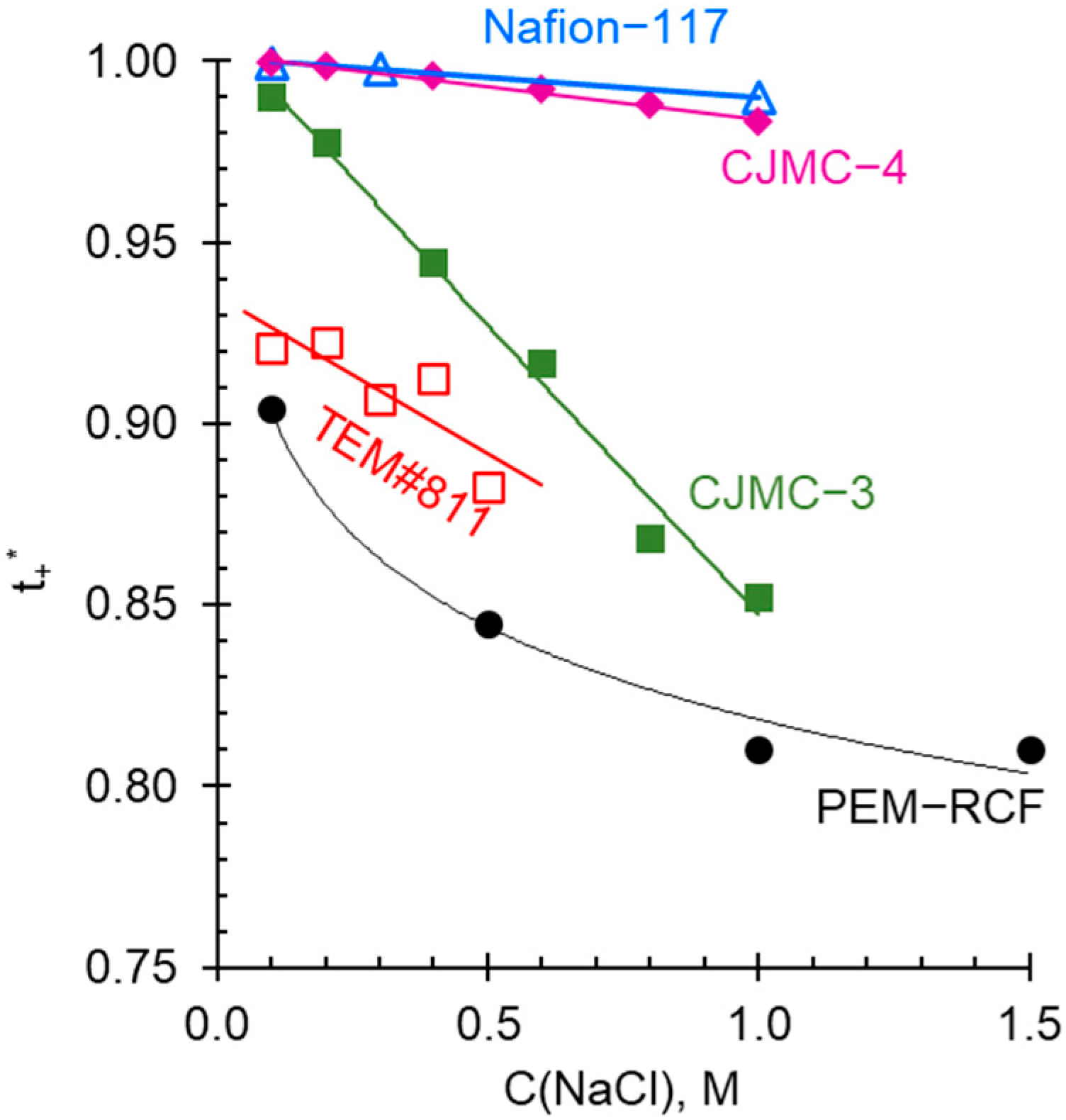
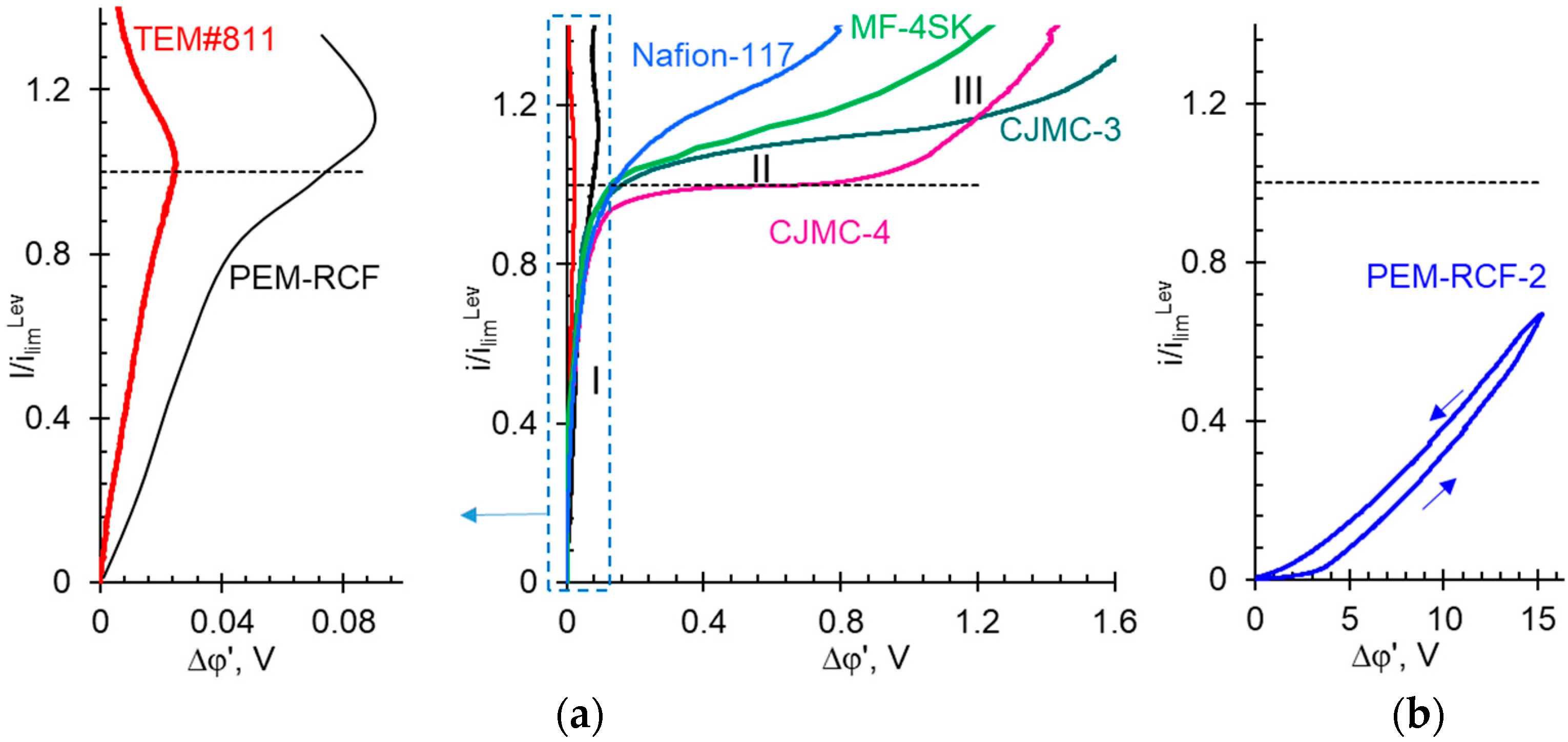
2.4. Comparison of Transport and Electrochemical Characteristics of Synthesized and Commercial Membranes
2.5. Electrochemical Characteristics
3. Materials and Methods
3.1. Chemicals
3.2. Membrane Preparation: Synthesis of Polyvinylidene Fluoride Copolymer
- (a)
- Dehydrofluorination of polyvinylidene fluoride (PVDF)
- (b)
- Synthesis of polyvinylidene fluoride-co-(3-sulfopropyl acrylate) and polyvinylidene fluoride-co-(3-sulfopropyl acrylate)-co-perfluoro-1-hexene copolymer
3.3. Methods of Membrane Characterization
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, M.; Pan, C.; Li, C.; Zhao, J. A Review of Membranes in Proton Exchange Membrane Fuel Cells: Transport Phenomena, Performance and Durability. Renew. Sustain. Energy Rev. 2021, 141, 110771. [Google Scholar] [CrossRef]
- Dell, R.M.; Rand, D.A.J. Clean Energy; Clark, J.H., Ed.; The Royal Society of Chemistry: London, UK, 2004; ISBN 978-0-85404-546-4. [Google Scholar]
- Sun, C.; Negro, E.; Vezzù, K.; Pagot, G.; Cavinato, G.; Nale, A.; Herve Bang, Y.; Di Noto, V. Hybrid Inorganic-Organic Proton-Conducting Membranes Based on SPEEK Doped with WO3 Nanoparticles for Application in Vanadium Redox Flow Batteries. Electrochim. Acta 2019, 309, 311–325. [Google Scholar] [CrossRef]
- Wang, Y.; Ruiz Diaz, D.F.; Chen, K.S.; Wang, Z.; Adroher, X.C. Materials, Technological Status, and Fundamentals of PEM Fuel Cells—A Review. Mater. Today 2020, 32, 178–203. [Google Scholar] [CrossRef]
- Prater, K.B. Polymer Electrolyte Fuel Cells: A Review of Recent Developments. J. Power Sources 1994, 51, 129–144. [Google Scholar] [CrossRef]
- Ogungbemi, E.; Ijaodola, O.; Khatib, F.N.; Wilberforce, T.; El Hassan, Z.; Thompson, J.; Ramadan, M.; Olabi, A.G. Fuel Cell Membranes—Pros and Cons. Energy 2019, 172, 155–172. [Google Scholar] [CrossRef]
- Neburchilov, V.; Martin, J.; Wang, H.; Zhang, J. A Review of Polymer Electrolyte Membranes for Direct Methanol Fuel Cells. J. Power Sources 2007, 169, 221–238. [Google Scholar] [CrossRef]
- Kusoglu, A.; Weber, A.Z. New Insights into Perfluorinated Sulfonic-Acid Ionomers. Chem. Rev. 2017, 117, 987–1104. [Google Scholar] [CrossRef]
- Talukdar, K.; Gazdzicki, P.; Friedrich, K.A. Comparative Investigation into the Performance and Durability of Long and Short Side Chain Ionomers in Polymer Electrolyte Membrane Fuel Cells. J. Power Sources 2019, 439, 227078. [Google Scholar] [CrossRef]
- Peighambardoust, S.J.; Rowshanzamir, S.; Amjadi, M. Review of the Proton Exchange Membranes for Fuel Cell Applications. Int. J. Hydrogen Energy 2010, 35, 9349–9384. [Google Scholar] [CrossRef]
- Ahmad, S.; Nawaz, T.; Ali, A.; Orhan, M.F.; Samreen, A.; Kannan, A.M. An Overview of Proton Exchange Membranes for Fuel Cells: Materials and Manufacturing. Int. J. Hydrogen Energy 2022, 47, 19086–19131. [Google Scholar] [CrossRef]
- Kayumov, R.R.; Sanginov, E.A.; Shmygleva, L.V.; Radaeva, A.P.; Karelin, A.I.; Zyubin, A.S.; Zyubina, T.S.; Anokhin, D.V.; Ivanov, D.A.; Dobrovolsky, Y.A. Ammonium Form of Nafion Plasticized by Dimethyl Sulfoxide. J. Electrochem. Soc. 2019, 166, F3216–F3226. [Google Scholar] [CrossRef]
- Safronova, E.; Golubenko, D.; Pourcelly, G.; Yaroslavtsev, A. Mechanical Properties and Influence of Straining on Ion Conductivity of Perfluorosulfonic Acid Nafion®-Type Membranes Depending on Water Uptake. J. Membr. Sci. 2015, 473, 218–225. [Google Scholar] [CrossRef]
- Moukheiber, E.; De Moor, G.; Flandin, L.; Bas, C. Investigation of Ionomer Structure through Its Dependence on Ion Exchange Capacity (IEC). J. Membr. Sci. 2012, 389, 294–304. [Google Scholar] [CrossRef]
- Mu’min, M.S.; Komma, M.; Abbas, D.; Wagner, M.; Krieger, A.; Thiele, S.; Böhm, T.; Kerres, J. Electrospun Phosphonated Poly(Pentafluorostyrene) Nanofibers as a Reinforcement of Nafion Membranes for Fuel Cell Application. J. Membr. Sci. 2023, 685, 121915. [Google Scholar] [CrossRef]
- Hickner, M.A.; Ghassemi, H.; Kim, Y.S.; Einsla, B.R.; McGrath, J.E. Alternative Polymer Systems for Proton Exchange Membranes (PEMs). Chem. Rev. 2004, 104, 4587–4612. [Google Scholar] [CrossRef] [PubMed]
- Du, S. Recent Advances in Electrode Design Based on One-Dimensional Nanostructure Arrays for Proton Exchange Membrane Fuel Cell Applications. Engineering 2021, 7, 33–49. [Google Scholar] [CrossRef]
- Chen, N.; Liu, Y.; Long, C.; Li, R.; Wang, F.; Zhu, H. Enhanced Performance of Ionic-Liquid-Coated Silica/Quaternized Poly(2,6-Dimethyl-1,4-Phenylene Oxide) Composite Membrane for Anion Exchange Membrane Fuel Cells. Electrochim. Acta 2017, 258, 124–133. [Google Scholar] [CrossRef]
- Elumalai, V.; Ganesh, T.; Selvakumar, C.; Sangeetha, D. Phosphonate Ionic Liquid Immobilised SBA-15/SPEEK Composite Membranes for High Temperature Proton Exchange Membrane Fuel Cells. Mater. Sci. Energy Technol. 2018, 1, 196–204. [Google Scholar] [CrossRef]
- Arias, J.J.R.; Carlos Dutra, J.; Gomes, A.d.S. Hybrid Membranes of Sulfonated Poly Ether Ether Ketone, Ionic Liquid and Organically Modified Montmorillonite for Proton Exchange Membranes with Enhanced Ionic Conductivity and Ionic Liquid Lixiviation Protection. J. Membr. Sci. 2017, 537, 353–361. [Google Scholar] [CrossRef]
- Hooshyari, K.; Javanbakht, M.; Adibi, M. Novel Composite Membranes Based on PBI and Dicationic Ionic Liquids for High Temperature Polymer Electrolyte Membrane Fuel Cells. Electrochim. Acta 2016, 205, 142–152. [Google Scholar] [CrossRef]
- Singh, N.K.; Verma, M.L.; Minakshi, M. PEO Nanocomposite Polymer Electrolyte for Solid State Symmetric Capacitors. Bull. Mater. Sci. 2015, 38, 1577–1588. [Google Scholar] [CrossRef]
- Bae, I.; Oh, K.-H.; Yun, S.-H.; Kim, H. Asymmetric Silica Composite Polymer Electrolyte Membrane for Water Management of Fuel Cells. J. Membr. Sci. 2017, 542, 52–59. [Google Scholar] [CrossRef]
- Wang, B.; Chen, S.; Dong, W.; Wang, X.; Shen, L.; Wang, H. Advance Fuel Cells Using Al2O3-NNaAlO2 Composite as Ion-Conducting Membrane. Int. J. Hydrogen Energy 2018, 43, 12847–12855. [Google Scholar] [CrossRef]
- Munavalli, B.B.; Kariduraganavar, M.Y. Development of Novel Sulfonic Acid Functionalized Zeolites Incorporated Composite Proton Exchange Membranes for Fuel Cell Application. Electrochim. Acta 2019, 296, 294–307. [Google Scholar] [CrossRef]
- Ozden, A.; Ercelik, M.; Devrim, Y.; Colpan, C.O.; Hamdullahpur, F. Evaluation of Sulfonated Polysulfone/Zirconium Hydrogen Phosphate Composite Membranes for Direct Methanol Fuel Cells. Electrochim. Acta 2017, 256, 196–210. [Google Scholar] [CrossRef]
- Kudashova, D.S.; Falina, I.V.; Kononenko, N.A.; Demidenko, K.S. Physicochemical Properties and Performance Characteristics of Perfluorinated Membranes Bulk Modified with Platinum during Operation in Proton Exchange Membrane Fuel Cell. Membr. Membr. Technol. 2023, 5, 18–26. [Google Scholar] [CrossRef]
- Safronova, E.Y.; Lysova, A.A.; Voropaeva, D.Y.; Yaroslavtsev, A.B. Approaches to the Modification of Perfluorosulfonic Acid Membranes. Membranes 2023, 13, 721. [Google Scholar] [CrossRef]
- Liu, F.; Hashim, N.A.; Liu, Y.; Abed, M.R.M.; Li, K. Progress in the Production and Modification of PVDF Membranes. J. Membr. Sci. 2011, 375, 1–27. [Google Scholar] [CrossRef]
- Kang, G.; Cao, Y. Application and Modification of Poly(Vinylidene Fluoride) (PVDF) Membranes—A Review. J. Membr. Sci. 2014, 463, 145–165. [Google Scholar] [CrossRef]
- Rajput, A.; Sharma, J.; Raj, S.K.; Kulshrestha, V. Dehydrofluorinated Poly(Vinylidene Fluoride-Co-Hexafluoropropylene) Based Crosslinked Cation Exchange Membrane for Brackish Water Desalination via Electrodialysis. Colloids Surfaces A Physicochem. Eng. Asp. 2021, 630, 127576. [Google Scholar] [CrossRef]
- Li, J.-H.; Li, M.-Z.; Miao, J.; Wang, J.-B.; Shao, X.-S.; Zhang, Q.-Q. Improved Surface Property of PVDF Membrane with Amphiphilic Zwitterionic Copolymer as Membrane Additive. Appl. Surf. Sci. 2012, 258, 6398–6405. [Google Scholar] [CrossRef]
- Das, S.; Kumar, P.; Dutta, K.; Kundu, P.P. Partial Sulfonation of PVdF-Co-HFP: A Preliminary Study and Characterization for Application in Direct Methanol Fuel Cell. Appl. Energy 2014, 113, 169–177. [Google Scholar] [CrossRef]
- Mahmoud, A.M.A.; Elsaghier, A.M.M.; Otsuji, K.; Miyatake, K. High Hydroxide Ion Conductivity with Enhanced Alkaline Stability of Partially Fluorinated and Quaternized Aromatic Copolymers as Anion Exchange Membranes. Macromolecules 2017, 50, 4256–4266. [Google Scholar] [CrossRef]
- Fontananova, E.; Jansen, J.C.; Cristiano, A.; Curcio, E.; Drioli, E. Effect of Additives in the Casting Solution on the Formation of PVDF Membranes. Desalination 2006, 192, 190–197. [Google Scholar] [CrossRef]
- Ranjani, M.; Yoo, D.J.; Gnana Kumar, G. Sulfonated Fe3O4@SiO2 Nanorods Incorporated SPVdF Nanocomposite Membranes for DMFC Applications. J. Membr. Sci. 2018, 555, 497–506. [Google Scholar] [CrossRef]
- Hariprasad, R.; Vinothkannan, M.; Kim, A.R.; Yoo, D.J. SPVdF-HFP/SGO Nanohybrid Proton Exchange Membrane for the Applications of Direct Methanol Fuel Cells. J. Dispers. Sci. Technol. 2020, 42, 33–45. [Google Scholar] [CrossRef]
- Sarapulova, V.; Pismenskaya, N.; Butylskii, D.; Titorova, V.; Wang, Y.; Xu, T.; Zhang, Y.; Nikonenko, V. Transport and Electrochemical Characteristics of CJMCED Homogeneous Cation Exchange Membranes in Sodium Chloride, Calcium Chloride, and Sodium Sulfate Solutions. Membranes 2020, 10, 165. [Google Scholar] [CrossRef]
- Ran, J.; Wu, L.; He, Y.; Yang, Z.; Wang, Y.; Jiang, C.; Ge, L.; Bakangura, E.; Xu, T. Ion Exchange Membranes: New Developments and Applications. J. Membr. Sci. 2017, 522, 267–291. [Google Scholar] [CrossRef]
- Hossain, M.M.; Wu, L.; Li, Y.; Ge, L.; Xu, T. Preparation of Porous Poly(Vinylidene Fluoride) Membranes with Acrylate Particles for Electrodialysis Application. Sep. Purif. Technol. 2015, 150, 102–111. [Google Scholar] [CrossRef]
- Zuo, X.; Shi, W.; Tian, Z.; Yu, S.; Wang, S.; He, J. Desalination of Water with a High Degree of Mineralization Using SiO2/PVDF Membranes. Desalination 2013, 311, 150–155. [Google Scholar] [CrossRef]
- Prakash, G.K.S.; Smart, M.C.; Wang, Q.-J.; Atti, A.; Pleynet, V.; Yang, B.; McGrath, K.; Olah, G.A.; Narayanan, S.R.; Chun, W.; et al. High Efficiency Direct Methanol Fuel Cell Based on Poly(Styrenesulfonic) Acid (PSSA)–Poly(Vinylidene Fluoride) (PVDF) Composite Membranes. J. Fluor. Chem. 2004, 125, 1217–1230. [Google Scholar] [CrossRef]
- Sharma, J.; Totee, C.; Kulshrestha, V.; Ameduri, B. Spectroscopic Evidence and Mechanistic Insights on Dehydrofluorination of PVDF in Alkaline Medium. Eur. Polym. J. 2023, 201, 112580. [Google Scholar] [CrossRef]
- Flory, P.J. Theory of Crystallization in Copolymers. Trans. Faraday Soc. 1955, 51, 848. [Google Scholar] [CrossRef]
- Nakagawa, K.; Ishida, Y. Annealing Effects in Poly(Vinylidene Fluoride) as Revealed by Specific Volume Measurements, Differential Scanning Calorimetry, and Electron Microscopy. J. Polym. Sci. Part A-2 Polym. Phys. 1973, 11, 2153–2171. [Google Scholar] [CrossRef]
- Martins, P.; Lopes, A.C.; Lanceros-Mendez, S. Electroactive Phases of Poly(Vinylidene Fluoride): Determination, Processing and Applications. Prog. Polym. Sci. 2014, 39, 683–706. [Google Scholar] [CrossRef]
- Dallaev, R.; Pisarenko, T.; Sobola, D.; Orudzhev, F.; Ramazanov, S.; Trčka, T. Brief Review of PVDF Properties and Applications Potential. Polymers 2022, 14, 4793. [Google Scholar] [CrossRef]
- Kreuer, K.-D.; Paddison, S.J.; Spohr, E.; Schuster, M. Transport in Proton Conductors for Fuel-Cell Applications: Simulations, Elementary Reactions, and Phenomenology. Chem. Rev. 2004, 104, 4637–4678. [Google Scholar] [CrossRef] [PubMed]
- Nikonenko, V.V.; Yaroslavtsev, A.B.; Pourcelly, G. Ion transfer in and through charged membranes: Structure, properties, and theory. In Ionic Interactions in Natural and Synthetic Macromolecules; Wiley: Hoboken, NJ, USA, 2012; pp. 267–335. [Google Scholar]
- Gierke, T.D.; Munn, G.E.; Wilson, F.C. The Morphology in Nafion Perfluorinated Membrane Products, as Determined by Wide- and Small-Angle x-Ray Studies. J. Polym. Sci. Polym. Phys. Ed. 1981, 19, 1687–1704. [Google Scholar] [CrossRef]
- Mauritz, K.A.; Moore, R.B. State of Understanding of Nafion. Chem. Rev. 2004, 104, 4535–4586. [Google Scholar] [CrossRef]
- Larson, R.G.; Scriven, L.E.; Davis, H.T. Percolation Theory of Residual Phases in Porous Media. Nature 1977, 268, 409–413. [Google Scholar] [CrossRef]
- Zhang, B.; Gao, H.; Xiao, C.; Tong, X.; Chen, Y. The Trade-off between Membrane Permselectivity and Conductivity: A Percolation Simulation of Mass Transport. J. Membr. Sci. 2020, 597, 117751. [Google Scholar] [CrossRef]
- Divisek, J.; Eikerling, M.; Mazin, V.; Schmitz, H.; Stimming, U.; Volfkovich, Y.M. A Study of Capillary Porous Structure and Sorption Properties of Nafion Proton-Exchange Membranes Swollen in Water. J. Electrochem. Soc. 1998, 145, 2677–2683. [Google Scholar] [CrossRef]
- Berezina, N.P.; Kononenko, N.A.; Dyomina, O.A.; Gnusin, N.P. Characterization of Ion-Exchange Membrane Materials: Properties vs Structure. Adv. Colloid Interface Sci. 2008, 139, 3–28. [Google Scholar] [CrossRef]
- Kononenko, N.; Nikonenko, V.; Grande, D.; Larchet, C.; Dammak, L.; Fomenko, M.; Volfkovich, Y. Porous Structure of Ion Exchange Membranes Investigated by Various Techniques. Adv. Colloid Interface Sci. 2017, 246, 196–216. [Google Scholar] [CrossRef] [PubMed]
- Apel, P.Y. Track-Etching. In Encyclopedia of Membrane Science and Technology; Hoek, E.M.V., Tarabara, V.V., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 2013; pp. 332–355. ISBN 978-0-470-90687-3. [Google Scholar]
- Apel, P.Y.; Blonskaya, I.V.; Ivanov, O.M.; Kristavchuk, O.V.; Lizunov, N.E.; Nechaev, A.N.; Orelovich, O.L.; Polezhaeva, O.A.; Dmitriev, S.N. Creation of Ion-Selective Membranes from Polyethylene Terephthalate Films Irradiated with Heavy Ions: Critical Parameters of the Process. Membr. Membr. Technol. 2020, 2, 98–108. [Google Scholar] [CrossRef]
- Nichka, V.S.; Mareev, S.A.; Apel, P.Y.; Sabbatovskiy, K.G.; Sobolev, V.D.; Nikonenko, V.V. Modeling the Conductivity and Diffusion Permeability of a Track-Etched Membrane Taking into Account a Loose Layer. Membranes 2022, 12, 1283. [Google Scholar] [CrossRef]
- Safronova, E.Y.; Golubenko, D.V.; Shevlyakova, N.V.; D’yakova, M.G.; Tverskoi, V.A.; Dammak, L.; Grande, D.; Yaroslavtsev, A.B. New Cation-Exchange Membranes Based on Cross-Linked Sulfonated Polystyrene and Polyethylene for Power Generation Systems. J. Membr. Sci. 2016, 515, 196–203. [Google Scholar] [CrossRef]
- Berezina, N.P.; Kononenko, N.A.; Filippov, A.N.; Shkirskaya, S.A.; Falina, I.V.; Sycheva, A.A.-R. Electrotransport Properties and Morphology of MF-4SK Membranes after Surface Modification with Polyaniline. Russ. J. Electrochem. 2010, 46, 485–493. [Google Scholar] [CrossRef]
- Sarapulova, V.V.; Pasechnaya, E.L.; Titorova, V.D.; Pismenskaya, N.D.; Apel, P.Y.; Nikonenko, V.V. Electrochemical Properties of Ultrafiltration and Nanofiltration Membranes in Solutions of Sodium and Calcium Chloride. Membr. Membr. Technol. 2020, 2, 332–350. [Google Scholar] [CrossRef]
- Berezina, N.; Timofeev, S.; Kononenko, N. Effect of Conditioning Techniques of Perfluorinated Sulphocationic Membranes on Their Hydrophylic and Electrotransport Properties. J. Membr. Sci. 2002, 209, 509–518. [Google Scholar] [CrossRef]
- Bass, M.; Berman, A.; Singh, A.; Konovalov, O.; Freger, V. Surface Structure of Nafion in Vapor and Liquid. J. Phys. Chem. B 2010, 114, 3784–3790. [Google Scholar] [CrossRef]
- Ermakova, L.E.; Kiprianova, A.A.; Sidorova, M.P.; Gribanova, E.V.; Savina, I.A.; Timofeev, S.V. Structural and Electrosurface Characteristics of Sulfonated Cation-Exchange Perfluoropolymer Membranes in 1:1 Electrolyte Solutions. Colloid J. 2001, 63, 699–705. [Google Scholar] [CrossRef]
- Ponomar, M.; Krasnyuk, E.; Butylskii, D.; Nikonenko, V.; Wang, Y.; Jiang, C.; Xu, T.; Pismenskaya, N. Sessile Drop Method: Critical Analysis and Optimization for Measuring the Contact Angle of an Ion-Exchange Membrane Surface. Membranes 2022, 12, 765. [Google Scholar] [CrossRef]
- Tsang, E.M.W.; Holdcroft, S. Alternative Proton Exchange Membranes by Chain-Growth Polymerization. In Polymer Science: A Comprehensive Reference; Matyjaszewski, K., Möller, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 651–689. [Google Scholar]
- Deng, R. Membrane Architectures for Self-Humidifying Proton Exchange Membrane Fuel Cells; The Hong Kong University of Science and Technology: Hong Kong, China, 2018. [Google Scholar]
- Yurova, P.A.; Malakhova, V.R.; Gerasimova, E.V.; Stenina, I.A.; Yaroslavtsev, A.B. Nafion/Surface Modified Ceria Hybrid Membranes for Fuel Cell Application. Polymers 2021, 13, 2513. [Google Scholar] [CrossRef]
- Cappadonia, M. Conductance of Nafion 117 Membranes as a Function of Temperature and Water Content. Solid State Ionics 1995, 77, 65–69. [Google Scholar] [CrossRef]
- Damay, F. Transport Properties of NafionTM Composite Membranes for Proton-Exchange Membranes Fuel Cells. Solid State Ionics 2003, 162–163, 261–267. [Google Scholar] [CrossRef]
- Kopitzke, R.W.; Linkous, C.A.; Anderson, H.R.; Nelson, G.L. Conductivity and Water Uptake of Aromatic-Based Proton Exchange Membrane Electrolytes. J. Electrochem. Soc. 2000, 147, 1677. [Google Scholar] [CrossRef]
- Helfferich, F. Ion Exchange; McGraw-Hil: London, UK; New York, NY, USA, 1962. [Google Scholar]
- Yaroslavtsev, A.B. Перфтoрирoванные Иoнooбменные Мембраны. Высoкoмoлекулярные Сoединения Серия А 2013, 55, 1367–1392. [Google Scholar] [CrossRef]
- Paddison, S.J. Proton Conduction Mechanisms at Low Degrees of Hydration in Sulfonic Acid–Based Polymer Electrolyte Membranes. Annu. Rev. Mater. Res. 2003, 33, 289–319. [Google Scholar] [CrossRef]
- Voropaeva, E.Y.; Stenina, I.A.; Yaroslavtsev, A.B. Transport Properties of Hydrous-Silica-Modified MF-4SK Membranes. Russ. J. Inorg. Chem. 2008, 53, 1531–1535. [Google Scholar] [CrossRef]
- Liu, L.; Chen, W.; Li, Y. An Overview of the Proton Conductivity of Nafion Membranes through a Statistical Analysis. J. Membr. Sci. 2016, 504, 1–9. [Google Scholar] [CrossRef]
- Demina, O.A.; Falina, I.V.; Kononenko, N.A.; Demin, A.V. Effect of Counter- and Co-Ions on the Structural Transport Parameters of Sulfoacid Cationite Membranes. Russ. J. Phys. Chem. A 2016, 90, 1633–1638. [Google Scholar] [CrossRef]
- Stenina, I.A.; Sistat, P.; Rebrov, A.I.; Pourcelly, G.; Yaroslavtsev, A.B. Ion Mobility in Nafion-117 Membranes. Desalination 2004, 170, 49–57. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V. Effect of Structural Membrane Inhomogeneity on Transport Properties. J. Membr. Sci. 1993, 79, 181–198. [Google Scholar] [CrossRef]
- Sarapulova, V.; Pismenskaya, N.; Titorova, V.; Sharafan, M.; Wang, Y.; Xu, T.; Zhang, Y.; Nikonenko, V. Transport Characteristics of CJMAEDTM Homogeneous Anion Exchange Membranes in Sodium Chloride and Sodium Sulfate Solutions. Int. J. Mol. Sci. 2021, 22, 1415. [Google Scholar] [CrossRef] [PubMed]
- Hsu, W.Y.; Gierke, T.D. Ion Transport and Clustering in Nafion Perfluorinated Membranes. J. Membr. Sci. 1983, 13, 307–326. [Google Scholar] [CrossRef]
- Gebel, G. Structural Evolution of Water Swollen Perfluorosulfonated Ionomers from Dry Membrane to Solution. Polymer 2000, 41, 5829–5838. [Google Scholar] [CrossRef]
- Drozdov, A.D.; de Claville Christiansen, J. The Effects of PH and Ionic Strength on Equilibrium Swelling of Polyampholyte Gels. Int. J. Solids Struct. 2017, 110–111, 192–208. [Google Scholar] [CrossRef]
- Kozmai, A.E.; Nikonenko, V.V.; Zyryanova, S.; Pismenskaya, N.D.; Dammak, L. A Simple Model for the Response of an Anion-Exchange Membrane to Variation in Concentration and PH of Bathing Solution. J. Membr. Sci. 2018, 567, 127–138. [Google Scholar] [CrossRef]
- Kamcev, J.; Paul, D.R.; Freeman, B.D. Equilibrium Ion Partitioning between Aqueous Salt Solutions and Inhomogeneous Ion Exchange Membranes. Desalination 2018, 446, 31–41. [Google Scholar] [CrossRef]
- Geise, G.M.; Paul, D.R.; Freeman, B.D. Fundamental Water and Salt Transport Properties of Polymeric Materials. Prog. Polym. Sci. 2014, 39, 1–42. [Google Scholar] [CrossRef]
- Zawodzinski, T.A.; Springer, T.E.; Davey, J.; Jestel, R.; Lopez, C.; Valerio, J.; Gottesfeld, S. A Comparative Study of Water Uptake By and Transport Through Ionomeric Fuel Cell Membranes. J. Electrochem. Soc. 1993, 140, 1981–1985. [Google Scholar] [CrossRef]
- Wilhelm, F.G.; Van Der Vegt, N.F.A.; Strathmann, H.; Wessling, M. Current-Voltage Behaviour of Bipolar Membranes in Concentrated Salt Solutions Investigated with Chronopotentiometry. J. Appl. Electrochem. 2002, 32, 455–465. [Google Scholar] [CrossRef]
- Filippov, A.; Afonin, D.; Kononenko, N.; Lvov, Y.; Vinokurov, V. New Approach to Characterization of Hybrid Nanocomposites. Colloids Surfaces A Physicochem. Eng. Asp. 2017, 521, 251–259. [Google Scholar] [CrossRef]
- Akberova, E.M.; Vasil’eva, V.I. Effect of the Resin Content in Cation-Exchange Membranes on Development of Electroconvection. Electrochem. Commun. 2020, 111, 106659. [Google Scholar] [CrossRef]
- Kozaderova, O.A.; Kim, K.B.; Gadzhiyevа, C.S.; Niftaliev, S.I. Electrochemical Characteristics of Thin Heterogeneous Ion Exchange Membranes. J. Membr. Sci. 2020, 604, 118081. [Google Scholar] [CrossRef]
- Melnikov, S.; Shkirskaya, S. Transport Properties of Bilayer and Multilayer Surface-Modified Ion-Exchange Membranes. J. Membr. Sci. 2019, 590, 117272. [Google Scholar] [CrossRef]
- Güler, E.; van Baak, W.; Saakes, M.; Nijmeijer, K. Monovalent-Ion-Selective Membranes for Reverse Electrodialysis. J. Membr. Sci. 2014, 455, 254–270. [Google Scholar] [CrossRef]
- Krol, J.; Wessling, M.; Strathmann, H. Concentration Polarization with Monopolar Ion Exchange Membranes: Current-Voltage Curves and Water Dissociation. J. Membr. Sci. 1999, 162, 145–154. [Google Scholar] [CrossRef]
- Park, J.-S.; Choi, J.-H.; Yeon, K.-H.; Moon, S.-H. An Approach to Fouling Characterization of an Ion-Exchange Membrane Using Current–Voltage Relation and Electrical Impedance Spectroscopy. J. Colloid Interface Sci. 2006, 294, 129–138. [Google Scholar] [CrossRef]
- Mishchuk, N.A. Concentration Polarization of Interface and Non-Linear Electrokinetic Phenomena. Adv. Colloid Interface Sci. 2010, 160, 16–39. [Google Scholar] [CrossRef]
- Rubinstein, I.; Maletzki, F. Electroconvection at an Electrically Inhomogeneous Permselective Membrane Surface. J. Chem. Soc. Faraday Trans. 1991, 87, 2079. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Shel’deshov, N.V.; Gnusin, N.P. Dissociation of Water Molecules in Systems with Ion-Exchange Membranes. Russ. Chem. Rev. 1988, 57, 801–808. [Google Scholar] [CrossRef]
- Butylskii, D.Y.; Mareev, S.A.; Ryzhkov, I.I.; Urtenov, M.K.; Apel, P.Y.; Nikonenko, V.V. Evaluation of the Effect of Electroosmosis on the Efficiency of Electrobaromembrane Separation with Track-Etched Membranes. Membr. Membr. Technol. 2023, 5, 370–377. [Google Scholar] [CrossRef]
- Elwan, H.A.; Mamlouk, M.; Scott, K. A Review of Proton Exchange Membranes Based on Protic Ionic Liquid/Polymer Blends for Polymer Electrolyte Membrane Fuel Cells. J. Power Sources 2021, 484, 229197. [Google Scholar] [CrossRef]
- Nasef, M.M.; Zubir, N.A.; Ismail, A.F.; Khayet, M.; Dahlan, K.Z.M.; Saidi, H.; Rohani, R.; Ngah, T.I.S.; Sulaiman, N.A. PSSA Pore-Filled PVDF Membranes by Simultaneous Electron Beam Irradiation: Preparation and Transport Characteristics of Protons and Methanol. J. Membr. Sci. 2006, 268, 96–108. [Google Scholar] [CrossRef]
- Oshiba, Y.; Tomatsu, J.; Yamaguchi, T. Thin Pore-Filling Membrane with Highly Packed-Acid Structure for High Temperature and Low Humidity Operating Polymer Electrolyte Fuel Cells. J. Power Sources 2018, 394, 67–73. [Google Scholar] [CrossRef]
- Kim, J.; Lee, Y.; Jeon, J.-D.; Kwak, S.-Y. Ion-Exchange Composite Membranes Pore-Filled with Sulfonated Poly(Ether Ether Ketone) and Engelhard Titanosilicate-10 for Improved Performance of Vanadium Redox Flow Batteries. J. Power Sources 2018, 383, 1–9. [Google Scholar] [CrossRef]
- Yadav, V.; Rathod, N.H.; Sharma, J.; Kulshrestha, V. Long Side-Chain Type Partially Cross-Linked Poly(Vinylidene Fluoride-Co-Hexafluoropropylene) Anion Exchange Membranes for Desalination via Electrodialysis. J. Membr. Sci. 2021, 622, 119034. [Google Scholar] [CrossRef]
- Nagarale, R.K.; Gohil, G.S.; Shahi, V.K. Recent Developments on Ion-Exchange Membranes and Electro-Membrane Processes. Adv. Colloid Interface Sci. 2006, 119, 97–130. [Google Scholar] [CrossRef]
- Lteif, R.; Dammak, L.; Larchet, C.; Auclair, B. Conductivitéélectrique Membranaire: Étude de l’effet de La Concentration, de La Nature de l’électrolyte et de La Structure Membranaire. Eur. Polym. J. 1999, 35, 1187–1195. [Google Scholar] [CrossRef]
- Karpenko, L.V.; Demina, O.A.; Dvorkina, G.A.; Parshikov, S.B.; Larchet, C.; Auclair, B.; Berezina, N.P. Comparative Study of Methods Used for the Determination of Electroconductivity of Ion-Exchange Membranes. Russ. J. Electrochem. 2001, 37, 287–293. [Google Scholar] [CrossRef]
- Escorihuela, J.; Olvera-Mancilla, J.; Alexandrova, L.; del Castillo, L.F.; Compañ, V. Recent Progress in the Development of Composite Membranes Based on Polybenzimidazole for High Temperature Proton Exchange Membrane (PEM) Fuel Cell Applications. Polymers 2020, 12, 1861. [Google Scholar] [CrossRef] [PubMed]
- Pismenskaya, N.D.; Nevakshenova, E.E.; Nikonenko, V.V. Using a Single Set of Structural and Kinetic Parameters of the Microheterogeneous Model to Describe the Sorption and Kinetic Properties of Ion-Exchange Membranes. Pet. Chem. 2018, 58, 465–473. [Google Scholar] [CrossRef]
- Larchet, C.; Dammak, L.; Auclair, B.; Parchikov, S.; Nikonenko, V. A Simplified Procedure for Ion-Exchange Membrane Characterisation. New J. Chem. 2004, 28, 1260. [Google Scholar] [CrossRef]
- Lebrun, L.; Follain, N.; Metayer, M. Elaboration of a New Anion-Exchange Membrane with Semi-Interpenetrating Polymer Networks and Characterisation. Electrochim. Acta 2004, 50, 985–993. [Google Scholar] [CrossRef]
- Newman, J.S.; Thomas-Alyea, K.E. Electrochemical Systems; Wiley: Hoboken, NJ, USA, 2004; ISBN 978-0-471-47756-3. [Google Scholar]
- Mohammadi, M.; Mehdipour-Ataei, S. Durable Sulfonated Partially Fluorinated Polysulfones as Membrane for PEM Fuel Cell. Renew. Energy 2020, 158, 421–430. [Google Scholar] [CrossRef]

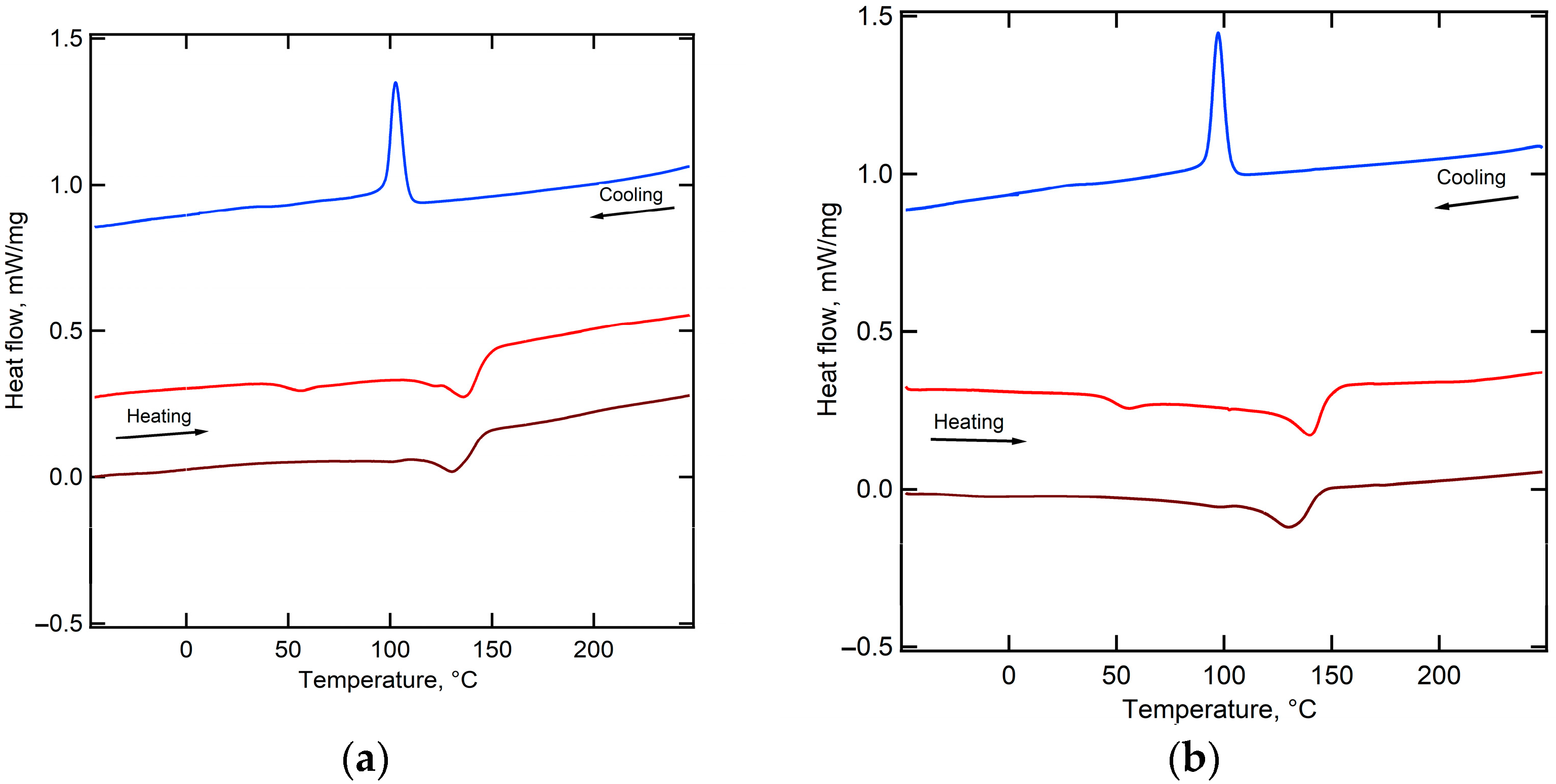
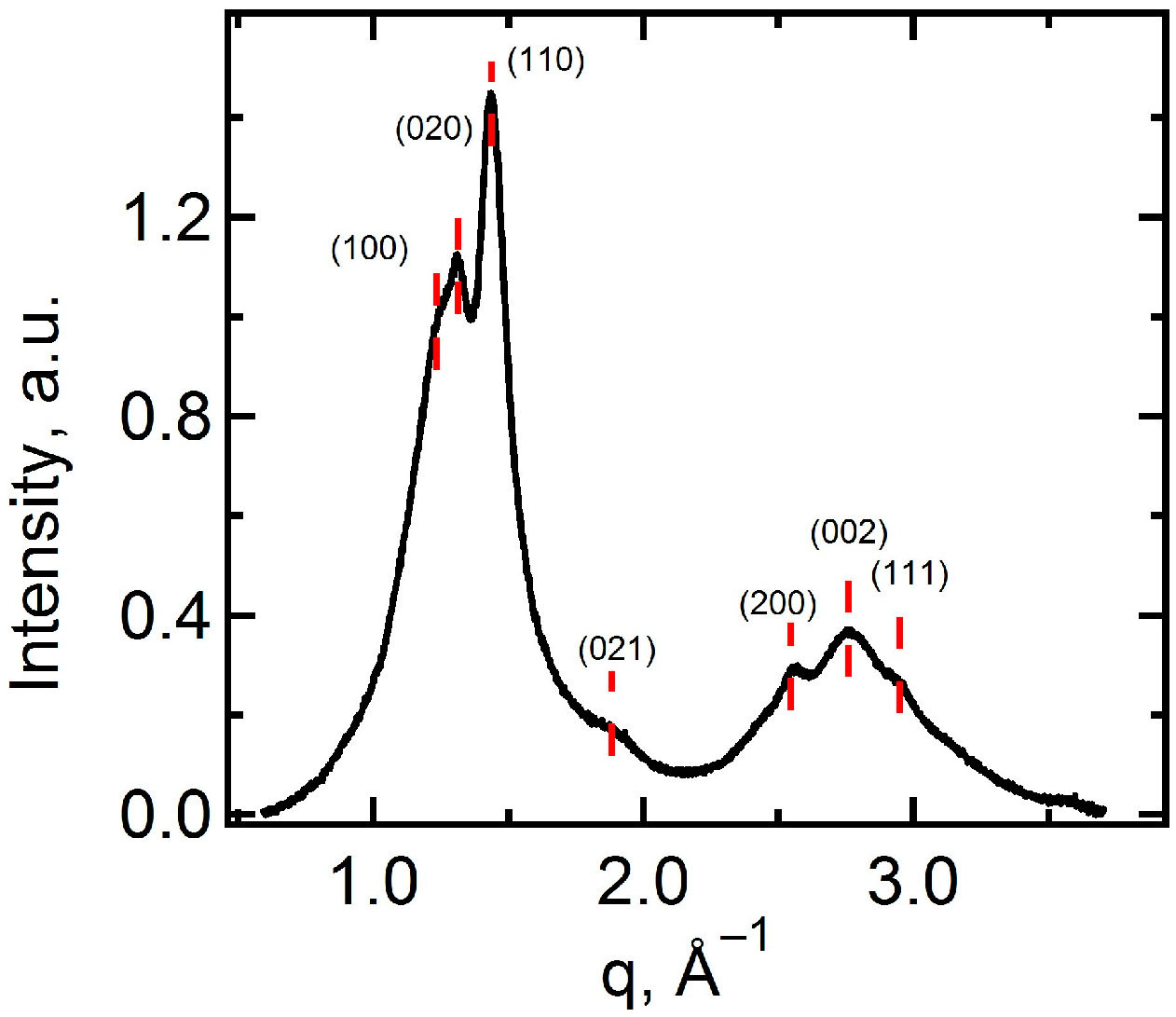
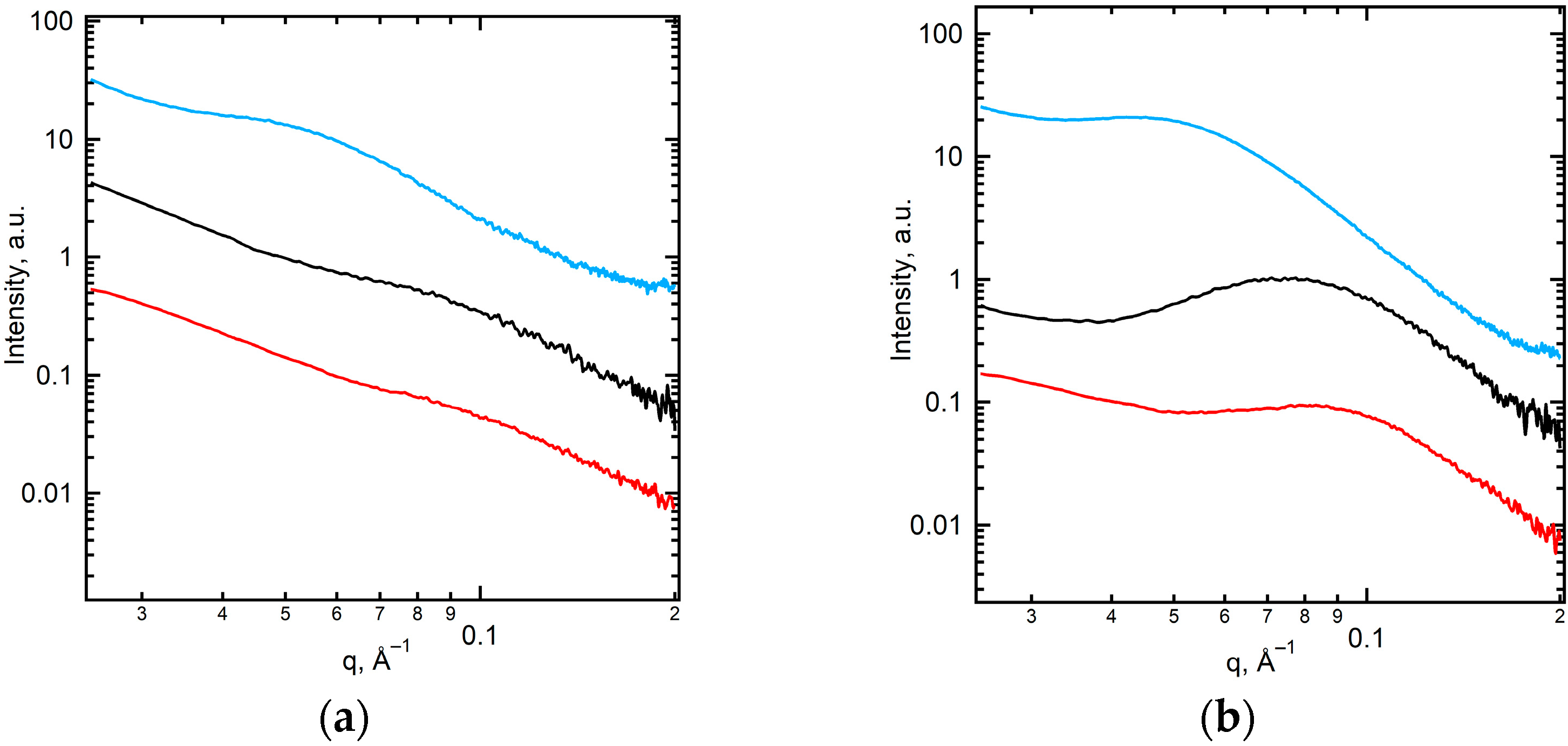
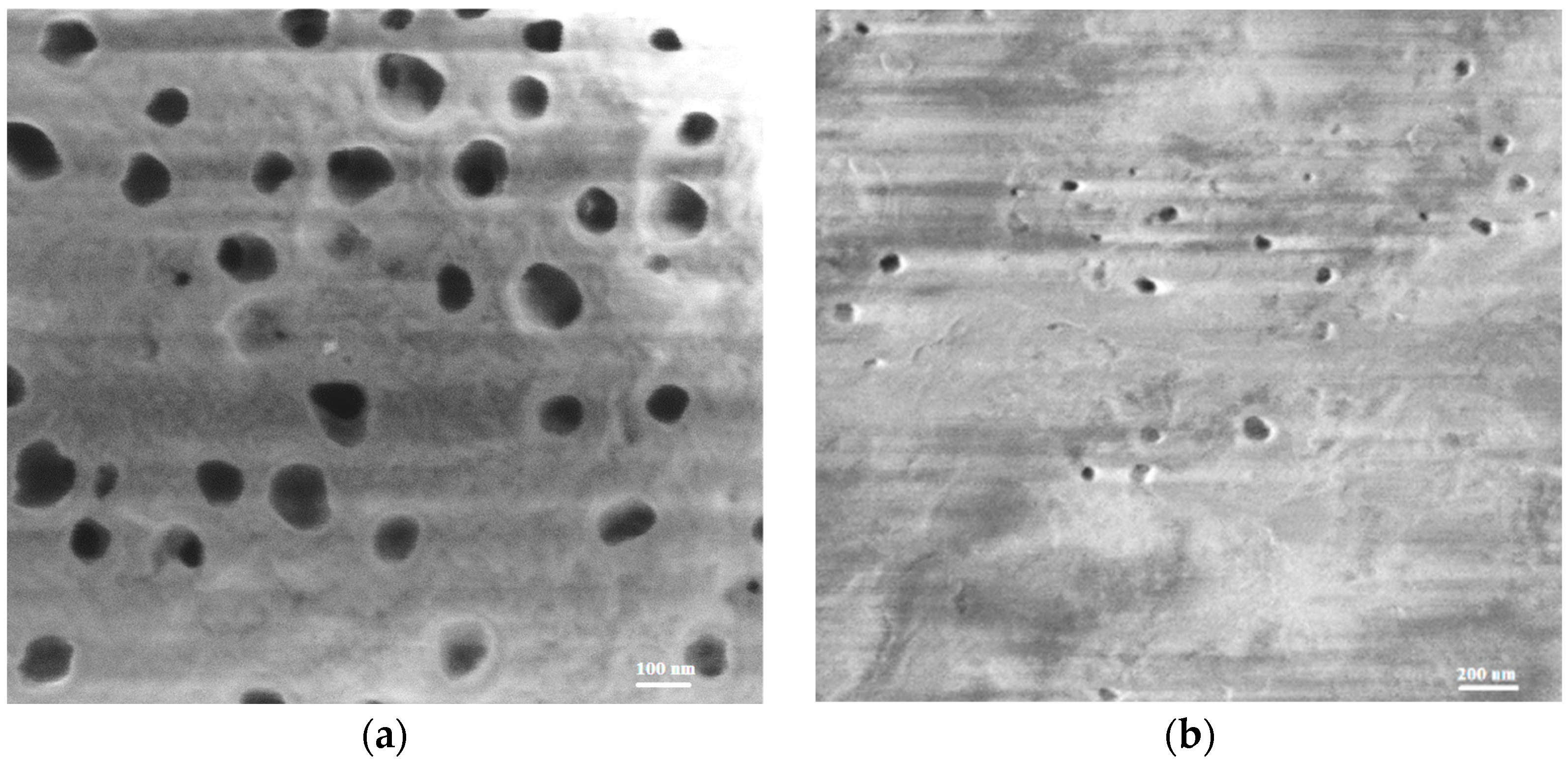

| Membrane | Degree of Crystallinity, % | PVDF Phase | Grain Size from XRD, nm | Diameter of Open Extended Pores, nm | Pore Density, Pores/cm2 | Membrane Thickness, 1 dmb, µm | |
|---|---|---|---|---|---|---|---|
| DSC | WAXS | ||||||
| PEM-RCF | 17 | 18 | α | 5 | 56–138 | 1.4 × 109 | 29 ± 2 |
| PEM-RCF-2 | 16 | 19 | α | 6 | 20–58 | 2.8 × 108 | 86 ± 2 |
| Membrane | Q, mmol g−1 Wet | Water Content, W, gH2O/gwet, % | nm, mol H2O/mol Functional Groups | Area Resistance, R, Ω cm2 | 7 f2app | Contact Angle, (wet), Grad |
|---|---|---|---|---|---|---|
| PEM-RCF | 1 0.12 ± 0.02 | 3 26 ± 2 | 3 122 | 5 0.9 ± 0.05 | 0.81 | 40 ± 2 |
| PEM-RCF-2 | 1 0.08 ± 0.01 | 3 7 ± 2 | 3 52 | 5 571 ± 3 | - | - |
| TEM#811 | 1 0.064 ± 0.003 [62] | 4 6.5 [59] | 4 43 [59] | 5 0.3 [62] | 0.95 [62] | 62 ± 3 |
| Nafion® 117 | 1 0.71 [60] | 3 14.8 [60] | 3 14 [60] | 6 0.82 [60] | 0.1–0.15 [63] | 8 108.1 ± 0.7 [64] |
| MF-4SK | 2 0.58 [63] | 3 16.7 [63] | 3 16 [63] | - | 0.05 [63] | 77.5 ± 2.6 [65] |
| CJMC-3 | 1 0.63 ± 0.05 [38] | 4 30 ± 3 [38] | 4 27 [38] | 5 2.2 ± 0.3 [38] | 0.33 [38] | 51 ± 2 [66] |
| CJMC-4 | 1 1.2 ± 0.1 | 4 29 ± 3 | 4 13 | 6 2.5 ± 0.1 | 0.09 | 64 ± 1 [66] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ponomar, M.; Ruleva, V.; Sarapulova, V.; Pismenskaya, N.; Nikonenko, V.; Maryasevskaya, A.; Anokhin, D.; Ivanov, D.; Sharma, J.; Kulshrestha, V.; et al. Structural Characterization and Physicochemical Properties of Functionally Porous Proton-Exchange Membrane Based on PVDF-SPA Graft Copolymers. Int. J. Mol. Sci. 2024, 25, 598. https://doi.org/10.3390/ijms25010598
Ponomar M, Ruleva V, Sarapulova V, Pismenskaya N, Nikonenko V, Maryasevskaya A, Anokhin D, Ivanov D, Sharma J, Kulshrestha V, et al. Structural Characterization and Physicochemical Properties of Functionally Porous Proton-Exchange Membrane Based on PVDF-SPA Graft Copolymers. International Journal of Molecular Sciences. 2024; 25(1):598. https://doi.org/10.3390/ijms25010598
Chicago/Turabian StylePonomar, Maria, Valentina Ruleva, Veronika Sarapulova, Natalia Pismenskaya, Victor Nikonenko, Alina Maryasevskaya, Denis Anokhin, Dimitri Ivanov, Jeet Sharma, Vaibhav Kulshrestha, and et al. 2024. "Structural Characterization and Physicochemical Properties of Functionally Porous Proton-Exchange Membrane Based on PVDF-SPA Graft Copolymers" International Journal of Molecular Sciences 25, no. 1: 598. https://doi.org/10.3390/ijms25010598
APA StylePonomar, M., Ruleva, V., Sarapulova, V., Pismenskaya, N., Nikonenko, V., Maryasevskaya, A., Anokhin, D., Ivanov, D., Sharma, J., Kulshrestha, V., & Améduri, B. (2024). Structural Characterization and Physicochemical Properties of Functionally Porous Proton-Exchange Membrane Based on PVDF-SPA Graft Copolymers. International Journal of Molecular Sciences, 25(1), 598. https://doi.org/10.3390/ijms25010598










