Numerical Simulation of S-Shaped Current–Voltage Curves Induced by Electron Traps in Inverted Organic Photovoltaics
Abstract
:1. Introduction
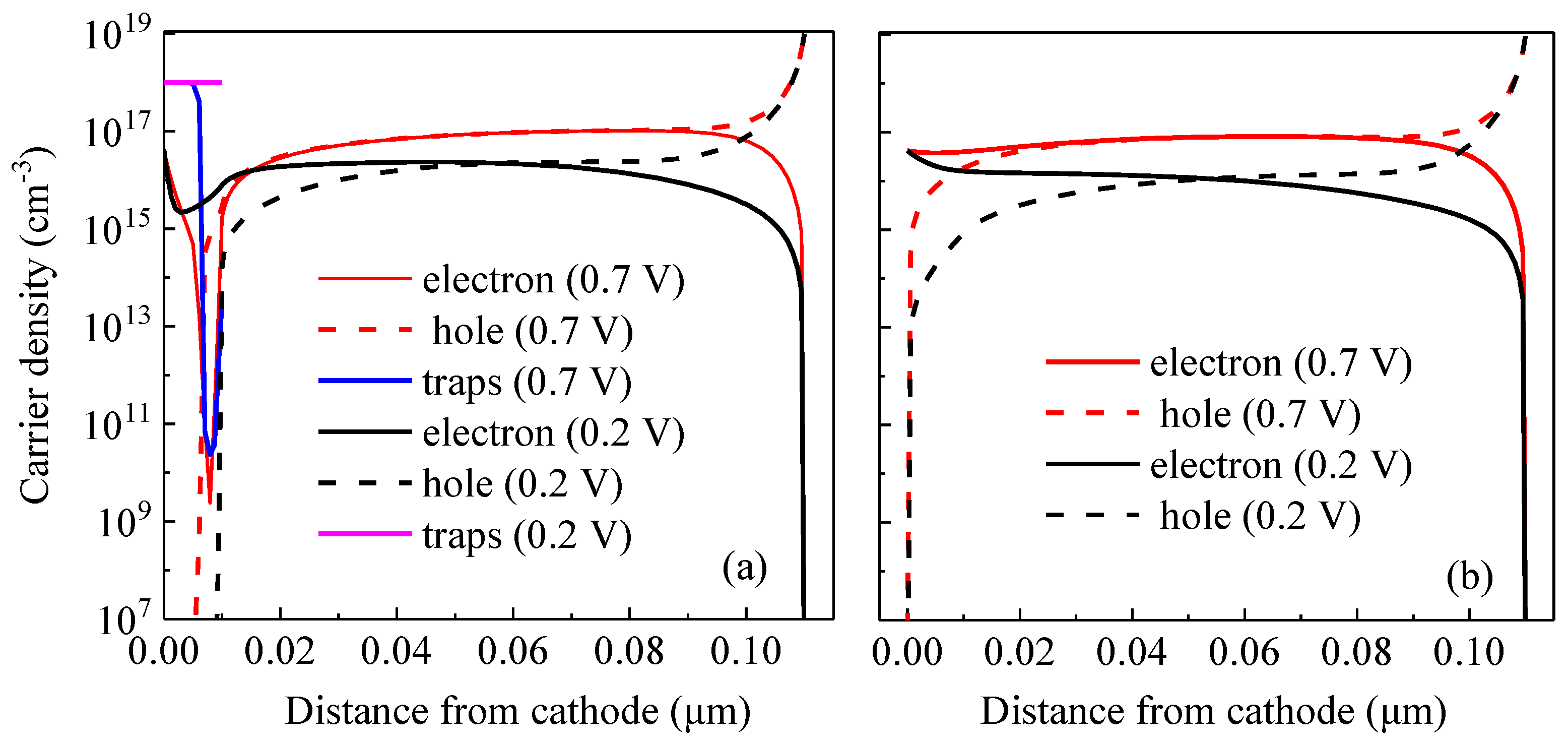
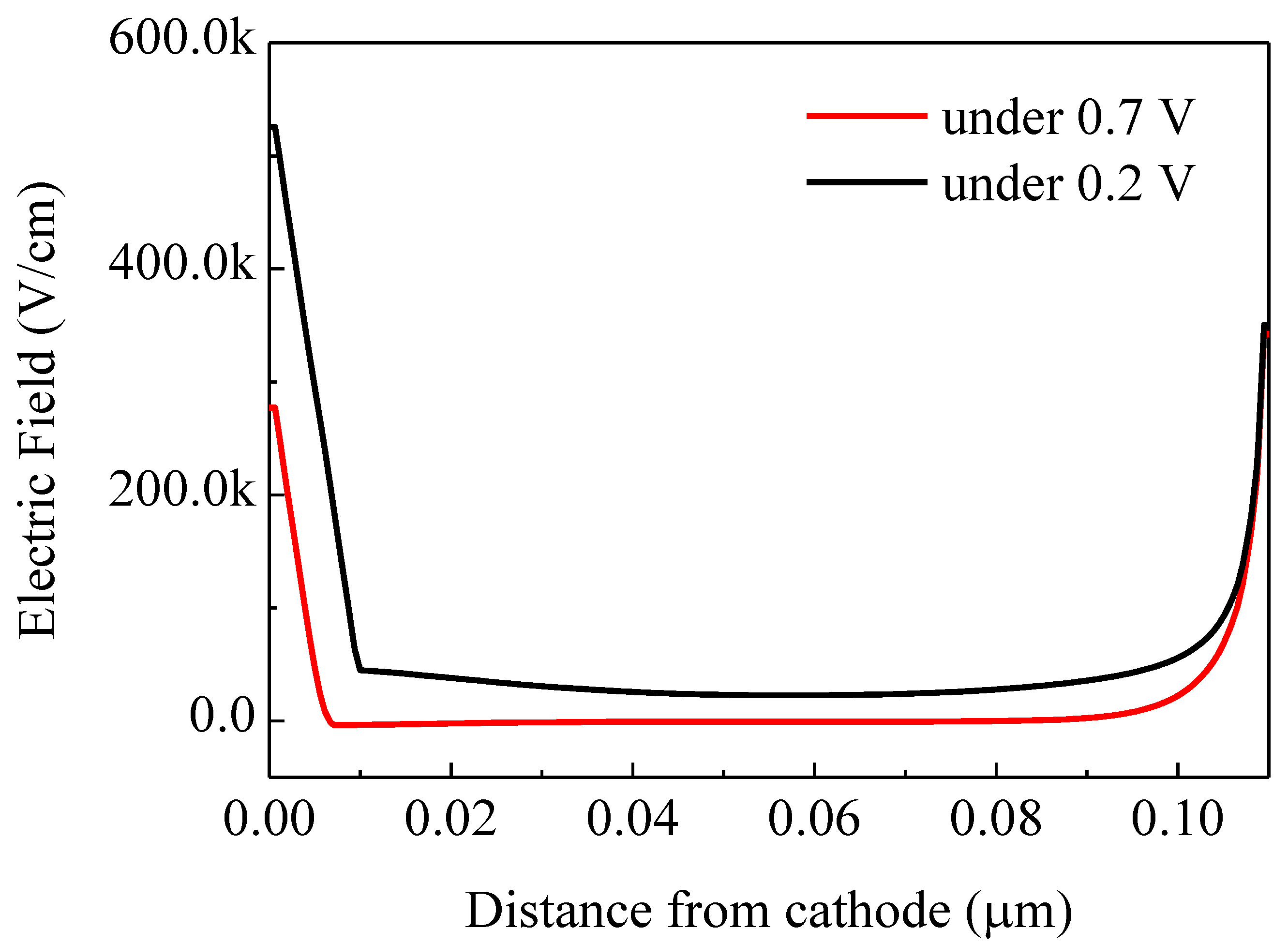
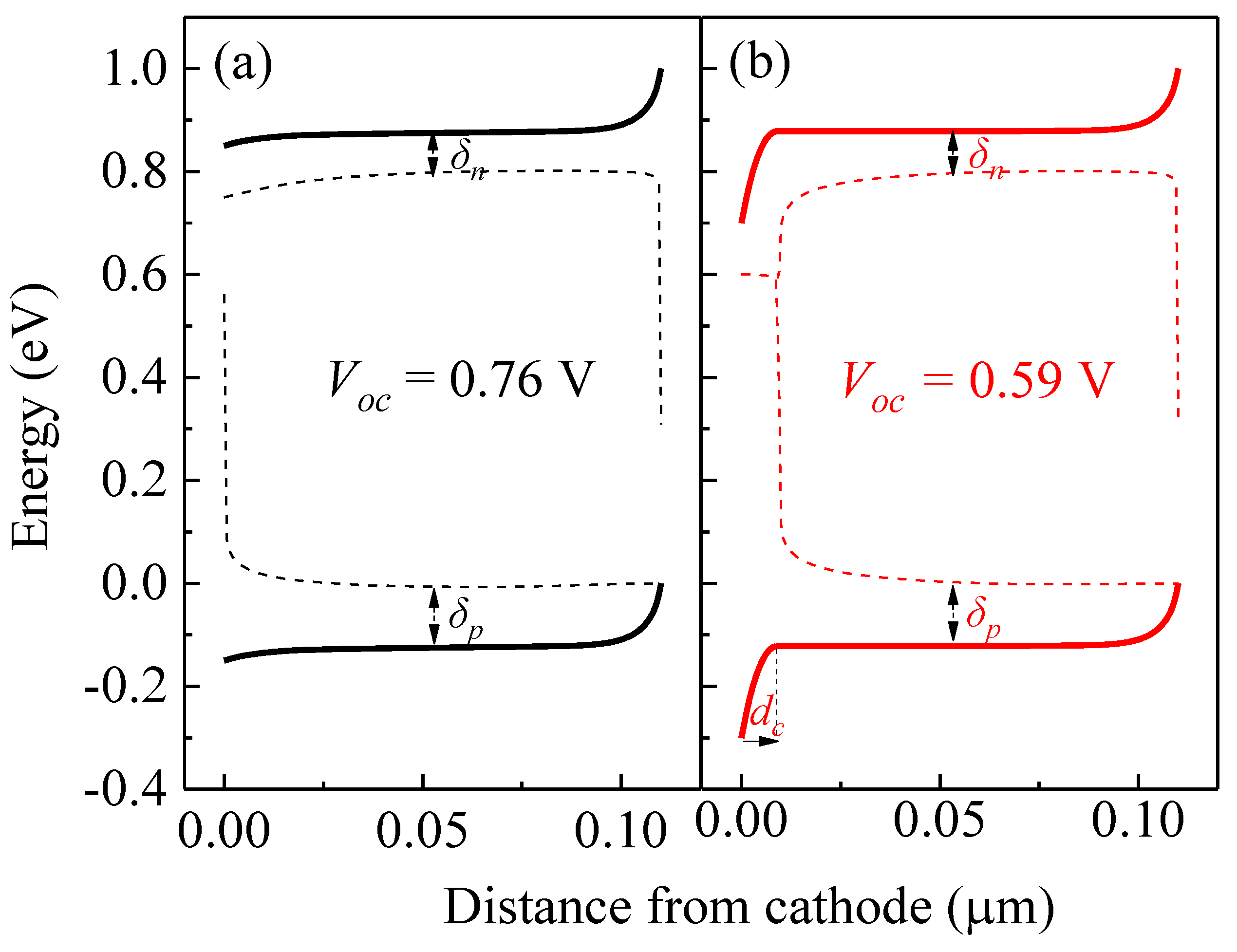
2. Results
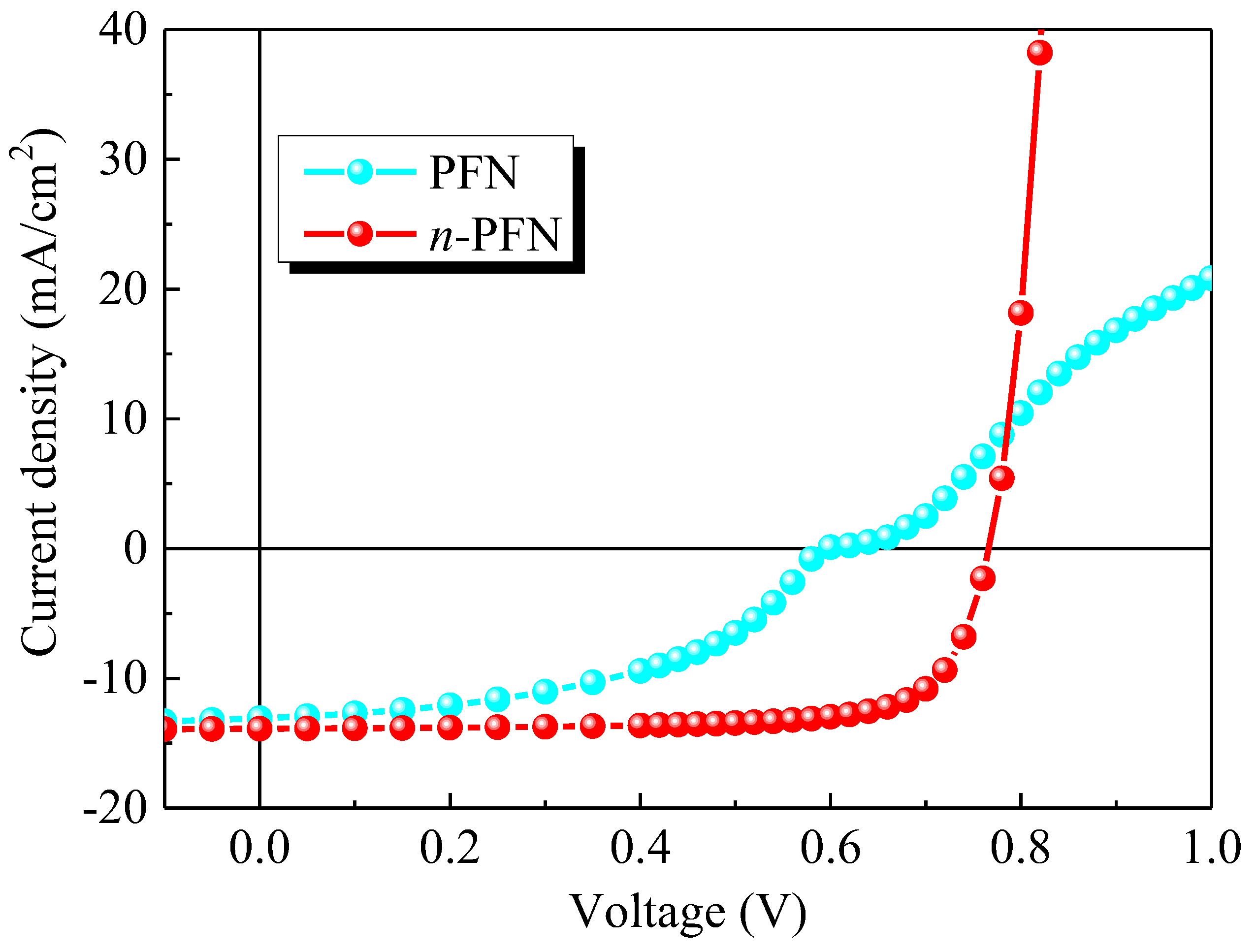
2.1. Device Performance
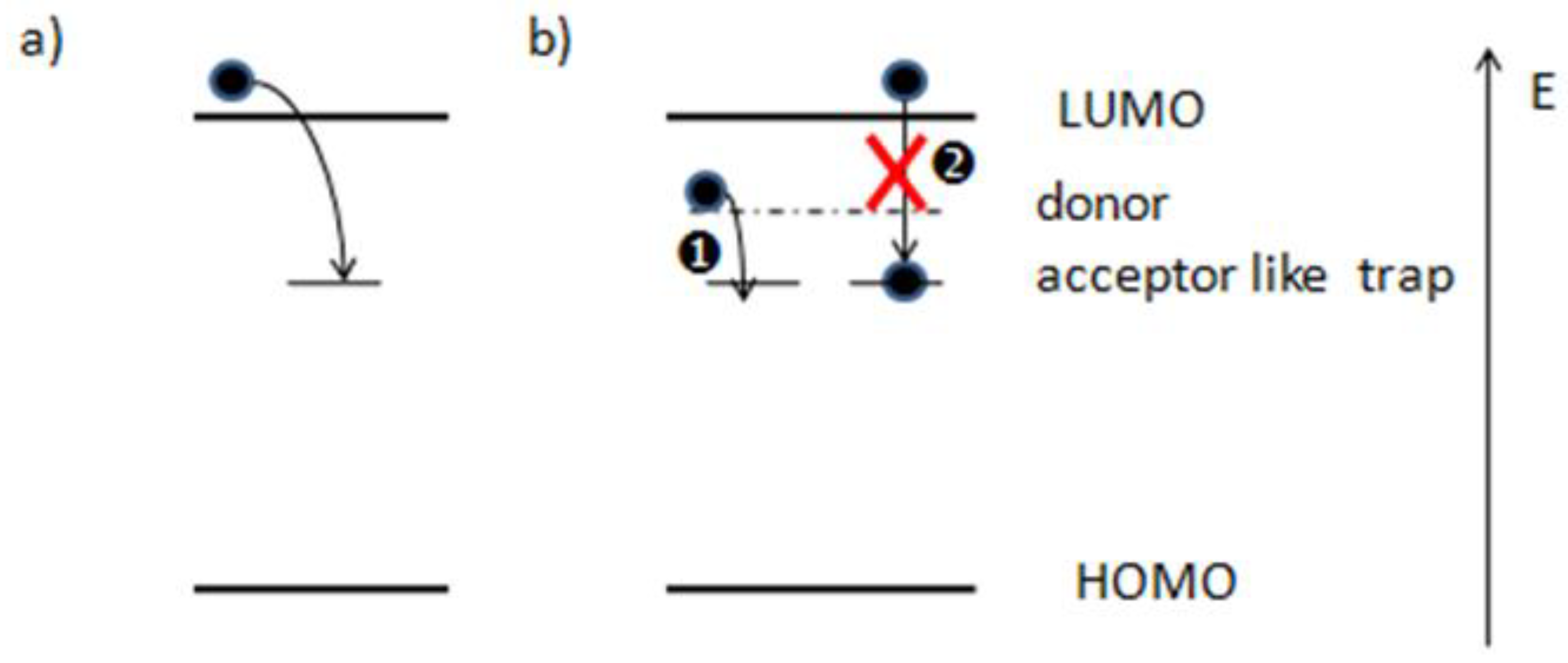
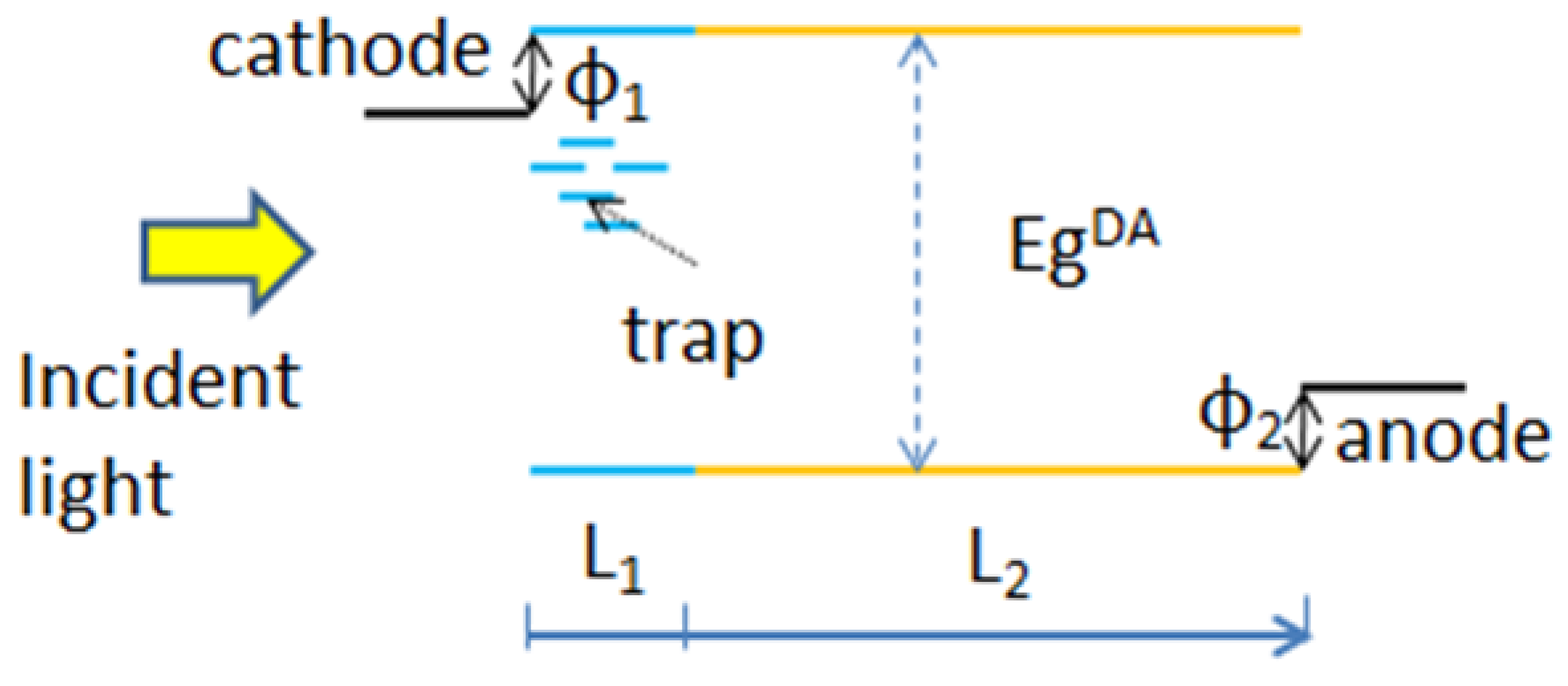
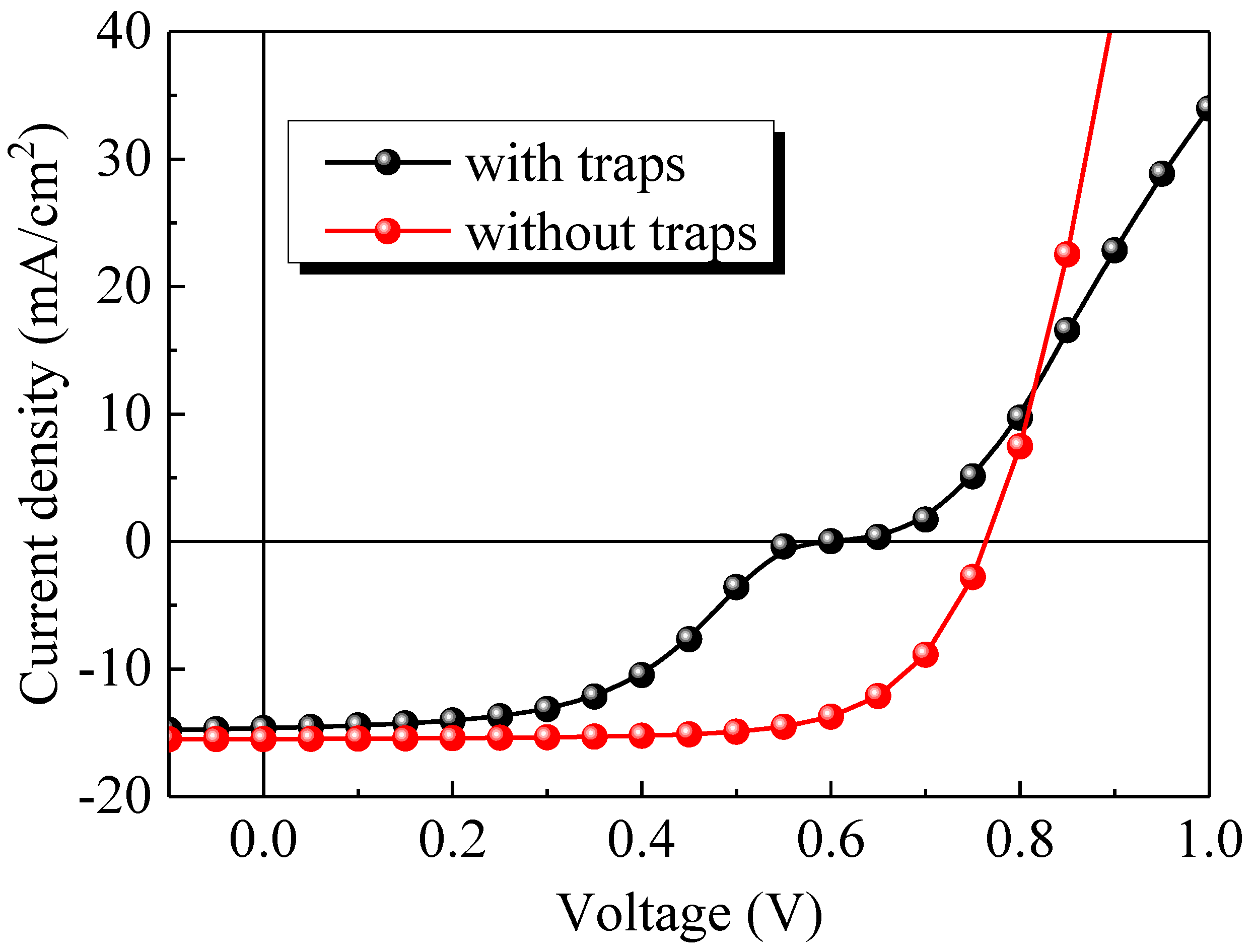
2.2. Numerical Model
3. Discussion
4. Materials and Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, Y.; Wang, Y.M.; Bergqvist, J.; Yao, H.F.; Hou, J.H. Wide-gap non-fullerene acceptor enabling high-performance organic photovoltaic cells for indoor applications. Nat. Energy 2019, 4, 768–775. [Google Scholar] [CrossRef]
- Li, G.; Zhu, R.; Yang, Y. Polymer solar cells. Nat. Photonics 2012, 6, 153–161. [Google Scholar] [CrossRef]
- He, Z.C.; Zhong, C.M.; Su, S.J.; Xu, M.; Wu, H.B.; Cao, Y. Enhanced power-conversion efficiency in polymer solar cells using an inverted device structure. Nat. Photonics 2012, 6, 591–595. [Google Scholar] [CrossRef]
- Lin, Y.B.; Adilbekova, B.; Firdaus, Y.; Yengel, E.; Faber, H.; Sajjad, M.; Zheng, X.P.; Yarali, E.; Seitkhan, A.; Bakr, O.M.; et al. 17% Efficient organic solar cells based on liquid exfoliated WS2 as a replacement for PEDOT:PSS. Adv. Mater. 2019, 31, 1902965. [Google Scholar] [CrossRef] [PubMed]
- Wagenpfahl, A.; Rauh, D.; Binder, M.; Deibel, C.; Dyakonov, V. S-shaped current-voltage characteristics of organic solar devices. Phys. Rev. B. 2010, 82, 115306. [Google Scholar] [CrossRef] [Green Version]
- Finck, B.Y.; Schwartz, B.J. Polymer/fullerene photovoltaics from drift-diffusion simulations. Appl. Phys. Lett. 2013, 103, 053306. [Google Scholar] [CrossRef] [Green Version]
- Nelson, J.; Kirkpatrick, J.; Ravirajan, P. Factors limiting the efficiency of molecular photovoltaic devices. Phys. Rev. B 2004, 69, 035337. [Google Scholar] [CrossRef]
- Mihailetchi, V.D.; Wildeman, J.; Blom, P.W.M. Space-charge limited photocurrent. Phys. Rev. Lett. 2005, 94, 126602. [Google Scholar] [CrossRef] [Green Version]
- Tress, W.; Petrich, A.; Hummert, M.; Hein, M.; Leo, K.; Riede, M. lmbalanced mobilities causing S-shaped IV curves in planar heterojunction organic solar cells. Appl. Phys. Lett. 2011, 98, 063301. [Google Scholar] [CrossRef]
- Schulze, K.; Uhrich, C.; Schuppel, R.; Leo, K.; Pfeiffer, M.; Brier, E.; Reinold, E.; Bauerle, P. Efficient vacuum-deposited organic solar cells based on a new low-bandgap oligothiophene and fullerene C60. Adv. Mater. 2006, 18, 2872–2875. [Google Scholar] [CrossRef]
- Uhrich, C.; Schueppel, R.; Petrich, A.; Pfeiffer, M.; Leo, K.; Brier, E.; Kilickiran, P.; Baeuerle, P. Organic thin-film photovoltaic cells based on oligothiophenes with reduced bandgap. Adv. Funct. Mater. 2010, 17, 2991–2999. [Google Scholar] [CrossRef]
- Sharma, A.; Franklin, J.B.; Singh, B.; Andersson, G.G.; Lewis, D.A. Electronic and chemical properties of ZnO in inverted organic photovoltaic devices. Org. Electron. 2015, 24, 131–136. [Google Scholar] [CrossRef]
- Kim, C.S.; Lee, S.S.; Gomez, E.D.; Kim, J.B.; Loo, Y.L. Transient photovoltaic behavior of air-stable, inverted organic solar cells with solution-processed electron transport layer. Appl. Phys. Lett. 2009, 94, 113302. [Google Scholar] [CrossRef]
- Tran, H.N.; Dao, D.Q.; Yoon, Y.J.; Shin, Y.S.; Choi, J.S.; Kim, J.Y.; Cho, S. Inverted polymer solar cells with annealing-free solution-processable NiO. Small 2021, 17, 2101729. [Google Scholar] [CrossRef]
- Li, Z.; Guo, J.; Lu, F.; Liu, C.; Zhang, X.; Shen, L.; Wu, H.; Guo, W. Eliminating light soaking effect of inverted polymer solar cells functionalized with a conjugated macroelectrolyte electron-collecting interlayer. Electrochim. Acta 2018, 281, 218–226. [Google Scholar] [CrossRef]
- Schmidt, H.; Zilberberg, K.; Schmale, S.; Fluegge, H.; Riedl, T.; Kowalsky, W. Transient characteristics of inverted polymer solar cells using titaniumoxide interlayers. Appl. Phys. Lett. 2010, 96, 243305. [Google Scholar] [CrossRef]
- Romero, B.; Pozo, G.D.; Destouesse, E.; Chambon, S.; Arredondo, B. Circuital modelling of S-shape removal in the current-voltage characteristic of TiOx inverted organic solar cells through white-light soaking. Organic. Electronics 2014, 15, 3546–3551. [Google Scholar]
- Zhang, D.; Choy, W.C.H.; Xie, F.X.; Sha, W.E.I.; Li, X.C.; Ding, B.F.; Zhang, K.; Huang, F.; Cao, Y. Plasmonic electrically functionalized TiO2 for high-performance organic solar cells. Adv. Funct. Mater. 2013, 23, 4255–4261. [Google Scholar] [CrossRef]
- Liu, Y.M.; Sun, Y.; Rockett, A. An improved algorithm for solving equations for intra-band tunneling current in heterojunction solar cells. Thin. Solid. Films. 2012, 520, 4947–4950. [Google Scholar] [CrossRef]
- Yan, H.; Manion, J.G.; Yuan, M.J.; Arquer, F.P.G.D.; Seferos, D.S. lncreasing polymer solar cell fill factor by trap-filling with F4-TCNQ at parts per thousand concentration. Adv. Mater. 2016, 28, 6491. [Google Scholar] [CrossRef]
- Liao, H.H.; Chen, L.M.; Xu, Z.; Li, G.; Yang, Y. Highly efficient inverted polymer solar cell by low temperature annealing of Cs2CO3 interlayer. Appl. Phys. Lett. 2008, 92, 173303. [Google Scholar] [CrossRef] [Green Version]
- Olthof, S.; Mehraeen, S.; Mohapatra, S.K.; Barlow, S.; Coropceanu, V.; Bredas, J.L.; Marder, S.R.; Kahn, A. Ultralow doping in organic semiconductors: Evidence of trap filling. Phys. Rev. Lett. 2012, 109, 176601. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Zhang, K.; Liu, X.; Jin, Y.; Jiang, X.-F.; Xu, Q.-H.; Huang, F.; Cao, Y. Alkali salt-doped highly transparent and thickness-insensitive electron-transport layer for high-performance polymer solar cell. ACS Appl. Mater. Interfaces 2018, 10, 1939–1947. [Google Scholar] [CrossRef] [PubMed]
- Koster, L.J.A.; Smits, E.C.P.; Mihailetchi, V.D.; Blom, P.W.M. Device model for the operation of polymer/fullerene bulk heterojunction solar cells. Phys. Rev. B 2005, 72, 085205. [Google Scholar] [CrossRef] [Green Version]
- Mihailetchi, V.D.; Xie, H.X.; Boer, B.D.; Koster, L.J.A.; Blom, P.W.M. Charge transport and photocurrent generation in poly(3-hexylthiophene): Methanofullerene bulk-heterojunction solar Cells. Adv. Funct. Mater. 2006, 16, 699–708. [Google Scholar] [CrossRef] [Green Version]
- Wehenkel, D.J.; Koster, L.J.A.; Wienk, M.M.; Janssen, R.A.J. Influence of injected charge carriers on photocurrents in polymer solar cells. Phys. Rev. B. 2012, 85, 125203. [Google Scholar] [CrossRef] [Green Version]
- Fonash, S.; Arch, J.; Cuifi, J.; Hou, J.; Howland, W.; McElheny, P.; Moquin, A.; Rogossky, M.; Rubinelli, M.; Tran, T.; et al. A Manual for AMPS-1D for Windows 95/NT; The Pennsylvania State University: Happy Valley, PA, USA, 1997; pp. 10–31. [Google Scholar]
- Zhu, H.; Kalkan, A.K.; Hou, J.Y.; Fonash, S.J. Applications of AMPS-1D for solar cell simulation. AIP Conf. Proc. 1999, 462, 309. [Google Scholar]
- The University of Illinois and Engineering Wiki Website. Available online: https://wiki.engr.illinois.edu/display/solarcellsim (accessed on 20 November 2021).
- Hall, R.N. Electron-hole recombination in germanium. Phys. Rev. 1952, 87, 387. [Google Scholar] [CrossRef]
- Shockley, W.; Read, W.T. Statistics of the recombinations of holes and electrons. Phys. Rev. 1952, 87, 835. [Google Scholar] [CrossRef]
- Sandberg, O.J.; Nyman, M.; Österbacka, R. Effect of contacts in organic bulk heterojunction solar cells. Phys. Rev. Appl. 2014, 1, 024003. [Google Scholar] [CrossRef]


| Parameter | Symbol | Numerical Value |
|---|---|---|
| Effective band gap | ||
| Electron mobility | ||
| Hole mobility | ||
| Relative static permittivity | 3.4 | |
| Injection barrier at cathode side | 0.1 eV | |
| Injection barrier at anode side | 0 eV | |
| Density of states at conduction band | ||
| Density of states at valence band | ||
| Distance to cathode | ||
| Distance to anode | ||
| Surface recombination velocity of electrons (cathode side) | ||
| Surface recombination velocity of holes (cathode side) | ||
| Surface recombination velocity of electrons (anode side) | ||
| Surface recombination velocity of holes (anode side) | ||
| Discrete acceptor-like gap state density | ||
| Capte cross section of electrons | ||
| Capture cross section of holes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, S.; Huo, M.; Xue, Q.; Xie, G. Numerical Simulation of S-Shaped Current–Voltage Curves Induced by Electron Traps in Inverted Organic Photovoltaics. Int. J. Mol. Sci. 2022, 23, 2039. https://doi.org/10.3390/ijms23042039
Luo S, Huo M, Xue Q, Xie G. Numerical Simulation of S-Shaped Current–Voltage Curves Induced by Electron Traps in Inverted Organic Photovoltaics. International Journal of Molecular Sciences. 2022; 23(4):2039. https://doi.org/10.3390/ijms23042039
Chicago/Turabian StyleLuo, Shanglin, Mingfang Huo, Qin Xue, and Guohua Xie. 2022. "Numerical Simulation of S-Shaped Current–Voltage Curves Induced by Electron Traps in Inverted Organic Photovoltaics" International Journal of Molecular Sciences 23, no. 4: 2039. https://doi.org/10.3390/ijms23042039
APA StyleLuo, S., Huo, M., Xue, Q., & Xie, G. (2022). Numerical Simulation of S-Shaped Current–Voltage Curves Induced by Electron Traps in Inverted Organic Photovoltaics. International Journal of Molecular Sciences, 23(4), 2039. https://doi.org/10.3390/ijms23042039







