Theoretical Evaluation of Sulfur-Based Reactions as a Model for Biological Antioxidant Defense
Abstract
:1. Introduction


2. Results
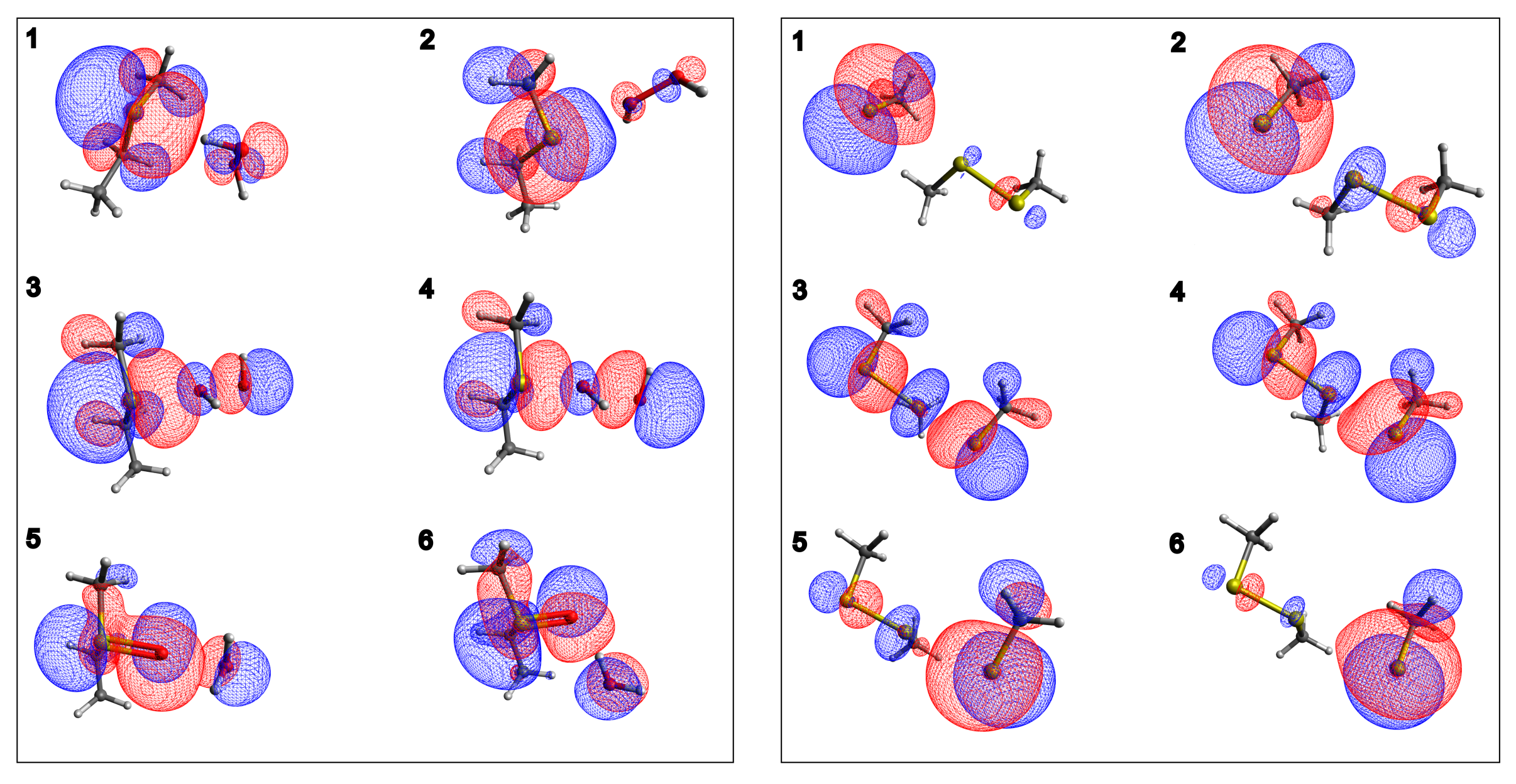
2.1. In Vacuum Reaction Pathways


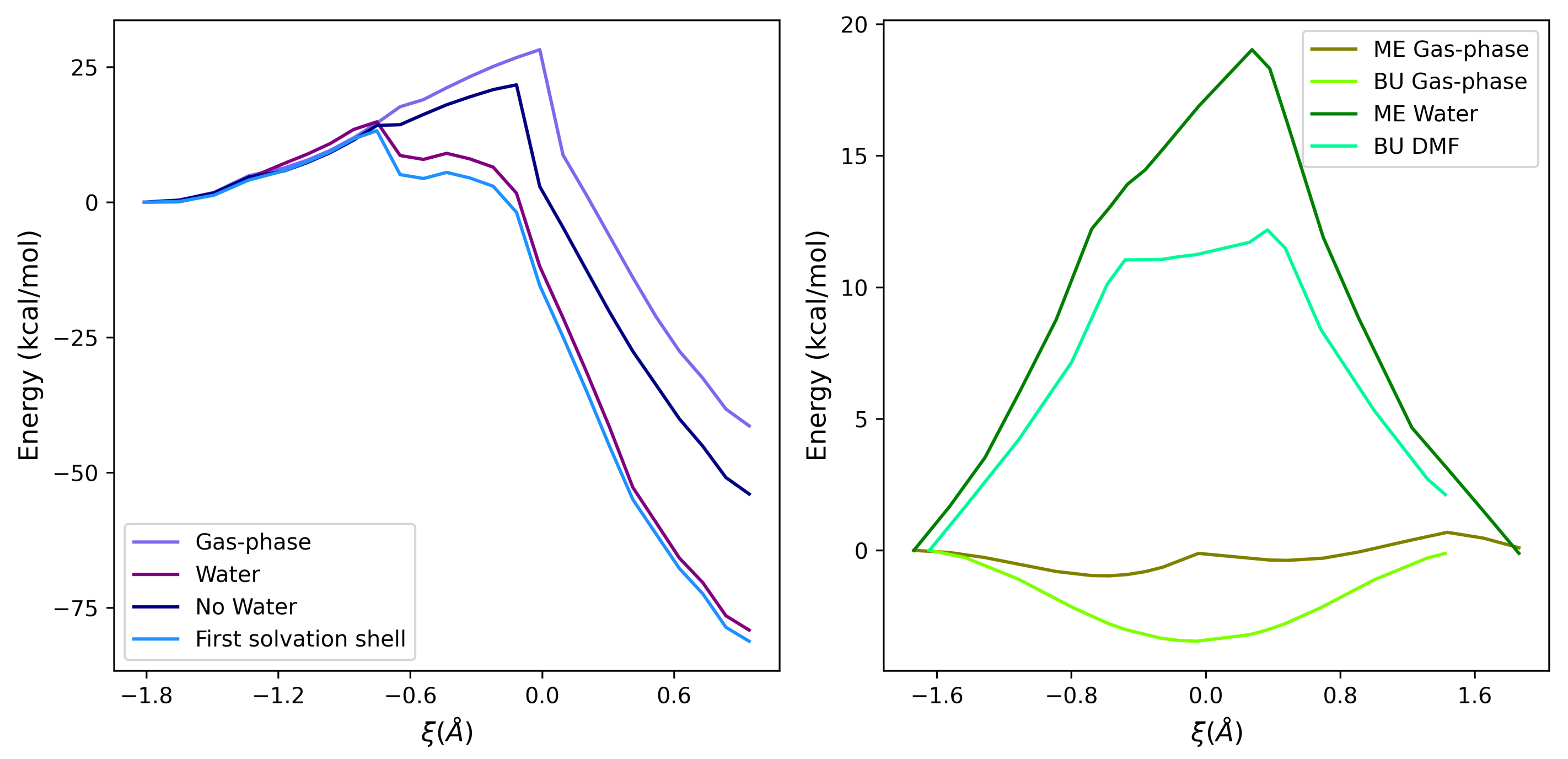
2.2. Effect of a Perturbing Environment on the Energy Barrier
2.3. Analysis of the Environment Perturbation
3. Discussion
4. Materials and Methods
4.1. Theoretical Background: The Perturbed Matrix Method (PMM)
4.2. Helmholtz Free Energy Change along a Reaction Coordinate
4.3. Computational Details
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pajares, M.; Jiménez-Moreno, N.; Dias, I.H.; Debelec, B.; Vucetic, M.; Fladmark, K.E.; Basaga, H.; Ribaric, S.; Milisav, I.; Cuadrado, A. Redox Control of Protein Degradation. Redox Biol. 2015, 6, 409–420. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murphy, M.P. How Mitochondria Produce Reactive Oxygen Species. Biochem. J. 2009, 417, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nordberg, J.; Arnér, E.S. Reactive oxygen species, antioxidants, and the mammalian thioredoxin system. Free Radical. Bio. Med. 2001, 31, 1287–1312. [Google Scholar] [CrossRef]
- Netto, L.E.S.; de Oliveira, M.A.; Monteiro, G.; Demasi, A.P.D.; Cussiol, J.R.R.; Discola, K.F.; Demasi, M.; Silva, G.M.; Alves, S.V.; Faria, V.G.; et al. Reactive cysteine in proteins: Protein folding, antioxidant defense, redox signaling and more. Comp. Biochem. Physiol. Part C Toxicol. Pharmacol. 2007, 146, 180–193. [Google Scholar] [CrossRef] [PubMed]
- Netto, L.E.S.; De Oliveira, M.A.; Tairum, C.A.; Da Silva Neto, J.F. Conferring specificity in redox pathways by enzymatic thiol/disulfide exchange reactions. Free Radic. Res. 2016, 50, 206–245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barford, D. The role of cysteine residues as redox-sensitive regulatory switches. Curr. Opin. Struct. Biol. 2004, 14, 679–686. [Google Scholar] [CrossRef] [PubMed]
- Davies, J.M. The oxidative environment and protein damage. Biochim. Biophys. Acta Proteins Proteom. 2005, 1703, 93–109. [Google Scholar] [CrossRef]
- Cao, Z.; Mitchell, L.; Hsia, O.; Scarpa, M.; Caldwell, T.S.; Alfred, A.D.; Gennaris, A.; Collet, J.F.; Hartley, R.C.; Bulleid, N.J. Methionine sulfoxide reductase B3 requires resolving cysteine residues for full activity and can act as a stereospecific methionine oxidase. Biochem. J. 2018, 475, 827–838. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, B.H.F. Thiol/Disulfide Exchange Equilibria Bond Stability and Disulfde. Meth. Enzymol. 1995, 251, 8–28. [Google Scholar]
- Bulaj, G. Formation of disulfide bonds in proteins and peptides. Biotechnol. Adv. 2005, 23, 87–92. [Google Scholar] [CrossRef]
- Houk, J.; Singh, R.; Whitesides, G.M. Measurement of Thiol-Disulfide Interchange Reactions and Thiol pKa Values. Meth. Enzymol. 1987, 143, 129–140. [Google Scholar]
- Houk, J.; Whitesides, G.M. Structure-Reactivity Relations for Thiol-Disulfide Interchange. J. Am. Chem. Soc. 1987, 109, 6825–6836. [Google Scholar] [CrossRef]
- Bach, R.D.; Dmitrenko, O.; Thorpe, C. Mechanism of thiolate-disulfide interchange reactions in biochemistry. J. Org. Chem. 2008, 73, 12–21. [Google Scholar] [CrossRef] [PubMed]
- Nagy, P. Kinetics and mechanisms of thiol-disulfide exchange covering direct substitution and thiol oxidation-mediated pathways. Antioxid. Redox. Signal. 2013, 18, 1623–1641. [Google Scholar] [CrossRef] [Green Version]
- Putzu, M.; Gräter, F.; Elstner, M.; Kubař, T. On the mechanism of spontaneous thiol-disulfide exchange in proteins. Phys. Chem. Chem. Phys. 2018, 20, 16222–16230. [Google Scholar] [CrossRef]
- Rajeeva, S.; Whiteside, G.M. Comparisons of Rate Constants for Thiolate-Disulfide Interchange in Water and in Polar Aprotic Solvents Using Dynamic 1H NMR Line Shape Analysis. J. Am. Chem. Soc. 1990, 112, 1190–1197. [Google Scholar]
- Goddard, D.R.; Michaelis, L. A Study on Keratin. J. Biol. Chem. 1934, 106, 605–614. [Google Scholar] [CrossRef]
- Kolthoff, I.M.; Stricks, W.; Kapoor, R.C. Equilibrium Constants of Exchange Reactions of Cystine with Glutathione and with Thioglycolic Acid Both in the Oxidized and Reduced State. J. Am. Chem. Soc. 1955, 77, 4733–4739. [Google Scholar] [CrossRef]
- Inaba, K.; Ito, K. Structure and mechanisms of the DsbB–DsbA disulfide bond generation machine. Biochim. Biophys. Acta 2008, 1783, 520–529. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Z.; Zhang, J.; Ballou, D.P.; Williams, C.H. Reactivity of thioredoxin as a protein thiol-disulfide oxidoreductase. Chem. Rev. 2011, 111, 5768–5783. [Google Scholar] [CrossRef] [Green Version]
- Ben-Lulu, S.; Ziv, T.; Admon, A.; Weisman-Shomer, P.; Benhar, M. A substrate trapping approach identifies proteins regulated by reversible S-nitrosylation. Mol. Cell. Proteomics. 2014, 13, 2573–2583. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kortemme, T.; Creighton, T.E. Ionisation of cysteine residues at the termini of model α-helical peptides. Relevance to unusual thiol pKa values in proteins of the thioredoxin family. J. Mol. Cell. Biol. 1995, 253, 799–812. [Google Scholar]
- Hagras, M.A.; Bellucci, M.A.; Marek, R.A.; Trout, B.L. Computational Modeling of the Disulfide Cross-Linking reaction. J. Phys. Chem. B 2020, 124, 9840–9851. [Google Scholar] [CrossRef] [PubMed]
- Roos, G.; Loverix, S.; Geerlings, P. Origin of the pKa perturbation of N-terminal cysteine in α- And 310-helices: A computational DFT study. J. Phys. Chem. B 2006, 110, 557–562. [Google Scholar] [CrossRef] [PubMed]
- Hol, W.G.J.; Van Duijnen, P.T.; Berendsen, H.J.C. The alpha-helix dipole and the properties of proteins. Nature 1978, 273, 443–446. [Google Scholar] [CrossRef]
- Drazic, A.; Winter, J. The physiological role of reversible methionine oxidation. Biochim. Biophys. Acta Proteins Proteom. 2014, 1844, 1367–1382. [Google Scholar] [CrossRef]
- Schöneich, C. Methionine oxidation by reactive oxygen species: Reaction mechanisms and relevance to Alzheimer’s disease. Biochim. Biophys. Acta Proteins Proteom. 2005, 1703, 111–119. [Google Scholar] [CrossRef]
- Lowther, W.T.; Brot, N.; Weissbach, H.; Matthews, B.W. Structure and Mechanism of Peptide Methionine Sulfoxide Reductase, an “Anti-Oxidation” Enzyme. Biochemistry 2000, 39, 13307–13312. [Google Scholar] [CrossRef]
- Di Marzo, N.; Chisci, E.; Giovannoni, R. The Role of Hydrogen Peroxide in Redox-Dependent Signaling: Homeostatic and Pathological Responses in Mammalian Cells. Cells 2018, 7, 156. [Google Scholar] [CrossRef] [Green Version]
- Rhee, S.G.; Chang, T.S.; Bae, Y.S.; Lee, S.R.; Kang, S.W. Cellular Regulation by Hydrogen Peroxide. JASN 2003, 14, S211–S215. [Google Scholar] [CrossRef] [Green Version]
- Sies, H. Hydrogen peroxide as a central redox signaling molecule in physiological oxidative stress: Oxidative eustress. Redox Biol. 2017, 11, 613–619. [Google Scholar] [CrossRef] [PubMed]
- Chu, J.W.; Trout, B.L. On the Mechanisms of Oxidation of Organic Sulfides by H2O2 in Aqueous Solutions. J. Am. Chem. Soc. 2004, 126, 900–908. [Google Scholar] [CrossRef]
- Chu, J.W.; Brooks, B.R.; Trout, B.L. Oxidation of Methionine Residues in Aqueous Solutions: Free Methionine and Methionine in Granulocyte Colony-Stimulating Factor. J. Am. Chem. Soc. 2004, 126, 16601–16607. [Google Scholar] [CrossRef] [PubMed]
- Chu, J.W.; Yin, J.; Wang, D.I.C.; Trout, B.L. A Structural and Mechanistic Study of the Oxidation of Methionine Residues in hPTH (1–34) via Experiments and Simulations. Biochemistry 2004, 43, 14139–14148. [Google Scholar] [CrossRef] [PubMed]
- Chu, J.; Yin, J.; Brooks, B.R.; Wang, D.I.; Ricci, M.S.; Brems, D.N.; Trout, B.L. A comprehensive picture of non-site specific oxidation of methionine residues by peroxides in protein pharmaceuticals. J. Pharm. Sci. 2004, 93, 3096–3102. [Google Scholar] [CrossRef] [PubMed]
- Sjöberg, B. Methionine oxidation by hydrogen peroxide in peptides and proteins: A theoretical and Raman spectroscopy study. J. Photochem. Photobiol. B Biol. 2018, 188, 95–99. [Google Scholar] [CrossRef]
- Pan, B.; Abel, J.; Ricci, M.S.; Brems, D.N.; Wang, D.I.C.; Trout, B.L. Comparative Oxidation Studies of Methionine Residues Reflect a structural effect on chemical kinetics in rhG-CSF. Biochemistry 2006, 45, 15430–15443. [Google Scholar] [CrossRef]
- Aussel, L.; Ezraty, B. Methionine Redox Homeostasis in Protein Quality Control. Front. Mol. Biosci. 2021, 8, 665492. [Google Scholar] [CrossRef]
- Kim, G.; Weiss, S.J.; Levine, R.L. Methionine oxidation and reduction in proteins. Biochim. Biophys. Acta Gen. Subj. 2014, 1840, 901–905. [Google Scholar] [CrossRef] [Green Version]
- Bettinger, J.Q.; Welle, K.A.; Hryhorenko, J.R.; Ghaemmaghami, S. Quantitative Analysis of in Vivo Methionine Oxidation of the Human Proteome. J. Proteome Res. 2020, 19, 624–633. [Google Scholar] [CrossRef]
- Stadtman, E.R.; Moskovitz, J.; Levine, R.L. Oxidation of Methionine Residues of Proteins: Biological Consequences. Antioxid. Redox Signal. 2003, 5, 577–582. [Google Scholar] [CrossRef] [PubMed]
- Bigelow, D.J.; Squier, T.C. Thioredoxin-dependent redox regulation of cellular signaling and stress response through reversible oxidation of methionines. Mol. BioSyst. 2011, 7, 2101. [Google Scholar] [CrossRef] [PubMed]
- Lourenço dos Santos, S.; Petropoulos, I.; Friguet, B. The Oxidized Protein Repair Enzymes Methionine Sulfoxide Reductases and Their Roles in Protecting against Oxidative Stress, in Ageing and in Regulating Protein Function. Antioxidants 2018, 7, 191. [Google Scholar] [CrossRef] [PubMed]
- Ursini, F. Redox homeostasis: The Golden Mean of healthy living. Redox Biol. 2016, 8, 205–215. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, P.A.; Ramos, M.J. Theoretical Insight into the Mechanism for Thiol/Disulfide Exchange. Chem. Eur. J. 2004, 10, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Rosenfield, R.E., Jr.; Parthasarathy, R.; Dunitz, J.D. Directional preferences of nonbonded atomic contacts with divalent sulfur. 1. Electrophiles and nucleophiles. J. Am. Chem. Soc. 1977, 99, 4860–4862. [Google Scholar] [CrossRef]
- Agrawal, N.J.; Dykstra, A.; Yang, J.; Yue, H.; Nguyen, X.; Kolvenbach, C.; Angell, N. Prediction of the Hydrogen Peroxide–Induced Methionine Oxidation Propensity in Monoclonal Antibodies. Eur. J. Pharm. Sci. 2018, 107, 1282–1289. [Google Scholar] [CrossRef]
- Vatsa, S. In silico prediction of post-translational modifications in therapeutic antibodies. mAbs 2022, 14, 2023938. [Google Scholar] [CrossRef]
- Wilson, J.M.; Bayer, R.J.; Hupe, D.J. Structure-Reactivity Correlations for the Thiol-Disulfide Interchange Reaction1. J. Am. Chem. Soc. 1977, 99, 7922–7926. [Google Scholar] [CrossRef]
- Zanetti-Polzi, L.; Bortolotti, C.A.; Daidone, I.; Aschi, M.; Amadei, A.; Corni, S. A few key residues determine the high redox potential shift in azurin mutants. Org. Biomol. Chem. 2015, 13, 11003–11013. [Google Scholar] [CrossRef]
- Segreto, G.E.; Alba, J.; Salvio, R.; D’Abramo, M. DNA cleavage by endonuclease I-DmoI: A QM/MM study and comparison with experimental data provide indications on the environmental effects. Theor. Chem. Acc. 2020, 139, 1–7. [Google Scholar] [CrossRef]
- Zanetti-Polzi, L.; Del Galdo, S.; Daidone, I.; D’Abramo, M.; Barone, V.; Aschi, M.; Amadei, A. Extending the perturbed matrix method beyond the dipolar approximation: Comparison of different levels of theory. Phys. Chem. Chem. Phys 2018, 20, 24369–24378. [Google Scholar] [CrossRef] [PubMed]
- Spezia, R.; Aschi, M.; Nola, A.D.; Amadei, A. Extension of the perturbed matrix method: Application to a water molecule. Chem. Phys. Lett. 2002, 365, 450–456. [Google Scholar] [CrossRef]
- D’Annibale, V.; Nardi, A.N.; Amadei, A.; D’Abramo, M. Theoretical Characterization of the Reduction Potentials of Nucleic Acids in Solution. J. Chem. Theory Comput. 2021, 17, 1301–1307. [Google Scholar] [CrossRef] [PubMed]
- Nardi, A.N.; Olivieri, A.; D’Abramo, M. Rationalizing Sequence and Conformational Effects on the Guanine Oxidation in Different DNA Conformations. J. Phys. Chem. B 2022, 126, 5017–5023. [Google Scholar] [CrossRef]
- Chen, C.G.; Nardi, A.N.; Giustini, M.; D’Abramo, M. Absorption behavior of doxorubicin hydrochloride in visible region in different environments: A combined experimental and computational study. Phys. Chem. Chem. Phys. 2022, 24, 12027–12035. [Google Scholar] [CrossRef]
- Zanetti-Polzi, L.; Daidone, I.; Amadei, A. Fully Atomistic Multiscale Approach for pKa Prediction. J. Phys. Chem. B 2020, 124, 4712–4722. [Google Scholar] [CrossRef]
- Amadei, A.; D’Alessandro, M.; Aschi, M. Statistical Mechanical Modeling of Chemical Reactions in Complex Systems: The Reaction Free Energy Surface. J. Phys. Chem. B 2004, 108, 16250–16254. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian˜16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Rassolov, V.A.; Ratner, M.A.; Pople, J.A.; Redfern, P.C.; Curtiss, L.A. 6-31G* Basis Set for Third-Row Atoms. J. Comput. Chem. 2001, 22, 976–984. [Google Scholar] [CrossRef]
- Abraham, M.J.D.; van der Spoel, E.L.B.H.; the GROMACS Development Team. GROMACS User Manual Version 2019; GROMACS Development Team: Uppsala, Sweden, 2019. [Google Scholar]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sousa da Silva, A.W.; Vranken, W.F. ACPYPE—AnteChamber PYthon Parser interfacE. BMC Res. Notes 2012, 5, 367. [Google Scholar] [CrossRef] [PubMed]


| Molecule | Solvent | ||||
|---|---|---|---|---|---|
| Methionine | 15.5 | 14.9 | 16.1 | 1.2 | |
| Mercaptoethanol | 16.2 | 19.0 | 21.9 | 2.9 | |
| Butanethiol | DMF | 11.1 | 12.2 | 13.7 | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Sciscio, M.L.; D’Annibale, V.; D’Abramo, M. Theoretical Evaluation of Sulfur-Based Reactions as a Model for Biological Antioxidant Defense. Int. J. Mol. Sci. 2022, 23, 14515. https://doi.org/10.3390/ijms232314515
De Sciscio ML, D’Annibale V, D’Abramo M. Theoretical Evaluation of Sulfur-Based Reactions as a Model for Biological Antioxidant Defense. International Journal of Molecular Sciences. 2022; 23(23):14515. https://doi.org/10.3390/ijms232314515
Chicago/Turabian StyleDe Sciscio, Maria Laura, Valeria D’Annibale, and Marco D’Abramo. 2022. "Theoretical Evaluation of Sulfur-Based Reactions as a Model for Biological Antioxidant Defense" International Journal of Molecular Sciences 23, no. 23: 14515. https://doi.org/10.3390/ijms232314515
APA StyleDe Sciscio, M. L., D’Annibale, V., & D’Abramo, M. (2022). Theoretical Evaluation of Sulfur-Based Reactions as a Model for Biological Antioxidant Defense. International Journal of Molecular Sciences, 23(23), 14515. https://doi.org/10.3390/ijms232314515