“Dividing and Conquering” and “Caching” in Molecular Modeling
Abstract
1. Introduction
2. Challenges in Molecular Modeling
2.1. Accurate Description of Molecular Interactions
2.2. Inherent Low Efficiency in Sampling of Configurational Space
3. DC and “Caching” in Traditional Molecular Modeling
3.1. Coarse Graining, a Partially Transferable “Caching” Strategy
3.2. Enhanced Sampling, a Nontransferable in Resolution DC and “Caching” Strategy
4. Machine Learning Improves “Caching”
4.1. Toward Ab Initio Accuracy of Molecular Simulation Potentials
4.2. Machine Learning and Coarse Graining
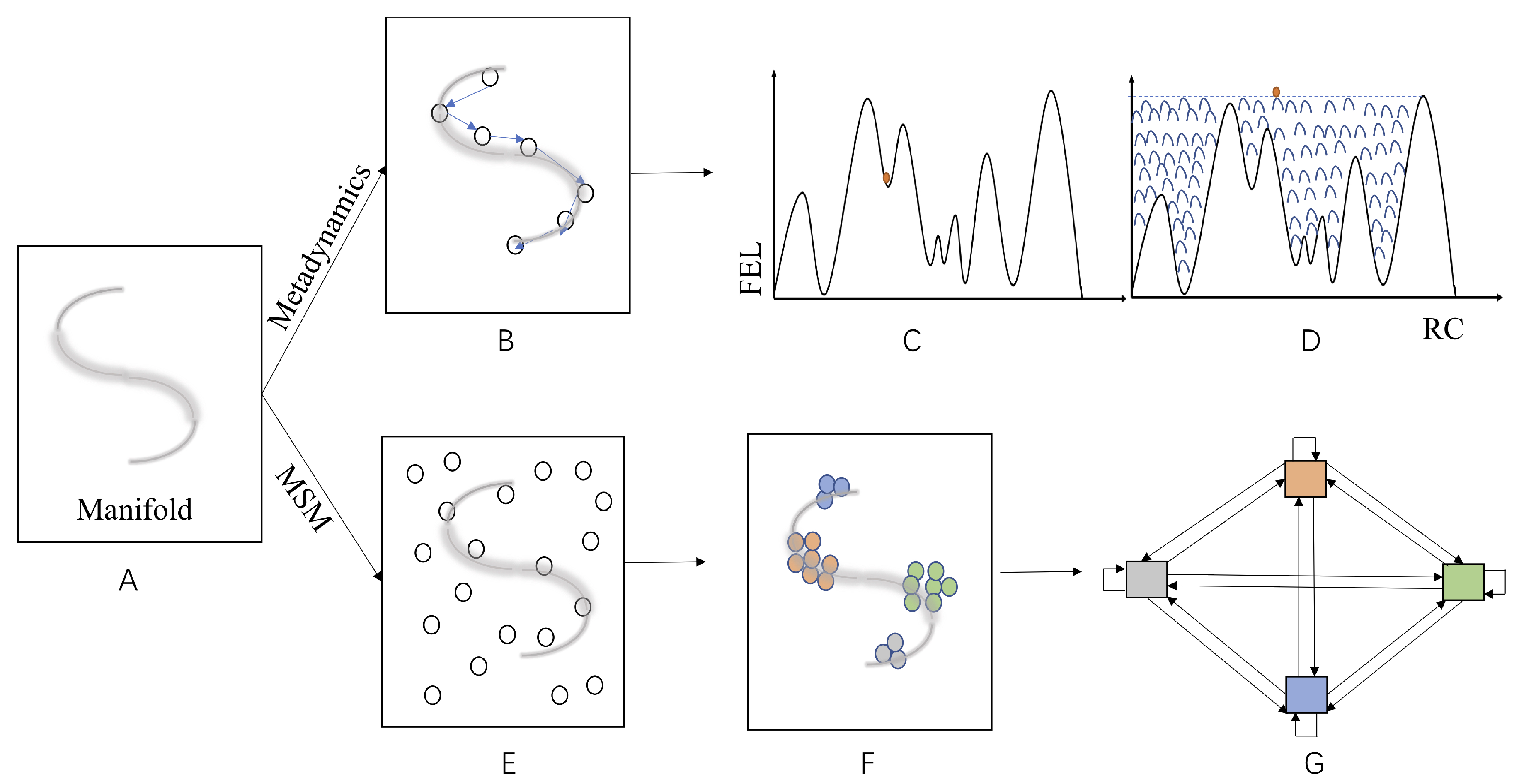
4.3. Machine Learning in Searching for RC/CVs and Construction of MSM
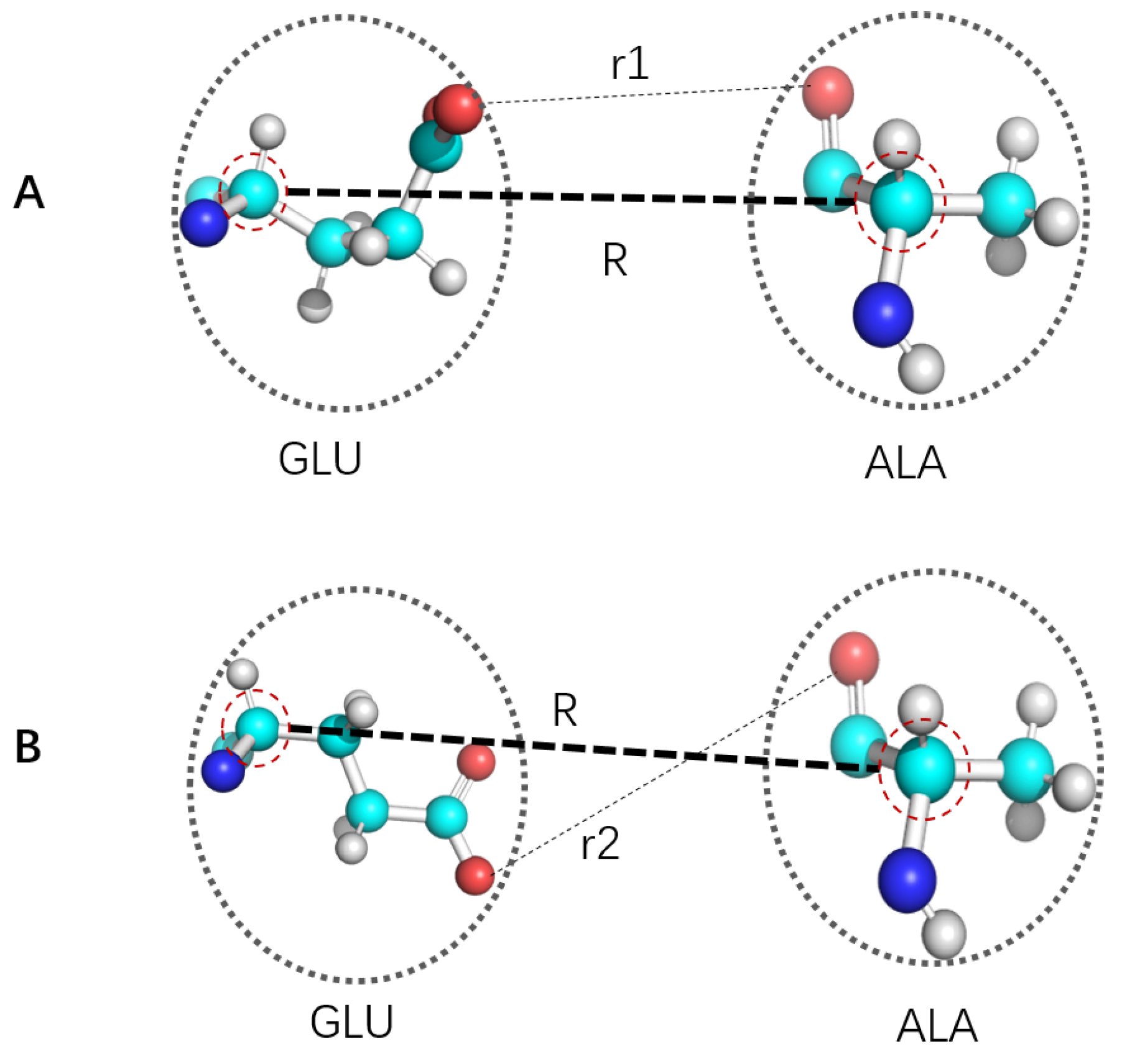
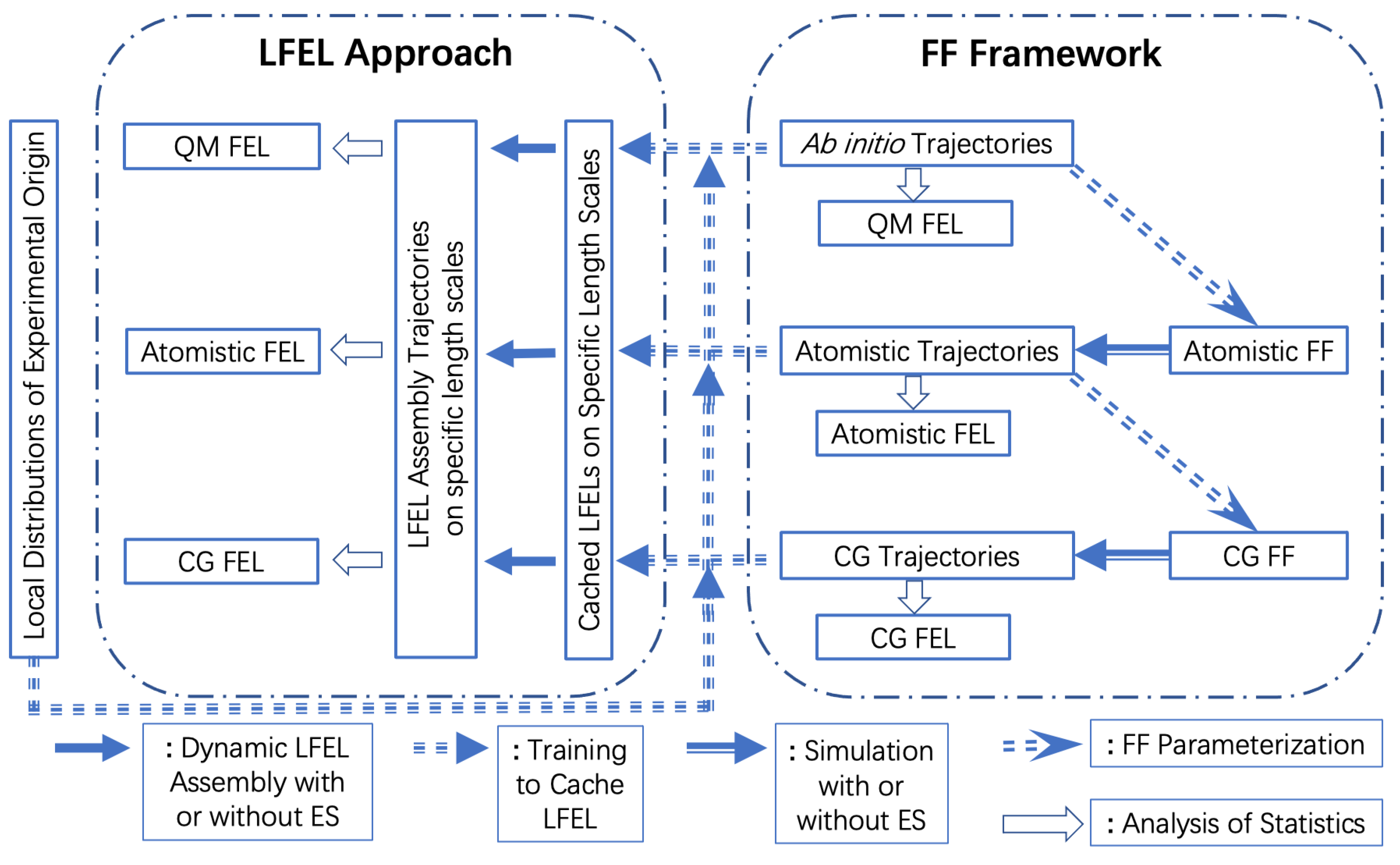
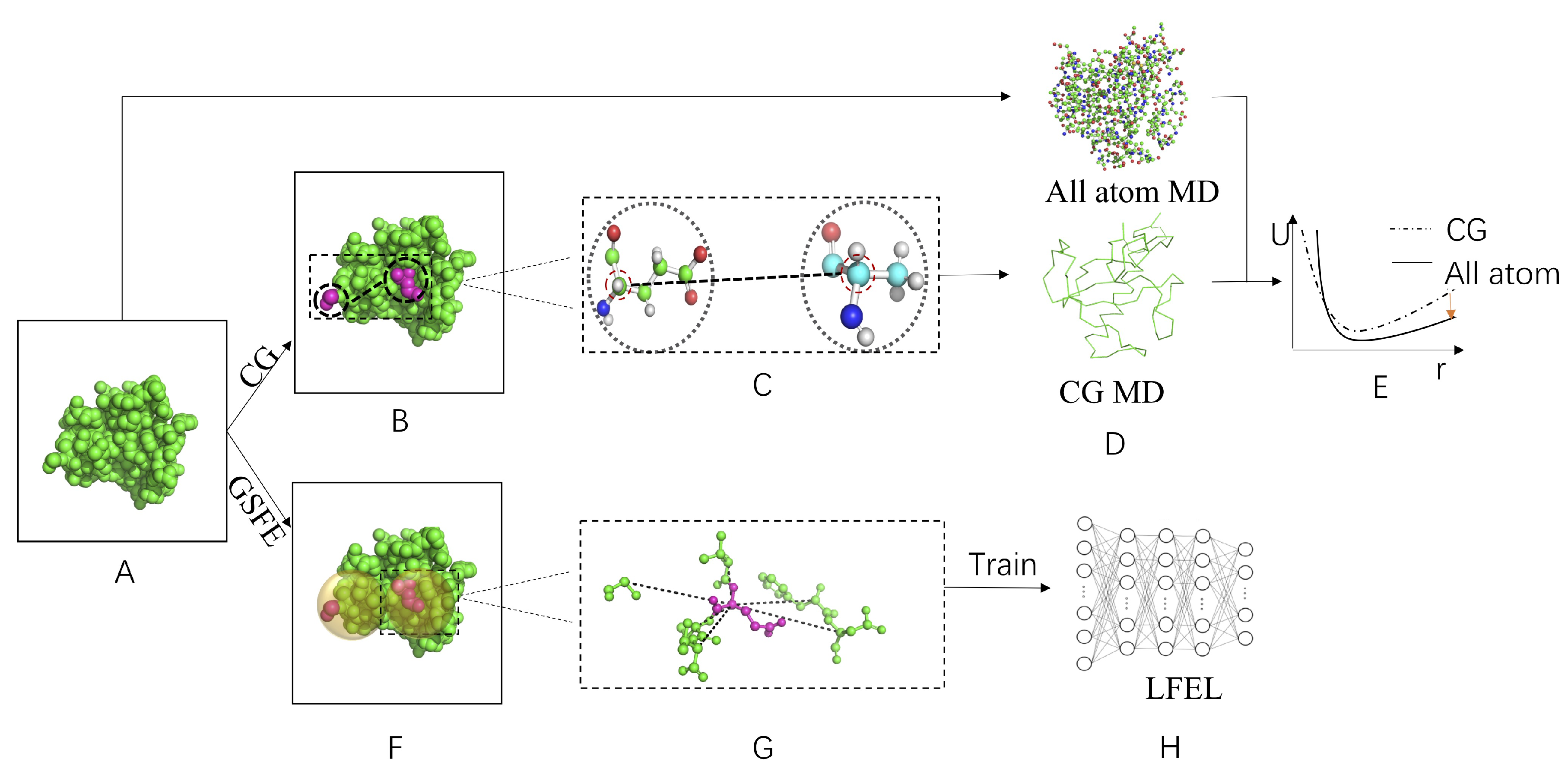
5. The Local Free Energy Landscape Approach
6. More on Connections among CG, ES and LFEL Approach
7. Conclusions and Prospect
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chodera, J.D.; Mobley, D.L.; Shirts, M.R.; Dixon, R.W.; Branson, K.; Pande, V.S. Alchemical free energy methods for drug discovery: Progress and challenges. Curr. Opin. Struct. Biol. 2011, 21, 150–160. [Google Scholar] [CrossRef]
- Dror, R.O.; Dirks, R.M.; Grossman, J.; Xu, H.; Shaw, D.E. Biomolecular Simulation: A Computational Microscope for Molecular Biology. Annu. Rev. Biophys. 2012, 41, 429–452. [Google Scholar] [CrossRef] [PubMed]
- Van der Kamp, M.W.; Mulholland, A.J. Combined Quantum Mechanics/Molecular Mechanics (QM/MM) Methods in Computational Enzymology. Biochemistry 2013, 52, 2708–2728. [Google Scholar] [CrossRef]
- Canchi, D.R.; Garcia, A.E. Cosolvent Effects on Protein Stability. Annu. Rev. Phys. Chem. 2013, 64, 273–293. [Google Scholar] [CrossRef]
- Hansen, N.; van Gunsteren, W.F. Practical Aspects of Free-Energy Calculations: A Review. J. Chem. Theory Comput. 2014, 10, 2632–2647. [Google Scholar] [CrossRef] [PubMed]
- Mobley, D.L.; Gilson, M.K. Predicting Binding Free Energies: Frontiers and Benchmarks. Annu. Rev. Biophys. 2017, 46, 531–558. [Google Scholar] [CrossRef]
- Wang, E.; Sun, H.; Wang, J.; Wang, Z.; Liu, H.; Zhang, J.Z.H.; Hou, T. End-Point Binding Free Energy Calculation with MM/PBSA and MM/GBSA: Strategies and Applications in Drug Design. Chem. Rev. 2019, 119, 9478–9508. [Google Scholar] [CrossRef]
- Enkavi, G.; Javanainen, M.; Kulig, W.; Rog, T.; Vattulainen, I. Multiscale Simulations of Biological Membranes: The Challenge To Understand Biological Phenomena in a Living Substance. Chem. Rev. 2019, 119, 5607–5774. [Google Scholar] [CrossRef]
- Bedrov, D.; Piquemal, J.-P.; Borodin, O.; MacKerell, A.D., Jr.; Roux, B.; Schroeder, C. Molecular Dynamics Simulations of Ionic Liquids and Electrolytes Using Polarizable Force Fields. Chem. Rev. 2019, 119, 7940–7995. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Corradi, V.; Souza, P.C.T.; Ingolfsson, H.I.; Tieleman, D.P.; Sansom, M.S.P. Computational Modeling of Realistic Cell Membranes. Chem. Rev. 2019, 119, 6184–6226. [Google Scholar] [CrossRef] [PubMed]
- Lee, A.C.-L.; Harris, J.L.; Khanna, K.K.; Hong, J.-H. A Comprehensive Review on Current Advances in Peptide Drug Development and Design. Int. J. Mol. Sci. 2019, 20, 2383. [Google Scholar] [CrossRef] [PubMed]
- Kang, L.; Liang, F.; Jiang, X.; Lin, Z.; Chen, C. First-Principles Design and Simulations Promote the Development of Nonlinear Optical Crystals. Accounts Chem. Res. 2020, 53, 209–217. [Google Scholar] [CrossRef] [PubMed]
- Nelson, T.R.; White, A.J.; Bjorgaard, J.A.; Sifain, A.E.; Zhang, Y.; Nebgen, B.; Fernandez-Alberti, S.; Mozyrsky, D.; Roitberg, A.E.; Tretiak, S. Non-adiabatic Excited-State Molecular Dynamics: Theory and Applications for Modeling Photophysics in Extended Molecular Materials. Chem. Rev. 2020, 120, 2215–2287. [Google Scholar] [CrossRef]
- Shaebani, M.R.; Wysocki, A.; Winkler, R.G.; Gompper, G.; Rieger, H. Computational models for active matter. Nat. Rev. Phys. 2020, 2, 181–199. [Google Scholar] [CrossRef]
- Spaggiari, G.; Di Pizio, A.; Cozzini, P. Sweet, umami and bitter taste receptors: State of the art of in silico molecular modeling approaches. Trends Food Sci. Technol. 2020, 96, 21–29. [Google Scholar] [CrossRef]
- Duncan, A.L.; Song, W.; Sansom, M.S.P. Lipid-Dependent Regulation of Ion Channels and G Protein-Coupled Receptors: Insights from Structures and Simulations. Annu. Rev. Pharmacol. Toxicol. 2020, 60, 31–50. [Google Scholar] [CrossRef] [PubMed]
- Rust, J. The New Palgrave Dictionary of Economics; Palgrave Macmillan UK: London, UK, 2016; pp. 1–26. [Google Scholar]
- Sambasivan, R.; Das, S.; Sahu, S.K. A Bayesian perspective of statistical machine learning for big data. Comput. Stat. 2020, 35, 893–930. [Google Scholar] [CrossRef]
- Rudzinski, J.F.; Noid, W.G. Coarse-graining entropy, forces, and structures. J. Chem. Phys. 2011, 135, 214101. [Google Scholar] [CrossRef]
- Marrink, S.J.; Tieleman, D.P. Perspective on the martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. [Google Scholar] [CrossRef]
- Noid, W.G. Perspective: Coarse-grained models for biomolecular systems. J. Chem. Phys. 2013, 139, 090901. [Google Scholar] [CrossRef] [PubMed]
- Saunders, M.G.; Voth, G.A. Coarse-graining methods for computational biology. Annu. Rev. Biophys. 2013, 42, 73–93. [Google Scholar] [CrossRef] [PubMed]
- Ruff, K.M.; Harmon, T.S.; Pappu, R.V. CAMELOT: A machine learning approach for Coarse-grained simulations of aggregation of block-copolymeric protein sequences. J. Chem. Phys. 2015, 143, 1–19. [Google Scholar] [CrossRef]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef]
- Hafner, A.E.; Krausser, J.; Saric, A. Minimal coarse-grained models for molecular self-organisation in biology. Curr. Opin. Struct. Biol. 2019, 58, 43–52. [Google Scholar] [CrossRef] [PubMed]
- Joshi, S.Y.; Deshmukh, S.A. A review of advancements in coarse-grained molecular dynamics simulations. Mol. Simul. 2020, 47, 1–18. [Google Scholar] [CrossRef]
- Gkeka, P.; Stoltz, G.; Barati Farimani, A.; Belkacemi, Z.; Ceriotti, M.; Chodera, J.D.; Lelièvre, T. Machine Learning Force Fields and Coarse-Grained Variables in Molecular Dynamics: Application to Materials and Biological Systems. J. Chem. Theory Comput. 2020, 16, 4757–4775. [Google Scholar] [CrossRef]
- Bernardi, R.C.; Melo, M.C.R.; Schulten, K. Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim. Biophys. Acta Gen. Subj. 2015, 1850, 872–877. [Google Scholar] [CrossRef]
- Mlynsky, V.; Bussi, G. Exploring RNA structure and dynamics through enhanced sampling simulations. Curr. Opin. Struct. Biol. 2018, 49, 63–71. [Google Scholar] [CrossRef]
- Yang, Y.I.; Shao, Q.; Zhang, J.; Yang, L.; Gao, Y.Q. Enhanced sampling in molecular dynamics. J. Chem. Phys. 2019, 151, 070902. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.-H.; Zhang, Z.-C.; Li, G.-H. Advances in Enhanced Sampling Molecular Dynamics Simulations for Biomolecules. Chin. J. Chem. Phys. 2019, 32, 277–286. [Google Scholar] [CrossRef]
- Okamoto, Y. Protein structure predictions by enhanced conformational sampling methods. Biophys. Phys. 2019, 16, 344–366. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Gómez-Bombarelli, R. Coarse-graining auto-encoders for molecular dynamics. NPJ Comput. Mater. 2019, 5, 1–9. [Google Scholar] [CrossRef]
- Lazim, R.; Suh, D.; Choi, S. Advances in Molecular Dynamics Simulations and Enhanced Sampling Methods for the Study of Protein Systems. Int. J. Mol. Sci. 2020, 21, 6339. [Google Scholar] [CrossRef]
- Liao, Q. Computational Approaches for Understanding Dynamical Systems: Protein Folding and Assembly; Progress in Molecular Biology and Translational Science; Strodel, B., Barz, B., Eds.; Academic Press Ltd.: London, UK; Elsevier Science Ltd.: London, UK, 2020; Volume 170, pp. 177–213. [Google Scholar]
- Long, S.; Tian, P. A simple neural network implementation of generalized solvation free energy for assessment of protein structural models. RSC Adv. 2019, 9, 36227–36233. [Google Scholar] [CrossRef]
- Čížek, J. On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods. J. Chem. Phys. 1966, 45, 4256–4266. [Google Scholar] [CrossRef]
- Reyes, A.; Moncada, F.; Charry, J. The any particle molecular orbital approach: A short review of the theory and applications. Int. J. Quantum Chem. 2019, 119, e25705. [Google Scholar] [CrossRef]
- Van Houten, J. A Century of Chemical Dynamics Traced through the Nobel Prizes. 1998: Walter Kohn and John Pople. J. Chem. Educ. 2002, 79, 1297. [Google Scholar] [CrossRef]
- Bensberg, M.; Neugebauer, J. Density functional theory based embedding approaches for transition-metal complexes. Phys. Chem. Chem. Phys. 2020, 22, 26093–26103. [Google Scholar] [CrossRef] [PubMed]
- Kraus, P. Basis Set Extrapolations for Density Functional Theory. J. Chem. Theory Comput. 2020, 16, 5712–5722. [Google Scholar] [CrossRef]
- Morgante, P.; Peverati, R. The devil in the details: A tutorial review on some undervalued aspects of density functional theory calculations. Int. J. Quantum Chem. 2020, 120, e26332. [Google Scholar] [CrossRef]
- Zhang, I.Y.; Xu, X. On the top rung of Jacob’s ladder of density functional theory: Toward resolving the dilemma ofSIEandNCE. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, 11, e1490. [Google Scholar] [CrossRef]
- Mackerell, A.D., Jr. Empirical force fields for biological macromolecules: Overview and issues. J. Comput. Chem. 2004, 25, 1584–1604. [Google Scholar] [CrossRef]
- Kumar, A.; Yoluk, O.; Mackerell, A.D., Jr. FFParam: Standalone package for CHARMM additive and Drude polarizable force field parametrization of small molecules. J. Comput. Chem. 2020, 41, 958–970. [Google Scholar] [CrossRef]
- Oweida, T.J.; Kim, H.S.; Donald, J.M.; Singh, A.; Yingling, Y.G. Assessment of AMBER Force Fields for Simulations of ssDNA. J. Chem. Theory Comput. 2021, 17, 1208–1217. [Google Scholar] [CrossRef]
- Huai, Z.; Shen, Z.; Sun, Z. Binding Thermodynamics and Interaction Patterns of Inhibitor-Major Urinary Protein-I Binding from Extensive Free-Energy Calculations: Benchmarking AMBER Force Fields. J. Chem. Inf. Model. 2021, 61, 284–297. [Google Scholar] [CrossRef]
- Alford, R.F.; Leaver-Fay, A.; Jeliazkov, J.R.; O’Meara, M.J.; DiMaio, F.P.; Park, H.; Gray, J.J. The Rosetta All-Atom Energy Function for Macromolecular Modeling and Design. J. Chem. Theory Comput. 2017, 13, 3031–3048. [Google Scholar] [CrossRef] [PubMed]
- Sasse, A.; de Vries, S.J.; Schindler, C.E.M.; de Beauchêne, I.C.; Zacharias, M. Rapid Design of Knowledge-Based Scoring Potentials for Enrichment of Near-Native Geometries in Protein-Protein Docking. PLoS ONE 2017, 12, e0170625. [Google Scholar] [CrossRef] [PubMed]
- Narykov, O.; Bogatov, D.; Korkin, D. DISPOT: A simple knowledge-based protein domain interaction statistical potential. Bioinformatics 2019, 35, 5374–5378. [Google Scholar] [CrossRef] [PubMed]
- Wang, S. Efficiently Calculating Anharmonic Frequencies of Molecular Vibration by Molecular Dynamics Trajectory Analysis. ACS Omega 2019, 4, 9271–9283. [Google Scholar] [CrossRef]
- Ferreiro, D.U.; Komives, E.A.; Wolynes, P.G. Frustration in biomolecules. Q. Rev. Biophys. 2014, 47, 285–363. [Google Scholar] [CrossRef] [PubMed]
- Sulkowska, J.I. On folding of entangled proteins: Knots, lassos, links and theta-curves. Curr. Opin. Struct. Biol. 2020, 60, 131–141. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Chen, X.; Schafer, N.P.; Clementi, C.; Komives, E.A.; Ferreiro, D.U.; Wolynes, P.G. Surveying biomolecular frustration at atomic resolution. Nat. Commun. 2020, 11, 5944. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Kato, M.; Pisliakov, A.V. Polarizable force fields: History, test cases, and prospects. J. Chem. Theory Comput. 2007, 3, 2034–2045. [Google Scholar] [CrossRef]
- Jing, Z.; Liu, C.; Cheng, S.Y.; Qi, R.; Walker, B.D.; Piquemal, J.-P.; Ren, P. Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications. Annu. Rev. Biophys. 2019, 48, 371–394. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.P.; Chen, J.; Van Voorhis, T. Systematic parametrization of oolarizable force fields from quantum chemistry data. J. Chem. Theory Comput. 2013, 9, 452–460. [Google Scholar] [CrossRef] [PubMed]
- Császár, A.G. Anharmonic molecular force fields. WIREs Comput. Mol. Sci. 2012, 2, 273–289. [Google Scholar] [CrossRef]
- Ulmschneider, J.P.; Ulmschneider, M.B. Molecular Dynamics Simulations Are Redefining Our View of Peptides Interacting with Biological Membranes. Accounts Chem. Res. 2018, 51, 1106–1116. [Google Scholar] [CrossRef]
- Jung, J.; Nishima, W.; Daniels, M.; Bascom, G.; Kobayashi, C.; Adedoyin, A.; Wall, M.; Lappala, A.; Phillips, D.; Fischer, W.; et al. Scaling molecular dynamics beyond 100,000 processor cores for large-scale biophysical simulations. J. Comput. Chem. 2019, 40, 1919–1930. [Google Scholar] [CrossRef]
- Wolf, S.; Lickert, B.; Bray, S.; Stock, G. Multisecond ligand dissociation dynamics from atomistic simulations. Nat. Commun. 2020, 11, 1–8. [Google Scholar] [CrossRef]
- Ferguson, A.L.; Panagiotopoulos, A.Z.; Kevrekidis, I.G.; Debenedetti, P.G. Nonlinear dimensionality reduction in molecular simulation: The diffusion map approach. Chem. Phys. Lett. 2011, 509, 1–11. [Google Scholar] [CrossRef]
- Springer. Rugged Free Energy Landscapes; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Westerlund, A.M.; Delemotte, L. InfleCS: Clustering Free Energy Landscapes with Gaussian Mixtures. J. Chem. Theory Comput. 2019, 15, 6752–6759. [Google Scholar] [CrossRef] [PubMed]
- Dick, T.J.; Madura, J.D. Chapter 5 A Review of the TIP4P, TIP4P-Ew, TIP5P, and TIP5P-E Water Models; Annual Reports in Computational Chemistry; Elsevier: Amsterdam, The Netherlands, 2005; Volume 1, pp. 59–74. [Google Scholar]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [PubMed]
- Van der Spoel, D. Systematic design of biomolecular force fields. Curr. Opin. Struct. Biol. 2021, 67, 18–24. [Google Scholar] [CrossRef] [PubMed]
- Michael, L.; Warshel, A. Computer simulation of protein folding. Nature 1975, 253, 694–698. [Google Scholar]
- Levitt, M. A simplified representation of protein conformations for rapid simulation of protein folding. J. Mol. Biol. 1976, 104, 59–107. [Google Scholar] [CrossRef]
- Field, M.J.; Bash, P.A.; Karplus, M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. J. Comput. Chem. 1990, 11, 700–733. [Google Scholar] [CrossRef]
- Gao, J. Reviews in Computational Chemistry; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2007; pp. 119–185. [Google Scholar]
- Messer, B.M.; Roca, M.; Chu, Z.T.; Vicatos, S.; Kilshtain, A.V.; Warshel, A. Multiscale simulations of protein landscapes: Using coarse-grained models as reference potentials to full explicit models. Proteins Struct. Funct. Bioinform. 2010, 78, 1212–1227. [Google Scholar] [CrossRef]
- Mukherjee, S.; Warshel, A. Realistic simulations of the coupling between the protomotive force and the mechanical rotation of the F0-ATPase. Proc. Natl. Acad. Sci. USA 2012, 109, 14876–14881. [Google Scholar] [CrossRef] [PubMed]
- Jones, L.O.; Mosquera, M.A.; Schatz, G.C.; Ratner, M.A. Embedding Methods for Quantum Chemistry: Applications from Materials to Life Sciences. J. Am. Chem. Soc. 2020, 142, 3281–3295. [Google Scholar] [CrossRef]
- Nochebuena, J.; Naseem-Khan, S.; Cisneros, G.A. Development and application of quantum mechanics/molecular mechanics methods with advanced polarizable potentials. WIREs Comput. Mol. Sci. 2021, e1515. [Google Scholar] [CrossRef]
- Chen, C.; Depa, P.; Sakai, V.G.; Maranas, J.K.; Lynn, J.W.; Peral, I.; Copley, J.R.D. A comparison of united atom, explicit atom, and coarse-grained simulation models for poly(ethylene oxide). J. Chem. Phys. 2006, 124, 234901. [Google Scholar] [CrossRef] [PubMed]
- Potter, T.D.; Walker, M.; Wilson, M.R. Self-assembly and mesophase formation in a non-ionic chromonic liquid crystal: Insights from bottom-up and top-down coarse-grained simulation models. Soft Matter 2020, 16, 9488–9498. [Google Scholar] [CrossRef] [PubMed]
- Tschöp, W.; Kremer, K.; Batoulis, J.; Bürger, T.; Hahn, O. Simulation of polymer melts. I. Coarse-graining procedure for polycarbonates. Acta Polym. 1998, 49, 61–74. [Google Scholar] [CrossRef]
- Español, P.; Warren, P.B. Perspective: Dissipative particle dynamics. J. Chem. Phys. 2017, 146, 150901. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.; Xu, S.; Wan, B.; Xiu, P.; Zhou, X. A novel multiscale scheme to accelerate atomistic simulations of bio-macromolecules by adaptively driving coarse-grained coordinates. J. Chem. Phys. 2020, 152, 114115. [Google Scholar] [CrossRef] [PubMed]
- Perdikari, T.M.; Jovic, N.; Dignon, G.L.; Kim, Y.C.; Fawzi, N.L.; Mittal, J. A coarse-grained model for position-specific effects of post-translational modifications on disordered protein phase separation. Biophys. J. 2021, 120, 1187–1197. [Google Scholar] [CrossRef]
- Elliott, J.A. Novel approaches to multiscale modelling in materials science. Int. Mater. Rev. 2011, 56, 207–225. [Google Scholar] [CrossRef]
- Jankowski, E.; Ellyson, N.; Fothergill, J.W.; Henry, M.M.; Leibowitz, M.H.; Miller, E.D.; Alberts, M.; Chesser, S.; Guevara, J.D.; Jones, C.D.; et al. Perspective on coarse-graining, cognitive load, and materials simulation. Comput. Mater. Sci. 2020, 171, 109129. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Laaksonen, A. Calculation of effective interaction potentials from radial distribution functions: A reverse Monte Carlo approach. Phys. Rev. E 1995, 52, 3730–3737. [Google Scholar] [CrossRef]
- Chiba, S.; Okuno, Y.; Honma, T.; Ikeguchi, M. Force-field parametrization based on radial and energy distribution functions. J. Comput. Chem. 2019, 40, 2577–2585. [Google Scholar] [CrossRef]
- Mironenko, A.V.; Voth, G.A. Density Functional Theory-Based Quantum Mechanics/Coarse-Grained Molecular Mechanics: Theory and Implementation. J. Chem. Theory Comput. 2020, 16, 6329–6342. [Google Scholar] [CrossRef] [PubMed]
- Noid, W.G.; Chu, J.-W.; Ayton, G.S.; Krishna, V.; Izvekov, S.; Voth, G.A.; Das, A.; Andersen, H.C. The multiscale coarse-graining method. I. A rigorous bridge between atomistic and coarse-grained models. J. Chem. Phys. 2008, 128, 244114. [Google Scholar] [CrossRef]
- Noid, W.G.; Liu, P.; Wang, Y.; Chu, J.-W.; Ayton, G.S.; Izvekov, S.; Andersen, H.C.; Voth, G.A. The multiscale coarse-graining method. II. Numerical implementation for coarse-grained molecular models. J. Chem. Phys. 2008, 128, 244115. [Google Scholar] [CrossRef]
- Jin, J.; Han, Y.; Pak, A.J.; Voth, G.A. A new one-site coarse-grained model for water: Bottom-up many-body projected water (BUMPer). I. General theory and model. J. Chem. Phys. 2021, 154, 044104. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Li, Y.; Ren, P.; Zhang, D.; Li, G. Anisotropic Coarse-Grained Model for Proteins Based On Gay–Berne and Electric Multipole Potentials. J. Chem. Theory Comput. 2014, 10, 731–750. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Shen, H.; Zhang, D.; Li, Y.; Wang, H. Coarse-Grained Modeling of Nucleic Acids Using Anisotropic Gay–Berne and Electric Multipole Potentials. J. Chem. Theory Comput. 2016, 12, 676–693. [Google Scholar] [CrossRef]
- Tanis, I.; Rousseau, B.; Soulard, L.; Lemarchand, C.A. Assessment of an anisotropic coarse-grained model for cis-1,4-polybutadiene: A bottom-up approach. Soft Matter 2021, 17, 621–636. [Google Scholar] [CrossRef] [PubMed]
- Dama, J.F.; Sinitskiy, A.V.; McCullagh, M.; Weare, J.; Roux, B.; Dinner, A.R.; Voth, G.A. The Theory of Ultra-Coarse-Graining. 1. General Principles. J. Chem. Theory Comput. 2013, 9, 2466–2480. [Google Scholar] [CrossRef] [PubMed]
- Davtyan, A.; Dama, J.F.; Sinitskiy, A.V.; Voth, G.A. The Theory of Ultra-Coarse-Graining. 2. Numerical Implementation. J. Chem. Theory Comput. 2014, 10, 5265–5275. [Google Scholar] [CrossRef]
- Jin, J.; Voth, G.A. Ultra-Coarse-Grained Models Allow for an Accurate and Transferable Treatment of Interfacial Systems. J. Chem. Theory Comput. 2018, 14, 2180–2197. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, Z.; Zhang, J.Z.; Xia, F. Double-Well Ultra-Coarse-Grained Model to Describe Protein Conformational Transitions. J. Chem. Theory Comput. 2020, 16, 6678–6689. [Google Scholar] [CrossRef]
- Jin, J.; Yu, A.; Voth, G.A. Temperature and Phase Transferable Bottom-up Coarse-Grained Models. J. Chem. Theory Comput. 2020, 16, 6823–6842. [Google Scholar] [CrossRef]
- Ueda, Y.; Taketomi, H.; Gō, N. Studies on protein folding, unfolding, and fluctuations by computer simulation. II. A. Three-dimensional lattice model of lysozyme. Biopolymers 1978, 17, 1531–1548. [Google Scholar] [CrossRef]
- Nymeyer, H.; García, A.E.; Onuchic, J.N. Folding funnels and frustration in off-lattice minimalist protein landscapes. Proc. Natl. Acad. Sci. USA 1998, 95, 5921–5928. [Google Scholar] [CrossRef] [PubMed]
- Tirion, M.M. Large Amplitude Elastic Motions in Proteins from a Single-Parameter, Atomic Analysis. Phys. Rev. Lett. 1996, 77, 1905–1908. [Google Scholar] [CrossRef]
- Atilgan, A.; Durell, S.; Jernigan, R.; Demirel, M.; Keskin, O.; Bahar, I. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 2001, 80, 505–515. [Google Scholar] [CrossRef]
- Togashi, Y.; Flechsig, H. Coarse-Grained Protein Dynamics Studies Using Elastic Network Models. Int. J. Mol. Sci. 2018, 19, 3899. [Google Scholar] [CrossRef] [PubMed]
- Haliloglu, T.; Bahar, I.; Erman, B. Gaussian Dynamics of Folded Proteins. Phys. Rev. Lett. 1997, 79, 3090–3093. [Google Scholar] [CrossRef]
- Wang, S.; Gong, W.; Deng, X.; Liu, Y.; Li, C. Exploring the dynamics of RNA molecules with multiscale Gaussian network model. Chem. Phys. 2020, 538, 110820. [Google Scholar] [CrossRef]
- Yang, L.-W.; Chng, C.-P. Coarse-Grained Models Reveal Functional Dynamics—I. Elastic Network Models—Theories, Comparisons and Perspectives. Bioinform. Biol. Insights 2008, 2, BBI-S460. [Google Scholar] [CrossRef]
- Chng, C.-P.; Yang, L.-W. Coarse-Grained Models Reveal Functional Dynamics—II. Molecular Dynamics Simulation at the Coarse-Grained Level—Theories and Biological Applications. Bioinform. Biol. Insights 2008, 2, BBI-S459. [Google Scholar] [CrossRef] [PubMed]
- Torrie, G.; Valleau, J. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Mezei, M. Adaptive umbrella sampling: Self-consistent determination of the non-Boltzmann bias. J. Comput. Phys. 1987, 68, 237–248. [Google Scholar] [CrossRef]
- Park, S.; Im, W. Theory of adaptive optimization for umbrella sampling. J. Chem. Theory Comput. 2014, 10, 2719–2728. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Shirts, M.R.; Chodera, J.D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. [Google Scholar] [CrossRef] [PubMed]
- Paliwal, H.; Shirts, M.R. Using Multistate Reweighting to Rapidly and E ffi ciently Explore Molecular Simulation Parameters Space for Nonbonded Interactions. J. Chem. Theory Comput. 2013, 9, 4700–4717. [Google Scholar] [CrossRef] [PubMed]
- Darve, E.; Pohorille, A. Calculating free energies using average force. J. Chem. Phys. 2001, 115, 9169–9183. [Google Scholar] [CrossRef]
- Zhao, T.; Fu, H.; Lehievre, T.; Shao, X.; Chipot, C.; Cai, W. The Extended Generalized Adaptive Biasing Force Algorithm for Multidimensional Free-Energy Calculations. J. Chem. Theory Comput. 2017, 13, 1566–1576. [Google Scholar] [CrossRef]
- Miao, M.; Fu, H.; Zhang, H.; Shao, X.; Chipot, C.; Cai, W. Avoiding non-equilibrium effects in adaptive biasing force calculations. Mol. Simul. 2020, 46, 1–5. [Google Scholar] [CrossRef]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
- Raniolo, S.; Limongelli, V. Ligand binding free-energy calculations with funnel metadynamics. Nat. Protoc. 2020, 15, 2837–2866. [Google Scholar] [CrossRef]
- Kondo, T.; Sasaki, T.; Ruiz-Barragan, S.; Ribas-Ariño, J.; Shiga, M. Refined metadynamics through canonical sampling using time-invariant bias potential: A study of polyalcohol dehydration in hot acidic solutions. J. Comput. Chem. 2021, 42, 156–165. [Google Scholar] [CrossRef]
- Comer, J.; Gumbart, J.C.; Hénin, J.; Lelièvre, T.; Pohorille, A.; Chipot, C. The Adaptive Biasing Force Method: Everything You Always Wanted To Know but Were Afraid To Ask. J. Phys. Chem. B 2015, 119, 1129–1151. [Google Scholar] [CrossRef]
- Fu, H.; Shao, X.; Cai, W.; Chipot, C. Taming Rugged Free Energy Landscapes Using an Average Force. Accounts Chem. Res. 2019, 52, 3254–3264. [Google Scholar] [CrossRef]
- Valsson, O.; Tiwary, P.; Parrinello, M. Enhancing Important Fluctuations: Rare Events and Metadynamics from a Conceptual Viewpoint. Annu. Rev. Phys. Chem. 2016, 67, 159–184. [Google Scholar] [CrossRef]
- Bussi, G.; Laio, A. Using metadynamics to explore complex free-energy landscapes. Nat. Rev. Phys. 2020, 2, 200–212. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer: New York, NY, USA; Berlin/Heidelberg, Germany; Hong Kong, China; Milan, Italy; Paris, France; Tokyo, Japan, 2002. [Google Scholar]
- Shan, P.; Zhao, Y.; Wang, Q.; Ying, Y.; Peng, S. Principal component analysis or kernel principal component analysis based joint spectral subspace method for calibration transfer. Spectrochim. Acta Part Mol. Biomol. Spectrosc. 2020, 227, 117653. [Google Scholar] [CrossRef] [PubMed]
- Cox, T.F.; Cox, M.A.A. Multidimensional SCALING; Chapman & HALL/CRC: London, UK, 2000. [Google Scholar]
- Tenenbaum, J.B.; Silva, V.D.; Langford, J.C. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- Roweis, S.T.; Saul, L.K. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Coifman, R.R.; Lafon, S.; Lee, A.B.; Maggioni, M.; Nadler, B.; Warner, F.; Zucker, S.W. Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps. Proc. Natl. Acad. Sci. USA 2005, 102, 7426–7431. [Google Scholar] [CrossRef]
- Coifman, R.R.; Lafon, S.; Lee, A.B.; Maggioni, M.; Nadler, B.; Warner, F.; Zucker, S.W. Geometric diffusions as a tool for harmonic analysis and structure definition of data: Multiscale methods. Proc. Natl. Acad. Sci. USA 2005, 102, 7432–7437. [Google Scholar] [CrossRef]
- Ceriotti, M.; Tribello, G.A.; Parrinello, M. Simplifying the representation of complex free-energy landscapes using sketch-map. Proc. Natl. Acad. Sci. USA 2011, 108, 13023–13028. [Google Scholar] [CrossRef]
- Dellago, C.; Bolhuis, P.G.; Geissler, P.L. Advances in Chemical Physics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003; pp. 1–78, Chapter 1. [Google Scholar]
- Rogal, J.; Bolhuis, P.G. Multiple state transition path sampling. J. Chem. Phys. 2008, 129, 224107. [Google Scholar] [CrossRef] [PubMed]
- Buijsman, P.; Bolhuis, P.G. Transition path sampling for non-equilibrium dynamics without predefined reaction coordinates. J. Chem. Phys. 2020, 152, 044108. [Google Scholar] [CrossRef]
- Yao, Y.; Cui, R.Z.; Bowman, G.R.; Silva, D.-A.; Sun, J.; Huang, X. Hierarchical Nyström methods for constructing Markov state models for conformational dynamics. J. Chem. Phys. 2013, 138, 174106. [Google Scholar] [CrossRef] [PubMed]
- Chodera, J.D.; Noé, F. Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol. 2014, 25, 135–144. [Google Scholar] [CrossRef]
- Husic, B.E.; Pande, V.S. Markov State Models: From an Art to a Science. J. Am. Chem. Soc. 2018, 140, 2386–2396. [Google Scholar] [CrossRef] [PubMed]
- Nagel, D.; Weber, A.; Stock, G. MSMPathfinder: Identification of Pathways in Markov State Models. J. Chem. Theory Comput. 2020, 16, 7874–7882. [Google Scholar] [CrossRef]
- Sadiq, S.K.; Noé, F.; De Fabritiis, G. Kinetic characterization of the critical step in HIV-1 protease maturation. Proc. Natl. Acad. Sci. USA 2012, 109, 20449–20454. [Google Scholar] [CrossRef]
- Kohlhoff, K.J.; Shukla, D.; Lawrenz, M.; Bowman, G.R.; Konerding, D.E.; Belov, D.; Altman, R.B.; Pande, V.S. Cloud-based simulations on Google Exacycle reveal ligand modulation of GPCR activation pathways. Nat. Chem. 2014, 6, 15–21. [Google Scholar] [CrossRef]
- Yang, M.; Tang, Y.; Weng, J.; Liu, Z.; Wang, W. The Role of Calcium in Regulating the Conformational Dynamics of d-Galactose/d-Glucose-Binding Protein Revealed by Markov State Model Analysis. J. Chem. Inf. Model. 2021, 61, 891–900. [Google Scholar] [CrossRef]
- Wu, H.; Noé, F. Variational Approach for Learning Markov Processes from Time Series Data. J. Nonlinear Sci. 2020, 30, 23–66. [Google Scholar] [CrossRef]
- Zuckerman, D.M.; Chong, L.T. Weighted Ensemble Simulation: Review of Methodology, Applications, and Software. Annu. Rev. Biophys. 2017, 46, 43–57. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C. Some comments on Boltzmann-Gibbs statistical mechanics. CHaos Solitons Fractals 1995, 6, 539–559. [Google Scholar] [CrossRef]
- Plastino, A. Why Tsallis’ statistics? Phys. A Stat. Mech. Its Appl. 2004, 344, 608–613. [Google Scholar] [CrossRef]
- Swendsen, R.H.; Wang, J.-S. Replica Monte Carlo Simulation of Spin-Glasses. Phys. Rev. Lett. 1986, 57, 2607–2609. [Google Scholar] [CrossRef]
- Appadurai, R.; Nagesh, J.; Srivastava, A. High resolution ensemble description of metamorphic and intrinsically disordered proteins using an efficient hybrid parallel tempering scheme. Nat. Commun. 2021, 12, 958. [Google Scholar] [CrossRef]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- Peng, C.; Wang, J.; Shi, Y.; Xu, Z.; Zhu, W. Increasing the Sampling Efficiency of Protein Conformational Change by Combining a Modified Replica Exchange Molecular Dynamics and Normal Mode Analysis. J. Chem. Theory Comput. 2021, 17, 13–28. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Landau, D.P. Efficient, Multiple-Range Random Walk Algorithm to Calculate the Density of States. Phys. Rev. Lett. 2001, 86, 2050–2053. [Google Scholar] [CrossRef]
- Gao, Y.Q. An integrate-over-temperature approach for enhanced sampling. J. Chem. Phys. 2008, 128, 064105. [Google Scholar] [CrossRef]
- Yang, L.; Liu, C.-W.; Shao, Q.; Zhang, J.; Gao, Y.Q. From Thermodynamics to Kinetics: Enhanced Sampling of Rare Events. Accounts Chem. Res. 2015, 48, 947–955. [Google Scholar] [CrossRef]
- Yang, Y.I.; Niu, H.; Parrinello, M. Combining Metadynamics and Integrated Tempering Sampling. J. Phys. Chem. Lett. 2018, 9, 6426–6430. [Google Scholar] [CrossRef]
- Behler, J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 2016, 145, 170901. [Google Scholar] [CrossRef]
- Ceriotti, M. Unsupervised machine learning in atomistic simulations, between predictions and understanding. J. Chem. Phys. 2019, 150, 150901. [Google Scholar] [CrossRef] [PubMed]
- Lunghi, A.; Sanvito, S. A unified picture of the covalent bond within quantum-accurate force fields: From organic molecules to metallic complexes’ reactivity. Sci. Adv. 2019, 5, eaaw2210. [Google Scholar] [CrossRef]
- Mueller, T.; Hernandez, A.; Wang, C. Machine learning for interatomic potential models. J. Chem. Phys. 2020, 152, 050902. [Google Scholar] [CrossRef] [PubMed]
- Noé, F.; Tkatchenko, A.; Müller, K.-R.; Clementi, C. Machine Learning for Molecular Simulation. Annu. Rev. Phys. Chem. 2020, 71, 361–390. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, A.; Seko, A.; Tanaka, I. Linearized machine-learning interatomic potentials for non-magnetic elemental metals: Limitation of pairwise descriptors and trend of predictive power. J. Chem. Phys. 2018, 148, 234106. [Google Scholar] [CrossRef]
- Deringer, V.L.; Csányi, G. Machine learning based interatomic potential for amorphous carbon. Phys. Rev. B 2017, 95, 094203. [Google Scholar] [CrossRef]
- Bartók, A.P.; Kermode, J.; Bernstein, N.; Csányi, G. Machine Learning a General-Purpose Interatomic Potential for Silicon. Phys. Rev. X 2018, 8, 041048. [Google Scholar] [CrossRef]
- Slepoy, A.; Peters, M.D.; Thompson, A.P. Searching for globally optimal functional forms for interatomic potentials using genetic programming with parallel tempering. J. Comput. Chem. 2007, 28, 2465–2471. [Google Scholar] [CrossRef]
- Qu, C.; Bowman, J.M. A fragmented, permutationally invariant polynomial approach for potential energy surfaces of large molecules: Application to N-methyl acetamide. J. Chem. Phys. 2019, 150, 141101. [Google Scholar] [CrossRef]
- Chmiela, S.; Sauceda, H.E.; Müller, K.-R. Towards exact molecular dynamics simulations with machine-learned force fields. Nat. Commun. 2018, 9, 3887. [Google Scholar] [CrossRef] [PubMed]
- Artrith, N.; Behler, J. High-dimensional neural network potentials for metal surfaces: A prototype study for copper. Phys. Rev. B 2012, 85, 045439. [Google Scholar] [CrossRef]
- Podryabinkin, E.V.; Tikhonov, E.V.; Shapeev, A.V.; Oganov, A.R. Accelerating crystal structure prediction by machine-learning interatomic potentials with active learning. Phys. Rev. B 2019, 99, 064114. [Google Scholar] [CrossRef]
- Jinnouchi, R.; Karsai, F.; Kresse, G. On-the-fly machine learning force field generation: Application to melting points. Phys. Rev. B 2019, 100, 014105. [Google Scholar] [CrossRef]
- Huan, T.D.; Batra, R.; Chapman, J.; Kim, C.; Chandrasekaran, A.; Ramprasad, R. Iterative-Learning Strategy for the Development of Application-Specific Atomistic Force Fields. J. Phys. Chem. C 2019, 123, 20715–20722. [Google Scholar] [CrossRef]
- Ghasemi, S.A.; Hofstetter, A.; Saha, S.; Goedecker, S. Interatomic potentials for ionic systems with density functional accuracy based on charge densities obtained by a neural network. Phys. Rev. B 2015, 92, 045131. [Google Scholar] [CrossRef]
- Ko, T.W.; Finkler, J.A.; Goedecker, S.; Behler, J. A fourth-generation high-dimensional neural network potential with accurate electrostatics including non-local charge transfer. Nat. Commun. 2021, 12, 398. [Google Scholar] [CrossRef]
- Harris, W.H. Machine Learning Transferable Physics-Based Force Fields using Graph Convolutional Neural Networks. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2020. [Google Scholar]
- Zhang, Y.; Hu, C.; Jiang, B. Embedded Atom Neural Network Potentials: Efficient and Accurate Machine Learning with a Physically Inspired Representation. J. Phys. Chem. Lett. 2019, 10, 4962–4967. [Google Scholar] [CrossRef]
- Chan, H.; Cherukara, M.J.; Narayanan, B.; Loeffler, T.D.; Benmore, C.; Gray, S.K.; Sankaranarayanan, S.K. Machine learning coarse grained models for water. Nat. Commun. 2019, 10, 1–14. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Aluru, N.R. Transfer-Learning-Based Coarse-Graining Method for Simple Fluids: Toward Deep Inverse Liquid-State Theory. J. Phys. Chem. Lett. 2019, 10, 1242–1250. [Google Scholar] [CrossRef]
- Wang, J.; Olsson, S.; Wehmeyer, C.; Pérez, A.; Charron, N.E.; De Fabritiis, G.; Noé, F.; Clementi, C. Machine Learning of Coarse-Grained Molecular Dynamics Force Fields. ACS Cent. Sci. 2019, 5, 755–767. [Google Scholar] [CrossRef]
- Zhang, L.; Han, J.; Wang, H.; Car, R.; Weinan, W.E. DeePCG: Constructing coarse-grained models via deep neural networks. J. Chem. Phys. 2018, 149, 034101. [Google Scholar] [CrossRef]
- Chakraborty, M.; Xu, C.; White, A.D. Encoding and selecting coarse-grain mapping operators with hierarchical graphs. J. Chem. Phys. 2018, 149, 134106. [Google Scholar] [CrossRef]
- Webb, M.A.; Delannoy, J.Y.; De Pablo, J.J. Graph-Based Approach to Systematic Molecular Coarse-Graining. J. Chem. Theory Comput. 2019, 15, 1199–1208. [Google Scholar] [CrossRef] [PubMed]
- Giulini, M.; Menichetti, R.; Shell, M.S.; Potestio, R. An information theory-based approach for optimal model reduction of biomolecules. J. Chem. Theory Comput. 2020, 16, 6795–6813. [Google Scholar] [CrossRef]
- Li, Z.; Wellawatte, G.P.; Chakraborty, M.; Gandhi, H.A.; Xu, C.; White, A.D. Graph neural network based coarse-grained mapping prediction. Chem. Sci. 2020, 11, 9524–9531. [Google Scholar] [CrossRef]
- Durumeric, A.E.; Voth, G.A. Adversarial-residual-coarse-graining: Applying machine learning theory to systematic molecular coarse-graining. J. Chem. Phys. 2019, 151, 124110. [Google Scholar] [CrossRef] [PubMed]
- Khot, A.; Shiring, S.B.; Savoie, B.M. Evidence of information limitations in coarse-grained models. J. Chem. Phys. 2019, 151, 244105. [Google Scholar] [CrossRef]
- Chen, W.; Tan, A.R.; Ferguson, A.L. Collective variable discovery and enhanced sampling using autoencoders: Innovations in network architecture and error function design. J. Chem. Phys. 2018, 149, 072312. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Ferguson, A.L. Molecular enhanced sampling with autoencoders: On-the-fly collective variable discovery and accelerated free energy landscape exploration. J. Comput. Chem. 2018, 39, 2079–2102. [Google Scholar] [CrossRef]
- Wehmeyer, C.; Noé, F. Time-lagged autoencoders: Deep learning of slow collective variables for molecular kinetics. J. Chem. Phys. 2018, 148, 241703. [Google Scholar] [CrossRef]
- Ribeiro, J.M.L.; Bravo, P.; Wang, Y.; Tiwary, P. Reweighted autoencoded variational Bayes for enhanced sampling (RAVE). J. Chem. Phys. 2018, 149, 241703. [Google Scholar] [CrossRef]
- Mardt, A.; Pasquali, L.; Wu, H.; Noé, F. VAMPnets for deep learning of molecular kinetics. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Tian, P. Molecular free energy optimization on a computational graph. RSC Adv. 2020, 11, 12929. [Google Scholar] [CrossRef]
- Khatib, F.; Cooper, S.; Tyka, M.D.; Xu, K.; Makedon, I.; Popović, Z.; Baker, D.; Players, F. Algorithm discovery by protein folding game players. Proc. Natl. Acad. Sci. USA 2011, 108, 18949–18953. [Google Scholar] [CrossRef]
- Feig, M. Computational protein structure refinement: Almost there, yet still so far to go. Wiley Interdiplinary Rev. Comput. Mol. Sci. 2017, 7, e1307. [Google Scholar] [CrossRef]
| Key Words | Number of Publications |
|---|---|
| Molecular dynamics simulation | 241,748 |
| Monte Carlo simulation | 189,550 |
| QM-MM (quantum mechanical—molecular mechanical) simulation | 9907 |
| Dissipative particle dynamics simulation | 3693 |
| Langevin dynamics simulation | 3893 |
| Molecular modeling | 2,072,091 |
| All of the above | 2,243,182 |
| Algorithm | Coarse Graining | Enhanced Sampling | LFEL Approach |
|---|---|---|---|
| Resolution | Lower | In | In |
| Transferable? | Partial | No | Partial |
| Dividing space | Physical | Configurational | Physical |
| Free energy unit | Partially Specified | Specified | Arbitrary |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Tian, P. “Dividing and Conquering” and “Caching” in Molecular Modeling. Int. J. Mol. Sci. 2021, 22, 5053. https://doi.org/10.3390/ijms22095053
Cao X, Tian P. “Dividing and Conquering” and “Caching” in Molecular Modeling. International Journal of Molecular Sciences. 2021; 22(9):5053. https://doi.org/10.3390/ijms22095053
Chicago/Turabian StyleCao, Xiaoyong, and Pu Tian. 2021. "“Dividing and Conquering” and “Caching” in Molecular Modeling" International Journal of Molecular Sciences 22, no. 9: 5053. https://doi.org/10.3390/ijms22095053
APA StyleCao, X., & Tian, P. (2021). “Dividing and Conquering” and “Caching” in Molecular Modeling. International Journal of Molecular Sciences, 22(9), 5053. https://doi.org/10.3390/ijms22095053






