Risk Prediction of Cardiovascular Events by Exploration of Molecular Data with Explainable Artificial Intelligence
Abstract
:1. Introduction
2. Results
2.1. Traditional Risk Scores Based on Clinical and Imaging Data
2.1.1. Predicting the Risk of Incident CVD with Survival Models
2.1.2. Predicting Recurrent Events with Survival Models
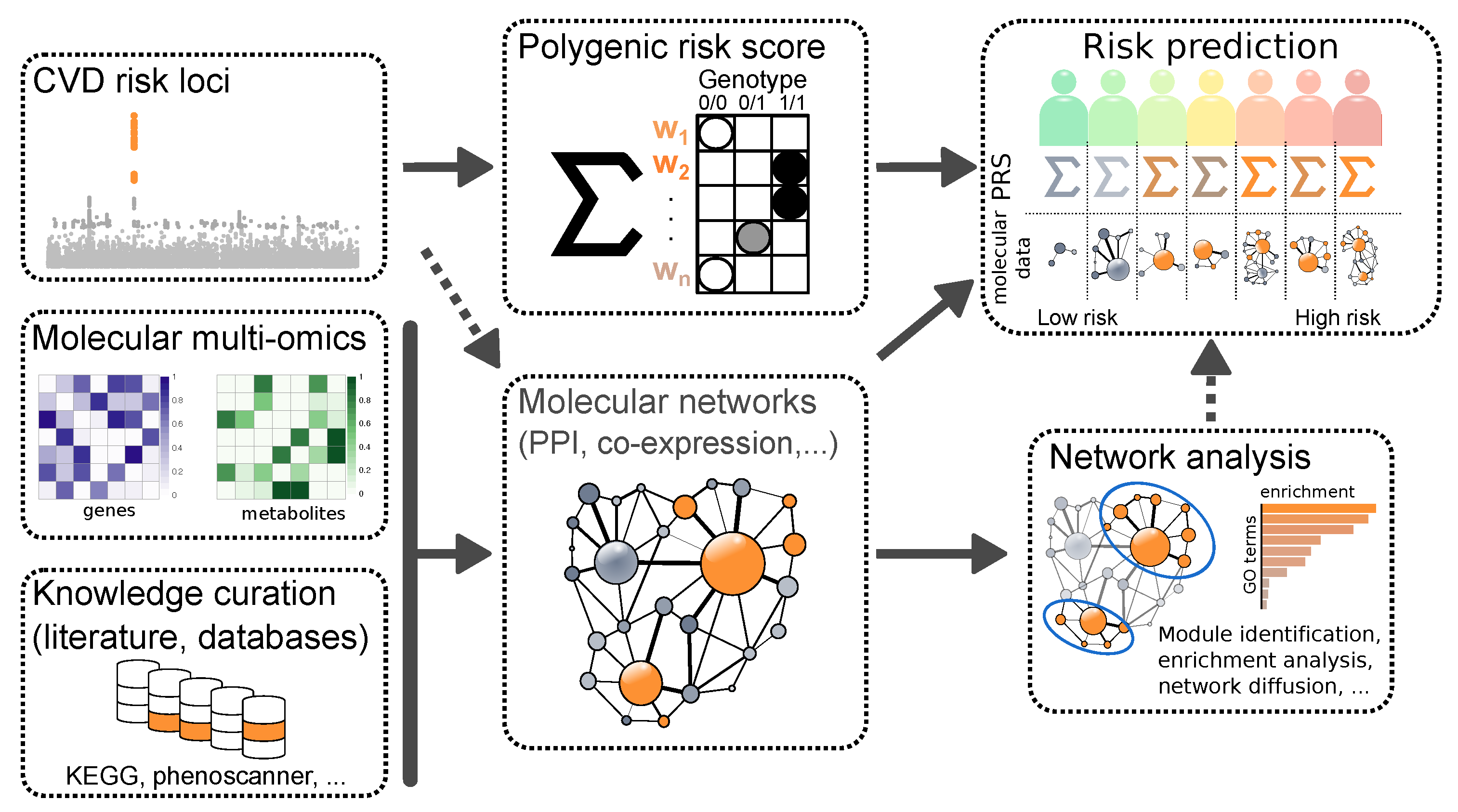
2.2. Molecular Aspects of Risk Prediction of Cardiovascular Events
2.2.1. Understanding CVD and Recurrent Events with Genotyping Data
2.2.2. Integration of (Multi-)Omics Data
2.3. Exploiting Artificial Intelligence for Risk Prediction of Cardiovascular Events
2.3.1. Brief Introduction to AI
2.3.2. Utilizing Clinical and Imaging Data in AI Risk Prediction
2.3.3. Utilizing Molecular Data in AI Models
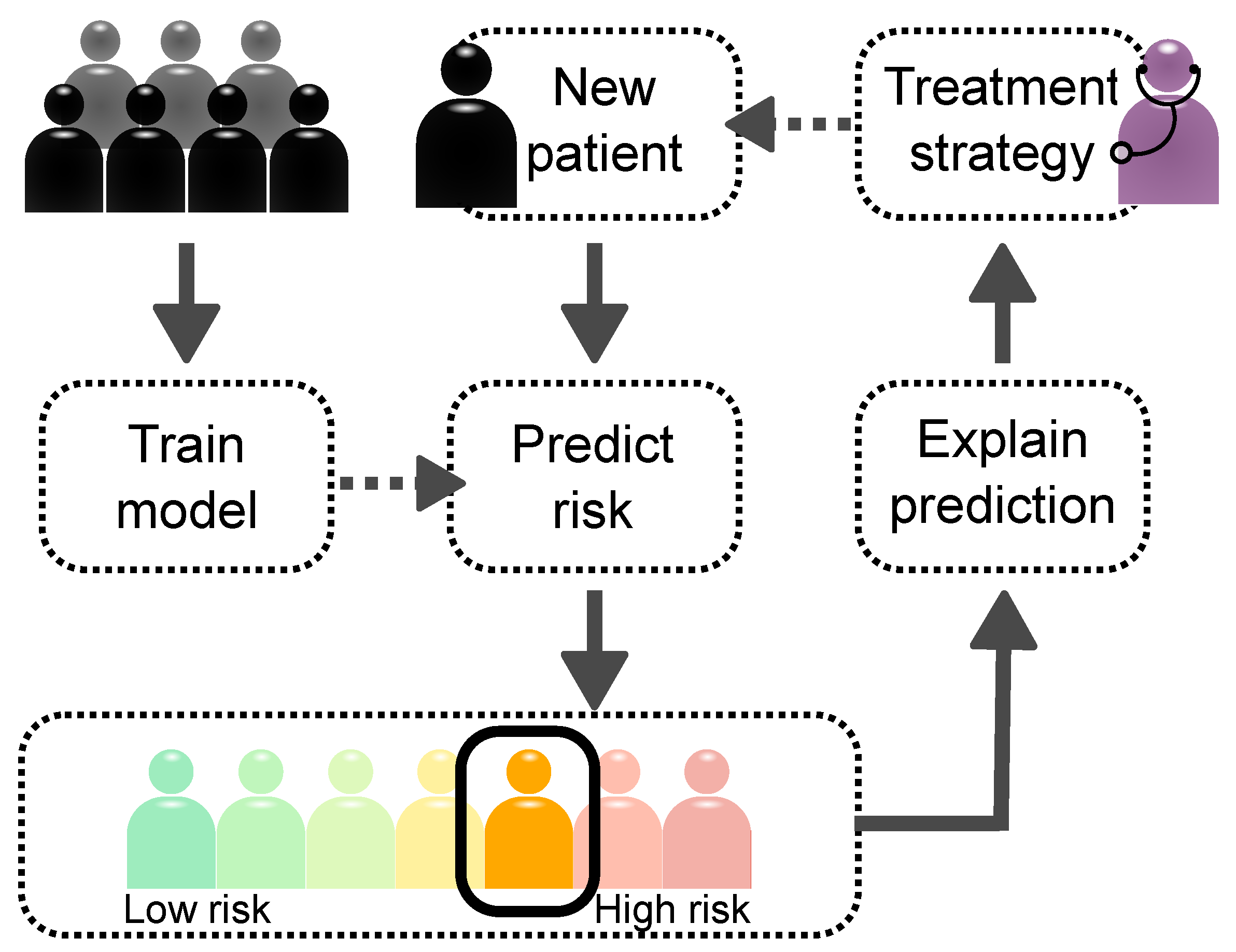
2.4. Explaining Decisions Made by AI Models
2.4.1. Model-Specific Relevance Explanations
2.4.2. Model-Agnostic Relevance Explanations
2.4.3. Clinical Applications of XAI
3. Discussion
Funding
Conflicts of Interest
Abbreviations
| CVD | Cardiovascular disease |
| CAD | Coronary artery disease |
| PAD | Peripheral artery disease |
| CeVD | Cerebrovascular disease |
| MR | magnetic resonance |
| CCTA | Coronary computed tomography angiography |
| GWAS | Genome-wide association studies |
| AI | Artificial intelligence |
| XAI | Explainable artificial intelligence |
| FRS | Framingham risk score |
| SCORE | Systematic COronary Risk Evaluation |
| ACC/AHA | American College of Cardiology/American Heart Association |
| TIMI | Thrombolysis In Myocardial Infarction |
| GRACE | Global Registry of Acute Coronary Events |
| SMART | Secondary Manifestations of ARTerial disease |
| REACH | REduction of Atherothrombosis for Continued Health |
| CONFIRM | COronary CT Angiography EvaluatioN For Clinical Outcomes: |
| An InteRnational Multicenter registry | |
| GENIUS-CHD | Genetics of Subsequent Coronary Heart Disease |
| PRS | Polygenic risk score |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| CNN | Convolutional neural networks |
| XGBoost | eXtreme Gradient Boosting |
References
- Ruan, Y.; Guo, Y.; Zheng, Y.; Huang, Z.; Sun, S.; Kowal, P.; Shi, Y.; Wu, F. Cardiovascular disease (CVD) and associated risk factors among older adults in six low-and middle-income countries: Results from SAGE Wave 1. BMC Public Health 2018, 18, 778. [Google Scholar] [CrossRef] [Green Version]
- Wilson, P.W.F.; D’Agostino Ralph, B.; Levy, D.; Belanger Albert, M.; Silbershatz, H.; Kannel William, B. Prediction of Coronary Heart Disease Using Risk Factor Categories. Circulation 1998, 97, 1837–1847. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Bacquer, D.; Ueda, P.; Reiner, Z.; De Sutter, J.; De Smedt, D.; Lovic, D.; Gotcheva, N.; Fras, Z.; Pogosova, N.; Mirrakhimov, E.; et al. Prediction of recurrent event in patients with coronary heart disease: The EUROASPIRE Risk Model: Results from a prospective study in 27 countries in the WHO European region—The EURObservational Research Programme (EORP) of the European Society of Cardiology (ESC). Eur. J. Prev. Cardiol. 2020, zwaa128. [Google Scholar] [CrossRef]
- Fox, K.A.A.; Dabbous, O.H.; Goldberg, R.J.; Pieper, K.S.; Eagle, K.A.; Werf, F.V.D.; Avezum, A.; Goodman, S.G.; Flather, M.D.; Anderson, F.A.; et al. Prediction of risk of death and myocardial infarction in the six months after presentation with acute coronary syndrome: Prospective multinational observational study (GRACE). BMJ 2006, 333, 1091. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilson, P.W.F.; D’Agostino, R.; Bhatt, D.L.; Eagle, K.; Pencina, M.J.; Smith, S.C.; Alberts, M.J.; Dallongeville, J.; Goto, S.; Hirsch, A.T.; et al. An International Model to Predict Recurrent Cardiovascular Disease. Am. J. Med. 2012, 125, 695–703.e1. [Google Scholar] [CrossRef]
- Dorresteijn, J.A.N.; Visseren, F.L.J.; Wassink, A.M.J.; Gondrie, M.J.A.; Steyerberg, E.W.; Ridker, P.M.; Cook, N.R.; van der Graaf, Y.; SMART Study Group. Development and validation of a prediction rule for recurrent vascular events based on a cohort study of patients with arterial disease: The SMART risk score. Heart 2013, 99, 866–872. [Google Scholar] [CrossRef]
- Fernández-Friera, L.; Fuster, V.; López-Melgar, B.; Oliva, B.; García-Ruiz, J.M.; Mendiguren, J.; Bueno, H.; Pocock, S.; Ibáñez, B.; Fernández-Ortiz, A.; et al. Normal LDL-Cholesterol Levels Are Associated With Subclinical Atherosclerosis in the Absence of Risk Factors. J. Am. Coll. Cardiol. 2017, 70, 2979–2991. [Google Scholar] [CrossRef] [PubMed]
- van’t Klooster, C.C.; van der Graaf, Y.; Nathoe, H.M.; Bots, M.L.; de Borst, G.J.; Visseren, F.L.J.; Leiner, T.; Asselbergs, F.W.; Nathoe, H.M.; de Borst, G.J.; et al. Added value of cardiovascular calcifications for prediction of recurrent cardiovascular events and cardiovascular interventions in patients with established cardiovascular disease. Int. J. Cardiovasc. Imaging 2021, 37, 2051–2061. [Google Scholar] [CrossRef] [PubMed]
- Motwani, M.; Dey, D.; Berman, D.S.; Germano, G.; Achenbach, S.; Al-Mallah, M.H.; Andreini, D.; Budoff, M.J.; Cademartiri, F.; Callister, T.Q.; et al. Machine learning for prediction of all-cause mortality in patients with suspected coronary artery disease: A 5-year multicentre prospective registry analysis. Eur. Heart J. 2017, 38, 500–507. [Google Scholar] [CrossRef] [PubMed]
- Meyer, H.V.; Dawes, T.J.W.; Serrani, M.; Bai, W.; Tokarczuk, P.; Cai, J.; de Marvao, A.; Henry, A.; Lumbers, R.T.; Gierten, J.; et al. Genetic and functional insights into the fractal structure of the heart. Nature 2020, 584, 589–594. [Google Scholar] [CrossRef]
- Bello, G.A.; Dawes, T.J.W.; Duan, J.; Biffi, C.; de Marvao, A.; Howard, L.S.G.E.; Gibbs, J.S.R.; Wilkins, M.R.; Cook, S.A.; Rueckert, D.; et al. Deep-learning cardiac motion analysis for human survival prediction. Nat. Mach. Intell. 2019, 1, 95–104. [Google Scholar] [CrossRef]
- Parker, J.S.; Mullins, M.; Cheang, M.C.; Leung, S.; Voduc, D.; Vickery, T.; Davies, S.; Fauron, C.; He, X.; Hu, Z.; et al. Supervised Risk Predictor of Breast Cancer Based on Intrinsic Subtypes. J. Clin. Oncol. 2009, 27, 1160–1167. [Google Scholar] [CrossRef] [PubMed]
- Visscher, P.M.; Wray, N.R.; Zhang, Q.; Sklar, P.; McCarthy, M.I.; Brown, M.A.; Yang, J. 10 Years of GWAS Discovery: Biology, Function, and Translation. Am. J. Hum. Genet. 2017, 101, 5–22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Z.; Schunkert, H. Genetics of coronary artery disease in the post GWAS era. J. Intern. Med. 2021; 1–13. [Google Scholar] [CrossRef]
- Wünnemann, F.; Sin Lo, K.; Langford-Avelar, A.; Busseuil, D.; Dubé, M.P.; Tardif, J.C.; Lettre, G. Validation of Genome-Wide Polygenic Risk Scores for Coronary Artery Disease in French Canadians. Circ. Genom. Precis. Med. 2019, 12, e002481. [Google Scholar] [CrossRef] [Green Version]
- Khera, A.V.; Chaffin, M.; Aragam, K.G.; Haas, M.E.; Roselli, C.; Choi, S.H.; Natarajan, P.; Lander, E.S.; Lubitz, S.A.; Ellinor, P.T.; et al. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nat. Genet. 2018, 50, 1219–1224. [Google Scholar] [CrossRef]
- Aragam, K.G.; Jiang, T.; Goel, A.; Kanoni, S.; Wolford, B.N.; Weeks, E.M.; Wang, M.; Hindy, G.; Zhou, W.; Grace, C.; et al. Discovery and systematic characterization of risk variants and genes for coronary artery disease in over a million participants. medRxiv 2021. [Google Scholar] [CrossRef]
- Zeng, L.; Moser, S.; Mirza-Schreiber, N.; Lamina, C.; Coassin, S.; Nelson, C.P.; Annilo, T.; Franzén, O.; Kleber, M.E.; Mack, S.; et al. Cis-epistasis at the LPA locus and risk of cardiovascular diseases. Cardiovasc. Res. 2021, cvab136. [Google Scholar] [CrossRef] [PubMed]
- Koyama, S.; Ito, K.; Terao, C.; Akiyama, M.; Horikoshi, M.; Momozawa, Y.; Matsunaga, H.; Ieki, H.; Ozaki, K.; Onouchi, Y.; et al. Population-specific and trans-ancestry genome-wide analyses identify distinct and shared genetic risk loci for coronary artery disease. Nat. Genet. 2020, 52, 1169–1177. [Google Scholar] [CrossRef]
- Gola, D.; Erdmann, J.; Müller-Myhsok, B.; Schunkert, H.; König, I.R. Polygenic risk scores outperform machine learning methods in predicting coronary artery disease status. Genet. Epidemiol. 2020, 44, 125–138. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Canela, M.; Hruby, A.; Clish, C.B.; Liang, L.; Martínez-González, M.A.; Hu, F.B. Comprehensive Metabolomic Profiling and Incident Cardiovascular Disease: A Systematic Review. J. Am. Heart Assoc. 2017, 6, e005705. [Google Scholar] [CrossRef] [Green Version]
- Kessler, T.; Schunkert, H. Coronary Artery Disease Genetics Enlightened by Genome-Wide Association Studies. JACC Basic Transl. Sci. 2021, 6, 610–623. [Google Scholar] [CrossRef]
- Damen, J.A.A.G.; Hooft, L.; Schuit, E.; Debray, T.P.A.; Collins, G.S.; Tzoulaki, I.; Lassale, C.M.; Siontis, G.C.M.; Chiocchia, V.; Roberts, C.; et al. Prediction models for cardiovascular disease risk in the general population: Systematic review. BMJ 2016, 353, i2416. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martin-Isla, C.; Campello, V.M.; Izquierdo, C.; Raisi-Estabragh, Z.; Baessler, B.; Petersen, S.E.; Lekadir, K. Image-Based Cardiac Diagnosis With Machine Learning: A Review. Front. Cardiovasc. Med. 2020, 7, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, S.K.; Greenspan, H.; Davatzikos, C.; Duncan, J.S.; Van Ginneken, B.; Madabhushi, A.; Prince, J.L.; Rueckert, D.; Summers, R.M. A Review of Deep Learning in Medical Imaging: Imaging Traits, Technology Trends, Case Studies with Progress Highlights, and Future Promises. Proc. IEEE 2021, 109, 820–838. [Google Scholar] [CrossRef]
- Mathur, P.; Srivastava, S.; Xu, X.; Mehta, J.L. Artificial Intelligence, Machine Learning, and Cardiovascular Disease. Clin. Med. Insights Cardiol. 2020, 14, 1179546820927404. [Google Scholar] [CrossRef]
- Doran, S.; Arif, M.; Lam, S.; Bayraktar, A.; Turkez, H.; Uhlen, M.; Boren, J.; Mardinoglu, A. Multi-omics approaches for revealing the complexity of cardiovascular disease. Briefings Bioinform. 2021, 22, bbab061. [Google Scholar] [CrossRef]
- Heinig, M. Using Gene Expression to Annotate Cardiovascular GWAS Loci. Front. Cardiovasc. Med. 2018, 5, 59. [Google Scholar] [CrossRef]
- Anderson, K.M.; Wilson, P.W.; Odell, P.M.; Kannel, W.B. An updated coronary risk profile. A statement for health professionals. Circulation 1991, 83, 356–362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Conroy, R.; Pyörälä, K.; Fitzgerald, A.; Sans, S.; Menotti, A.; De Backer, G.; De Bacquer, D.; Ducimetière, P.; Jousilahti, P.; Keil, U.; et al. Estimation of ten-year risk of fatal cardiovascular disease in Europe: The SCORE project. Eur. Heart J. 2003, 24, 987–1003. [Google Scholar] [CrossRef]
- Goff, D.C.; Lloyd-Jones, D.M.; Bennett, G.; Coady, S.; D’Agostino, R.B.; Gibbons, R.; Greenland, P.; Lackland, D.T.; Levy, D.; O’Donnell, C.J.; et al. 2013 ACC/AHA Guideline on the Assessment of Cardiovascular Risk. Circulation 2014, 129, S49–S73. [Google Scholar] [CrossRef] [Green Version]
- Hippisley-Cox, J.; Stables, D.; Pringle, M. QRESEARCH: A new general practice database for research. J. Innov. Health Inform. 2004, 12, 49–50. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, K.; Okamura, T.; Watanabe, M.; Nakai, M.; Takegami, M.; Higashiyama, A.; Kokubo, Y.; Okayama, A.; Miyamoto, Y. Predicting Coronary Heart Disease Using Risk Factor Categories for a Japanese Urban Population, and Comparison with the Framingham Risk Score: The Suita Study. J. Atheroscler. Thromb. 2014, 21, 784–798. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- D’Agostino, R.B.; Vasan Ramachandran, S.; Pencina Michael, J.; Wolf Philip, A.; Cobain, M.; Massaro Joseph, M.; Kannel William, B. General Cardiovascular Risk Profile for Use in Primary Care. Circulation 2008, 117, 743–753. [Google Scholar] [CrossRef] [Green Version]
- Hippisley-Cox, J.; Coupland, C.; Vinogradova, Y.; Robson, J.; May, M.; Brindle, P. Derivation and validation of QRISK, a new cardiovascular disease risk score for the United Kingdom: Prospective open cohort study. BMJ 2007, 335, 136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Investigators, G. Rationale and design of the GRACE (Global Registry of Acute Coronary Events) Project: A multinational registry of patients hospitalized with acute coronary syndromes. Am. Heart J. 2001, 141, 190–199. [Google Scholar] [CrossRef]
- Ohman, E.M.; Bhatt, D.L.; Steg, P.G.; Goto, S.; Hirsch, A.T.; Liau, C.S.; Mas, J.L.; Richard, A.J.; Röther, J.; Wilson, P.W.F.; et al. The REduction of Atherothrombosis for Continued Health (REACH) Registry: An international, prospective, observational investigation in subjects at risk for atherothrombotic events-study design. Am. Heart J. 2006, 151, 786.e1–786.e10. [Google Scholar] [CrossRef] [PubMed]
- Kotseva, K. The EUROASPIRE surveys: Lessons learned in cardiovascular disease prevention. Cardiovasc. Diagn. Ther. 2017, 7, 633–639. [Google Scholar] [CrossRef] [Green Version]
- Bohula, E.A.; Bonaca, M.P.; Braunwald, E.; Aylward, P.E.; Corbalan, R.; De Ferrari, G.M.; He, P.; Lewis, B.S.; Merlini, P.A.; Murphy, S.A.; et al. Atherothrombotic Risk Stratification and the Efficacy and Safety of Vorapaxar in Patients With Stable Ischemic Heart Disease and Previous Myocardial Infarction. Circulation 2016, 134, 304–313. [Google Scholar] [CrossRef]
- Min, J.K.; Dunning, A.; Lin, F.Y.; Achenbach, S.; Al-Mallah, M.H.; Berman, D.S.; Budoff, M.J.; Cademartiri, F.; Callister, T.Q.; Chang, H.J.; et al. Rationale and design of the CONFIRM (COronary CT Angiography EvaluatioN For Clinical Outcomes: An InteRnational Multicenter) Registry. J. Cardiovasc. Comput. Tomogr. 2011, 5, 84–92. [Google Scholar] [CrossRef]
- Simons, P.C.; Algra, A.; van de Laak, M.F.; Grobbee, D.E.; van der Graaf, Y. Second manifestations of ARTerial disease (SMART) study: Rationale and design. Eur. J. Epidemiol. 1999, 15, 773–781. [Google Scholar] [CrossRef]
- Patel, R.S.; Tragante, V.; Schmidt, A.F.; McCubrey, R.O.; Holmes, M.V.; Howe Laurence, J.; Kenan, D.; Axel, Å.; Karin, L.; Virani Salim, S.; et al. Subsequent Event Risk in Individuals with Established Coronary Heart Disease. Circ. Genom. Precis. Med. 2019, 12, e002470. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hadamitzky, M.; Achenbach, S.; Al-Mallah, M.; Berman, D.; Budoff, M.; Cademartiri, F.; Callister, T.; Chang, H.J.; Cheng, V.; Chinnaiyan, K.; et al. Optimized Prognostic Score for Coronary Computed Tomographic Angiography: Results From the CONFIRM Registry (COronary CT Angiography EvaluatioN For Clinical Outcomes: An InteRnational Multicenter Registry). J. Am. Coll. Cardiol. 2013, 62, 468–476. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alaa, A.M.; Bolton, T.; Angelantonio, E.D.; Rudd, J.H.F.; van der Schaar, M. Cardiovascular disease risk prediction using automated machine learning: A prospective study of 423,604 UK Biobank participants. PLoS ONE 2019, 14, e0213653. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Woodward, M.; Brindle, P.; Tunstall-Pedoe, H.; SIGN Group on Risk Estimation. Adding social deprivation and family history to cardiovascular risk assessment: The ASSIGN score from the Scottish Heart Health Extended Cohort (SHHEC). Heart 2007, 93, 172–176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hippisley-Cox, J.; Coupland, C.; Brindle, P. Development and validation of QRISK3 risk prediction algorithms to estimate future risk of cardiovascular disease: Prospective cohort study. BMJ 2017, 357, j2099. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Collins, G.S.; Altman, D.G. Predicting the 10 year risk of cardiovascular disease in the United Kingdom: Independent and external validation of an updated version of QRISK2. BMJ 2012, 344, e4181. [Google Scholar] [CrossRef] [Green Version]
- Cardiovascular Disease: Risk Assessment and Reduction, Including Lipid Modification. National Institute for Health and Care Excellence. 2016. Available online: https://www.nice.org.uk/guidance/cg181 (accessed on 23 July 2021).
- Collet, J.P.; Thiele, H.; Barbato, E.; Barthélémy, O.; Bauersachs, J.; Bhatt, D.L.; Dendale, P.; Dorobantu, M.; Edvardsen, T.; Folliguet, T.; et al. 2020 ESC Guidelines for the management of acute coronary syndromes in patients presenting without persistent ST-segment elevation: The Task Force for the management of acute coronary syndromes in patients presenting without persistent ST-segment elevation of the European Society of Cardiology (ESC). Eur. Heart J. 2021, 42, 1289–1367. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; FitzGerald, G.; Goldberg, R.J.; Gore, J.; McManus, R.H.; Awad, H.; Waring, M.E.; Allison, J.; Saczynski, J.S.; Kiefe, C.I.; et al. Performance of the GRACE Risk Score 2.0 Simplified Algorithm for Predicting 1-year Death Following Hospitalization for an Acute Coronary Syndrome in a Contemporary Multiracial Cohort. Am. J. Cardiol. 2016, 118, 1105–1110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- van Rosendael, A.R.; Maliakal, G.; Kolli, K.K.; Beecy, A.; Al’Aref, S.J.; Dwivedi, A.; Singh, G.; Panday, M.; Kumar, A.; Ma, X.; et al. Maximization of the usage of coronary CTA derived plaque information using a machine learning based algorithm to improve risk stratification; insights from the CONFIRM registry. J. Cardiovasc. Comput. Tomogr. 2018, 12, 204–209. [Google Scholar] [CrossRef]
- Al-Shamsi, S.; Govender, R.D. Validation of the REduction of Atherothrombosis for Continued Health (REACH) prediction model for recurrent cardiovascular disease among United Arab Emirates Nationals. BMC Res. Notes 2020, 13, 484. [Google Scholar] [CrossRef]
- Rossello, X.; Dorresteijn, J.A.; Janssen, A.; Lambrinou, E.; Scherrenberg, M.; Bonnefoy-Cudraz, E.; Cobain, M.; Piepoli, M.F.; Visseren, F.L.; Dendale, P.; et al. Risk prediction tools in cardiovascular disease prevention: A report from the ESC Prevention of CVD Programme led by the European Association of Preventive Cardiology (EAPC) in collaboration with the Acute Cardiovascular Care Association (ACCA) and the Association of Cardiovascular Nursing and Allied Professions (ACNAP). Eur. J. Prev. Cardiol. 2019, 26, 1534–1544. [Google Scholar] [CrossRef] [PubMed]
- van’t Klooster, C.C.; Bhatt, D.L.; Steg, P.G.; Massaro, J.M.; Dorresteijn, J.A.N.; Westerink, J.; Ruigrok, Y.M.; de Borst, G.J.; Asselbergs, F.W.; van der Graaf, Y.; et al. Predicting 10-year risk of recurrent cardiovascular events andcardiovascular interventions in patients with established cardiovascular disease: Results from UCC-SMART and REACH. Int. J. Cardiol. 2021, 325, 140–148. [Google Scholar] [CrossRef] [PubMed]
- Inouye, M.; Abraham, G.; Nelson, C.P.; Wood, A.M.; Sweeting, M.J.; Dudbridge, F.; Lai, F.Y.; Kaptoge, S.; Brozynska, M.; Wang, T.; et al. Genomic Risk Prediction of Coronary Artery Disease in 480,000 Adults. J. Am. Coll. Cardiol. 2018, 72, 1883–1893. [Google Scholar] [CrossRef] [PubMed]
- Oemrawsingh, R.M.; Cheng, J.M.; Akkerhuis, K.M.; Kardys, I.; Degertekin, M.; van Geuns, R.J.; Daemen, J.; Boersma, E.; Serruys, P.W.; van Domburg, R.T. High-sensitivity C-reactive protein predicts 10-year cardiovascular outcome after percutaneous coronary intervention. EuroIntervention 2016, 12, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Goncalves, I.; Bengtsson, E.; Colhoun, H.M.; Shore, A.C.; Palombo, C.; Natali, A.; Edsfeldt, A.; Duner, P.; Fredrikson, G.N.; Björkbacka, H.; et al. Elevated Plasma Levels of MMP-12 Are Associated with Atherosclerotic Burden and Symptomatic Cardiovascular Disease in Subjects With Type 2 Diabetes. Arterioscler. Thromb. Vasc. Biol. 2015, 35, 1723–1731. [Google Scholar] [CrossRef] [Green Version]
- Eggers, K.M.; Kempf, T.; Larsson, A.; Lindahl, B.; Venge, P.; Wallentin, L.; Wollert, K.C.; Lind, L. Evaluation of Temporal Changes in Cardiovascular Biomarker Concentrations Improves Risk Prediction in an Elderly Population from the Community. Clin. Chem. 2016, 62, 485–493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rezaee, M.; Putrenko, I.; Takeh, A.; Ganna, A.; Ingelsson, E. Development and validation of risk prediction models for multiple cardiovascular diseases and Type 2 diabetes. PLoS ONE 2020, 15, e0235758. [Google Scholar] [CrossRef] [PubMed]
- Khera, A.V.; Kathiresan, S. Genetics of coronary artery disease: Discovery, biology and clinical translation. Nat. Rev. Genet. 2017, 18, 331–344. [Google Scholar] [CrossRef]
- Hughes, M.F.; Saarela, O.; Stritzke, J.; Kee, F.; Silander, K.; Klopp, N.; Kontto, J.; Karvanen, J.; Willenborg, C.; Salomaa, V.; et al. Genetic Markers Enhance Coronary Risk Prediction in Men: The MORGAM Prospective Cohorts. PLoS ONE 2012, 7, e40922. [Google Scholar] [CrossRef] [Green Version]
- Mega, J.L.; Stitziel, N.O.; Smith, J.G.; Chasman, D.I.; Caulfield, M.J.; Devlin, J.J.; Nordio, F.; Hyde, C.L.; Cannon, C.P.; Sacks, F.M.; et al. Genetic risk, coronary heart disease events, and the clinical benefit of statin therapy: An analysis of primary and secondary prevention trials. Lancet 2015, 385, 2264–2271. [Google Scholar] [CrossRef] [Green Version]
- Schunkert, H.; Samani, N.J. Statin treatment: Can genetics sharpen the focus? Lancet 2015, 385, 2227–2229. [Google Scholar] [CrossRef]
- Hall, K.T.; Kessler, T.; Buring, J.E.; Passow, D.; Sesso, H.D.; Zee, R.Y.L.; Ridker, P.M.; Chasman, D.I.; Schunkert, H. Genetic variation at the coronary artery disease risk locus GUCY1A3 modifies cardiovascular disease prevention effects of aspirin. Eur. Heart J. 2019, 40, 3385–3392. [Google Scholar] [CrossRef]
- Marston, N.A.; Kamanu, F.K.; Nordio, F.; Gurmu, Y.; Roselli, C.; Sever, P.S.; Pedersen, T.R.; Keech, A.C.; Wang, H.; Lira Pineda, A.; et al. Predicting Benefit From Evolocumab Therapy in Patients With Atherosclerotic Disease Using a Genetic Risk Score. Circulation 2020, 141, 616–623. [Google Scholar] [CrossRef]
- Damask, A.; Steg, P.G.; Schwartz, G.G.; Szarek, M.; Hagström, E.; Badimon, L.; Chapman, M.J.; Boileau, C.; Tsimikas, S.; Ginsberg, H.N.; et al. Patients With High Genome-Wide Polygenic Risk Scores for Coronary Artery Disease May Receive Greater Clinical Benefit From Alirocumab Treatment in the ODYSSEY OUTCOMES Trial. Circulation 2020, 141, 624–636. [Google Scholar] [CrossRef]
- Ehret, G.B.; Ferreira, T.; Chasman, D.I.; Jackson, A.U.; Schmidt, E.M.; Johnson, T.; Thorleifsson, G.; Luan, J.; Donnelly, L.A.; Kanoni, S.; et al. The genetics of blood pressure regulation and its target organs from association studies in 342,415 individuals. Nat. Genet. 2016, 48, 1171–1184. [Google Scholar] [CrossRef]
- Liu, H.H.; Cao, Y.X.; Jin, J.L.; Zhang, H.W.; Hua, Q.; Li, Y.F.; Guo, Y.L.; Zhu, C.G.; Wu, N.Q.; Gao, Y.; et al. Association of lipoprotein(a) levels with recurrent events in patients with coronary artery disease. Heart 2020, 106, 1228–1235. [Google Scholar] [CrossRef]
- Hilvo, M.; Meikle, P.J.; Pedersen, E.R.; Tell, G.S.; Dhar, I.; Brenner, H.; Schöttker, B.; Lääperi, M.; Kauhanen, D.; Koistinen, K.M.; et al. Development and validation of a ceramide- and phospholipid-based cardiovascular risk estimation score for coronary artery disease patients. Eur. Heart J. 2020, 41, 371–380. [Google Scholar] [CrossRef] [Green Version]
- Laaksonen, R.; Ekroos, K.; Sysi-Aho, M.; Hilvo, M.; Vihervaara, T.; Kauhanen, D.; Suoniemi, M.; Hurme, R.; März, W.; Scharnagl, H.; et al. S Plasma ceramides predict cardiovascular death in patients with stable coronary artery disease and acute coronary syndromes beyond LDL-cholesterol. Eur. Heart J. 2016, 37, 1967–1976. [Google Scholar] [CrossRef] [PubMed]
- Patel, R.S.; Schmidt, A.F.; Tragante, V.; McCubrey, R.O.; Holmes, M.V.; Howe Laurence, J.; Kenan, D.; Axel, Å.; Karin, L.; Virani Salim, S.; et al. Association of Chromosome 9p21 With Subsequent Coronary Heart Disease Events. Circ. Genom. Precis. Med. 2019, 12, e002471. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahmoodi, B.K.; Tragante, V.; Kleber Marcus, E.; Holmes, M.V.; Schmidt, A.F.; McCubrey Raymond, O.; Howe Laurence, J.; Kenan, D.; Hooman, A.; Baranova Ekaterina, V.; et al. Association of Factor V Leiden With Subsequent Atherothrombotic Events. Circulation 2020, 142, 546–555. [Google Scholar] [CrossRef] [PubMed]
- Helgadottir, A.; Thorleifsson, G.; Manolescu, A.; Gretarsdottir, S.; Blondal, T.; Jonasdottir, A.; Jonasdottir, A.; Sigurdsson, A.; Baker, A.; Palsson, A.; et al. A Common Variant on Chromosome 9p21 Affects the Risk of Myocardial Infarction. Science 2007, 316, 1491–1493. [Google Scholar] [CrossRef]
- Talukdar, H.A.; Asl, H.F.; Jain, R.K.; Ermel, R.; Ruusalepp, A.; Franzén, O.; Kidd, B.A.; Readhead, B.; Giannarelli, C.; Kovacic, J.C.; et al. Cross-Tissue Regulatory Gene Networks in Coronary Artery Disease. Cell Syst. 2016, 2, 196–208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lempiäinen, H.; Brænne, I.; Michoel, T.; Tragante, V.; Vilne, B.; Webb, T.R.; Kyriakou, T.; Eichner, J.; Zeng, L.; Willenborg, C.; et al. Network analysis of coronary artery disease risk genes elucidates disease mechanisms and druggable targets. Sci. Rep. 2018, 8, 3434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Foroughi Asl, H.; Talukdar, H.A.; Kindt, A.S.; Jain, R.K.; Ermel, R.; Ruusalepp, A.; Nguyen, K.D.H.; Dobrin, R.; Reilly, D.F.; Schunkert, H.; et al. Expression Quantitative Trait Loci Acting Across Multiple Tissues Are Enriched in Inherited Risk for Coronary Artery Disease. Circ. Cardiovasc. Genet. 2015, 8, 305–315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, L.; Pennells, L.; Kaptoge, S.; Nelson, C.P.; Ritchie, S.C.; Abraham, G.; Arnold, M.; Bell, S.; Bolton, T.; Burgess, S.; et al. Polygenic risk scores in cardiovascular risk prediction: A cohort study and modelling analyses. PLoS Med. 2021, 18, e1003498. [Google Scholar] [CrossRef]
- Levin, M.G.; Rader, D.J. Polygenic Risk Scores and Coronary Artery Disease. Circulation 2020, 141, 637–640. [Google Scholar] [CrossRef]
- Howe, L.J.; Dudbridge, F.; Schmidt, A.F.; Finan, C.; Denaxas, S.; Asselbergs, F.W.; Hingorani, A.D.; Patel, R.S. Polygenic risk scores for coronary artery disease and subsequent event risk amongst established cases. Hum. Mol. Genet. 2020, 29, 1388–1395. [Google Scholar] [CrossRef]
- Qian, J.; Tanigawa, Y.; Du, W.; Aguirre, M.; Chang, C.; Tibshirani, R.; Rivas, M.A.; Hastie, T. A fast and scalable framework for large-scale and ultrahigh-dimensional sparse regression with application to the UK Biobank. PLoS Genet. 2020, 16, e1009141. [Google Scholar] [CrossRef] [PubMed]
- Bycroft, C.; Freeman, C.; Petkova, D.; Band, G.; Elliott, L.T.; Sharp, K.; Motyer, A.; Vukcevic, D.; Delaneau, O.; O’Connell, J.; et al. The UK Biobank resource with deep phenotyping and genomic data. Nature 2018, 562, 203–209. [Google Scholar] [CrossRef] [Green Version]
- Elliott, J.; Bodinier, B.; Bond, T.A.; Chadeau-Hyam, M.; Evangelou, E.; Moons, K.G.M.; Dehghan, A.; Muller, D.C.; Elliott, P.; Tzoulaki, I. Predictive Accuracy of a Polygenic Risk Score-Enhanced Prediction Model vs. a Clinical Risk Score for Coronary Artery Disease. J. Am. Med. Assoc. 2020, 323, 636–645. [Google Scholar] [CrossRef]
- Bauer, A.; Zierer, A.; Gieger, C.; Büyüközkan, M.; Müller-Nurasyid, M.; Grallert, H.; Meisinger, C.; Strauch, K.; Prokisch, H.; Roden, M.; et al. Comparison of genetic risk prediction models to improve prediction of coronary heart disease in two large cohorts of the MONICA/KORA study. Genet. Epidemiol. 2021, 45, 633–650. [Google Scholar] [CrossRef]
- Weijmans, M.; de Bakker, P.I.W.; van der Graaf, Y.; Asselbergs, F.W.; Algra, A.; de Borst, G.J.; Spiering, W.; Visseren, F.L.J. Incremental value of a genetic risk score for the prediction of new vascular events in patients with clinically manifest vascular disease. Atherosclerosis 2015, 239, 451–458. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Zheng, Q.; Han, Y.; Qiao, S.; Chen, J.; Yuan, Z.; Yu, B.; Ge, L.; Jia, J.; Gong, Y.; et al. Genetic predisposition to coronary artery disease is predictive of recurrent events: A Chinese prospective cohort study. Hum. Mol. Genet. 2020, 29, 1044–1053. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, M.; Probst, P.; Hornung, R.; Jurinovic, V.; Boulesteix, A.L. Large-scale benchmark study of survival prediction methods using multi-omics data. Briefings Bioinform. 2021, 22, bbaa167. [Google Scholar] [CrossRef] [PubMed]
- Blanco-Colio, L.M.; Mendez-Barbero, N.; Pello Lazaro, A.M.; Acena, A.; Tarin, N.; Cristobal, C.; Martinez-Milla, J.; Gonzalez-Lorenzo, O.; Martin-Ventura, J.L.; Huelmos, A.; et al. MCP-1 Predicts Recurrent Cardiovascular Events in Patients with Persistent Inflammation. J. Clin. Med. 2021, 10, 1137. [Google Scholar] [CrossRef]
- Tunon, J.; Blanco-Colio, L.; Cristóbal, C.; Tarín, N.; Higueras, J.; Huelmos, A.; Alonso, J.; Egido, J.; Asensio, D.; Lorenzo, O.; et al. Usefulness of a combination of monocyte chemoattractant protein-1, galectin-3, and N-terminal probrain natriuretic peptide to predict cardiovascular events in patients with coronary artery disease. Am. J. Cardiol. 2014, 113, 434–440. [Google Scholar] [CrossRef]
- Nguyen, N.D.; Wang, D. Multiview learning for understanding functional multiomics. PLoS Comput. Biol. 2020, 16, e1007677. [Google Scholar] [CrossRef]
- Miller, C.L.; Pjanic, M.; Wang, T.; Nguyen, T.; Cohain, A.; Lee, J.D.; Perisic, L.; Hedin, U.; Kundu, R.K.; Majmudar, D.; et al. Integrative functional genomics identifies regulatory mechanisms at coronary artery disease loci. Nat. Commun. 2016, 7, 12092. [Google Scholar] [CrossRef]
- Barbeira, A.N.; Bonazzola, R.; Gamazon, E.R.; Liang, Y.; Park, Y.; Kim-Hellmuth, S.; Wang, G.; Jiang, Z.; Zhou, D.; Hormozdiari, F.; et al. Exploiting the GTEx resources to decipher the mechanisms at GWAS loci. Genome Biol. 2021, 22, 49. [Google Scholar] [CrossRef]
- Huan, T.; Zhang, B.; Wang, Z.; Joehanes, R.; Zhu, J.; Johnson, A.D.; Ying, S.; Munson, P.J.; Raghavachari, N.; Wang, R.; et al. A Systems Biology Framework Identifies Molecular Underpinnings of Coronary Heart Disease. Arterioscler. Thromb. Vasc. Biol. 2013, 33, 1427–1434. [Google Scholar] [CrossRef] [Green Version]
- Heinig, M.; Adriaens, M.E.; Schafer, S.; van Deutekom, H.W.M.; Lodder, E.M.; Ware, J.S.; Schneider, V.; Felkin, L.E.; Creemers, E.E.; Meder, B.; et al. Natural genetic variation of the cardiac transcriptome in non-diseased donors and patients with dilated cardiomyopathy. Genome Biol. 2017, 18, 170. [Google Scholar] [CrossRef]
- Gene Ontology Consortium. Gene Ontology Consortium: Going forward. Nucleic Acids Res. 2015, 43, D1049–D1056. [Google Scholar] [CrossRef]
- Kanehisa, M.; Goto, S. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef]
- Yao, F.; Zhang, K.; Zhang, Y.; Guo, Y.; Li, A.; Xiao, S.; Liu, Q.; Shen, L.; Ni, J. Identification of Blood Biomarkers for Alzheimer’s Disease Through Computational Prediction and Experimental Validation. Front. Neurol. 2019, 9, 1158. [Google Scholar] [CrossRef]
- Kanuri, S.H.; Ipe, J.; Kassab, K.; Gao, H.; Liu, Y.; Skaar, T.C.; Kreutz, R.P. Next generation MicroRNA sequencing to identify coronary artery disease patients at risk of recurrent myocardial infarction. Atherosclerosis 2018, 278, 232–239. [Google Scholar] [CrossRef]
- Ghatge, M.; Sharma, A.; Maity, S.; Kakkar, V.V.; Vangala, R.K. Danger-recognizing proteins, beta-defensin-128 and histatin-3, as potential biomarkers of recurrent coronary events. Int. J. Mol. Med. 2017, 40, 531–538. [Google Scholar] [CrossRef]
- Seifert, S.; Gundlach, S.; Junge, O.; Szymczak, S. Integrating biological knowledge and gene expression data using pathway-guided random forests: A benchmarking study. Bioinformatics 2020, 36, 4301–4308. [Google Scholar] [CrossRef] [PubMed]
- Nazarieh, M.; Rajula, H.S.R.; Helms, V. Topology Consistency of Disease-specific Differential Co-regulatory Networks. BMC Bioinform. 2019, 20, 550. [Google Scholar] [CrossRef] [PubMed]
- Zuo, Y.; Cui, Y.; Yu, G.; Li, R.; Ressom, H.W. Incorporating prior biological knowledge for network-based differential gene expression analysis using differentially weighted graphical LASSO. BMC Bioinform. 2017, 18, 99. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Hu, J.; Zhou, J.; Guo, F.; Yao, T.; Zhang, L. Weighed Gene Coexpression Network Analysis Screens the Potential Long Noncoding RNAs and Genes Associated with Progression of Coronary Artery Disease. Comput. Math. Methods Med. 2020, 2020, e8183420. [Google Scholar] [CrossRef] [PubMed]
- Franzén, O.; Ermel, R.; Cohain, A.; Akers, N.K.; Narzo, A.D.; Talukdar, H.A.; Foroughi-Asl, H.; Giambartolomei, C.; Fullard, J.F.; Sukhavasi, K.; et al. Cardiometabolic risk loci share downstream cis- and trans-gene regulation across tissues and diseases. Science 2016, 353, 827–830. [Google Scholar] [CrossRef] [Green Version]
- Ritchie, M.D.; Holzinger, E.R.; Li, R.; Pendergrass, S.A.; Kim, D. Methods of integrating data to uncover genotype–phenotype interactions. Nat. Rev. Genet. 2015, 16, 85–97. [Google Scholar] [CrossRef] [PubMed]
- Tragante, V.; Hemerich, D.; Alshabeeb, M.; Brænne, I.; Lempiäinen, H.; Patel, R.S.; den Ruijter, H.M.; Barnes, M.R.; Moore, J.H.; Schunkert, H.; et al. Druggability of Coronary Artery Disease Risk Loci. Circ. Genom. Precis. Med. 2018, 11, e001977. [Google Scholar] [CrossRef] [Green Version]
- Zeng, L.; Talukdar, H.A.; Koplev, S.; Giannarelli, C.; Ivert, T.; Gan, L.M.; Ruusalepp, A.; Schadt, E.E.; Kovacic, J.C.; Lusis, A.J.; et al. Contribution of Gene Regulatory Networks to Heritability of Coronary Artery Disease. J. Am. Coll. Cardiol. 2019, 73, 2946–2957. [Google Scholar] [CrossRef] [PubMed]
- Sumathipala, M.; Weiss, S.T. Predicting miRNA-based disease-disease relationships through network diffusion on multi-omics biological data. Sci. Rep. 2020, 10, 8705. [Google Scholar] [CrossRef] [PubMed]
- Chou, C.H.; Shrestha, S.; Yang, C.D.; Chang, N.W.; Lin, Y.L.; Liao, K.W.; Huang, W.C.; Sun, T.H.; Tu, S.J.; Lee, W.H.; et al. miRTarBase update 2018: A resource for experimentally validated microRNA-target interactions. Nucleic Acids Res. 2018, 46, D296–D302. [Google Scholar] [CrossRef] [PubMed]
- Hamosh, A.; Scott, A.F.; Amberger, J.; Valle, D.; McKusick, V.A. Online Mendelian Inheritance In Man (OMIM). Hum. Mutat. 2000, 15, 57–61. [Google Scholar] [CrossRef]
- Piñero, J.; Ramírez-Anguita, J.M.; Saüch-Pitarch, J.; Ronzano, F.; Centeno, E.; Sanz, F.; Furlong, L.I. The DisGeNET knowledge platform for disease genomics: 2019 update. Nucleic Acids Res. 2020, 48, D845–D855. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghafouri-Fard, S.; Gholipour, M.; Taheri, M. Role of MicroRNAs in the Pathogenesis of Coronary Artery Disease. Front. Cardiovasc. Med. 2021, 8, 632392. [Google Scholar] [CrossRef]
- Oughtred, R.; Rust, J.; Chang, C.; Breitkreutz, B.; Stark, C.; Willems, A.; Boucher, L.; Leung, G.; Kolas, N.; Zhang, F.; et al. The BioGRID database: A comprehensive biomedical resource of curated protein, genetic, and chemical interactions. Protein Sci. Publ. Protein Soc. 2021, 30, 187–200. [Google Scholar] [CrossRef]
- Szklarczyk, D.; Gable, A.L.; Lyon, D.; Junge, A.; Wyder, S.; Huerta-Cepas, J.; Simonovic, M.; Doncheva, N.T.; Morris, J.H.; Bork, P.; et al. STRING v11: Protein-protein association networks with increased coverage, supporting functional discovery in genome-wide experimental datasets. Nucleic Acids Res. 2019, 47, D607–D613. [Google Scholar] [CrossRef] [Green Version]
- Kamburov, A.; Pentchev, K.; Galicka, H.; Wierling, C.; Lehrach, H.; Herwig, R. ConsensusPathDB: Toward a more complete picture of cell biology. Nucleic Acids Res. 2011, 39, D712–D717. [Google Scholar] [CrossRef] [Green Version]
- Bader, G.D.; Cary, M.P.; Sander, C. Pathguide: A Pathway Resource List. Nucleic Acids Res. 2006, 34, D504–D506. [Google Scholar] [CrossRef]
- Ghatge, M.; Nair, J.; Sharma, A.; Vangala, R.K. Integrative gene ontology and network analysis of coronary artery disease associated genes suggests potential role of ErbB pathway gene EGFR. Mol. Med. Rep. 2018, 17, 4253–4264. [Google Scholar] [CrossRef]
- Du, P.; Feng, G.; Flatow, J.; Song, J.; Holko, M.; Kibbe, W.A.; Lin, S.M. From disease ontology to disease-ontology lite: Statistical methods to adapt a general-purpose ontology for the test of gene-ontology associations. Bioinformatics 2009, 25, i63–i68. [Google Scholar] [CrossRef]
- Liu, H.; Liu, W.; Liao, Y.; Cheng, L.; Liu, Q.; Ren, X.; Shi, L.; Tu, X.; Wang, Q.K.; Guo, A.Y. CADgene: A comprehensive database for coronary artery disease genes. Nucleic Acids Res. 2011, 39, D991–D996. [Google Scholar] [CrossRef]
- Kazeminia, S.; Baur, C.; Kuijper, A.; van Ginneken, B.; Navab, N.; Albarqouni, S.; Mukhopadhyay, A. GANs for medical image analysis. Artif. Intell. Med. 2020, 109, 101938. [Google Scholar] [CrossRef]
- Christiansen, F.; Epstein, E.L.; Smedberg, E.; Åkerlund, M.; Smith, K.; Epstein, E. Ultrasound image analysis using deep neural networks for discriminating between benign and malignant ovarian tumors: Comparison with expert subjective assessment. Ultrasound Obstet. Gynecol. 2021, 57, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Matek, C.; Schwarz, S.; Spiekermann, K.; Marr, C. Human-level recognition of blast cells in acute myeloid leukaemia with convolutional neural networks. Nat. Mach. Intell. 2019, 1, 538–544. [Google Scholar] [CrossRef]
- Schouten, J.P.E.; Matek, C.; Jacobs, L.F.P.; Buck, M.C.; Bošnački, D.; Marr, C. Tens of images can suffice to train neural networks for malignant leukocyte detection. Sci. Rep. 2021, 11, 7995. [Google Scholar] [CrossRef] [PubMed]
- Bai, W.; Suzuki, H.; Huang, J.; Francis, C.; Wang, S.; Tarroni, G.; Guitton, F.; Aung, N.; Fung, K.; Petersen, S.E.; et al. A population-based phenome-wide association study of cardiac and aortic structure and function. Nat. Med. 2020, 26, 1654–1662. [Google Scholar] [CrossRef]
- Warnat-Herresthal, S.; Schultze, H.; Shastry, K.L.; Manamohan, S.; Mukherjee, S.; Garg, V.; Sarveswara, R.; Händler, K.; Pickkers, P.; Aziz, N.A.; et al. Swarm Learning for decentralized and confidential clinical machine learning. Nature 2021, 594, 265–270. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional neural networks: An overview and application in radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ward, A.; Sarraju, A.; Chung, S.; Li, J.; Harrington, R.; Heidenreich, P.; Palaniappan, L.; Scheinker, D.; Rodriguez, F. Machine learning and atherosclerotic cardiovascular disease risk prediction in a multi-ethnic population. NPJ Digit. Med. 2020, 3, 125. [Google Scholar] [CrossRef] [PubMed]
- Junwei, K.; Yang, H.; Junjiang, L.; Zhijun, Y. Dynamic prediction of cardiovascular disease using improved LSTM. Int. J. Crowd Sci. 2019, 3, 14–25. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M.E.; Uddin, S.; Khan, A. Network analytics and machine learning for predictive risk modelling of cardiovascular disease in patients with type 2 diabetes. Expert Syst. Appl. 2021, 164, 113918. [Google Scholar] [CrossRef]
- D’Ascenzo, F.; Filippo, O.D.; Gallone, G.; Mittone, G.; Deriu, M.A.; Iannaccone, M.; Ariza-Solé, A.; Liebetrau, C.; Manzano-Fernández, S.; Quadri, G.; et al. Machine learning-based prediction of adverse events following an acute coronary syndrome (PRAISE): A modelling study of pooled datasets. Lancet 2021, 397, 199–207. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Bai, W.; Sinclair, M.; Tarroni, G.; Oktay, O.; Rajchl, M.; Vaillant, G.; Lee, A.M.; Aung, N.; Lukaschuk, E.; Sanghvi, M.M.; et al. Automated cardiovascular magnetic resonance image analysis with fully convolutional networks. J. Cardiovasc. Magn. Reson. 2018, 20, 65. [Google Scholar] [CrossRef] [Green Version]
- Wolterink, J.M.; Leiner, T.; de Vos, B.D.; Coatrieux, J.L.; Kelm, B.M.; Kondo, S.; Salgado, R.A.; Shahzad, R.; Shu, H.; Snoeren, M.; et al. An evaluation of automatic coronary artery calcium scoring methods with cardiac CT using the orCaScore framework. Med. Phys. 2016, 43, 2361. [Google Scholar] [CrossRef]
- Litjens, G.; Ciompi, F.; Wolterink, J.M.; de Vos, B.D.; Leiner, T.; Teuwen, J.; Išgum, I. State-of-the-Art Deep Learning in Cardiovascular Image Analysis. JACC Cardiovasc. Imaging 2019, 12, 1549–1565. [Google Scholar] [CrossRef]
- Zhou, J.; Troyanskaya, O.G. Predicting effects of noncoding variants with deep learning–based sequence model. Nat. Methods 2015, 12, 931–934. [Google Scholar] [CrossRef] [Green Version]
- Talukder, A.; Barham, C.; Li, X.; Hu, H. Interpretation of deep learning in genomics and epigenomics. Briefings Bioinform. 2021, 22, bbaa177. [Google Scholar] [CrossRef]
- Eraslan, G.; Avsec, Z.; Gagneur, J.; Theis, F.J. Deep learning: New computational modelling techniques for genomics. Nat. Rev. Genet. 2019, 20, 389–403. [Google Scholar] [CrossRef] [PubMed]
- Yin, B.; Balvert, M.; van der Spek, R.A.A.; Dutilh, B.E.; Bohté, S.; Veldink, J.; Schönhuth, A. Using the structure of genome data in the design of deep neural networks for predicting amyotrophic lateral sclerosis from genotype. Bioinformatics 2019, 35, i538–i547. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dutta, A.; Batabyal, T.; Basu, M.; Acton, S.T. An efficient convolutional neural network for coronary heart disease prediction. Expert Syst. Appl. 2020, 159, 113408. [Google Scholar] [CrossRef]
- Linden, A.; Yarnold, P.R. Modeling time-to-event (survival) data using classification tree analysis. J. Eval. Clin. Pract. 2017, 23, 1299–1308. [Google Scholar] [CrossRef]
- Chen, X.; Ishwaran, H. Pathway hunting by random survival forests. Bioinformatics 2013, 29, 99–105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Katzman, J.L.; Shaham, U.; Cloninger, A.; Bates, J.; Jiang, T.; Kluger, Y. DeepSurv: Personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med. Res. Methodol. 2018, 18, 24. [Google Scholar] [CrossRef]
- Kvamme, H.; Borgan, O.; Scheel, I. Time-to-Event Prediction with Neural Networks and Cox Regression. J. Mach. Learn. Res. 2019, 20, 1–30. [Google Scholar]
- Schäfer, J.; Strimmer, K. An empirical Bayes approach to inferring large-scale gene association networks. Bioinformatics 2005, 21, 754–764. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 2008, 9, 432–441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hawe, J.S.; Theis, F.J.; Heinig, M. Inferring Interaction Networks From Multi-Omics Data. Front. Genet. 2019, 10, 535. [Google Scholar] [CrossRef] [PubMed]
- Zierer, J.; Pallister, T.; Tsai, P.C.; Krumsiek, J.; Bell, J.T.; Lauc, G.; Spector, T.D.; Menni, C.; Kastenmüller, G. Exploring the molecular basis of age-related disease comorbidities using a multi-omics graphical model. Sci. Rep. 2016, 6, 37646. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manatakis, D.V.; Raghu, V.K.; Benos, P.V. piMGM: Incorporating multi-source priors in mixed graphical models for learning disease networks. Bioinformatics 2018, 34, i848–i856. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.M.; Liang, L.; Liu, L.; Tang, M.J. Graph Neural Networks and Their Current Applications in Bioinformatics. Front. Genet. 2021, 12, 690049. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Shao, W.; Huang, Z.; Tang, H.; Zhang, J.; Ding, Z.; Huang, K. MOGONET integrates multi-omics data using graph convolutional networks allowing patient classification and biomarker identification. Nat. Commun. 2021, 12, 3445. [Google Scholar] [CrossRef]
- Schulte-Sasse, R.; Budach, S.; Hnisz, D.; Marsico, A. Integration of multiomics data with graph convolutional networks to identify new cancer genes and their associated molecular mechanisms. Nat. Mach. Intell. 2021, 3, 513–526. [Google Scholar] [CrossRef]
- Chereda, H.; Bleckmann, A.; Menck, K.; Perera-Bel, J.; Stegmaier, P.; Auer, F.; Kramer, F.; Leha, A.; Beißbarth, T. Explaining decisions of graph convolutional neural networks: Patient-specific molecular subnetworks responsible for metastasis prediction in breast cancer. Genome Med. 2021, 13, 42. [Google Scholar] [CrossRef]
- Rhee, S.; Seo, S.; Kim, S. Hybrid Approach of Relation Network and Localized Graph Convolutional Filtering for Breast Cancer Subtype Classification. arXiv 2018, arXiv:1711.05859. [Google Scholar]
- Young, J.; Modat, M.; Cardoso, M.J.; Mendelson, A.; Cash, D.; Ourselin, S. Accurate multimodal probabilistic prediction of conversion to Alzheimer’s disease in patients with mild cognitive impairment. Neuroimage Clin. 2013, 2, 735–745. [Google Scholar] [CrossRef] [Green Version]
- DeGrave, A.J.; Janizek, J.D.; Lee, S.I. AI for radiographic COVID-19 detection selects shortcuts over signal. Nat. Mach. Intell. 2021, 3, 610–619. [Google Scholar] [CrossRef]
- Samek, W.; Montavon, G.; Lapuschkin, S.; Anders, C.J.; Müller, K.R. Explaining Deep Neural Networks and Beyond: A Review of Methods and Applications. Proc. IEEE 2021, 109, 247–278. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Fleetwood, O.; Kasimova, M.A.; Westerlund, A.M.; Delemotte, L. Molecular Insights from Conformational Ensembles via Machine Learning. Biophys. J. 2020, 118, 765–780. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Montavon, G.; Lapuschkin, S.; Binder, A.; Samek, W.; Müller, K.R. Explaining nonlinear classification decisions with deep Taylor decomposition. Pattern Recognit. 2017, 65, 211–222. [Google Scholar] [CrossRef]
- Eichler, G.S.; Reimers, M.; Kane, D.; Weinstein, J.N. The LeFE algorithm: Embracing the complexity of gene expression in the interpretation of microarray data. Genome Biol. 2007, 8, R187. [Google Scholar] [CrossRef] [Green Version]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Hausken, K.; Mohr, M. The value of a player in n-person games. Soc. Choice Welf. 2001, 18, 465–483. [Google Scholar] [CrossRef]
- Eitel, F.; Soehler, E.; Bellmann-Strobl, J.; Brandt, A.U.; Ruprecht, K.; Giess, R.M.; Kuchling, J.; Asseyer, S.; Weygandt, M.; Haynes, J.D.; et al. Uncovering convolutional neural network decisions for diagnosing multiple sclerosis on conventional MRI using layer-wise relevance propagation. Neuroimage Clin. 2019, 24, 102003. [Google Scholar] [CrossRef] [PubMed]
- Böhle, M.; Eitel, F.; Weygandt, M.; Ritter, K. Layer-Wise Relevance Propagation for Explaining Deep Neural Network Decisions in MRI-Based Alzheimer’s Disease Classification. Front. Aging Neurosci. 2019, 11, 194. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Dataset | Cohort Size | Attributes | Follow Up | Ref. |
|---|---|---|---|---|
| FRS attributes: | ||||
| age, sex, | ||||
| American Framingham | ∼15,000 | diabetes, | 12 years | [29] |
| heart study | LDL and HDL | |||
| cholesterol, smoking, | ||||
| systolic blood pressure | ||||
| Sex, smoking, | ||||
| SCORE pooled dataset | ∼21,000 | total cholestrol, | Average | [30] |
| (12 European cohorts) | tot. chol./HDL ratio, | 13 years | ||
| systolic blood pressure | ||||
| ACC/AHA | FRS attributes, tot. chol. | |||
| pooled | ∼25,000 | treated/untreated | ≥12 years | [31] |
| cohort | systolic blood pressure | |||
| FRS attributes, | ||||
| QRESEARCH | social deprivation, | |||
| (No diabetes or | ∼10 million | family history, | 17 years | [32] |
| CVD at baseline) | BMI, LV function, | (study length) | ||
| antihypertensive | ||||
| agent treatment | ||||
| Suita dataset | ∼5600 | FRS attributes, CKD | 11.8 years | [33] |
| Risk Score | Dataset | Clinical Question | Method | Performance | Ref. |
|---|---|---|---|---|---|
| 0.733–0.841/ | |||||
| Framingham | American | 10-year risk; | 0.769–0.847 | ||
| risk score | Framingham | CAD, | Cox PH | (C-statistic, | [34] |
| heart study | CVD events | events average, | |||
| male/female) | |||||
| SCORE | 10-year risk; | 0.71–0.84 | |||
| SCORE | pooled | CAD/CVD | Weibull | (AUC-ROC, | [30] |
| dataset | mortality | EU countries) | |||
| ACC/AHA | ACC/AHA | 10-year risk; | 0.713–0.818 | ||
| pooled cohort | pooled | atherosclerotic | Cox PH | (C-statistic, | [31] |
| equations | cohort | CVD events | sex/race average) | ||
| 10-year risk; | 0.7674/0.7879 | ||||
| QRISK | QRESEARCH | CVD (MI, CAD, | Cox PH | (AUC-ROC, | [35] |
| stroke, TIA) | male/female) | ||||
| Suita | Suita dataset | 10-year risk; | Cox PH | 0.835 | [33] |
| CAD | (C-statistic) |
| Dataset | Cohort Size | Type of Data | Baseline | Follow Up | Ref. |
|---|---|---|---|---|---|
| Clinical | |||||
| (a) GRACE | ∼102,000 | risk | ACS | 6 months | [36] |
| registry | (30 countries) | factors | |||
| Clinical risk | CVD | ||||
| (b) REACH | ∼68,000 | factors, | (CAD, CeVD, | 1–2 years | [37] |
| registry | (44 countries) | demographics | PAD) | ||
| Clinical | |||||
| (c) EuroAspire | IV/V: ∼16,000 | risk factors, | CAD | 0.5–3 years | [38] |
| (27 countries) | lifestyle | ||||
| Clinical | |||||
| (d) TIMI | ∼8600 | risk | ACS | 2.5 years | [39] |
| factors | (median) | ||||
| CCTA images, | |||||
| (e) CONFIRM | ∼50,000 | clinical | suspected | 2.3 years | [40] |
| registry | (6 countries) | risk factors | CAD | (median) | |
| Clinical risk | |||||
| factors, carotid | |||||
| (f) UCC-SMART | ∼13,000 | ultrasound, | CVD | 4.7 years | [41] |
| (567 patients with CCTA images | (median) | ||||
| ∼186,000 | |||||
| (g) GENIUS-CHD | (57 studies, | Genotype | CAD | 1–15 years | [42] |
| 18 countries) |
| Risk score | Dataset | Clinical Question | Method | Performance | Ref. |
|---|---|---|---|---|---|
| GRACE registry | 6-month risk; | 0.7/0.82 | |||
| (a) GRACE | (43,810 patients, | death, or | Cox PH | (C-statistic, | [4] |
| 14 countries) | death/MI | death/death-MI) | |||
| REACH | 20-month risk; | 0.67 [0.66, 0.68]/ | |||
| registry | CVD events, | 0.75 [0.73, 0.77] | |||
| (b) REACH | (49,689 patients, | cardiovasc. | Cox PH | (C-statistic, | [5] |
| 44 countries) | death | 95% CI, | |||
| CVD/death) | |||||
| EuroAspire | 2-year risk; | ||||
| (c) EuroAspire | (IV/V, | CVD events | Weibull | 0.67 [0.64, 0.70] | [3] |
| 27 countries, | or | (C-statistic, | |||
| 12,484 patients) | interventions | 95% CI) | |||
| 3-year risk; | |||||
| (d) TRS2P | TIMI | Cardiovasc. | Cox PH | 0.67 [0.65, 0.69] | [39] |
| (8598 patients, | death, MI, | (C-statistic, | |||
| 9 predictors) | stroke | 95% CI) | |||
| CONFIRM | 2-year risk; | ||||
| (e) CONFIRM | registry | death | Cox PH | 0.682 | [43] |
| (20,300 patients) | (C-statistic) | ||||
| UCC-SMART | 10-year risk; | 0.68 [0.64, 0.71] | |||
| (f) SMART | (5788 patients, | CVD events | Cox PH | (C-statistic, | [6] |
| 14 predictors) | 95% CI) |
| Metric | Description | Math. Definition |
|---|---|---|
| True positive | A positive sample correctly | |
| (TP) | predicted by the model. | |
| True negative | A negative sample correctly | |
| (TN) | predicted by the model. | |
| False positive | A sample wrongly classified as | |
| (FP) | positive by the model. | |
| False negative | A sample wrongly classified as | |
| (FN) | negative by the model. | |
| Precision | Fraction of true positives among | |
| the predicted positives. | ||
| Recall | Fraction of positives that are | |
| (Sensitivity) | correctly predicted. | |
| Specificity | Fraction of negatives that are | |
| correctly predicted. | ||
| Accuracy | Fraction of correctly predicted | |
| positives and negatives. | ||
| ROC curve | A curve indicating performance | |
| (Receiver Operating | of a classifier. The Y-axis shows | |
| Characteristic) | recall and the X-axis shows | |
| s = (1-specificity) | ||
| AUC-ROC | Quantitative performance | |
| (Area Under the Curve | measure based on ROC curve. | |
| - ROC) | Ranges from 0 to 1, where 1 | |
| corresponds to perfect, and 0.5 | ||
| to random, classification. | ||
| C-statistic | Equivalent to AUC-ROC. Can | |
| be used for censored data | ||
| (missing patient outcomes). | ||
| —predicted risk of patient i | ||
| —time to event, patient i | ||
| - whether (event) | ||
| information exists. | ||
| PR curve | Similar to ROC curve. Y-axis | |
| (Precision Recall) | shows precision and X-axis | |
| recall (r). | ||
| AUC-PR | Quantitative performance | |
| (AUC—Precision-Recall) | measure based on PR curve. | |
| Alternative to AUC-ROC. |
| Risk Score/ | Dataset | Clinical | Prediction | Comparison | Ref. |
|---|---|---|---|---|---|
| Method | Question | Performance | (Cox PH) | ||
| (a) Auto- | UK Biobank | 5 year-risk; | AUC-ROC, 95% CI: | All attributes: | |
| prognosis | (clinical data, | Fatal or | 0.774 | 0.758 | |
| framework | 423,604 | non-fatal | [0.768, 0.780] | [0.753, 0.763] | [44] |
| patients) | CVD event | FRS attributes: | |||
| 0.734 | |||||
| [0.729, 0.739] | |||||
| (b) CAD CNN | NHANES | Predict | AUC-ROC: | - | |
| (1) CNN | (clinial, lab, | presence | (1) 76.87 | ||
| (2) LR | demographic | of CAD | (2) 71.29 | [141] | |
| (3) SVM | data, | (3) 77.64 | |||
| (4) RF | 37,079 | (4) 76.24 | |||
| (5) AdaBoost | patients) | (5) 71.63 | |||
| (6) MLP | (6) 72.61 | ||||
| (c) ASC AI | EHR | 5-year risk; | AUC-ROC, 95% CI: | ACC/AHA: | |
| (clinical data, | MI, stroke, | (full/reduced) | (full/reduced) | ||
| (1) GBM | socioecomics | or fatal CAD | (1) 0.835 / 0.779 | - /0.775 | |
| 262,923/ | [0.825, 0.846]/ | [-, -]/ | |||
| 131,721 | [0.760, 0.790] | [0.755, 0.794] | |||
| (2) LR– | patients) | (2) 0.784/0.825 | |||
| [0.765, 0.802]/ | |||||
| [0.812, 0.839] | |||||
| (3) XGBoost | (3) 0.784/0.830 | [126] | |||
| [0.766, 0.803]/ | |||||
| [0.816, 0.843] | |||||
| (4) RF | (4) 0.773/0.831 | ||||
| [0.760,0.793]/ | |||||
| [0.820,0.842] | |||||
| (5) LR- | (5) 0.749/0.808 | ||||
| [0.729,0.770]/ | |||||
| [0.795,0.820] | |||||
| (d) PRAISE | BleeMACS, | 1-year risk; | AUC-ROC, 95% CI: | - | |
| (AdaBoost) | RENAMI | (1) Death, | (1) 0.82 [0.78, 0.85] | ||
| (clinical data, | (2) MI, | (2) 0.74 [0.70, 0.78] | [129] | ||
| 19,826 | (3) bleeding | (3) 0.70 [0.66,0.75] | |||
| patients) | (ACS at baseline) | ||||
| (e) CONFIRM | CONFIRM | 5-year risk; | AUC-ROC, 95% CI: | FRS: | |
| (logit-boost) | registry | Death | 0.79 | 0.61 | [9] |
| (10,030 patients) | (suspected CAD | [0.77, 0.81] | [0.59, 0.64] | ||
| at baseline) | |||||
| Method | Question | Performance | (Cox PH) | ||
| (f) 4D-survival | NPHS | Survival-times | C-statistic, 95% CI: | Clinical/imaging: | |
| (survival | (MR imaging, | (pulmonary | 0.75 | 0.64 | [11] |
| autoencoder) | clinical data, | hypertension | [0.70, 0.79] | [0.57, 0.70] | |
| 302 patients) | at baseline) | ||||
| (g) CAD PRS | GerMIFS I-V, | Genetic risk; | AUC-ROC, 95% CI: | - | |
| (1) PRS | LURIC | CAD | (1) 0.92 [0.90, 0.94] | ||
| (2) SVM | (∼ 2.8M SNPs, | (2) 0.82 [0.80, 0.85] | [20] | ||
| (3) NB | 15,709 patients) | (3) 0.82 [0.79, 0.84] | |||
| (4) RF | (4) 0.75 [0.72, 0.78] | ||||
| (5) XGBoost | (5) 0.74 [0.71, 0.77] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Westerlund, A.M.; Hawe, J.S.; Heinig, M.; Schunkert, H. Risk Prediction of Cardiovascular Events by Exploration of Molecular Data with Explainable Artificial Intelligence. Int. J. Mol. Sci. 2021, 22, 10291. https://doi.org/10.3390/ijms221910291
Westerlund AM, Hawe JS, Heinig M, Schunkert H. Risk Prediction of Cardiovascular Events by Exploration of Molecular Data with Explainable Artificial Intelligence. International Journal of Molecular Sciences. 2021; 22(19):10291. https://doi.org/10.3390/ijms221910291
Chicago/Turabian StyleWesterlund, Annie M., Johann S. Hawe, Matthias Heinig, and Heribert Schunkert. 2021. "Risk Prediction of Cardiovascular Events by Exploration of Molecular Data with Explainable Artificial Intelligence" International Journal of Molecular Sciences 22, no. 19: 10291. https://doi.org/10.3390/ijms221910291
APA StyleWesterlund, A. M., Hawe, J. S., Heinig, M., & Schunkert, H. (2021). Risk Prediction of Cardiovascular Events by Exploration of Molecular Data with Explainable Artificial Intelligence. International Journal of Molecular Sciences, 22(19), 10291. https://doi.org/10.3390/ijms221910291







