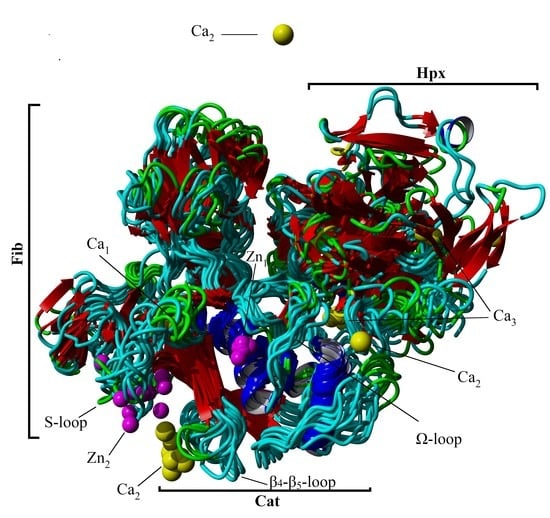
Conformation and Domain Movement Analysis of Human Matrix Metalloproteinase-2: Role of Associated Zn2+ and Ca2+ Ions
Abstract
1. Introduction
2. Results and Discussion
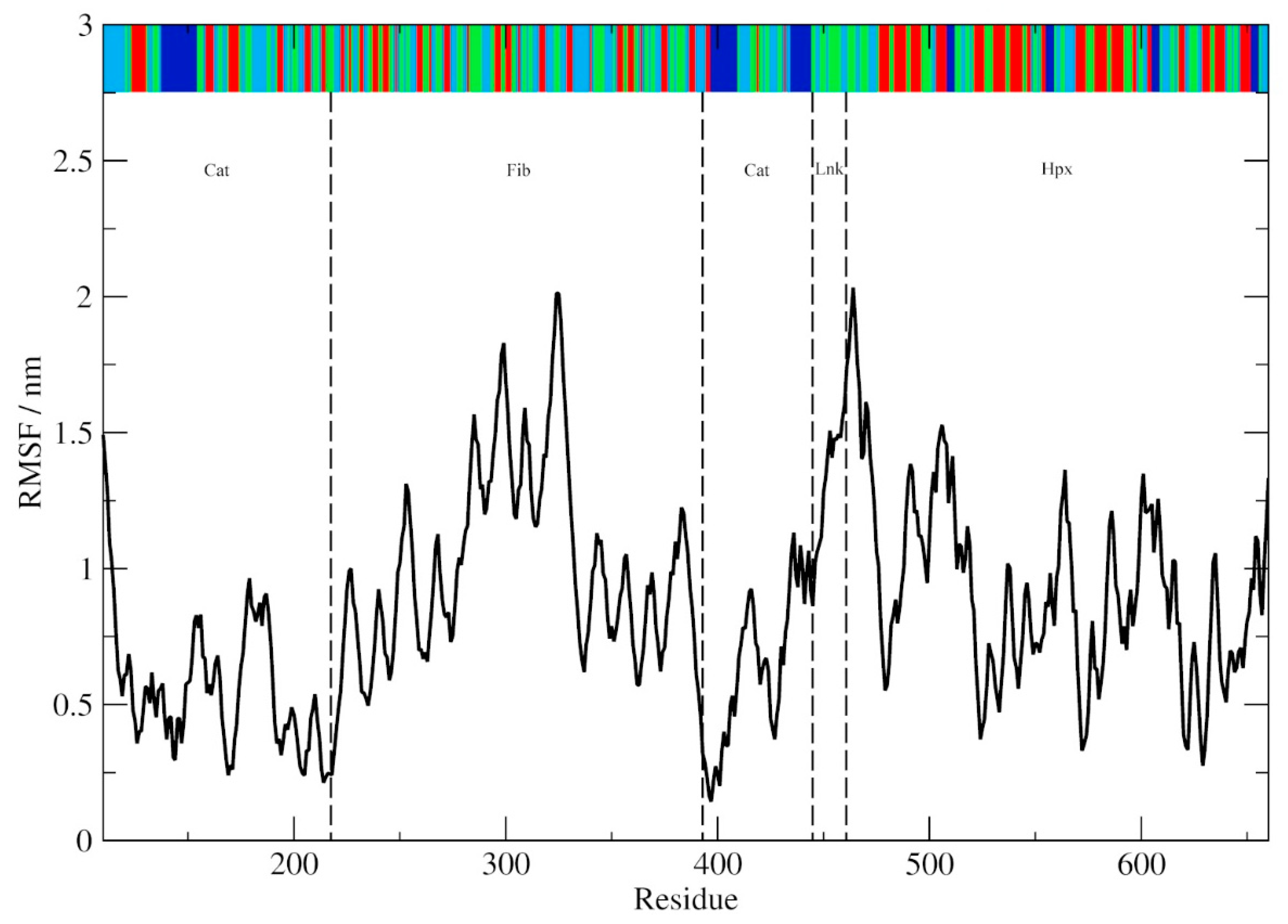
2.1. System Equilibration and Conformational Stability
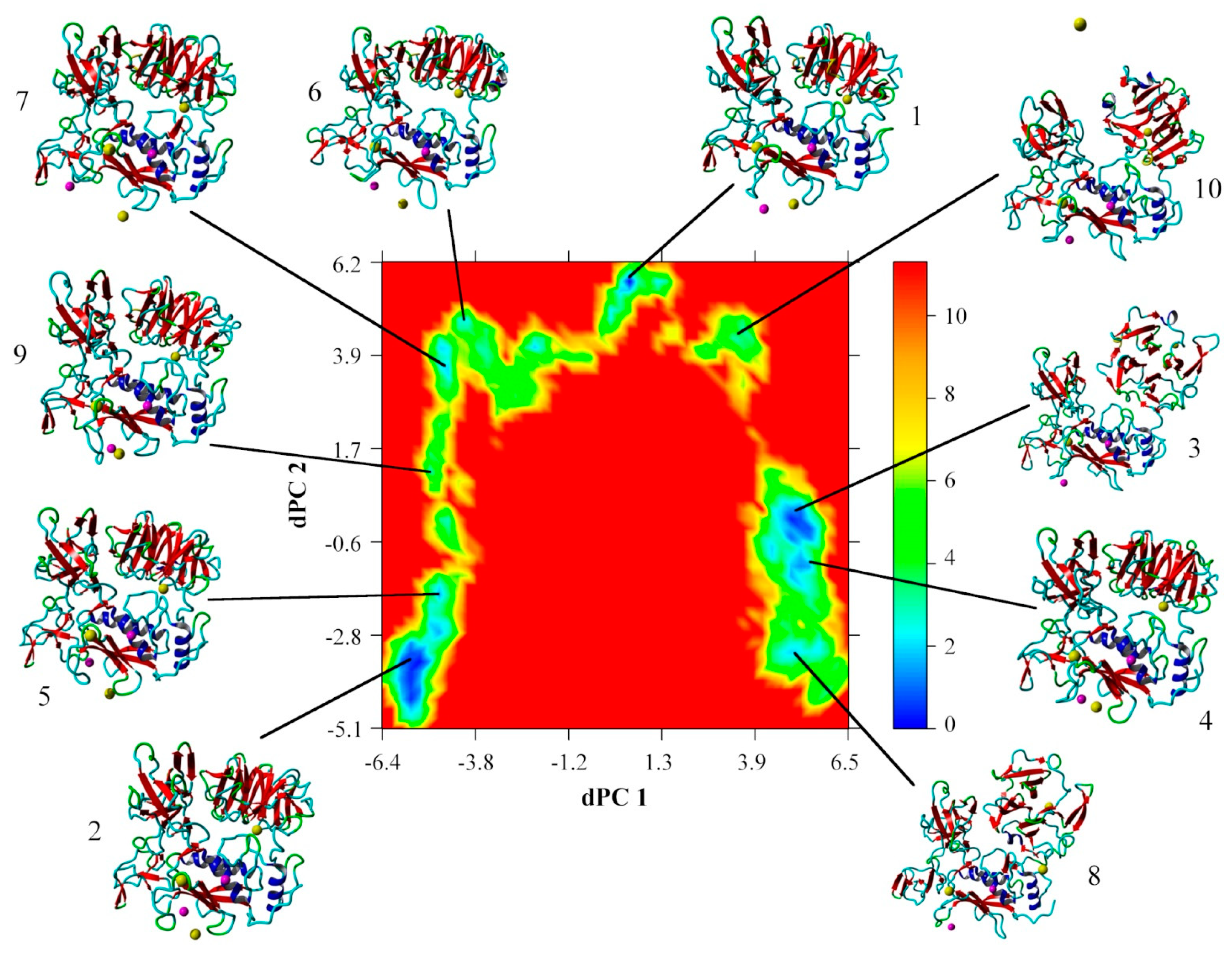
2.2. Conformational Analysis
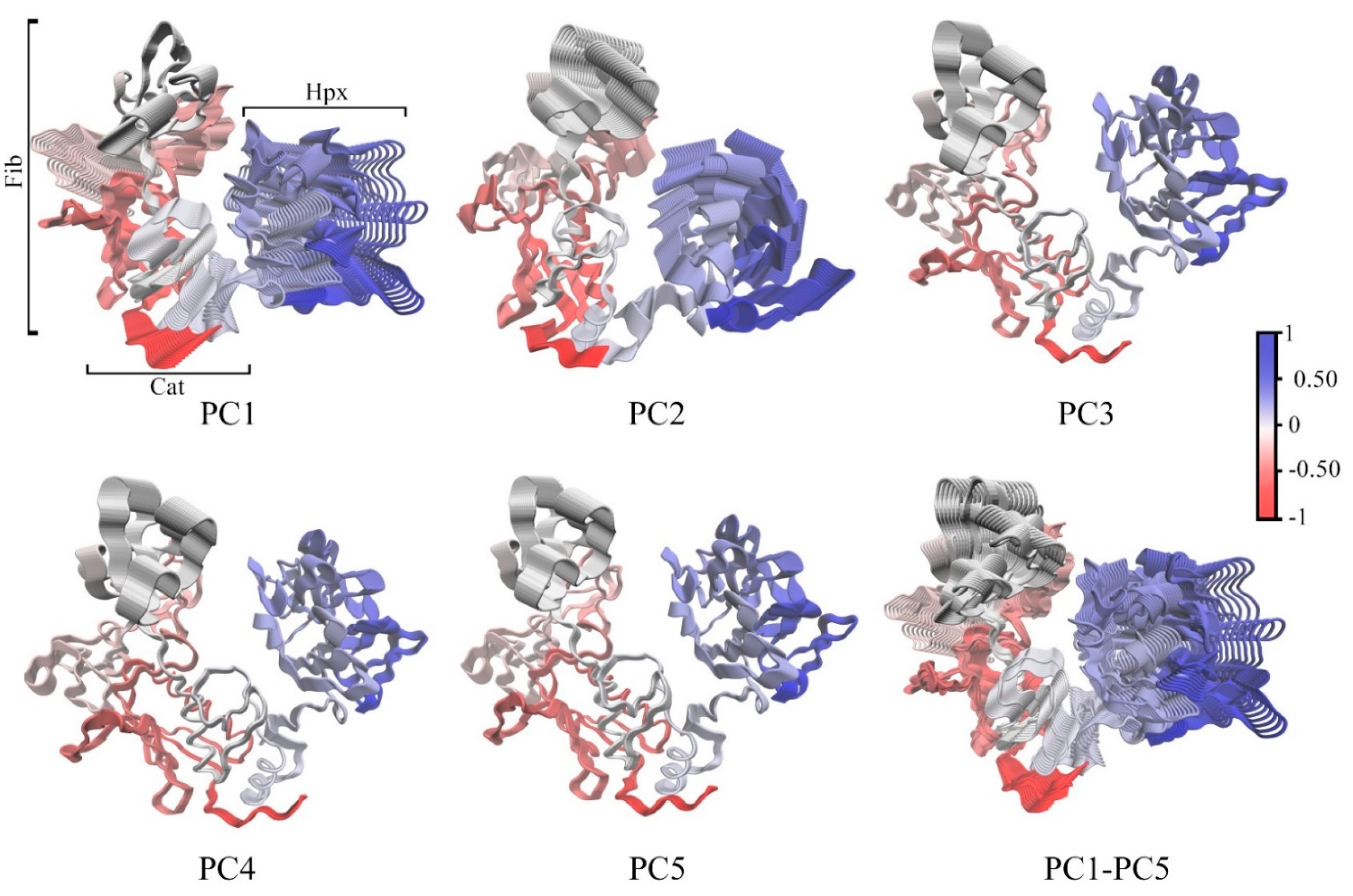
2.3. Domain Movement Analysis
2.4. Protein-Metal Ion Interaction Energies
3. Materials and Methods
3.1. Matrix Metalloprotease-2 Starting Conformation
3.2. Molecular Dynamics
3.3. Biophysical Properties
3.4. Conformational Analysis
3.5. Dynamic Cross-Correlation Matrix
3.6. Interaction Energy
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CN | Coordination number |
| dPCA | Dihedral principle component analysis |
| DCCM | Domain cross-correlation matrix |
| DSSP | Database of secondary structure assignments for all protein entries in the Protein Data Bank |
| MD | Molecular dynamics |
| MMP-2 | Matrix metalloproteinase-2 |
| MMPBSA-IE | Molecular mechanics Poisson Boltzman surface area – interaction entropy |
| NVT | Constant number, volume, and temperature |
| NPT | Constant number, pressure, and temperature |
| PDB | Protein databank |
| PME | Particle mesh Ewald |
| RMSD | Root mean square deviation |
| RMSF | Root mean square fluctuation |
| SASA | Solvent exposed surface area |
References
- Basbaum, C.B.; Werb, Z. Focalized proteolysis: Spatial and temporal regulation of extracellular matrix degradation at the cell surface. Curr. Opin. Cell Biol. 1996, 8, 731–738. [Google Scholar] [CrossRef]
- Birkedal-Hansen, H.; Moore, W.G.; Bodden, M.K.; Windsor, L.J.; Birkedal-Hansen, B.; DeCarlo, A.; Engler, J.A. Matrix metalloproteinases: A review. Crit. Rev. Oral Biol. Med. 1993, 4, 197–250. [Google Scholar] [CrossRef]
- Maskos, K. Crystal structure of MMPs in complex with physiological and pharmacological inhibitors. Biochimie 2005, 87, 249–263. [Google Scholar] [CrossRef] [PubMed]
- Ra, H.-J.; Parks, W.C. Control of Matrix Metalloproteinase Catalytic Activity. Matrix Biol. 2007, 26, 587–596. [Google Scholar] [CrossRef] [PubMed]
- Verma, R.P.; Hansch, C. Matrix metalloproteinases (MMPs): Chemical-biological functions and (Q) SARs. Bioorg. Med. Chem. 2007, 15, 2223–2268. [Google Scholar] [CrossRef] [PubMed]
- van Meurs, J.; van Lent, P.; Holthuysen, A.; Lambrou, D.; Bayne, E.; Singer, I.; van den Berg, W. Active matrix metalloproteinases are present in cartilage during immune complex mediated arthritis: A pivotal role for stromelysin-1 in cartilage destruction. J. Immunol. 1999, 163, 5633–5639. [Google Scholar]
- Nagase, H.; Woessner, J.F., Jr. Matrix metalloproteinases. J. Biol. Chem. 1999, 274, 21491–21494. [Google Scholar] [CrossRef]
- Steffensen, B.; Häkkinen, L.; Larjava, H. Proteolytic events of wound-healing-coordinated interactions among matrix metalloproteinases (MMPs), integrins, and extracellular matrix molecules. Crit. Rev. Oral Biol. Med. 2001, 12, 373–398. [Google Scholar] [CrossRef]
- Egeblad, M.; Werb, Z. New functions for the matrix metalloproteinases in cancer progression. Nat. Rev. Cancer 2002, 2, 163–176. [Google Scholar] [CrossRef]
- Fingleton, B. Matrix metalloproteinases: Roles in cancer and metastasis. Front. Biosci. 2006, 11, 479–491. [Google Scholar] [CrossRef]
- Butler, G.S.; Overall, C.M. Updated biological roles for matrix metalloproteinases and new “intracellular” substrates revealed by degradomics. Biochemistry 2009, 48, 10830–10845. [Google Scholar] [CrossRef]
- Rodríguez, D.; Morrison, C.J.; Overall, C.M. Matrix metalloproteinases: What do they not do? New substrates and biological roles identified by murine models and proteomics. Biochim. Biophys. Acta 2010, 1803, 39–54. [Google Scholar] [CrossRef] [PubMed]
- Morgunov, E.; Tuuttila, A.; Bergmann, U.; Isupov, M.; Lindqvist, Y.; Schneider, G.; Tryggvason, K. Structure of Human Pro-Matrix Metalloproteinase-2: Activation Mechanism Revealed. Science 1999, 284, 1667–1670. [Google Scholar] [CrossRef]
- Díaz, N.; Suárez, D.; Valdés, H. From the X-ray Compact Structure to the Elongated form of the Full-Length MMP-2 Enzyme in Solution: A Molecular Dynamics Study. J. Am. Chem. Soc. 2008, 130, 14070–14071. [Google Scholar] [CrossRef]
- Díaz, N.; Suárez, D. Alternative Interdomain Configurations of the Full-Length MMP-2 Enzyme Explored by Molecular Dynamics Simulations. J. Phys. Chem. B 2012, 116, 2677–2686. [Google Scholar] [CrossRef]
- Krieger, E.; Vriend, G. YASARA View—Molecular graphics for all devices—From smartphones to workstations. Bioinformatics 2011, 30, 2981–2982. [Google Scholar] [CrossRef]
- Zheng, H.; Chruszcz, M.; Lasota, P.; Lebioda, L.; Minor, M. Data mining of metal ion environments present in protein structures. J. Inorg. Biochem. 2008, 102, 1765–1776. [Google Scholar] [CrossRef]
- Zheng, H.; Cooper, D.R.; Porebski, P.J.; Shabalin, I.G.; Handing, K.B.; Minor, W. CheckMyMetal: A macromolecular metal-binding validation tool. Acta Cryst. 2017, 73, 223–233. [Google Scholar] [CrossRef] [PubMed]
- Amadei, A.; Ceruso, M.A.; Di Nola, A. On the convergence of the conformational coordinates basis set obtained by the essential dynamics analysis of proteins’ molecular dynamics simulations. Proteins 1999, 36, 419–424. [Google Scholar] [CrossRef]
- Hayward, S.; de Groot, B.L. Normal modes and essential dynamics. In Methods in Molecular Biology: Molecular Modeling of Proteins; Kukol, A., Ed.; Humana Press: New York, NY, USA, 2008; Volume 443, pp. 89–106. ISBN 978-1-59745-177-2. [Google Scholar]
- Andricioaei, I.; Karplus, M. On the calculation of entropy from covariance matrices of the atomic fluctuations. J. Chem. Phys. 2001, 115, 6289–6292. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: http://www.R-project.org/ (accessed on 2 January 2019).
- Maechler, M.; Rousseeuw, P.; Struyf, A.; Hubert, M.; Hornik, K.; Studer, M.; Roudier, P.; Gonzalez, J.; Kozlowski, K. Cluster: Methods for Cluster Analysis. Available online: https://cran.r-project.org/web/packages/cluster/ (accessed on 2 January 2019).
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Steffensen, B.; Wallon, U.M.; Overall, C.M. Extracellular matrix binding properties of recombinant fibronectin type II-like modules of human 72-kDa gelatinase/type IV collagenase. High affinity binding to native type I collagen but not native type IV collagen. J. Biol. Chem. 1995, 270, 11555–11566. [Google Scholar] [CrossRef]
- Gehrmann, M.L.; Douglas, J.T.; Bányai, L.; Hedvig, T.; Patthy, L.; Llinás, M. Modular autonomy, ligand specificity, and functional cooperativity of the three in-tandem fibronectin type II repeats from human matrix metalloproteinase 2. J. Biol. Chem. 2004, 279, 46921–46929. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Wang, Y.; Lauer-Fields, J.L.; Fields, G.B.; Steffensen, B. Contributions of the MMP-2 collagen binding domain to gelatin cleavage. Substrate binding via the collagen binding domain is required for hydrolysis of gelatin but not short peptides. Matrix Biol. 2004, 23, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Mikhailova, M.; Llangovan, U.; Chen, Z.; Yu, A.; Pal, S.; Hinck, A.P.; Steffensen, B. Nuclear magnetic resonance mapping and functional confirmation of the collagen binding sites of matrix metalloproteinase-2. Biochemistry 2009, 48, 5822–5831. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Díaz, N.; Suárez, D. Molecular dynamics simulations of the active matrix metalloproteinase-2: Positioning of the N-terminal fragment and binding of a small peptide substrate. Proteins 2008, 72, 50–61. [Google Scholar] [CrossRef]
- Díaz, N.; Suárez, D. Molecular Dynamics Simulations of Matrix Metalloproteinase 2: Role of the Structural Metal Ions. Biochemistry 2007, 46, 8943–8952. [Google Scholar] [CrossRef]
- Díaz, N.; Suárez, D. Peptide Hydrolysis Catalyzed by Matrix Metalloproteinase 2: A computational Study. J. Phys. Chem. B 2008, 112, 8412–8424. [Google Scholar] [CrossRef]
- Duan, L.; Liu, X.; Zhang, J.Z.H. Interaction Entropy: A New Paradigm for Highly Efficient and Reliable Computation of Protein-Ligand Binding Free Energy. J. Am. Chem. Soc. 2016, 138, 5722–5728. [Google Scholar] [CrossRef]
- Springman, E.B.; Nagase, H.; Birkedal-Hansen, H.; Van Wart, H.E. Zinc content and function in human fibroblast collagenase. Biochemistry 1995, 34, 15713–15720. [Google Scholar] [CrossRef]
- Li, S.; Hong, M. Protonation, Tautomerization, and Rotameric Structure of Histidine: A comprehensive Study by Magic-Angle-Spinning Solid-State NMR. J. Am. Chem. Soc. 2011, 133, 1534–1544. [Google Scholar] [CrossRef]
- Langella, E.; Improta, R.; Barone, V. Checking the pH-Induced Conformational Transition of Prion Protein by Molecular Dynamics Simulations: Effect of Protonation of Histidine Residues. Biophys. J. 2004, 87, 3623–3632. [Google Scholar] [CrossRef]
- Cates, M.S.; Teodoro, M.L.; Phillips, G.N., Jr. Molecular Mechanisms of Calcium and Magnesium Binding to Parvalbumin. Biophys. J. 2002, 82, 1133–1146. [Google Scholar] [CrossRef][Green Version]
- Engel, C.K.; Pirard, B.; Schimanski, S.; Kirsch, R.; Habermann, J.; Klingler, O.; Schlotte, V.; Weithmann, K.U.; Wendt, K.U. Structural basis for the highly selective inhibition of MMP-13. Chem. Biol. 2005, 12, 181–189. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Abraham, M.J.; van der Spoel, D.; Lindahl, E.; Hess, B.; the GROMACS Development Team. GROMACS User Manual ver. 5.1.2 2016. Available online: http://www.gromacs.org (accessed on 2 January 2019).
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmüller, H.; MacKerell, A.D., Jr. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.; Mittal, J.; Feig, M.; Mackerell, A.D., Jr. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef]
- MacKerell, A.D., Jr.; Feig, M.; Brooks, C.L., III. Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004, 25, 1400–1415. [Google Scholar] [CrossRef]
- MacKerell, A.D., Jr.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics Studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Bjelkmar, P.; Larsson, P.; Cuendet, M.A.; Bess, B.; Lindahl, E. Implementation of the CHARMM force field in GROMACS: Analysis of protein stability effects from correction maps, virtual interaction sites, and water models. J. Chem. Theory Comput. 2010, 6, 459–466. [Google Scholar] [CrossRef]
- Li, P.; Roberts, B.P.; Chakravorty, D.K.; Merz, K.M., Jr. Rational Design of Particle Mesh Ewald Compatible Lennard-Jones Parameters for +2 Metal Cations in Explicit Solvent. J. Chem. Theory Comput. 2013, 9, 2733–2748. [Google Scholar] [CrossRef]
- Stote, R.H.; Karplus, M. Zinc Binding in Proteins and Solution: A Simple but Accurate Nonbonded Representation. Proteins 1995, 23, 12–31. [Google Scholar] [CrossRef]
- Foote, J.W.; Delves, H.T. Determination of non-protein-bound zinc in human serum using ultrafiltration and atomic absorption spectrometry with electrothermal atomisation. Analyst 1988, 113, 911–915. [Google Scholar] [CrossRef]
- Forman, D.T.; Lorenzo, L. Ionized Calcium: Its significance and Clinical Usefulness. Ann. Clin. Lab. Sci. 1991, 21, 297–304. [Google Scholar]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A Linear Constraint Solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Hess, B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem Theory Comput. 2008, 4, 116–122. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8592. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- White, A.D.; Keefe, A.J.; Ella-Menye, J.R.; Nowinski, A.K.; Shao, Q.; Pfaendtner, J.; Jiang, S. Free energy of solvated salt bridges: A simulation and experimental study. J. Phys. Chem. B 2013, 117, 7254–7259. [Google Scholar] [CrossRef]
- Nguyen, B.L.; Pettitt, B.M. Effects of Acids, Bases, and Heteroatoms on Proximal Radial Distribution Functions for Proteins. J. Chem. Theory Comput. 2015, 11, 1399–1409. [Google Scholar] [CrossRef]
- Mu, Y.; Nguyen, P.H.; Stock, G. Energy landscape of a small peptide revealed by dihedral angle principal component analysis. Proteins 2005, 58, 45–52. [Google Scholar] [CrossRef]
- Altis, A.; Nguyen, P.H.; Hegger, R.; Stock, G. Dihedral Angle Principal Component Analysis of Molecular Dynamics Simulations. J. Chem. Phys. 2007, 126, 216–225. [Google Scholar] [CrossRef]
- Ligges, U.; Mächler, M. Scatterplot3d—An R Package for Visualizing Multivariate Data. J. Stat. Softw. 2003, 8, 1–20. [Google Scholar] [CrossRef]
- Akima, H.; Gebhardt, A.; Petzold, T.; Maechler, M. akima: Interpolation of Irregularly and Regularly Spaced Data. Available online: https://CRAN.R-project.org/package=akima (accessed on 2 January 2019).
- Sarkar, D.; Andrews, F. latticeExtra: Extra Graphical Utilities Based on Lattice. Available online: https://CRAN.R-project.org/package=latticeExtra (accessed on 2 January 2019).
- Tan, P.-N.; Steinbach, M.; Kumar, V. Cluster Analysis: Basic Concepts and Algorithms in Introduction to Data Mining, 2nd ed.; Pearson Press: New York, NY, USA, 2005; Chapter 8; pp. 487–568. ISBN 978-0321321367. [Google Scholar]
- Tan, P.-N.; Steinbach, M.; Kumar, V. Cluster Analysis: Additional Issues and Algorithms in Introduction to Data Mining, 2nd ed.; Pearson Press: New York, NY, USA, 2005; Chapter 9; pp. 569–650. ISBN 978-0321321367. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–56. [Google Scholar] [CrossRef]
- Thinsungnoena, T.; Kaoungkub, N.; Durongdumronchaib, P.; Kerdprasopb, K.; Kerdprasopb, N. The Clustering Validity with Silhouette and Sum of Squared Errors. In Proceedings of the 3rd International Conference on Industrial Application Engineering, Kitakyushu, Japan, 28–31 March 2015; Volume 3, pp. 44–51. [Google Scholar] [CrossRef]
- Romanowska, J.; Nowínski, K.S.; Trylska, J. Determining Geometrically Stable Domains in Molecular Conformation Sets. J. Chem. Theory Comput. 2012, 8, 2588–2599. [Google Scholar] [CrossRef]
- Grant, B.J.; Rodrigues, A.P.; El Sawy, K.M.; McCammon, J.A.; Caves, L.S. Bio3d: An R Package for the Comparative Analysis of Protein Structures. Available online: https://CRAN.R-project.org/package=bio3d (accessed on 2 January 2019).
- Grant, B.J.; Rodrigues, A.P.; El Sawy, K.M.; McCammon, J.A.; Caves, L.S. Bio3d: An R package for the comparative analysis of protein structures. Bioinformatics 2006, 22, 2695–2696. [Google Scholar] [CrossRef]
- Pearson, K. Notes on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]
- Hünenberger, P.H.; Mark, A.E.; van Gunsteren, W.F. Fluctuation and cross-correlation analysis of protein motions observed in nanosecond molecular dynamics simulations. J. Mol. Biol. 1995, 252, 492–503. [Google Scholar] [CrossRef]
- Kumari, R.; Kumar, R.; Lynn, A. g_mmpbsa: A GROMACS tool for high-throughput MMPBSA calculations. J. Chem. Inf. Model. 2014, 54, 1951–1962. [Google Scholar] [CrossRef]
- Baker, N.A.; Sept, D.; Joseph, S.; Holst, M.J.; McCammon, J.A. Electrostatics of nanosystems: Application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA 2001, 98, 10037–10041. [Google Scholar] [CrossRef]
- Sitkoff, D.; Sharp, K.A.; Honig, B. Accurate Calculation of Hydration Free-Energies Using Macroscopic Solvent Models. J. Phys. Chem. 1994, 98, 1978–1988. [Google Scholar] [CrossRef]
- Sun, A.; Yan, Y.N.; Yang, M.; Zhang, J.Z.H. Interaction entropy for protein-protein binding. J. Chem. Phys. 2017, 146, 124124. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Reading, MA, USA, 1977; p. 688. ISBN 0-201-07616-0. [Google Scholar]
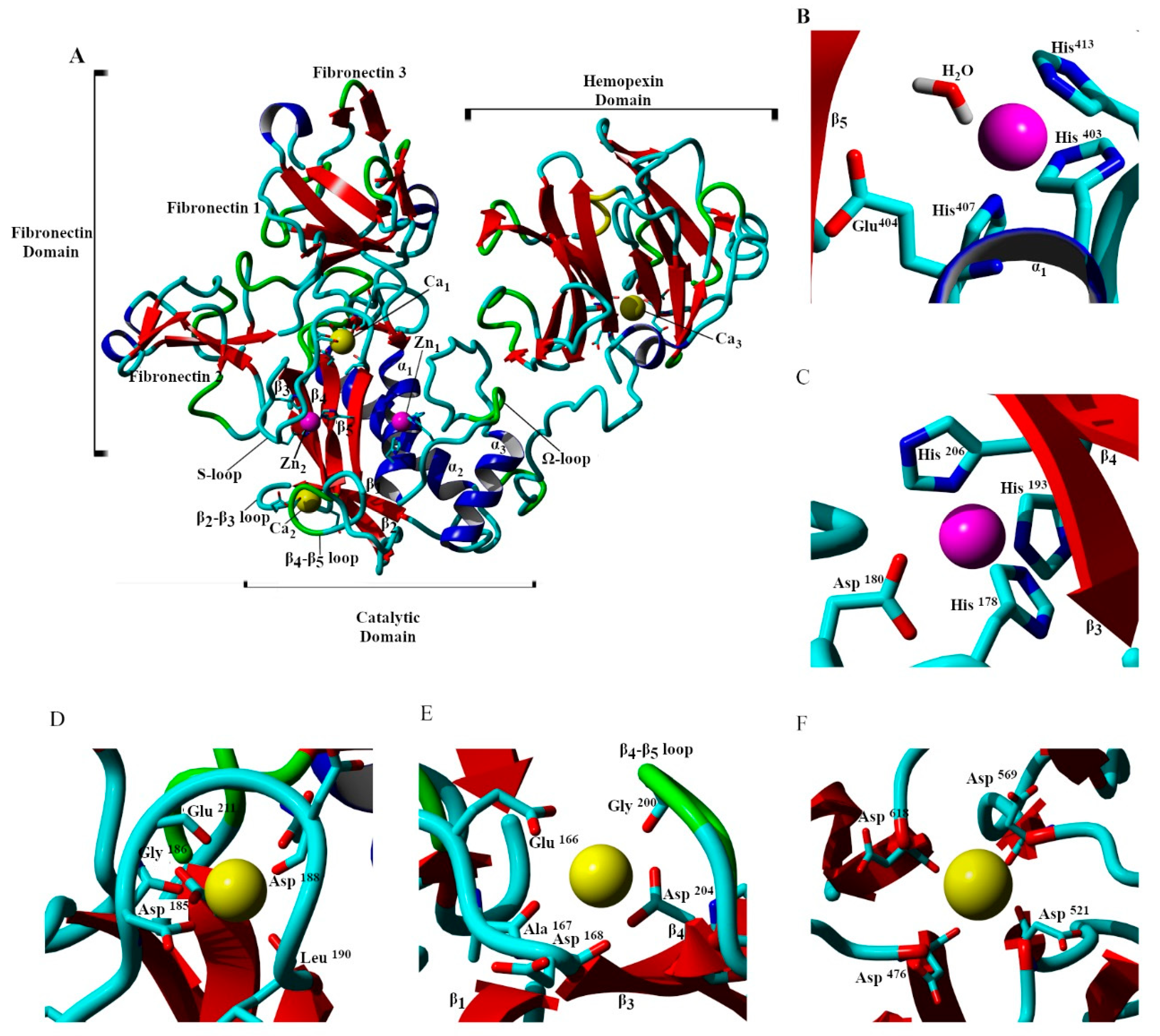
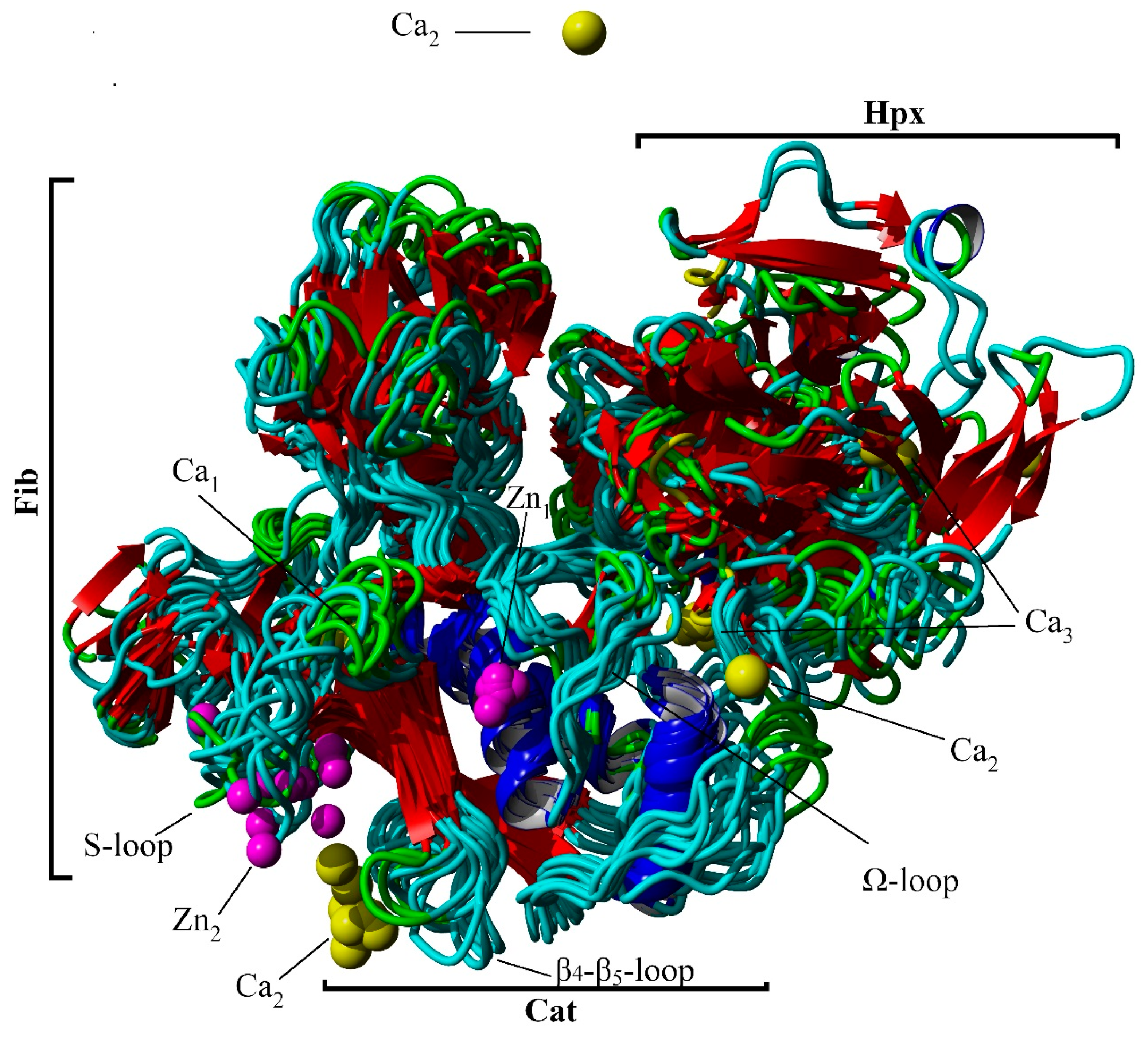

| Protein Atom | Geometry | Distance/nm | ||||
|---|---|---|---|---|---|---|
| Zn2+ ion 1 | Zn2+ ion 2 | Ca2+ ion 1 | Ca2+ ion 2 | Ca2+ ion 3 | ||
| His403:Nε2 | tetrahedral | 0.23 | ||||
| His407:Nε2 | tetrahedral | 0.22 | ||||
| His413:Nε2 | tetrahedral | 0.25 | ||||
| Water:O | tetrahedral | 0.25 | ||||
| Glu404:Oε1 | 0.83 | |||||
| Glu404:Oε2 | 0.76 | |||||
| His178:Nε2 | trigonal bipyramidal | 0.21 | ||||
| Asp180:Oδ2 | trigonal bipyramidal | 0.23 | ||||
| His193:Nε2 | trigonal bipyramidal | 0.21 | ||||
| His206:Nδ1 | trigonal bipyramidal | 0.21 | ||||
| Asp185:C=O | octahedral | 0.29 | ||||
| Gly186:C=O | octahedral | 0.24 | ||||
| Asp188:C=O | octahedral | 0.26 | ||||
| Leu198:C=O | octahedral | 0.25 | ||||
| Asp208:Oδ2 | octahedral | 0.25 | ||||
| Glu211:Oε2 | octahedral | 0.27 | ||||
| Ala167:C=0 | poorly coordinated | 0.29 | ||||
| Asp168:C=O | poorly coordinated | 0.29 | ||||
| Gly200:C=O | poorly coordinated | 0.27 | ||||
| Asp476:C=O | square planar | 0.25 | ||||
| Asp521:C=O | square planar | 0.28 | ||||
| Asp569:C=O | square planar | 0.27 | ||||
| Asp618:C=O | square planar | 0.27 | ||||
| All | Cat w/ Fib | Fib | Cat w/o Fib | Hpx | Lnk | |
|---|---|---|---|---|---|---|
| RMSD/nm | 3.20 ± 0.14 | 3.34 ± 0.02 | 3.69 ± 0.03 | 0.50 ± 0.03 | 0.34 ± 0.04 | 0.54 ± 0.08 |
| Zn2+ ion 1 | Zn2+ ion 2 | Ca2+ ion 1 | Ca2+ ion 2 | Ca2+ ion 3 | |
|---|---|---|---|---|---|
| RMSF/nm | 0.593 | 0.882 | 0.571 | 2.906 | 1.062 |
| Property | Zn2+ ion 1 | Zn2+ ion 2 | Ca2+ ion 1 | Ca2+ ion 2 | Ca2+ ion 3 |
|---|---|---|---|---|---|
| ρ (1st shell) | 0.20 | 0.26 | 0.07 | 0.23 | 0.25 |
| ρ (2nd shell) | 0.29 | 0.41 | 0.22 | 0.44 | 0.41 |
| SASA/nm2 | 0.002 ± 0.010 | 0.046 ± 0.030 | 0.021 ± 0.013 | 0.311 ± 0.110 | 0.302 ± 0.119 |
| CN | 1 to 2 | 2 | 1 | 3 | 3 |
| Mean ± Standard Deviation/kJ mol−1 | |||||||
|---|---|---|---|---|---|---|---|
| Ion(s) | ∆Evdw | ∆Eelec | ∆Gpolar | ∆Gnon-polar | −T∆S | ∆Ebinding | ∆Gbinding |
| All ions | 95.04 ± 2.92 | −9264.45 ± 194.34 | 3142.58 ± 81.6 | −3.95 ± 0.13 | 6.77 | −6020.73 ± 116.75 | −6013.96 ± 116.75 |
| Zn2+ ion 1 | 25.41 ± 0.77 | −2427.66 ± 72.19 | 1291.3 ± 42.75 | −0.88 ± 0.04 | 0.63 | −1114.16 ± 27.12 | −1113.51 ± 27.12 |
| Zn2+ ion 2 | 13.79 ± 0.96 | −799.35 ± 63.45 | 188.73 ± 35.14 | −0.47 ± 0.04 | 0.52 | −598.61 ± 29.09 | −598.09 ± 29.09 |
| Ca2+ ion 1 | 38.15 ± 1.90 | −1796.42 ± 89.21 | 605.84 ± 30.55 | −1.14 ± 0.07 | 1.03 | −1154.73 ± 56.65 | −1153.69 ± 56.65 |
| Ca2+ ion 2 | 6.52 ± 0.58 | −367.21 ± 36.96 | 73.71 ± 9.94 | −0.35 ± 0.05 | 0.18 | −289.24 ± 27.33 | −298.07 ± 27.33 |
| Ca2+ ion 3 | 14.94 ± 0.57 | −1480.59 ± 42.61 | 320.38 ± 11.31 | −1.32 ± 0.05 | 0.23 | −1147.96 ± 30.78 | −1147.73 ± 30.78 |
| Protein Atom | ∆Ebinding | Geometry | Zn2+ Ion 1 | Zn2+ ion 2 | Ca2+ ion 1 | Ca2+ ion 2 | Ca2+ ion 3 |
|---|---|---|---|---|---|---|---|
| †*Glu404:Oε1 | −154.8223 | 0.46 ± 0.05 | |||||
| †*Glu404:Oε2 | 0.48 ± 0.06 | ||||||
| †*His403:Nε2 | −72.1511 | trigonal pyramidal | 0.21 ± 0.01 | ||||
| †*His407:Nε2 | −66.3450 | trigonal pyramidal | 0.21 ± 0.01 | ||||
| †*His413:Nε2 | −61.5998 | trigonal pyramidal | 0.21 ± 0.01 | ||||
| †*Asp180:Oδ1 | −92.3424 | linear | 0.19 ± 0.01 | ||||
| †*Asp180:Oδ2 | linear | 0.19 ± 0.01 | |||||
| †*Asp185:Oδ1 | seesaw | 0.29 ± 0.16 | |||||
| †*Asp185:Oδ2 | seesaw | 0.28 ± 0.16 | |||||
| †*Glu211:Oε1 | −147.6924 | seesaw | 0.33 ± 0.11 | ||||
| †*Glu211:Oε2 | seesaw | 0.35 ± 0.10 | |||||
| †*Asp208:Oδ1 | −142.7074 | seesaw | 0.34 ± 0.09 | ||||
| †*Asp208:Oδ2 | seesaw | 0.24 ± 0.02 | |||||
| *Asp210:Oδ1 | −112.8532 | seesaw | 0.33 ± 0.14 | ||||
| *Asp210:Oδ2 | seesaw | 0.35 ± 0.14 | |||||
| Asp168:Oδ1 | N/C | 2.57 ± 1.59 | |||||
| Asp168:Oδ2 | N/C | 2.54 ± 1.60 | |||||
| †Ala167:C=O | −1.3321 | N/C | 2.52 ± 1.75 | ||||
| †Gly200:C=O | 0.3799 | N/C | 2.57 ± 1.70 | ||||
| †Gly202:C=O | −1.0605 | N/C | 2.55 ± 1.56 | ||||
| *Asp521:Oδ2 | N/C | 0.98 ± 0.16 | |||||
| †*Asp569:C=O | −79.0260 | N/C | 0.71 ± 0.18 | ||||
| *Asp569:Oδ1 | N/C | 0.92 ± 0.15 | |||||
| *Asp569:Oδ2 | N/C | 0.91 ± 0.15 | |||||
| *Asp490:Oδ1 | −69.0106 | N/C | 1.19 ± 0.11 | ||||
| *Asp490:Oδ2 | N/C | 1.19 ± 0.11 | |||||
| *Asp615:Oδ1 | −68.1150 | N/C | 1.29 ± 0.14 | ||||
| *Asp615:Oδ2 | N/C | 1.30 ± 0.14 | |||||
| *Asp153:Oδ1 | −63.3125 | N/C | 2.52 ± 0.96 | ||||
| *Asp153:Oδ2 | N/C | 2.51 ± 0.95 | |||||
| *Asp472:Oδ1 | −54.3377 | N/C | 1.54 ± 0.15 | ||||
| *Asp472:Oδ2 | N/C | 1.54 ± 0.15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voit-Ostricki, L.; Lovas, S.; Watts, C.R. Conformation and Domain Movement Analysis of Human Matrix Metalloproteinase-2: Role of Associated Zn2+ and Ca2+ Ions. Int. J. Mol. Sci. 2019, 20, 4194. https://doi.org/10.3390/ijms20174194
Voit-Ostricki L, Lovas S, Watts CR. Conformation and Domain Movement Analysis of Human Matrix Metalloproteinase-2: Role of Associated Zn2+ and Ca2+ Ions. International Journal of Molecular Sciences. 2019; 20(17):4194. https://doi.org/10.3390/ijms20174194
Chicago/Turabian StyleVoit-Ostricki, Leah, Sándor Lovas, and Charles R. Watts. 2019. "Conformation and Domain Movement Analysis of Human Matrix Metalloproteinase-2: Role of Associated Zn2+ and Ca2+ Ions" International Journal of Molecular Sciences 20, no. 17: 4194. https://doi.org/10.3390/ijms20174194
APA StyleVoit-Ostricki, L., Lovas, S., & Watts, C. R. (2019). Conformation and Domain Movement Analysis of Human Matrix Metalloproteinase-2: Role of Associated Zn2+ and Ca2+ Ions. International Journal of Molecular Sciences, 20(17), 4194. https://doi.org/10.3390/ijms20174194