Four-Reference State-Specific Brillouin-Wigner Coupled-Cluster Method: Study of the IBr Molecule

Abstract

We implemented the state-specific Brillouin–Wigner coupled-cluster method for the complete model space spanned by four reference configurations generated by two electrons in two active orbitals. We applied the method (together with the previously suggested a posteriori size-extensivity correction) to the calculation of spectroscopic constants of the IBr molecule, using averaged relativistic effective core potential.

1. Introduction

This paper is a continuation of our previous studies [1,2,3,4,5,6,7,8,9] on the development of a multi-reference coupled-cluster (MRCC) method that would be free of the problem of intruder states and that would be amenable to treatment of systems requiring more than two reference configurations. Avoidance of intruder states was achieved by using the Brillouin-Wigner (BW) resolvent, and simplicity of the method and feasibility of calculations were achieved by subjecting the BWCCSD method to a state-specific form [2,3,4]. Although the method so developed was general in respect to the number of reference configurations, its implementation [4] in the ACES II program [10] was limited to two-reference cases, where HOMO and LUMO orbitals have different spatial symmetry and only two closed-shell configurations can contribute to the wave function. In order to be able to treat molecules with quasidegenerate HOMO and LUMO orbitals with the same spatial symmetry, we extended our original implementation of the BWCCSD method for open shell reference configurations. For merits of the state-specific BW theory we paid the price that the method was not size extensive any longer. We developed therefore an a posteriori correction [5,6] for eliminating the size-inconsistent terms in the amplitudes. Again, the correction in its original implementation [6] was confined to two-reference cases. In this paper it has been generalized and calculated for four reference configurations.

The IBr molecule was selected for testing. Its HOMO and LUMO are of the same symmetry and the two singly excited configurations (determinants) HOMO → LUMO have to be included in the reference space. One of us (J. P.) was a coauthor of a paper [11] dealing with single‑reference calculations on IBr. Results of these calculations are used in this paper for judging the performance of BWCCSD. Finally, IBr was selected for that reason that this molecule is also interesting experimentally and the MR BWCCSD calculations could be helpful for the theoretical interpretation.

The IBr has been studied for several decades.

The early measurements of spectra of IBr in visible [12] and ultraviolet [13] have found bands corresponding to transitions to higher electronic states. Further studies confirmed these findings [14] and gave refined values of rotational and vibrational constants from high resolution far infrared absorption spectra [15]. The value of dissociation energy was obtained from isotopically selective velocity mapping measurements [16]. The predissociation of IBr has been studied by resonance Raman spectroscopy [17], pump‑probe experiments [18] and time dependent wave packet dynamics [19]. Recently ion imaging methods were used to investigate the photolysis of IBr [20].

Early theoretical calculations of electronic structure on IBr [21] were performed at Hartree‑Fock level. Subsequent ab initio studies with inclusion of relativistic effects provided values of spectroscopic [11,22,23] and electric [22,24,25] properties.

2. Theory

Since the derivation of the state-specific Brillouin-Wigner coupled-cluster theory has been presented for the general multireference case previously [3,5], and details of the implementation for closed-shell molecules have also been published [4], we give here only a brief review of the method and the relevant working equations.

We use the notation that i, j and a, b indices represent occupied and unoccupied spin-orbitals, respectively, while p, q are generic spin‑orbital indices. Moreover, we reserve the letters k and c for denoting the internal excitations (thus these indices are fixed for a given pair of reference configurations μ, ν), while i, j, a, b are used as general or summation indices. For many systems, including the IBr molecule, k is the HOMO and c is the LUMO orbital and the four (spin‑unrestricted) reference configurations are generated by all possible occupations of these two orbitals by two electrons.

The model function for the ground state is assumed in the form

$${{\displaystyle \mathrm{\Psi }}}_0^P={\displaystyle \sum _{\mu =0}^M{{\displaystyle C}}_{\mu }}{{\displaystyle \mathrm{\Phi }}}_{\mu }$$

(1)

where M is the number of reference configurations. For the exact ground‑state wave function Ψ₀ and exact energy ${\tilde{E}}_0$ it holds

$${{\displaystyle \mathrm{\Psi }}}_0={{\displaystyle \mathrm{\Omega }}}_0{{\displaystyle \mathrm{\Psi }}}_0^P$$

(2)

and

$${{\displaystyle H}}^{eff}{{\displaystyle \mathrm{\Psi }}}_0^P={{\displaystyle \tilde{E}}}_0{{\displaystyle \mathrm{\Psi }}}_0^P$$

(3)

The "effective" Hamiltonian H^eff is defined as

$${{\displaystyle H}}^{eff}=PH{{\displaystyle \mathrm{\Omega }}}_{0}P$$

(4)

where P is the projection operator onto the model space spanned by M configurations

$$P={\displaystyle \sum _{\mu =0}^M|{{\displaystyle \mathrm{\Phi }}}_{\mu }\rangle }\langle {{\displaystyle \mathrm{\Phi }}}_{\mu }|$$

(5)

Assuming the CCSD cluster operator T(μ) = T₁(μ) + T₂(μ) with respect to configuration μ as Fermi vacuum, the wave operator Ω₀ in the Hilbert space ansatz [26]

$${{\displaystyle \mathrm{\Omega }}}_0={\displaystyle \sum _{\mu =0}^M{{\displaystyle e}}^{T(\mu )}}|{{\displaystyle \mathrm{\Phi }}}_{\mu }\rangle \langle {{\displaystyle \mathrm{\Phi }}}_{\mu }|$$

(6)

is subject to the state-specific Brillouin-Wigner analogue of the Bloch equation

$${{\displaystyle \mathrm{\Omega }}}_0={{\displaystyle 1+B}}_{0}V{{\displaystyle \mathrm{\Omega }}}_0$$

(7)

where B₀ is the Brillouin-Wigner resolvent

$${{\displaystyle B}}_0={\displaystyle \sum _{q>M}\frac{|{{\displaystyle \mathrm{\Phi }}}_q\rangle \langle {{\displaystyle \mathrm{\Phi }}}_q|}{{{\displaystyle \tilde{E}}}_0-{{\displaystyle E}}_q}}$$

(8)

Here ${\tilde{E}}_0$ denotes the exact energy (lowest eigenvalue of H^eff), while E_q are the unperturbed energies corresponding to Φ_q similarly as in the Rayleigh‑Schrödinger resolvent, and the notation q >M in Eq. (8) means that internal excitations (the ones relating Φ_μ and Φ_ν, μ,ν ≤ M) are excluded.

The diagonal matrix elements of the effective Hamiltonian read

$${{\displaystyle H}}_{\mu \mu }^{eff}={{\displaystyle H}}_{\mu \mu }+\langle {{\displaystyle \mathrm{\Phi }}}_{\mu }|{{\displaystyle H}}_N{\displaystyle (\mu )}{{\displaystyle e}}^{T(\mu )}|{{\displaystyle \mathrm{\Phi }}}_{\mu }\rangle$$

(9)

where H_μμ is Hamiltonian expectation value for reference configuration Φ_μ and H_N(μ) is the Hamiltonian normally ordered with respect to Fermi vacuum Φ_μ. They can be computed by a modified routine for energy in single-reference CCSD [4]. Coupling between the reference configurations is furnished by the off-diagonal elements

$${{\displaystyle H}}_{\nu \mu }^{eff}=\langle {{\displaystyle \mathrm{\Phi }}}_{\nu }|{{\displaystyle H}}_N{\displaystyle (\mu )}{{\displaystyle e}}^{T(\mu )}|{{\displaystyle \mathrm{\Phi }}}_{\mu }\rangle$$

(10)

These have to be treated separately for cases when Φ_ν and Φ_μ are single- or double-excitations with respect to each other. In the former case we can write either ${\mathrm{\Phi }}_{\nu }={({\mathrm{\Phi }}_{\mu })}_k^c$ or ${\mathrm{\Phi }}_{\nu }={({\mathrm{\Phi }}_{\mu })}_{\overline{k}}^{\overline{c}}$ and the matrix elements are obtained as r.h.s. of the T₁ amplitude update equations. In the latter ${\mathrm{\Phi }}_{\nu }={({\mathrm{\Phi }}_{\mu })}_{k\overline{k}}^{c\overline{c}}$ and the matrix element is obtained from the T₂ amplitude equations as described in [4]. Presently, our implementation does not support reference configurations which would be mutually more than biexcited.

The final equations for T₁ amplitudes read

$$\left[{{\displaystyle F}}_{ii}^{\mu }-{{\displaystyle F}}_{aa}^{\mu }+{{\displaystyle \tilde{E}}}_0-{{\displaystyle H}}_{\mu \mu }^{eff}\right]{{\displaystyle t}}_i^a=\left\{\langle {{\displaystyle \mathrm{\Phi }}}_i^a(\mu )|{{\displaystyle H}}_N(\mu ){{\displaystyle e}}^{T(\mu )}{|{{\displaystyle \mathrm{\Phi }}}_{\mu }\rangle }_C+\left[{{\displaystyle F}}_{ii}^{\mu }-{{\displaystyle F}}_{aa}^{\mu }\right]{{\displaystyle t}}_i^a\right\}$$

(11)

where the r.h.s. is the same as in the case of single reference CCSD, except that the amplitudes of internal excitations are set to zero. In the T₂ case we have

$$\begin{array}{l}({{\displaystyle \tilde{E}}}_0-{{\displaystyle H}}_{\mu \mu }^{eff}+{{\displaystyle F}}_{ii}^{\mu }+{{\displaystyle F}}_{jj}^{\mu }-{{\displaystyle F}}_{aa}^{\mu }-{{\displaystyle F}}_{bb}^{\mu }){\left({{\displaystyle t}}_{ij}^{ab}+{{\displaystyle t}}_i^a{{\displaystyle t}}_j^b-{{\displaystyle t}}_j^a{{\displaystyle t}}_i^b\right)}_{\mu }=\\ =\left\{\langle {{\displaystyle \mathrm{\Phi }}}_{ij}^{ab}(\mu )|{{\displaystyle H}}_N(\mu ){{\displaystyle e}}^{T(\mu )}{|{{\displaystyle \mathrm{\Phi }}}_{\mu }\rangle }_C+\left[{{\displaystyle F}}_{ii}^{\mu }+{{\displaystyle F}}_{jj}^{\mu }-{{\displaystyle F}}_{aa}^{\mu }-{{\displaystyle F}}_{bb}^{\mu }\right]{\left({{\displaystyle t}}_{ij}^{ab}+{{\displaystyle t}}_i^a{{\displaystyle t}}_j^b-{{\displaystyle t}}_j^a{{\displaystyle t}}_i^b\right)}_{\mu }\right\}+\\ {{\displaystyle +P}}_{ij}{{\displaystyle P}}_{ab}\left[{{\displaystyle t}}_i^a\langle {{\displaystyle \mathrm{\Phi }}}_j^b(\mu )|{{\displaystyle H}}_N(\mu ){{\displaystyle e}}^{T(\mu )}{|{{\displaystyle \mathrm{\Phi }}}_{\mu }\rangle }_C\right]\end{array}$$

(12)

where P_ij is antisymmetrization operator acting on the i, j indices. The r.h.s. term in curly brackets can be identified with the r.h.s. of the single reference CCSD equations computed with internal amplitudes set to zero. As described in[6], the amplitudes obtained by this method need to be corrected for retaining size-extensivity. The idea is to make BWCC a posteriori close to its Rayleigh-Schrödinger (RS) version. Since our BW variant of the Bloch equation (7) contains only a denominator of the type $({\tilde{E}}_0-E_q)$, it can be cast into the form

$${{\displaystyle \mathrm{\Omega }}}_0=1+{\displaystyle \sum _{q>M}\frac{|{{\displaystyle \mathrm{\Phi }}}_q\rangle \langle {{\displaystyle \mathrm{\Phi }}}_q|}{{{\displaystyle E}}_0-{{\displaystyle E}}_q}}V{{\displaystyle \mathrm{\Omega }}}_0+{\displaystyle \sum _{q>M}\frac{-\Delta {{\displaystyle \tilde{E}}}_0|{{\displaystyle \mathrm{\Phi }}}_q\rangle \langle {{\displaystyle \mathrm{\Phi }}}_q|}{\left({{\displaystyle \tilde{E}}}_0-{{\displaystyle E}}_q\right)\left({{\displaystyle E}}_0-{{\displaystyle E}}_q\right)}}V{{\displaystyle \mathrm{\Omega }}}_0$$

(13)

where

$$\Delta {\tilde{E}}_0={\tilde{E}}_0-E_0$$

(14)

The first two terms on the r.h.s. of Eq. (13) are size-extensive because they may be viewed as the analog of the usual RS form of the Bloch equation. However, the "additional" third term on the r.h.s. of Eq. (13) gives, on iterating the BWCCSD equations, size-inextensive terms. Computationally, it is simplest to identify the size-inextensive terms in the amplitude update equations and eliminate them in an additional a posteriori iteration. For T₁ amplitudes the only term responsible for size-inextensivity is $[{\tilde{E}}_0-H_{\mu \mu }^{eff}]t_i^a$ on the l.h.s of Eq. (11). With the T₂ amplitudes it is the $({\tilde{E}}_0-H_{\mu \mu }^{eff}){(t_{ij}^{ab}+t_i^a{t}_j^b-t_j^a{t}_i^b)}_{\mu }$ term on the l.h.s of Eq. (12) and the last term on the r.h.s. of Eq. (12). From the corrected amplitudes we construct a new H^eff matrix, and by its diagonalization we obtain the final energy. Note that the size-inextensive terms cannot be eliminated during iterations, since the only coupling between amplitudes of different reference configurations, provided by ${\tilde{E}}_0$, would be lost.

The BWCCSD calculation proceeds iteratively. After a standard initial guess of amplitudes, the H^eff matrix elements are calculated and H^eff is diagonalized. The lowest eigenvalue is then used as ${\tilde{E}}_0$ and new T₁ and T₂ amplitudes for all reference configurations are computed according to Eqs. (11) and (12). This procedure is repeated, employing the DIIS convergence acceleration, until amplitudes converge. Subsequently the a posteriori size-extensivity correction is performed in an additional iteration.

Note that the absence of explicit coupling of amplitudes from different reference sets makes the method simple and computationally feasible for larger molecules. The computational demands per iteration for the M-reference BWCCSD method are thus only marginally higher than M times the demands for single-reference CCSD procedure.

3. Computational

In molecules containing heavy atoms, such as iodine or bromine, relativistic effects, and spin‑orbit (LS) interactions in particular, cannot be neglected and in some cases even first-order perturbative treatment is not accurate enough. Moreover, in order to obtain potential energy (PE) curve accurate enough in the whole range of internuclear distances, inclusion of both statical and dynamical electron correlation in a sophisticated way is absolutely essential. The ground state of the IBr molecule is ¹Σ+. Since it has zero angular and spin momentum, it is not subject to spin-orbit splitting, however, scalar relativistic effects play an important role. Therefore in our calculations the inner-shell electrons have been treated using recent averaged relativistic effective core potentials (AREP)[27]. We employed two valence basis sets: the basis set supplied together with the AREP of the size (6s6p1d/3s3p1d) for both I and Br labeled A, and basis set augmented by diffuse functions of size (8s8p3d/5s5p3d) for both atoms, labeled B, which is described in [11] and serves mainly for comparison with that paper. For each internuclear geometry, we performed first a CASSCF calculation with two electrons in the HOMO and LUMO active orbitals, i.e. the same active space as in BWCCSD. The canonical CASSCF orbitals were used in the subsequent BWCCSD treatment based on the four spin‑unrestricted reference configurations possible in this active space. Since the BWCCSD calculation is performed in a spin-unrestricted form, three eigenvalues of H^eff correspond to singlet states and one to a triplet. It has been checked that no spin contamination occurs in numerical procedure. The CASSCF was chosen for the description of the reference state because it is size extensive and correctly describes the static correlation.

For all coupled cluster calculations reported in this paper, we used our implementation of the BW CCSD method [4] and of the a posteriori correction [6] within the ACES II program [10]. The MR-CISD results reported in this work were obtained using the GAMESS-UK program [19].

The spectroscopic constants were obtained from the polynomial expansion of the energy by means of the Dunham analysis. D_e values were obtained as difference between the minimum and the dissociation limit of the potential energy curves. Rovibrational levels (cf. Table 2) have been calculated by the program LEVEL [17].

4. Results and Discussion

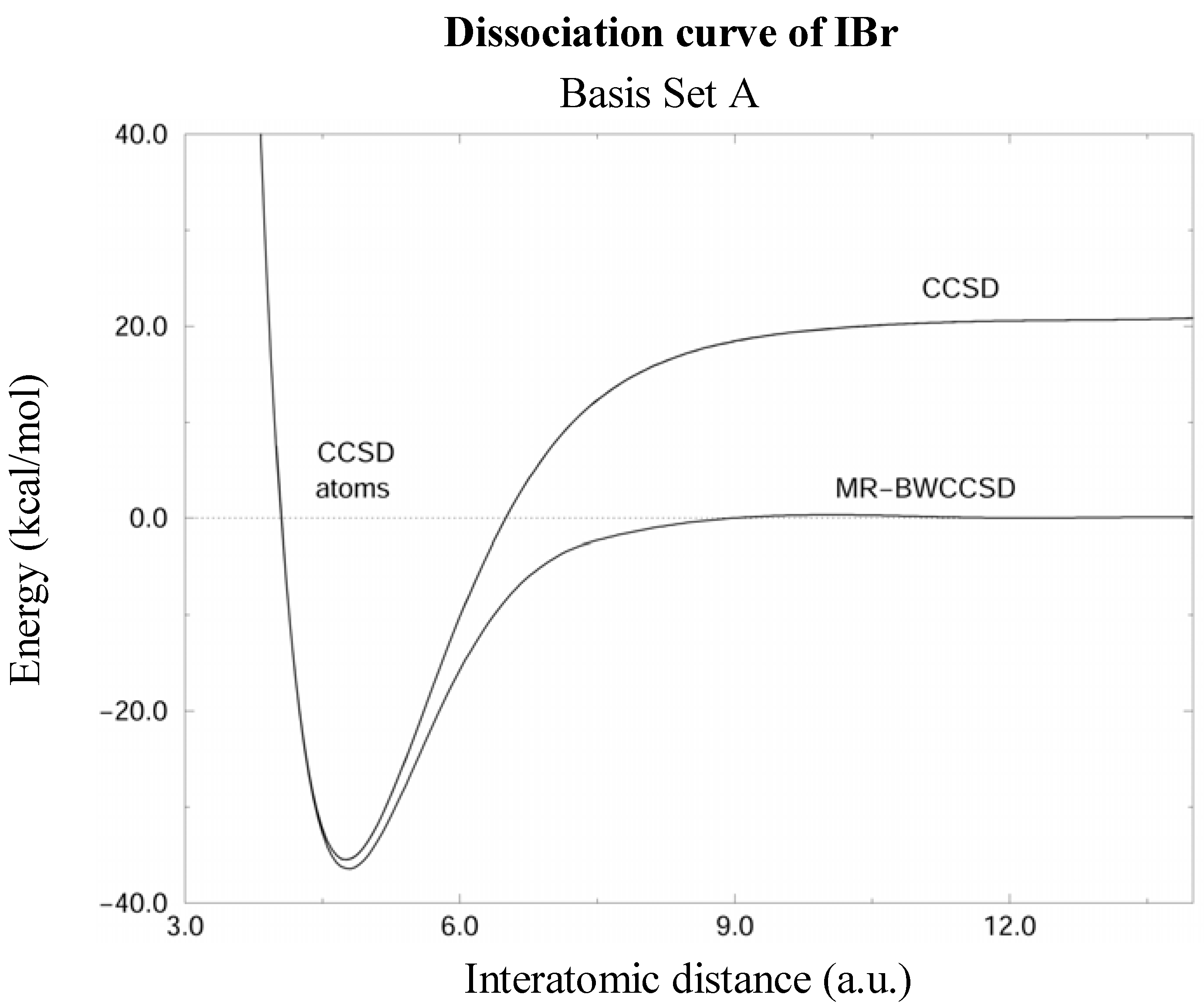
The MR-BWCCSD potential energy curves of IBr computed in basis sets A and B are shown in Figs. 1 and 2, respectively. CCSD curves are shown for comparison and it can be seen that the single reference method fails to meet the correct dissociation limit indicated by the dashed line. This clearly shows the need for a multireference description for larger interatomic distances, while near the equilibrium the single-reference description is quite reliable.

The calculated spectroscopic constants are compared with the sample results of previous works [11,22,23] in Table 1. We also computed a set of rovibrational levels, given in Table 2.

First we tested the size extensivity, and we found that the size-consistency error was small. It was only 0.10 kcal/mol with the basis set A and 0.11 kcal/mol with the basis set B. This is because the CASSCF orbitals are localized for large interatomic distances, which is beneficial for size consistency, making thus BWCCSD near size consistent even without the a posteriori correction.

On comparing the calculated spectroscopic constants with those obtained from single‑reference calculations [11], using both the same basis set B and the pseudopotential, it can be seen that the dissociation energy D_e has decreased from 47.7 kcal/mol (CCSD) to 38.0 kcal/mol (MR BWCCSD), due to the multireference description at large internuclear separation. The equilibrium bond length r_e has increased by approximately 0.01 Å, while the vibrational frequency ω_e has decreased slightly and the anharmonicity ω_ex_e remained almost same. They are also very similar to values obtained by the MR-CISD method (cf. Table 1). The lack of improvement of the multi-reference method for r_e, ω_e and ω_ex_e with respect to single reference CCSD can be explained by a low contribution of the excited references near the equilibrium geometry and therefore effective reduction of BWCCSD to a single reference CCSD, since the values of r_e, ω_e, and ω_ex_e are determined by the shape of the PES curve near equilibrium. Additional inclusion of dynamical correlation by means of connected triples, when implemented, should result in an improvement of the obtained spectroscopic constants.

Figure 1. Potential energy curves of the IBr molecule calculated by the CCSD and MR-BWCCSD methods in the basis set A (see text) shown by solid lines. Energy scale is relative to the sum of energies of isolated atoms, which is indicated by the dashed line. Notice the incorrect dissociation limit of the single-reference CCSD.

Figure 1. Potential energy curves of the IBr molecule calculated by the CCSD and MR-BWCCSD methods in the basis set A (see text) shown by solid lines. Energy scale is relative to the sum of energies of isolated atoms, which is indicated by the dashed line. Notice the incorrect dissociation limit of the single-reference CCSD.

Figure 2. Potential energy curves of the IBr molecule calculated by the CCSD and MR-BWCCSD methods in the basis set B (see text) shown by solid lines. Energy scale is relative to the sum of energies of isolated atoms, which is indicated by the dashed line. Notice the incorrect dissociation limit of the single-reference CCSD.

Figure 2. Potential energy curves of the IBr molecule calculated by the CCSD and MR-BWCCSD methods in the basis set B (see text) shown by solid lines. Energy scale is relative to the sum of energies of isolated atoms, which is indicated by the dashed line. Notice the incorrect dissociation limit of the single-reference CCSD.

Table 1. Spectroscopic constants of IBr

Methoda	Basis set	re(Å)	ωe(cm‑1)	ωexe(cm‑1)	De(kcal mol-1)
NR-HF [22]	apVDZ	2.508	284		18.4
NR-HF [22]	apVTZ	2.472	295		25.7
DC-HF[22]	apVDZ	2.510	276		8.0
DC-HF [22]	apVTZ	2.475	287		14.5
NR-MP2[22]	apVDZ	2.537	264		40.2
NR-MP2[22]	apVTZ	2.483	283		50.5
DC-MP2 [22]	apVDZ	2.541	246		30.9
DC-MP2 [22]	apVTZ	2.486	275		40.4
NR-CCSD [22]	apVDZ	2.552	255		37.2
NR-CCSD [22]	apVTZ	2.497	275		44.0
DC-CCSD [22]	apVDZ	2.557	246		28.0
DC-CCSD [22]	apVTZ	2.501	266		34.1
NR-CCSD(T) [22]	apVDZ	2.562	247		39.5
NR-CCSD(T) [22]	apVTZ	2.506	267		47.1
DC-CCSD(T) [22]	apVDZ	2.568	237		30.4
DC-CCSD(T) [22]	apVTZ	2.511	258		37.4
HFb [23]	(3s3p1d)	2.489	281		16.8
KRHFb [23]	(3s3p1d)	2.499	272		7.1
MP2b [23]	(3s3p1d)	2.510	267		42.6
KRMP2b [23]	(3s3p1d)	2.522	255		33.0
MR-CISDb,c,e	B	2.534	249		37.9
MR-CISDb,d,e	B	2.537	247		39.3
CCSDb,e [11]	B	2.520	253	0.87	47.7
MR-BWCCSDb,f	A	2.531	252	0.87	36.5
MR-BWCCSDb,f	B	2.534	250	0.89	38.0
experiment [30]		2.469	269	0.81	42.3

^a NR means nonrelativistic, DC relativistic.

^b Using a relativistic effective core potential.

^c The same reference configurations as in MR-BWCCSD; without size-extensivity correction.

^d The same reference configurations as in MR-BWCCSD; with Davidson correction.

^e Based on RHF molecular orbitals.

^f Based on CASSCF molecular orbitals.

Table 1. Spectroscopic constants of IBr

Methoda	Basis set	re(Å)	ωe(cm‑1)	ωexe(cm‑1)	De(kcal mol-1)
NR-HF [22]	apVDZ	2.508	284		18.4
NR-HF [22]	apVTZ	2.472	295		25.7
DC-HF[22]	apVDZ	2.510	276		8.0
DC-HF [22]	apVTZ	2.475	287		14.5
NR-MP2[22]	apVDZ	2.537	264		40.2
NR-MP2[22]	apVTZ	2.483	283		50.5
DC-MP2 [22]	apVDZ	2.541	246		30.9
DC-MP2 [22]	apVTZ	2.486	275		40.4
NR-CCSD [22]	apVDZ	2.552	255		37.2
NR-CCSD [22]	apVTZ	2.497	275		44.0
DC-CCSD [22]	apVDZ	2.557	246		28.0
DC-CCSD [22]	apVTZ	2.501	266		34.1
NR-CCSD(T) [22]	apVDZ	2.562	247		39.5
NR-CCSD(T) [22]	apVTZ	2.506	267		47.1
DC-CCSD(T) [22]	apVDZ	2.568	237		30.4
DC-CCSD(T) [22]	apVTZ	2.511	258		37.4
HFb [23]	(3s3p1d)	2.489	281		16.8
KRHFb [23]	(3s3p1d)	2.499	272		7.1
MP2b [23]	(3s3p1d)	2.510	267		42.6
KRMP2b [23]	(3s3p1d)	2.522	255		33.0
MR-CISDb,c,e	B	2.534	249		37.9
MR-CISDb,d,e	B	2.537	247		39.3
CCSDb,e [11]	B	2.520	253	0.87	47.7
MR-BWCCSDb,f	A	2.531	252	0.87	36.5
MR-BWCCSDb,f	B	2.534	250	0.89	38.0
experiment [30]		2.469	269	0.81	42.3

^a NR means nonrelativistic, DC relativistic.

^b Using a relativistic effective core potential.

^c The same reference configurations as in MR-BWCCSD; without size-extensivity correction.

^d The same reference configurations as in MR-BWCCSD; with Davidson correction.

^e Based on RHF molecular orbitals.

^f Based on CASSCF molecular orbitals.

Table 2. Rovibrational energy levels of IBr obtained from potential curve calculated by MR BWCCSD in basis B (cm^‑1)

	J
v	0	1	2	3	4	5	6
0	0.00	0.11	0.32	0.65	1.08	1.62	2.27
1	245.57	245.68	245.90	246.22	246.65	247.19	247.84
2	489.16	489.27	489.48	489.80	490.23	490.77	491.42
3	730.66	730.77	730.98	731.30	731.73	732.27	732.91
4	969.94	970.04	970.26	970.58	971.01	971.54	972.18

Table 2. Rovibrational energy levels of IBr obtained from potential curve calculated by MR BWCCSD in basis B (cm^‑1)

	J
v	0	1	2	3	4	5	6
0	0.00	0.11	0.32	0.65	1.08	1.62	2.27
1	245.57	245.68	245.90	246.22	246.65	247.19	247.84
2	489.16	489.27	489.48	489.80	490.23	490.77	491.42
3	730.66	730.77	730.98	731.30	731.73	732.27	732.91
4	969.94	970.04	970.26	970.58	971.01	971.54	972.18

As our experience with MR-BWCCSD shows, our previous results are very close to those of state-universal MR‑CCSD [4,8,31,32]. We believe that in case of IBr this will be similar. Unfortunately we did not find such a result from state-universal MR-CCSD method for comparison.

The dependence of the calculated values of r_e, ω_e and ω_ex_e show a very small difference between the two basis sets used. That means that adding extra diffuse functions to the basis set does not have a large effect on the ground state wave function in the equilibrium interatomic distance range. However the D_e value, which is slightly more sensitive, has changed by approximately 1.5 kcal mol^-1 towards the experimental value.

5. Conclusions

The BWCCSD method developed previously has been shown in this paper to be computationally feasible for a four-reference problem. The calculations performed for the IBr molecule yielded a smooth potential curve in the whole range of interatomic distances assumed (4 to 80 au). The potential curve has the correct dissociation limit, and the spectroscopic constants compare well with the experimental and best available theoretical data. The results obtained for IBr also provide another numerical evidence that the size-extensivity error of the MR BWCCSD method is small.