Maximum Topological Distances Based Indices as Molecular Descriptors for QSPR. 4. Modeling the Enthalpy of Formation of Hydrocarbons from Elements

doi:10.3390/i2020121

This article is

freely available
re-usable

Int. J. Mol. Sci. 2001, 2(2), 121-132; doi:10.3390/i2020121

Article

Maximum Topological Distances Based Indices as Molecular Descriptors for QSPR. 4. Modeling the Enthalpy of Formation of Hydrocarbons from Elements

Andrés Mercader ¹, Eduardo A. Castro ¹^,* and Andrey A. Toropov ¹

¹ CEQUINOR, Departamento de Química, Facultad de Ciencias Exactas, Universidad Nacional de la Plata, C.C. 962, La Plata 1900, Argentina ² Andrey A. Toropov, Vostok Innovation Company, S. Azimstreet 4, 100047 Tashkent, Uzbekistan

* Author to whom correspondence should be addressed.

Received: 9 April 2001 / Accepted: 15 June 2001 / Published: 28 June 2001

Download PDF Full-Text [196 KB, uploaded 11 September 2008 16:07 CET]

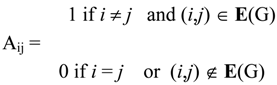
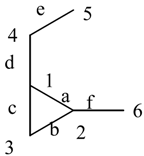
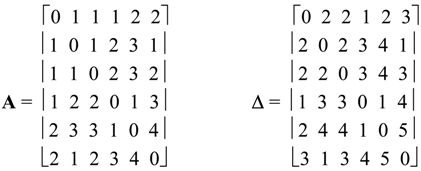
Abstract: The enthalpy of formation of a set of 60 hydroarbons is calculated on the basis of topological descriptors defined from the distance and detour matrices within the realm of the QSAR/QSPR theory. Linear and non-linear polynomials fittings are made and results show the need to resort to higher-order regression equations in order to get better concordances between theoretical results and experimental available data. Besides, topological indices computed from maximum order distances seems to yield rather satisfactory predictions of heats of formation for hydrocarbons.

Keywords: QSPR theory; Detour matrix; Enthalpy of formation; Hydrocarbons; Topological indices

Article Statistics

Click here to load and display the download statistics.

Cite This Article

MDPI and ACS Style

Mercader, A.; Castro, E.A.; Toropov, A.A. Maximum Topological Distances Based Indices as Molecular Descriptors for QSPR. 4. Modeling the Enthalpy of Formation of Hydrocarbons from Elements. Int. J. Mol. Sci. 2001, 2, 121-132.

AMA Style

Mercader A., Castro E.A., Toropov A.A. Maximum Topological Distances Based Indices as Molecular Descriptors for QSPR. 4. Modeling the Enthalpy of Formation of Hydrocarbons from Elements. International Journal of Molecular Sciences. 2001; 2(2):121-132.

Chicago/Turabian Style

Mercader, Andrés; Castro, Eduardo A.; Toropov, Andrey A. 2001. "Maximum Topological Distances Based Indices as Molecular Descriptors for QSPR. 4. Modeling the Enthalpy of Formation of Hydrocarbons from Elements." Int. J. Mol. Sci. 2, no. 2: 121-132.

Int. J. Mol. Sci. EISSN 1422-0067 Published by MDPI Publishing, Basel, Switzerland RSS E-Mail Table of Contents Alert