Meshless Method with Operator Splitting Technique for Transient Nonlinear Bioheat Transfer in Two-Dimensional Skin Tissues
Abstract
:1. Introduction
2. Numerical Results and Discussion
2.1. Verification of the Proposed Method
| Thermal Parameters | Value |
|---|---|
| Thermal conductivity k | 0.5 Wm−1·K−1 |
| Density of blood ρb | 1000 kg·m−3 |
| Specific heat of blood cb | 4200 J·kg−1·K−1 |
| Spatial heat Qr | 30,000 Wm−3 |
| Metabolic heat Qm | 4200 Wm−3 |
| Arterial temperature Tb | 37 °C |
| Temperature of body core Tc | 37 °C |
| Temperature of skin surface Ts | 25 °C |
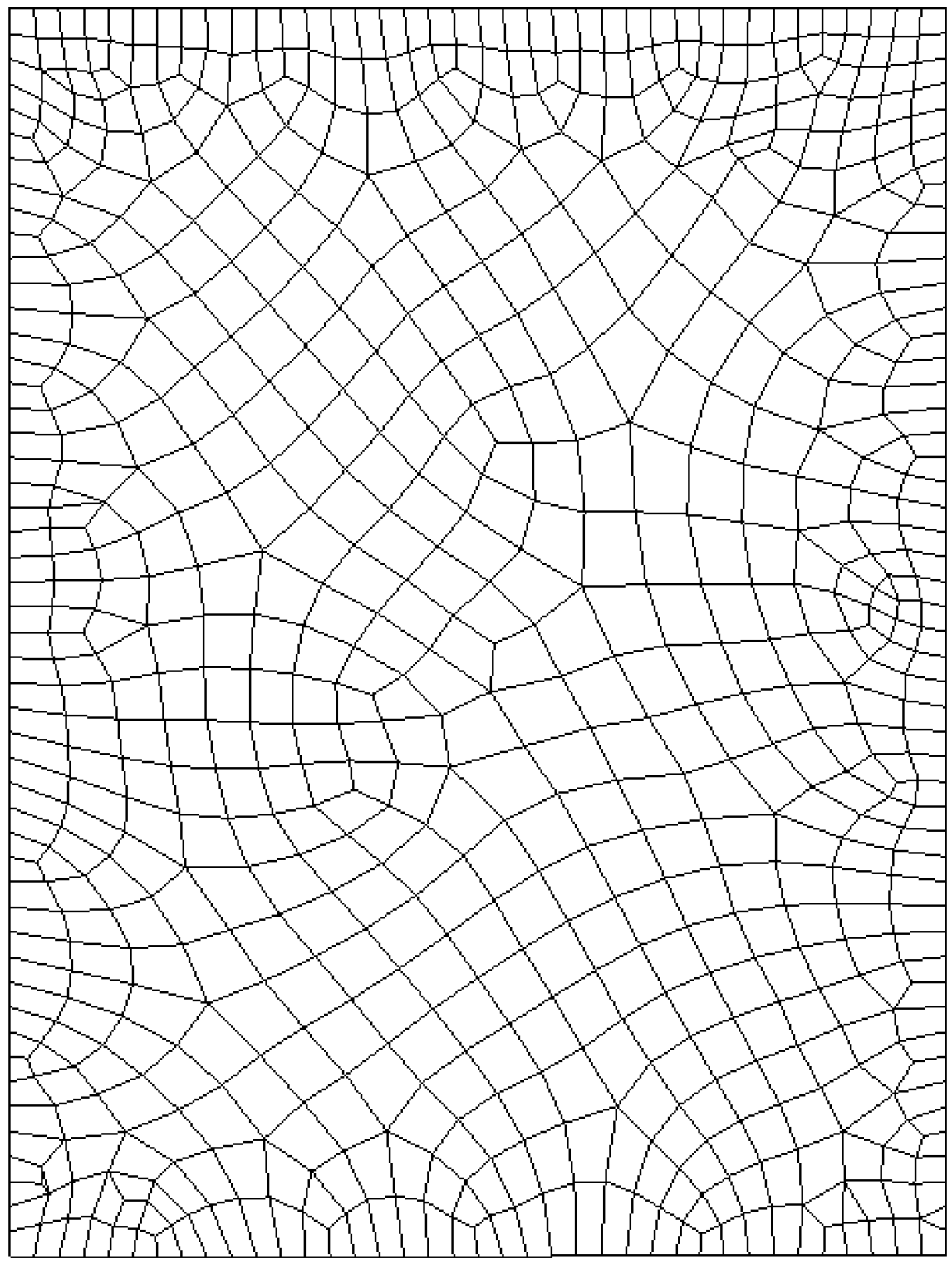
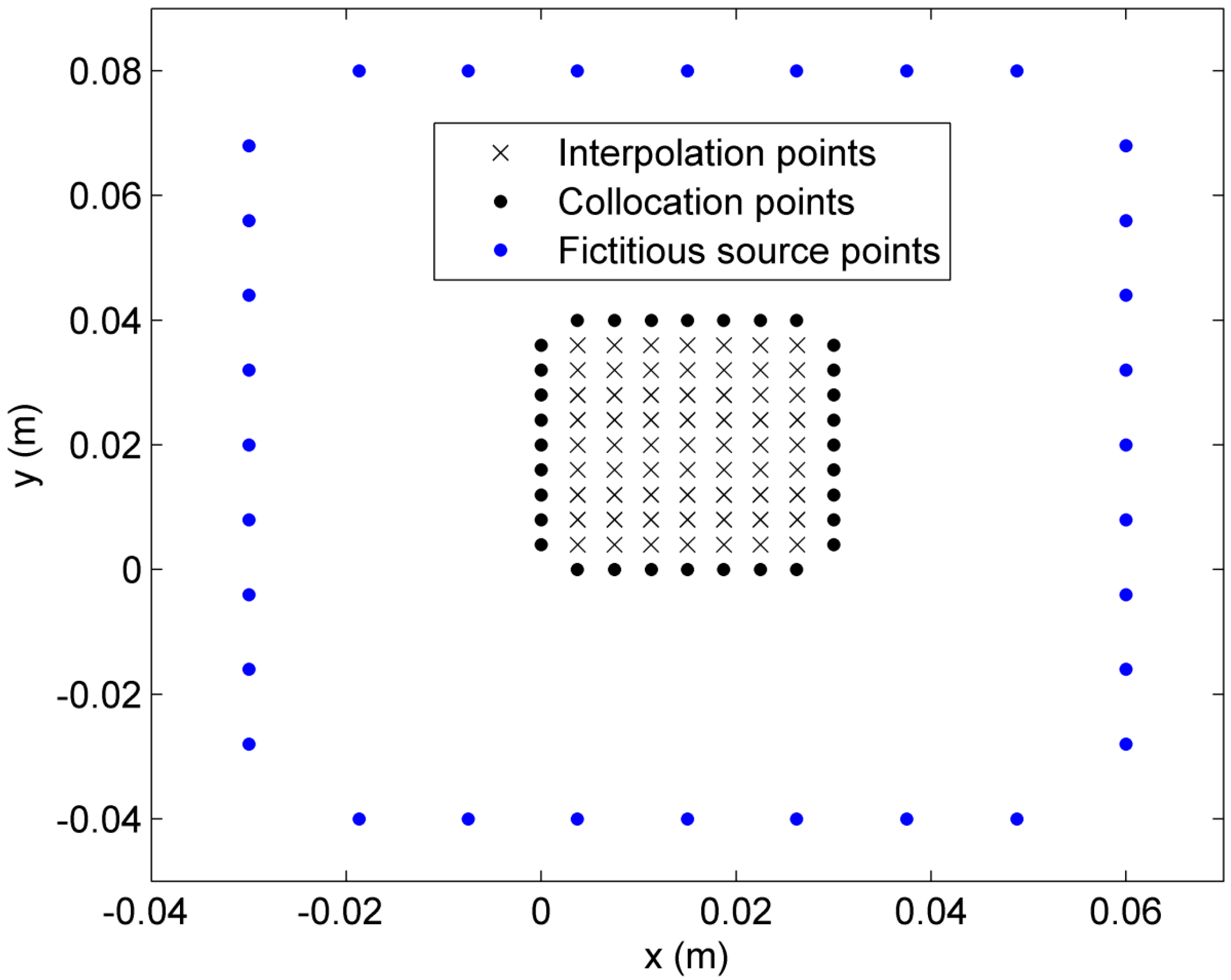
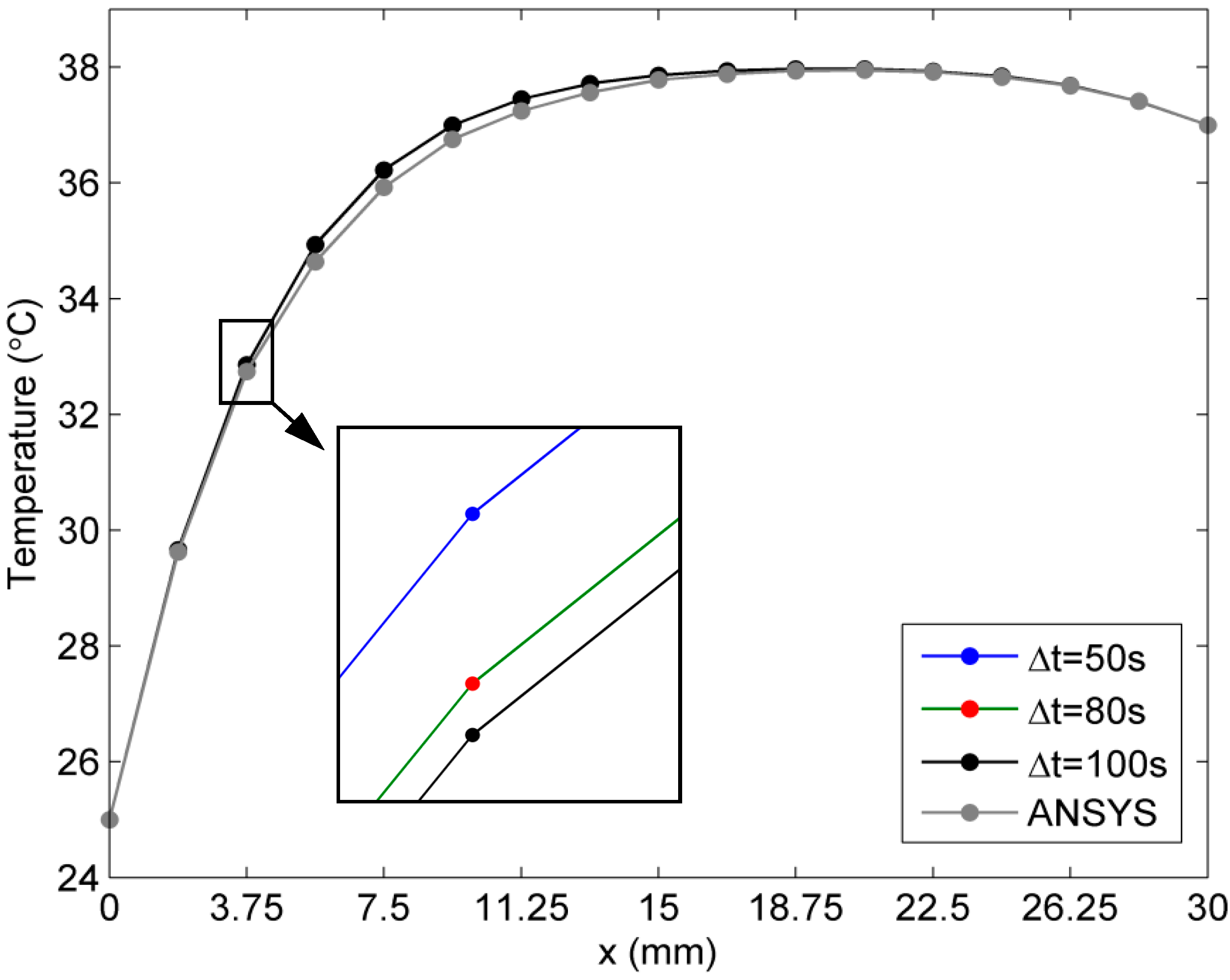
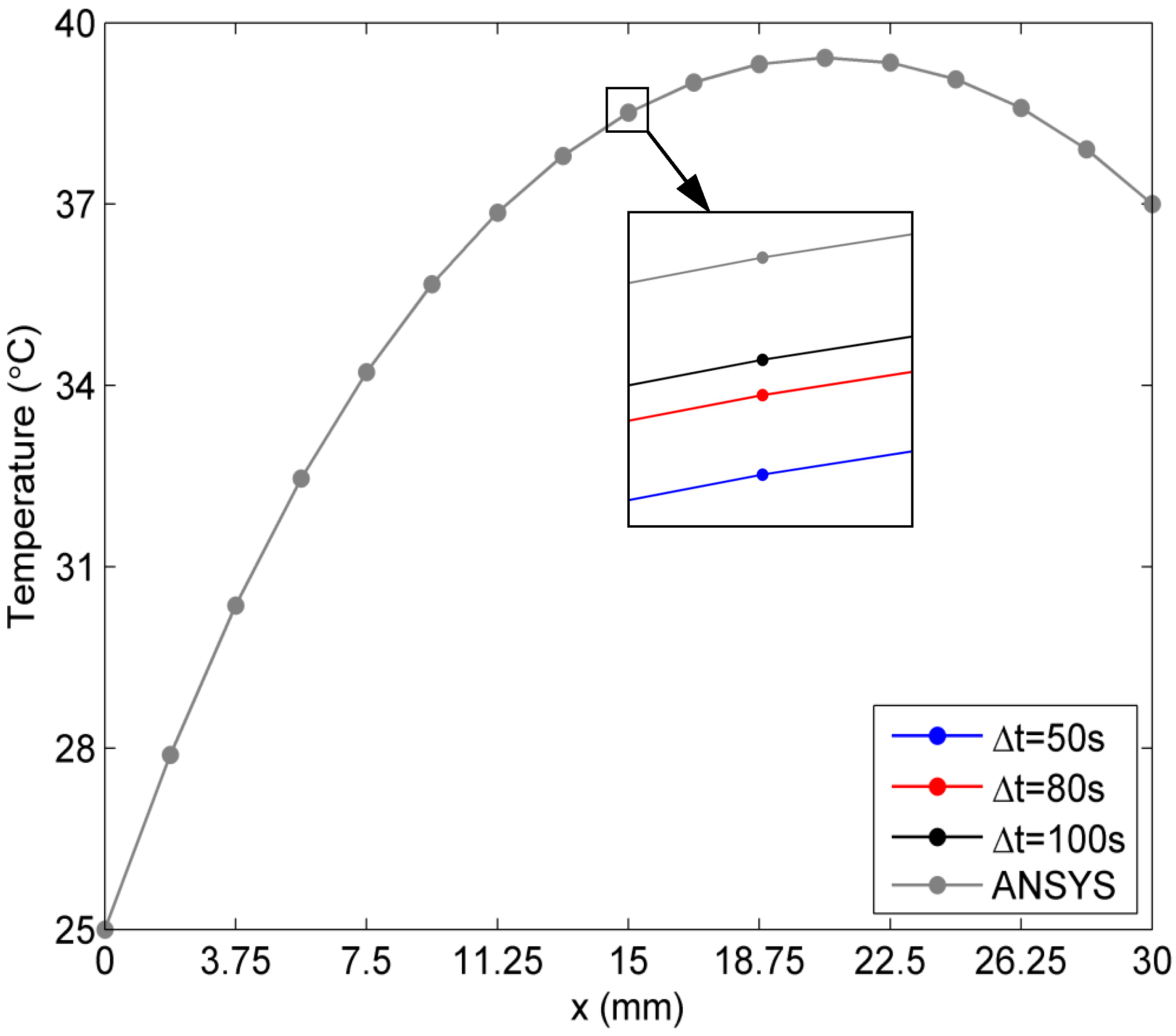
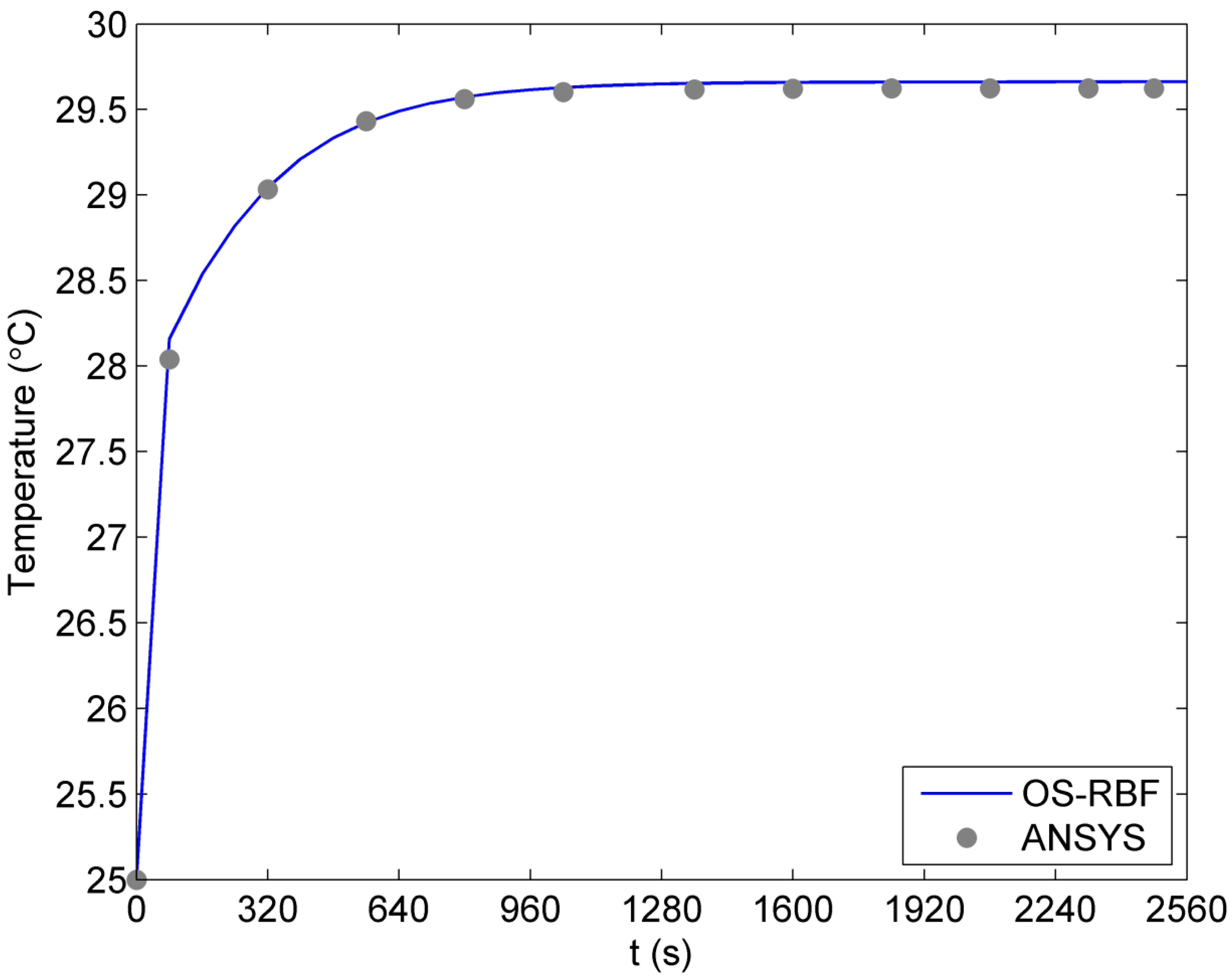

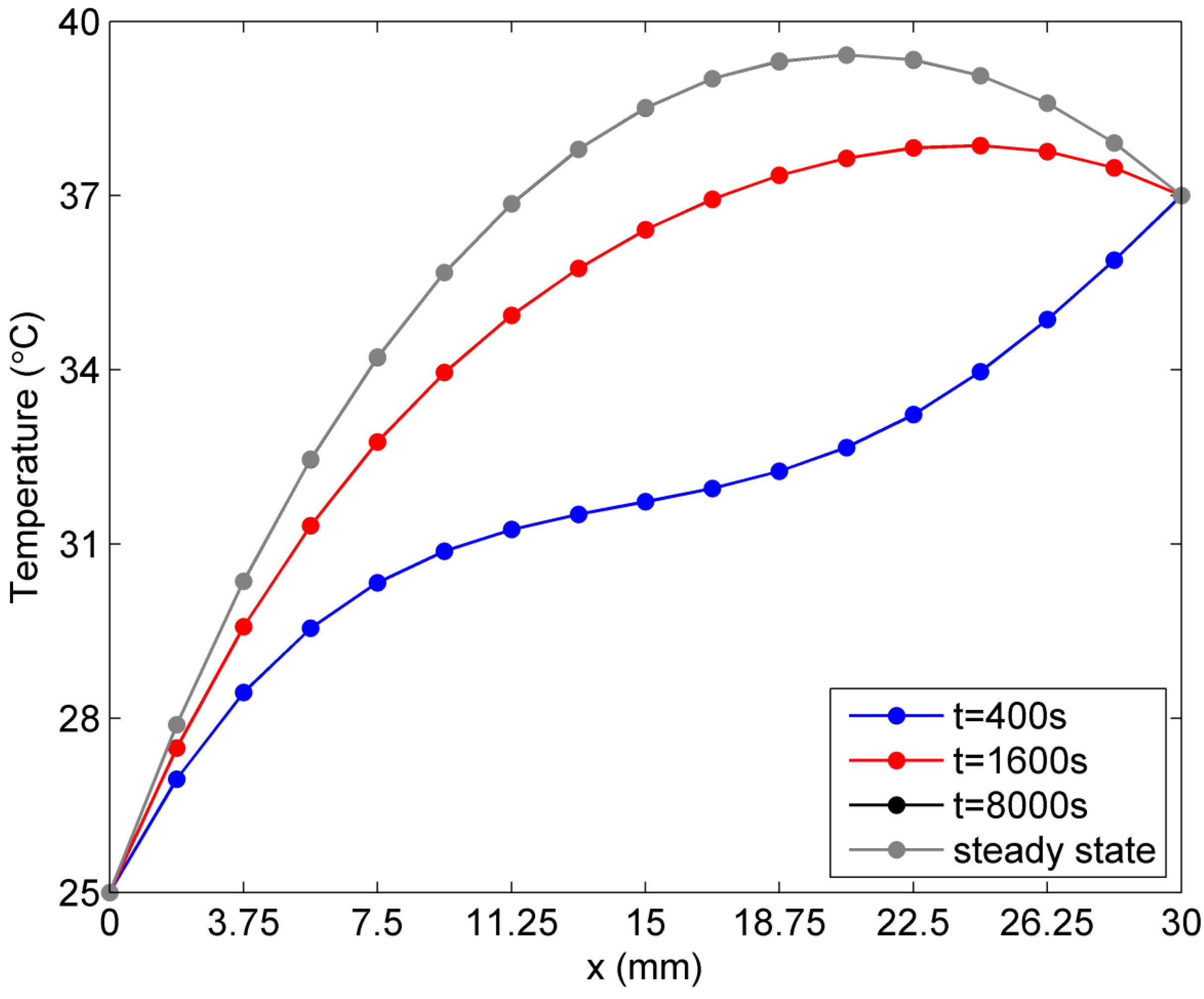
2.2. Sensitivity of Temperature to Variation of Constants ai in Linear Case of Blood Perfusion Rate

2.3. Sensitivity of Temperature to Variation of ai in the Exponential Case of Blood Perfusion Rate

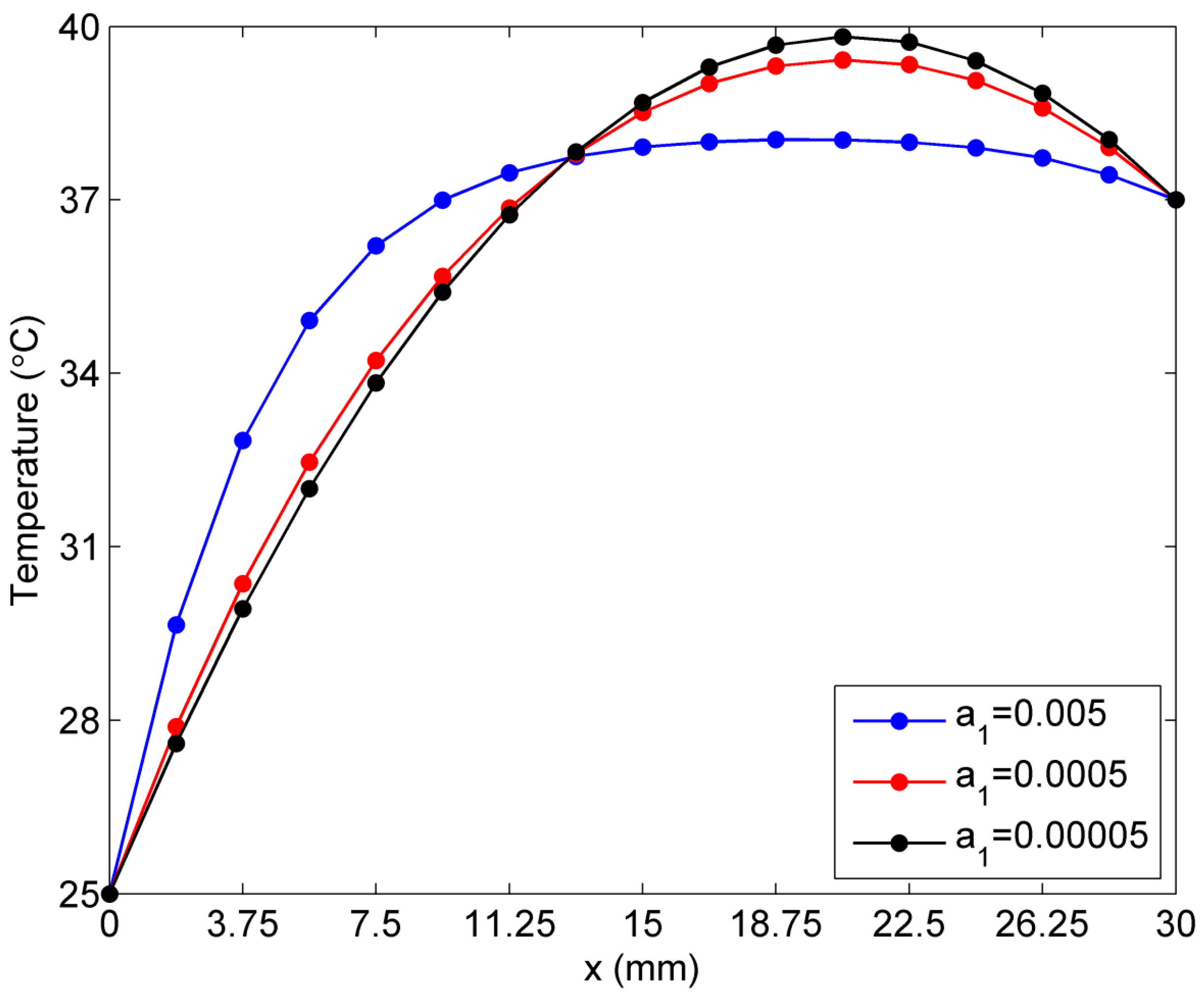
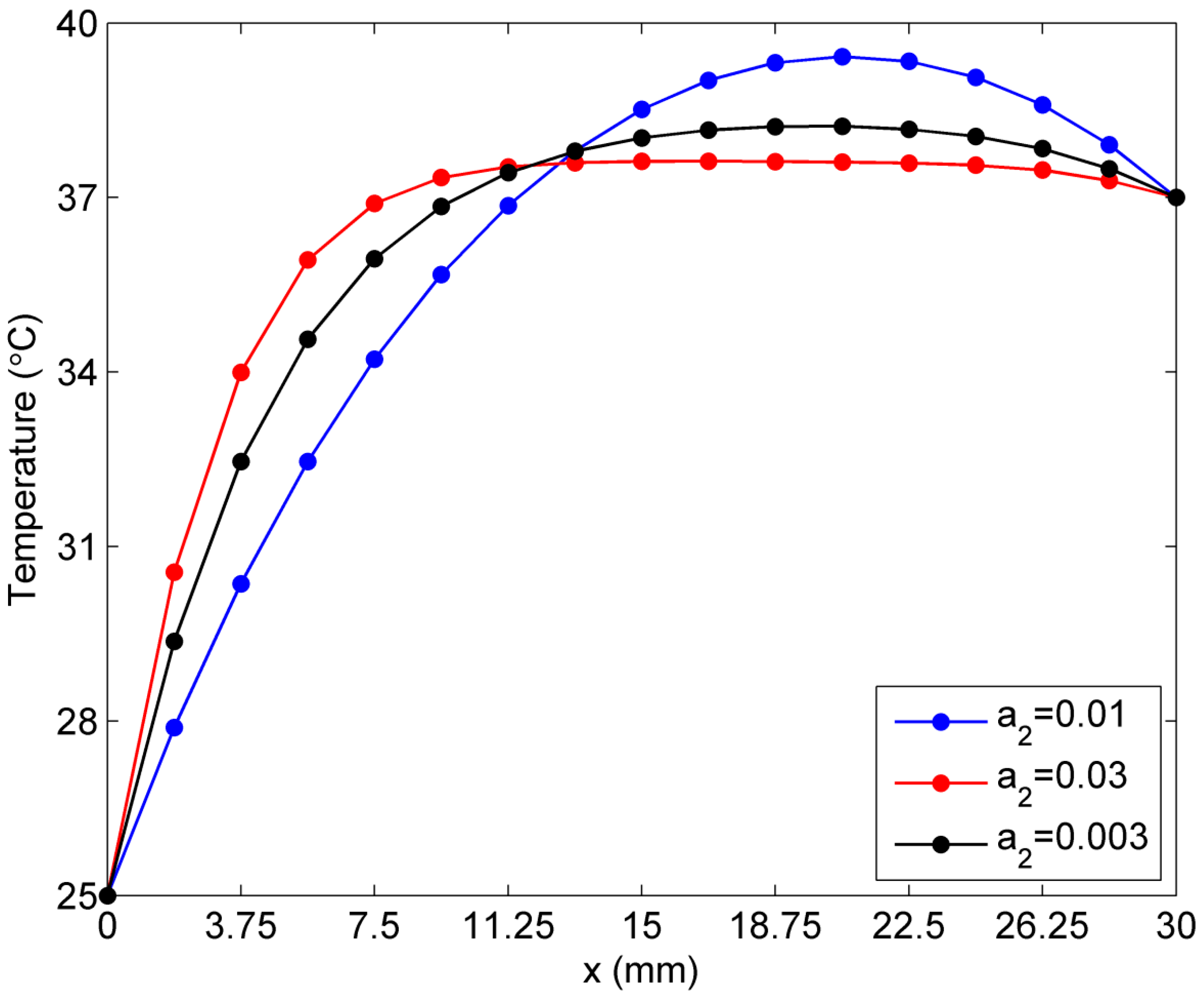
3. Mathematical Bioheat Transfer Model in 2D Skin Tissue
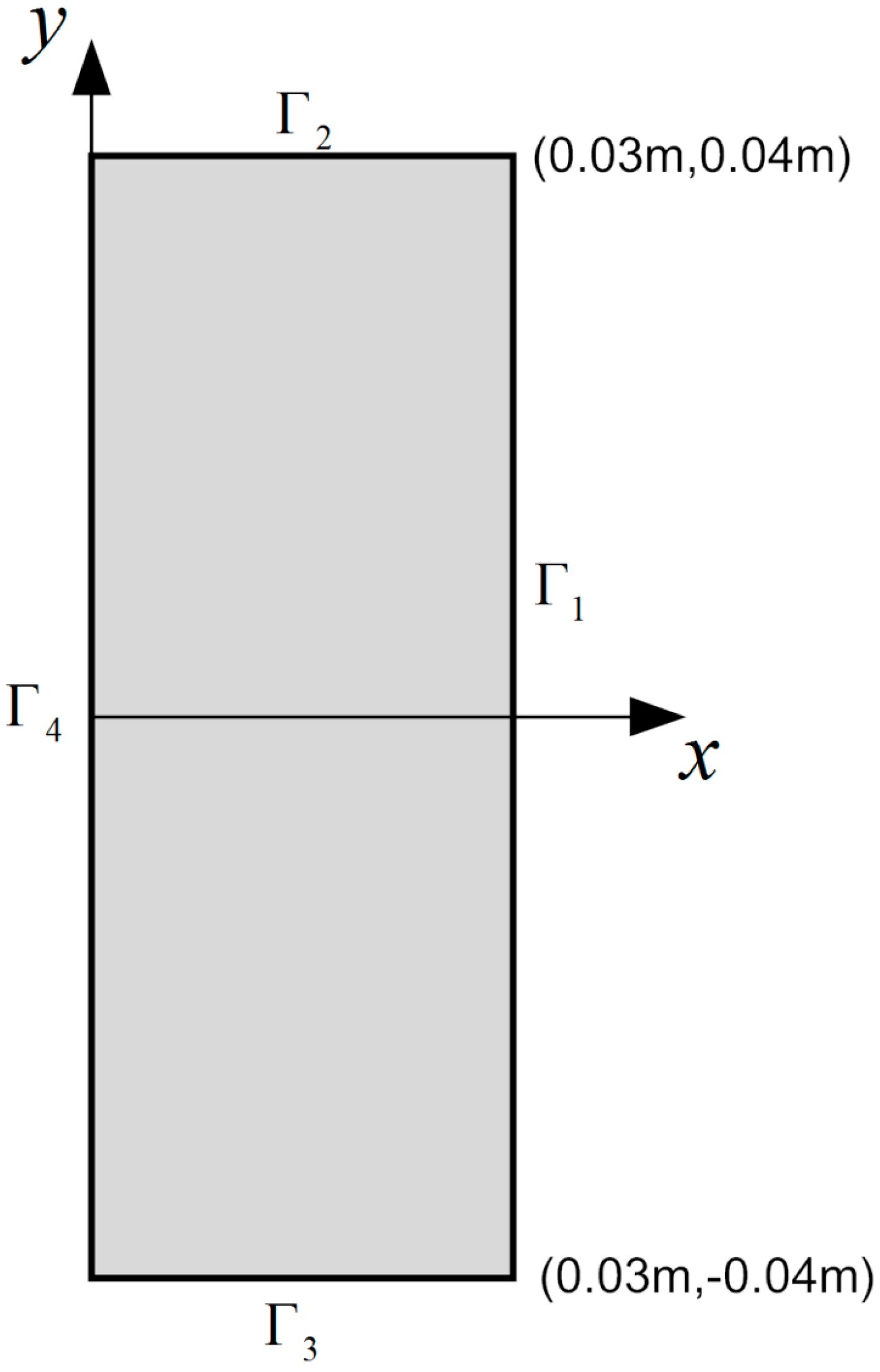
4. Solution Procedure
4.1. The Operator Splitting Method
4.2. Solution of the Modified Helmholtz System
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xu, F.; Lu, T.J.; Seffen, K.A. Biothermomechanics of skin tissues. J. Mech. Phys. Solids 2008, 56, 1852–1884. [Google Scholar] [CrossRef]
- Fuentes, D.; Walker, C.; Elliott, A.; Shetty, A.; Hazle, J.; Stafford, R. Magnetic resonance temperature imaging validation of a bioheat transfer model for laser-induced thermal therapy. Int. J. Hyperth. 2011, 27, 453–464. [Google Scholar] [CrossRef]
- Ng, E.Y.K.; Tan, H.M.; Ooi, E.H. Prediction and parametric analysis of thermal profiles within heated human skin using the boundary element method. Philos. Trans. Math. Phys. Eng. Sci. 2010, 368, 655–678. [Google Scholar] [CrossRef]
- Ng, E.Y.K.; Tan, H.M.; Ooi, E.H. Boundary element method with bioheat equation for skin burn injury. Burns 2009, 35, 987–997. [Google Scholar] [CrossRef] [PubMed]
- Lang, J.; Erdmann, B.; Seebass, M. Impact of nonlinear heat transfer on temperature control in regional hyperthermia. IEEE Trans. Biomed. Eng. 1999, 46, 1129–1138. [Google Scholar] [CrossRef] [PubMed]
- Tzou, D.Y. A unified field approach for heat conduction from macro-to micro-scales. J. Heat. Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Bourantas, G.C.; Loukopoulos, V.C.; Burganos, V.N.; Nikiforidis, G.C. A meshless point collocation treatment of transient bioheat problems. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 587–601. [Google Scholar] [CrossRef]
- Wang, H.; Qin, Q.H. FE approach with green’s function as internal trial function for simulating bioheat transfer in the human eye. Arch. Mech. 2010, 62, 493–510. [Google Scholar]
- Akbarzadeh, A.H.; Pasini, D. Phase-lag heat conduction in multilayered cellular media with imperfect bonds. Int. J. Heat Mass Transf. 2014, 75, 656–667. [Google Scholar] [CrossRef]
- Akbarzadeh, A.H.; Chen, Z.T. Heat conduction in one-dimensional functionally graded media based on the dual-phase-lag theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 744–759. [Google Scholar] [CrossRef]
- Ezzat, M.A.; El-Bary, A.A.; Fayik, M.A. Fractional fourier law with three-phase lag of thermoelasticity. Mech. Adv. Mater. Struct. 2013, 20, 593–602. [Google Scholar] [CrossRef]
- Narasimhan, A.; Jha, K.K. Bio-heat transfer simulation of retinal laser irradiation. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 547–559. [Google Scholar] [CrossRef]
- Trakic, A.; Liu, F.; Crozier, S. Transient temperature rise in a mouse due to low-frequency regional hyperthermia. Phys. Med. Biol. 2006, 51, 1673–1691. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Fuentes, D.; Hawkins, A.; Bass, J.; Rylander, M.; Elliott, A.; Shetty, A.; Stafford, R.J.; Oden, J.T. Nanoshell-mediated laser surgery simulation for prostate cancer treatment. Eng. Comput. 2009, 25, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.S.; Liu, J. Parametric studies on the phase shift method to measure the blood perfusion of biological bodies. Med. Eng. Phys. 2000, 22, 693–702. [Google Scholar] [CrossRef] [PubMed]
- Majchrzak, E. Numerical modelling of bio-heat transfer using the boundary element method. J. Theor. Appl. Mech. 1998, 36, 437–455. [Google Scholar]
- Cao, L.L.; Qin, Q.H.; Zhao, N. An RBF-MFS model for analysing thermal behaviour of skin tissues. Int. J. Heat Mass Transf. 2010, 53, 1298–1307. [Google Scholar] [CrossRef]
- Chen, C.S.; Rashed, Y.F.; Golberg, M.A. A mesh-free method for linear diffusion equations. Numer. Heat Transf. B 1998, 33, 469–486. [Google Scholar] [CrossRef]
- Golberg, M.A.; Chen, C.S. An efficient mesh-free method for nonlinear reaction-diffusion equations. Comput. Model. Eng. Sci. 2001, 2, 87–95. [Google Scholar]
- Balakrishnan, K.; Sureshkumar, R.; Ramachandran, P.A. An operator splitting-radial basis function method for the solution of transient nonlinear poisson problems. Comput. Math. Appl. 2002, 43, 289–304. [Google Scholar] [CrossRef]
- Peaceman, D.W.; Rachford JR, H.H. The numerical solution of parabolic and elliptic differential equations. J. Soc. Ind. Appl. Math. 1955, 3, 28–41. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Wang, H.; Qin, Q.H. Method of fundamental solutions for nonlinear skin bioheat model. J. Mech. Med. Biol. 2014, 14. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Wang, H.; Qin, Q.H. Transient bioheat simulation of the laser-tissue interaction in human skin using hybrid finite element formulation. Mol. Cell. Biomech. 2012, 9, 31–53. [Google Scholar] [PubMed]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [PubMed]
- Xu, L.; Zhu, L.; Holmes, K. Thermoregulation in the canine prostate during transurethral microwave hyperthermia, part II: Blood flow response. Int. J. Hyperth. 1998, 14, 65–73. [Google Scholar] [CrossRef]
- Kim, B.M.; Jacques, S.L.; Rastegar, S.; Thomsen, S.; Motamedi, M. Nonlinear finite-element analysis of the role of dynamic changes in blood perfusion and optical properties in laser coagulation of tissue. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 922–933. [Google Scholar] [CrossRef]
- Wang, H.; Qin, Q.H. A fundamental solution-based finite element model for analyzing multi-layer skin burn injury. J. Mech. Med. Biol. 2012, 12. [Google Scholar] [CrossRef]
- Wang, H.; Qin, Q.H. A meshless method for generalized linear or nonlinear poisson-type problems. Eng. Anal. Bound. Elem. 2006, 30, 515–521. [Google Scholar] [CrossRef]
- Wang, H.; Qin, Q.H.; Kang, Y.L. A meshless model for transient heat conduction in functionally graded materials. Comput. Mech. 2006, 38, 51–60. [Google Scholar] [CrossRef]
- Qin, Q.H. The Trefftz Finite and Boundary Element Method; WIT Press: Southampton, UK, 2000. [Google Scholar]
- Wang, H.; Qin, Q.H. Some problems with the method of fundamental solution using radial basis functions. Acta Mech. Solida Sin. 2007, 20, 21–29. [Google Scholar] [CrossRef]
- Wang, H.; Qin, Q.H.; Kang, Y.L. A new meshless method for steady-state heat conduction problems in anisotropic and inhomogeneous media. Arch. Appl. Mech. 2005, 74, 563–579. [Google Scholar]
- Chen, C.S.; Kuhn, G.; Li, J.; Mishuris, G. Radial basis functions for solving near singular poisson problems. Comm. Numer. Meth. Eng. 2003, 19, 333–347. [Google Scholar] [CrossRef]
- Wang, H.; Qin, Q.H. Meshless approach for thermo-mechanical analysis of functionally graded materials. Eng. Anal. Bound. Elem. 2008, 32, 704–712. [Google Scholar] [CrossRef]
- Brebbia, C.A. Boundary Element Methods in Engineering; Springer: New York, NY, USA, 1982. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.-W.; Wang, H.; Qin, Q.-H. Meshless Method with Operator Splitting Technique for Transient Nonlinear Bioheat Transfer in Two-Dimensional Skin Tissues. Int. J. Mol. Sci. 2015, 16, 2001-2019. https://doi.org/10.3390/ijms16012001
Zhang Z-W, Wang H, Qin Q-H. Meshless Method with Operator Splitting Technique for Transient Nonlinear Bioheat Transfer in Two-Dimensional Skin Tissues. International Journal of Molecular Sciences. 2015; 16(1):2001-2019. https://doi.org/10.3390/ijms16012001
Chicago/Turabian StyleZhang, Ze-Wei, Hui Wang, and Qing-Hua Qin. 2015. "Meshless Method with Operator Splitting Technique for Transient Nonlinear Bioheat Transfer in Two-Dimensional Skin Tissues" International Journal of Molecular Sciences 16, no. 1: 2001-2019. https://doi.org/10.3390/ijms16012001
APA StyleZhang, Z.-W., Wang, H., & Qin, Q.-H. (2015). Meshless Method with Operator Splitting Technique for Transient Nonlinear Bioheat Transfer in Two-Dimensional Skin Tissues. International Journal of Molecular Sciences, 16(1), 2001-2019. https://doi.org/10.3390/ijms16012001







