Monovalent Ions and Water Dipoles in Contact with Dipolar Zwitterionic Lipid Headgroups-Theory and MD Simulations
Abstract
:1. Introduction
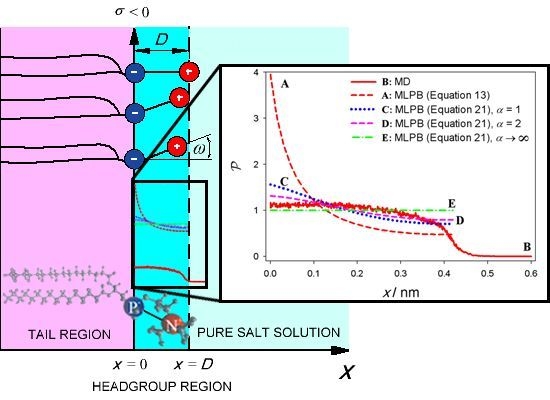
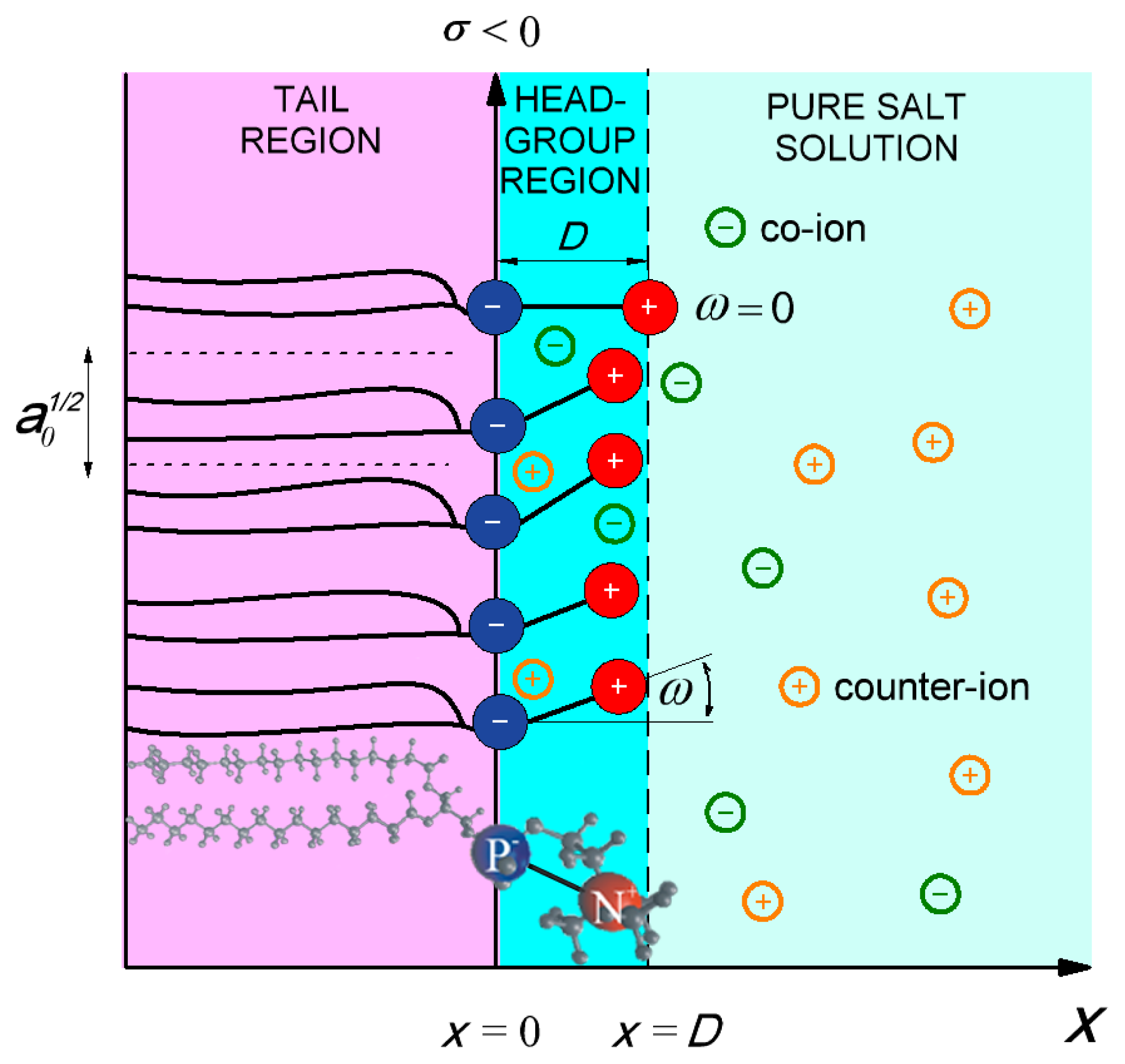
2. Model
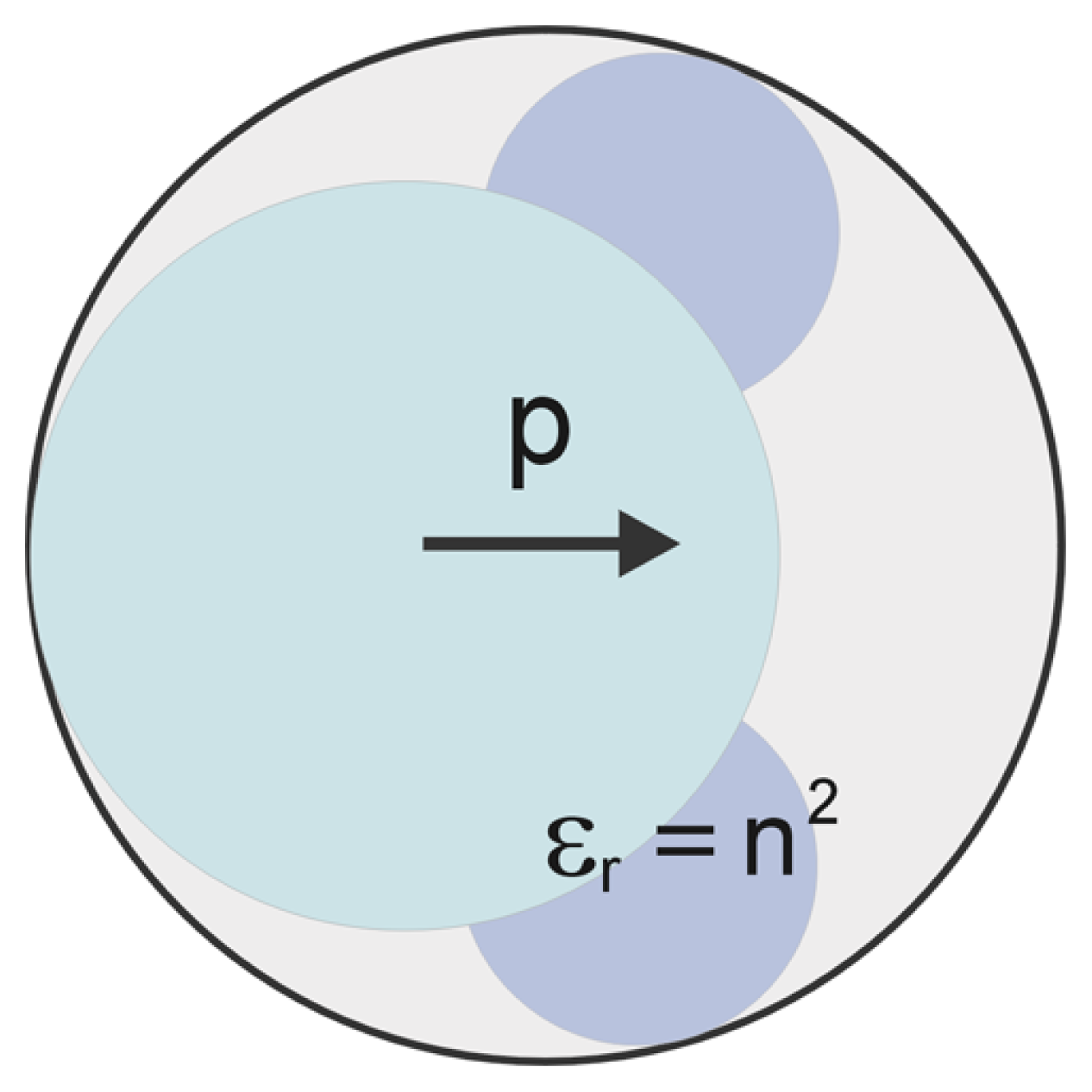
2.1. Modified Langevin-Poisson-Boltzmann (MLPB) Model
2.2. Poisson Equation
2.3. Molecular Dynamics Simulations (MD)
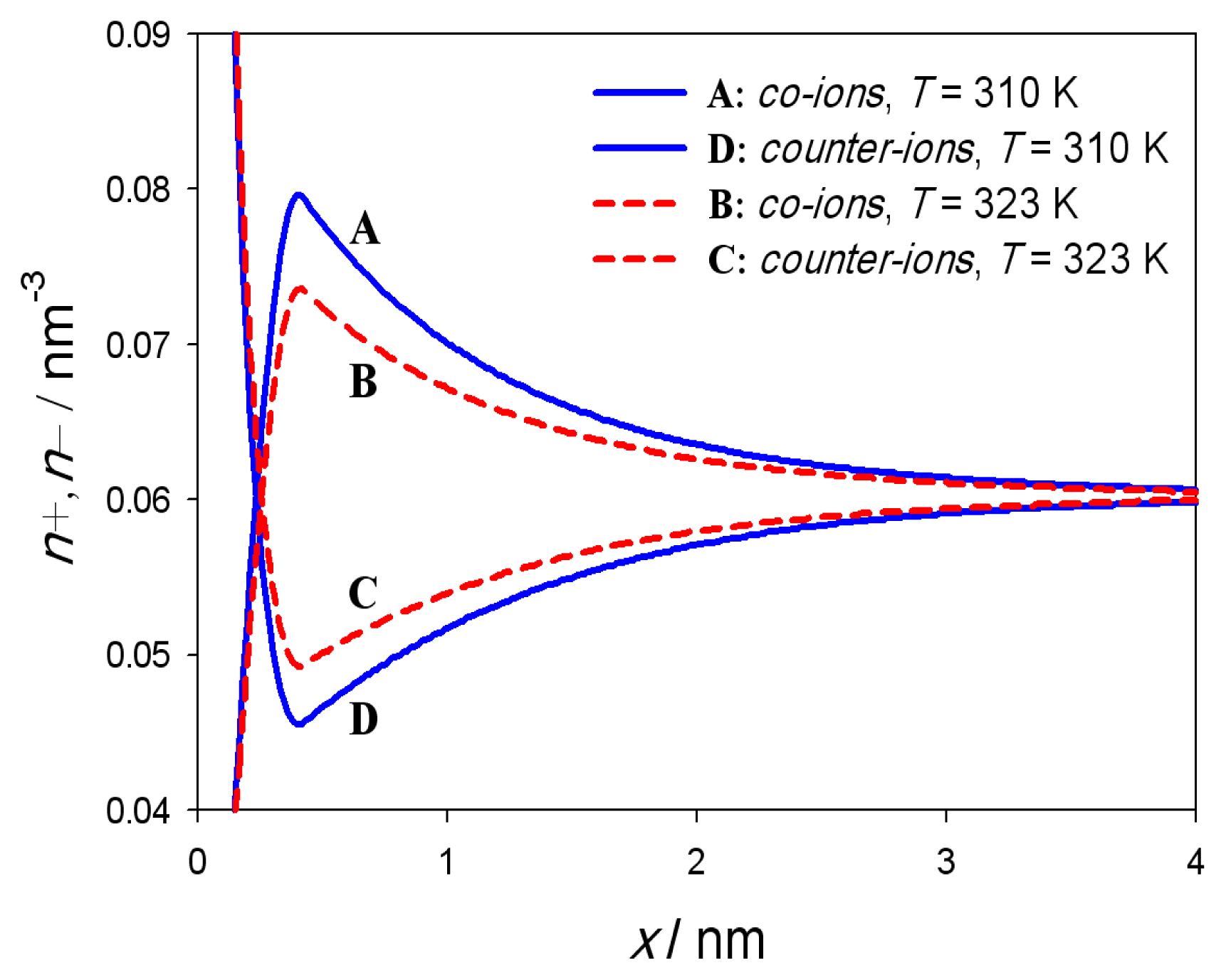
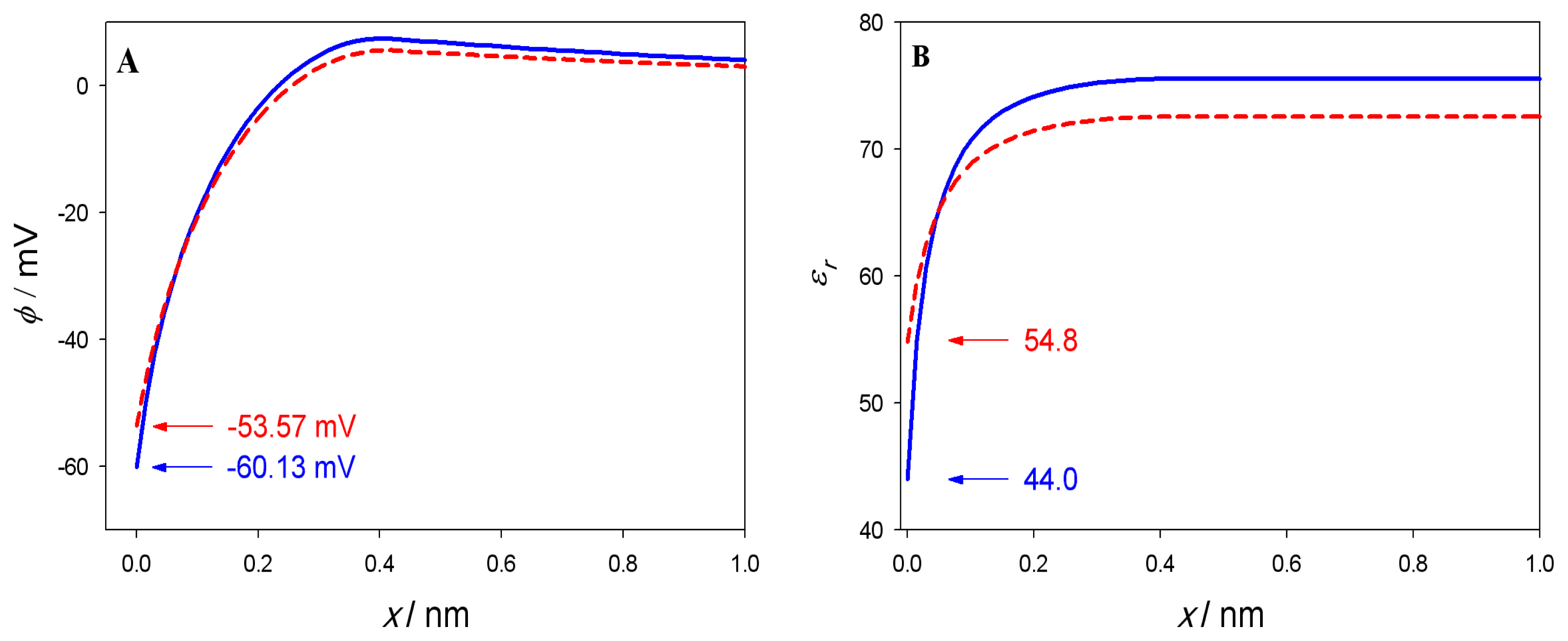
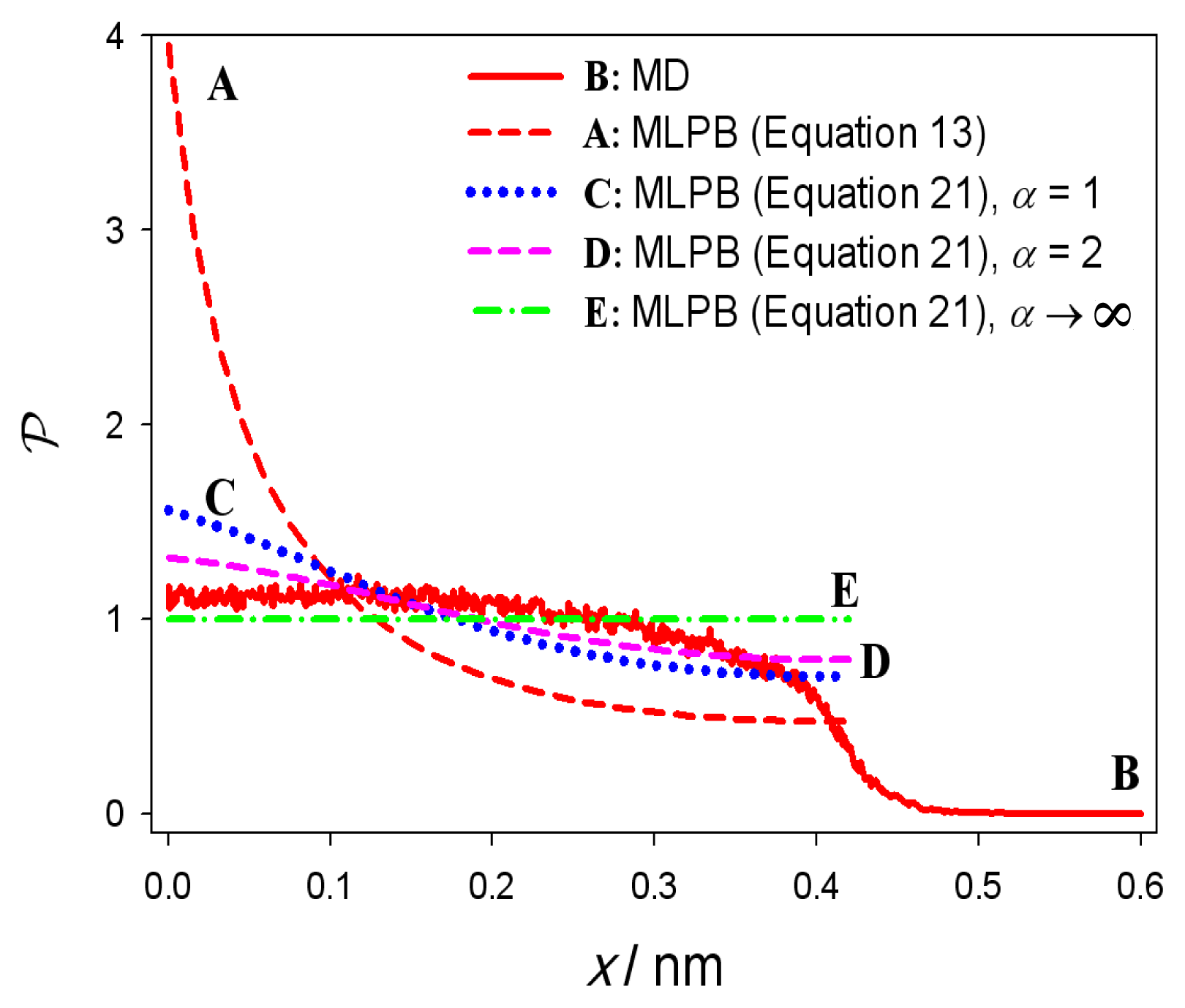
3. Results
4. Discussion and Conclusions
Acknowledgements
References
- Sackmann, E. Molecular and global structure and dynamics of membranes and lipid bilayers. Can. J. Phys 1990, 68, 999–1012. [Google Scholar]
- Sackmann, E. Biological Membranes Architecture and Function. In Structure and Dynamics of Membranes; Lipowsky, R., Sackmann, E., Eds.; Elsevier: Amsterdam, The Netherlands, 1995; pp. 1–63. [Google Scholar]
- Šuštar, V.; Zelko, J.; Lopalco, P.; Lobasso, S.; Ota, A.; Ulrih, N.P.; Corcelli, A.; Kralj-Iglič, V. Morphology, biophysical properties and protein-mediated fusion of archaeosomes. PLoS One 2012, 7, e39401. [Google Scholar]
- Kralj-Iglič, V. Stability of membranous nanostructures: A possible key mechanism in cancer progression. Int. J. Nanomed 2012, 7, 3579–3596. [Google Scholar]
- Šuštar, V.; Bedina Zavec, A.; Štukelj, R.; Frank, M.; Bobojevič, G.; Janša, R.; Ogorevc, E.; Kruljc, P.; Mam, K.; Šimunič, B.; et al. Nanoparticles isolated from blood: A reflection of vesiculability of blood cells during the isolation process. Int. J. Nanomed 2011, 6, 2737–2748. [Google Scholar]
- Rappolt, M.; Pabst, G. Flexibility and Struture of Fluid Bilyer Interfaces. In Structure and Dynamics of Membranous Interfaces; Nag, K., Ed.; John Wiley and Sons, Inc: Hoboken, NJ, USA, 2008; pp. 45–81. [Google Scholar]
- Yaghmur, A.; Rappolt, M. Structural characterization of lipidic systems under nonequilibrium conditions. Eur. Biophys. J 2012, 41, 831–840. [Google Scholar]
- Tien, H.T.; Ottova-Leitmannova, A. The Lipid Bilayer Concept: Experimental Realization and Current Application. In Planar Lipid Bilayers (BLMs) And Their Application; Tien, H.T., Ottova-Leitmannova, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2003; pp. 1–73. [Google Scholar]
- Luckey, M. Membrane Structural Biology, 1st ed.; Cambridge University Press: New York, NY, USA, 2008; pp. 1–67. [Google Scholar]
- Kramar, P.; Miklavčič, D.; Kotulska, M.; Maček Lebar, A. Voltage- and Current-clamp Methods for Determination of Planar Lipid Bilayer Properties. In Advances in Planar Lipid Bilayers and Liposomes, Volume 11; Iglič, A., Ed.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 29–69. [Google Scholar]
- Polak, A.; Mulej, B.; Kramar, P. System for measuring planar lipid bilayer properties. J. Membrane Biol 2012, 24, 625–632. [Google Scholar]
- Kramar, P.; Miklavčič, D.; Maček Lebar, A. A system for the determination of planar lipid bilayer breakdown voltage and its applications. IEEE Trans. Nanobiosci 2009, 8, 132–138. [Google Scholar]
- Gongadze, E.; Iglič, A. Decrease of permittivity of an electrolyte solution near a charged surface due to saturation and excluded volume effects. Bioelectrochemistry 2012, 87, 199–203. [Google Scholar]
- Cevc, G. Phospholipid Handbook, 1st ed; Marcel Dekker: New York, NY, USA, 1993. [Google Scholar]
- Rappolt, M.; Laggner, P.; Pabst, G. Structure and Elasticity of Phospholipid Bilayers in the LαPhase: A Comparison of Phosphatidylcholine and Phosphatidylethanolamine Membranes. In Recent Research Development in Biophysics; Pandalai, S.G., Ed.; Trivandrum-Transworld Research Network: Kerala, India, 2004; Volume 3, pp. 363–392. [Google Scholar]
- Kramar, P.; Miklavčič, D.; Maček Lebar, A. Determination of the lipid bilayer breakdown voltage by means of a linear rising signal. Bioelectrochemistry 2007, 70, 23–27. [Google Scholar]
- Kramar, P.; Delemotte, L.; Maček Lebar, A.; Kotulska, M.; Tarek, M.; Miklavčič, D. Molecular-level characterization of lipid membrane electroporation using linearly rising current. J. Membrane Biol 2012, 245, 651–659. [Google Scholar]
- Sabotin, I.; Maček Lebar, A.; Miklavčič, D.; Kramar, P. Measurement protocol for planar lipid bilayer viscoelastic properties. IEEE Trans. Diel. El. Insul 2009, 15, 1236–1242. [Google Scholar]
- Vácha, R.; Siu, S.W.I.; Petrov, M.; Böckmann, R.A.; Barucha-Kraszewska, J.; Jurkiewicz, P.; Hof, M.; Berkowitz, M.L.; Jungwirth, P. Effects of alkali cations and halide anions on the DOPC lipid membrane. J. Chem. Phys. A 2009, 113, 7235–7243. [Google Scholar]
- McLaughlin, S. The electrostatic properties of membranes. Ann. Rev. Biophys. Chem 1989, 18, 113–136. [Google Scholar]
- Gongadze, E.; van Rienen, U.; Kralj-Iglič, V.; Iglič, A. Langevin Poisson-Boltzmann equation: Point-like ions and water dipoles near a charged surface. Gen. Physiol. Biophys 2011, 30, 130–137. [Google Scholar]
- Gongadze, E.; van Rienen, U.; Kralj-Iglič, V.; Iglič, A. Spatial variation of permittivity of an electrolyte solution in contact with a charged metal surface: A mini review. Comput. Meth. Biomech. Biomed. Eng. 2012, pp. 1–18. Available online: http://dx.org/10.1080/10255842.2011.624769 accessed on 18 September 2012. [CrossRef]
- Cevc, G. Memrane electrostatics. Biochim. Biophys. Acta 1990, 1031, 311–382. [Google Scholar]
- Kralj-Iglič, V.; Iglič, A. A simple statistical mechanical approach to the free energy of the electric double layer including the excluded volume effect. J. Phys. II France 1996, 6, 477–491. [Google Scholar]
- Lamperski, S.; Outhwaite, C.W. Exclusion volume term in the inhomogeneous poisson-boltzmann theory for high surface charge. Langmuir 2002, 18, 3423. [Google Scholar]
- Bazant, M.Z.; Kilic, M.S.; Storey, B.; Ajdari, A. Advances in colloid and interface science. Adv. Colloid Interface Sci 2009, 152, 48. [Google Scholar]
- Butt, H.J.; Graf, K.; Kappl, M. Physics and Chemistry of Interfaces, 2nd ed; Wiley-VCH Verlag: Weinheim, Germany, 2003. [Google Scholar]
- Outhwaite, C.W. A treatment of solvent effects in the potential theory of electrolyte solutions. Mol. Phys 1976, 31, 1345–1357. [Google Scholar]
- Outhwaite, C.W. Towards a mean electrostatic potential treatment of an ion-dipole mixture or a dipolar system next to a plane wall. Mol. Phys 1983, 48, 599–614. [Google Scholar]
- Iglič, A.; Gongadze, E.; Bohinc, K. Excluded volume effect and orientational ordering near charged surface in solution of ions and Langevin dipoles. Bioelectrochemistry 2010, 79, 223. [Google Scholar]
- Das, S; Chakraborty, S.; Mitra, S.K. Redefining electrical double layer thickness in narrow confinements: Effect of solvent polarization. Phys. Rev. E 2012, 85, 051508. [Google Scholar]
- Fröhlich, H. Theory of Dielectrics, 1st ed; Clarendon Press: Oxford, UK, 1964. [Google Scholar]
- Marsh, D. An incteracting spin label study of lateral expansion in dipalmitoyllecithin-cholesterol bilayers. Biochim. Biophys. Acta 1974, 363, 373–386. [Google Scholar]
- Kale, L.; Skeel, R.; Bhandarkar, M.; Brunner, R.; Gursoy, A.; Krawetz, N.; Phillips, J.; Shinozaki, A.; Varadarajan, K.; Schulten, K. NAMD2: Greater scalability for parallel molecular dynamics. J. Comp. Phys 1999, 151, 283–312. [Google Scholar]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comp. Chem 2005, 26, 1781–1802. [Google Scholar]
- Dardenn, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys 1993, 98, 10089. [Google Scholar]
- Essmann, U.; Perera, L.; Berkowitz, M.L. The origin of the hydration interaction of lipid bilayers from MD simulation of dipalmitoylphosphatidylcholine membranes in gel and liquid crystalline phases. Langmuir 1995, 11, 4519–4531. [Google Scholar]
A. Derivation of Equations for Matlab
A.1. Variant A
A.2. Variant B
B. Average Orientation of Lipid Head-Groups

© 2013 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Velikonja, A.; Perutkova, Š.; Gongadze, E.; Kramar, P.; Polak, A.; Maček-Lebar, A.; Iglič, A. Monovalent Ions and Water Dipoles in Contact with Dipolar Zwitterionic Lipid Headgroups-Theory and MD Simulations. Int. J. Mol. Sci. 2013, 14, 2846-2861. https://doi.org/10.3390/ijms14022846
Velikonja A, Perutkova Š, Gongadze E, Kramar P, Polak A, Maček-Lebar A, Iglič A. Monovalent Ions and Water Dipoles in Contact with Dipolar Zwitterionic Lipid Headgroups-Theory and MD Simulations. International Journal of Molecular Sciences. 2013; 14(2):2846-2861. https://doi.org/10.3390/ijms14022846
Chicago/Turabian StyleVelikonja, Aljaž, Šarka Perutkova, Ekaterina Gongadze, Peter Kramar, Andraž Polak, Alenka Maček-Lebar, and Aleš Iglič. 2013. "Monovalent Ions and Water Dipoles in Contact with Dipolar Zwitterionic Lipid Headgroups-Theory and MD Simulations" International Journal of Molecular Sciences 14, no. 2: 2846-2861. https://doi.org/10.3390/ijms14022846
APA StyleVelikonja, A., Perutkova, Š., Gongadze, E., Kramar, P., Polak, A., Maček-Lebar, A., & Iglič, A. (2013). Monovalent Ions and Water Dipoles in Contact with Dipolar Zwitterionic Lipid Headgroups-Theory and MD Simulations. International Journal of Molecular Sciences, 14(2), 2846-2861. https://doi.org/10.3390/ijms14022846