Dynamics of Order Reconstruction in a Nanoconfined Nematic Liquid Crystal with a Topological Defect
Abstract
:1. Introduction
2. Theoretical Basis
2.1. Free Energy
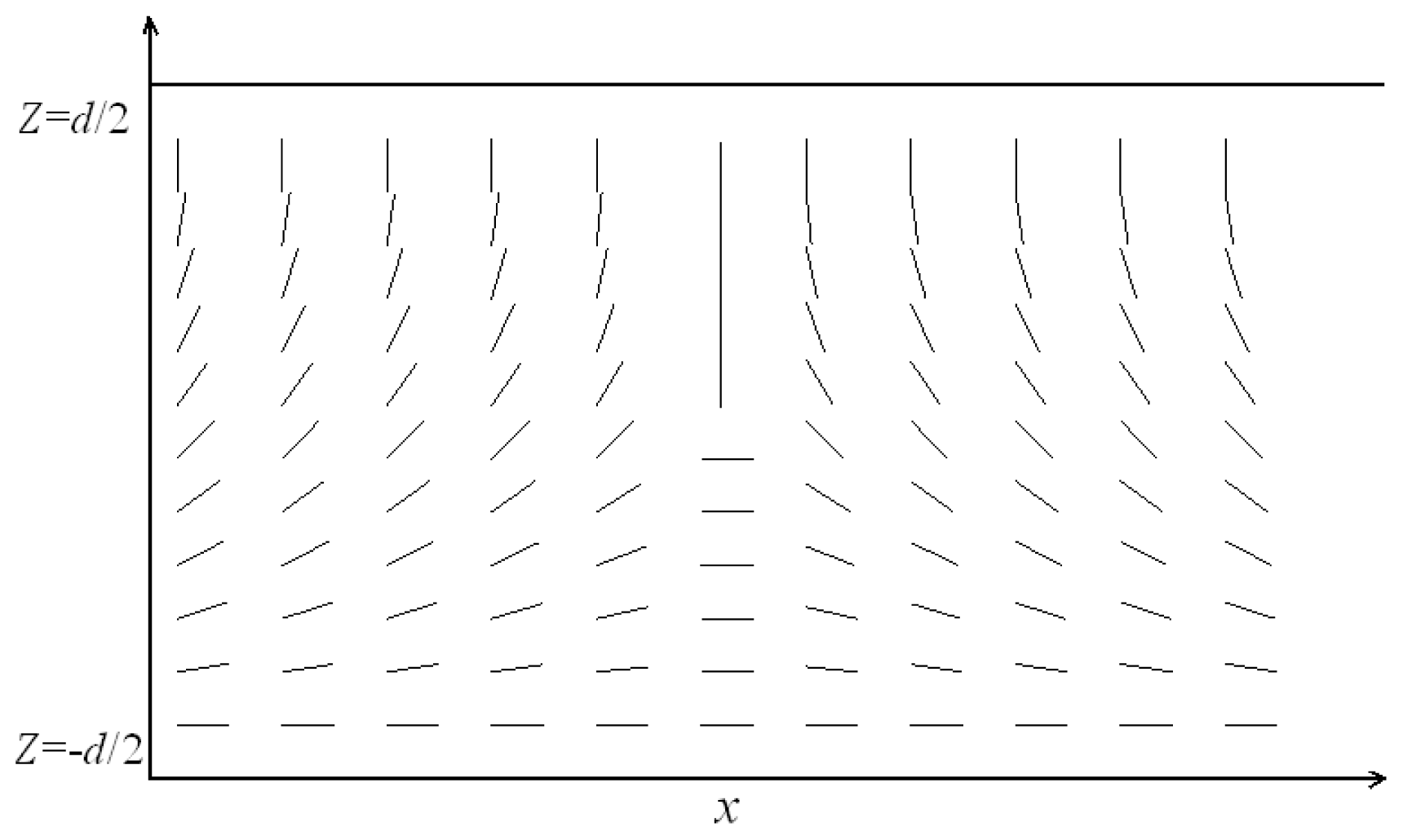
2.2. Geometry of the Problem
2.3. Numerical Methods
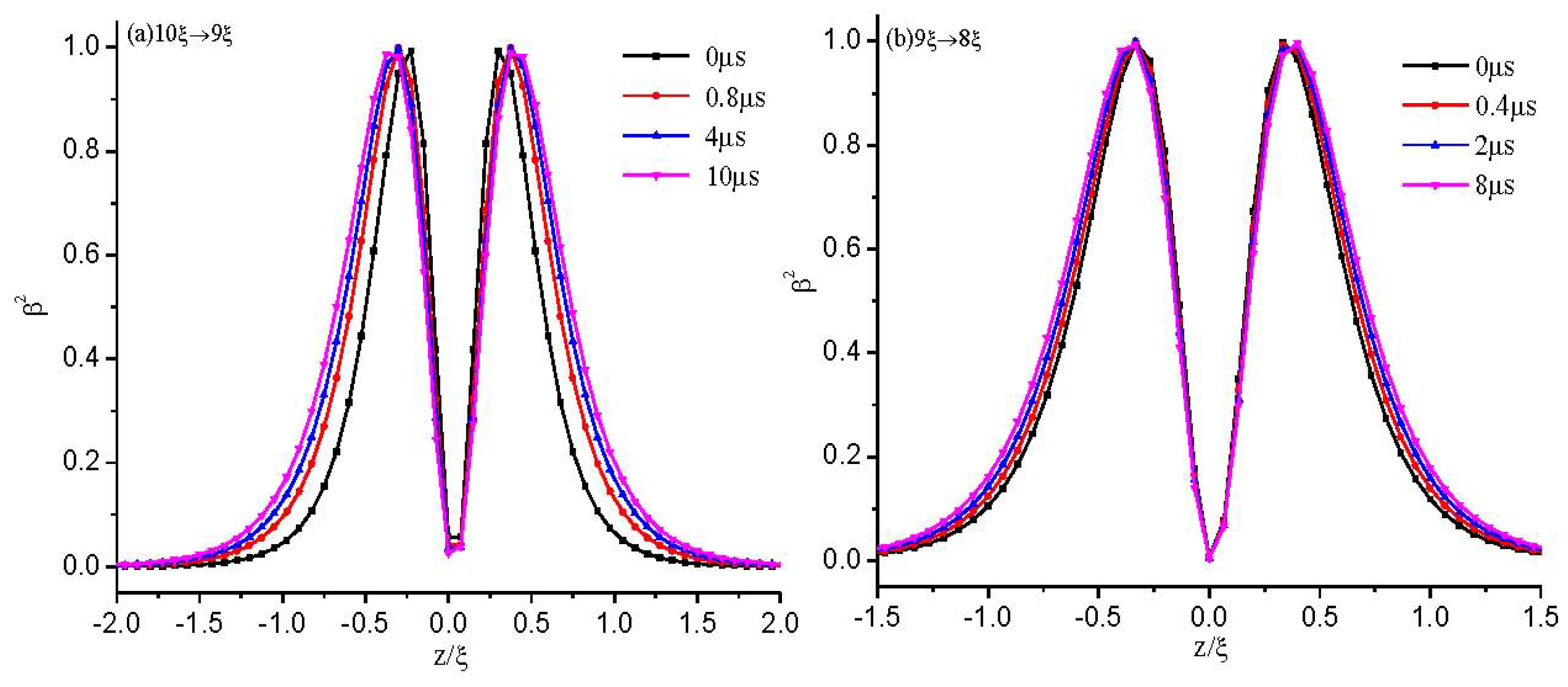
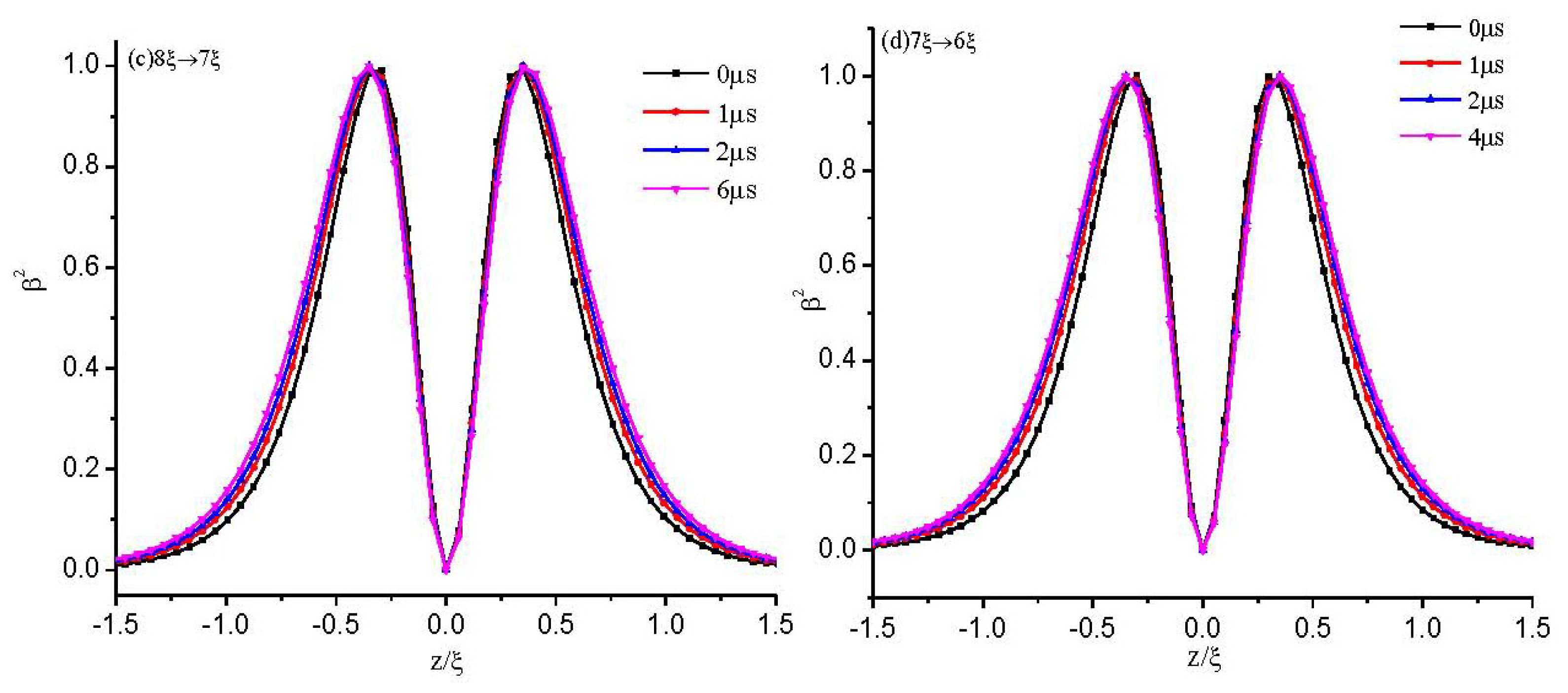
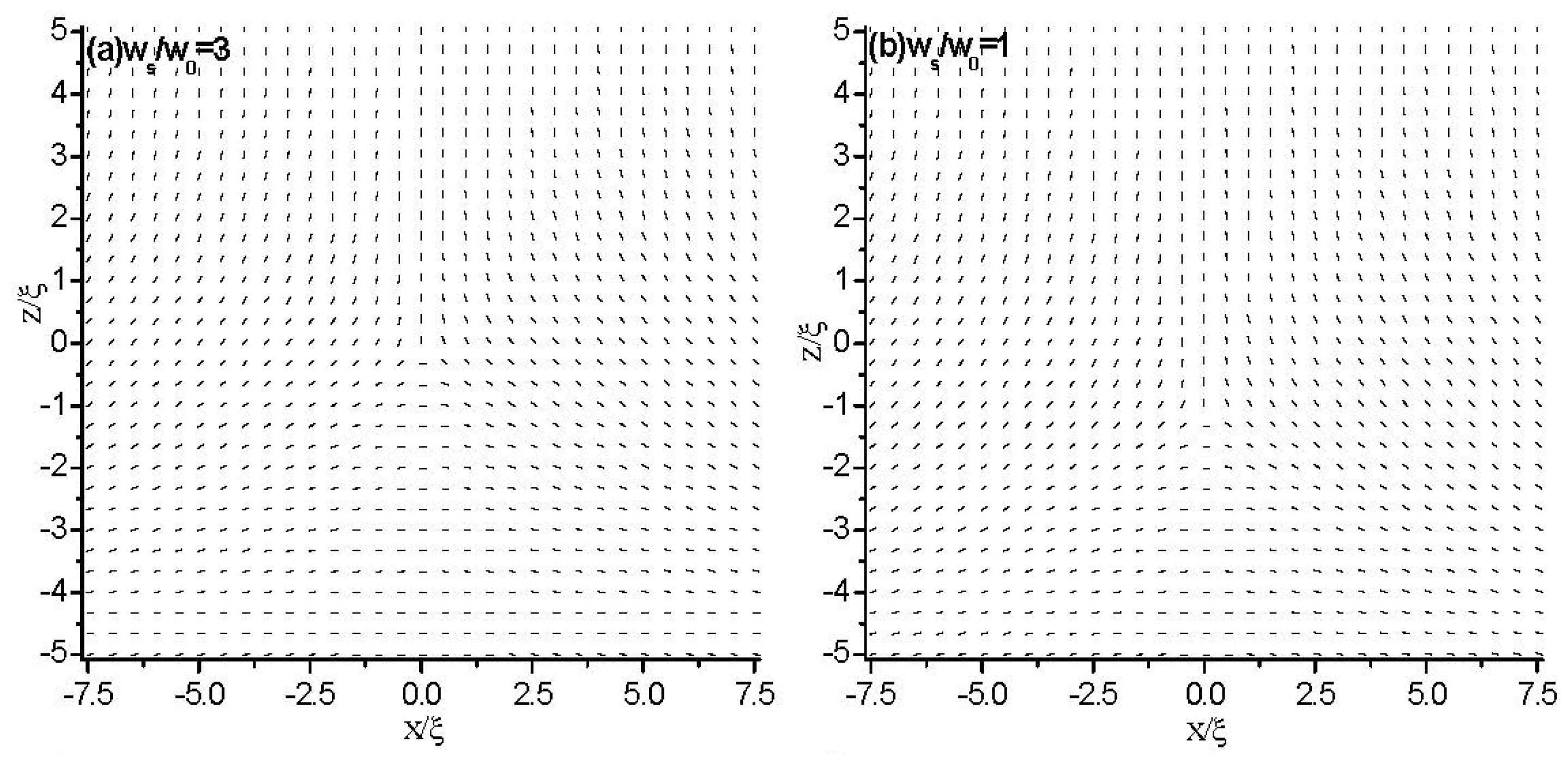
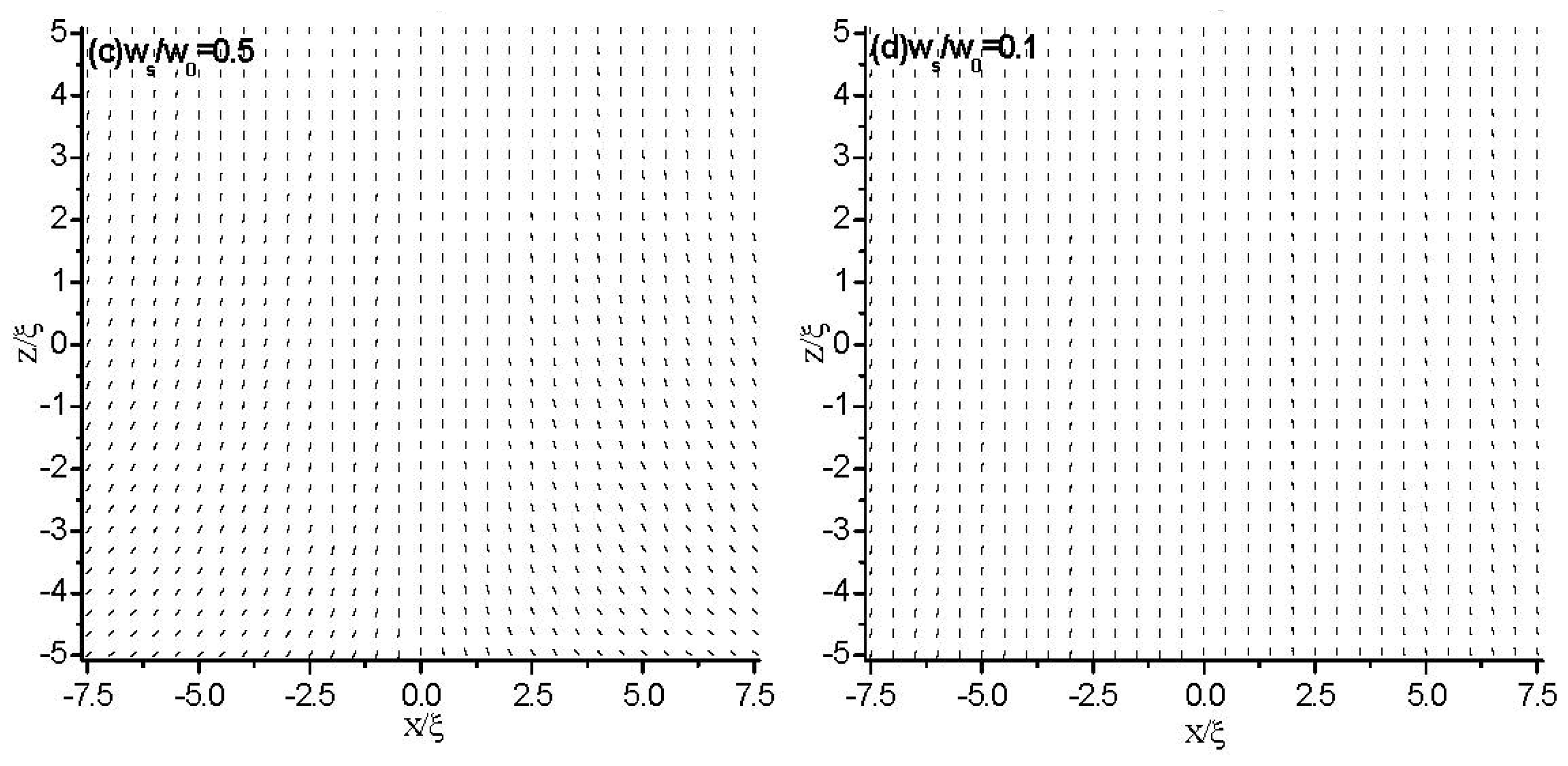
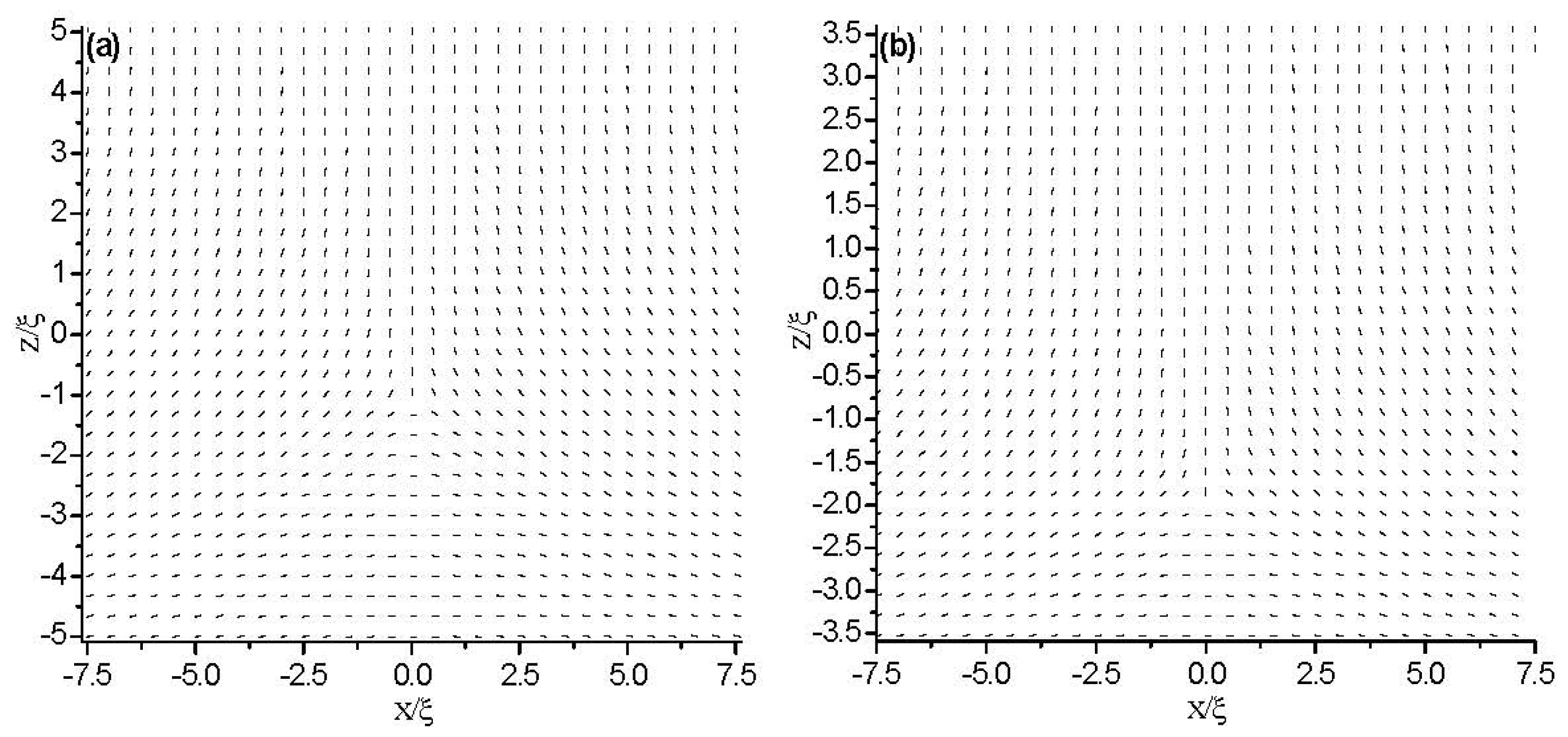
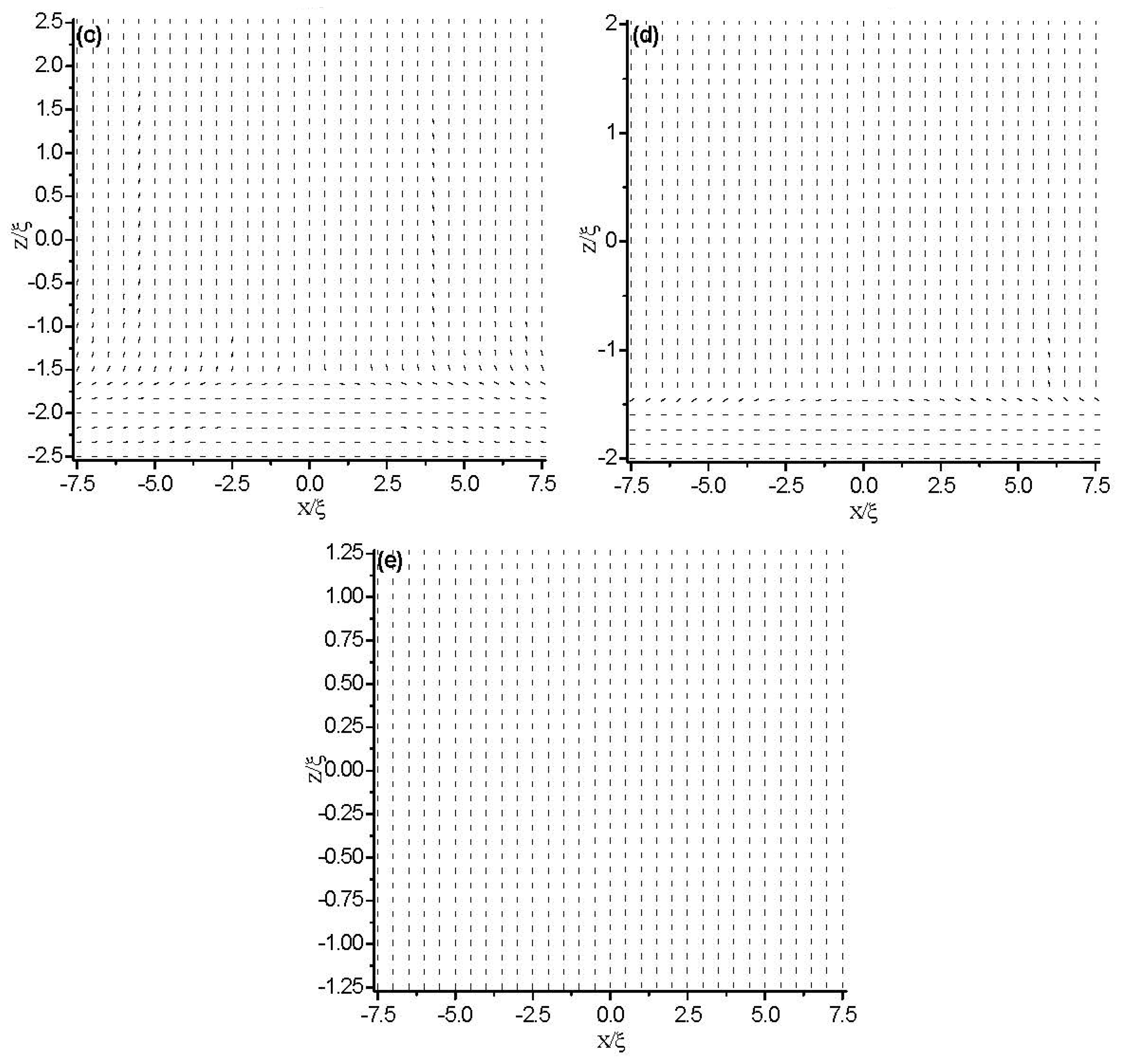
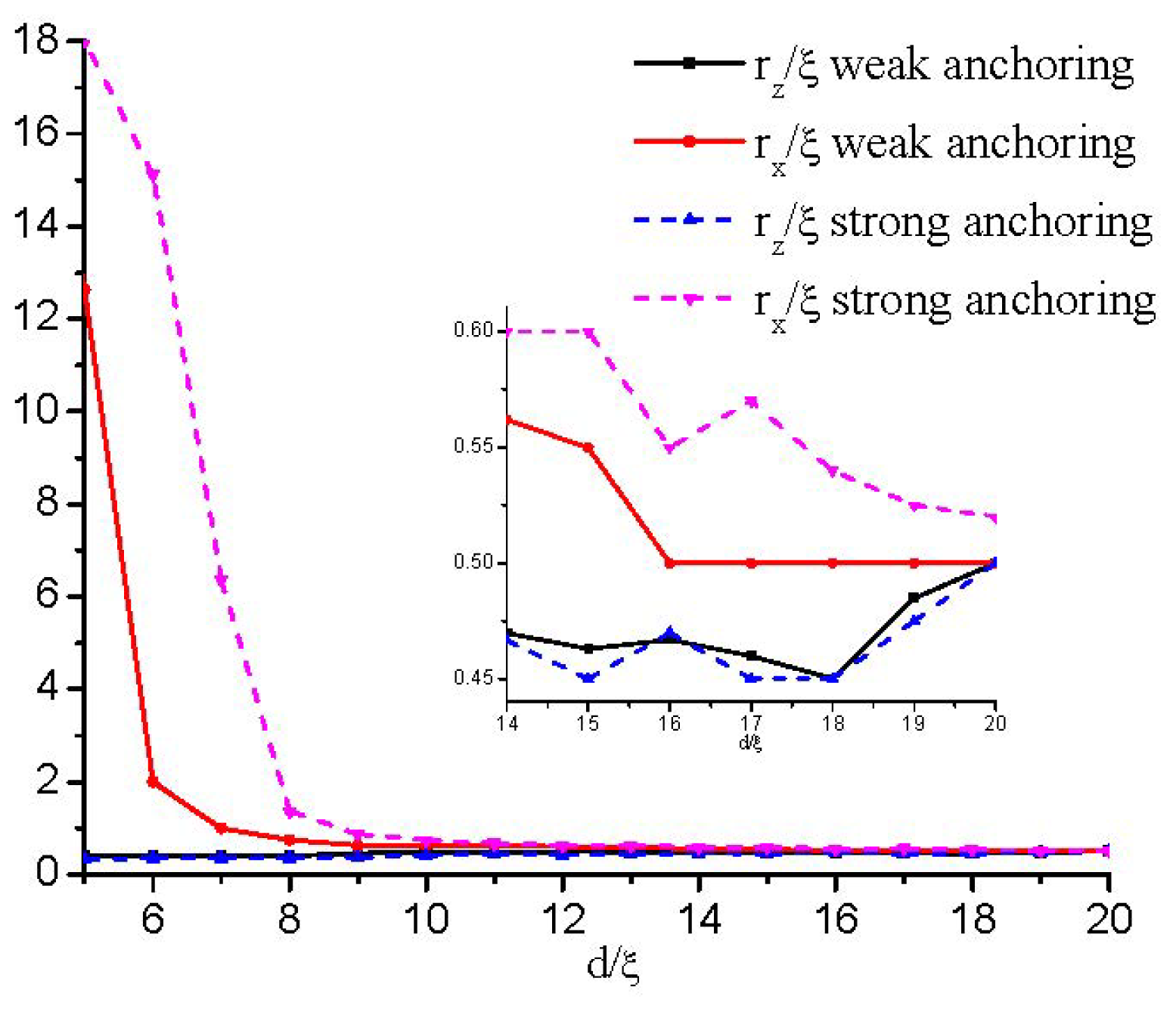
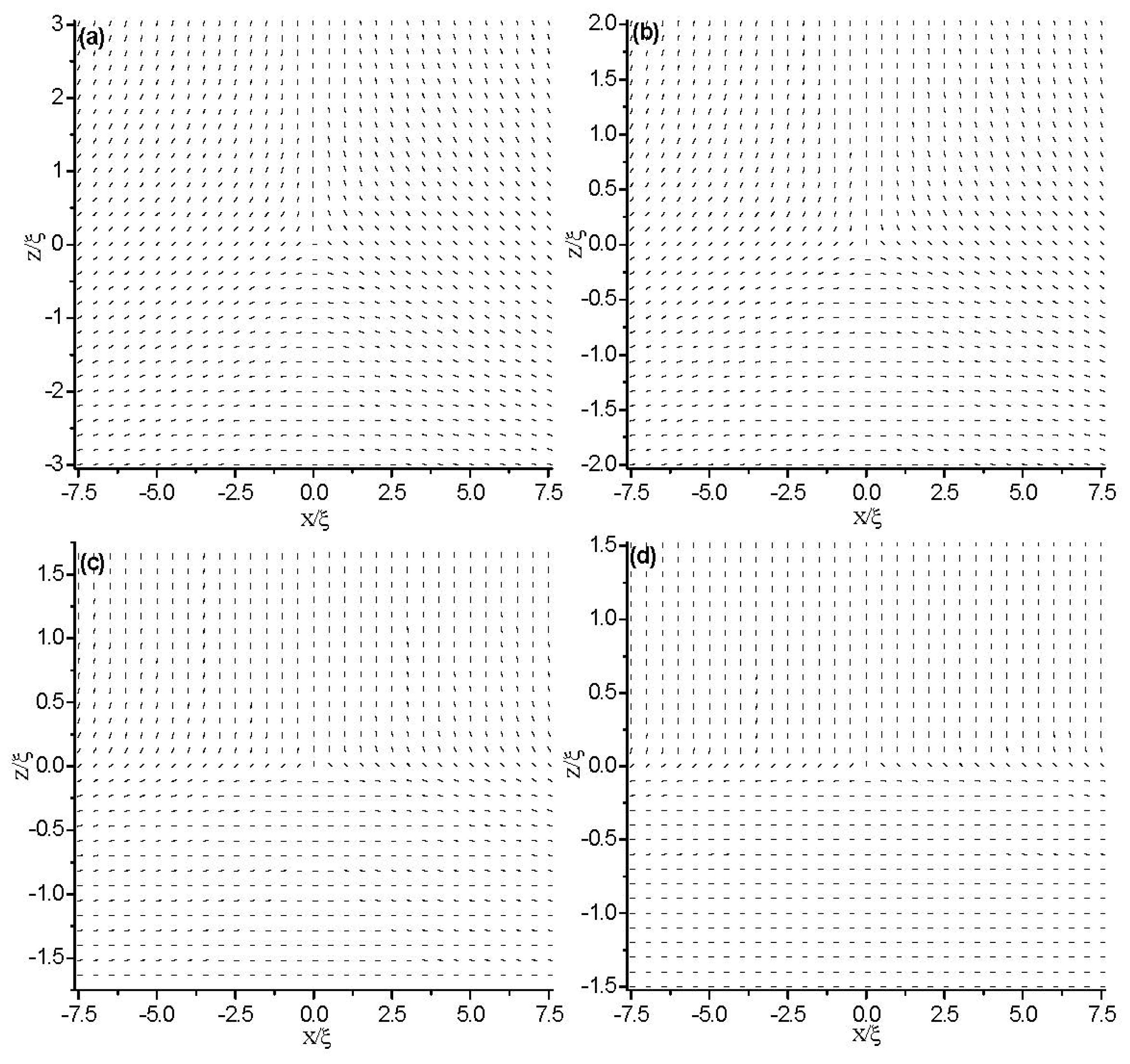
3. Results
3.1. Strong Anchoring Boundary Conditions
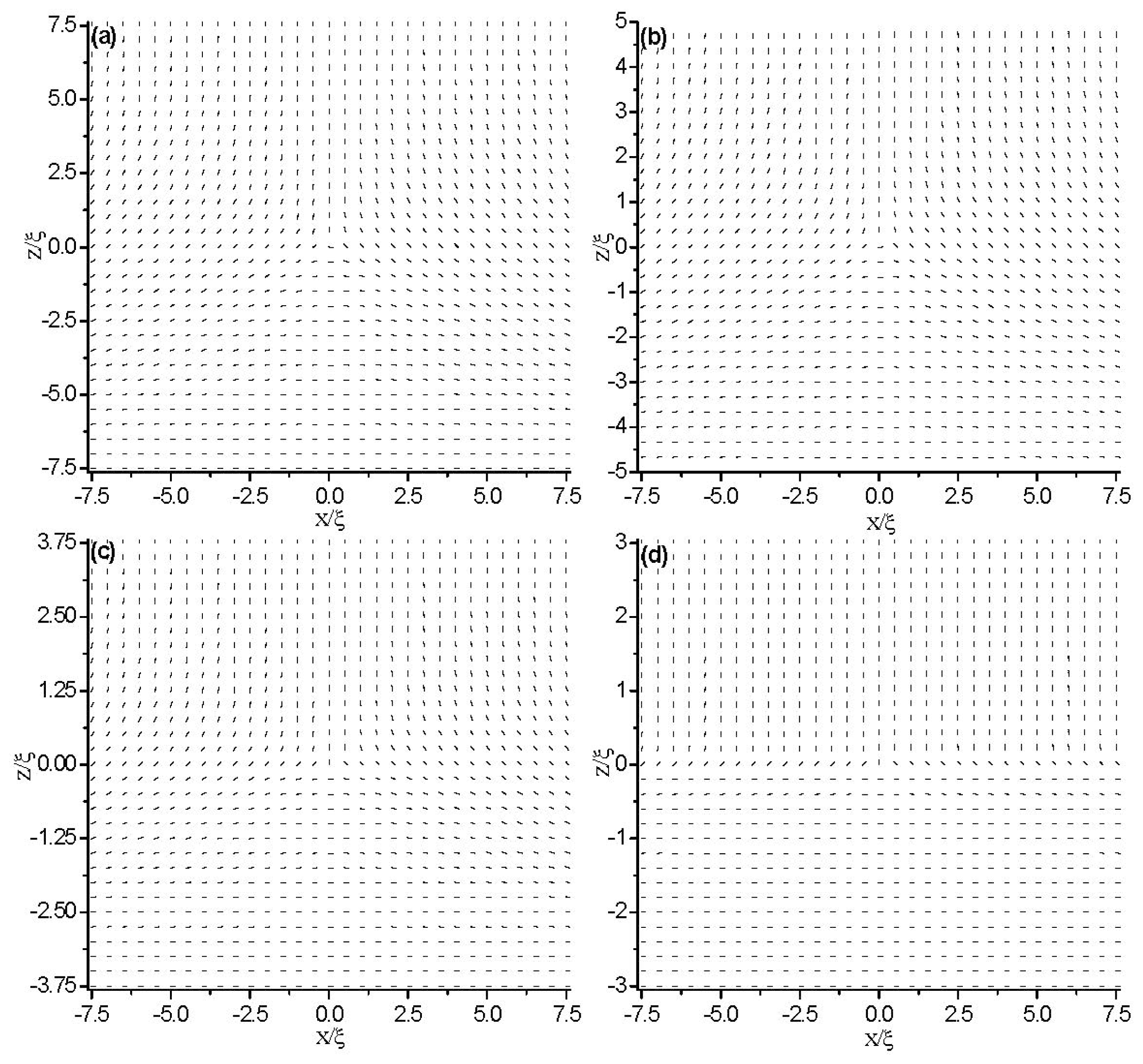
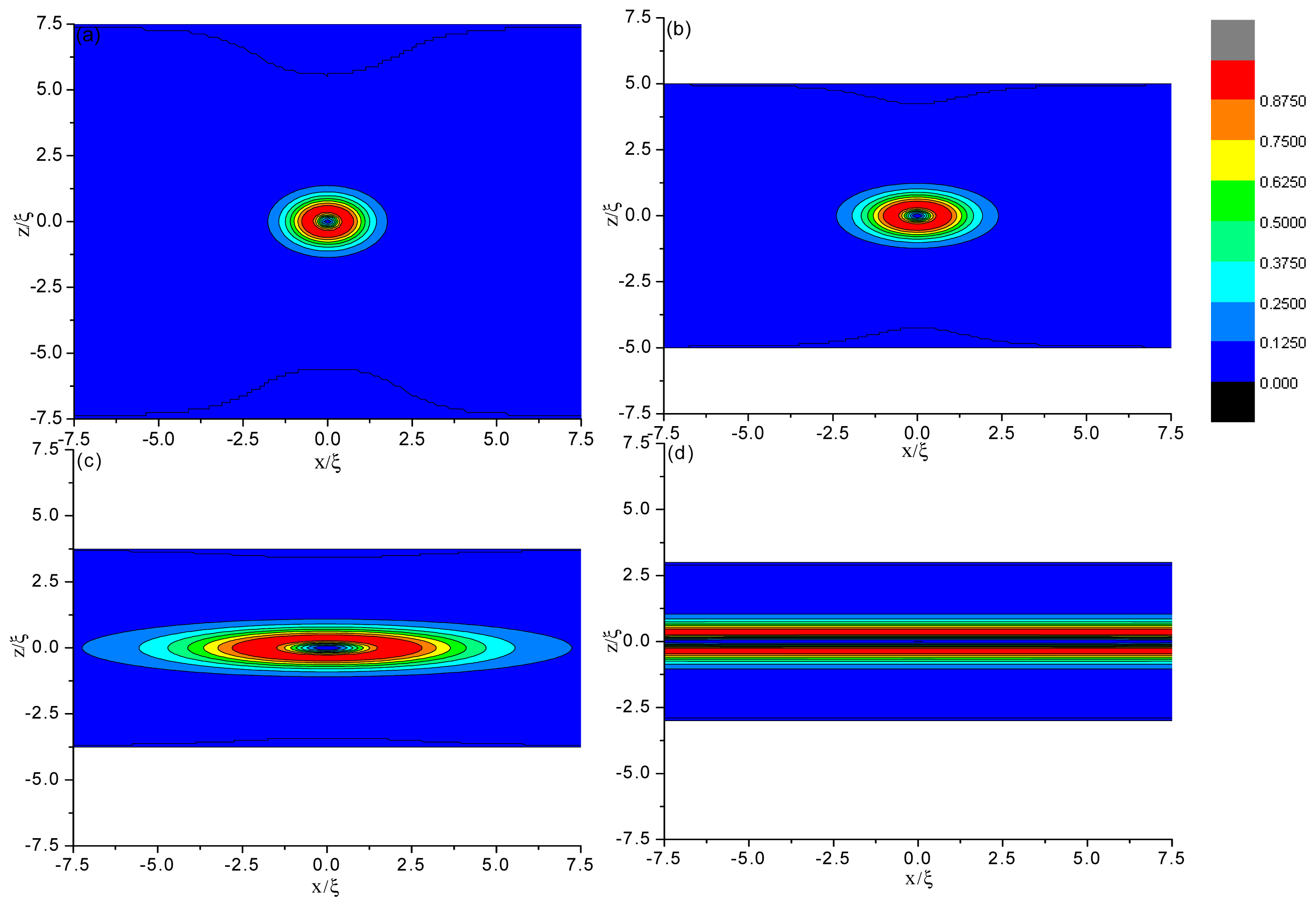
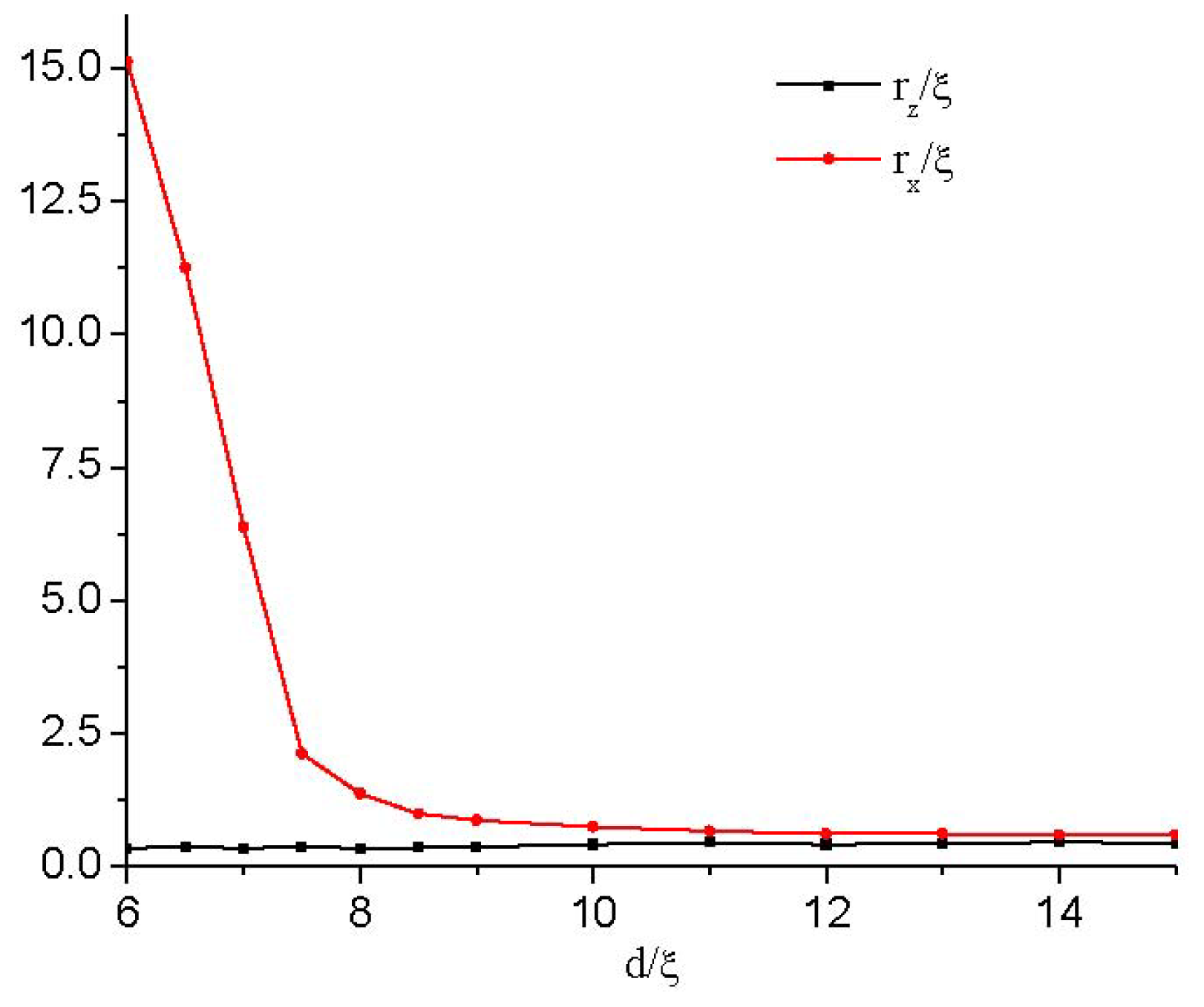
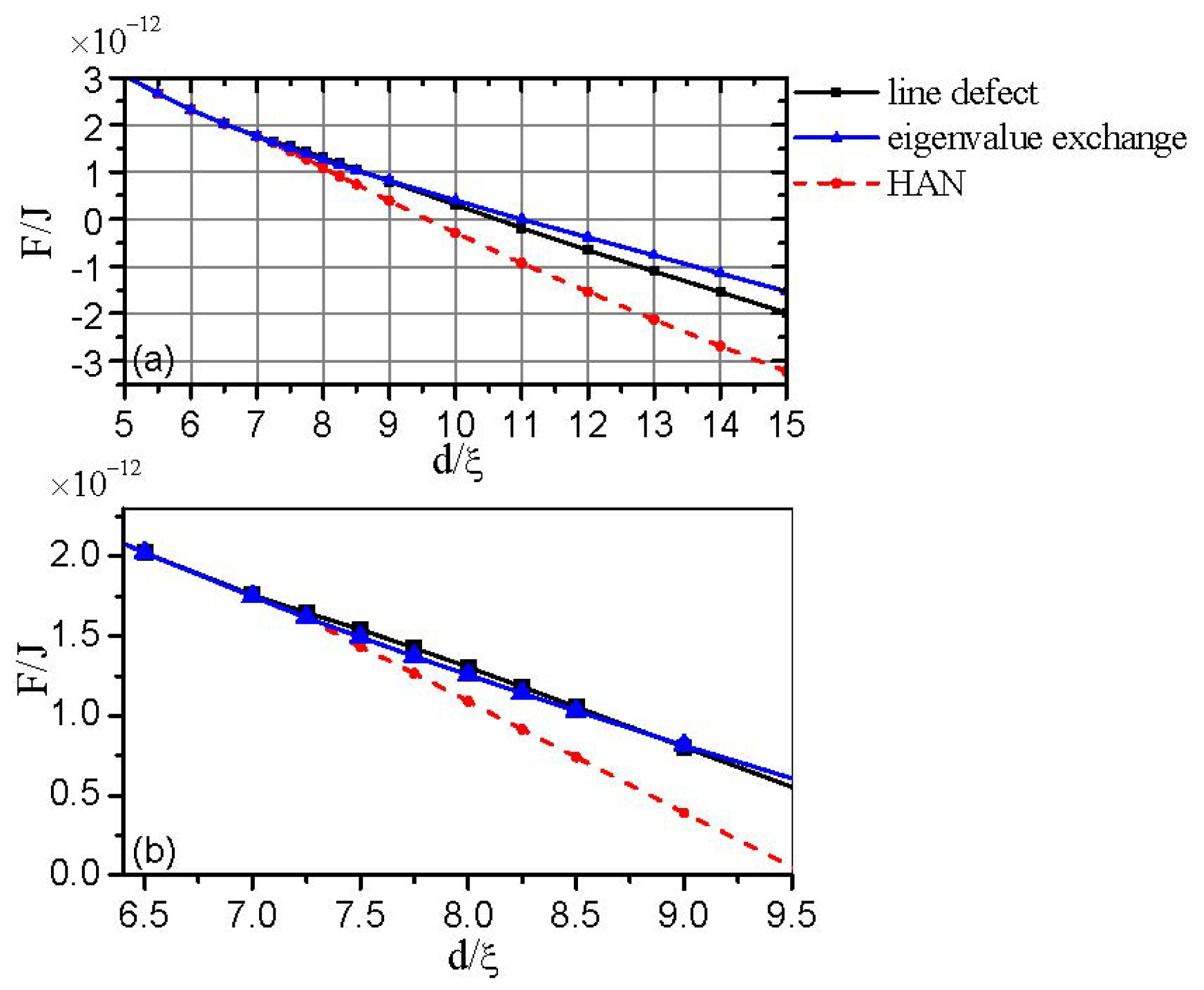
3.1.1. The Structure at Equilibrium State
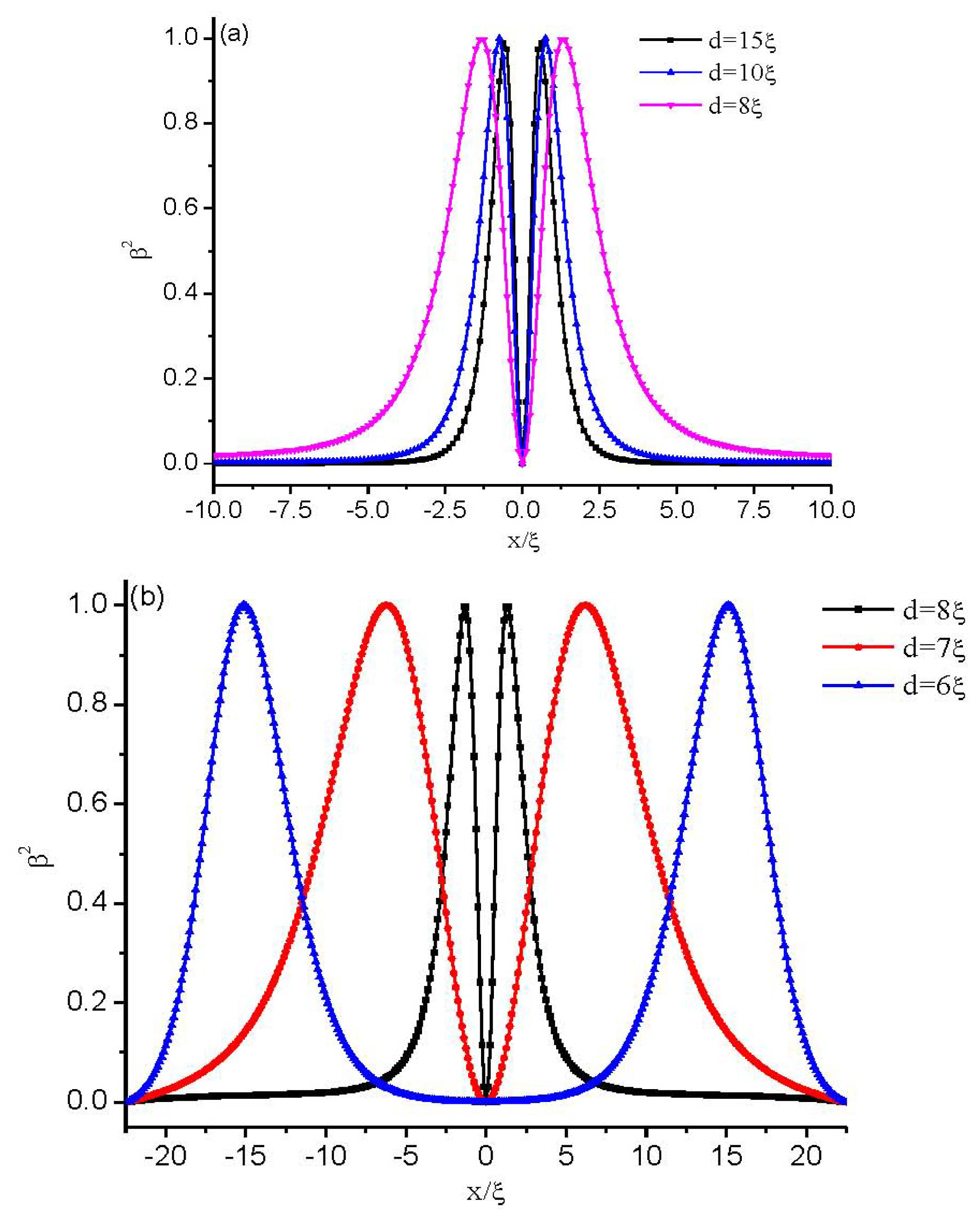
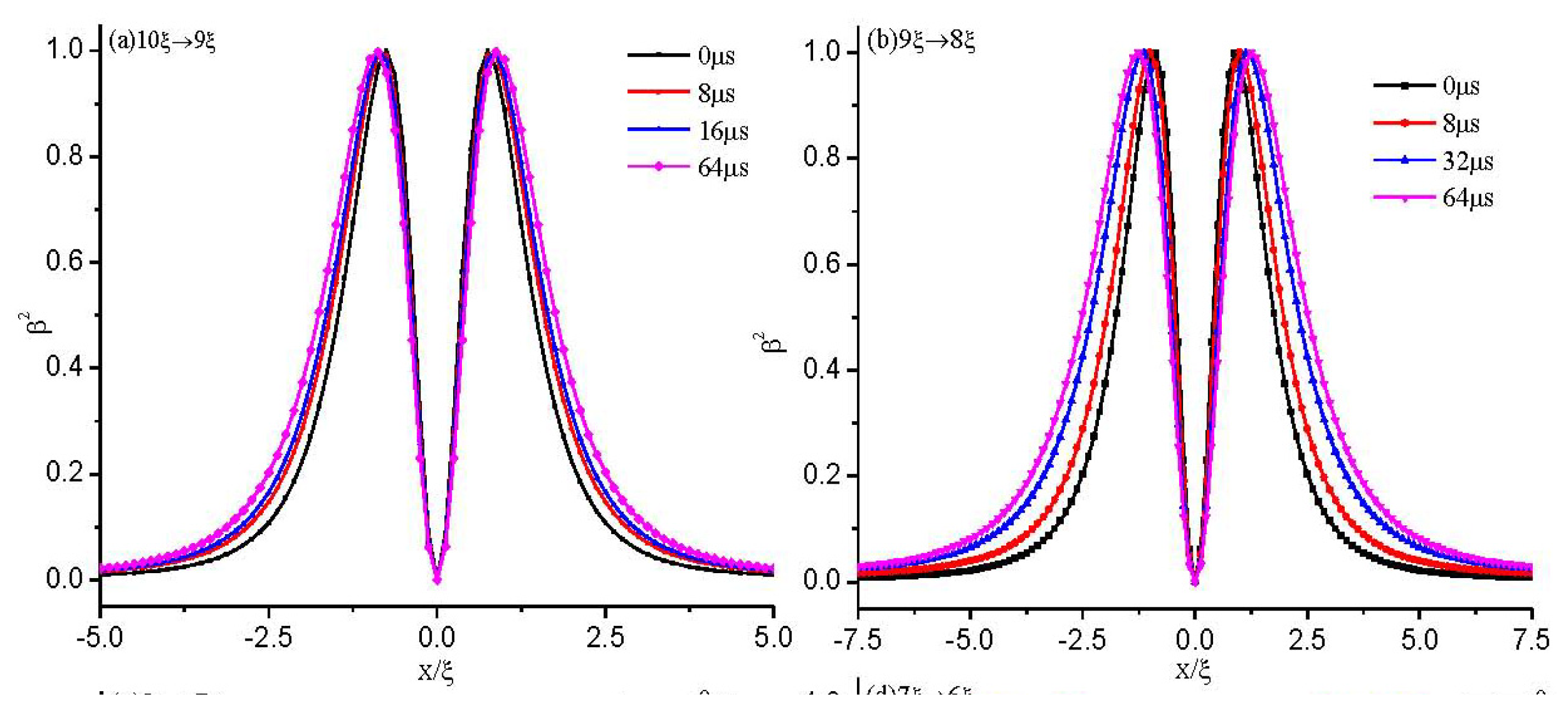
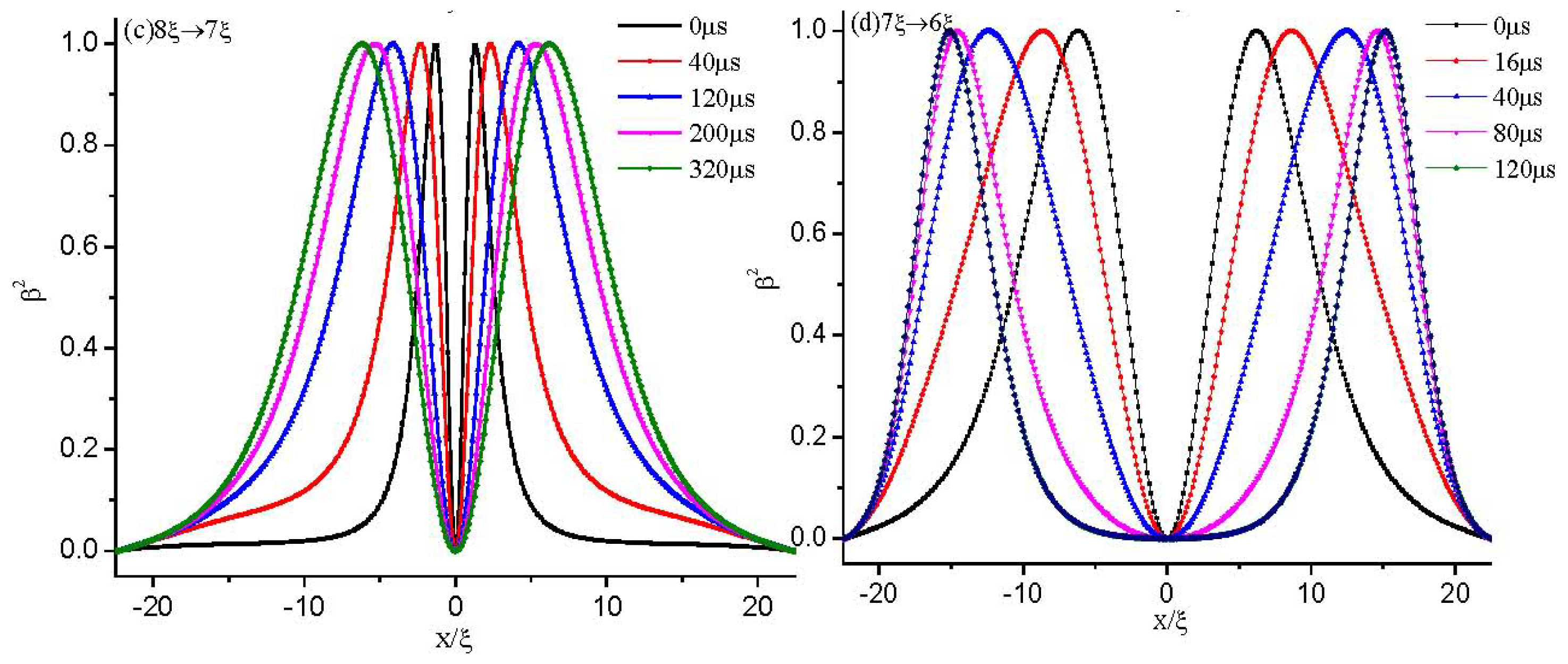
3.1.2. Dynamical Evolution
3.2. Weak Anchoring Boundary Conditions
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Mermin, N.D. Topological theory of defects. Rev. Mod. Phys 1979, 51, 591–648. [Google Scholar]
- Trebin, H.-R. The topology of non-uniform media in condensed matter physics. Adv. Phys 1982, 31, 195–254. [Google Scholar]
- Chaikin, P.M.; Lubensky, T.C. Principles of Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Kléman, M. Points, Lines and Walls. In Liquid Crystals, Magnetic Systems and Various Disordered Media; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Kurik, M.V.; Lavrentovich, O.D. Defects in liquid crystals: Homotopy theory and experimental studies. Sov. Phys. Usp 1988, 31, 196–224. [Google Scholar]
- Kralj, S.; Virga, E.G. Universal fine structure of nematic hedgehogs. J. Phys. A 2001, 34, 829–838. [Google Scholar]
- Schopohl, N.; Sluckin, T.J. Defect core structure in nematic liquid crystals. Phys. Rev. Lett 1987, 59, 2582–2584. [Google Scholar]
- Palffy-Muhoray, P.; Gartland, E.C.; Kelly, J.R. A new configuration transition in inhomogeneous nematics. Liq. Cryst 1994, 16, 713–718. [Google Scholar]
- Bisi, F.; Gartland, E.C.; Rosso, R.; Virga, E.G. Order reconstruction in frustrated nematic twisted cells. Phys. Rev. E 2003, 68, 021707:1–021707:11. [Google Scholar]
- Kralj, S.; Virga, E.G.; Žumer, S. Biaxial torus around nematic point defects. Phys. Rev. E 1999, 60, 1858–1866. [Google Scholar]
- Lombardo, G.; Ayeb, H.; Ciuchi, F.; de Santo, M.P.; Barberi, R.; Bartolino, R.; Virga, E.G.; Durand, G.E. Inhomogeneous bulk nematic order reconstruction. Phys. Rev. E 2008, 77, 020702:1–020702:4. [Google Scholar]
- Ambrožič, M.; Kralj, S.; Virga, E.G. Defect-enhanced nematic surface order reconstruction. Phys. Rev. E 2007, 75. [Google Scholar] [CrossRef]
- Kralj, S.; Rosso, R.; Virga, E.G. Finite-size effects on order reconstruction around nematic defects. Phys. Rev. E 2010, 81, 021703:1–021703:15. [Google Scholar]
- Barberi, R.; Ciuchi, F.; Durand, G.E.; Iovane, M.; Sikharulidze, D.; Sonnet, A.M.; Virga, E.G. Electric field induced order reconstruction in a nematic cell. Eur. Phys. J. E 2004, 13, 61–71. [Google Scholar]
- Martinot-Lagarde, P.; Dreyfus-Lambez, H.; Dozov, I. Biaxial melting of the nematic order under a strong electric field. Phys. Rev. E 2003, 67, 051710:1–051710:4. [Google Scholar]
- Barberi, R.; Ciuchi, F.G.; Lombardo, G.; Bartolino, R.; Durand, G.E. Time resolved experimental analysis of the electric field induced biaxial order reconstruction in nematics. Phys. Rev. Lett 2004, 93, 137801:1–137801:4. [Google Scholar]
- Guzmán, O.; Abbott, N.L.; de Pablo, J.J. Quenched disorder in a liquid-crystal biosensor: Adsorbed nanoparticles at confining walls. J. Chem. Phys 2005, 122, 184711:1–184711:10. [Google Scholar]
- Carbone, G.; Lombardo, G.; Barberi, R. Mechanically induced biaxial transition in a nanoconfined nematic liquid crystal with a topological defect. Phys. Rev. Lett 2009, 103, 167806:1–167806:4. [Google Scholar]
- Koèevar, K.; Muševiè, I. Structural forces near phase transitions of liquid crystals. Chem. Phys. Chem 2003, 4, 1049–1056. [Google Scholar]
- Carbone, G.; Barberi, R.; Muševiè, I.; Kržiè, U. Atomic force microscope study of presmectic modulation in the nematic and isotropic phases of the liquid crystal octylcyanobiphenyl using piezoresistive force detection. Phys. Rev. E 2005, 71, 051704:1–051704:5. [Google Scholar]
- Muševič, I.; Kočevar, K.; Kržič, U.; Carbone, G. Force spectroscopy based on temperature controlled atomic force microscope head using piezoresistive cantilevers. Rev. Sci. Instrum 2005, 76, 043701:1–043701:4. [Google Scholar]
- Rasing, T.; Muševič, I. Surfaces and Interfaces of Liquid Crystals; Springer Berlin: Heidelberg; Springer, Berlin, Germany, 2004. [Google Scholar]
- Koèevar, K.; Muševiè, I. Surface-induced nematic and smectic order at a liquid-crystal-silanated-glass interface observed by atomic force spectroscopy and Brewster angle ellipsometry. Phys. Rev. E 2002, 65, 021703:1–021703:10. [Google Scholar]
- Koèevar, K.; Blinc, R.; Muševiè, I. Atomic force microscope evidence for the existence of smecticlike surface layers in the isotropic phase of a nematic liquid crystal. Phys. Rev. E 2000, 62, R3055–R3058. [Google Scholar]
- Koèevar, K.; Muševiè, I. Forces in the isotropic phase of a confined nematic liquid crystal 5CB. Phys. Rev. E 2001, 64, 051711:1–051711:8. [Google Scholar]
- Koèevar, K.; Borštnik, A.; Muševiè, I.; Žumer, S. Capillary condensation of a nematic liquid crystal observed by force spectroscopy. Phys. Rev. Lett 2001, 86, 5914–5917. [Google Scholar]
- Lombardo, G.; Ayeb, H.; Barberi, R. Dynamical numericalr model for biaxial nematic order reconstruction. Phys. Rev. E 2008, 77, 051708:1–051708:10. [Google Scholar]
- Amoddeo, A.; Barberi, R.; Lombardo, G. Moving mesh partial differential equations to describe nematic order dynamics. Comput. Math. Appl 2010, 60, 2239–2252. [Google Scholar]
- Ayeb, H.; Lombardo, G.; Ciuchi, F.; Hamdi, R.; Gharbi, A.; Durand, G.; Barberi, R. Surface order reconstruction in nematics. Appl. Phys. Lett 2010, 97, 104104:1–104104:3. [Google Scholar]
- Amoddeo, A.; Barberi, R.; Lombardo, G. Surface and bulk contributions to nematic order reconstruction. Phys. Rev. E 2012, 85, 061705:1–061705:10. [Google Scholar]
- Lombardo, G.; Amoddeo, A.; Hamdi, R.; Ayeb, H.; Barberi, R. Biaxial surface order dynamics in calamitic nematics. Eur. Phys. J. E 2012, 35. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Virga, E.G. Variational Theories for Liquid Crystals; Chapman Hall: London, UK, 1994. [Google Scholar]
- Kaiser, P.; Wiese, W.; Hess, S. Stability and instability of an uniaxial alignment against biaxial distortions in the isotropic and nematic phases of liquid crystals. J. Non-Equilib. Thermodyn 1992, 17, 153–169. [Google Scholar]
- Zhou, X.; Zheng, G.L.; Zhang, Z.D. Defect core structures in twisted nematic and twisted chiral liquid crystals. J. Mod. Phys 2013, 4, 272–279. [Google Scholar]
- Qian, T.Z.; Sheng, P. Orientational states and phase transitions induced by microtextured substrates. Phys. Rev. E 1997, 55, 7111–7120. [Google Scholar]
- Chen, K.M.; Gauza, S.; Xianyu, H.; Wu, S.T. Hysteresis effects in blue-phase liquid crystals. J. Disp. Technol 2010, 6, 318–322. [Google Scholar]
- Smalyukh, I.I.; Lavrentovich, O.D. Anchoring-mediated interaction of edge dislocations with bounding surfaces in confined cholesteric liquid crystals. Phys. Rev. Lett 2003, 90, 085503:1–085503:4. [Google Scholar]
- Barberi, R.; Barbero, G. Variational Calculus and Simple Applications of Continuum Theory. In Physics of Liquid Crystalline Materials, 2nd ed; Khoo, I., Simoni, F., Eds.; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1991; Volume 3, pp. 225–231. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhou, X.; Zhang, Z. Dynamics of Order Reconstruction in a Nanoconfined Nematic Liquid Crystal with a Topological Defect. Int. J. Mol. Sci. 2013, 14, 24135-24153. https://doi.org/10.3390/ijms141224135
Zhou X, Zhang Z. Dynamics of Order Reconstruction in a Nanoconfined Nematic Liquid Crystal with a Topological Defect. International Journal of Molecular Sciences. 2013; 14(12):24135-24153. https://doi.org/10.3390/ijms141224135
Chicago/Turabian StyleZhou, Xuan, and Zhidong Zhang. 2013. "Dynamics of Order Reconstruction in a Nanoconfined Nematic Liquid Crystal with a Topological Defect" International Journal of Molecular Sciences 14, no. 12: 24135-24153. https://doi.org/10.3390/ijms141224135
APA StyleZhou, X., & Zhang, Z. (2013). Dynamics of Order Reconstruction in a Nanoconfined Nematic Liquid Crystal with a Topological Defect. International Journal of Molecular Sciences, 14(12), 24135-24153. https://doi.org/10.3390/ijms141224135



