3. Results and Discussion
The numerical values of all 10 structural parameters derived from the quantum-chemical calculations
in vacuo with the use of the 6–31G (d, p) method for all 12 examined compounds are presented in
Table 1. In
Table 2 they are presented with the 6–31G (3d, 3p) method used.
The values of 15 structural parameters derived from the PCM calculations in the aquatic environment using 6–31G (d, p) are presented in
Table 3.
Table 4 presents the same for the 6–31G (3d, 3p) method.
The values of the parameters determining the lipophilicity and biological activity of the compounds in question are presented in
Table 5.
A preliminary comparison, of the structural parameters calculated using the 6–31G (d, p) and 6–31G (3d, 3p) methods reveals that some differences in the values calculated for isolated molecules (in vacuuo) and molecules in an aqueous medium (PCM model) are only observed for the electron charge on the atoms (the largest positive charge MAX_POS, the largest negative charge MAX_NEG, and the difference between the charges ΔQ) standing at about 30%, and for IPOL (isotropic polarisability) ranging between 15–20%. Minor differences (within 5%) occur for the values of the total dipole moment. This comparison was only an approximate estimation of the values obtained directly from Gaussian software. In order to evaluate the usefulness of the calculations using 6–31G (d, p) and 6–31G (3d, 3p) it was necessary to conduct a multiregression analysis.
Before initiating the multiregression analysis, the data set was subject to cross-validation in the aggregate PLS analysis and in the traditional manner.
i.e., by sequential removal of one case followed by a statistical analysis of the remaining 11 cases. Then, the mean values were calculated: the directional factors of the independent variables, the intercept and the regression coefficient based on those cases of the regression dependence where, the independent variables were most likely to repeat. Finally, the obtained values were compared with the values derived from the full set of cases (
n = 12). The results of the multiregression analysis are presented in
Tables 6–
12.
Geometry optimization and calculation of the structural parameters of the enlarged function base (3d, 3p instead of d, p) does not yield any significant differences in the resulting multiregression relationships. This may be due to the fact that the structural parameters involving the highest observed differences (MAX_POS, MAX_NEG, ΔQ, and IPOL) do not occur at all, or appear sporadically as a third variable. The values of the structural parameters that have the greatest impact on the empirical parameters generally differ by less than 5%, and in some cases by even less than 1% for both functional bases.
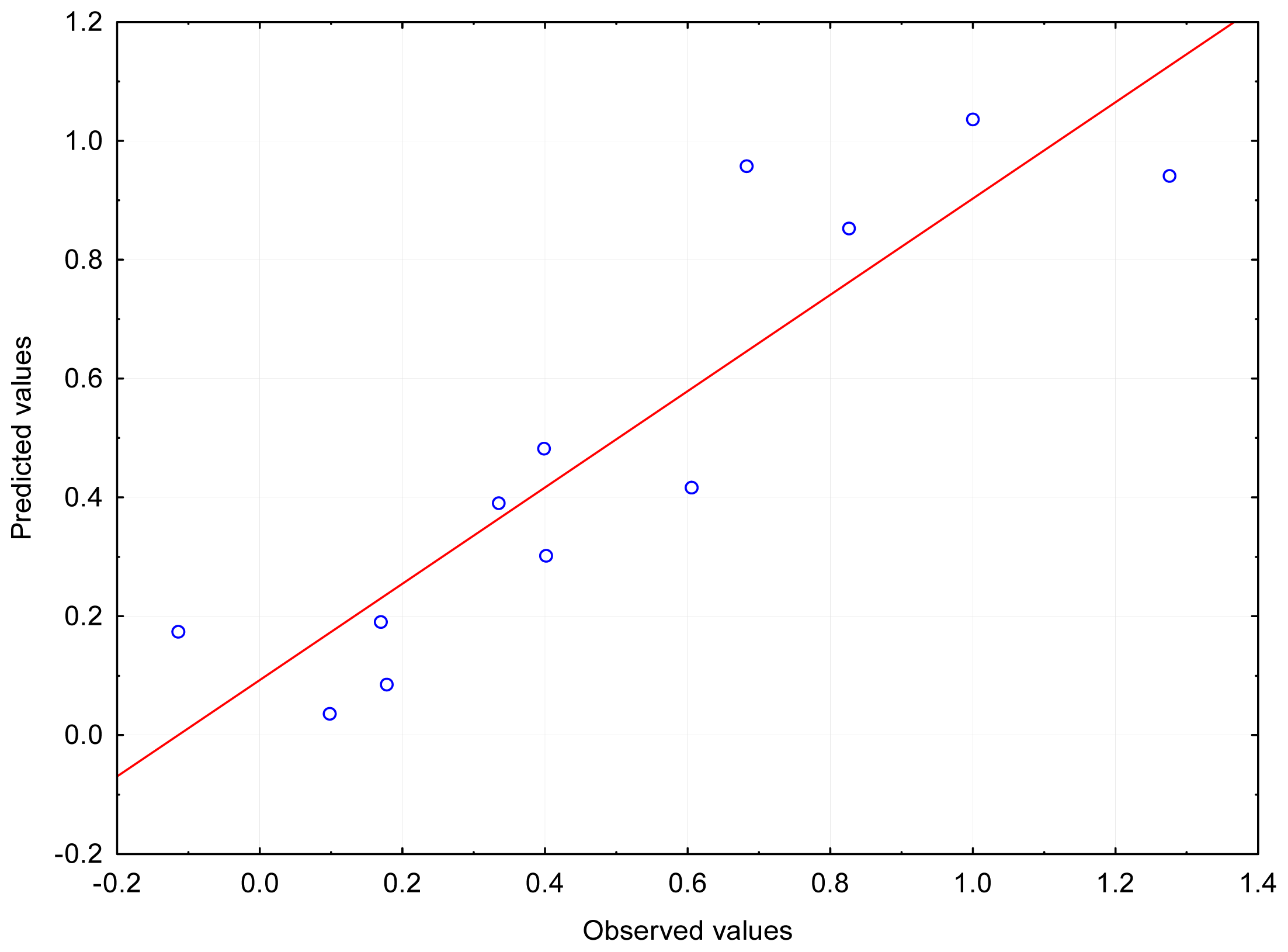
The logarithm of the retention factor, log
k, for isolated molecules (
in vacuo) depends primarily on the electron spatial extent (ESE), than on the value of the total dipole moment (TDM). The best agreement (R~0.9) was obtained for those two independent variables (
Figure 2). The situation is analogous in aqueous medium (R~0.9). During the cross-validation, dependence was found occasionally for three independent variables: ESE, TDM and MAX_POS (R~0.98) in 11 cases. The logarithm of the partition coefficient, clog
P, calculated by the authors [
4] under the classical Hansch method [
5] also shows a very similar dependence for both the isolated molecules and those in the aquatic environment–ESE as a single variable, and ESE with TDM in the case of two variables (R~0.89). The relationship of two variables can be considered satisfactory. Occasionally, for all 12 cases, relationships of three variables were observed: ESE, TDM, and MAX_POS for isolated molecules, and ESE, TDM, and ΔQ for the particles in an aqueous medium (R~0.93–0.94).
The LD
50 parameter was given for biological activity [
4]. This was supplemented with the log (1/LD
50) parameter being directly proportional to the force of action. The logarithm of the inverse of LD
50 is proven in having slightly better correspondence with the structural parameters. Isolated molecules (
in vacuo) demonstrated dependence on only one parameter—the lowest energy unoccupied molecular orbitals (E_LUMO) with R~0.89–0.90 (LD
50) and R~0.91 (log (1/LD
50)).
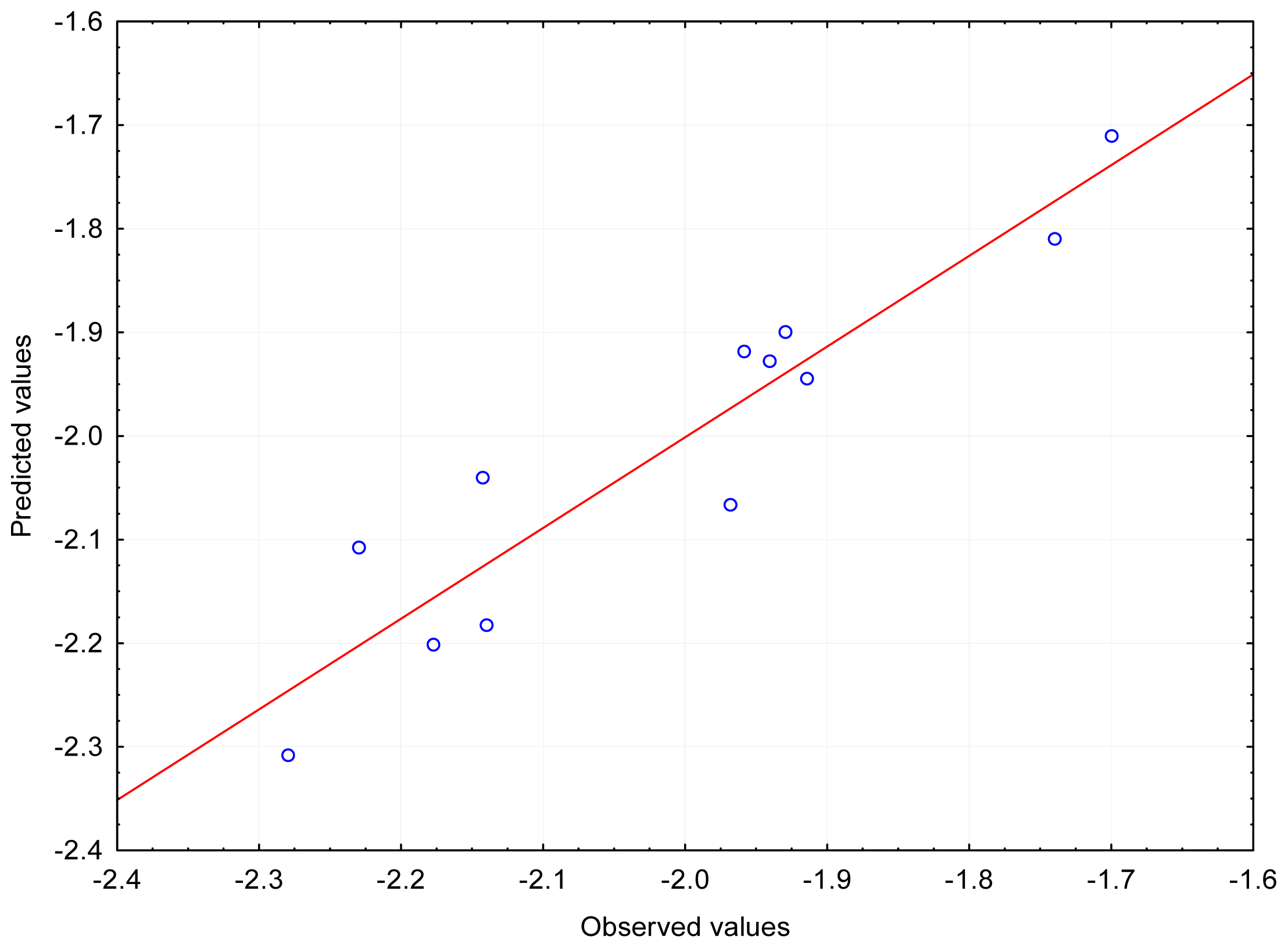
When the particles were optimized in the aquatic environment a shift of the structural parameters was recorded. This may be due to the fact that more parameters, not noted for isolated molecules, were taken into account for the aquatic environment. Moreover, there were more variables than cases so the calculation matrix became “oversquare”. The first important variable was the energy of dispersion (ED), although the dependence on E_LUMO for the log (1/LD
50) occurred sporadically during cross-validation; the, R values were: ~0.83 (LD
50) and ~0.84 (log (1/LD
50)). A dependence was also found for two other variables: DE and E_LUMO with R~0.91–0.92 (LD
50) and R~0.93–0.94 (log (1/LD
50), presented on
Figure 3). In addition, for log (1/LD
50) a relationship was found between the following three variables: DE, E_LUMO, and the energy of interaction of the polarized solute-solvent (PSSIE), with R~0.96–0.97.
Among the parameters determining the lipophilicity of the molecules (chromatographic, log k, and calculated, clog P) those of the greatest impact are as follows: electron spatial extent (ESE) reflecting the particles’ dispersion ability and the London force interactions. Coming second in significance is the total dipole moment (TDM) reflecting the targeted electrostatic interactions. Incidentally, the influence of the electrical charges on the atoms (the largest positive difference MAX_POS and maximum positive and negative ΔQ) also appeared to be associated with more local electrostatic interactions. The coefficients of proportionality occurring for the ESE and TDM values are positive, which indicates that lipophilicity is directly proportional to these two parameters. The charges on atoms (or their difference) occasionally appearing in the equations as the third parameter show negative values for the proportionality coefficients, which leads to reduction of lipophilicity.
In the case of the parameters determining antiproliferative activity we observe competition between the energy of lowest unoccupied molecular orbitals and energy of dispersion. The energy of the LUMO orbitals, according to Koopman’s theorem, carries the physical sense of electron affinity (EA). A positive value of the LUMO energy in the thermodynamic convention denotes the energy, which must be supplied to the system in order to attach an additional electron to the molecule or otherwise convert it to an anion). On the other hand, negative LUMO energy denotes the energy provided by the system, which means that the process is exergonic. EA = −E_LUMO, and is the measure of electrophilicity of a molecule that is particularly important in the modeling of molecular properties and reactivity (radical reactions). The energy of dispersion (DE) denotes the share of the dispersive effect energy of the total energy of the solute-solvent interactions. The dispersion energy term is often collated with the repulsion into a unique term defining the so-called van der Waals contribution to the interaction energy of molecules [
10,
12]. The proportionality coefficients of the two independent variables (E_LUMO and DE) have negative signs (in the dependency for log (1/LD
50)), the E_LUMO values are positive, while the DE values are negative. The exact numerical values are determined by the values of free expression. Increase of the LUMO energy leads to a reduction in antiproliferative activity, whereas increase of DE leads to growth in the antiproliferative activity. The third and incidentally occurring variable,
i.e., the energy of the solute-solvent impacts, increases antiproliferative activity just like the energy of dispersion. The interaction energies of the solute and solvent, and particularly the dispersion component in the polar solvent,
i.e., water, can serve as a model for interactions of substances demonstrating antiproliferative activity of cellular receptors. They represent non-specific interactions. This is indicated in the conclusions of the work [
4] about the relationship between lipophilic and biological activities. The meaning of LUMO orbital energy should be interpreted differently. All examined compounds have positive values of LUMO orbital energy, which means that E_LUMO reduces the value of log (1/LD
50) (the positive value of E_LUMO signifies that no anions are formed). If the E_LUMO values were negative, then the element described by this parameter would be positive and increase the value of log (1/LD
50) (anions of the molecules in question would form, as well as possible additional interactions with the polar groups and the positively charged cellular structures).
As was shown in the cited work by Hollósy
et al. [
4], for the regressions between the parameters of lipophilicity and biological activity for each separate subset of the compounds under consideration,
i.e, derivatives of furan and thiophene, it was decided to examine how the presented empirical parameters depend on the structural parameters in each subset. The presented results of those statistical analyses were only indicative and approximate due to the fact that they formed a small subset (
n = 6) and the compounds contained in them differ in structure to a lesser degree than the full set of compounds.
In the subgroup of the furan derivatives, the lipophilicity parameters for the isolated molecules (in vacuo), just like the full set, depend mainly on the electron spatial extent (ESE) with R~0.85–0.90. The antiproliferative activity (only LD50 value) depends on the isotropic polarisability (IPOL), with R~0.82–0.85. Thus, the most important independent variables are: the structural parameters determining the possibility of dispersion and London force interactions.
In the aqueous medium all parameters,
i.e., lipophilicity and biological activity, depend on the dispersive energy (ED), with R~0.93, and R~0.89 for the activity expressed as log (1/LD
50). The correlation between LD
50 and ED is therefore slightly closer than the correlation found by the authors [
4] between LD
50 and log
k.
In the subgroup of the thiophene derivatives the lipophilicity parameters and biological activity for the isolated molecules (in vacuo) depend on the energy of the lowest unoccupied molecular orbitals (E_LUMO). However, with LD50, dependence on the electron spatial extent (ESE) occurred for the particles optimized on the (d, p) base alongside the two parametric dependencies on the ESE and the energy of the highest unoccupied molecular orbitals (E_HOMO). The regression coefficients characteristic for most of the dependencies are: R~0.85–0.89, R~0.92–0.93 for the log k dependencies, and R~0.99 for the two parametric dependencies for LD50.
In the aqueous medium all parameters,
i.e., of both lipophilicity and proliferative activity, depend mainly on the energy of repulsion (repulsion between the solute and solvent particles)—RE. The values of regression coefficients were identified at R~0.93–0.96. The correlation between the biological parameters and the RE was also slightly better than that between the LD
50 and log
k presented in the work [
4]. Furthermore, two-parametric dependencies developed with isotropic polarisability (IPOL) or total energy of non-electrostatic interactions (Tne) with the values of R~0.98–0.99 coming in as the prevailing second parameter.
The statistical analysis of the compound subsets indicates that the parameters of lipophilicity and biological activity are generally best correlated to the structural parameters describing the effect commonly referred as non-polar interactions, which confirms the conclusions drawn in the work by Hollósy
et al. [
4].