Abstract
The structures, electron affinities and bond dissociation energies of BrO4F/BrO4F− species have been investigated with five density functional theory (DFT) methods with DZP++ basis sets. The planar F-Br…O2…O2 complexes possess 3A′ electronic state for neutral molecule and 4A′ state for the corresponding anion. Three types of the neutral-anion energy separations are the adiabatic electron affinity (EAad), the vertical electron affinity (EAvert), and the vertical detachment energy (VDE). The EAad value predicted by B3LYP method is 4.52 eV. The bond dissociation energies De (BrO4F → BrO4-mF + Om) (m = 1–4) and De− (BrO4F− → BrO4-mF− + Om and BrO4F− → BrO4-mF + Om−) are predicted. The adiabatic electron affinities (EAad) were predicted to be 4.52 eV for F-Br…O2…O2 (3A′←4A′) (B3LYP method).
1. Introduction
In recent days, density functional theory (DFT) has been enjoying tremendous success in electronic structure calculations for molecules and solids alike [1–8]. The DFT methods are able to describe the electronic structure of these systems with accuracies comparable to traditional correlated molecular orbital methods at a decreased computational cost. Furthermore these techniques are observed to assign more bonding character to the Lewis system in which the nucleophilic reaction occurs [9]. The DFT-based global and local properties (namely, DFT descriptors), such as Fukui functions, global and local hardness or softness [10,11], have already been used for reliable predictions in various types of electrophilic and nucleophilic reactions on a diversity of material structures [1–9,12–16]. In some sense, the DFT-descriptors provide us with more rigorous alternatives than the classical frontier orbital analysis. Chatterjee’s group have already used the DFT-descriptors for predictions in electrophilic and nucleophilic reactions in the case of zeolites and clay materials with or without solvent environment [1–7].
On the other hand, the bromine, chlorine, and fluorine oxides are known to be important in lower stratospheric ozone depletion, and have been the subjects of intense studies in recent years [17–26, and references cited therein]. Relevant bromine oxide fluorides, represent intriguing ternary molecules involving covalent bond between highly electronegative atoms, possessing a large number of unpaired electrons, resulting in strong lone pair-lone pair repulsions. Therefore, the hypervalent structures of these species could be characterized. As early as 1972, Johnson et al. [27] reported the thermodynamic properties of Br(VII) FBrO3 species. In 1976, Appelman et al. [28] characterized the molecular structure of gaseous perbromyl fluoride (FBrO3), and Gillespie and Spekkens [29] prepared and characterized potassium difluorodioxobromate (BrO2F2−) and tetrafluoro-oxobromate (BrOF4−). In 1978, Christe et al. [30] reported the vibrational frequencies and assignment of BrOF3. In 2005, Lehmann et al. [31] reported synthesis and characterization of salts containing the bromine (VII) BrO3F2− anion; last year, Lehmann et al. [32] also reported the characterization of BrO3F and ClO3F to [XO2][SbF6] (X = Cl, Br) by single crystal X-ray diffraction, raman spectroscopy, and computational methods. The results showed that of a few computational methods, the DFT functional, B3LYP in combination with the aug-cc-pVTZ basis set, and the QCISD and CCSD(T) calculations provided the most reliable correlation with the experimental geometry and vibrational frequencies of BrO2+ [33] and likely provide reliable estimates of the geometric parameters and vibrational frequencies of BrO3+, as well as benchmarks for calculations involving bromine fluoride and oxide fluoride species [33]. Correspondingly, the density functional theory (DFT) in conjunction with DZP++ basis set has also localized these Br-hypervalent ternary structures to be minimum on the potential energy surfaces (PES) [34,35]. The planar/lineaer FBrO/FBrO-, pseudo-trigonal bipyramid F(F2)Br=O (Cs symmetric) [34] and [F-(:BrO2)-F]− (C2v) anionic [29], and quasi-octahedral (OBr-F4)− (C4v) [34,29] Br(V) structures have been found to be the lowest-lying isomers. However, the hypervalent FBrO2, FBrO3 [35], and their corresponding anionic isomers are local minima on the PES. These DFT methods, especially the hybrid DFT methods (BHLYP and B3LYP) are reliable to predict the bond lengths and bond angles [32]. Besides the rich fluoride chemistry of the III and V oxidation states of Br oxides, the fluoride ion transfer reactions containing Br(VII) are scarce and have only been established by the syntheses of the ternary bromine oxide fluorides, BrO3F2− [31]. In this work, we report the systemic theoretical investigation of the similar BrO4F/BrO4F− species, which may be of importance in atmospheric chemistry.
DFT/DZP++ scheme has been shown to be successful in prediction of electron affinities (EAs) of many species, such as BrOFn/BrOFn−, FBrO2/FBrO3, Br2On/Br2On−, BrClFn/BrClFn and SF5On/SF5On− (n = 1–3) species [34–38]. These studies and others have demonstrated that the DFT/DZP++ methods can predict electron affinities (EAs) in a good accuracy [39]. In addition, these methods are reliable for the geometry optimization of the neutral radicals and their anion.
The aim of the present work is to apply five DFT methods to predict the electron affinities of ternary bromine oxide fluoride, BrO4F, as well as the equilibrium geometries, harmonic vibrational frequencies, and bond dissociation energies. Four forms of the electron affinities are calculated, evaluated as the neutral–anion energy separations in the following manners. The adiabatic electron affinities (EAad) are determined by, EAad = E(optimized neutral) – E(optimized anion), zero-point corrected adiabatic electron affinities (EAzero) are determined by, EAzero = E(zero-point corrected neutral) – E(zero-point corrected anion), the vertical electron affinities (EAvert) by, EAvert = E(optimized neutral) – E(anion at optimized neutral geometry), and the vertical detachment energies (VDE) of the anion by, VDE = E(neutral at optimized anion geometry) – E(optimized anion). The DFT descriptors, such as Fukui functions, global and local hardness or softness [10,11], also have been used for the reliable predictions in the stability of BrO4F isomers.
2. Theory
Just like Chatterjee et al. [1–5] rationalized the structure-property relationship in different clays and observed that the hydroxyl groups present in the clay structure play a crucial role in the catalytic activity. We have explored the role of O and F atoms on the structure and properties of different bromine oxygen fluoides [34,35].
The hard-soft acid-base (HSAB) principles categorize the interaction between acids and bases in terms of global softness. Pearson proposed the global HSAB principle [40]. The global hardness was the second derivative of energy with respect to the number of electrons at constant temperature and external potential, which includes the nuclear field. The nonchemical meaning of the word “hardness” is resistance to deformation or change.
The global softness is the inverse of this. Pearson also pointed out a principle of maximum hardness (PMH) [41], which stated that, for a constant external potential, the system with the maximum global hardness is the most stable.
DFT-based local properties, like Fukui functions and local softness [10], have already been used for reliable predictions of electrophilic and nucleophilic reactions [1–8]. Generally, compared to a gas-phase calculation, the solvent environment alters the charge distribution of a molecule. There is an increase in the dipole moment of molecules such as water and BrF, which enhances the intrinsic reactivity of polar molecules toward nucleophilic and electrophilic attack [15]. Our aim in the current work is to explore the role of On chain in the structure and bonding of BrO4F species. DFT-based local descriptors have been used for calculating the reactivity index within the helm of the HSAB principle [11–15]. It is used to determine the possible correlation between BrO4F isomers.
In density functional theory, hardness (η) [40] is defined as:
where E is the total energy, N is the number of electrons of the chemical species, and μ is the chemical potential.
The global softness, S, is defined as the inverse of the global hardness, η:
Using the finite difference approximation, S can be approximated as:
where IE and EA are the first ionization energy and electron affinity of the molecule, respectively.
The Fukui function f(r) is defined by [10]:
The function f is thus a local quantity, which has different values at different points in the species, N is the total number of electrons, μ is the chemical potential, and v is the potential acting on an electron due to all nuclei present. Since ρ(r) as a function of N has slope discontinuities, equation 1 provides the following three reaction indices [10]:
In a finite difference approximation, the condensed Fukui function [16] of an atom, say x, in a molecule with N electrons is defined as:
where qx is the electronic population of atom x in a molecule. The local softness s(r) can be defined as:
Equation(3) can also be written as:
Thus, local softness contains the same information as the Fukui function f(r) plus additional information about the total molecular softness, which is related to the global reactivity with respect to a reaction partner, as stated in the HSAB principle. Atomic softness values can easily be calculated by using equation 4, namely:
3. Methodology
The five different DFT exchange-correlation functionals employed in this work range from generalized gradient approximation (GGA) [BLYP, BP86] to hybrid-GGA [BHLYP, B3P86, and B3LYP]. These hybrid Hartree-Fock/density functionals include: (a) Becke’s half and half HF/DFT hybrid exchange functional (BH) [42] with the Lee, Yang, and Parr correlation functional (LYP) [43] (BHLYP); (b) Becke’s three parameter functional [44] (B3) plus Perdew’s correlation functional (P86) [45] (B3P86); (c) B3 combined with LYP functionals (B3LYP) [44,43]; (d) incorporation of Becke’s 1988 exchange functional (B) [46] with Perdew’s correlation functional (P86) (BP86); (e) B along with LYP (BLYP) [46,43]. The standard double-ζ plus polarization (DZP) basis set augmented with diffuse functions (DZP++) were utilized. The basis set for bromine was comprised of Ahlrichs’ standard doublẹ-spd set plus a set of d-type polarization functions [αd (Br) = 0.389] [47] plus diffuse functions [αs (Br) = 0.0469 and αp (Br) = 0.0465]. For oxygen and fluorine, the basis sets were composed of the standard Huzinaga-Dunning [48,49] doublẹ-ζ set plus one set of polarization functions [αd (O) = 0.85, αd (F) = 1.00] augmented with one set of diffuse functions [αs (O) = 0.08227, αp (O) = 0.06508, and αs (F) = 0.1049, αp (F) = 0.0826]. The final contracted basis sets are thus designated as Br (15s12p6d/9s7p3d), O (10s6p1d/5s3p1d), and F (10s6p1d/5s3p1d). All of the molecular structures and the electron affinities have been determined using the Gaussian 03 program suite [50]. The fine integration grid (99 590) was used. All stationary point geometries were characterized by the evaluation of their harmonic vibrational frequencies at the five different levels of theory. Unless otherwise reported, the geometries in figures were found to be minima after determining the harmonic vibrational frequencies via analytical second derivatives for the corresponding stationary point structures for each function.
Besides the electron affinities, the bond dissociation energies for BrO4F/BrO4F− are also determined as the difference in total energies in the following manners:
The bond dissociation energies for the neutrals refer to the reactions:
The bond dissociation energies for the anions refer to the reactions:
The natrural bond orbital (NBO) analysis [51] was carried out at the B3LYP/DZP++ level for some species, corresponding Wiberg bond index (WBI) and atomic charges are obtained. Unless otherwise stated, we use the B3LYP result for molecular structures and energetics. The counterpoise (CP) method [52] was used to correct the basis set superposition error (BSSE) [7,53] using the Boys-Bernardi method in the calculation of the binding energy for the current basis. For these complexes of Lewis species, the single point calculations of the cation and anion of each molecule at the optimized geometry of the neutral molecule were also carried out to evaluate Fukui functions, global and local softness [10]. The condensed Fukui function and atomic softness were evaluated using equations 3 and 6 in Section 2. Theory, respectively. The gross atomic charges were evaluated using the technique of Mulliken charges, due to the Br atomic charge can hardly be evaluated by using the technique of electrostatic potential (ESP) driven charges.
4. Results and Discussion
With the present five DFT methods, the optimized O-F bond length for single OF molecule ranges from 1.331 Å (BHLYP) to 1.385 Å (BLYP) (not shown). The trend of bond lengths predicted for O-F is BHLYP < B3P86 < B3LYP < BP86 < BLYP. The DZP++ B3LYP method gives the result closest to the experimental O-F bond length (re) of 1.3541 Å, obtained from Raman spectroscopy [18 and references cited therein]. The B3LYP method also obtain the best prediction result for dissociation energy (De) of OF [23] and BrO [21]. For a discussion of the reliability of B3LYP thermochemistry, see the recent work of Boese, Martin, and Handy [54]. Therefore, in the following discussion, unless otherwise stated, we use the B3LYP result for molecular structures and energetics.
For neutral BrO4F species, the molecular chain FBr…OO…OO structure with a terminal F-Br moiety connected by OO…OO chain lies the lowest energetically. This structure in its 5A′ state (all of the five DFT methods) or 3A′ state (both BP86 and BLYP pure DFT methods) corresponds a very loose van der Waals complex between BrF…OO and O2, possessing a binding energy of about zero and the very long Br…O (2.719–3.004 Å in 5A′ state and 2.618, 2.719 Å in 3A′ state) and (O)O…O(O) (5.220–7.095 Å in 5A′ state, and 5.746, 6.014 Å in 3A′ state) distances (not shown). It is favorable to dissociate into BrF + 2O2 (3Σg−) or BrF + O2 (1Δg) + O2 (3Σg−).
The FBr…OO…OO structures in 3A′ state (a: 3A′) optimized by three hybrid DFT methods (BHLYP, B3P86 and B3LYP) and in 1A′ (b: 1A′) (BHLYP) or 1A (b: 1A) state (with the rest four DFT methods) are reported in Figure 1. The optimized geometries for both Br- and F-terminal structures, including cis- and trans- BrOO…OOF (c: 1A and d: 1A), and BrOO(O)…OF (e: 1A), and those of Br-hypervalent structures, O2Br…OOF (f: 1A) and FBrO3...O (g: C3v, 3A1) are also displayed in Figure 1. The optimized geometries for anionic BrO4F− species, including (FBr…OO)−…OO (aa: 4A′) chain, and [FBr(O2)...OO]− (ab: 2A′), (FO…BrO3)− (ac: 2A′) Br-hypervalent structures are shown in Figure 2. They may represent an important intermediate in atmospheric reactions.
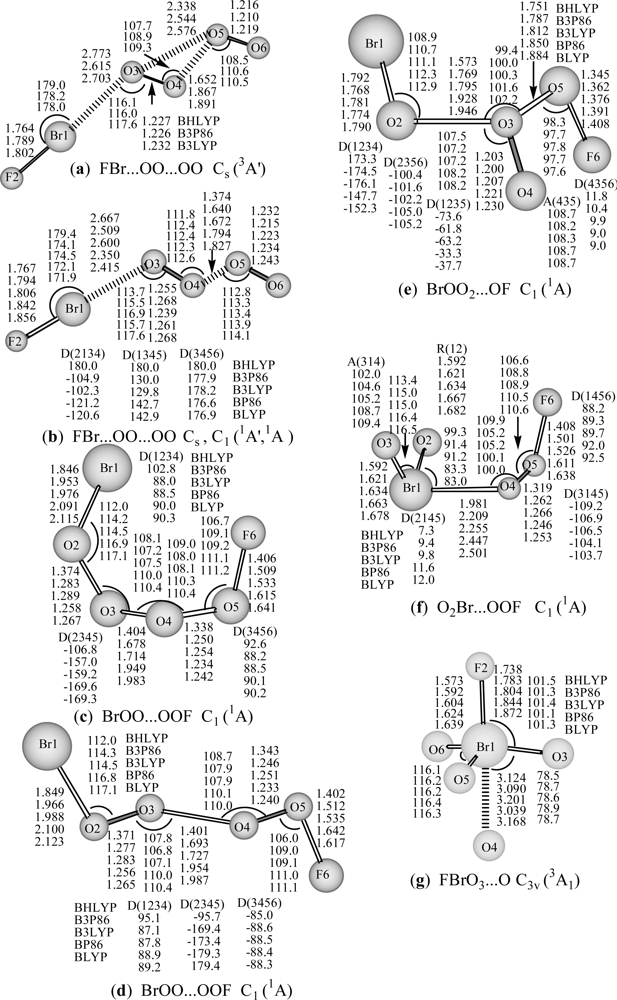
Figure 1.
Optimized geometries of neutral BrO4F (a-g) with DFT/DZP++ approach (bond lengths in Å, bond angles and dihedral angles in degrees). A: represents bond angle, D: represents torsion angle.
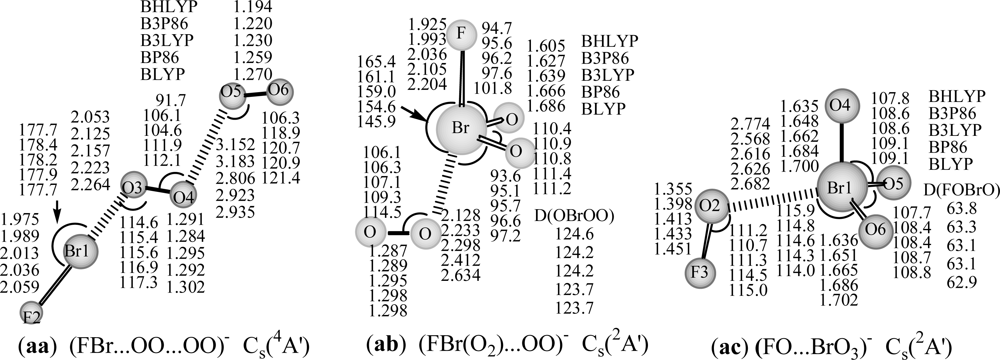
Figure 2.
Optimized geometries of anionic BrO4F− (aa-ac) with DFT/DZP++ approach (bond lengths in Å, bond angles and dihedral angles in degrees). A: represents bond angle, D: represents torsion angle.
The calculated energies (Table 1) show that the FBr…OO…OO structure in its 5A′ state or its dissociation products (FBr...OO (3A″) + O2 (3Σg−)) lies lower than the corresponding 3A′ (a) and 1A′ or 1A (b) states by about 33 and 60 kcal/mol respectively with the B3LYP method. This state also lies much lower than the cis-, trans- BrOO…OOF (c: 1A and d: 1A) and BrOO2…OF (e: 1A) isomers by ca.64, 64, and 95 kcal/mol (Table 1) respectively (B3LYP). The O2Br…OOF (f: 1A) and FBrO3...O (g: C3v, 3A1) Br-hypervalent structures lie much higher than the 5A′ state by ca. 78 and 130 kcal/mol (Table 1) respectively. With a few exceptions, the two pure DFT methods (BP86 and BLYP) predict much smaller relative energies and the bond dissociation energies than three hybrid DFT methods. All these discrepancies indicate that BrO4F is a challenging target for DFT methods.

Table 1.
Relative energies in kcal·mol−1 for BrO4F and its dissociation products species a
As can be seen from Figure 1, for the FBr…OO…OO structure in its 3A′ state, the covalent bond lengths are predicted to be 1.764–1.802 Å for the Br-F bond, and 1.227–1.232 Å for interim O-O and 1.216–1.219 Å for the terminal O-O bond, and the complex bond distances are 2.615–2.773 Å for Br…O, and 1.652–1.891 Å for (O)O…O(O) with three hybrid DFT methods. At the B3LYP level, Br-F bond length, the interim O-O and terminal O-O bond lengths in the 3A′ state (a in Figure 1) are 1.802, 1.232, and 1.219 Å respectively, and Br…O or (O)O…O(O) complex distance is 2.703 or 1.891 Å respectively. These structure parameters are similar to those of the corresponding 1A′ state or 1A state of (b in Figure 1), in which, the Br-F bond distance, the interim O-O and terminal O-O bond lengths (b in Figure 1) are slightly elongated (1.806, 1.239, and 1.223 Å respectively at B3LYP level), and Br…O or (O)O…O(O) complex distance is significantly shortened (2.600 or 1.672 Å respectively). The geometric and electronic structures show that the F-Br terminal moiety connected by OO…OO chain structure in 3A′ (hybrid DFT methods) or in singlet state may be viewed as a van der Waals complex between BrF moiety and OO-OO covalent-like chain respectively. NBO analyses (B3LYP) show that the 3A′ state possesses stronger single Br-F (WBI: 0.795 vs 0.781) and double O-O (WBI: 1.462 vs 1.436 for interim O-O; 1.524 vs 1.519 for terminal O-O) bonds than the singlet state, and that the covalent OO-OO (WBI: 0.418 vs 0.717) and complex Br…O (WBI: 0.063 vs 0.089) bonds in 3A′ state are weaker than those in singlet state. Compared with the 3A″ state of FBr...OO [35], the Br-F and interim O-O bonds in 3A′ state of FBr...OO-OO are slightly elongated by 0.01 Å, whereas Br...O distance is significantly shorter by 0.26 Å (B3LYP), and the terminal O-O bond distance is very similar to that in free O2 (3Σg−) (1.194–1.245 Å) [55].
It is worthy to note that the geometries predicted using the five functionals are all similar, with small variations in bond lengths and angles. The general trend for the covalent bond lengths is BLYP > BP86 > B3LYP > B3P86 > BHLYP. According to previous studies on geometries of BrOFn/BrOFn−, FBrO2/FBrO3, BrClFn/BrClFn and BrFn species [34,35,37,56], the hybrid DFT methods (BHLYP, B3P86 or B3LYP method) are excellent methods for the prediction of covalent bond lengths. The B3LYP method taking the median position may be regarded as a compromise between the reliabilities of geometry and thermochemical parameter predictions. This order coincides with that predicted for the FO molecule [25] where comparison with experiment indicates the B3LYP method to be the most accurate in prediction of geometry, and for BrO in predictions of bond dissociation and adiabatic electron affinity (EAad) [21].
The attachment of an electron to FBr…OO…OO complex, results in the 4A′ ground state for anion (aa: 4A′ in Figure 2). As might be expected, this structure is more stable than other anionic BrO4F− Br-hypervalent structures (ab: 2A′ and ac: 2A′ in Figure 2) by 32 and 78 kcal/mol at B3LYP/DZP++ level. The covalent bond lengths are predicted to be 1.975–2.059 Å for the Br-F bond, and 1.284–1.302 Å for interim O-O and 1.194–1.270 Å for the terminal O-O bond, and the complex bond distances are 2.053–2.264 Å for Br…O, and 2.806–3.183 Å for (O)O…O(O) in the 4A′ state of BrO4F−. Comparison with the similar neutral isomer shows that there is a substantial change in geometry between neutral 3A′ state and anionic 4A′ state. The Br-F bond (2.013 Å at B3LYP level), the interim O-O bond (1.295 Å) and Br…O bond (2.157 Å) in anionic 4A′ state are analogous to those of (FBr-OO)− (2.038 Å for Br-F, 1.302 Å for O-O, and 2.135 Å for Br…O) [35]; the terminal O-O bond in the 4A′ state of BrO4F− (1.230 Å) is similar to that of free O2 (1.219 Å at B3LYP level) [55]; the (O)O…O(O) distance of 2.806 Å in anionic BrO4F− is substantially longer than the corresponding (O)O…O(O) distance (1.891 Å) in 3A′ state of neutral BrO4F. Thus, this BrO4F− structure in 4A′ state could be regarded as a van der Waals complex between (FBr-OO)− [35] and O2 (3Σg−) due to suitable Br…O and (O)O…O(O) bonding distances, and the high negative charge of FBr-OO moiety (near to −1 from NBO analysis). Neither theoretical nor experimental values of BrO4F/BrO4F− are available for comparison. For this structure in its doublet 2A′ state, the results of all five DFT methods are suspect due to the large spin contamination, with <S2> = 1.77 or 1.76.
For the cis- and trans- BrOO…OOF (c: 1A and d: 1A in Figure 1) structures, the bond lengths are calculated to be 1.846–2.123 Å for the Br-O bond (that in cis-form tinily shorter than in trans-like), 1.402–1.642 Å for the F-O bond, 1.401–1.987 Å for the central single O–O bond, and 1.233–1.374 Å for outer O–O bonds connected by Br and F. In the cis- BrOO…OOF, the O…OO fragment nearly in a planar, both BrO and FO bonds are almost perpendicular to this planar, however, in the trans- BrOO…OOF, the OO…OO chain nearly in a planar, the BrO and FO bonds are also almost perpendicular to this planar. At B3LYP level, both BrOO…OOF isomers nearly possess the same stability. This BrOO…OOF conformation could be viewed as a complex comprising of unstable BrOO and FOO molecules, furthermore, the DFT methods predict it thermodynamic instability with respect to dissociation into BrOO + FOO (not shown).
For the BrOO2…OF (e: 1A) structures, the bond lengths are calculated to be 1.768–1.792 Å for the Br-O bond, 1.345–1.408 Å for the F-O bond, 1.200–1.230 Å for the central double O–O bond and 1.573–1.946 Å, 1.7514–1.884 Å for outer single O–O bonds connected by Br and F, respectively. At B3LYP level, the Br-O (1.781 Å) or F-O (1.376 Å) bond is slightly longer than that in BrO [21] or FO [25]. Thus, this BrOO2…OF (e: 1A) structures could be regarded as a complex comprising of simple BrO, O2 and FO molecules. The hybrid DFT methods predict it thermodynamic instability with respect to dissociation into BrO + O2 + OF (not shown), whereas the pure DFT methods predict the reaction energy of about 10 (BP86) and 6 kcal/mol (BLYP) for BrOO2…OF (e: 1A) → BrO + O2 + OF (not shown).
For Br-hypervalent structures: O2Br…OOF (f: 1A), the bond lengths are predicted to be 1.592–1.682 Å for Br-Oterm (with an oxygen atom at the terminal position), 1.981–2.501 Å for Br-Omid (with O atom at the middle position), and 1.246–1.319 Å for O-O, and 1.408–1.638 Å for F-O. The predicted Br-Oterm length is comparable to that of OBrO (1.649 Å) [21], F-O or O-O bond distances are slightly shorter or longer than those in FOO (1.649 or 1.200 Å) [18]. This structure could be thought as a complex between BrO2 and FOO. Likewise, the hybrid DFT methods predict it thermodynamic instability with respect to dissociation into BrO2 + FOO (not shown), and the pure DFT methods predict the dissociation energy of O2Br…OOF (f: 1A) → BrO2 + FOO reaction is about 2.3 (BP86) and 0.5 kcal/mol (BLYP) respectively (not shown).
For the rare Br(VII) FBrO3...O (g: C3v, 3A1) complex between FBrO3 and O atom, the bond lengths are predicted to be 1.573–1.639 Å for Br-O, 1.738–1.832 Å for Br-F, and 3.039–3.168 Å for Br…O. At B3LYP level, Br-O bond long is 1.604 Å, analogous to that in BrO4− (1.603 Å) [21] or BrO3F2− (1.601 Å) [31], and longer than that in FBrO3 (1.582 Å) [35], however, significantly shorter than that in BrO3− (1.648 Å) [21]. The Br-F bond length is 1.804 Å, being significantly shorter than that in BrO3F2− (1.872 or 1.849 Å) [31], while substantially longer than that in FBrO3 (1.708 Å) [35]. ∠FBrO and ∠OBrO angles are 101.4 and 116.2° respectively, slightly narrower than those in FBrO3 theoretically (101.9 and 115.9) or experimentally (103.3 and 114.9°) [27]. Generally, the predicted lengths are comparable to those of FBrO3 (C3v) and BrO3F2− anion [31]. The DFT methods predict the dissociation energy of FBrO3...O (g: C3v, 3A1) → FBrO3 (C3v) + O reaction is about 1 kcal/mol (Table 1), demonstrating that this Br(VII) FBrO3...O (g: C3v, 3A1) hypervalent structure is bound for dissociation to FBrO3 and O.
The corresponding anion eventually to dissociation into FBr(O2)−...OO (ab: 2A′) complex structure, Br-F and Br-O bonds are elongated to be 2.036 and 1.639 Å (B3LYP), the Br…O complex distance and O-O bond length are about 2.3 and 1.30 Å. The DFT methods predict the dissociation energy of FBr(O2)−...OO (ab: 2A′) → BrF− + O2 (3Σg−) +O2 (1Δg) reaction being in the range of 7–48 kcal/mol, the BHLYP result is too small (7 kcal/mol). This is not unexpected, given the large fraction of exact exchange in the BHLYP method [57]. For the global minimum FBr…OO…OO anion (aa: 4A′), the predictions of five different DFT methods for the dissociation energies for aa to dissociate to its components [FBr...OO−(2A″) + O2, FBr...OO (3A″) + O2−, or BrF−+ 2O2(3Σg−)] show the same trend, i.e. the pure DFT (BP86 and BLYP) methods predict higher dissociation energies than the hybrid DFT methods, and the BHLYP result is the smallest.
For the higher-lying hypervalent anionic (FO…BrO3)− complex structure (ac: 2A′), the bond lengths are predicted to be 1.635–1.702 Å for Br-O bonds, 1.355–1.451Å for F-O bond, 1.355–1.451Å for F-O bond, and 2.568–2.774 Å for Br…O complex bond. The theoretical dissociation energies for (FO…BrO3)− → BrO3− (C3v) + FO is in the range of 2.8–17.9 kcal/mol (Table 2). Likewise, the pure DFT methods predict higher dissociation energies, and the BHLYP result is the lowest.

Table 2.
Relative energies (corrected with ZPVE) in kcal mol−1 for the BrO4F− species a
Generally, the theoretical dissociation energies (De) for BrO4F/BrO4F− species can be evaluated from the data in Tables 1 and 2. For the anionic BrO4F− species, all of five DFT methods predict almost consistent relative energies and bond dissociation energies, with the exception of the lowest BHLYP results (Table 2) (vide supra). In contrast, for the neutral BrO4F species (Table 1), the relative energies and bond dissociation energies predicted by BHLYP method are nearly the biggest. It is noted that BHLYP method perform poorly for bond-breaking process [57] due to the large (50%) contribution from Hartree-Fock or exact exchange. Based on the previous studies of the BrOn species [21] and the anionic BrO4F− species (vide supra), the B3LYP methods should predict reasonable dissociation energies and relative energies, however, caution is urged because of the complex of BrO4F ternary system.
At B3LYP level, for the lowest energies species, the theoretical bond dissociation energies for neutral BrO4F refer to the reactions: BrO4F→ BrO4-mF + Om (m = 1–4). For BrO4F → BrO2F (3A″) [35] + O2, the theoretical reaction energies (ca. zero) are much smaller than those of BrO4F→ BrO3F (1A’) + O (range from 84 to 109 kcal/mol, about 100 kcal/mol at B3LYP level) and BrO4F→ BrOF (1A’) + O3 (range from 48 to 101 kcal/mol, ca. 71 kcal/mol at B3LYP level), indicating the dissociation reaction is favored, which is consistent with the FBr…O2…O2 complex structure.
The most reliable B3LYP method predicts the dissociation energy (De) for F-Br…O2…O2 (5A′) → BrF + 2O2 and (F-Br…O2…O2)− (4A′) → BrF− + 2O2 are only 0.0 and 9.1 kcal/mol, respectively (Tables 1 and 2), suggesting a weak van der Waals interaction between the BrF or BrF− and O2 moieties.
For the anionic BrO4F− species, the De of BrO4F− → BrO4-mF− + Om and BrO4F− → BrO4-mF + Om−predicted (Table 2). The bond dissociation energies for BrO4F− → BrO2F− + O2 are smaller positive values, from 1.0 to 1.5 kcal/mol for three hybrid DFT methods and 4.4 or 4.9 kcal/mol for BP86 or BLYP (two pure DFT) methods. The De values predicted by BHLYP method are too low to be reliable. The De value of 1.4 kcal/mol predicted by B3LYP is much smaller than those of BrO4F− → BrO3F− + O (71 kcal/mol) and BrO4F− → OBrF− + O3 (60 kcal/mol).
For BrO4F− → BrO4-mF + Om− reactions, the higher bond dissociation energies are predicted, the De value (58 kcal/mol) of BrO4F− → BrO2F + O2− is also smaller than those of BrO4F− → BrO3F + O− (136 kcal/mol) and BrO4F− → OBrF + O3− (81 kcal/mol), and demonstrating that complex BrOnF [34,35] species have higher electron affinities than the free Om species [55]. For the challenging BrOmF/BrOmF− (m = 1–4) species, minima on PES were found with all of DFT methods employed. However, the thermodynamic stabilities decrease with n (vide supra).
The EAad for FBr-O2-O2 (a: 3A′← aa: 4A′) are predicted to be 4.95 eV(BHLYP), 4.97 eV(B3P86), and 4.52 eV(B3LYP), zero-point corrected EAad (EAzero) is only increased about 0.05 eV. At B3LYP level, EAzero is 4.57 eV, larger than those of FBr-OOO [35] and FBrO [34] by about 0.1 and 1.9 eV respectively, and much smaller than those of FBr-OO by 1.3 eV (B3LYP). Those with odd n (n = 1 and 3, closed shell) have smaller EAs than those of species for the even number of n (n = 2 and 4), which are open-shell triplet state. The EAvert values range from 2.13 to 3.55 eV. The range of VDE is from 4.49 to 4.98eV. No experimental data are available.
The harmonic vibrational frequencies and IR active intensities of BrO4F/BrO4F− species predicted by B3LYP method are available in Tables 3 and 4. For triplet state FBr...O2...O2 (a) (Cs, 3A′), the calculated infrared spectrum is characterized by three strong bands around 1561 (terminal O-O symmetri stretch(s.s.)), 1440 (middle O-O s.s.), 628 cm−1(F-Br s.s.), all other modes give rise to weak intensities. For singlet state FBr...OOOO (b) (C1, 1A), the bands of ca. 1508 (terminal O-O s.s.), 1391 (middle O-O s.s.), and 620 cm−1(F-Br s.s.) possess the stronger intensities. For BrOO...OOF chain structures (c) and (d), the predicted infrared spectrum are characterized by three stronger bands around 1223, 1376 (F-connected O-O s.s.), 1107, 1276 (Br-connected O-O s.s.), and 720, 667 cm−1(F-O-O bend), respectively, the rest modes yield weak intensities. For BrOO2...OF structure (e), four bands around 1209, 934, 862, and 718 cm−1 exist the stronger intensities, the corresponding modes are O-O (O2) s.s., F-O s.s., Br-O s.s., and O...O stretch.

Table 3.
Predicted total energies(Etotal) in hartree, zero-point vibrational energies (ZPE) in kcal mol−1, and harmonic vibrational frequencies (Freq) in cm−1and the infrared intensities (in parenthese, in km·mol−1) for the minimum-energy BrO4F (a, b, c, d, and e) structures at the B3LYP/DZP++ level.

Table 4.
Predicted total energies(Etotal) in hartree, zero-point vibrational energies (ZPE) in kcal mol−1, and harmonic vibrational frequencies (Freq) in cm−1and the infrared intensities (in parenthese, in km mol−1) for the minimum-energy BrO4F/BrO4F− (f, g/aa, ac) structures at the B3LYP/DZP++ level.
For O2Br...OOF structure (f), four bands around 1529, 1055, 732, and 618 cm−1 possess the stronger intensities, the corresponding modes are O-O stretch, OBrO asymmetric bend, OBrO symmetric bend, and FOO bend. For the highest symmetric Br(VII) FBrO3...O (g), theoretical infrared spectrum are characterized by the stronger bands around θ: 955 cm−1 (BrO3 asymmetric stretch (a.s.)); η: 864 cm−1 (BrO3 symm.bend); ζ: 567 cm−1(F-Br s.s.); ɛ: 364 cm−1(OBrO in the planar bend); δ: 345 cm−1 (OBrO out of planar bend), the harmonic vibrational frequencies of BrO3 radical are larger than the corresponding BrO3+ [32] (966, 850, 329, and 231 cm−1). For anionic quartet state FBr...OO...OO (aa) (Cs, 4A′) species, four bands around 1532, 1226, 383, and 227 cm−1 possess the stronger intensities. For anionic hypervalency structure [FO...Br(O)O2] − (ac) (Cs, 2A′), four bands around 957, 812, 805, 789 cm−1 possess the stronger intensities.
Isodesmic reactions, which have been typically used to obtain the heats of formation for many molecules, are those in which the reactants and products contain the same types of bonds, i.e., the number of bonds broken and formed is conserved [58]. An isodesmic reaction scheme requires that the heats of formation of all the molecules involved in the reaction to be known with the exception of the heat of formation of the particular isomer. Because of this property, errors in the energy that might occur due to defects in the basis set and electron correlation cancel, to a large extent. The isodesmic scheme used here is BrOOOOF + 4HOH → 3HOOH + HOBr + HOF. During the calculation of the heat of formation of BrOOOOF using the isodesmic scheme, literature values for the heats of formation of HOH (−57.10 kcal mol−1) [59], HOOH (−31.02 kcal mol−1) [59], and HOBr (−10.93 kcal mol−1) [60], HOF (−22.47 kcal mol−1) [61], were used. Using these results we were able to calculate the heats of reaction. For cis BrOOOOF (c), the heat of formation is predicted to be 50 kcalmol−1 at B3LYP level of theory (Table 5). Using the relative energies (Table 1) along with the heat of formation of BrOOOOF (c), we obtained a value of 19 kcal mol−1 for FBrOOOO(a), 83 kcal mol−1 for BrOO2…OF (e), 64 kcal mol−1 for O2Br…OOF (f), and 116 kcal mol−1 for FBrO3…O (g) (shown in Table 6). To further assess these results, we have listed all five DFT methods heats of formation of the isomers in Table 6. At present, there are no experimental measurements to which be mainly due to the incompleteness of the basis sets and only partial allowance for electron correlation.

Table 5.
Isodesmic heats of reaction (kcal mol−1) and heats of formation of BrOOOOF (c)

Table 6.
Heats of formation (kcal mol−1) of BrO4F isomers.
For these complexes of Lewis acid (BrF) and base (lone pair Om chains), we treated as a local version of the hard and soft acid base (HSAB) principle [40]. The DFT-based local reactivity descriptors such as the global or local softness or hardness, condensed Fukui functions can be used to explain the stability of isomers. The predicted global hardness (η) and softness (GS) for the minimum-energy BrO4F structures (a, b, c, d, e, f, and g isomers) with five DFT methods are shown in Tables 7 and 8 respectively. The local softness (Sx+ and Sx−), and ratios of them (Sx−/Sx+) for the minimum BrO4F structures (a, b, c, d, e, f, and g isomers) at the B3LYP/DZP++ level are tabulated in Table 9. According the Pearson’s PMH suggestion [41], the Br(VII) structure (g) FBrO3…O in this work has the largest global hardness (Table 7), and smallest global softness (Table 8), thus triplet state FBrO3…O structure is the most stable isomer. For BrO4F isomers, the maximum value (from 5.1 to 8.2, at B3LYP/DZZ++ level, as 8.2) of global hardness (Table 7) set in the highest symmetric Br(VII) FBrO3...O structure (g), whereas the minimum value (from 2.9 to 3.2) of hardness assign to singlet BrOO...OOF isomer (b), inversely, the isomers (g) or (b) possesses the smallest or largest global softness (Table 8), respectively, namely, from 0.06 to 1.0, or from 0.16 to 0.17. For Br in the different isomers presents almost either the largest or smallest Sx−/Sx+ values (Table 9), corresponding to different bonds stabilities. An important finding from this investigation is that Br may reveal the flexibility in which the bromine atom shares valence electrons and orbitals to form a variety of hypervalent species, even the extend hypervalent system.

Table 7.
Global hardness Approximated as: η = 1/2(IE − EA) of BrO4F isomers.

Table 8.
Global softness approximated as: GS = 1/(2η) = 1/(IE − EA) of BrO4F isomers.

Table 9.
Predicted global softness (GS), local softness (Sx+ and Sx−), and ratio of them for the BrO4F (a, b, c, d, e, f, and g) isomers.
5. Conclusions
The structures, electron affinities and bond dissociation energies of BrO4F/BrO4F− species have been studied with five DFT methods. The B3LYP method is the most reliable method for predicting the geometry and electron affinities for this ternary species. The EAad value predicted by the B3LYP method is 4.52 eV for BrO4F. The EAad values for OBrF [34], FBrOO, and FBrOOO [35] species are 3.64, 5.83 and 4.43 eV, respectively. and close to those of other interhalogen compounds, such as BrCIFn and BrFn [37,56]. Those with odd n (n = 1 and 3, closed shell) have smaller EAad than those of even n (n = 2 and 4) species, which are open-shell triplet state. These substantial electron affinities suggest that the corresponding anion may have the lifetimes as independent species under atmospheric conditions.
Similar to the case of the electron affinities, the hybrid DFT methods especial BHLYP predict the discrepant values of bond dissociation energies for BrO4F/BrO4F dissociation reactions and relative energies from two pure DFT methods, demonstrating that this system is a challenge for DFT methods.
Although the FBr-O2-O2/(FBr-O2-O2)− chain structures have been found to be the most stable isomers, yet there is no workable reaction mechanism for the formation of these species considering only BrF or BrF−, BrO and O2 or O2− as starting materials. According recently report on bromine (VII) BrO3F2− anion [31], we conclude that the Br(VII) structure, FBrO3...O (g: C3v, 3A1) are the most likely structure for neutral BrO4F, and the BrO4F− may have Br(V) (FO…BrO3)− (ac: 2A′) complex structure. The DFT-based local reactivity descriptors such as the global or local softness or hardness, condensed Fukui functions can demonstrate this suggestion.
The DFT methods are able to describe the electronic structure of these systems with accuracies comparable to traditional correlated molecular orbital methods at a decreased computational cost. Furthermore these DFT-based local descriptors techniques are observed to assign more bonding character to the BrO4F Lewis system.
Acknowledgments
This work was supported by the China Sustentation Fund of Scientific and Technological Development Project of Beijing Municipal Education Commission (No. KM200810017007). We thank the editors and reviewers for their time, patience and help.
References and Notes
- Chatterjee, A; Iwasaki, T; Hayashi, H; Ebina, T; Torri, K. Electronic and structural properties of montmorillonite—a quantum chemical study. J. Mol. Catal 1998, 136, 195–202. [Google Scholar]
- Chatterjee, A; Ebina, T; Mizukami, F. Effects of Water on the structure and bonding of resorcinol in the interlayer of montmorillonite nanocomposite: A periodic first principle study. J. Phys. Chem. B 2005, 109, 7306–7313. [Google Scholar]
- Chatterjee, A; Iwasaki, T; Ebina, T; Miyamoto, A. A DFT study on clay–cation–water interaction in montmorillonite and beidellite. Comput. Mater. Sci 1999, 14, 119–124. [Google Scholar]
- Chatterjee, A; Iwasaki, T; Ebina, T. A novel method to correlate layer charge and the catalytic activity of 2:1 dioctahedral smectite clays in terms of binding the interlayer cation surrounded by monohydrate. J. Phys. Chem A 2000, 104, 8216–8223. [Google Scholar]
- Chatterjee, A; Ebina, T; Onodera, Y; Mizukami, F. Effect of exchangeable cation on the swelling property of 2:1 dioctahedral smectite—A periodic first principle study. J. Chem. Phys 2004, 120, 3414–3422. [Google Scholar]
- Chatterjee, A; Iwasaki, T; Ebina, T. Sorbent for dioxins and furans: reactivity index study. J. Phys. Chem. A 2002, 106, 641–648. [Google Scholar]
- Chatterjee, A; Niwa, S; Mizukami, F. Structure and property correlation for Ag deposition on α-Al2O3 - a first principle study. J. Mol. Graph. Model 2005, 23, 447–456. [Google Scholar]
- Szöllösi, G; Chatterjee, A; Forgó, P; Bartók, M; Mizukami, F. Structure-property relationship in py-hexahydrocinchonidine diastereomers: ab Initio and NMR study. J. Phys. Chem. A 2005, 109, 860–868. [Google Scholar]
- Parr, RG. How I came about working in conceptual DFT. In Chemical Reactivity Theory: A Density Functional Theory View; Chattaraj, PK, Ed.; Taylor & Francis Group: London, UK, 2009. [Google Scholar]
- Parr, RG; Yang, W. Density functional approach to the frontier-electron theory of chemical reactivity. J. Am. Chem. Soc 1984, 106, 4049–4050. [Google Scholar]
- Geerlings, P; De Proft, F; Langenaekar, W. Conceptual density functional theory. J. Chem. Rev 2003, 103, 1793–1873. [Google Scholar]
- Nguyen, LT; Le, TN; De Proft, F; Chandra, AK; Langenaeker, W; Nguyen, MT; Geerlings, P. Mechanism of [2 + 1] cycloadditions of hydrogen isocyanide to alkynes: molecular orbital and density functional theory study. J. Am. Chem. Soc 1999, 121, 5992–6001. [Google Scholar]
- Langenaeker, W; De Proft, F; Geerlings, P. Ab initio and density functional theory study of the geometry and reactivity of benzyne, 3-fluorobenzyne, 4-fluorobenzyne, and 4,5-Didehydro-pyrimidine. J. Phys. Chem. A 1998, 102, 5944–5950. [Google Scholar]
- Chandra, AK; Geerlings, P; Nguyen, MT. On the asynchronism of isocyanide addition to dipolarophiles: Application of local softness. J. Org. Chem 1997, 62, 6419. [Google Scholar]
- Sivanesan, D; Amutha, R; Subramanian, V; Nair, BU; Ramaswami, T. Assessment of the importance of the solvent in the calculation of condensed Fukui function: a self-consistent reaction field calculation study. Chem. Phys. Lett 1999, 308, 223–228. [Google Scholar]
- Yang, W; Mortier, MJ. The use of global and local molecular parameters for the analysis of the gas-phase basicity of amines. J. Am. Chem. Soc 1986, 108, 5708–5711. [Google Scholar]
- Hebestreit, K; Stutz, J; Rosen, D; Matveiv, V; Peleg, M; Luria, M; Platt, U. DOAS Measurements of tropospheric bromine oxide in mid-latitudes. Science 1999, 283, 55–57. [Google Scholar]
- Karton, A; Parthiban, S; Martin, JML. Post-CCSD(T) ab initio thermochemistry of halogen Oxides and related hydrides XOX, XOOX, HOX, XO, and HXO (X = F, Cl), and evaluation of DFT methods for these systems. J. Phys. Chem. A 2009, 113, 4802–4816. [Google Scholar]
- Matus, MH; Nguyen, MT; Dixon, DA; Peterson, KA; Francisco, JS. ClClO2 is the most stable isomer of Cl2O2. Accurate coupled cluster energetics and electronic spectra of Cl2O2 isomers. J. Phys. Chem. A 2009, 112, 9623–9627. [Google Scholar]
- Li, Z; Francisco, JS. A density functional study of structure and heat of formation for Br2O4 and Br2O5. Chem. Phys. Lett 2002, 354, 109–119. [Google Scholar]
- Xie, Y; Schaefer, HF; Wang, Y; Fu, X; Liu, R. Electron affinities of the bromine oxides BrOn, n = 1–4. Mol. Phys 2000, 98, 879–890. [Google Scholar]
- Martin, JML. Heats of formation of perchloric acid, HClO4, and perchloric anhydride, Cl2O7. Probing the limits of W1 and W2 theory. J. Mol. Struct.: THEOCHEM 2006, 771, 19–26. [Google Scholar]
- Ju, XH; Wang, ZY; Yan, XF; Xiao, HM. Density functional theory studies on dioxygen difluoride and other fluorine/oxygen binary compounds: Availability and shortcoming. J. Mol. Struct.: THEOCHEM 2007, 804, 95–100. [Google Scholar]
- Prascher, BP; Wilson, AK. A computational study of dihalogen-l-dichalcogenides: XAAX (X = F, Cl, Br; A = S, Se). J. Mol. Struct. : THEOCHEM 2007, 814, 1–10. [Google Scholar]
- Feller, D; Dixon, DA. Coupled cluster theory and multireference configuration interaction study of FO, F2O, FO2, and FOOF. J. Phys. Chem. A 2003, 107, 9641–9651. [Google Scholar]
- Kraka, E; He, Y; Cremer, D. Quantum chemical descriptions of FOOF: the unsolved problem of predicting its equilibrium geometry. J. Phys. Chem. A 2001, 105, 3269–3276. [Google Scholar]
- Johnson, GK; O’Hare, PAG; Appelman, EH. Thermodynamic properties of perbromyl fluoride (BrO3F). Inorg. Chem 1972, 11, 800–802. [Google Scholar]
- Appelman, EH; Beagley, B; Cruickshank, DWJ; Foord, A; Rustad, S; Ulbrecht, V. An electron-diffraction study of the molecular structure of gaseous perbromyl fluoride and calculation of its force field and vibrational amplitudes. J. Mol. Struct. : THEOCHEM 1976, 35, 139–148. [Google Scholar]
- Gillespie, RJ; Spekkens, P. Preparation and characterization of potassiumdifluorodioxobromate and tetrafluoro-oxobromate. J Chem Soc Dalton Trans 1976, 2391–2396. [Google Scholar]
- Christe, KO; Curtis, EC; Bougon, R. Bromine trifluoride oxide. Vibrational spectrum, force constants and thermodynamic properties. Inorg. Chem 1978, 17, 1533–1539. [Google Scholar]
- Lehmann, JF; Schrobilgen, GJ. Synthesis and characterization of salts containing the BrO3F2− anion; A rare example of a bromine (VII) species. J. Am. Chem. Soc 2005, 127, 9416–9427. [Google Scholar]
- Lehmann, JF; Riedel, S; Schrobilgen, GJ. Behavior of BrO3F and ClO3F Toward strong lewis acids and the characterization of [XO2][SbF6] (X = Cl, Br) by single cCrystal X-ray diffraction, raman spectroscopy, and computational methods. Inorg. Chem 2008, 47, 8343–8356. [Google Scholar]
- Francisco, JS. Structure, vibrational spectra and energetics of OBrO+. Chem. Phys. Lett 1998, 288, 307–310. [Google Scholar]
- Gong, L; Li, Q; Xie, Y; Schaefer, HF. Novel bromine oxyfluorides: Structures, thermochemistry and electron affinities of BrOFn/BrOFn− (n = 1–5). Mol. Phys 2005, 103, 1995–2008. [Google Scholar]
- Li, S; Gong, L; Wu, X; Guo, W. Structures and electron affinities of BrO2F and BrO3F. Chem. Phys. Lett 2007, 439, 395–401. [Google Scholar]
- Pak, C; Xie, Y; Schaefer, HF. Electron affinities of the dibromine oxides: Br2On (n = 0–4). Mol. Phys 2003, 101, 211–225. [Google Scholar]
- Ignatyev, IS; Schaefer, HF. Bromine halides: The neutral molecules BrClFn (n = 1–5) and their anions structures, energetics, and electron affinities. J. Am. Chem. Soc 1999, 121, 6904–6910. [Google Scholar]
- Xu, W; Cheng, S; Lu, SX. Structures, vibrational frequencies, and electron affinities of SF5On/SF5On− (n = 1–3). J. Mol. Struct. : THEOCHEM 2009, 900, 77–83. [Google Scholar]
- Rienstra-Kiracofe, JC; Tschumper, GS; Schaefer, HF; Nandi, S; Ellison, GB. Atomic and molecular electron affinities: Photoelectron experiments and theoretical computations. Chem. Rev 2002, 102, 231–282. [Google Scholar]
- Parr, RG; Pearson, RG. Absolute Hardness: Companion parameter to absolute electronegativity. J. Am. Chem. Soc 1983, 105, 7512–7516. [Google Scholar]
- Pearson, RG. Recent advances in the concept of hard and soft acids and bases. J. Chem. Educ 1987, 64, 561–567. [Google Scholar]
- Becke, AD. A new mixing of Hartree–Fock and local density-functional theories. J Chem Phys 1993, 98, 1372, BHandHLYP method in the Gaussian programs has 0.5*Ex(LSDA)+0.5*Ex(HF)+0.5*Delta-Ex(B88)+Ec(LYP) formula, which is not precisely the formulation proposed in his paper.. [Google Scholar]
- Lee, C; Yang, W; Parr, RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar]
- Becke, AD. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys 1993, 98, 5648–5652. [Google Scholar]
- Perdew, JP. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar]
- Becke, AD. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar]
- Schafer, A; Horn, H; Ahlrichs, R. Br Basis sets. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys 1992, 97, 2571–2577. [Google Scholar]
- Huzinaga, S. F and O Basis setsGaussian-Type Functions for Polyatomic Systems I. J. Chem. Phys 1965, 42, 1293–1302. [Google Scholar]
- Dunning, TH. Gaussian Basis Functions for Use in Molecular Calculations. I. Contraction of (9s5p) Atomic Basis Sets for the First-Row Atoms F and O Basis sets. J. Chem. Phys 1970, 53, 2823–2833. [Google Scholar]
- Frisch, MJ; Trucks, GW; Schlegel, HB; Scuseria, GE; Robb, MA; Cheeseman, JR, Jr; Montgomery, JA; Vreven, T; Kudin, KN; Burant, JC; Millam, JM; Iyengar, SS; Tomasi, J; Barone, V; Mennucci, B; Cossi, M; Scalmani, G; Rega, N; Petersson, GA; Nakatsuji, H; Hada, M; Ehara, M; Toyota, K; Fukuda, R; Hasegawa, J; Ishida, M; Nakajima, T; Honda, Y; Kitao, O; Nakai, H; Klene, M; Li, X; Knox, JE; Hratchian, HP; Cross, JB; Adamo, C; Jaramillo, J; Gomperts, R; Stratmann, RE; Yazyev, O; Austin, AJ; Cammi, R; Pomelli, C; Ochterski, JW; Ayala, PY; Morokuma, K; Voth, GA; Salvador, P; Dannenberg, JJ; Zakrzewski, VG; Dapprich, S; Daniels, AD; Strain, MC; Farkas, O; Malick, DK; Rabuck, AD; Raghavachari, K; Foresman, JB; Ortiz, JV; Cui, Q; Baboul, AG; Clifford, S; Cioslowski, J; Stefanov, BB; Liu, G; Liashenko, A; Piskorz, P; Komaromi, I; Martin, RL; Fox, DJ; Keith, T; Al-Laham, MA; Peng, CY; Nanayakkara, A; Challacombe, M; Gill, PMW; Johnson, B; Chen, W; Wong, MW; Gonzalez, C; Pople, JA. Gaussian 03: IA32W-G03RevC 02 12-Jun-2004; Gaussian, Inc: Wallingford, CT, USA, 2004. [Google Scholar]
- Reed, AE; Curtiss, LA; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev 1988, 88, 899–926. [Google Scholar]
- Boys, SF; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys 1970, 19, 553–557. [Google Scholar]
- Orita, H; Itoh, N; Inada, Y. A comparison of CO adsorption on Pt(211), Ni(211), and Pd(211) surfaces using density functional theory. Surf. Sci 2004, 571, 161–172. [Google Scholar]
- Boese, AD; Martin, JML; Handy, NC. The role of the basis set: Assessing density functional theory. J. Chem. Phys 2003, 119, 3005–3015. [Google Scholar]
- Tschumper, GS; Schaefer, HF, III. Predicting electron affinities with density functional theory: Some positive results for negative ions. J. Chem. Phys 1997, 107, 2529–2541. [Google Scholar]
- Pak, C; Xie, Y; Van Huis, TJ; Schaefer, HF. Electron affinities of the bromine fluorides, BrFn (n = 1–7). J. Am. chem. Soc 1998, 120, 11115–11121. [Google Scholar]
- Roos, BJ. Ab Initio Methods in Quantum Chemistry; Lawley, KP, Ed.; John Wiley & Sons: New York, USA, 1987; pp. 399–445. [Google Scholar]
- Guha, S; Francisco, JS. Structures, vibrational spectra, and relative energetics of CH3BrO3 isomers. J. Phys. Chem A 2000, 104, 3239–3245. [Google Scholar]
- Chase, MW; Davies, CA; Downey, JR; Frurip, DJ; McDonald, RA; Syverud, AN. NIST-JANAF Thermochemical Tables. J. Phys. Chem. Ref. Data 1985, 1, 146–147. [Google Scholar]
- Ruscic, R; Berkowitz, J. Experiment determination of ΔHfθ (HOBr) and ionization potentials (HOBr): Implications for the corresponding properties of HOI. J. Chem. Phys 1994, 101, 7795–7803. [Google Scholar]
- Chase, MW; Davies, CA; Downey, JR; Frurip, DJ; McDonald, RA; Syverud, AN. JANAF Thermochemical Tables, 3rd ed. J Phys Chem Ref Data 1985, 14(Suppl. 1), 8–9. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).