Abstract
The free energy of solvation,
, in octanol of organic compunds is quantitatively predicted from the molecular structure. The model, involving only three molecular descriptors, is obtained by multiple linear regression analysis from a data set of 147 compounds containing diverse organic functions, namely, halogenated and non-halogenated alkanes, alkenes, alkynes, aromatics, alcohols, aldehydes, ketones, amines, ethers and esters; covering a
range from about −50 to 0 kJ·mol−1. The model predicts the free energy of solvation with a squared correlation coefficient of 0.93 and a standard deviation, 2.4 kJ·mol−1, just marginally larger than the generally accepted value of experimental uncertainty. The involved molecular descriptors have definite physical meaning corresponding to the different intermolecular interactions occurring in the bulk liquid phase. The model is validated with an external set of 36 compounds not included in the training set.
1. Introduction
Octanol is a straight chain fatty alcohol with eight carbon atoms and molecular formula CH3(CH2)7OH which is used as a good surrogate for the lipids in aquatic and animal biota, and for the organic matter in soils and sediments. Lipophilicity is widely recognized as one of the key physicochemical descriptors used to assess and model the distribution and transport potential of pollutants in biological and environmental compartments, such as solubility in water, octanol-water partitioning, bioconcentration in aquatic organisms, and soil or sediment sorption phenomena [,]. The free energy of solvation in octanol may be used as a measure of the lipophilic nature of chemicals, i.e., as a key parameter to quantify their lipophilicity.
Gibbs free energy is arguably the most important general concept in physical chemistry, as it determines equilibrium constants and the direction of spontaneous chemical changes at constant T and P. The most theoretical work defines the standard-state free energy of solvation,
, as the free energy change involved in the transfer of 1 mol of solute from the gas phase into certain solvent, taking as standard state a concentration 1 mol L−1 in both the gas phase and solution. In addition to its fundamental interest,
may be combined with other thermodynamic data to predict a variety of equilibrium properties, the more important of which are solubility and the partitioning of a solute between immiscibles phases; for instance, the calculation octanol-air partition coefficient and the octanol-water partition coefficient requires of reliable values of the free energy of solvation in octanol. The above coefficients are the critical importance in drug design, extractions and environmental applications [].
The best developed classical method to compute free energies of solvation is the use of multivariate quantitative structure-property relationship (QSPR) models. These methods can be classified into two broad categories, namely group contribution methods, which capitalize on the additive-constitutive nature of
, and regression methods, which quantify the weights of different structure descriptors on the principle of least square deviation [].
The main criticism of QSPR methods relies on the difficulty of the physical interpretation of the descriptors involved in the correlation equations; however, even within this limitation QSPR modeling represents a good alternative for rapid estimation of a property, since it requires both less computational requirements, hardware and software, and much less computation time in comparison to quantum mechanical and discrete methods (MD and MC simulations) [,].
Although for octanol related partition coefficients (octanol/water or octanol/air partition coefficients) there are numerous QSPR studies reported in literature; the direct prediction of free energy of solvation in octanol, by QSPR methodology, has been much less studied preventing to have a simple model for the rapid and direct estimation of
. Currently, free energy of solvation is estimated from some derived parameter, such as the Ostwald solubility or octanol/water partition coefficient [].
In this article, we report a simple QSPR model for predicting free energy of solvation in octanol of 147 structurally different organic compounds containing diverse organic functions. The model, involving only three molecular descriptors, allows the prediction of
with a square correlation coefficient, R2, of 0.93 and a root-mean-square deviation of 2.41. The model is validated with an external set of 36 compounds not included in the training set.
2. Experimental
2.1. Chemical data
The data set of free energy of solvation in octanol used to develop the model was taken from the data reported by Kollman et al. []. The data set contains 147 structurally different compounds containing diverse organic functions: alkanes, alkenes, alkynes, aromatics, alcohols, aldehydes, ethers, ketones, esters, amines, nitriles, halogenated and nitro hydrocarbons covering a
range from about – 50 to 0 kJ/mol. The data for the validation set was collected from several literature sources [–].
2.2. Computational methodology
Initial three-dimensional geometries for all 147 chemicals in their ground state were generated using the Hyperchem 7.0 molecular modeling package []. Subsequent quantum chemical calculations in gas phase were performed using the AMPAC program [] with AMI parameterization. The output files of AMPAC containing the refined geometries and electron wave functions of individual compounds were loaded into the CODESSA program [] in order to calculate a total of 453 molecular descriptors. This pool of descriptors was reduced by objective feature selection in order to remove those descriptors that do not provide useful information for the prediction of
. Pairwise correlations between descriptors were examined so that only one descriptor was retained from a pair contributing similar information. Finally, with this reduced pool of descriptors the best multiple linear regression model was searched with SigmaStat [] by fitting the descriptors to the experimental data and respective correlation analysis.
3. Results and Discussion
In this study, a total of 453 molecular descriptors were calculated for all 147 compounds. The molecular descriptors can be grouped as constitutional, geometric, topological, electrostatic, and quantum chemical. However, bearing in mind that the main interactions between uncharged molecules are originated by polar, dispersion and hydrogen-bonding interactions; we have focused on descriptors encoding those features, and in this way the number of potential descriptors useful for the prediction of
was reduced to 119.
The best multiple linear regression model found involves only the following three molecular descriptors: the gravitation index (GI), HA dependent HDCA-2, and the number of fluorine atoms (NF); which will be defined further on. The resulting equation is:
and its respective statistics is shown in Tables 1 and 2. The statistical parameters are the following: R the correlation coefficient, RCV the leave-one-out crossvalidated correlation coefficient, Rdf the correlation coefficient adjusted for degrees of freedom, s the standard deviation, F the Fisher test value, P the probability to retain the null hypothesis, i.e. the independent variables have no predictive value and therefore the observed relationship occurred just by chance; and VTF, the variation inflation factor, is a measurement of the collinearity between the independent variables. If the VIF value is 1, there is no collinearity. If its value is large, about 10 or more, serious collinearity is present.

Table 1.
Statistical parameters for the best QSPR model.

Table 2.
Analysis of variance of the best QSPR model.
The squared correlation coefficient value, R2, indicates that the model as fitted explains 93% of the variability of the property. The squared crossvalidated correlation coefficient, R2CV, provides an estimation of the stability of the obtained regression model, i.e. the sensitivity of the model to the elimination of any single data point. For the model the value of this parameter is equal to the squared correlation coefficient value indicating a good stability of the regression model. The correlation coefficient adjusted for degrees of freedom is a useful figure for comparing models with different numbers of independent variables. In determining whether the model can be simplified, all the P-values on the independent variables are less than 0.001, which means that all descriptors are statistically significant at the 99% confidence level. Therefore, it is concluded that all the independent variables included in the model are relevant. The standardized coefficients represent the change in response for a change of one standard deviation in a predictor. The use of these standardized coefficients removes the problem of the predictor's underlying scale of units. On the other hand, the VIF values, equal to 1, confirm the orthogonality of the involved descriptors.
The P-value for the correlation is less than 0.001, therefore there is a statistically significant relationship between the property and the independent variables at the 99% confidence level. However, it is also observed from this Table that the value of the constant is less than the respective error and the respective P-value to retain the null hypothesis is quite large, indicating the constant has no additional predictive value over and above that contributed by the independent variables. On the other hand, the generally accepted value of experimental uncertainty for the free energy of solvation is about 1.7 kJ·mol−1 [], value greater than the value of the constant. For all these reasons the constant can be eliminated from the model without loss of predictive quality and without need of refitting because the orthogonality of the involved descriptors assure the correlation coefficients and statistics remain the same. Therefore, the model is reduced to:
The experimental and calculated values of
along with the values of the descriptors involved in the model are shown in Table 3. The respective scatter plot is shown in Figure 1.

Table 3.
Molecular descriptors and values of experimental and calculated
for the training set.
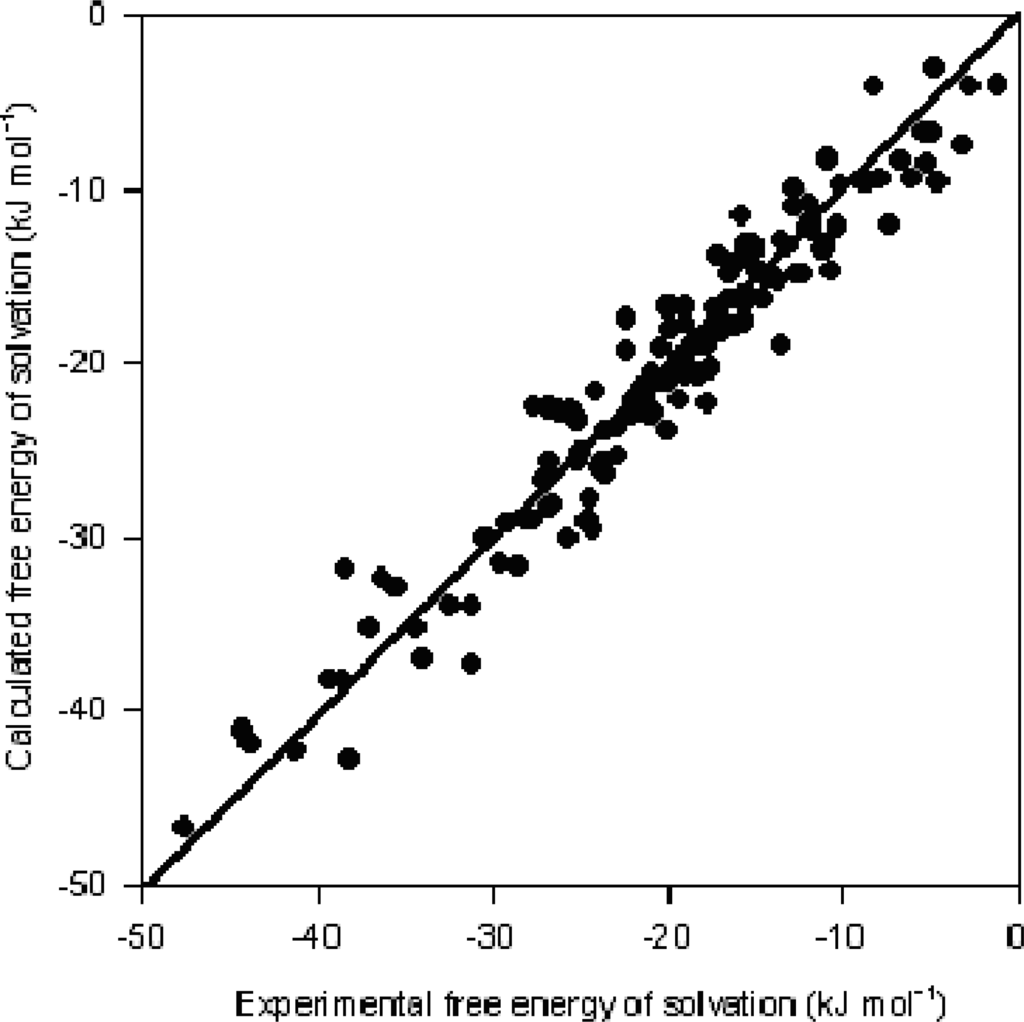
Figure 1.
Scatter plot of calculated vs experimental
values.
The last column column of this Table shows the standardized residuals, i.e., the residuals expressed in standard deviation units. These residuals are used in order to better detect unusual observations. In general, if the residuals are normally distributed about the regression, about 66% of the standardized residuals have values between −1 and +1, and about 95% of the standardized residuals have values between −2 and +2. A larger standardized residual indicates that the point is far from the regression; the suggested value flagged as an outlier is 2.5. In this study, only 8 observations out of the 147 data points of the training set have standardized residual values greater than 2, of which only 3 have values over 2.5.
To check the predictive capability of the model, it was tested with an external set of chemicals not included in the training set. The validation data set included 36 diverse chemicals, including fluorotelomer alcohols and sulfur containing compounds. In Table 4, the values of the molecular descriptors along with the experimental and calculated values of
for the validation set are shown. The statistics for the validation is as follows: R2 = 0.93, s = 2.5, F= 153. For this data, only two observations have standardized residual values greater than the threshold value of 2.5 These results confirm the prediction capability of the model.

Table 4.
Molecular descriptors and values of experimental and calculated
for the validation set.
3.1. Physical meaning of the descriptors involved
The more relevant descriptor in the correlation is the gravitation index (all bonds), GI, accounting for about the 52% of the variability of the property. This descriptor reflects the effective mass distribution in the molecule and it is defined as:
where mi, and mj are the atomic masses of the bonded atoms and rij denotes the respective bond lengths, has been associated to size-dependent bulk effects, dispersion and cavity formation, in the bulk liquid media []. The correlation coefficient for this descriptor is negative, as expected, indicating the solvation process is favored by these effects, leading to lower
values.
The second more relevant descriptor is the hydrogen acceptor dependent hydrogen donors charged surface area based on Zefirov charges (HA dependent HDCA-2) []:
where SD is the solvent accessible surface area of H-bonding donor H atoms, qD is the partial charge on H-bonding donor H atoms, and Stot is the total solvent accessible molecular surface area. This descriptor, which accounts for about the 25% of the variability of the
, is connected with the hydrogen-bonding ability of the molecule. It is expected the solvation will be favored, more negative value of
, by the presence of hydrogen bonding interactions between solute and solvent molecules. The negative value of the coefficient for this descriptor corroborates this assumption.
Lastly, the third descriptor is the number of F atoms (NF). The introduction of substituents into organic compounds with increasing differences in electronegativity with respect to carbon produces a charge separation in the bond originating a dipole moment. Therefore this descriptor encodes information related to polar interactions. The question which remain is, why the molecular dipole moment then is not involved in the model ?. The answer is apparently for the deficiency of the AM1 method to calculate partial charges in molecules containing fluorine atoms. As result, the NF appears to be a better descriptor for the quantitative prediction of
. Finally, since this descriptor encodes information relative to the polarity of the molecule, it is expected this descriptor disfavors the solvation process in octanol, a paradigm of hydrophobic solvent. Consequently, the correlation coefficient for this descriptor is positive showing the
increases its value as the number of fluorine atoms also increases.
4. Conclusions
The merit of the QSPR model developed in this article lays in its simplicity. The model allows the prediction of
of a wider variety of organics compounds with less parameters and better statistics than other models reported in literature []. Free energy of solvation can be predicted straightforwardly from only three molecular descriptors accounting for the different components which comprise the free energy of solvation: electrostatic, cavitation and van der Waals components. The three involved descriptors can be calculated solely from the molecular structure, therefore the model is independent of previous group contribution fitting and consequently is applicable to new or developing compounds for which group contribution has not been determined.
Acknowledgments
The author acknowledges financial support from the Directión de Investigatión, Universidad de Concepción, Grant N0 207.022.023–1.0.
References
- Ruelle, P. The n-octanol and n-hexane/water partition coefficient of environmentally relevant chemicals predicted from the mobile order and disorder (MOD) thermodynamics. Chemosphere 2000, 40, 457–512. [Google Scholar]
- Sandier, SI. Unusual chemical thermodynamics. J. Chem. Thermodynam 1999, 31, 3–25. [Google Scholar]
- Leo, A. Octanol/water partition coefficient. In Handbook of Property Estimation Methods for Chemicals, Environmental and Health Sciences; Boethling, RS, Mackay, D, Eds.; Lewis Publishers: Boca Ratón, FL, USA, 2000; pp. 89–114. [Google Scholar]
- Delgado, EJ; Alderete, JB; Jaña, GA. DFT derived solvation models for organic compounds in alkane solvents. Chem. Phys 2006, 325, 220–224. [Google Scholar]
- Cramer, CJ; Truhlar, DG. Implicit solvation models: Equilibria, structure, spectra, and dynamics. Chem. Rev 1999, 99, 2161–2200. [Google Scholar]
- Duffy, EM; Jorgensen, WL. Prediction of properties from simulations: Free energies of solvation in hexadecane, octanol, and water. J. Am. Chem. Soc 2000, 122, 2878–2888. [Google Scholar]
- Katritzky, AR; Oliferenko, AA; Oliferenko, PV; Petrukhin, R; Tatham, DB; Maran, U; Lomaka, A; Acree, WE. A general treatment of solubility. 1. The QSPR correlation of solvation free energies of single solutes in series of solvents. J. Chem. Inf. Comput. Sci 2003, 43, 1794–1805. [Google Scholar]
- Wang, J; Wang, W; Huo, S; Lee, M; Kollman, PA. Solvation model on weighted solvent accessible surface area. J. Phys. Chem B 2001, 105, 5055–5067. [Google Scholar]
- Sepassi, K; Yalkowsky, SH. Simplified estimation of the octanol-air partition coefficient. Ind. Eng. Chem. Res 2007, 46, 2220–2223. [Google Scholar]
- Thuens, S; Dreyer, A; Sturm, R; Temme, C; Ebingaus, R. Determination of the octanol-air partition coefficients (KOA) of fluorotelomer alcohols. J. Chem. Eng. Data 2008, 53, 223–227. [Google Scholar]
- Staikova, M; Wania, F; Donaldson, DJ. Molecular polarizability as a single-parameter predictor of vapour pressures and octanol-air partitioning coefficients of non-polar compounds: A priori approach and results. Atmos. Environ 2004, 38, 213–225. [Google Scholar]
- Hyperchem 7.0; Hypercube, Inc.: Gainesville, FL, USA, 2002.
- Ampac 5.0; Semichem, Inc.: Shawnee, KS, USA, 1994.
- Codessa 2.63; Semichem, Inc.: Shawnee, KS, USA, 1999.
- SigmaStat 30; SPSS Inc: Chicago, IL, USA, 2003.
- Li, J; Zhu, T; Hawkins, GD; Winget, P; Liotard, DA; Cramer, CJ; Truhlar, DG. Extension of the platform of applicability of the SM5.42R universal solvation model. Theor. Chem. Ace 1999, 103, 9–63. [Google Scholar]
- Katritzky, AR; Mu, L; Lobanov, VS; Karelson, M. Correlation of boiling points with molecular structure. 1. A training set of 298 diverse organics and a test set of 9 simple organics. J. Phys. Chem 1996, 100, 10400–10407. [Google Scholar]
- Stanton, DT; Jurs, PC. Development and use of charged partial surface area structural descriptors in computer-assisted quantitative structure-property relationship studies. Anal. Chem 1990, 62, 2323–2329. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/). This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).