Magnitude of the First and Second Neighbour Magnetic Interactions in the Spin Chain Compound Li2CuO2
Abstract
:1. Introduction
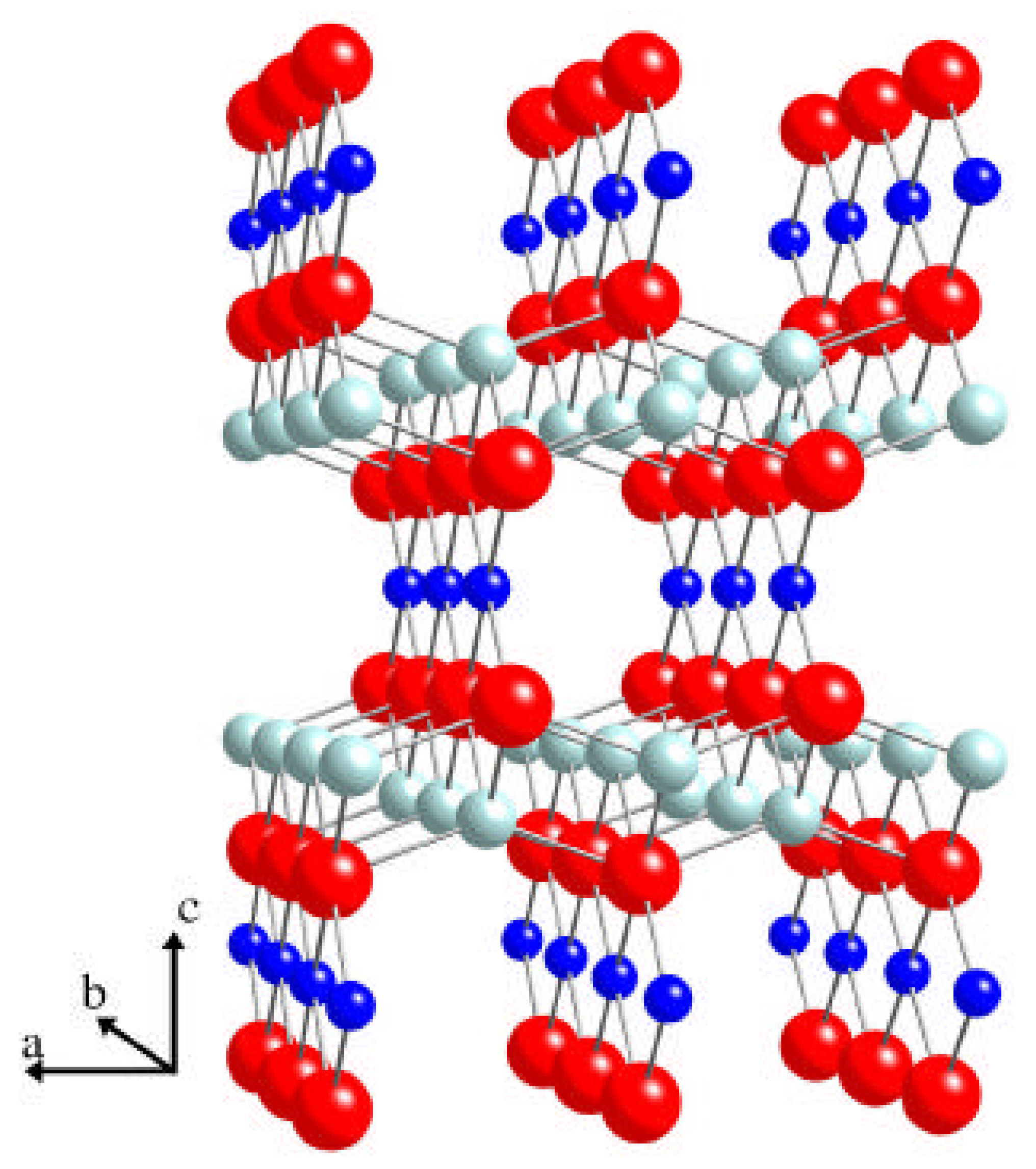
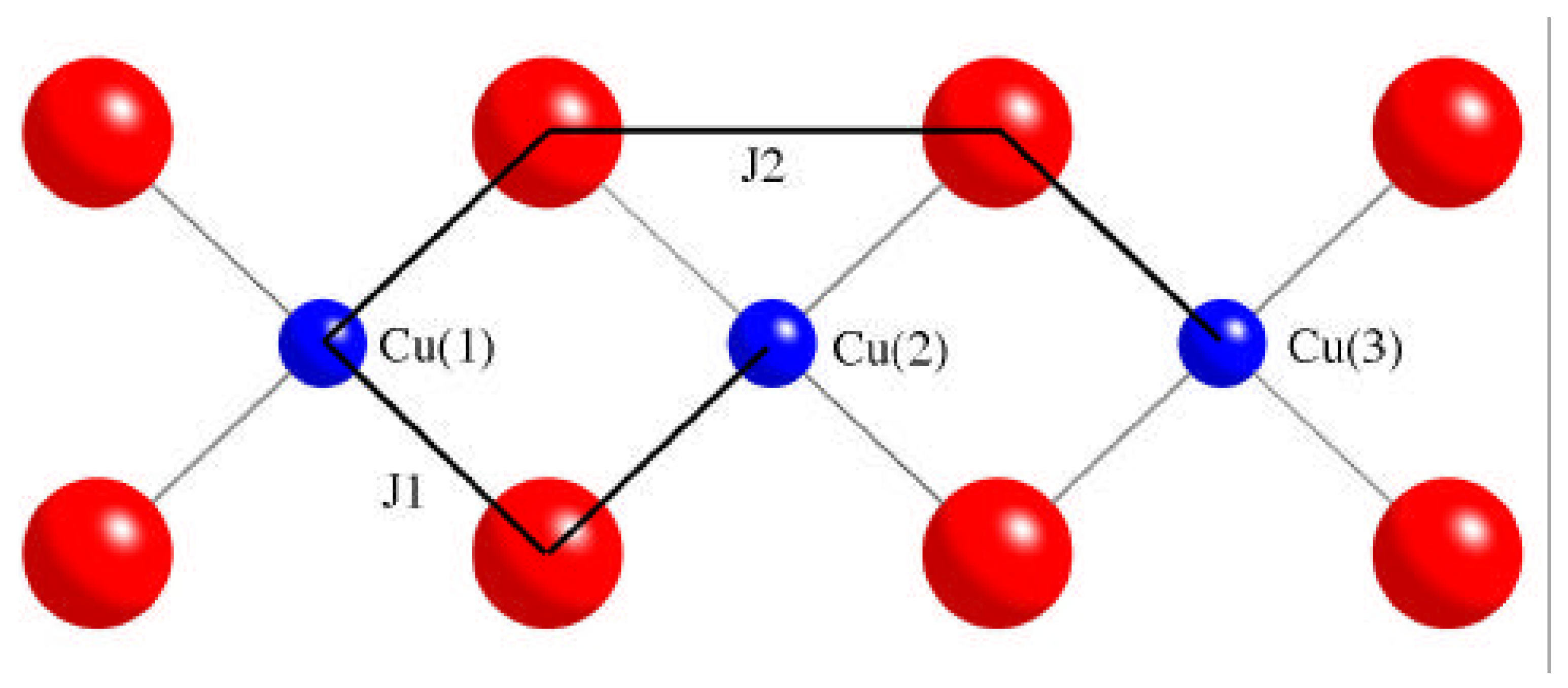
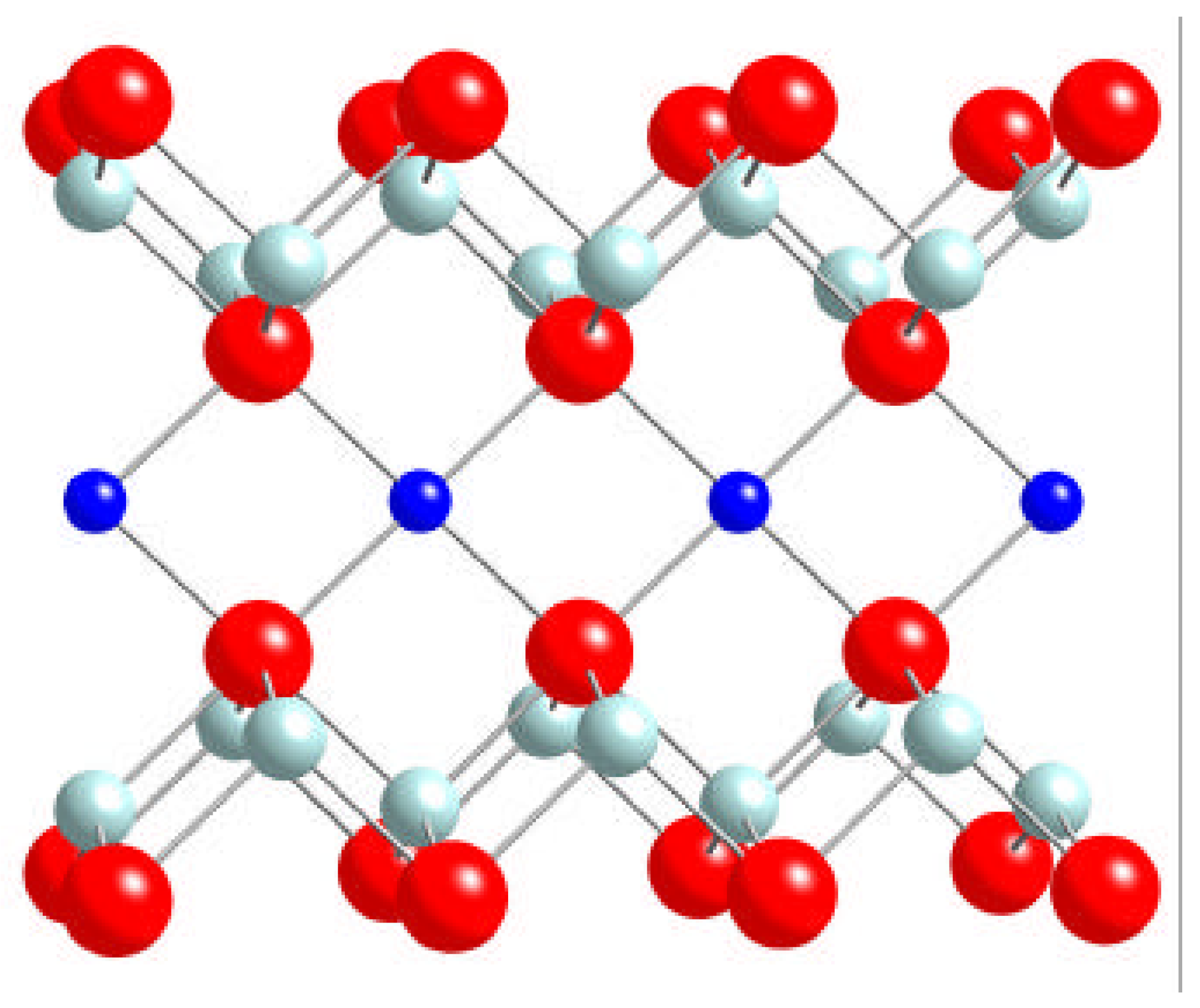
2. Computational strategy
3. Methods
4. Results and Discussion
A. Accurate Determination of J1 and J2
| Material | CASSCF | CASPT2 | DDCI3 | |||
| model | J1 | J2 | J1 | J2 | J1 | J2 |
| Cu3O8 | 3.5 | -1.5 | 11.6 | -8.1 | 10.6 | -8.8 |
| Cu3O8Li6 | 3.8 | -0.2 | 13.1 | -1.8 | 12.2 | -1.7 |
| Cu2O6 | 3.5 | – | 11.1 | – | 13.4 | – |
| Cu2O6Li4 | 3.8 | – | 12.7 | – | 15.4 | – |
| Cu2O8 | – | -1.3 | – | -7.9 | – | -10.8 |
| Cu2O8Li6 | – | -0.3 | – | -2.3 | – | -2.3 |
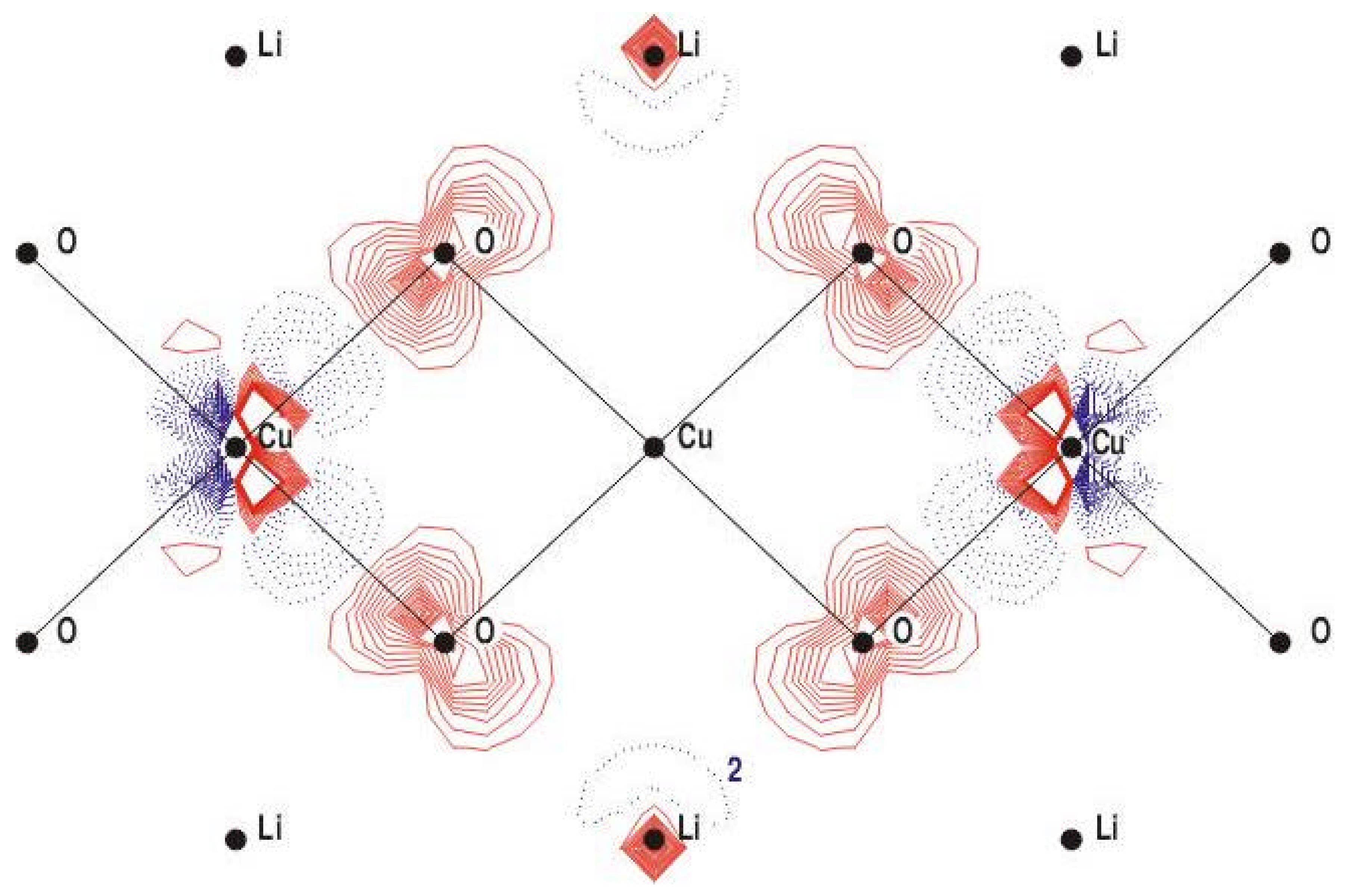
B. Basis Set and Cluster Size Check
| CASSCF | CASPT2 | |
| Basis A | 3.8 | 12.7 |
| Basis B | 3.8 | 13.0 |
| Basis C | 4.0 | 13.7 |
| Basis D | 3.9 | 13.0 |
| Basis E | 3.8 | 12.7 |
| cluster | CASSCF | CASPT2 | ||
| J1 | J2 | J1 | J2 | |
| Cu2O6 | 3.5 | – | 11.4 | – |
| Cu2O6Li4 | 3.9 | – | 13.0 | – |
| Cu2O6Li20 | 4.1 | – | 13.2 | – |
| Cu2O6Li20O16 | 4.1 | – | 13.5 | – |
| Cu3O8 | 3.5 | -1.5 | 11.9 | -8.5 |
| Cu3O8Li6 | 3.8 | -0.3 | 13.2 | -1.9 |
| Cu3O8Li10 | 3.9 | -0.2 | 13.3 | -1.9 |
| Cu3O8Li26 | 4.2 | -0.3 | 14.4 | -2.3 |
| Cu3O8Li26O12 | 4.1 | -0.3 | 14.1 | -2.2 |
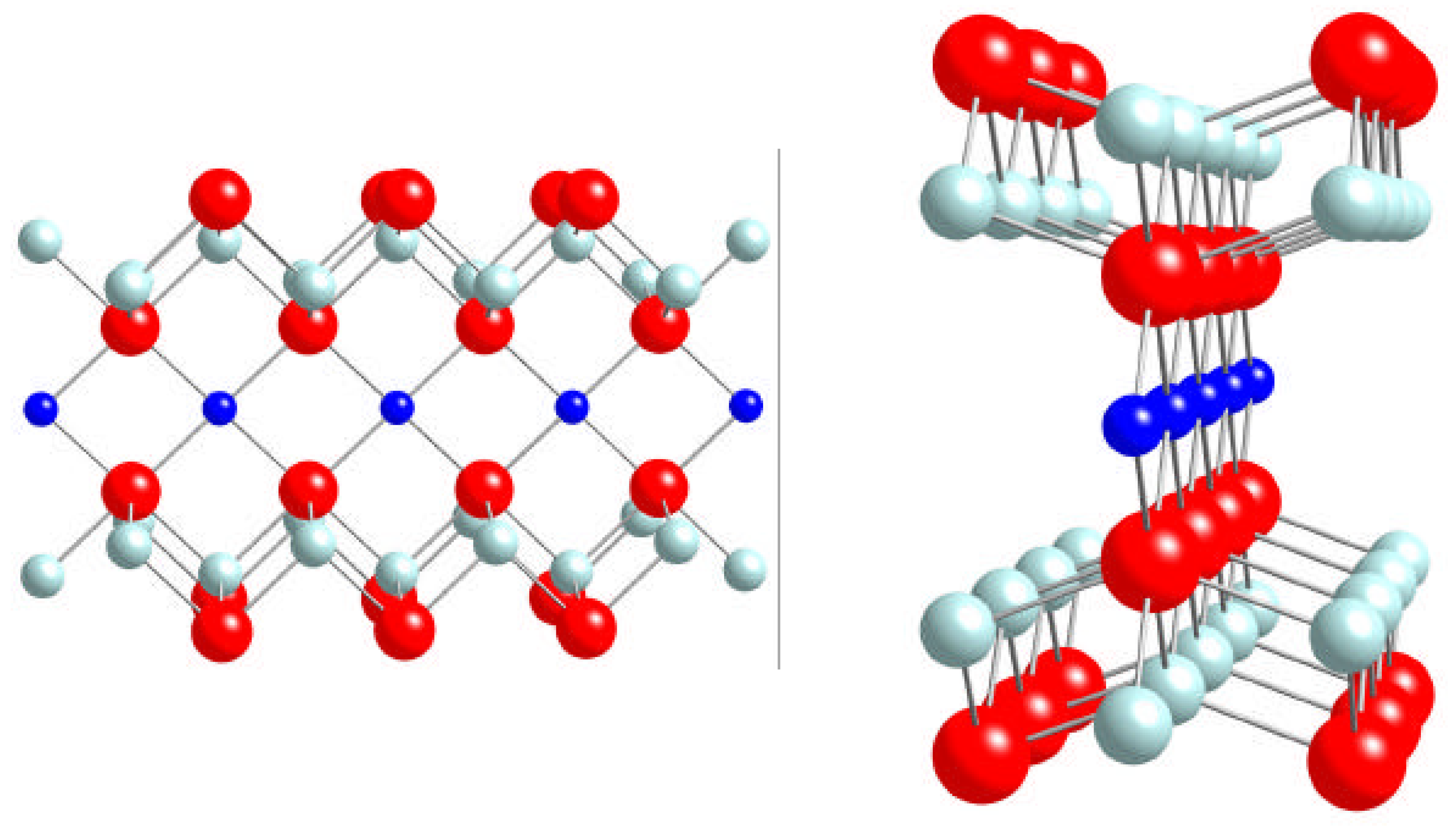
C. Magnetic Moments
5. Summary
Acknowldgements
References and Notes
- Goodenough, J. B. Theory of the role of covalence in the perovskite-type manganites [La,M(II)] MnO3. Phys. Rev. 1955, 100, 564–573. [Google Scholar] [CrossRef]
- Kanamori, J. J. Phys. Chem. Solids 1959, 10, 87. [CrossRef]
- Anderson, P. W. Theory of magnetic exchange interaction: Exchange in insulators and semicon-ductors. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: New York, 1963; Vol. 14, pp. 99–214. [Google Scholar]
- van Oosten, A. B.; Mila, F. Ab initio determination of exchange integrals and Néel temperature in the chain cuprates. Chem. Phys. Lett. 1998, 295, 359–365. [Google Scholar] [CrossRef]
- Mizuno, Y.; Tohyama, T.; Maekawa, S. Superexchange interactions in cuprates. Phys. Rev. B. 1998, 58, 14713–14716. [Google Scholar] [CrossRef]
- Lorenzana, J.; Eder, R. Dynamics of the one dimensional Heisenberg model and optical absorption of spinons in cuprate antiferromagnetic chains. Phys. Rev. B. 1997, 55, 3358–3359. [Google Scholar] [CrossRef]
- Rosner, H.; Eschrig, H.; Hayn, R.; Drechsler, S.-L.; Málek, J. Electronic structure and magnetic properties of the linear chain cuprates Sr2CuO3 and Ca2CuO3. Phys. Rev. B. 1997, 56, 3402–3412. [Google Scholar] [CrossRef]
- de Graaf, C.; de P. R. Moreira, I.; Illas, F.; Martin, R. L. Ab Initio study of the Magnetic Interactions in the Spin Ladder Compound SrCu2O3. Phys. Rev. B. 1999, 60, 3457–3464. [Google Scholar] [CrossRef]
- Sugai, S.; Shinoda, T.; Kobayashi, N.; Hiroi, Z.; Takano, M. Anisotropic exchange integrals in the two-leg spin ladder LaCuO2.5. Phys. Rev. B. 1999, 60, 6969–6972. [Google Scholar] [CrossRef]
- Sapiña, F.; Rodríguez-Carvajal, J.; Sanchis, M. J.; Ibáñez, R.; Beltrán, A.; Beltrán, D. Crystal and Magnetic Structure of Li2CuO2. Solid Sate Comm. 1990, 74, 779–784. [Google Scholar] [CrossRef]
- Mizuno, Y.; Tohyama, T.; Maekawa, S.; Osafune, T.; Motoyama, N.; Eisaki, H.; Uchida, S. Electronic states and magnetic properties of edge-sharing Cu - O chains. Phys. Rev. B. 1998, 57, 5326–5335. [Google Scholar] [CrossRef]
- Boehm, M.; Coad, S.; Roessli, B.; Zheludev, A.; Zolliker, M.; Böni, P.; Paul, D. M.; Eisaki, H.; Motoyama, N.; Uchida, S. Competing exchange interactions in Li2CuO2. Europhys. Lett. 1998, 43, 77–82. [Google Scholar] [CrossRef]
- Weht, R.; Pickett, W. E. Extended Moment Formation and Second Neighbor Coupling in Li2CuO2. Phys. Rev. Lett. 1998, 81, 2502–2505. [Google Scholar] [CrossRef]
- de P. R. Moreira, I.; Illas, F.; Calzado, C. J.; Sanz, J. F.; Malrieu, J.-P.; Ben Amor, N.; Maynau, D. The Local Character of Magnetic Coupling in Ionic Solids. Phys. Rev. B. 1999, 59, 6593–6596. [Google Scholar] [CrossRef]
- de P. R. Moreira, I.; Illas, F. Ab Initio theoretical comparative study of magnetic coupling in KNiF3 and K2NiF4. Phys. Rev. B. 1997, 55, 4129–4137. [Google Scholar] [CrossRef]
- Illas, F.; de P. R. Moreira, I.; de Graaf, C.; Barone, V. Magnetic coupling in biradicals, binuclear complexes and wide gap insulators: A survey of ab initio Wave Function and Density Functional Theory approaches. Theor. Chem. Acc. 2000, 104, 265–272. [Google Scholar] [CrossRef]
- Winter, N. W.; Pitzer, R. M.; Temple, D. K. Theoretical study of a Cu+ ion impurity in a NaF host. J. Chem. Phys. 1987, 86, 3549–3556. [Google Scholar] [CrossRef]
- Pou-Amérigo, R.; Merchán, M.; Nebot-Gil, I.; Widmark, P.-O.; Roos, B.O. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. Theor. Chim. Acta. 1995, 92, 149–181. [Google Scholar] [CrossRef]
- Widmark, P.-O.; Malmqvist, P.-Å.; Roos, B.O. Density matrix averaged atomic natural orbitals (ANO) basis sets for correlated molecular wave functions. I First row atoms. Theor. Chim. Acta. 1990, 77, 291–306. [Google Scholar] [CrossRef]
- Malrieu, J.-P. Cancellations occurring in the calculation of transition energies by a perturbation development of Configuration Interaction Matrices. J. Chem. Phys. 1967, 47, 4555–4558. [Google Scholar] [CrossRef]
- Miralles, J.; Castell, O.; Caballol, R.; Malrieu, J.-P. Specific CI calculation of energy differences: transition energies and bond energies. Chem. Phys. 1993, 172, 33–43. [Google Scholar] [CrossRef]
- Andersson, K.; Malmqvist, P.-Å.; Roos, B. O.; Sadlej, A. J.; Wolinski, K. Second-Order Perturbation Theory with a CASSCF Reference Function. J. Phys. Chem. 1990, 94, 5483–5488. [Google Scholar] [CrossRef]
- Andersson, K.; Malmqvist, P.-Å.; Roos, B. O. Second-Order Perturbation Theory with a Complete Active Space Self-Consistent Field Reference Function. J. Chem. Phys. 1992, 96, 1218–1226. [Google Scholar] [CrossRef]
- de Graaf, C.; Broer, R.; Nieuwpoort, W. C. Comparison of the superexchange interaction in NiO and in a NiO [100] surface. Chem. Phys. Lett. 1997, 271, 372–376. [Google Scholar] [CrossRef]
- de Graaf, C.; Sousa, C.; Illas, F.; de P. R. Moreira, I. Magnetic interactions in biradicals, molecular complexes and ionic insulators: A comparison of the Difference Dedicated CI and CASPT2 methods. Work in progress. 2000. [Google Scholar]
- Andersson, K.; Blomberg, M. R. A.; Fülscher, M. P.; Karlström, G.; Lindh, R.; Malmqvist, P.-Å.; Neogrády, P.; Olsen, J.; Roos, B. O.; Sadlej, A. J.; Schütz, M.; Seijo, L.; Serrano-Andrés, L.; Siegbahn, P. E. M.; Widmark, P.-O. MOLCAS version 4. University of Lund: Sweden, 1997.
- Maynau, D.; Ben Amor, N. CASDI suite of programs. Toulouse, 1997. [Google Scholar]
- Illas, F.; de P. R. Moreira, I.; de Graaf, C.; Castell, O.; Casanovas, J. Absence of collective effects in Heisenberg systems with localized magnetic moments. Phys. Rev. B. 1997, 56, 5069–5072. [Google Scholar] [CrossRef]
- Okuda, K.; Noguchi, S.; Konishi, K.; Deguchi, H.; Takeda, K. Magnetism of one-dimensional copper oxides related to HTSC. J. Magn. Magn. Mat. 1992, 104-107, 817–818. [Google Scholar] [CrossRef]
- Martin, R. L.; Illas, F. Antiferromagnetic Exchange Interactions from Hybrid Density Functional Theory. Phys. Rev. Lett. 1997, 79, 1539–1542. [Google Scholar] [CrossRef]
© 2000 by MDPI (http://www.mdpi.org).
Share and Cite
De Graaf, C.; Moreira, I.D.P.R.; Illas, F. Magnitude of the First and Second Neighbour Magnetic Interactions in the Spin Chain Compound Li2CuO2. Int. J. Mol. Sci. 2000, 1, 28-38. https://doi.org/10.3390/ijms1030028
De Graaf C, Moreira IDPR, Illas F. Magnitude of the First and Second Neighbour Magnetic Interactions in the Spin Chain Compound Li2CuO2. International Journal of Molecular Sciences. 2000; 1(3):28-38. https://doi.org/10.3390/ijms1030028
Chicago/Turabian StyleDe Graaf, C., I. De P. R. Moreira, and F. Illas. 2000. "Magnitude of the First and Second Neighbour Magnetic Interactions in the Spin Chain Compound Li2CuO2" International Journal of Molecular Sciences 1, no. 3: 28-38. https://doi.org/10.3390/ijms1030028
APA StyleDe Graaf, C., Moreira, I. D. P. R., & Illas, F. (2000). Magnitude of the First and Second Neighbour Magnetic Interactions in the Spin Chain Compound Li2CuO2. International Journal of Molecular Sciences, 1(3), 28-38. https://doi.org/10.3390/ijms1030028




