A Cost-Effective Treatment of Spin–Orbit Couplings in the State-Averaged Driven Similarity Renormalization Group Second-Order Perturbation Theory
Abstract
1. Introduction
2. Theory
2.1. State-Averaged Driven Similarity Renormalization Group Second-Order Perturbation Theory
2.2. Incorporating Spin–Orbit Coupling in SA-DSRG-PT2
3. Implementation
4. Numerical Results
4.1. Calibration of the Parameters of BP1-SA-DSRG-PT2c
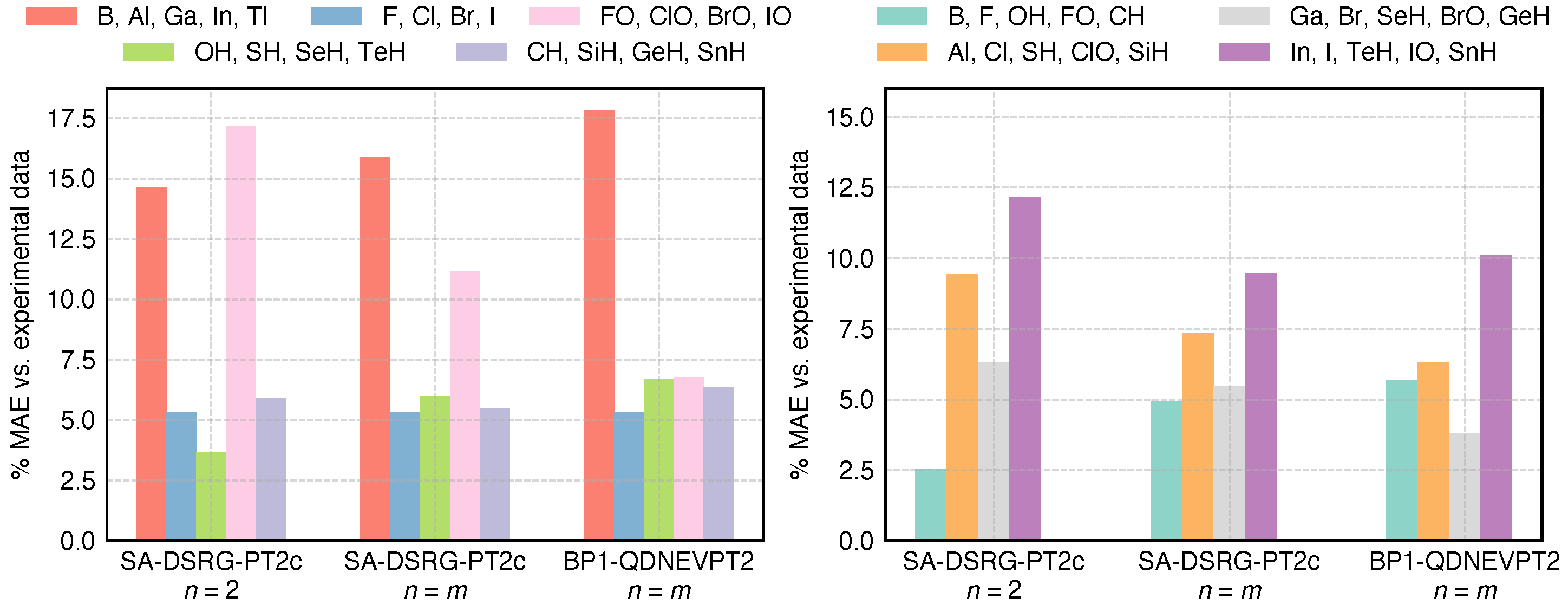
4.2. Main-Group Atoms and Diatomic Molecules
4.3. Transition-Metal Elements: Cu, Ag, and Au
4.4. Actinide Oxides: [UO2]+ and [NpO2]2+
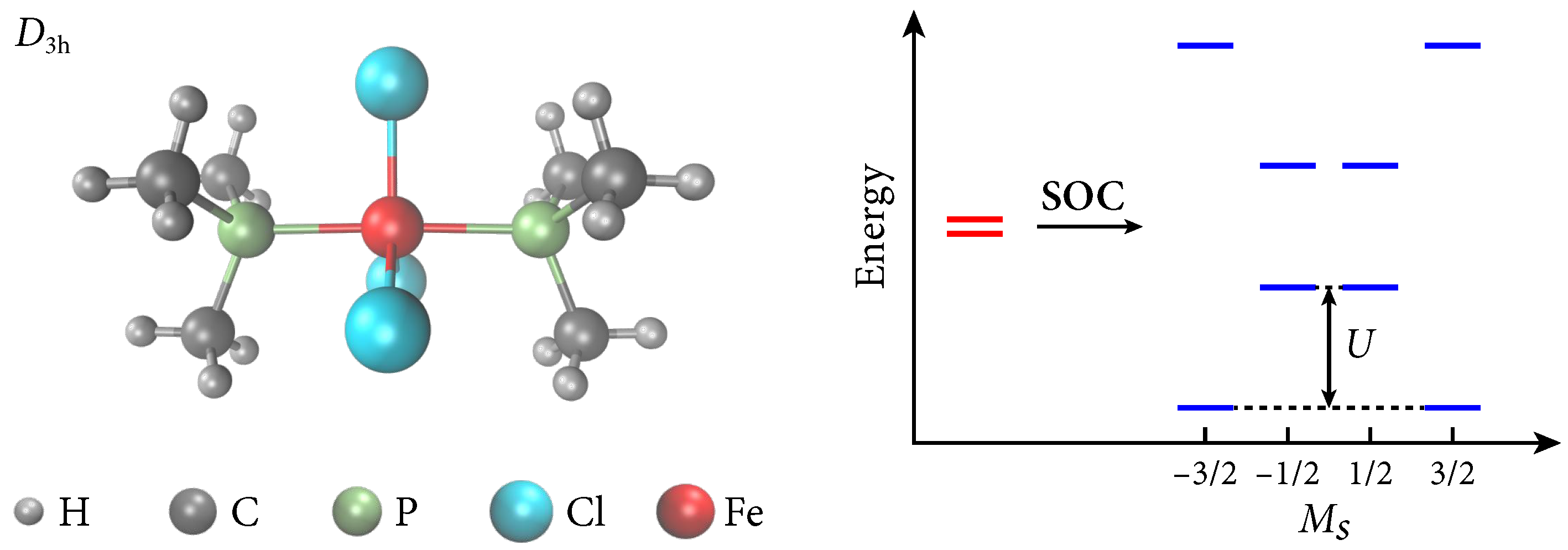
4.5. Mononuclear Single-Molecule Magnet: (PMe3)2FeCl3
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Andersson, K.; Malmqvist, P.Å.; Roos, B.O. Second-order perturbation theory with a complete active space self-consistent field reference function. J. Chem. Phys. 1992, 96, 1218–1226. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.P. Introduction of n-electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
- Hirao, K. Multireference Møller–Plesset method. Chem. Phys. Lett. 1992, 190, 374–380. [Google Scholar] [CrossRef]
- Sinha Mahapatra, U.; Datta, B.; Mukherjee, D. Molecular Applications of a Size-Consistent State-Specific Multireference Perturbation Theory with Relaxed Model-Space Coefficients. J. Phys. Chem. A 1999, 103, 1822–1830. [Google Scholar] [CrossRef]
- Khait, Y.G.; Song, J.; Hoffmann, M.R. Explication and revision of generalized Van Vleck perturbation theory for molecular electronic structure. J. Chem. Phys. 2002, 117, 4133–4145. [Google Scholar] [CrossRef]
- Rolik, Z.; Szabados, Á.; Surján, P.R. On the perturbation of multiconfiguration wave functions. J. Chem. Phys. 2003, 119, 1922–1928. [Google Scholar] [CrossRef]
- Hannon, K.P.; Li, C.; Evangelista, F.A. An integral-factorized implementation of the driven similarity renormalization group second-order multireference perturbation theory. J. Chem. Phys. 2016, 144, 204111. [Google Scholar] [CrossRef] [PubMed]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.P. n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants. J. Chem. Phys. 2002, 117, 9138–9153. [Google Scholar] [CrossRef]
- Finley, J.; Malmqvist, P.Å.; Roos, B.O.; Serrano-Andrés, L. The multi-state CASPT2 method. Chem. Phys. Lett. 1998, 288, 299–306. [Google Scholar] [CrossRef]
- Angeli, C.; Borini, S.; Cestari, M.; Cimiraglia, R. A quasidegenerate formulation of the second order n-electron valence state perturbation theory approach. J. Chem. Phys. 2004, 121, 4043–4049. [Google Scholar] [CrossRef]
- Nakano, H. Quasidegenerate perturbation theory with multiconfigurational self-consistent-field reference functions. J. Chem. Phys. 1993, 99, 7983–7992. [Google Scholar] [CrossRef]
- Lei, Y.; Liu, W.; Hoffmann, M.R. Further development of SDSPT2 for strongly correlated electrons. Mol. Phys. 2017, 115, 2696–2707. [Google Scholar] [CrossRef]
- Sharma, S.; Jeanmairet, G.; Alavi, A. Quasi-degenerate perturbation theory using matrix product states. J. Chem. Phys. 2016, 144, 34103. [Google Scholar] [CrossRef]
- Yanai, T.; Saitow, M.; Xiong, X.G.; Chalupský, J.; Kurashige, Y.; Guo, S.; Sharma, S. Multistate Complete-Active-Space Second-Order Perturbation Theory Based on Density Matrix Renormalization Group Reference States. J. Chem. Theory Comput. 2017, 13, 4829–4840. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Evangelista, F.A. Driven similarity renormalization group for excited states: A state-averaged perturbation theory. J. Chem. Phys. 2018, 148, 124106. [Google Scholar] [CrossRef]
- Li, C.; Evangelista, F.A. Multireference Theories of Electron Correlation Based on the Driven Similarity Renormalization Group. Annu. Rev. Phys. Chem. 2019, 70, 245–273. [Google Scholar] [CrossRef]
- Evangelisti, S.; Daudey, J.P.; Malrieu, J.P. Qualitative intruder-state problems in effective Hamiltonian theory and their solution through intermediate Hamiltonians. Phys. Rev. A 1987, 35, 4930–4941. [Google Scholar] [CrossRef]
- Paldus, J.; Piecuch, P.; Pylypow, L.; Jeziorski, B. Application of Hilbert-space coupled-cluster theory to simple (H2)2 model systems: Planar models. Phys. Rev. A 1993, 47, 2738–2782. [Google Scholar] [CrossRef]
- Wang, M.; Fang, W.H.; Li, C. Assessment of State-Averaged Driven Similarity Renormalization Group on Vertical Excitation Energies: Optimal Flow Parameters and Applications to Nucleobases. J. Chem. Theory Comput. 2023, 19, 122–136. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; Zhai, H.; Fang, W.H. Driven similarity renormalization group with a large active space: Applications to oligoacenes, zeaxanthin, and chromium dimer. arXiv 2025, arXiv:2503.01299. [Google Scholar]
- Huang, M.; Li, C.; Evangelista, F.A. Theoretical Calculation of Core-Excited States along Dissociative Pathways beyond Second-Order Perturbation Theory. J. Chem. Theory Comput. 2022, 18, 219–233. [Google Scholar] [CrossRef]
- Huang, M.; Evangelista, F.A. A study of core-excited states of organic molecules computed with the generalized active space driven similarity renormalization group. J. Chem. Phys. 2023, 158, 124112. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Evangelista, F.A. Benchmark Study of Core-Ionization Energies with the Generalized Active Space-Driven Similarity Renormalization Group. J. Chem. Theory Comput. 2024, 20, 7990–8000. [Google Scholar] [CrossRef]
- Garner, S.M.; Haugen, E.A.; Leone, S.R.; Neuscamman, E. Spin Coupling Effect on Geometry-Dependent X-Ray Absorption of Diradicals. J. Am. Chem. Soc. 2024, 146, 2387–2397. [Google Scholar] [CrossRef]
- Athanasakis-Kaklamanakis, M.; Wilkins, S.G.; Skripnikov, L.V.; Koszorús, Á.; Breier, A.A.; Ahmad, O.; Au, M.; Bai, S.W.; Belošević, I.; Berbalk, J.; et al. Electron correlation and relativistic effects in the excited states of radium monofluoride. Nat. Commun. 2025, 16, 2139. [Google Scholar] [CrossRef] [PubMed]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef] [PubMed]
- McAdams, S.G.; Ariciu, A.M.; Kostopoulos, A.K.; Walsh, J.P.; Tuna, F. Molecular single-ion magnets based on lanthanides and actinides: Design considerations and new advances in the context of quantum technologies. Coord. Chem. Rev. 2017, 346, 216–239. [Google Scholar] [CrossRef]
- Marian, C.M. Spin–orbit coupling and intersystem crossing in molecules. WIREs Comput. Mol. Sci. 2012, 2, 187–203. [Google Scholar] [CrossRef]
- Samanta, P.K.; Kim, D.; Coropceanu, V.; Brédas, J.L. Up-Conversion Intersystem Crossing Rates in Organic Emitters for Thermally Activated Delayed Fluorescence: Impact of the Nature of Singlet vs Triplet Excited States. J. Am. Chem. Soc. 2017, 139, 4042–4051. [Google Scholar] [CrossRef]
- Shen, L.; Xie, B.; Li, Z.; Liu, L.; Cui, G.; Fang, W.H. Role of Multistate Intersections in Photochemistry. J. Phys. Chem. Lett. 2020, 11, 8490–8501. [Google Scholar] [CrossRef]
- Pyykkö, P. Relativistic Effects in Chemistry: More Common Than You Thought. Annu. Rev. Phys. Chem. 2012, 63, 45–64. [Google Scholar] [CrossRef]
- Saue, T. Relativistic Hamiltonians for Chemistry: A Primer. ChemPhysChem 2011, 12, 3077–3094. [Google Scholar] [CrossRef]
- Kutzelnigg, W. Solved and unsolved problems in relativistic quantum chemistry. Chem. Phys. 2012, 395, 16–34. [Google Scholar] [CrossRef]
- Liu, W. Essentials of relativistic quantum chemistry. J. Chem. Phys. 2020, 152, 180901. [Google Scholar] [CrossRef]
- Eliav, E.; Kaldor, U.; Hess, B.A. The relativistic Fock-space coupled-cluster method for molecules: CdH and its ions. J. Chem. Phys. 1998, 108, 3409–3415. [Google Scholar] [CrossRef]
- Shiozaki, T.; Mizukami, W. Relativistic Internally Contracted Multireference Electron Correlation Methods. J. Chem. Theory Comput. 2015, 11, 4733–4739. [Google Scholar] [CrossRef] [PubMed]
- Vilkas, M.J.; Ishikawa, Y.; Koc, K. Relativistic multireference many-body perturbation theory for quasidegenerate systems: Energy levels of ions of the oxygen isoelectronic sequence. Phys. Rev. A 1999, 60, 2808–2821. [Google Scholar] [CrossRef]
- Abe, M.; Nakajima, T.; Hirao, K. The relativistic complete active-space second-order perturbation theory with the four-component Dirac Hamiltonian. J. Chem. Phys. 2006, 125, 234110. [Google Scholar] [CrossRef]
- Masuda, Y.; Noda, K.; Iwamuro, S.; Hada, M.; Nakatani, N.; Abe, M. Relativistic CASPT2/RASPT2 Program along with DIRAC Software. J. Chem. Theory Comput. 2025, 21, 1249–1258. [Google Scholar] [CrossRef]
- Zhao, Z.; Evangelista, F.A. Toward Accurate Spin–Orbit Splittings from Relativistic Multireference Electronic Structure Theory. J. Phys. Chem. Lett. 2024, 15, 7103–7110. [Google Scholar] [CrossRef]
- Dyall, K.G. An exact separation of the spin-free and spin-dependent terms of the Dirac–Coulomb–Breit Hamiltonian. J. Chem. Phys. 1994, 100, 2118–2127. [Google Scholar] [CrossRef]
- Reiher, M.; Wolf, A. Exact decoupling of the Dirac Hamiltonian. I. General theory. J. Chem. Phys. 2004, 121, 2037–2047. [Google Scholar] [CrossRef] [PubMed]
- Filatov, M.; Dyall, K.G. On convergence of the normalized elimination of the small component (NESC) method. Theor. Chem. Acc. 2007, 117, 333–338. [Google Scholar] [CrossRef]
- Li, Z.; Xiao, Y.; Liu, W. On the spin separation of algebraic two-component relativistic Hamiltonians. J. Chem. Phys. 2012, 137, 154114. [Google Scholar] [CrossRef]
- Kutzelnigg, W.; Liu, W. Quasirelativistic theory equivalent to fully relativistic theory. J. Chem. Phys. 2005, 123, 241102. [Google Scholar] [CrossRef] [PubMed]
- Dyall, K.G. Interfacing relativistic and nonrelativistic methods. IV. One- and two-electron scalar approximations. J. Chem. Phys. 2001, 115, 9136–9143. [Google Scholar] [CrossRef]
- Iliaš, M.; Saue, T. An infinite-order two-component relativistic Hamiltonian by a simple one-step transformation. J. Chem. Phys. 2007, 126, 064102. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Peng, D. Exact two-component Hamiltonians revisited. J. Chem. Phys. 2009, 131, 031104. [Google Scholar] [CrossRef]
- Peng, D.; Reiher, M. Exact decoupling of the relativistic Fock operator. Theor. Chem. Acc. 2012, 131, 1081. [Google Scholar] [CrossRef]
- Cheng, L.; Gauss, J. Perturbative treatment of spin-orbit coupling within spin-free exact two-component theory. J. Chem. Phys. 2014, 141, 164107. [Google Scholar] [CrossRef]
- Liu, W. Advances in relativistic molecular quantum mechanics. Phys. Rep. 2014, 537, 59–89. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
- Dyall, K.G.; van Lenthe, E. Relativistic regular approximations revisited: An infinite-order relativistic approximation. J. Chem. Phys. 1999, 111, 1366–1372. [Google Scholar] [CrossRef]
- Douglas, M.; Kroll, N.M. Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. 1974, 82, 89–155. [Google Scholar] [CrossRef]
- Hess, B.A. Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators. Phys. Rev. A 1986, 33, 3742–3748. [Google Scholar] [CrossRef]
- Wolf, A.; Reiher, M.; Hess, B.A. The generalized Douglas–Kroll transformation. J. Chem. Phys. 2002, 117, 9215–9226. [Google Scholar] [CrossRef]
- Nakajima, T.; Hirao, K. The Douglas–Kroll–Hess Approach. Chem. Rev. 2012, 112, 385–402. [Google Scholar] [CrossRef] [PubMed]
- Breit, G. Approximately Relativistic Equations. Phys. Rev. 1938, 53, 153–173. [Google Scholar] [CrossRef]
- Fedorov, D.G.; Koseki, S.; Schmidt, M.W.; Gordon, M.S. Spin-orbit coupling in molecules: Chemistry beyond the adiabatic approximation. Int. Rev. Phys. Chem. 2003, 22, 551–592. [Google Scholar] [CrossRef]
- Malmqvist, P.Å.; Roos, B.O.; Schimmelpfennig, B. The restricted active space (RAS) state interaction approach with spin–orbit coupling. Chem. Phys. Lett. 2002, 357, 230–240. [Google Scholar] [CrossRef]
- Roos, B.O.; Malmqvist, P.Å. Relativistic quantum chemistry: The multiconfigurational approach. Phys. Chem. Chem. Phys. 2004, 6, 2919. [Google Scholar] [CrossRef]
- Sayfutyarova, E.R.; Chan, G.K.L. A state interaction spin-orbit coupling density matrix renormalization group method. J. Chem. Phys. 2016, 144, 234301. [Google Scholar] [CrossRef] [PubMed]
- Zhai, H.; Chan, G.K.L. A comparison between the one- and two-step spin–orbit coupling approaches based on the ab initio density matrix renormalization group. J. Chem. Phys. 2022, 157, 164108. [Google Scholar] [CrossRef] [PubMed]
- Fedorov, D.G.; Finley, J.P. Spin-orbit multireference multistate perturbation theory. Phys. Rev. A 2001, 64, 042502. [Google Scholar] [CrossRef]
- Majumder, R.; Sokolov, A.Y. Simulating Spin–Orbit Coupling with Quasidegenerate N -Electron Valence Perturbation Theory. J. Phys. Chem. A 2023, 127, 546–559. [Google Scholar] [CrossRef]
- Majumder, R.; Sokolov, A.Y. Consistent Second-Order Treatment of Spin–Orbit Coupling and Dynamic Correlation in Quasidegenerate N-Electron Valence Perturbation Theory. J. Chem. Theory Comput. 2024, 20, 4676–4688. [Google Scholar] [CrossRef]
- Cheng, L.; Gauss, J. Analytic energy gradients for the spin-free exact two-component theory using an exact block diagonalization for the one-electron Dirac Hamiltonian. J. Chem. Phys. 2011, 135, 084114. [Google Scholar] [CrossRef]
- Meitei, O.R.; Houck, S.E.; Mayhall, N.J. Spin–Orbit Matrix Elements for a Combined Spin-Flip and IP/EA approach. J. Chem. Theory Comput. 2020, 16, 3597–3606. [Google Scholar] [CrossRef]
- Heß, B.A.; Marian, C.M.; Wahlgren, U.; Gropen, O. A mean-field spin-orbit method applicable to correlated wavefunctions. Chem. Phys. Lett. 1996, 251, 365–371. [Google Scholar] [CrossRef]
- Berning, A.; Schweizer, M.; Werner, H.J.; Knowles, P.J.; Palmieri, P. Spin-orbit matrix elements for internally contracted multireference configuration interaction wavefunctions. Mol. Phys. 2000, 98, 1823–1833. [Google Scholar] [CrossRef]
- Neese, F. Efficient and accurate approximations to the molecular spin-orbit coupling operator and their use in molecular g-tensor calculations. J. Chem. Phys. 2005, 122, 034107. [Google Scholar] [CrossRef]
- Kutzelnigg, W.; Mukherjee, D. Normal order and extended Wick theorem for a multiconfiguration reference wave function. J. Chem. Phys. 1997, 107, 432–449. [Google Scholar] [CrossRef]
- Evangelista, F.A. A driven similarity renormalization group approach to quantum many-body problems. J. Chem. Phys. 2014, 141, 054109. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Evangelista, F.A. Multireference Driven Similarity Renormalization Group: A Second-Order Perturbative Analysis. J. Chem. Theory Comput. 2015, 11, 2097–2108. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Lindh, R.; Evangelista, F.A. Dynamically weighted multireference perturbation theory: Combining the advantages of multi-state and state-averaged methods. J. Chem. Phys. 2019, 150, 144107. [Google Scholar] [CrossRef] [PubMed]
- Netz, J.; Mitrushchenkov, A.O.; Köhn, A. On the Accuracy of Mean-Field Spin-Orbit Operators for 3d Transition-Metal Systems. J. Chem. Theory Comput. 2021, 17, 5530–5537. [Google Scholar] [CrossRef]
- Li, C.; Evangelista, F.A. Driven similarity renormalization group: Third-order multireference perturbation theory. J. Chem. Phys. 2017, 146, 124132. [Google Scholar] [CrossRef]
- Smith, D.G.A.; Burns, L.A.; Simmonett, A.C.; Parrish, R.M.; Schieber, M.C.; Galvelis, R.; Kraus, P.; Kruse, H.; Di Remigio, R.; Alenaizan, A.; et al. Psi4 1.4: Open-source software for high-throughput quantum chemistry. J. Chem. Phys. 2020, 152, 184108. [Google Scholar] [CrossRef]
- Evangelista, F.A.; Li, C.; Verma, P.; Hannon, K.P.; Schriber, J.B.; Zhang, T.; Cai, C.; Wang, S.; He, N.; Stair, N.H.; et al. Forte: A suite of advanced multireference quantum chemistry methods. J. Chem. Phys. 2024, 161, 062502. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, X.; Banerjee, S.; Bao, P.; Barbry, M.; Blunt, N.S.; Bogdanov, N.A.; Booth, G.H.; Chen, J.; Cui, Z.H.; et al. Recent developments in the PySCF program package. J. Chem. Phys. 2020, 153, 024109. [Google Scholar] [CrossRef]
- Sun, Q. The updates in Libcint 6: More integrals, API refinements, and SIMD optimization techniques. J. Chem. Phys. 2024, 160, 174116. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Berkelbach, T.C.; Blunt, N.S.; Booth, G.H.; Guo, S.; Li, Z.; Liu, J.; McClain, J.D.; Sayfutyarova, E.R.; Sharma, S.; et al. PySCF: The Python-based simulations of chemistry framework. WIREs Comput. Mol. Sci. 2018, 8, e1340. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.Å.; Veryazov, V.; Widmark, P.O. Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set. J. Phys. Chem. A 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
- Stoychev, G.L.; Auer, A.A.; Neese, F. Automatic Generation of Auxiliary Basis Sets. J. Chem. Theory Comput. 2017, 13, 554–562. [Google Scholar] [CrossRef]
- Sansonetti, J.E.; Martin, W.C. Handbook of Basic Atomic Spectroscopic Data. J. Phys. Chem. Ref. Data 2005, 34, 1559–2259. [Google Scholar] [CrossRef]
- Huber, K.P.; Herzberg, G. Constants of diatomic molecules. In Molecular Spectra and Molecular Structure; Springer: Boston, MA, USA, 1979. [Google Scholar]
- Ram, R.; Bernath, P. Fourier Transform Infrared Emission Spectroscopy of SeH. J. Mol. Spectrosc. 2000, 203, 9–15. [Google Scholar] [CrossRef] [PubMed]
- Fink, E.; Setzer, K.; Ramsay, D.; Vervloet, M. Near-infrared emission bands of TeH and TeD. J. Mol. Spectrosc. 1989, 138, 19–28. [Google Scholar] [CrossRef]
- Miller, C.E.; Drouin, B.J. The X12Π3/2 and X22Π1/2 Potential Energy Surfaces of FO. J. Mol. Spectrosc. 2001, 205, 312–318. [Google Scholar] [CrossRef]
- Drouin, B.J.; Miller, C.E.; Cohen, E.A.; Wagner, G.; Birk, M. Further Investigations of the ClO Rotational Spectrum. J. Mol. Spectrosc. 2001, 207, 4–9. [Google Scholar] [CrossRef]
- Drouin, B.J.; Miller, C.E.; Müller, H.S.; Cohen, E.A. The Rotational Spectra, Isotopically Independent Parameters, and Interatomic Potentials for the X12Π3/2 and X22Π1/2 States of BrO. J. Mol. Spectrosc. 2001, 205, 128–138. [Google Scholar] [CrossRef]
- Gilles, M.K.; Polak, M.L.; Lineberger, W.C. Photoelectron spectroscopy of IO−. J. Chem. Phys. 1991, 95, 4723–4724. [Google Scholar] [CrossRef]
- Infante, I.; Severo Pereira Gomes, A.; Visscher, L. On the performance of the intermediate Hamiltonian Fock-space coupled-cluster method on linear triatomic molecules: The electronic spectra of NpO2+, NpO22+, and PuO22+. J. Chem. Phys. 2006, 125, 074301. [Google Scholar] [CrossRef] [PubMed]
- Gendron, F.; Pritchard, B.; Bolvin, H.; Autschbach, J. Magnetic Resonance Properties of Actinyl Carbonate Complexes and Plutonyl(VI)-tris-nitrate. Inorg. Chem. 2014, 53, 8577–8592. [Google Scholar] [CrossRef] [PubMed]
- Knecht, S.; Keller, S.; Autschbach, J.; Reiher, M. A Nonorthogonal State-Interaction Approach for Matrix Product State Wave Functions. J. Chem. Theory Comput. 2016, 12, 5881–5894. [Google Scholar] [CrossRef]
- Sarkar, A.; Gagliardi, L. Multiconfiguration Pair-Density Functional Theory for Vertical Excitation Energies in Actinide Molecules. J. Phys. Chem. A 2023, 127, 9389–9397. [Google Scholar] [CrossRef]
- Wang, X.; Sharma, S. Relativistic Semistochastic Heat-Bath Configuration Interaction. J. Chem. Theory Comput. 2023, 19, 848–855. [Google Scholar] [CrossRef]
- Infante, I.; Eliav, E.; Vilkas, M.J.; Ishikawa, Y.; Kaldor, U.; Visscher, L. A Fock space coupled cluster study on the electronic structure of the UO2, UO2+, U4+, and U5+ species. J. Chem. Phys. 2007, 127, 124308. [Google Scholar] [CrossRef]
- Merritt, J.M.; Han, J.; Heaven, M.C. Spectroscopy of the UO2+ cation and the delayed ionization of UO2. J. Chem. Phys. 2008, 128, 084304. [Google Scholar] [CrossRef]
- Feng, X.; Hwang, S.J.; Liu, J.l.; Chen, Y.c.; Tong, M.l.; Nocera, D.G. Slow Magnetic Relaxation in Intermediate Spin S = 3/2 Mononuclear Fe(III) Complexes. J. Am. Chem. Soc. 2017, 139, 16474–16477. [Google Scholar] [CrossRef]
- Roy Chowdhury, S.; Mishra, S. Ab initio investigation of magnetic anisotropy in intermediate spin iron( iii ) complexes. J. Chem. Phys. 2018, 149, 234302. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Balabanov, N.B.; Peterson, K.A. Systematically convergent basis sets for transition metals. I. All-electron correlation consistent basis sets for the 3d elements Sc–Zn. J. Chem. Phys. 2005, 123, 064107. [Google Scholar] [CrossRef] [PubMed]
- Alessio, M.; Krylov, A.I. Equation-of-Motion Coupled-Cluster Protocol for Calculating Magnetic Properties: Theory and Applications to Single-Molecule Magnets. J. Chem. Theory Comput. 2021, 17, 4225–4241. [Google Scholar] [CrossRef]
- Mussard, B.; Sharma, S. One-Step Treatment of Spin–Orbit Coupling and Electron Correlation in Large Active Spaces. J. Chem. Theory Comput. 2018, 14, 154–165. [Google Scholar] [CrossRef] [PubMed]
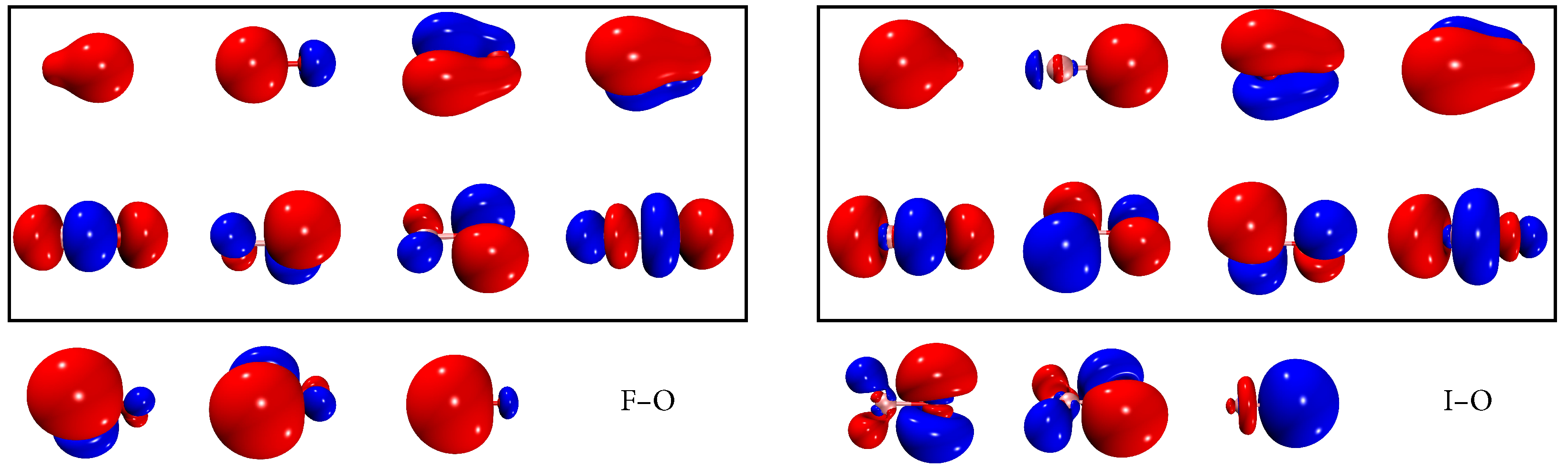


| System | SA-DSRG-PT2c a | QD-NEVPT2 b | 4c-DSRG-MRPT2 c | Experiment | ||
|---|---|---|---|---|---|---|
| ZFS | Ref. | |||||
| B | 14.7 | 14.9 | 15.0 | 13.99 | 15.3 | [85] |
| Al | 104.0 | 105.8 | 107.6 | 106.70 | 112 | [85] |
| Ga | 844.0 | 865.7 | 887.4 | 743.28 | 826 | [85] |
| In | 2459.6 | 2470.5 | 2560.8 | 2213 | [85] | |
| Tl | 11,591.0 | 12,065.6 | 12,475.8 | 7793 | [85] | |
| F | 401.5 | 401.5 | 401.5 | 384.70 | 404 | [85] |
| Cl | 789.7 | 789.7 | 789.7 | 867.69 | 882 | [85] |
| Br | 3574.4 | 3574.4 | 3574.4 | 3546.46 | 3685 | [85] |
| I | 8150.1 | 8150.1 | 8150.0 | 7603 | [85] | |
| CH | 27.8 | 28.5 | 29.0 | 27 | [86] | |
| SiH | 131.2 | 131.9 | 128.0 | 142 | [86] | |
| GeH | 880.4 | 864.1 | 864.1 | 892 | [86] | |
| SnH | 2433.1 | 2311.8 | 2286.3 | 2178 | [86] | |
| OH | 139.8 | 149.2 | 152.5 | 139 | [86] | |
| SH | 354.7 | 374.4 | 375.6 | 377 | [86] | |
| SeH | 1742.9 | 1832.7 | 1836.7 | 1763 | [87] | |
| TeH | 4080.9 | 4271.0 | 4293.5 | 3816 | [88] | |
| FO | 187.8 | 180.0 | 180.0 | 197 | [89] | |
| ClO | 270.0 | 280.3 | 299.7 | 322 | [90] | |
| BrO | 741.4 | 853.2 | 961.9 | 975 | [91] | |
| IO | 1593.3 | 1871.7 | 2303.8 | 2091 | [92] | |
| System | State | SA-CASSCF a | SA-DSRG-PT2c a | CASPT2 b | DMRG c | Exp. d |
|---|---|---|---|---|---|---|
| Cu | 2D (no SOC) | 1.66 | 1.36 | 1.49 | ||
| 2D5/2 | 1.55 | 1.26 | 1.43 | 1.31 | 1.39 | |
| 2D3/2 | 1.81 | 1.52 | 1.69 | 1.57 | 1.64 | |
| ZFS | 0.26 | 0.26 | 0.26 | 0.26 | 0.25 | |
| Ag | 2D (no SOC) | 4.46 | 3.98 | 3.97 | ||
| 2D5/2 | 4.23 | 3.75 | 3.75 | |||
| 2D3/2 | 4.80 | 4.33 | 4.30 | |||
| ZFS | 0.58 | 0.58 | 0.55 | |||
| Au | 2D (no SOC) | 2.30 | 1.74 | 1.58 | 1.62 | 1.74 |
| 2D5/2 | 1.61 | 1.05 | 0.97 | 1.02 | 1.14 | |
| 2D3/2 | 3.33 | 2.77 | 2.49 | 2.55 | 2.66 | |
| ZFS | 1.72 | 1.72 | 1.51 | 1.53 | 1.52 |
| Method | 2Δ3/2u | 2Φ7/2u | 2Δ5/2u |
|---|---|---|---|
| SA-DSRG-PT2c a,b | 0.35 | 0.85 | 0.99 |
| QD-NEVPT2 a,c | 0.36 | 0.80 | 0.98 |
| CASPT2 a,d | 0.32 | 0.83 | 0.98 |
| QD-NEVPT2 a,e | 0.35 | 0.76 | 0.95 |
| IHFSCCSD f | 0.34 | 0.71 | 0.81 |
| Exp. g | 0.33 |
| Method | 2Δ3/2u | 2Φ7/2u | 2Δ5/2u |
|---|---|---|---|
| SA-DSRG-PT2c a,b | 0.38 | 1.02 | 1.16 |
| QD-NEVPT2 a,c | 0.45 | 1.00 | 1.15 |
| XMS-CASPT2 a,d | 0.45 | 0.98 | 1.18 |
| CASPT2 a,e | 0.38 | 1.00 | 1.15 |
| QD-NEVPT2 a,f | 0.45 | 0.94 | 1.11 |
| IHFSCCSD g | 0.44 | 0.90 | 1.11 |
| SHCI h | 0.43 | 0.89 | 1.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Li, C. A Cost-Effective Treatment of Spin–Orbit Couplings in the State-Averaged Driven Similarity Renormalization Group Second-Order Perturbation Theory. Molecules 2025, 30, 2082. https://doi.org/10.3390/molecules30092082
Wang M, Li C. A Cost-Effective Treatment of Spin–Orbit Couplings in the State-Averaged Driven Similarity Renormalization Group Second-Order Perturbation Theory. Molecules. 2025; 30(9):2082. https://doi.org/10.3390/molecules30092082
Chicago/Turabian StyleWang, Meng, and Chenyang Li. 2025. "A Cost-Effective Treatment of Spin–Orbit Couplings in the State-Averaged Driven Similarity Renormalization Group Second-Order Perturbation Theory" Molecules 30, no. 9: 2082. https://doi.org/10.3390/molecules30092082
APA StyleWang, M., & Li, C. (2025). A Cost-Effective Treatment of Spin–Orbit Couplings in the State-Averaged Driven Similarity Renormalization Group Second-Order Perturbation Theory. Molecules, 30(9), 2082. https://doi.org/10.3390/molecules30092082





