Research Progress on Micro/Nanopore Flow Behavior
Abstract
1. Introduction
1.1. Background
1.2. Research Status and Problems
2. Basic Theory of Fluid Properties in Micro/Nanopores
2.1. Difference Between Microflow and Macro Flow
2.2. Characteristics of Microfluidic Systems
2.3. Theoretical Model and Description Method
3. Experimental Study on Microscopic Seepage Phenomena
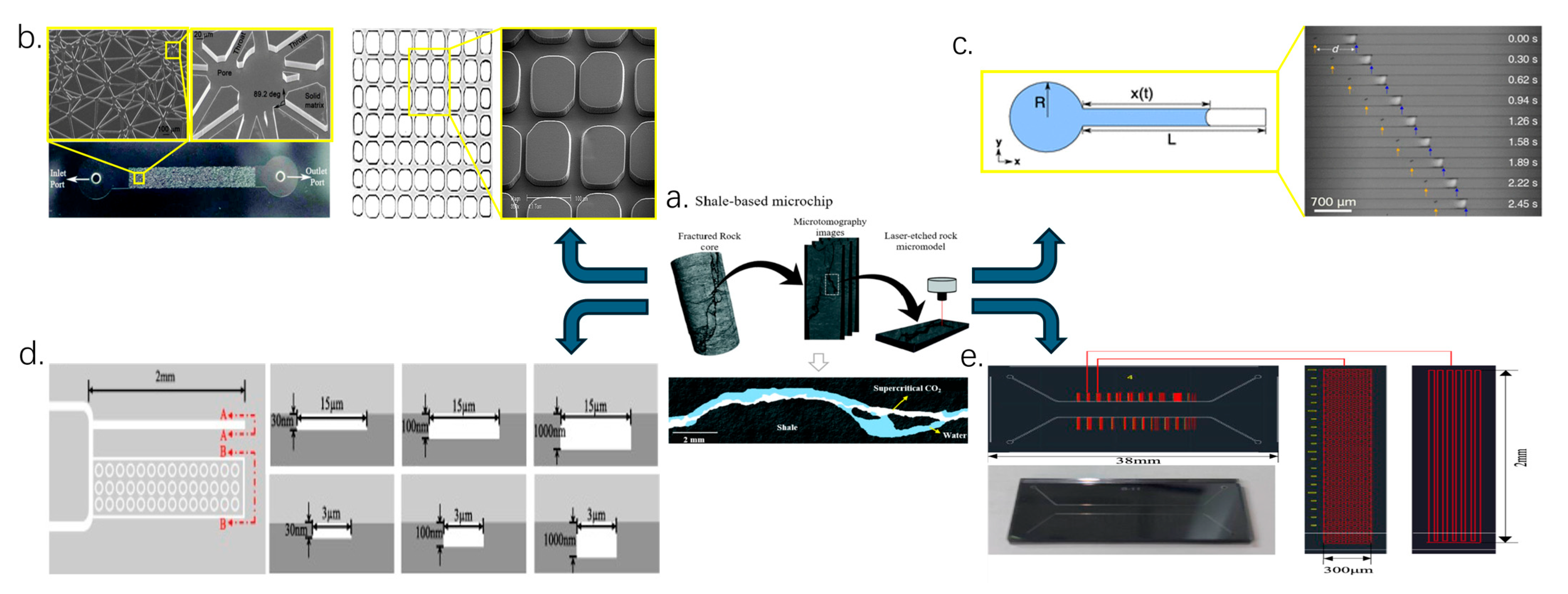
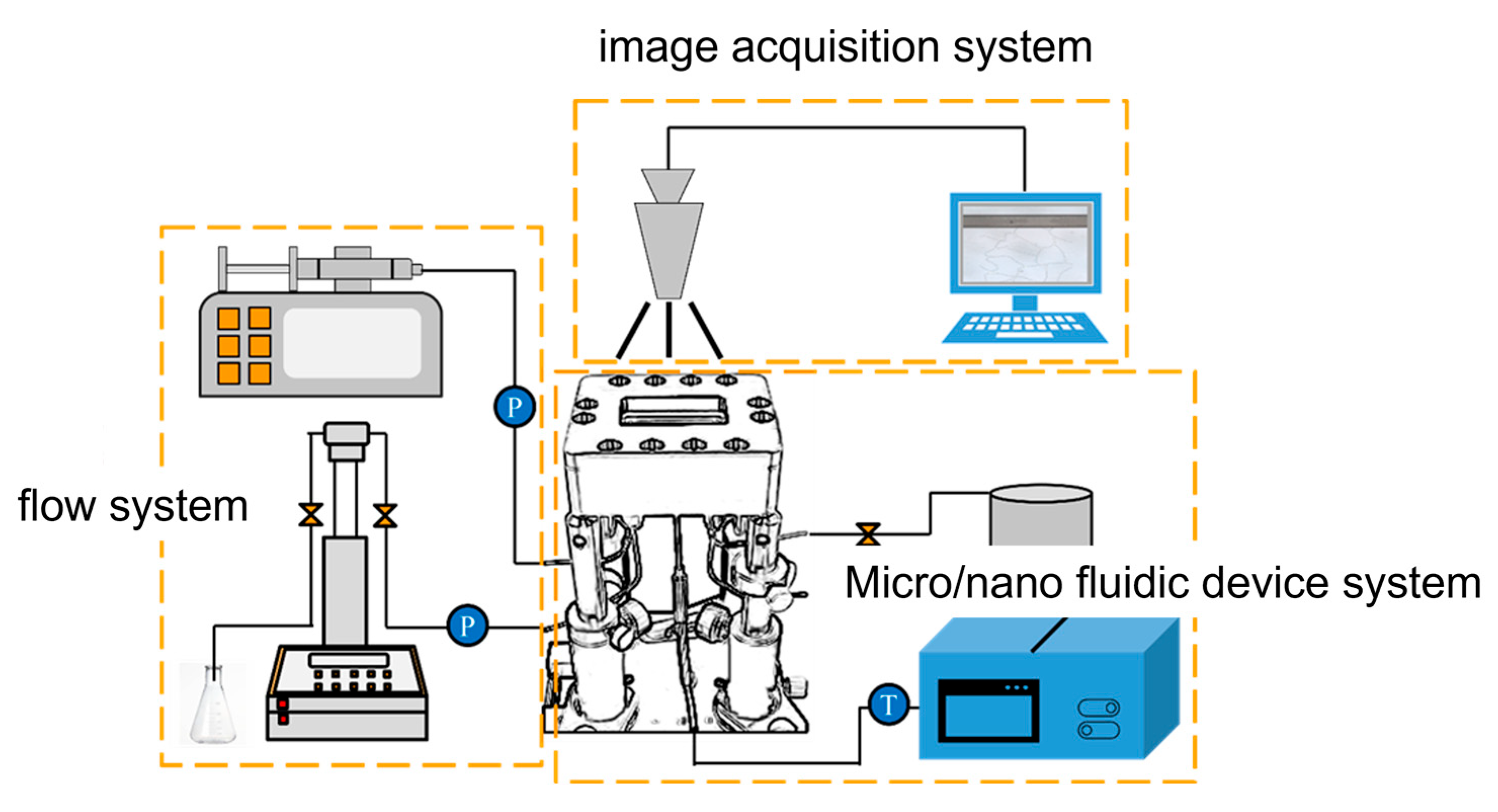
3.1. Evolution and Visualization of Microscopic Seepage Experimental Systems
3.2. Typical Experimental Research Results
3.2.1. Fluid Transport Characteristics in Multi Scale Pore Networks
3.2.2. The Influence of Nanoscale Effects on Transport Processes
3.2.3. The Influence of Pore Structure on Fluid Distribution
3.3. Limitations of Experimental Research
4. Numerical Simulation Study on Microscopic Seepage Flow
4.1. Formation and Improvement of the LBM
4.1.1. Breakthrough of the LBM in Multiphase Flow Research
4.1.2. Application of the LBM in Complex Porous Media Seepage
4.2. Introduction and Development of MD
4.2.1. Nano Confined Fluid Transport Characteristics
4.2.2. Nanofluid Drive Mechanism and Regulation
5. Limitations and Future Perspectives
5.1. Limitations
5.2. Future Perspectives
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, L.; Zhang, D.; Su, Y.; Zhang, X.; Lu, M.; Wang, H. Microfluidic Insights into CO2 Sequestration and Enhanced Oil Recovery in Laminated Shale Reservoirs: Post-Fracturing Interface Dynamics and Micro-Scale Mechanisms. Adv. Geo-Energy Res. 2024, 13, 203–217. [Google Scholar] [CrossRef]
- Han, B.; Wang, S.; Zhang, Z.; Wang, Y. Numerical Simulation of Geothermal Reservoir Thermal Recovery of Heterogeneous Discrete Fracture Network-Rock Matrix System. Energy 2024, 305, 132306. [Google Scholar] [CrossRef]
- Jangda, Z.; Menke, H.; Busch, A.; Geiger, S.; Bultreys, T.; Lewis, H.; Singh, K. Pore-Scale Visualization of Hydrogen Storage in a Sandstone at Subsurface Pressure and Temperature Conditions: Trapping, Dissolution and Wettability. J. Colloid Interface Sci. 2023, 629, 316–325. [Google Scholar] [CrossRef]
- Hou, Y.; Deng, H.; Pan, F.; Chen, W.; Du, Q.; Jiao, K. Pore-Scale Investigation of Catalyst Layer Ingredient and Structure Effect in Proton Exchange Membrane Fuel Cell. Appl. Energy 2019, 253, 113561. [Google Scholar] [CrossRef]
- Chang, Y.; Yang, Z.; Zhang, Y.; Niu, Z.; Chen, X. Micro-Nano Scale Confined Flow Characteristics and Mechanism in Tight Reservoir: Insights from Experimental and Molecular Simulation Studies. Geoenergy Sci. Eng. 2023, 231, 212317. [Google Scholar] [CrossRef]
- Ranjbarzadeh, R.; Sappa, G. Numerical and Experimental Study of Fluid Flow and Heat Transfer in Porous Media: A Review Article. Energies 2025, 18, 976. [Google Scholar] [CrossRef]
- Fani, M.; Pourafshary, P.; Mostaghimi, P.; Mosavat, N. Application of Microfluidics in Chemical Enhanced Oil Recovery: A Review. Fuel 2022, 315, 123225. [Google Scholar] [CrossRef]
- Bao, B.; Zhao, S. A Review of Experimental Nanofluidic Studies on Shale Fluid Phase and Transport Behaviors. J. Nat. Gas Sci. Eng. 2021, 86, 103745. [Google Scholar] [CrossRef]
- Cai, J.; Qin, X.; Xia, X.; Jiao, X.; Chen, H.; Wang, H.; Xia, Y. Numerical Modeling of Multiphase Flow in Porous Media Considering Micro- and Nanoscale Effects: A Comprehensive Review. Gas Sci. Eng. 2024, 131, 205441. [Google Scholar] [CrossRef]
- Liehui, Z.; Baochao, S.; Yulong, Z.; Zhaoli, G. Review of Micro Seepage Mechanisms in Shale Gas Reservoirs. Int. J. Heat Mass Transf. 2019, 139, 144–179. [Google Scholar] [CrossRef]
- Yin, Y.; Cui, Y.; Jing, L. Clogging and Unclogging of Fine Particles in Porous Media: Micromechanical Insights from an Analog Pore System. WATER Resour. Res. 2024, 60, e2023WR034628. [Google Scholar] [CrossRef]
- Forouzandeh, F.; Zhu, X.; Alfadhel, A.; Ding, B.; Walton, J.P.; Cormier, D.; Frisina, R.D.; Borkholder, D.A. A Nanoliter Resolution Implantable Micropump for Murine Inner Ear Drug Delivery. J. Control. Release 2019, 298, 27–37. [Google Scholar] [CrossRef]
- Jiang, X.; He, G.; Cai, J.; Xiao, W. Microscale Flow and Separation Process Analysis in the Nanoporous Crystal Layer. In New Polymer Nanocomposites for Environmental Remediation; Hussain, C., Mishra, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; p. 206. ISBN 978-0-12-811034-8. [Google Scholar]
- Foroozesh, J.; Kumar, S. Nanoparticles Behaviors in Porous Media: Application to Enhanced Oil Recovery. J. Mol. Liq. 2020, 316, 113876. [Google Scholar] [CrossRef]
- Pengfei, J.; Pengwan, W.; Shangwen, Z.; Huaichang, W.; Xiangyang, C. Study on the Microscopic Pore Structures of Coal Measure Reservoirs in the Shanxi Formation, Eastern Ordos Basin. Front. Earth Sci. 2022, 10, 903588. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G.; Wang, Z.; Chen, J.; Pang, X.; Wang, S.; Zhou, Z.; He, Z.; Qin, Z.; Fan, X. A Review on Pore Structure Characterization in Tight Sandstones. Earth-Sci. Rev. 2018, 177, 436–457. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.; Ge, L.; Hu, F.; Li, C.; Li, X.; Yu, J.; Xu, H.; Lu, S.; Xue, Q. Pore-Scale Characterization of Tight Sandstone in Yanchang Formation Ordos Basin China Using Micro-CT and SEM Imaging from Nm-to Cm-Scale. Fuel 2017, 209, 254–264. [Google Scholar] [CrossRef]
- Tian, W.; Lu, S.; Huang, W.; Wang, S.; Gao, Y.; Wang, W.; Li, J.; Xu, J.; Zhan, Z. Study on the Full-Range Pore Size Distribution and the Movable Oil Distribution in Glutenite. Energy Fuels 2019, 33, 7028–7042. [Google Scholar] [CrossRef]
- Bakhshian, S.; Hosseini, S.A.; Shokri, N. Pore-Scale Characteristics of Multiphase Flow in Heterogeneous Porous Media Using the Lattice Boltzmann Method. Sci. Rep. 2019, 9, 3377. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, Q.; Tian, Q.; Ke, Y.; Wang, Q. Small Angle Neutron Scattering Studies of Shale Oil Occurrence Status at Nanopores. Adv. Geo-Energy Res. 2024, 11, 230–240. [Google Scholar] [CrossRef]
- Neto, C.; Evans, D.R.; Bonaccurso, E.; Butt, H.-J.; Craig, V.S. Boundary Slip in Newtonian Liquids: A Review of Experimental Studies. Rep. Prog. Phys. 2005, 68, 2859. [Google Scholar] [CrossRef]
- Qi, D.; Hoelzle, D.J.; Rowat, A.C. Probing Single Cells Using Flow in Microfluidic Devices. Eur. Phys. J. Spec. Top. 2012, 204, 85–101. [Google Scholar] [CrossRef]
- Stokes, G.G. On the Theories of the Internal Friction of Fluids in Motion, and of the Equilibrium and Motion of Elastic Solids. In Classics of Elastic Wave Theory; Society of Exploration Geophysicists: Houston, TX, USA, 2007. [Google Scholar]
- Navier, C. Mémoire Sur Les Lois Du Mouvement Des Fluides; Mémoires de l’Académie Royale des Sciences de l’Institut de France: Paris, France, 1822. [Google Scholar]
- Huang, D.M.; Sendner, C.; Horinek, D.; Netz, R.R.; Bocquet, L. Water Slippage versus Contact Angle: A Quasiuniversal Relationship. Phys. Rev. Lett. 2008, 101, 226101. [Google Scholar] [CrossRef] [PubMed]
- Karim, K.E.; Kim, B. First Law of Thermodynamics on the Boundary for Flow through a Carbon Nanotube. Phys. Rev. E 2021, 103, 053115. [Google Scholar] [CrossRef]
- Zhang, R.L.; Du, G.J.; Wang, M.F.; Li, S.Y. Controlling Water Flow in Pattern-Charged Nanotubes. J. Nano Res. 2022, 72, 1–10. [Google Scholar] [CrossRef]
- Wei, N.; Peng, X.; Xu, Z. Breakdown of Fast Water Transport in Graphene Oxides. Phys. Rev. E 2014, 89, 012113. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, F.; Yin, S.; Wallace, C.D.; Soltanian, M.R.; Dai, Z.; Ritzi, R.W.; Ma, Z.; Zhan, C.; Lü, X. Application of Upscaling Methods for Fluid Flow and Mass Transport in Multi-Scale Heterogeneous Media: A Critical Review. Appl. Energy 2021, 303, 117603. [Google Scholar] [CrossRef]
- Tomo, Y.; Askounis, A.; Ikuta, T.; Takata, Y.; Sefiane, K.; Takahashi, K. Superstable Ultrathin Water Film Confined in a Hydrophilized Carbon Nanotube. Nano Lett. 2018, 18, 1869–1874. [Google Scholar] [CrossRef]
- Thomas, J.A.; McGaughey, A.J.; Kuter-Arnebeck, O. Pressure-Driven Water Flow through Carbon Nanotubes: Insights from Molecular Dynamics Simulation. Int. J. Therm. Sci. 2010, 49, 281–289. [Google Scholar] [CrossRef]
- Thomas, J.A.; McGaughey, A.J. Reassessing Fast Water Transport through Carbon Nanotubes. Nano Lett. 2008, 8, 2788–2793. [Google Scholar] [CrossRef]
- Holt, J.K. Methods for Probing Water at the Nanoscale. Microfluid. Nanofluid. 2008, 5, 425–442. [Google Scholar] [CrossRef]
- Hummer, G.; Rasaiah, J.; Noworyta, J. Nanoscale Hydrodynamics: Enhanced Flow in Carbon Nanotubes. Nature 2001, 414, 188. [Google Scholar] [CrossRef] [PubMed]
- Jing, W.; Zhang, L.; Li, A.; Liu, T.; Cheng, Y.; Sun, H.; Yang, Y.; Zhu, G.; Yao, J.; Zhong, J. Phase Behaviors of Gas Condensate at Pore Scale: Direct Visualization via Microfluidics and in-Situ CT Scanning. SPE J. 2024, 29, 2566–2577. [Google Scholar] [CrossRef]
- Tang, M.; Zhang, T.; Ma, Y.; Hao, D.; Yang, X.; Li, Y. Experimental Study on Fracture Effect on the Multiphase Flow in Ultra-Low Permeability Sandstone Based on LF-NMR. Geoenergy Sci. Eng. 2023, 222, 211399. [Google Scholar] [CrossRef]
- Gogoi, S.; Gogoi, S.B. Review on Microfluidic Studies for EOR Application. J. Pet. Explor. Prod. Technol. 2019, 9, 2263–2277. [Google Scholar] [CrossRef]
- Anbari, A.; Chien, H.; Datta, S.S.; Deng, W.; Weitz, D.A.; Fan, J. Microfluidic Model Porous Media: Fabrication and Applications. Small 2018, 14, 1703575. [Google Scholar] [CrossRef]
- Mostowfi, F.; Molla, S.; Tabeling, P. Determining Phase Diagrams of Gas–Liquid Systems Using a Microfluidic PVT. Lab A Chip 2012, 12, 4381–4387. [Google Scholar] [CrossRef]
- Zheng, B.; Tice, J.D.; Roach, L.S.; Ismagilov, R.F. A Droplet-based, Composite PDMS/Glass Capillary Microfluidic System for Evaluating Protein Crystallization Conditions by Microbatch and Vapor-diffusion Methods with On-chip X-ray Diffraction. Angew. Chem. Int. Ed. 2004, 43, 2508–2511. [Google Scholar] [CrossRef]
- Verma, N.; Pandya, A. Challenges and Opportunities in Micro/Nanofluidic and Lab-on-a-Chip. Prog. Mol. Biol. Transl. Sci. 2022, 186, 289–302. [Google Scholar]
- Rodríguez, C.F.; Andrade-Pérez, V.; Vargas, M.C.; Mantilla-Orozco, A.; Osma, J.F.; Reyes, L.H.; Cruz, J.C. Breaking the Clean Room Barrier: Exploring Low-Cost Alternatives for Microfluidic Devices. Front. Bioeng. Biotechnol. 2023, 11, 1176557. [Google Scholar] [CrossRef]
- Cobos, S.; Carvalho, M.; Alvarado, V. Flow of Oil-Water Emulsions through a Constricted Capillary. Int. J. Multiph. FLOW 2009, 35, 507–515. [Google Scholar] [CrossRef]
- Wang, H.; Wang, E.; Liu, Z.; Gao, D.; Yuan, R.; Sun, L.; Zhu, Y. A Novel Carbon Nanotubes Reinforced Superhydrophobic and Superoleophilic Polyurethane Sponge for Selective Oil-Water Separation through a Chemical Fabrication. J. Mater. Chem. A 2015, 3, 266–273. [Google Scholar] [CrossRef]
- Gong, D.; Grimes, C.A.; Varghese, O.K.; Hu, W.; Singh, R.S.; Chen, Z.; Dickey, E.C. Titanium Oxide Nanotube Arrays Prepared by Anodic Oxidation. J. Mater. Res. 2001, 16, 3331–3334. [Google Scholar] [CrossRef]
- Fuquan, S.; Xiao, H.; Genmin, Z.; Weiyao, Z. The Characteristics of Water Flow Displaced by Gas in Nano Arrays. Chin. J. Theor. Appl. Mech. 2018, 50, 553–560. [Google Scholar]
- Wegner, J.; Ganzer, L. Rock-on-a-Chip Devices for High p, T Conditions and Wettability Control for the Screening of EOR Chemicals; SPE: Paris, France, 2017; p. D041S010R007. [Google Scholar]
- Lee, H.; Lee, S.G.; Doyle, P.S. Photopatterned Oil-Reservoir Micromodels with Tailored Wetting Properties. Lab A Chip 2015, 15, 3047–3055. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Sanati-Nezhad, A.; Hejazi, S.H. Geo-Material Surface Modification of Microchips Using Layer-by-Layer (LbL) Assembly for Subsurface Energy and Environmental Applications. Lab A Chip 2018, 18, 285–295. [Google Scholar] [CrossRef]
- Wang, H.; Su, Y.; Wang, W.; Li, G.; Zhang, Q. Simulation on Liquid Flow in Shale Nanoporous Media Based on Lattice Boltzmann Method. Acta Pet. Sin. 2023, 44, 534. [Google Scholar]
- Zheng, J.; Ju, Y.; Wang, M. Pore-scale Modeling of Spontaneous Imbibition Behavior in a Complex Shale Porous Structure by Pseudopotential Lattice Boltzmann Method. J. Geophys. Res. Solid Earth 2018, 123, 9586–9600. [Google Scholar] [CrossRef]
- Zhang, J.; Song, H.; Zhu, W.; Wang, J. Liquid Transport through Nanoscale Porous Media with Strong Wettability. Transp. Porous Media 2021, 140, 697–711. [Google Scholar] [CrossRef]
- Wu, S.; Li, Z.; Zhang, C.; Lv, G.; Zhou, P. Nanohydrodynamic Model and Transport Mechanisms of Tight Oil Confined in Nanopores Considering Liquid–Solid Molecular Interaction Effect. Ind. Eng. Chem. Res. 2021, 60, 18154–18165. [Google Scholar] [CrossRef]
- Xing, L.; Zhang, Y. A Many-Body Dissipative Particle Dynamics Simulation of Flow Performance in Capillary Channel. Comput. Mater. Sci. 2024, 242, 113080. [Google Scholar] [CrossRef]
- Sasaki, K.; Ishiwatari, Y.; Ueno, K.; Kojima, T.; Banno, T.; Arai, N. Molecular Modelling of Active Oil Droplet Propulsion: Insights from Dissipative Particle Dynamics Simulation. Chem. Phys. Lett. 2024, 857, 141680. [Google Scholar] [CrossRef]
- Musharaf, H.M.; Roshan, U.; Mudugamuwa, A.; Trinh, Q.T.; Zhang, J.; Nguyen, N.-T. Computational Fluid-Structure Interaction in Microfluidics. Micromachines 2024, 15, 897. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Xu, H.; Fan, J.; Zhu, Y.-B.; Wang, F.; Wu, H. Transport of Shale Gas in Microporous/Nanoporous Media: Molecular to Pore-Scale Simulations. Energy Fuels 2020, 35, 911–943. [Google Scholar] [CrossRef]
- Kavokine, N.; Netz, R.R.; Bocquet, L. Fluids at the Nanoscale: From Continuum to Subcontinuum Transport. Annu. Rev. Fluid Mech. 2021, 53, 377–410. [Google Scholar] [CrossRef]
- Han, W.; Li, W.; Zhang, H. A Comprehensive Review on the Fundamental Principles, Innovative Designs, and Multidisciplinary Applications of Micromixers. Phys. Fluids 2024, 36, 101306. [Google Scholar] [CrossRef]
- Wang, L.; Fan, J. Nanofluids Research: Key Issues. Nanoscale Res. Lett. 2010, 5, 1241–1252. [Google Scholar] [CrossRef]
- Reynolds, O. XXIX. An Experimental Investigation of the Circumstances Which Determine Whether the Motion of Water Shall Be Direct or Sinuous, and of the Law of Resistance in Parallel Channels. Philos. Trans. R. Soc. Lond. 1883, 174, 935–982. [Google Scholar]
- Qin, X.; Wu, J.; Xia, Y.; Wang, H.; Cai, J. Multicomponent Image-Based Modeling of Water Flow in Heterogeneous Wet Shale Nanopores. Energy 2024, 298, 131367. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000; ISBN 1-139-64346-0. [Google Scholar]
- Kundu, P.K.; Cohen, I.M.; Dowling, D.R.; Capecelatro, J. Fluid Mechanics; Elsevier: Amsterdam, The Netherlands, 2024; ISBN 0-12-819808-7. [Google Scholar]
- Jamali, J.; Shoghl, S.N. Computational Fluid Dynamics Modeling of Fluid Flow and Heat Transfer in the Central Pore of Carbon Nanopipes. RSC Adv. 2014, 4, 57958–57966. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.; Li, J.; Li, X.; Xu, J.; Dong, X. Wettability Effect on Nanoconfined Water Flow. Proc. Natl. Acad. Sci. USA 2017, 114, 3358–3363. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017; ISBN 0-19-252470-4. [Google Scholar]
- Tian, Y.; Ju, B.; Wang, X.; Wang, H.; Hu, J.; Huang, Y.; Liu, N.; Dong, Y. Study on Phase Behavior of CO2/Hydrocarbons in Shale Reservoirs Considering Sieving Effect and Capillary Pressure. Nat. Resour. Res. 2021, 30, 3533–3549. [Google Scholar] [CrossRef]
- Feng, Q.; Xu, S.; Xing, X.; Zhang, W.; Wang, S. Advances and Challenges in Shale Oil Development: A Critical Review. Adv. Geo-Energy Res. 2020, 4, 406–418. [Google Scholar] [CrossRef]
- Joseph, S.; Aluru, N.R. Why Are Carbon Nanotubes Fast Transporters of Water? Nano Lett. 2008, 8, 452–458. [Google Scholar] [CrossRef]
- Priezjev, N.V. Effect of Surface Roughness on Rate-Dependent Slip in Simple Fluids. J. Chem. Phys. 2007, 127, 144708. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.E. Nanoscale Slip Length Prediction with Machine Learning Tools. Sci. Rep. 2021, 11, 12520. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Zhong, J.; Abedini, A.; Xu, L.; Xu, Y.; Qi, Z.; Mostowfi, F.; Sinton, D. Nanomodel Visualization of Fluid Injections in Tight Formations. Nanoscale 2018, 10, 21994–22002. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, T.; Liu, S.; Ding, K.; Liu, T.; Yao, J.; Sun, H.; Yang, Y.; Zhang, L.; Wang, W.; et al. Unveiling Nanoscale Fluid Miscible Behaviors with Nanofluidic Slim-Tube. Energy Environ. Sci. 2024, 17, 9635–9651. [Google Scholar] [CrossRef]
- Ally, J.; Molla, S.; Mostowfi, F. Condensation in Nanoporous Packed Beds. Langmuir 2016, 32, 4494–4499. [Google Scholar] [CrossRef]
- Kim, M.; Sell, A.; Sinton, D. Aquifer-on-a-Chip: Understanding Pore-Scale Salt Precipitation Dynamics during CO2 Sequestration. Lab A Chip 2013, 13, 2508–2518. [Google Scholar] [CrossRef]
- Bao, B.; Zandavi, S.H.; Li, H.; Zhong, J.; Jatukaran, A.; Mostowfi, F.; Sinton, D. Bubble Nucleation and Growth in Nanochannels. Phys. Chem. Chem. Phys. 2017, 19, 8223–8229. [Google Scholar] [CrossRef]
- Alfi, M.; Nasrabadi, H.; Banerjee, D. Experimental Investigation of Confinement Effect on Phase Behavior of Hexane, Heptane and Octane Using Lab-on-a-Chip Technology. Fluid Phase Equilibria 2016, 423, 25–33. [Google Scholar] [CrossRef]
- Jatukaran, A.; Zhong, J.; Persad, A.H.; Xu, Y.; Mostowfi, F.; Sinton, D. Direct Visualization of Evaporation in a Two-Dimensional Nanoporous Model for Unconventional Natural Gas. ACS Appl. Nano Mater. 2018, 1, 1332–1338. [Google Scholar] [CrossRef]
- Porter, M.L.; Jiménez-Martínez, J.; Martinez, R.; McCulloch, Q.; Carey, J.W.; Viswanathan, H.S. Geo-Material Microfluidics at Reservoir Conditions for Subsurface Energy Resource Applications. Lab A Chip 2015, 15, 4044–4053. [Google Scholar] [CrossRef]
- Nguyen, P.; Carey, J.W.; Viswanathan, H.S.; Porter, M. Effectiveness of Supercritical-CO2 and N2 Huff-and-Puff Methods of Enhanced Oil Recovery in Shale Fracture Networks Using Microfluidic Experiments. Appl. Energy 2018, 230, 160–174. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, C.; Qu, C.; Wei, M.; He, X.; Bai, B. Fabrication and Verification of a Glass–Silicon–Glass Micro-/Nanofluidic Model for Investigating Multi-Phase Flow in Shale-like Unconventional Dual-Porosity Tight Porous Media. Lab Chip 2019, 19, 4071–4082. [Google Scholar] [CrossRef]
- Kelly, S.A.; Torres-Verdín, C.; Balhoff, M.T. Subsurface to Substrate: Dual-Scale Micro/Nanofluidic Networks for Investigating Transport Anomalies in Tight Porous Media. Lab A Chip 2016, 16, 2829–2839. [Google Scholar] [CrossRef]
- Jatukaran, A.; Zhong, J.; Abedini, A.; Sherbatian, A.; Zhao, Y.; Jin, Z.; Mostowfi, F.; Sinton, D. Natural Gas Vaporization in a Nanoscale Throat Connected Model of Shale: Multi-Scale, Multi-Component and Multi-Phase. Lab A Chip 2019, 19, 272–280. [Google Scholar] [CrossRef]
- Ling, B.; Sodwatana, M.; Kohli, A.; Ross, C.M.; Jew, A.; Kovscek, A.R.; Battiato, I. Probing Multiscale Dissolution Dynamics in Natural Rocks through Microfluidics and Compositional Analysis. Proc. Natl. Acad. Sci. USA 2022, 119, e2122520119. [Google Scholar] [CrossRef]
- Gunda, N.S.K.; Bera, B.; Karadimitriou, N.K.; Mitra, S.K.; Hassanizadeh, S.M. Reservoir-on-a-Chip (ROC): A New Paradigm in Reservoir Engineering. Lab A Chip 2011, 11, 3785–3792. [Google Scholar] [CrossRef]
- Auset, M.; Keller, A.A. Pore-scale Processes That Control Dispersion of Colloids in Saturated Porous Media. Water Resour. Res. 2004, 40, 3. [Google Scholar] [CrossRef]
- Kolliopoulos, P.; Jochem, K.S.; Lade, R.K., Jr.; Francis, L.F.; Kumar, S. Capillary Flow with Evaporation in Open Rectangular Microchannels. Langmuir 2019, 35, 8131–8143. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lei, Z.; Sun, L.; Pan, X.; Liu, Y.; Xu, Z.; Zheng, X.; Wang, Y.; Liu, P. Study on the Minimum Miscibility Pressure and Phase Behavior of CO2–Shale Oil in Nanopores. Chem. Eng. J. 2024, 497, 154493. [Google Scholar] [CrossRef]
- Pan, X.; Sun, L.; Chen, F.; Huo, X.; Wang, Y.; Feng, C.; Zheng, X.; Zhang, Z. Minimum Miscibility Pressure of the CO2-Hydrocarbon System Based on Nanofluidics. Energy Fuels 2024, 38, 10904–10913. [Google Scholar] [CrossRef]
- de Winter, D.A.M.; Weishaupt, K.; Scheller, S.; Frey, S.; Raoof, A.; Hassanizadeh, S.M.; Helmig, R. The Complexity of Porous Media Flow Characterized in a Microfluidic Model Based on Confocal Laser Scanning Microscopy and Micro-PIV. Transp. Porous Media 2021, 136, 343–367. [Google Scholar] [CrossRef]
- Ivanova, A.; Mitiurev, N.; Cheremisin, A.; Orekhov, A.; Kamyshinsky, R.; Vasiliev, A. Characterization of Organic Layer in Oil Carbonate Reservoir Rocks and Its Effect on Microscale Wetting Properties. Sci. Rep. 2019, 9, 10667. [Google Scholar] [CrossRef] [PubMed]
- Jahanbakhsh, A.; Wlodarczyk, K.L.; Hand, D.P.; Maier, R.R.; Maroto-Valer, M.M. Review of Microfluidic Devices and Imaging Techniques for Fluid Flow Study in Porous Geomaterials. Sensors 2020, 20, 4030. [Google Scholar] [CrossRef]
- Teng, X.; Li, F.; Lu, C. Visualization of Materials Using the Confocal Laser Scanning Microscopy Technique. Chem. Soc. Rev. 2020, 49, 2408–2425. [Google Scholar] [CrossRef]
- Cui, S.S.; Li, Z.A.; Sun, X.D.; Liu, X.B. Laser Confocal Scanning Microscope Analysis on Micro-Pore Structures and Occurrence State of Organic Matter in Tight Rocks; Springer: Singapore, 2021; pp. 2995–3006. [Google Scholar]
- Rathnaweera, T.D.; Ranjith, P.G.; Perera, M.S.A.; Haque, A.; Lashin, A.; Al Arifi, N.; Chandrasekharam, D.; Yang, S.-Q.; Xu, T.; Wang, S.H.; et al. CO2-Induced Mechanical Behaviour of Hawkesbury Sandstone in the Gosford Basin: An Experimental Study. Mater. Sci. Eng. A 2015, 641, 123–137. [Google Scholar] [CrossRef]
- Kannan, M. Scanning Electron Microscopy: Principle, Components and Applications. In A Textbook on Fundamentals and Applications of Nanotechnology; Biogreen: Hunter Valley, NSW, Australia, 2018; pp. 81–92. [Google Scholar]
- Li, J.; Jiang, H.; Wang, C.; Zhao, Y.; Gao, Y.; Pei, Y.; Wang, C.; Dong, H. Pore-Scale Investigation of Microscopic Remaining Oil Variation Characteristics in Water-Wet Sandstone Using CT Scanning. J. Nat. Gas Sci. Eng. 2017, 48, 36–45. [Google Scholar] [CrossRef]
- Landis, E.N.; Keane, D.T. X-Ray Microtomography. Mater. Charact. 2010, 61, 1305–1316. [Google Scholar] [CrossRef]
- Jackson, S.J.; Niu, Y.; Manoorkar, S.; Mostaghimi, P.; Armstrong, R.T. Deep Learning of Multiresolution X-Ray Micro-Computed-Tomography Images for Multiscale Modeling. Phys. Rev. Appl. 2022, 17, 054046. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhang, D. RockGPT: Reconstructing Three-Dimensional Digital Rocks from Single Two-Dimensional Slice with Deep Learning. Comput. Geosci. 2022, 26, 677–696. [Google Scholar] [CrossRef]
- Fu, J.; Xiao, D.; Li, D.; Thomas, H.R.; Li, C. Stochastic Reconstruction of 3D Microstructures from 2D Cross-Sectional Images Using Machine Learning-Based Characterization. Comput. Methods Appl. Mech. Eng. 2022, 390, 114532. [Google Scholar] [CrossRef]
- Delpisheh, M.; Ebrahimpour, B.; Fattahi, A.; Siavashi, M.; Mir, H.; Mashhadimoslem, H.; Abdol, M.A.; Ghorbani, M.; Shokri, J.; Niblett, D.; et al. Leveraging Machine Learning in Porous Media. J. Mater. Chem. A 2024, 12, 20717–20782. [Google Scholar] [CrossRef]
- Zhou, L.; Sun, H.; Fan, D.; Zhang, L.; Imani, G.; Fu, S.; Yang, Y.; Zhang, K.; Yao, J. Flow Prediction of Heterogeneous Nanoporous Media Based on Physical Information Neural Network. Gas Sci. Eng. 2024, 125, 205307. [Google Scholar] [CrossRef]
- Alhadri, M.; Raza, J.; Yashkun, U.; Lund, L.A.; Maatki, C.; Khan, S.U.; Kolsi, L. Response Surface Methodology (RSM) and Artificial Neural Network (ANN) Simulations for Thermal Flow Hybrid Nanofluid Flow with Darcy-Forchheimer Effects. J. Indian Chem. Soc. 2022, 99, 100607. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Shoaib, M.; Khan, Z.; Zuhra, S.; Saleel, C.A.; Nisar, K.S.; Islam, S.; Khan, I. Supervised Neural Networks Learning Algorithm for Three Dimensional Hybrid Nanofluid Flow with Radiative Heat and Mass Fluxes. Ain Shams Eng. J. 2022, 13, 101573. [Google Scholar] [CrossRef]
- Ishola, O.; Vilcáez, J. Machine Learning Modeling of Permeability in 3D Heterogeneous Porous Media Using a Novel Stochastic Pore-Scale Simulation Approach. Fuel 2022, 321, 124044. [Google Scholar] [CrossRef]
- Purcell, W.R. Capillary Pressures—Their Measurement Using Mercury and the Calculation of Permeability Therefrom. J. Pet. Technol. 1949, 1, 39–48. [Google Scholar] [CrossRef]
- McNamara, G.R.; Zanetti, G. Use of the Boltzmann Equation to Simulate Lattice-Gas Automata. Phys. Rev. Lett. 1988, 61, 2332. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Øren, P.-E.; Bakke, S.; Arntzen, O.J. Extending Predictive Capabilities to Network Models. SPE J. 1998, 3, 324–336. [Google Scholar] [CrossRef]
- Piri, M.; Blunt, M.J. Three-Dimensional Mixed-Wet Random Pore-Scale Network Modeling of Two-and Three-Phase Flow in Porous Media. II. Results. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2005, 71, 026302. [Google Scholar] [CrossRef]
- Piri, M.; Blunt, M.J. Three-Dimensional Mixed-Wet Random Pore-Scale Network Modeling of Two-and Three-Phase Flow in Porous Media. I. Model Description. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2005, 71, 026301. [Google Scholar] [CrossRef]
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Modelling Two-Phase Flow in Porous Media at the Pore Scale Using the Volume-of-Fluid Method. J. Comput. Phys. 2012, 231, 5653–5668. [Google Scholar] [CrossRef]
- Jettestuen, E.; Helland, J.O.; Prodanović, M. A Level Set Method for Simulating Capillary-controlled Displacements at the Pore Scale with Nonzero Contact Angles. Water Resour. Res. 2013, 49, 4645–4661. [Google Scholar] [CrossRef]
- Ungerer, P.; Lachet, V.; Tavitian, B. Applications of Molecular Simulation in Oil and Gas Production and Processing. Oil Gas Sci. Technol.-Rev. IFP 2006, 61, 387–403. [Google Scholar] [CrossRef]
- Welch, W.R.; Piri, M. Molecular Dynamics Simulations of Retrograde Condensation in Narrow Oil-Wet Nanopores. J. Phys. Chem. C 2015, 119, 10040–10047. [Google Scholar] [CrossRef]
- Didar, B.R.; Akkutlu, I.Y. Pore-Size Dependence of Fluid Phase Behavior and Properties in Organic-Rich Shale Reservoirs. In Proceedings of the SPE: International Symposium on Oilfield Chemistry, The Woodlands, TX, USA, 8−10 April 2013; p. SPE-164099. [Google Scholar]
- Frisch, U.; Hasslacher, B.; Pomeau, Y. Lattice-Gas Automata for the Navier-Stokes Equation. Phys. Rev. Lett. 1986, 56, 1505. [Google Scholar] [CrossRef]
- Rothman, D.H.; Zaleski, S. Lattice-Gas Models of Phase Separation: Interfaces, Phase Transitions, and Multiphase Flow. Rev. Mod. Phys. 1994, 66, 1417. [Google Scholar] [CrossRef]
- Zhu, J.; Ma, J. Extending a Gray Lattice Boltzmann Model for Simulating Fluid Flow in Multi-Scale Porous Media. Sci. Rep. 2018, 8, 5826. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Zhao, T. Lattice Boltzmann Model for Incompressible Flows through Porous Media. Phys. Rev. E 2002, 66, 036304. [Google Scholar] [CrossRef]
- Kang, Q.; Zhang, D.; Lichtner, P.C.; Tsimpanogiannis, I.N. Lattice Boltzmann Model for Crystal Growth from Supersaturated Solution. Geophys. Res. Lett. 2004, 31, 21. [Google Scholar] [CrossRef]
- Asadolahpour, S.R.; Jiang, Z.; Lewis, H.; Chao, M. Deep Learning for Pore-Scale Two-Phase Flow: Modelling Drainage in Realistic Porous Media. Pet. Explor. Dev. 2024, 51, 1301–1315. [Google Scholar] [CrossRef]
- Wang, H.; Su, Y.; Wang, W.; Jin, Z.; Chen, H. CO2-Oil Diffusion, Adsorption and Miscible Flow in Nanoporous Media from Pore-Scale Perspectives. Chem. Eng. J. 2022, 450, 137957. [Google Scholar] [CrossRef]
- Zhang, D.; Li, S.; Li, Y. Lattice Boltzmann Simulation of Three Phase Reactive Flow in Random Porous Media at Pore-Scale. Appl. Therm. Eng. 2021, 194, 117140. [Google Scholar] [CrossRef]
- Mahrous, M.; Curti, E.; Churakov, S.V.; Prasianakis, N.I. Petrophysical Initialization of Core-Scale Reactive Transport Simulations on Indiana Limestones: Pore-Scale Characterization, Spatial Autocorrelations, and Representative Elementary Volume Analysis. J. Pet. Sci. Eng. 2022, 213, 110389. [Google Scholar] [CrossRef]
- Jiang, M.; Xu, Z.; Zhou, Z. Pore-Scale Investigation on Reactive Flow in Porous Media Considering Dissolution and Precipitation by LBM. J. Pet. Sci. Eng. 2021, 204, 108712. [Google Scholar] [CrossRef]
- Wang, H.; Cai, J.; Su, Y.; Jin, Z.; Zhang, M.; Wang, W.; Li, G. Pore-Scale Study on Shale Oil–CO2–Water Miscibility, Competitive Adsorption, and Multiphase Flow Behaviors. Langmuir 2023, 39, 12226–12234. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann Model for Simulating Flows with Multiple Phases and Components. Phys. Rev. E 1993, 47, 1815. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, H. Pore-Scale Modeling of Immiscible Two-Phase Flow in Complex Porous Media. Appl. Therm. Eng. 2016, 93, 1394–1402. [Google Scholar] [CrossRef]
- McDonald, P.; Turner, M. Combining Effective Media and Multi-Phase Methods of Lattice Boltzmann Modelling for the Characterisation of Liquid-Vapour Dynamics in Multi-Length Scale Heterogeneous Structural Materials. Model. Simul. Mater. Sci. Eng. 2015, 24, 015010. [Google Scholar] [CrossRef]
- Ou, Z.; Xue, Q.; Wan, Y.; Wei, H.; Liu, L.; Gharibi, F.; Thévenin, D. A One-Field Fluid/Meso-Structure Coupling Approach for Multiscale Transport in Heterogeneous Porous Media. Phys. Fluids 2024, 36, 113112. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Saeibehrouzi, A.; Abolfathi, S.; Denissenko, P.; Holtzman, R. Pore-Scale Modeling of Solute Transport in Partially-Saturated Porous Media. Earth-Sci. Rev. 2024, 256, 104870. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, J.; Wang, H.; Xia, Y.; Cai, J. Single Phase Flow Simulation in Porous Media by Physical-Informed Unet Network Based on Lattice Boltzmann Method. J. Hydrol. 2024, 639, 131501. [Google Scholar] [CrossRef]
- Wang, D.; Liu, F.; Sun, J.; Li, Y.; Wang, Q.; Jiao, Y.; Song, K.; Wang, S.; Ma, R. Lattice-Boltzmann Simulation of Two-Phase Flow in Carbonate Porous Media Retrieved from Computed Microtomography. Chem. Eng. Sci. 2023, 270, 118514. [Google Scholar] [CrossRef]
- Choi, C.-S.; Lee, Y.-K.; Song, J.-J. Equivalent Pore Channel Model for Fluid Flow in Rock Based on Microscale X-Ray CT Imaging. Materials 2020, 13, 2619. [Google Scholar] [CrossRef]
- Jin, Y. A Pore-Scale Resolved Direct Numerical Simulation Study for Scaling Analysis of the Solutal Convection in Porous Media. J. Fluid Mech. 2024, 1000, A21. [Google Scholar] [CrossRef]
- Hoang, H.; Galliero, G. Local Viscosity of a Fluid Confined in a Narrow Pore. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2012, 86, 021202. [Google Scholar] [CrossRef]
- Zhang, L.; Tan, M.; Liu, X.; Lu, X.; Wang, Q.; Wang, S.; Tian, M.; Wang, J. Insights into Adsorption Behaviors of Multi-Component Shale Oil in Illite Nanopores under Different Reservoir Conditions by Molecular Simulation. Nanomaterials 2025, 15, 235. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Yang, L.; Xiao, P.; Liang, Y.; Hua, X.; Tian, W.; Fang, W.; Liu, B. Molecular Insight into CO2 Improving Oil Mobility in Shale Inorganic Nanopores Containing Water Films. Langmuir 2024, 40, 17568–17576. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Wu, S.; Tian, S.; Huang, D.; Xiong, G.; Luo, T. Molecular-Level Understanding of the Effect of Water on Oil Transport in Graphene Nanochannels. J. Phys. Chem. C 2023, 127, 3671–3681. [Google Scholar] [CrossRef]
- Yu, H.; Chen, J.; Zhu, Y.; Wang, F.; Wu, H. Multiscale Transport Mechanism of Shale Gas in Micro/Nano-Pores. Int. J. Heat Mass Transf. 2017, 111, 1172–1180. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.; Li, J.; Lei, Z.; Xu, J.; Wang, K.; Li, R.; Dong, X.; Peng, Y.; Yang, S.; et al. Nanoconfinement Effect on N-Alkane Flow. J. Phys. Chem. C 2019, 123, 16456–16461. [Google Scholar] [CrossRef]
- Barisik, M.; Beskok, A. Scale Effects in Gas Nano Flows. Phys. Fluids 2014, 26, 052003. [Google Scholar] [CrossRef]
- Hoang, H.; Galliero, G. Shear Viscosity of Inhomogeneous Fluids. J. Chem. Phys. 2012, 136, 124902. [Google Scholar] [CrossRef]
- Chen, G.; Liu, Z. Effect of Modification on the Fluid Diffusion Coefficient in Silica Nanochannels. Molecules 2021, 26, 4030. [Google Scholar] [CrossRef]
- Xiong, H.; Devegowda, D.; Huang, L. Water Bridges in Clay Nanopores: Mechanisms of Formation and Impact on Hydrocarbon Transport. Langmuir 2020, 36, 723–733. [Google Scholar] [CrossRef]
- Babu, J.S.; Sathian, S.P. The Role of Activation Energy and Reduced Viscosity on the Enhancement of Water Flow through Carbon Nanotubes. J. Chem. Phys. 2011, 134, 194509. [Google Scholar] [CrossRef]
- Köhler, M.H.; da Silva, L.B. Size Effects and the Role of Density on the Viscosity of Water Confined in Carbon Nanotubes. Chem. Phys. Lett. 2016, 645, 38–41. [Google Scholar] [CrossRef]
- Alexiadis, A.; Kassinos, S. Molecular Simulation of Water in Carbon Nanotubes. Chem. Rev. 2008, 108, 5014–5034. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Ye, H.; Zheng, Y.; Zhang, Z. Prediction of the Viscosity of Water Confined in Carbon Nanotubes. Microfluid. Nanofluid. 2011, 10, 403–414. [Google Scholar] [CrossRef]
- Ghorbanian, J.; Beskok, A. Scale Effects in Nano-Channel Liquid Flows. Microfluid. Nanofluid. 2016, 20, 121. [Google Scholar] [CrossRef]
- Sendner, C.; Horinek, D.; Bocquet, L.; Netz, R.R. Interfacial Water at Hydrophobic and Hydrophilic Surfaces: Slip, Viscosity, and Diffusion. Langmuir 2009, 25, 10768–10781. [Google Scholar] [CrossRef]
- Bakli, C.; Chakraborty, S. Slippery to Sticky Transition of Hydrophobic Nanochannels. Nano Lett. 2015, 15, 7497–7502. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.; Xu, J.; Hu, Y.; Li, J.; Dong, X.; Liu, Y.; Chen, M. A Universal Model of Water Flow Through Nanopores in Unconventional Reservoirs: Relationships Between Slip, Wettability and Viscosity; SPE: Dubai, United Arab Emirates, 2016; p. D021S027R009. [Google Scholar]
- Kobayashi, Y.; Arai, N.; Yasuoka, K. Correlation between Ordering and Shear Thinning in Confined OMCTS Liquids. J. Chem. Phys. 2022, 157, 114506. [Google Scholar] [CrossRef]
- Liu, H.; Xiong, H.; Yu, H.; Wu, K. Effect of Water Behaviour on the Oil Transport in Illite Nanopores: Insights from a Molecular Dynamics Study. J. Mol. Liq. 2022, 354, 118854. [Google Scholar] [CrossRef]
- Xie, Q.; Alibakhshi, M.A.; Jiao, S.; Xu, Z.; Hempel, M.; Kong, J.; Park, H.G.; Duan, C. Fast Water Transport in Graphene Nanofluidic Channels. Nat. Nanotechnol. 2018, 13, 238–245. [Google Scholar] [CrossRef]
- Li, Y.; Xu, J.; Li, D. Molecular Dynamics Simulation of Nanoscale Liquid Flows. Microfluid. Nanofluid. 2010, 9, 1011–1031. [Google Scholar] [CrossRef]
- Nazari, M.; Davoodabadi, A.; Huang, D.; Luo, T.; Ghasemi, H. Transport Phenomena in Nano/Molecular Confinements. ACS Nano 2020, 14, 16348–16391. [Google Scholar] [CrossRef]
- Abdelrazik, A.; Sayed, M.A.; Omar, A.M.; FM, F.A.; Alshimaa, H.; Oulguidoum, A.; Kotob, E.; Helmy, M.H. Potential of Molecular Dynamics in the Simulation of Nanofluids Properties and Stability. J. Mol. Liq. 2023, 381, 121757. [Google Scholar] [CrossRef]



| Kn Value Range | Applicable Models |
|---|---|
| Kn < 0.001 | Application of Navier–Stokes equations (for continuous medium flow) |
| 0.001 < Kn < 0.1 | Slip flow needs to be corrected |
| 0.1 < Kn < 10 | Transition flow, Navier–Stokes failure |
| Kn > 10 | Free molecular flow requires molecular dynamics (MD) |
| Scale of Experiment | Fluid Type | Research Content | References |
|---|---|---|---|
| 106 nanopores, pore size 60 nm, microchannel connection (200 μm) | Light crude oil (West Texas Crude), N2, CO2 | CO2, N2 enhanced oil recovery | [74] |
| Glass–silicon–glass structure, pore size 100 nm–10 μm | CO2, n-heptane, pentane–dodecane mixture | CO2 miscibility pressure | [75] |
| Microfluidic chip with 150 nm SiO2 particles in ordered/disordered packing | Propane (C3H8), CO2 | CO2, propane capillary condensation pressure | [76] |
| Single straight-through channel with pore diameter of 250 μm, random pore structure with pore diameter 50–400 μm | CO2, high-salinity brine (4.7 mM NaCl) | CO2 injection efficiency and salt precipitation relationship | [77] |
| Channel depth 88 nm, width 7 μm | Propane (C3H8) | Bubble growth dominant conditions | [78] |
| 20 parallel nanofluidic channels (depth 50 nm, width 5 μm) | Hexane, heptane, octane | Bubble nucleation temperature under 50 nm confinement | [79] |
| Pore depth 9 nm, width 225 nm | Propane (C3H8) | Evaporation pressure | [80] |
| Shale micromodel with pore width 50–400 μm | n-Decane, supercritical CO2, brine | Capillary effect and matrix wettability relationship; fracture roughness and CO2 migration resistance | [81] |
| Fracture width 400–1000 μm, depth 500 μm | n-Decane, supercritical CO2, N2 | Comparison of CO2 and N2 huff-n-puff recovery efficiency | [82] |
| Matrix pores 3–10 μm, microfractures 100–200 μm | n-Decane, deionized water | Residual oil distribution | [83] |
| Nanopores 200 nm–5 μm, microfractures 10–100 μm | Deionized water, isopropanol, fluorescent-labeled oil phase | Flow behavior in microfractures and nanopores | [84] |
| 100 nm macropores, 5 nm throat | Methane–propane–pentane mixture (10%/40%/50%) | Light and heavy hydrocarbon gas release rate under 5 nm throat conditions | [85] |
| Pore size 0.1–1 μm, fracture width 1–1000 μm | 1% HCl, CO2 gas | Differences in fracture and pore structure between high and low carbonate rocks | [86] |
| Research Object | LBM Model | Validation Method | References |
|---|---|---|---|
| Shale/tight oil reservoir | Multiple relaxation time lattice Boltzmann method (MRT-LBM), considering fluid–fluid and fluid–surface interaction forces | 1. Fick’s second law calibration for diffusion; 2. Molecular dynamics (MD) calibration for adsorption; 3. MD calibration for miscible flow rate | [126] |
| Random porous media | Multicomponent multiphase LBM (MCMP-LBM), Shan–Chen interaction force model | 1. Droplet contact angle validation; 2. Reaction–diffusion experiment comparison; 3. Fracture acidizing simulation | [127] |
| Indiana limestone | MRT-LBM combined with μ-CT data, permeability calculation using Darcy’s Law | 1. REV analysis to determine the minimum representative volume; 2. Pore-permeability log-normal distribution validation | [128] |
| Dissolution–precipitation coupled reactive flow in porous media, CO2 geological sequestration | Multicomponent multiphase LBM (MCMP-LBM) coupled with heat-mass transfer model | 1. Poiseuille flow validation; 2. Natural convection experiment comparison; 3. Grid independence analysis | [129] |
| Shale oil–CO2–water multiphase flow behavior, CO2 huff-n-puff process | Improved MCMP-LBM, considering competitive adsorption and interfacial tension | 1. Laplace pressure test; 2. Contact angle calibration; 3. MD calibration for diffusion | [130] |
| Application of LBM in multiphase multicomponent flow simulation, phase change, and interfacial tension | Shan–Chen type multiphase LBM, introducing non-ideal gas state equation | 1. Laplace test; 2. Phase separation simulation; 3. Diffusion coefficient validation | [131] |
| Immiscible two-phase flow in complex porous media | Shan–Chen multiphase LBM, combined with micro-CT reconstructed pore structure | 1. Laplace pressure validation; 2. Wettability experiment comparison; 3. FVM-VOF comparison | [132] |
| Multiscale porous media flow, improved gray LBM | Two-parameter gray LBM, independently controlling effective viscosity and permeability | 1. Darcy–Brinkman equation validation; 2. Velocity profile analysis; 3. Isotropy test | [122] |
| Multiscale heterogeneous material liquid–vapor dynamics | Shan–Chen LBM combined with WBS partial bounce-back method | 1. Maxwell construction validation; 2. Laplace law test; 3. Complex pore experiment comparison | [133] |
| Multiscale transport in heterogeneous porous media | Single-field coupling model, implicitly describing effective parameters for solid influence | 1. DBS method comparison; 2. Scalar transport validation; 3. Isotropy test | [134] |
| Simulation Scale | Model and Research Object | Validation | References |
|---|---|---|---|
| Width W = 5~10σ, NEMD 107 steps | Local average density model (LADM) combined with hard-rod weighting function to study shear flow of fluids in confined pores | NEMD computes shear viscosity, Green–Kubo method calculates local viscosity, error < 5%. | [141] |
| Illite pore diameter 8 nm, shale oil simulation 8 ns | Multicomponent shale oil adsorption layer model to study shale oil adsorption in nanoscale pores | Adsorption layer thickness computed and compared with experiments, 20 MPa methane/octane NPT calculation error 2.47%. | [142] |
| Quartz pore 8 nm, CO2 50% proportion | CO2–oil interface friction reduction model to study CO2 in aqueous film environments | NPT computes octane density, compared with NIST data (0.69 g/cm3), error < 3%. | [143] |
| Graphene channel 50 × 25 × 90 Å3 | Water film-enhanced oil transport model to study the impact of water on oil transport in graphene nanochannels | Compute oil–water interface potential energy distribution, radial distribution function (RDF) analyzes oil–water molecular interaction. | [144] |
| Pore diameter 2 nm~1 mm | Slip/adsorption/surface diffusion transport mechanism study of shale gas transport in micro/nanopores across multiple scales | LBM simulation of apparent permeability, Knudsen number comparison error < 5%. | [145] |
| Pore diameter 2–10 nm, NEMD 2 ns | Study of interfacial and viscous resistance effects on the flow behavior of n-alkanes in nanopores | Field validation (NIST data error < 3%), slip length analysis of different pore flow rate changes. | [146] |
| Channel height 5.4, 54 nm | Knudsen number-dependent transport model to study gas transport in nanochannels | MD computes velocity distribution, DSMC computes Knudsen minimum point location, error < 3%. | [147] |
| Simulation box 18 × 10.5 × 10.5σ | Shear stress and viscosity decomposition model to study local shear viscosity in non-uniform fluids | Shear rate verification of velocity distribution, Green–Kubo computes viscosity, compared with experiments. | [148] |
| 40 Å wide silicon nanochannel, 32.28 × 73.90 × 40.00 Å3 | Einstein relation (MSD) + Green–Kubo formula to calculate diffusion coefficient in silicon nanochannels | MSD and Green–Kubo method calculation of diffusion coefficients are consistent. | [149] |
| Pore size 5, 10, 15 nm | P-H (potassium–hydroxyl structure) and H-H (hydroxyl–hydroxyl structure) pore water bridge formation mechanism to study the role of water bridges in clay nanopores | Compute water bridge interfacial potential energy, PMF calculates hydrocarbon adhesion potential under different pore sizes. | [150] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Du, M.; Zhang, Y.; Chen, X.; Yang, Z. Research Progress on Micro/Nanopore Flow Behavior. Molecules 2025, 30, 1807. https://doi.org/10.3390/molecules30081807
Yu J, Du M, Zhang Y, Chen X, Yang Z. Research Progress on Micro/Nanopore Flow Behavior. Molecules. 2025; 30(8):1807. https://doi.org/10.3390/molecules30081807
Chicago/Turabian StyleYu, Jinbo, Meng Du, Yapu Zhang, Xinliang Chen, and Zhengming Yang. 2025. "Research Progress on Micro/Nanopore Flow Behavior" Molecules 30, no. 8: 1807. https://doi.org/10.3390/molecules30081807
APA StyleYu, J., Du, M., Zhang, Y., Chen, X., & Yang, Z. (2025). Research Progress on Micro/Nanopore Flow Behavior. Molecules, 30(8), 1807. https://doi.org/10.3390/molecules30081807






