Structural Evolution Leading to the Thermosalient Phase Transition of Oxitropium Bromide
Abstract
:1. Introduction
2. Results
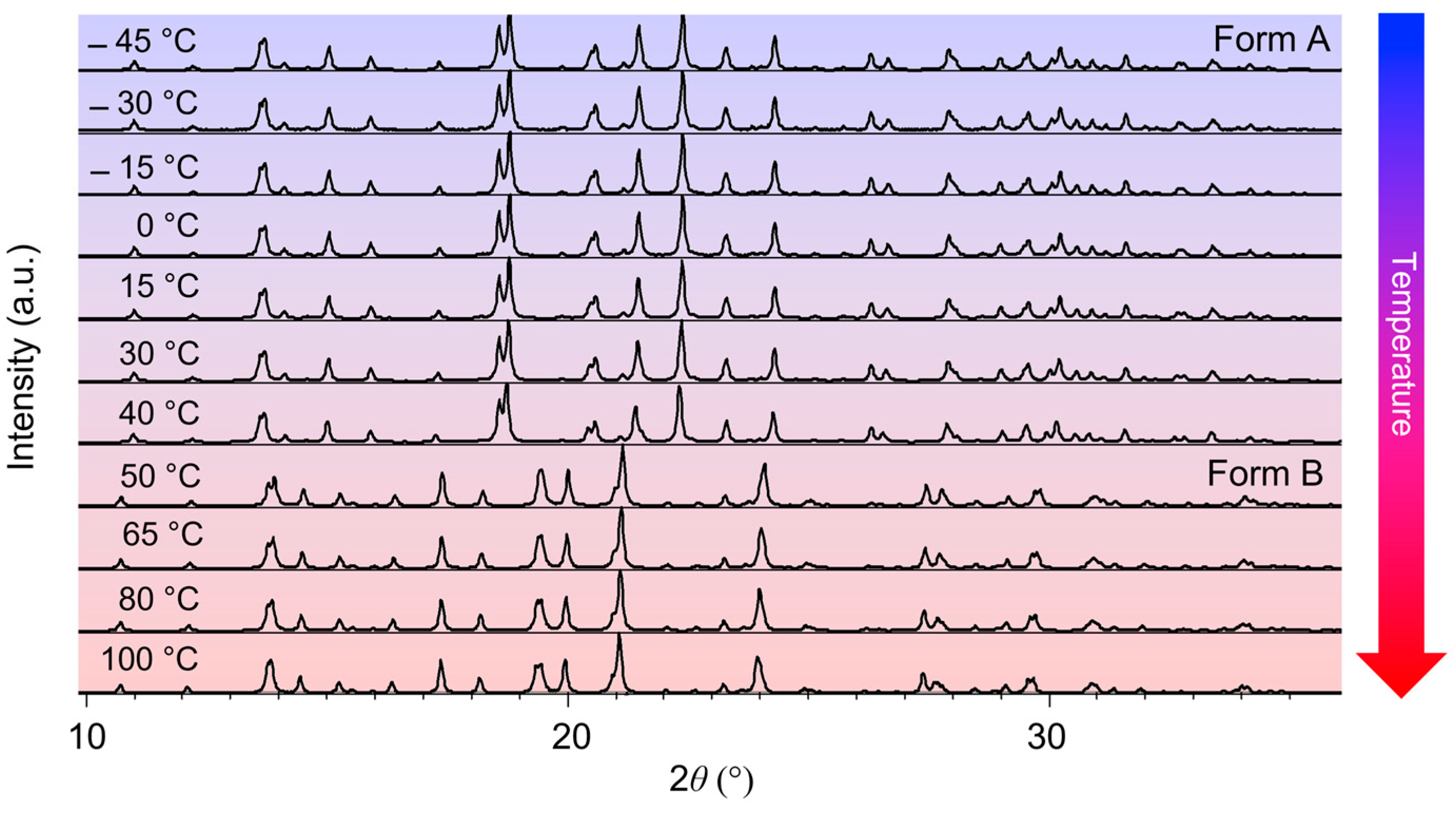
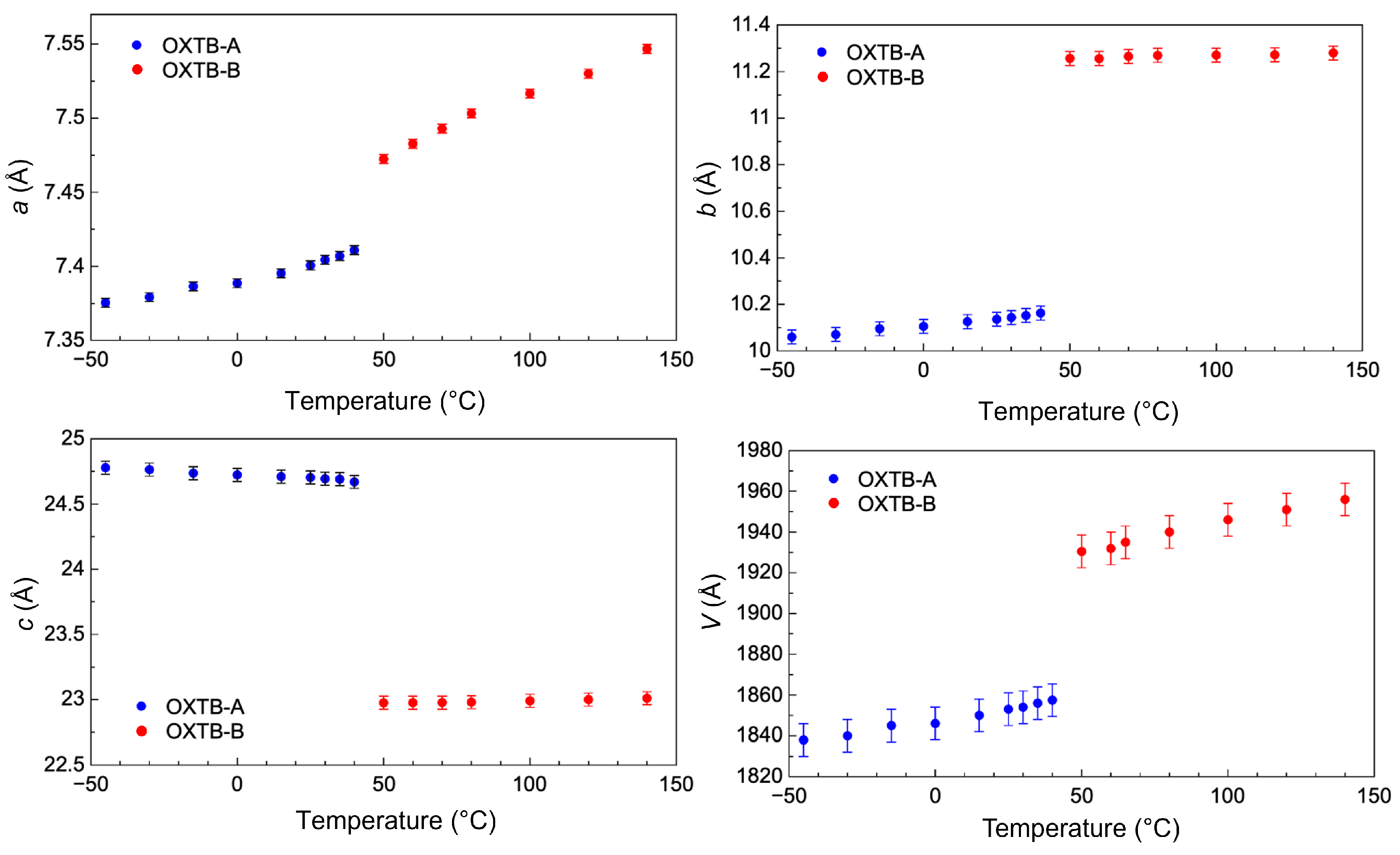
2.1. In Situ Variable-Temperature X-Ray Powder Diffraction
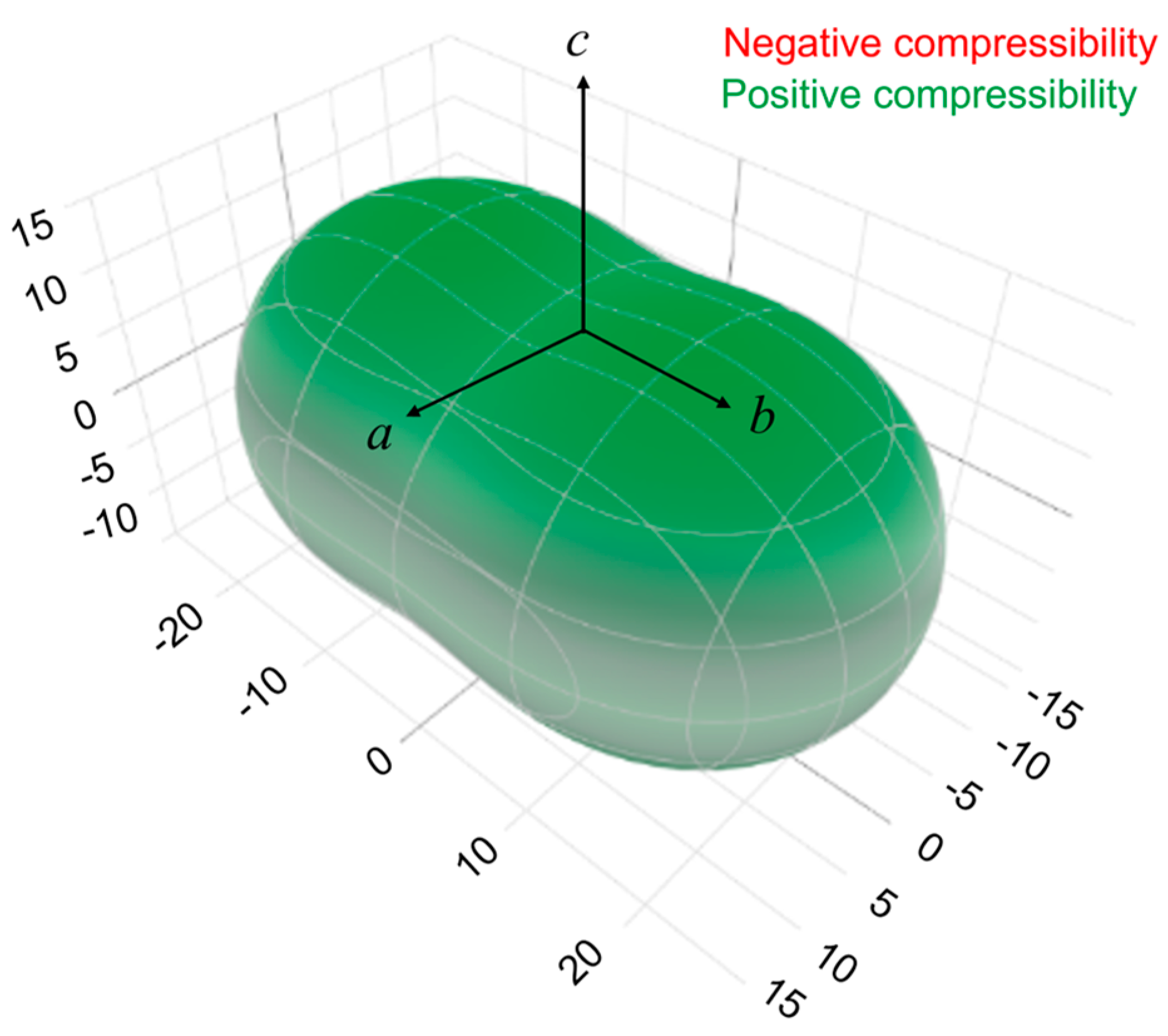
2.2. Elastic Properties of Oxitropium Bromide
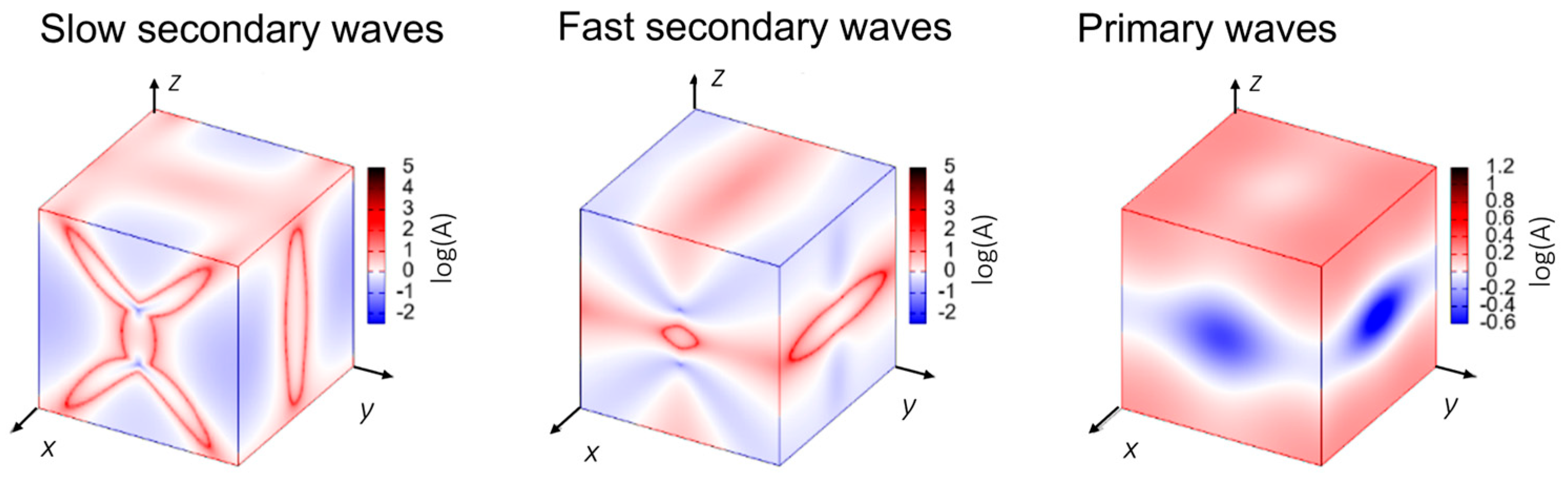
2.3. Sound Propagation and Anisotropy in the Oxitropium Bromide
3. Materials and Methods
3.1. Variable Temperature X-Ray Powder Diffraction
3.2. Density Functional Theory Calculations
3.3. Sound Propagation Studies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Etter, M.C.; Siedle, A.R. Solid-State Rearrangement of (Phenylazophenyl)Palladium Hexafluoroacetylacetonate. J. Am. Chem. Soc. 1983, 105, 641–643. [Google Scholar] [CrossRef]
- Ding, J.; Herbst, R.; Praefcke, K.; Kohne, B.; Saenger, W. A Crystal That Hops in Phase Transition, the Structure of Trans, Trans, Anti, Trans, Trans-perhydropyrene. Acta Crystallogr. Sect. B 1991, 47, 739–742. [Google Scholar] [CrossRef]
- Steiner, T.; Hinrichs, W.; Saenger, W.; Gigg, R. ‘Jumping Crystals’: X-ray Structures of the Three Crystalline Phases of (±)-3,4-di-O-acetyl-1,2,5,6-tetra-O-benzyl-myo-inositol. Acta Crystallogr. Sect. B 1993, 49, 708–718. [Google Scholar] [CrossRef]
- Zamir, S.; Bernstein, J. A Single Crystal to Single Crystal Reversible Phase Transition Which Exhibits the “Hopping Effect”. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A Mol. Cryst. Liq. Cryst. 1994, 242, 193–200. [Google Scholar] [CrossRef]
- Crottaz, O.; Kubel, F.; Schmid, H. Jumping Crystals of the Spinels NiCr2O4 and CuCr2O4. J. Mater. Chem. 1997, 7, 143. [Google Scholar] [CrossRef]
- Lieberman, H.F.; Davey, R.J.; Newsham, D.M.T. Br···Br and Br···H Interactions in Action: Polymorphism, Hopping, and Twinning in 1,2,4,5-Tetrabromobenzene. Chem. Mater. 2000, 12, 490–494. [Google Scholar] [CrossRef]
- Siegrist, T.; Besnard, C.; Haas, S.; Schiltz, M.; Pattison, P.; Chernyshov, D.; Batlogg, B.; Kloc, C. A Polymorph Lost and Found: The High-Temperature Crystal Structure of Pentacene. Adv. Mater. 2007, 19, 2079–2082. [Google Scholar] [CrossRef]
- Skoko, Ž.; Zamir, S.; Naumov, P.; Bernstein, J. The Thermosalient Phenomenon. “Jumping Crystals” and Crystal Chemistry of the Anticholinergic Agent Oxitropium Bromide. J. Am. Chem. Soc. 2010, 132, 14191–14202. [Google Scholar] [CrossRef]
- Sahoo, S.C.; Panda, M.K.; Nath, N.K.; Naumov, P. Biomimetic Crystalline Actuators: Structure-Kinematic Aspects of the Self-Actuation and Motility of Thermosalient Crystals. J. Am. Chem. Soc. 2013, 135, 12241–12251. [Google Scholar] [CrossRef]
- Sahoo, S.C.; Sinha, S.B.; Kiran, M.S.R.N.; Ramamurty, U.; Dericioglu, A.F.; Reddy, C.M.; Naumov, P. Kinematic and Mechanical Profile of the Self-Actuation of Thermosalient Crystal Twins of 1,2,4,5-Tetrabromobenzene: A Molecular Crystalline Analogue of a Bimetallic Strip. J. Am. Chem. Soc. 2013, 135, 13843–13850. [Google Scholar] [CrossRef]
- Lusi, M.; Bernstein, J. On the Propulsion Mechanism of “Jumping” Crystals. Chem. Commun. 2013, 49, 9293. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, S.C.; Nath, N.K.; Zhang, L.; Semreen, M.H.; Al-Tel, T.H.; Naumov, P. Actuation Based on Thermo/Photosalient Effect: A Biogenic Smart Hybrid Driven by Light and Heat. RSC Adv. 2014, 4, 7640. [Google Scholar] [CrossRef]
- Nath, N.K.; Panda, M.K.; Sahoo, S.C.; Naumov, P. Thermally Induced and Photoinduced Mechanical Effects in Molecular Single Crystals—A Revival. CrystEngComm 2014, 16, 1850. [Google Scholar] [CrossRef]
- Panda, M.K.; Runčevski, T.; Chandra Sahoo, S.; Belik, A.A.; Nath, N.K.; Dinnebier, R.E.; Naumov, P. Colossal Positive and Negative Thermal Expansion and Thermosalient Effect in a Pentamorphic Organometallic Martensite. Nat. Commun. 2014, 5, 4811. [Google Scholar] [CrossRef] [PubMed]
- Shima, T.; Muraoka, T.; Hoshino, N.; Akutagawa, T.; Kobayashi, Y.; Kinbara, K. Thermally Driven Polymorphic Transition Prompting a Naked-Eye-Detectable Bending and Straightening Motion of Single Crystals. Angew. Chem.—Int. Ed. 2014, 53, 7173–7178. [Google Scholar] [CrossRef] [PubMed]
- Naumov, P.; Chizhik, S.; Panda, M.K.; Nath, N.K.; Boldyreva, E. Mechanically Responsive Molecular Crystals. Chem. Rev. 2015, 115, 12440–12490. [Google Scholar] [CrossRef]
- Panda, M.K.; Runčevski, T.; Husain, A.; Dinnebier, R.E.; Naumov, P. Perpetually Self-Propelling Chiral Single Crystals. J. Am. Chem. Soc. 2015, 137, 1895–1902. [Google Scholar] [CrossRef]
- Commins, P.; Desta, I.T.; Karothu, D.P.; Panda, M.K.; Naumov, P. Crystals on the Move: Mechanical Effects in Dynamic Solids. Chem. Commun. 2016, 52, 13941–13954. [Google Scholar] [CrossRef] [PubMed]
- Nauha, E.; Naumov, P.; Lusi, M. Fine-Tuning of a Thermosalient Phase Transition by Solid Solutions. CrystEngComm 2016, 18, 4699–4703. [Google Scholar] [CrossRef]
- Panda, M.K.; Centore, R.; Causà, M.; Tuzi, A.; Borbone, F.; Naumov, P. Strong and Anomalous Thermal Expansion Precedes the Thermosalient Effect in Dynamic Molecular Crystals. Sci. Rep. 2016, 6, 29610. [Google Scholar] [CrossRef] [PubMed]
- Karothu, D.P.; Weston, J.; Desta, I.T.; Naumov, P. Shape-Memory and Self-Healing Effects in Mechanosalient Molecular Crystals. J. Am. Chem. Soc. 2016, 138, 13298–13306. [Google Scholar] [CrossRef]
- Khalil, A.; Ahmed, E.; Naumov, P. Metal-Coated Thermosalient Crystals as Electrical Fuses. Chem. Commun. 2017, 53, 8470–8473. [Google Scholar] [CrossRef] [PubMed]
- Lončarić, I.; Popović, J.; Despoja, V.; Burazer, S.; Grgičević, I.; Popović, D.; Skoko, Ž. Reversible Thermosalient Effect of N′-2-Propylidene-4-Hydroxybenzohydrazide Accompanied by an Immense Negative Compressibility: Structural and Theoretical Arguments Aiming toward the Elucidation of Jumping Phenomenon. Cryst. Growth Des. 2017, 17, 4445–4453. [Google Scholar] [CrossRef]
- Panda, M.K.; Etter, M.; Dinnebier, R.E.; Naumov, P. Acoustic Emission from Organic Martensites. Angew. Chem.—Int. Ed. 2017, 56, 8104–8109. [Google Scholar] [CrossRef] [PubMed]
- Tamboli, M.I.; Karothu, D.P.; Shashidhar, M.S.; Gonnade, R.G.; Naumov, P. Effect of Crystal Packing on the Thermosalient Effect of the Pincer-Type Diester Naphthalene-2,3-diyl-bis(4-fluorobenzoate): A New Class II Thermosalient Solid. Chem.—A Eur. J. 2018, 24, 4133–4139. [Google Scholar] [CrossRef]
- Zakharov, B.A.; Michalchuk, A.A.L.; Morrison, C.A.; Boldyreva, E.V. Anisotropic Lattice Softening near the Structural Phase Transition in the Thermosalient Crystal 1,2,4,5-Tetrabromobenzene. Phys. Chem. Chem. Phys. 2018, 20, 8523–8532. [Google Scholar] [CrossRef]
- Alimi, L.O.; van Heerden, D.P.; Lama, P.; Smith, V.J.; Barbour, L.J. Reversible Thermosalience of 4-Aminobenzonitrile. Chem. Commun. 2018, 54, 6208–6211. [Google Scholar] [CrossRef] [PubMed]
- Janiak, A.; Esterhuysen, C.; Barbour, L.J. A Thermo-Responsive Structural Switch and Colossal Anisotropic Thermal Expansion in a Chiral Organic Solid. Chem. Commun. 2018, 54, 3727–3730. [Google Scholar] [CrossRef]
- Klaser, T.; Popović, J.; Fernandes, J.A.; Tarantino, S.C.; Zema, M.; Skoko, Ž. Does Thermosalient Effect Have to Concur with a Polymorphic Phase Transition? The Case of Methscopolamine Bromide. Crystals 2018, 8, 301. [Google Scholar] [CrossRef]
- Kamo, Y.; Nagaya, I.; Sugino, R.; Hagiwara, H. Jumping Crystals of Stacked Planar Cobalt Complexes: Thermosalient Effect Promoted by Hydrogen-Bonded Lattice Solvent Release. Chem. Lett. 2019, 48, 1077–1080. [Google Scholar] [CrossRef]
- Takeda, T.; Ozawa, M.; Akutagawa, T. Jumping Crystal of a Hydrogen-Bonded Organic Framework Induced by the Collective Molecular Motion of a Twisted π System. Angew. Chem. Int. Ed. 2019, 58, 10345–10352. [Google Scholar] [CrossRef]
- Zaczek, A.J.; Catalano, L.; Naumov, P.; Korter, T.M. Mapping the Polymorphic Transformation Gateway Vibration in Crystalline 1,2,4,5-Tetrabromobenzene. Chem. Sci. 2019, 10, 1332–1341. [Google Scholar] [CrossRef]
- Seki, T.; Mashimo, T.; Ito, H. Anisotropic Strain Release in a Thermosalient Crystal: Correlation between the Microscopic Orientation of Molecular Rearrangements and the Macroscopic Mechanical Motion. Chem. Sci. 2019, 10, 4185–4191. [Google Scholar] [CrossRef]
- Duan, Y.; Semin, S.; Tinnemans, P.; Cuppen, H.; Xu, J.; Rasing, T. Robust Thermoelastic Microactuator Based on an Organic Molecular Crystal. Nat. Commun. 2019, 10, 4573. [Google Scholar] [CrossRef] [PubMed]
- Colin-Molina, A.; Karothu, D.P.; Jellen, M.J.; Toscano, R.A.; Garcia-Garibay, M.A.; Naumov, P.; Rodríguez-Molina, B. Thermosalient Amphidynamic Molecular Machines: Motion at the Molecular and Macroscopic Scales. Matter 2019, 1, 1033–1046. [Google Scholar] [CrossRef]
- Seki, T.; Mashimo, T.; Ito, H. Crystal Jumping of Simple Hydrocarbons: Cooling-Induced Salient Effect of Bis-, Tri-, and Tetraphenylethene through Anisotropic Lattice Dimension Changes without Thermal Phase Transitions. Chem. Lett. 2020, 49, 174–177. [Google Scholar] [CrossRef]
- Omoto, K.; Nakae, T.; Nishio, M.; Yamanoi, Y.; Kasai, H.; Nishibori, E.; Mashimo, T.; Seki, T.; Ito, H.; Nakamura, K.; et al. Thermosalience in Macrocycle-Based Soft Crystals via Anisotropic Deformation of Disilanyl Architecture. J. Am. Chem. Soc. 2020, 142, 12651–12657. [Google Scholar] [CrossRef]
- Naumov, P.; Karothu, D.P.; Ahmed, E.; Catalano, L.; Commins, P.; Mahmoud Halabi, J.; Al-Handawi, M.B.; Li, L. The Rise of the Dynamic Crystals. J. Am. Chem. Soc. 2020, 142, 13256–13272. [Google Scholar] [CrossRef] [PubMed]
- Mei, L.; An, S.; Hu, K.; Wang, L.; Yu, J.; Huang, Z.; Kong, X.; Xia, C.; Chai, Z.; Shi, W. Molecular Spring-like Triple-Helix Coordination Polymers as Dual-Stress and Thermally Responsive Crystalline Metal–Organic Materials. Angew. Chem. Int. Ed. 2020, 59, 16061–16068. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Semin, S.; Tinnemans, P.; Xu, J.; Rasing, T. Fully Controllable Structural Phase Transition in Thermomechanical Molecular Crystals with a Very Small Thermal Hysteresis. Small 2021, 17, 2006757. [Google Scholar] [CrossRef] [PubMed]
- Rath, B.B.; Gallo, G.; Dinnebier, R.E.; Vittal, J.J. Reversible Thermosalience in a One-Dimensional Coordination Polymer Preceded by Anisotropic Thermal Expansion and the Shape Memory Effect. J. Am. Chem. Soc. 2021, 143, 2088–2096. [Google Scholar] [CrossRef] [PubMed]
- Karothu, D.P.; Naumov, P. Thermosalience of 1,2,4,5-Tetrachlorobenzene. Isr. J. Chem. 2021, 61, 557–562. [Google Scholar] [CrossRef]
- Dharmarwardana, M.; Pakhira, S.; Welch, R.P.; Caicedo-Narvaez, C.; Luzuriaga, M.A.; Arimilli, B.S.; McCandless, G.T.; Fahimi, B.; Mendoza-Cortes, J.L.; Gassensmith, J.J. Rapidly Reversible Organic Crystalline Switch for Conversion of Heat into Mechanical Energy. J. Am. Chem. Soc. 2021, 143, 5951–5957. [Google Scholar] [CrossRef]
- Mahmoud Halabi, J.; Séguy, I.; Salvagnac, L.; Leïchlé, T.; Saya, D.; Mathieu, F.; Duployer, B.; Karothu, D.P.; Nicu, L.; Naumov, P. Microelectromechanical Devices Driven by Thermosalient Effects. Cell Rep. Phys. Sci. 2022, 3, 101133. [Google Scholar] [CrossRef]
- Zheng, Y.; Jia, X.; Li, K.; Xu, J.; Bu, X.H. Energy Conversion in Single-Crystal-to-Single-Crystal Phase Transition Materials. Adv. Energy Mater. 2022, 12, 202100324. [Google Scholar] [CrossRef]
- Takazawa, K.; Inoue, J.; Matsushita, Y. Repeatable Actuations of Organic Single Crystal Fibers Driven by Thermosalient-Phase-Transition-Induced Buckling. Small 2022, 18, e2204500. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Xiao, Y.; Qi, L.; Bai, Y.; Sun, Y.; Ye, Y.; Xie, C. An Attempt to Design Thermosalient Crystals by Co-Crystallization: The Twisted Angle between Aromatic Rings. Crystals 2023, 13, 701. [Google Scholar] [CrossRef]
- Masuda, S.; Kusumoto, S.; Okamura, M.; Hikichi, S.; Tokunaga, R.; Hayami, S.; Kim, Y.; Koide, Y. Thermosalient Effect of a Naphthalene Diimide and Tetrachlorocobaltate Hybrid and Changes of Color and Magnetic Properties by Ammonia Vapor. Dalton Trans. 2023, 52, 10531–10536. [Google Scholar] [CrossRef]
- Di, Q.; Al-Handawi, M.B.; Li, L.; Naumov, P.; Zhang, H. A Thermosalient and Mechanically Compliant Organic Crystalline Optical Waveguide Switcher. Angew. Chem. Int. Ed. 2024, 63, e202403914. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.A.; Martín, R.; Gámez-Valenzuela, S.; Echeverri, M.; Ruiz Delgado, M.C.; Gutiérrez Puebla, E.; Monge, A.; Gómez-Lor, B. Giant Thermosalient Effect in a Molecular Single Crystal: Dynamic Transformations and Mechanistic Insights. J. Am. Chem. Soc. 2024, 146, 27690–27700. [Google Scholar] [CrossRef]
- Ghasemlou, S.; Li, X.; Galimberti, D.R.; Nikitin, T.; Fausto, R.; Xu, J.; Holleman, S.; Rasing, T.; Cuppen, H.M. Identifying and Controlling the Order Parameter for Ultrafast Photoinduced Phase Transitions in Thermosalient Materials. Proc. Natl. Acad. Sci. USA 2024, 121, e2408366121. [Google Scholar] [CrossRef]
- Harsha, P.; Das, D. Bidirectional Strain Release in a Thermosalient Organic Salt Crystal Induced by Anisotropic Thermal Expansion and Phase Transformation. Chem. Commun. 2024, 60, 14105–14108. [Google Scholar] [CrossRef] [PubMed]
- Mladineo, B.; Lončarić, I. Thermosalient Phase Transitions from Machine Learning Interatomic Potential. Cryst. Growth Des. 2024, 24, 8167–8173. [Google Scholar] [CrossRef]
- Ragan, A.N.; Kraemer, Y.; Chaudhary, S.K.; Fonoti, O.J.; Cook, C.; Liu, G.; Trapp, N.; Koski, K.J.; Pitts, C.R. Tetrafluoro(Aryl)Sulfanylated Bicyclopentane Crystals That Self-Destruct upon Cooling. J. Am. Chem. Soc. 2025, 147, 1463–1473. [Google Scholar] [CrossRef] [PubMed]
- Shi, R.; Wang, Z.; Cheng, P.; Zheng, Y.; Xu, J. Side Chain Vibration Triggers the Thermosalient Effect in an Organic Crystal of Asymmetric Fluorenone Derivatives. Cryst. Growth Des. 2025, 25, 30–37. [Google Scholar] [CrossRef]
- Ghosh, S.; Mishra, M.K.; Ganguly, S.; Desiraju, G.R. Dual Stress and Thermally Driven Mechanical Properties of the Same Organic Crystal: 2,6-Dichlorobenzylidene-4-Fluoro-3-Nitroaniline. J. Am. Chem. Soc. 2015, 137, 9912. [Google Scholar] [CrossRef]
- Spackman, P.R.; Grosjean, A.; Thomas, S.P.; Karothu, D.P.; Naumov, P.; Spackman, M.A. Quantifying Mechanical Properties of Molecular Crystals: A Critical Overview of Experimental Elastic Tensors. Angew. Chem. Int. Ed. 2022, 61, e202110716. [Google Scholar] [CrossRef]
- Karothu, D.P.; Mahmoud Halabi, J.; Ahmed, E.; Ferreira, R.; Spackman, P.R.; Spackman, M.A.; Naumov, P. Global Analysis of the Mechanical Properties of Organic Crystals. Angew. Chem. Int. Ed. 2022, 61, e202113988. [Google Scholar] [CrossRef] [PubMed]
- Jaeken, J.W.; Cottenier, S. Solving the Christoffel Equation: Phase and Group Velocities. Comput. Phys. Commun. 2016, 207, 445–451. [Google Scholar] [CrossRef]
- Ross, R.B. Metallic Materials Specification Handbook; Springer: Boston, MA, USA, 1992; ISBN 978-0-412-36940-7. [Google Scholar]
- Kube, C.M. Elastic Anisotropy of Crystals. AIP Adv. 2016, 6, 095209. [Google Scholar] [CrossRef]
- Cliffe, M.J.; Goodwin, A.L. IUCr PASCal: A Principal Axis Strain Calculator for Thermal Expansion and Compressibility Determination. J. Appl. Crystallogr. 2012, 45, 1321–1329. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Garrity, K.F.; Bennett, J.W.; Rabe, K.M.; Vanderbilt, D. Pseudopotentials for High-Throughput DFT Calculations. Comput. Mater Sci. 2014, 81, 446–452. [Google Scholar] [CrossRef]
- Berland, K.; Cooper, V.R.; Lee, K.; Schröder, E.; Thonhauser, T.; Hyldgaard, P.; Lundqvist, B.I. Van Der Waals Forces in Density Functional Theory: A Review of the VdW-DF Method. Rep. Prog. Phys. 2015, 78, 066501. [Google Scholar] [CrossRef]
- Sun, D.; Kim, D.-H.; Le, D.; Borck, Ø.; Berland, K.; Kim, K.; Lu, W.; Zhu, Y.; Luo, M.; Wyrick, J.; et al. Publisher’s Note: Effective Elastic Properties of a van Der Waals Molecular Monolayer at a Metal Surface. Phys. Rev. B 2010, 82, 239903, Erratum in Phys. Rev. B 2010, 82, 201410. [Google Scholar] [CrossRef]
- Dal Corso, A. Elastic Constants of Beryllium: A First-Principles Investigation. J. Phys. Condens. Matter 2016, 28, 075401. [Google Scholar] [CrossRef] [PubMed]






| Component of xi Along the Crystallographic Axes | ||||
|---|---|---|---|---|
| Principal Axis, i | ) for Form A | a | b | c |
| 1 | −47 (2) | 0 | 0 | 1 |
| 2 | 55 (3) | 1 | 0 | 0 |
| 3 | 117 (4) | 0 | 1 | 0 |
| Component of xi Along the Crystallographic Axes | ||||
|---|---|---|---|---|
| Principal Axis, i | ) for Form A | a | b | c |
| 1 | 21 (3) | 0 | 1 | 0 |
| 2 | 18 (1) | 0 | 0 | 1 |
| 3 | 104 (4) | 1 | 0 | 0 |
| Component of xi Along the Crystallographic Axes | ||||
|---|---|---|---|---|
| Principal Axis, i | Ki (TPa−1) for Form A | a | b | c |
| 1 | 15.8 | 1 | 0 | 0 |
| 2 | 26.2 | 0 | 1 | 0 |
| 3 | 12.9 | 0 | 0 | 1 |
| Anisotropy Parameters | |||
|---|---|---|---|
| AL | AU | AC | |
| Form A | 0.20945 | 0.52453 | 0.045754 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klaser, T.; Popović, J.; Lončarić, I.; Skoko, Ž. Structural Evolution Leading to the Thermosalient Phase Transition of Oxitropium Bromide. Molecules 2025, 30, 1107. https://doi.org/10.3390/molecules30051107
Klaser T, Popović J, Lončarić I, Skoko Ž. Structural Evolution Leading to the Thermosalient Phase Transition of Oxitropium Bromide. Molecules. 2025; 30(5):1107. https://doi.org/10.3390/molecules30051107
Chicago/Turabian StyleKlaser, Teodoro, Jasminka Popović, Ivor Lončarić, and Željko Skoko. 2025. "Structural Evolution Leading to the Thermosalient Phase Transition of Oxitropium Bromide" Molecules 30, no. 5: 1107. https://doi.org/10.3390/molecules30051107
APA StyleKlaser, T., Popović, J., Lončarić, I., & Skoko, Ž. (2025). Structural Evolution Leading to the Thermosalient Phase Transition of Oxitropium Bromide. Molecules, 30(5), 1107. https://doi.org/10.3390/molecules30051107








