Identifying Inhibitor-SARS-CoV2-3CLpro Binding Mechanism Through Molecular Docking, GaMD Simulations, Correlation Network Analysis and MM-GBSA Calculations
Abstract
1. Introduction
2. Results
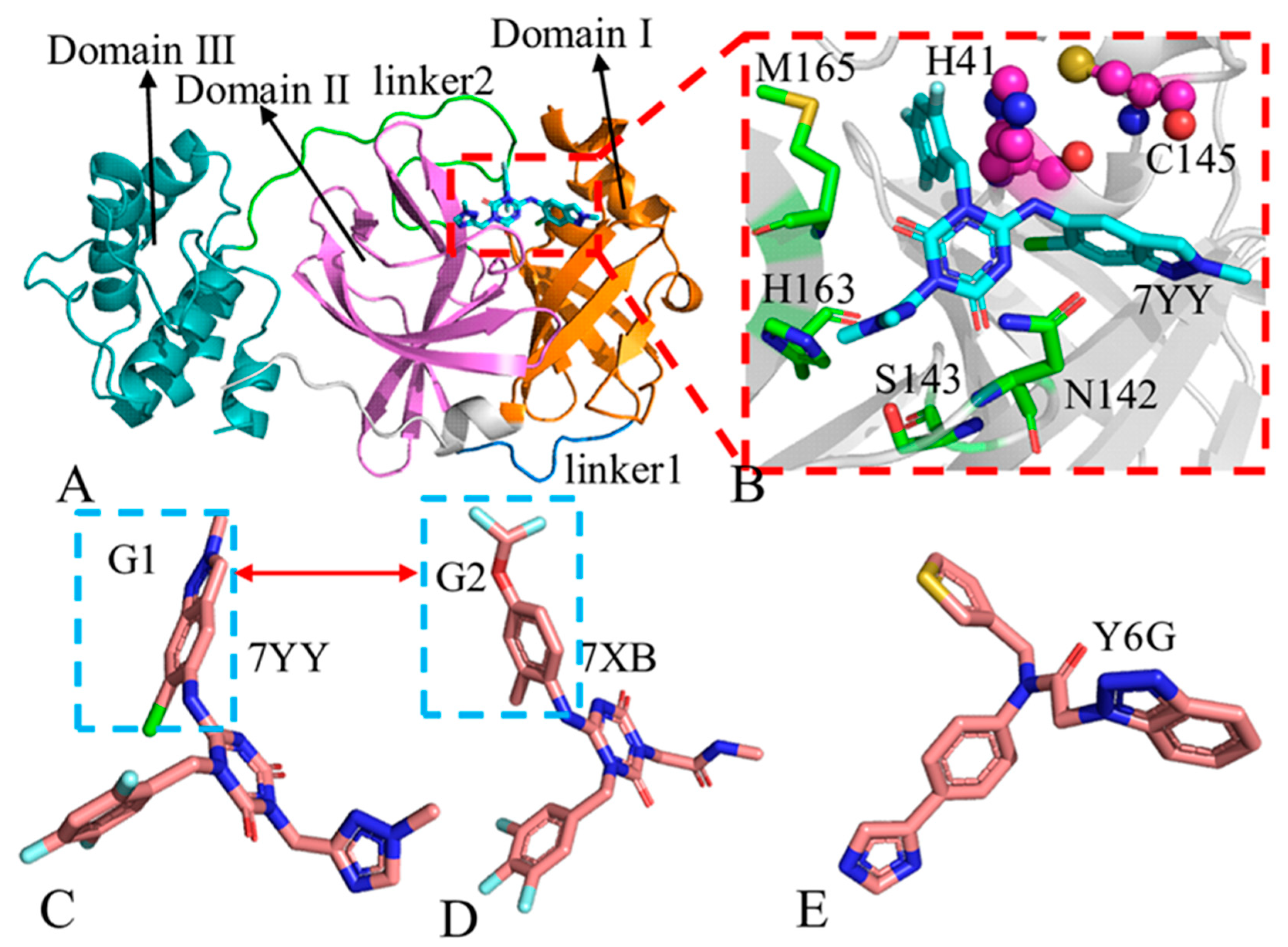
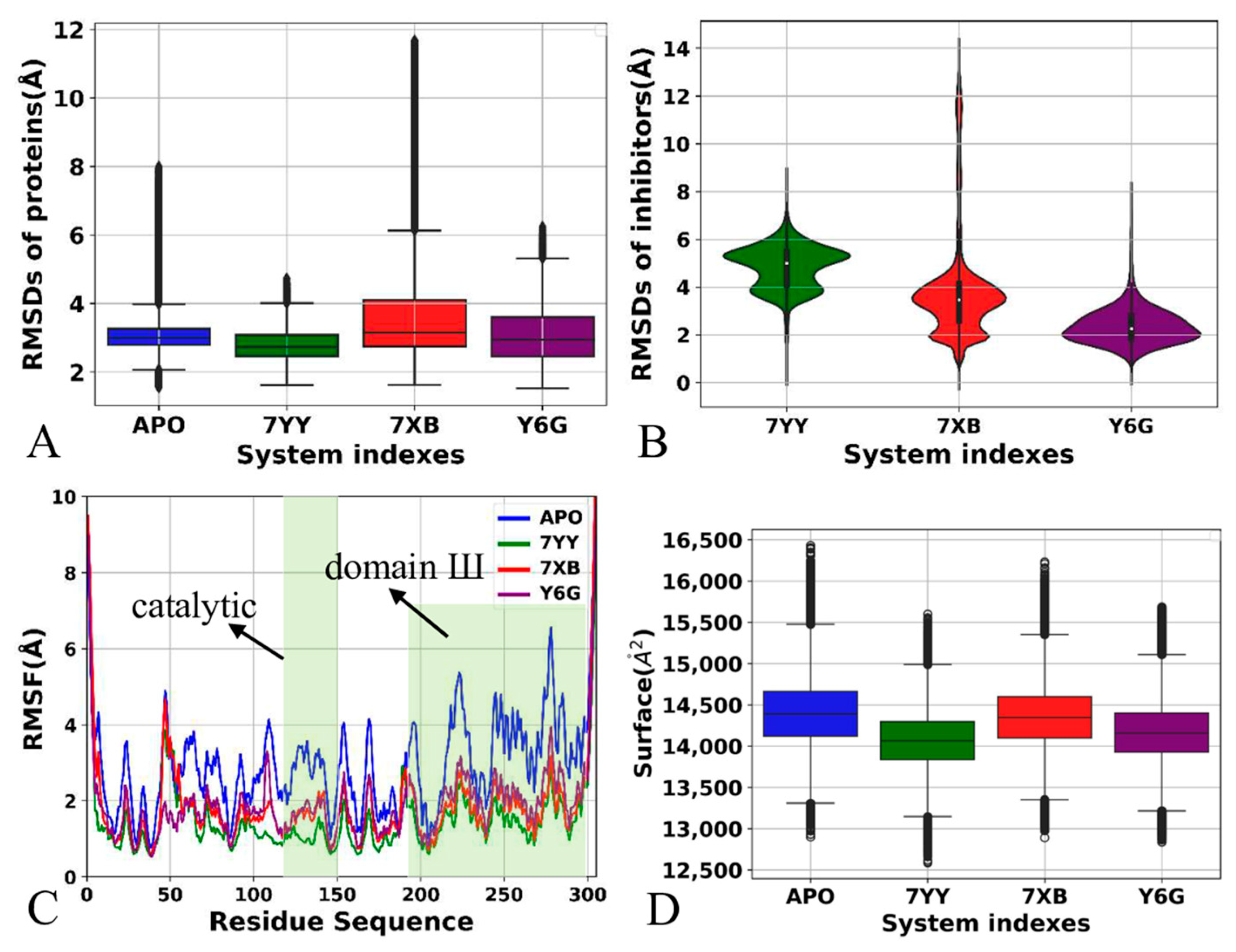
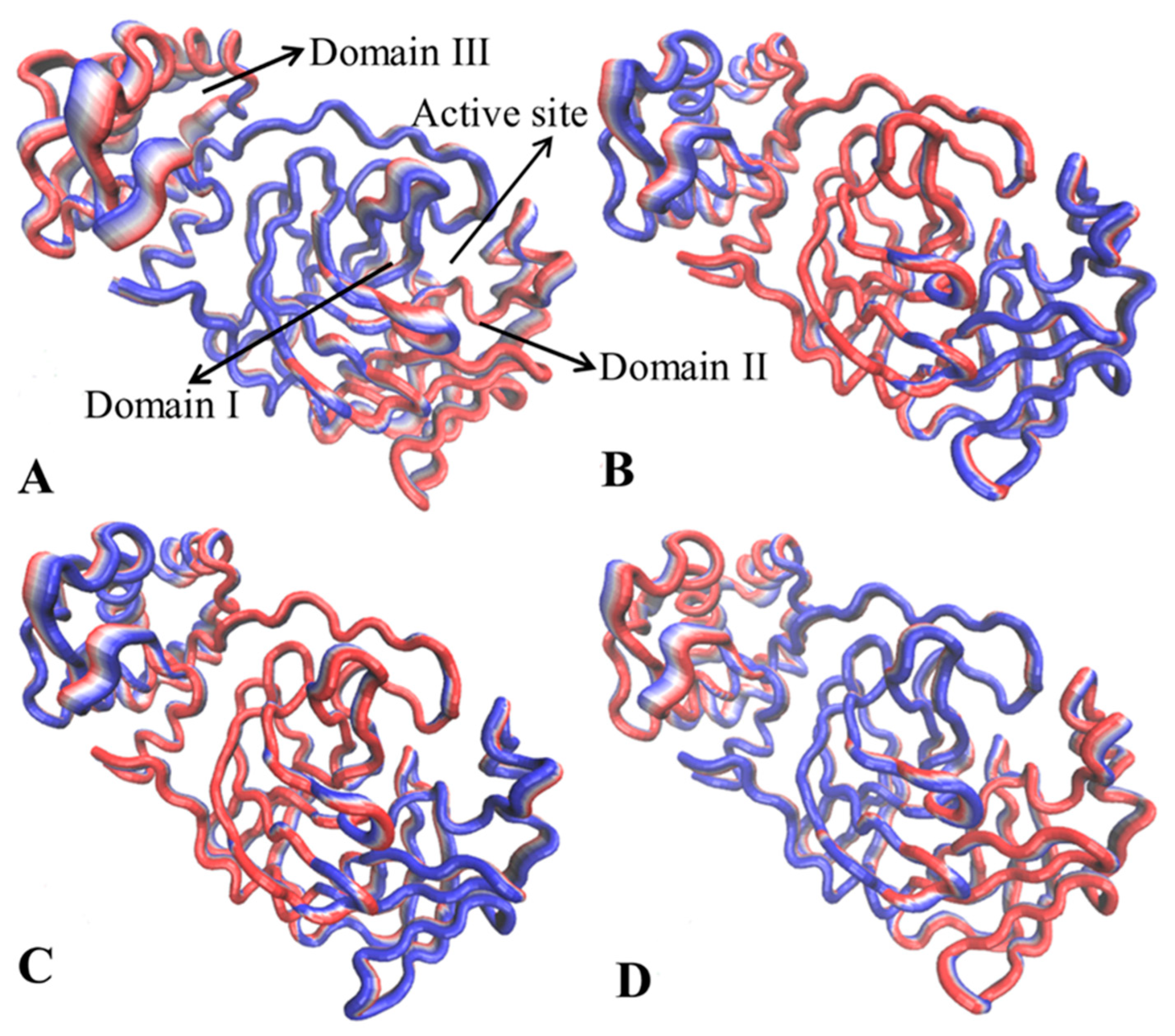
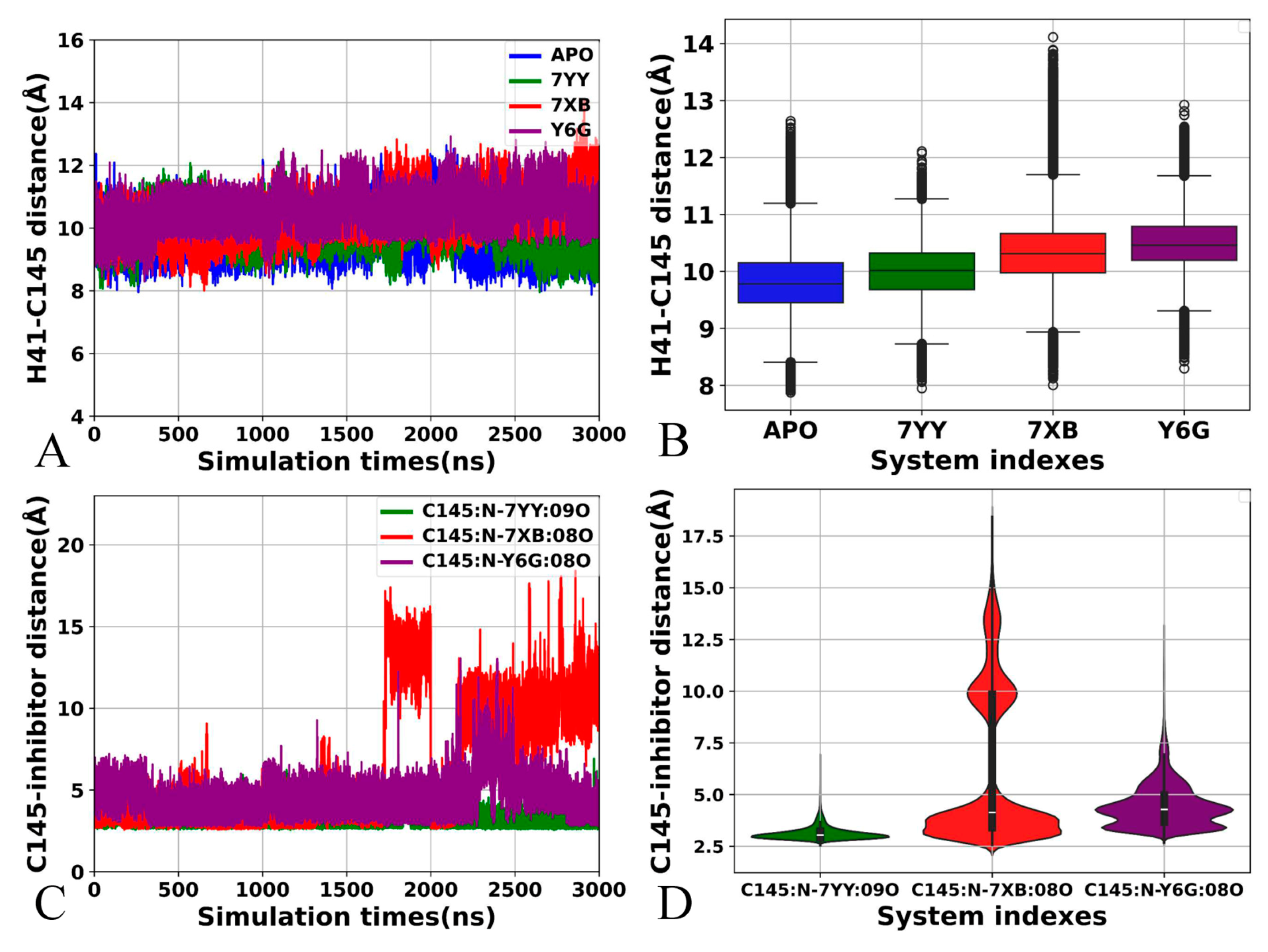
2.1. Structural Properties of 3CLpro Revealed by GaMD Simulations
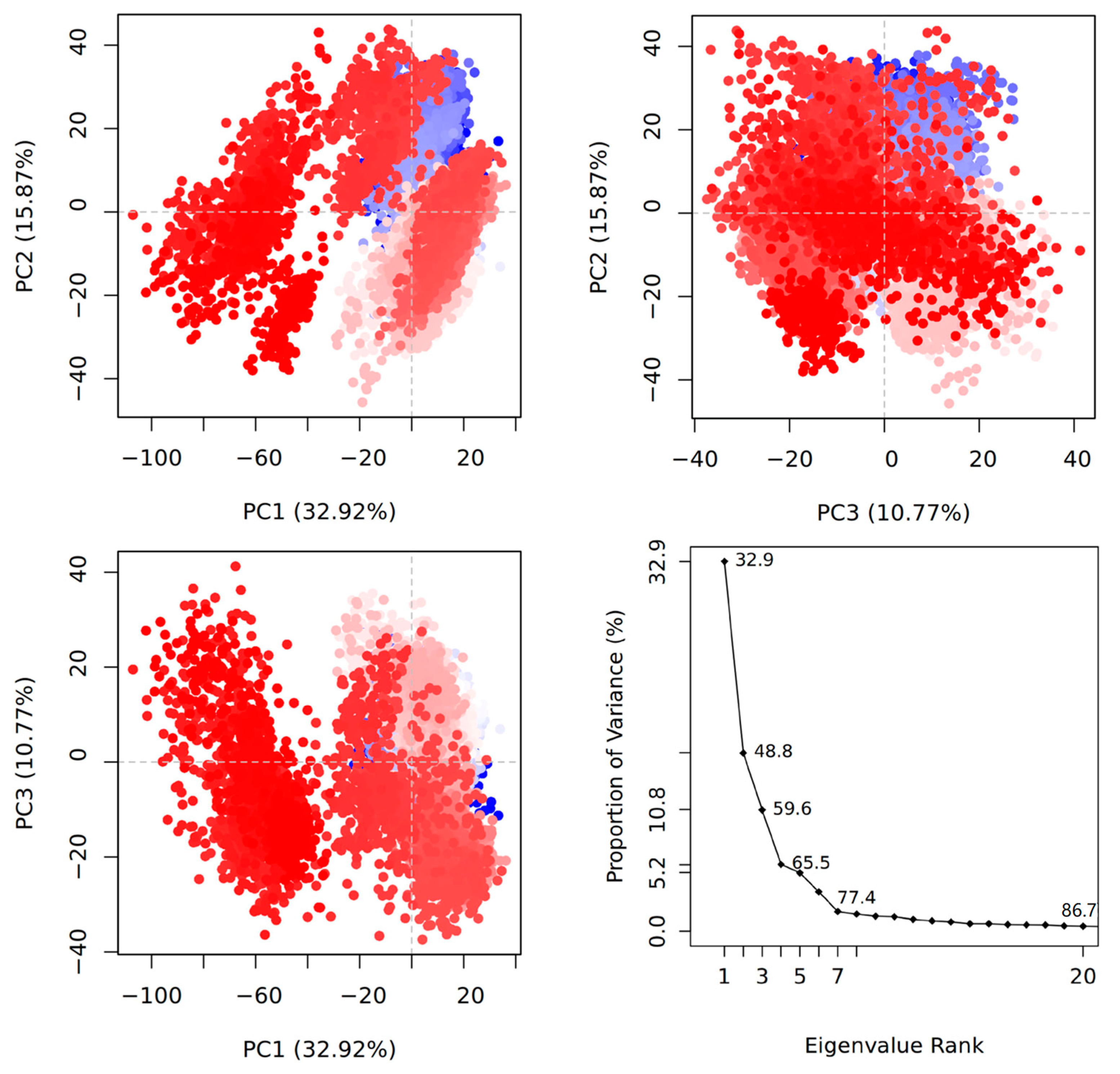
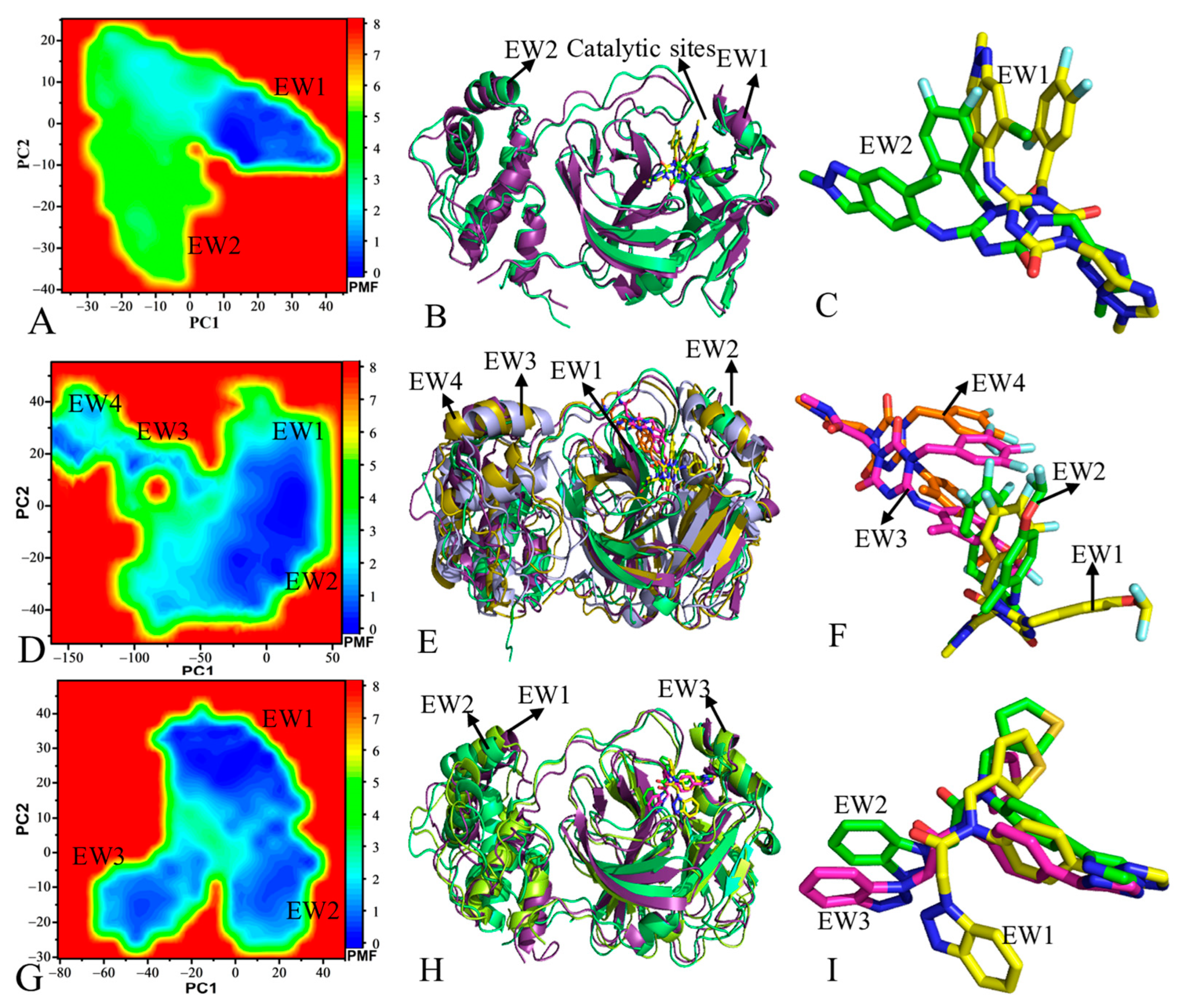
2.2. Principal Component Analysis and Free Energy Profiles of 3CLpro
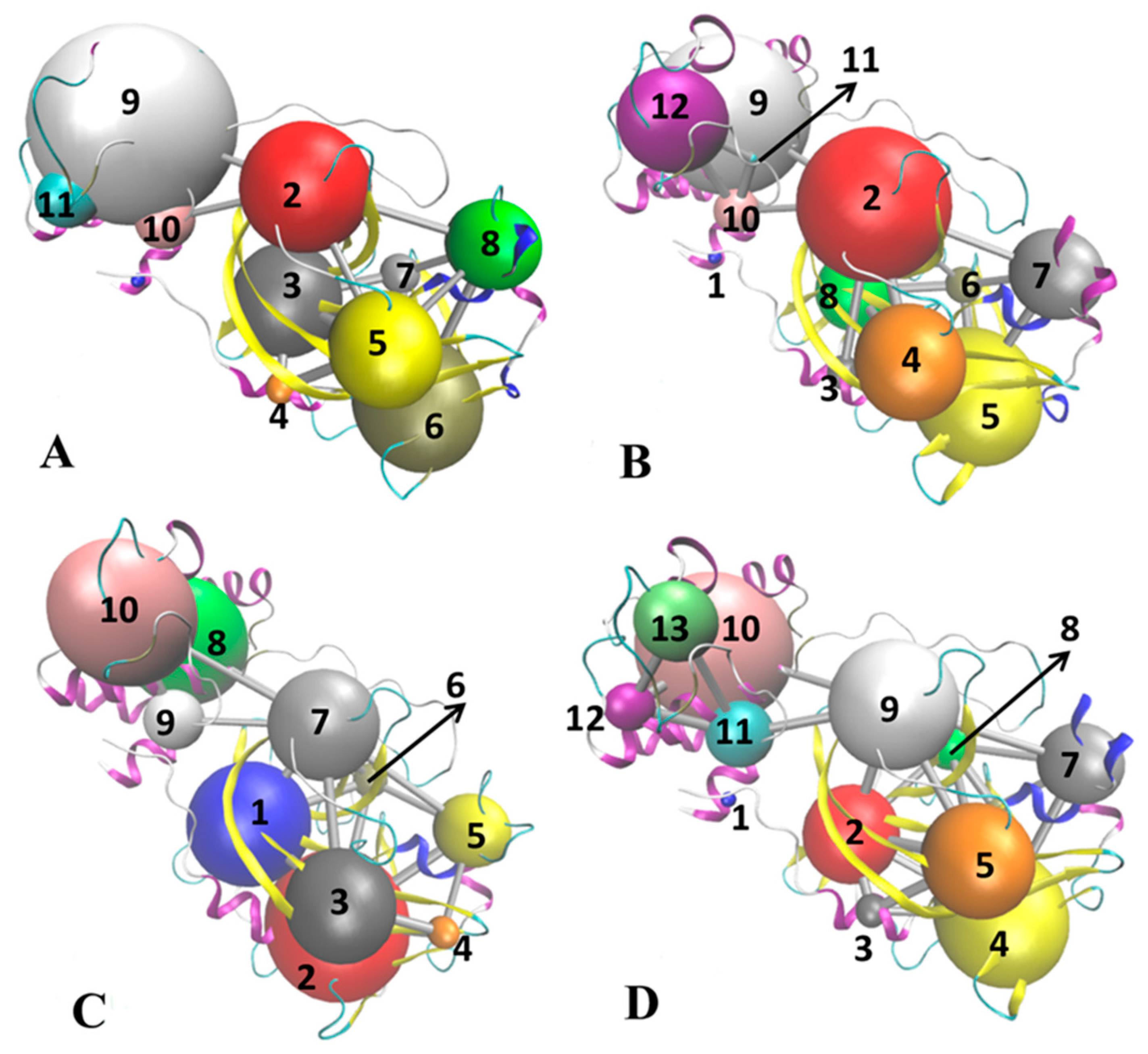
2.3. Normal Mode Analysis and Correlation Network Analysis
2.4. Calculations of MM-GBSA and QM/MM-GBSA
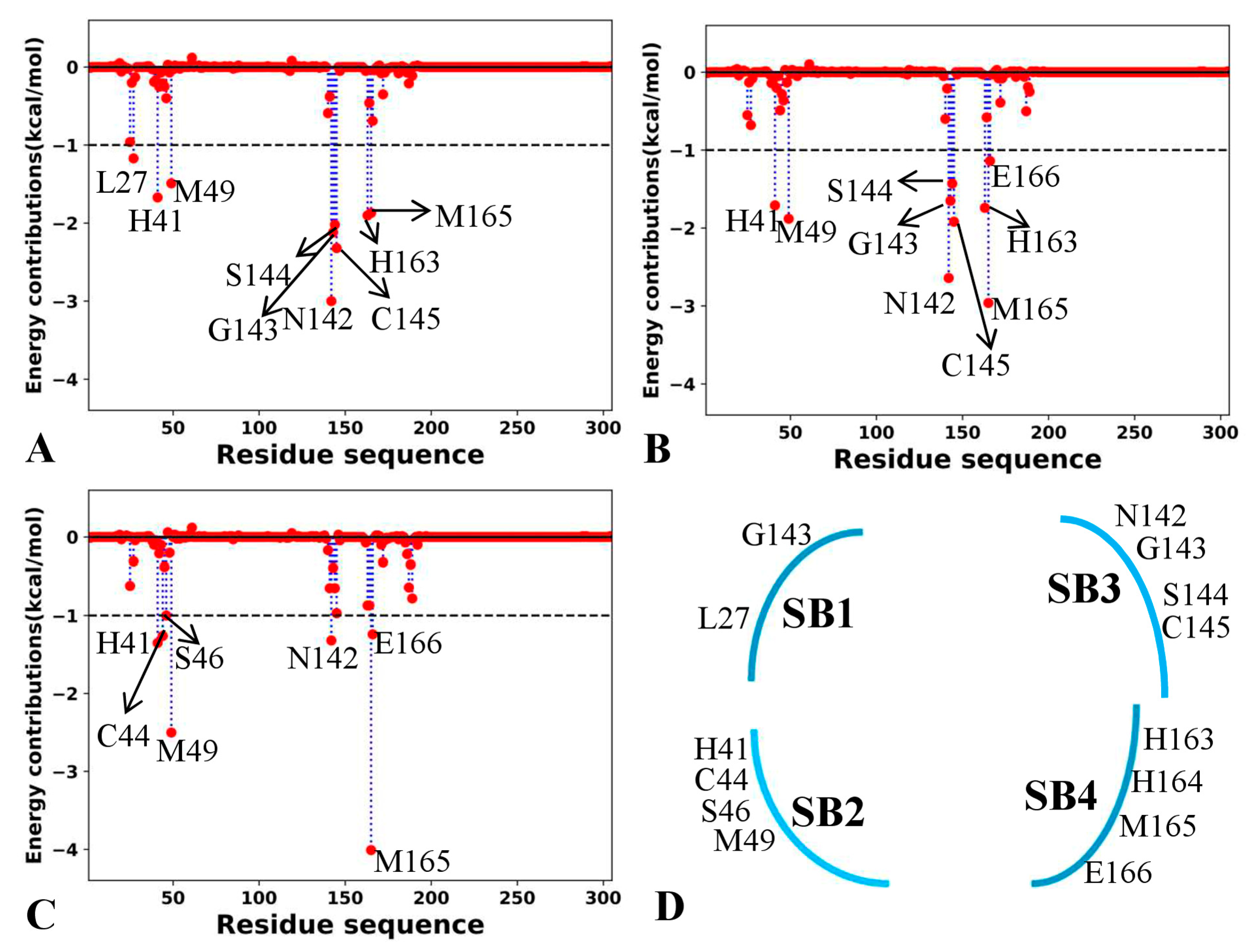
2.5. Target Sites to 3CLpro Identified by Residue-Based Free Energy Decomposition
3. Theory and Methods
3.1. Setup of Simulation Systems
3.2. GaMD Simulations
3.3. Free Energy Landscapes
3.4. Calculation of MM-GBSA and QM/MM-GBSA
3.5. Normal Mode Analysis and Correlation Network Analysis
3.6. Molecular Docking
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- WHO. Coronavirus (COVID-19) Dashboard. Available online: https://covid19.who.int (accessed on 12 January 2024).
- WHO. Target Product Profiles for COVID-19 Therapeutics for Non-Hospitalized Patients. Available online: https://www.who.int/publications/m/item/who-target-product-profiles-for-covid-19-therapeutics-for-non-hospitalized-patients (accessed on 12 January 2024).
- Wu, F.; Zhao, S.; Yu, B.; Chen, Y.-M.; Wang, W.; Song, Z.-G.; Hu, Y.; Tao, Z.-W.; Tian, J.-H.; Pei, Y.-Y.; et al. A new coronavirus associated with human respiratory disease in China. Nature 2020, 579, 265–269. [Google Scholar] [CrossRef]
- Zhou, P.; Yang, X.-L.; Wang, X.-G.; Hu, B.; Zhang, L.; Zhang, W.; Si, H.-R.; Zhu, Y.; Li, B.; Huang, C.-L.; et al. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature 2020, 579, 270–273. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, D.; Du, G.; Du, R.; Zhao, J.; Jin, Y.; Fu, S.; Gao, L.; Cheng, Z.; Lu, Q.; et al. Remdesivir in adults with severe COVID-19: A randomised, double-blind, placebo-controlled, multicentre trial. Lancet 2020, 395, 1569–1578. [Google Scholar] [CrossRef] [PubMed]
- Beigel, J.H.; Tomashek, K.M.; Dodd, L.E.; Mehta, A.K.; Zingman, B.S.; Kalil, A.C.; Hohmann, E.; Chu, H.Y.; Luetkemeyer, A.; Kline, S.; et al. Remdesivir for the Treatment of COVID-19—Final Report. N. Engl. J. Med. 2020, 383, 1813–1826. [Google Scholar] [CrossRef]
- Morse, J.S.; Lalonde, T.; Xu, S.; Liu, W.R. Learning from the Past: Possible Urgent Prevention and Treatment Options for Severe Acute Respiratory Infections Caused by 2019-nCoV. ChemBioChem 2020, 21, 730–738. [Google Scholar] [CrossRef] [PubMed]
- Dömling, A.; Gao, L. Chemistry and Biology of SARS-CoV-2. Chem 2020, 6, 1283–1295. [Google Scholar] [CrossRef]
- Cannalire, R.; Cerchia, C.; Beccari, A.R.; Di Leva, F.S.; Summa, V. Targeting SARS-CoV-2 Proteases and Polymerase for COVID-19 Treatment: State of the Art and Future Opportunities. J. Med. Chem. 2022, 65, 2716–2746. [Google Scholar] [CrossRef] [PubMed]
- Gil, C.; Ginex, T.; Maestro, I.; Nozal, V.; Barrado-Gil, L.; Cuesta-Geijo, M.Á.; Urquiza, J.; Ramírez, D.; Alonso, C.; Campillo, N.E.; et al. COVID-19: Drug Targets and Potential Treatments. J. Med. Chem. 2020, 63, 12359–12386. [Google Scholar] [CrossRef] [PubMed]
- Fan, K.; Wei, P.; Feng, Q.; Chen, S.; Huang, C.; Ma, L.; Lai, B.; Pei, J.; Liu, Y.; Chen, J.; et al. Biosynthesis, Purification, and Substrate Specificity of Severe Acute Respiratory Syndrome Coronavirus 3C-like Proteinase. J. Biol. Chem. 2004, 279, 1637–1642. [Google Scholar] [CrossRef] [PubMed]
- Barretto, N.; Jukneliene, D.; Ratia, K.; Chen, Z.; Mesecar, A.D.; Baker, S.C. The Papain-Like Protease of Severe Acute Respiratory Syndrome Coronavirus Has Deubiquitinating Activity. J. Virol. 2005, 79, 15189–15198. [Google Scholar] [CrossRef]
- Ullrich, S.; Nitsche, C. The SARS-CoV-2 main protease as drug target. Bioorg. Med. Chem. Lett. 2020, 30, 127377. [Google Scholar] [CrossRef]
- El Khoury, L.; Jing, Z.; Cuzzolin, A.; Deplano, A.; Loco, D.; Sattarov, B.; Hédin, F.; Wendeborn, S.; Ho, C.; El Ahdab, D.; et al. Computationally driven discovery of SARS-CoV-2 Mpro inhibitors: From design to experimental validation. Chem. Sci. 2022, 13, 3674–3687. [Google Scholar] [CrossRef] [PubMed]
- Qiao, J.; Li, Y.-S.; Zeng, R.; Liu, F.-L.; Luo, R.-H.; Huang, C.; Wang, Y.-F.; Zhang, J.; Quan, B.; Shen, C.; et al. SARS-CoV-2 Mpro inhibitors with antiviral activity in a transgenic mouse model. Science 2021, 371, 1374–1378. [Google Scholar] [CrossRef]
- Dampalla, C.S.; Zheng, J.; Perera, K.D.; Wong, L.-Y.R.; Meyerholz, D.K.; Nguyen, H.N.; Kashipathy, M.M.; Battaile, K.P.; Lovell, S.; Kim, Y.; et al. Postinfection treatment with a protease inhibitor increases survival of mice with a fatal SARS-CoV-2 infection. Proc. Natl. Acad. Sci. USA 2021, 118, e2101555118. [Google Scholar] [CrossRef] [PubMed]
- Marzi, M.; Vakil, M.K.; Bahmanyar, M.; Zarenezhad, E. Paxlovid: Mechanism of Action, Synthesis, and In Silico Study. BioMed Res. Int. 2022, 2022, 7341493. [Google Scholar] [CrossRef] [PubMed]
- Burki, T. The future of Paxlovid for COVID-19. Lancet Respir. Med. 2022, 10, e68. [Google Scholar] [CrossRef] [PubMed]
- Dai, W.; Zhang, B.; Jiang, X.-M.; Su, H.; Li, J.; Zhao, Y.; Xie, X.; Jin, Z.; Peng, J.; Liu, F.; et al. Structure-based design of antiviral drug candidates targeting the SARS-CoV-2 main protease. Science 2020, 368, 1331–1335. [Google Scholar] [CrossRef] [PubMed]
- Su, H.-X.; Yao, S.; Zhao, W.-F.; Li, M.-J.; Liu, J.; Shang, W.-J.; Xie, H.; Ke, C.-Q.; Hu, H.-C.; Gao, M.-N.; et al. Anti-SARS-CoV-2 activities in vitro of Shuanghuanglian preparations and bioactive ingredients. Acta Pharmacol. Sin. 2020, 41, 1167–1177. [Google Scholar] [CrossRef] [PubMed]
- Vuong, W.; Khan, M.B.; Fischer, C.; Arutyunova, E.; Lamer, T.; Shields, J.; Saffran, H.A.; McKay, R.T.; van Belkum, M.J.; Joyce, M.A.; et al. Feline coronavirus drug inhibits the main protease of SARS-CoV-2 and blocks virus replication. Nat. Commun. 2020, 11, 4282. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Xu, M.; Chen, C.Z.; Guo, H.; Shen, M.; Hu, X.; Shinn, P.; Klumpp-Thomas, C.; Michael, S.G.; Zheng, W. Identification of SARS-CoV-2 3CL Protease Inhibitors by a Quantitative High-Throughput Screening. ACS Pharmacol. Transl. Sci. 2020, 3, 1008–1016. [Google Scholar] [CrossRef] [PubMed]
- Dampalla, C.S.; Kim, Y.; Bickmeier, N.; Rathnayake, A.D.; Nguyen, H.N.; Zheng, J.; Kashipathy, M.M.; Baird, M.A.; Battaile, K.P.; Lovell, S.; et al. Structure-Guided Design of Conformationally Constrained Cyclohexane Inhibitors of Severe Acute Respiratory Syndrome Coronavirus-2 3CL Protease. J. Med. Chem. 2021, 64, 10047–10058. [Google Scholar] [CrossRef] [PubMed]
- Owen, D.R.; Allerton, C.M.N.; Anderson, A.S.; Aschenbrenner, L.; Avery, M.; Berritt, S.; Boras, B.; Cardin, R.D.; Carlo, A.; Coffman, K.J.; et al. An oral SARS-CoV-2 Mpro inhibitor clinical candidate for the treatment of COVID-19. Science 2021, 374, 1586–1593. [Google Scholar] [CrossRef] [PubMed]
- Unoh, Y.; Uehara, S.; Nakahara, K.; Nobori, H.; Yamatsu, Y.; Yamamoto, S.; Maruyama, Y.; Taoda, Y.; Kasamatsu, K.; Suto, T.; et al. Discovery of S-217622, a Noncovalent Oral SARS-CoV-2 3CL Protease Inhibitor Clinical Candidate for Treating COVID-19. J. Med. Chem. 2022, 65, 6499–6512. [Google Scholar] [CrossRef]
- Hoffman, R.L.; Kania, R.S.; Brothers, M.A.; Davies, J.F.; Ferre, R.A.; Gajiwala, K.S.; He, M.; Hogan, R.J.; Kozminski, K.; Li, L.Y.; et al. Discovery of Ketone-Based Covalent Inhibitors of Coronavirus 3CL Proteases for the Potential Therapeutic Treatment of COVID-19. J. Med. Chem. 2020, 63, 12725–12747. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Iketani, S.; Zask, A.; Khanizeman, N.; Bednarova, E.; Forouhar, F.; Fowler, B.; Hong, S.J.; Mohri, H.; Nair, M.S.; et al. Development of optimized drug-like small molecule inhibitors of the SARS-CoV-2 3CL protease for treatment of COVID-19. Nat. Commun. 2022, 13, 1891. [Google Scholar] [CrossRef]
- Hou, N.; Shuai, L.; Zhang, L.; Xie, X.; Tang, K.; Zhu, Y.; Yu, Y.; Zhang, W.; Tan, Q.; Zhong, G.; et al. Development of Highly Potent Noncovalent Inhibitors of SARS-CoV-2 3CLpro. ACS Cent. Sci. 2023, 9, 217–227. [Google Scholar] [CrossRef] [PubMed]
- Clyde, A.; Galanie, S.; Kneller, D.W.; Ma, H.; Babuji, Y.; Blaiszik, B.; Brace, A.; Brettin, T.; Chard, K.; Chard, R.; et al. High-Throughput Virtual Screening and Validation of a SARS-CoV-2 Main Protease Noncovalent Inhibitor. J. Chem. Inf. Model. 2022, 62, 116–128. [Google Scholar] [CrossRef]
- Albani, S.; Costanzi, E.; Hoang, G.L.; Kuzikov, M.; Frings, M.; Ansari, N.; Demitri, N.; Nguyen, T.T.; Rizzi, V.; Schulz, J.B.; et al. Unexpected Single-Ligand Occupancy and Negative Cooperativity in the SARS-CoV-2 Main Protease. J. Chem. Inf. Model. 2024, 64, 892–904. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, W.; Zhao, L.; Wei, B.; Chen, J. Binding Mechanism of Inhibitors to BRD4 and BRD9 Decoded by Multiple Independent Molecular Dynamics Simulations and Deep Learning. Molecules 2024, 29, 1857. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Wang, Z.; Wang, L.; Tian, S.; Hou, T.; Sun, H. Predicting the mutation effects of protein–ligand interactions via end-point binding free energy calculations: Strategies and analyses. J. Cheminf. 2022, 14, 56. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Huai, Z.; Sun, Z. Host Dynamics under General-Purpose Force Fields. Molecules 2023, 28, 5940. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Ni, D.; Fan, J.; Li, M.; Zhang, J.; Hua, C.; Nussinov, R.; Lu, S. Markov State Models and Molecular Dynamics Simulations Reveal the Conformational Transition of the Intrinsically Disordered Hypervariable Region of K-Ras4B to the Ordered Conformation. J. Chem. Inf. Model. 2022, 62, 4222–4231. [Google Scholar] [CrossRef] [PubMed]
- Luo, D.; Zhang, Y.; Li, Y.; Liu, Z.; Wu, H.; Xue, W. Structural Models of Human Norepinephrine Transporter Ensemble Reveal the Allosteric Sites and Ligand-Binding Mechanism. J. Phys. Chem. B 2024, 128, 8651–8661. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, Z.; Wang, L.; Wang, Q.; Tang, R.; Xiang, S.; Deng, Q.; Hou, T.; Sun, H. Deciphering the Shared and Specific Drug Resistance Mechanisms of Anaplastic Lymphoma Kinase via Binding Free Energy Computation. Research 2023, 6, 0170. [Google Scholar] [CrossRef]
- Wei, M.; Zhang, X.; Pan, X.; Wang, B.; Ji, C.; Qi, Y.; Zhang, J.Z.H. HobPre: Accurate prediction of human oral bioavailability for small molecules. J. Cheminform. 2022, 14, 1. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Huai, Z.; He, Q.; Liu, Z. A General Picture of Cucurbit [8]uril Host–Guest Binding. J. Chem. Inf. Model. 2021, 61, 6107–6134. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Wang, Y.; Fan, J.; Zhuang, H.; Liu, Y.; Ji, D.; Lu, S. Mechanistic Insights into the Long-range Allosteric Regulation of KRAS Via Neurofibromatosis Type 1 (NF1) Scaffold Upon SPRED1 Loading. J. Mol. Biol. 2022, 434, 167730. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Yang, F.; Wang, P.; Zheng, G.; Chen, Y.; Yao, X.; Zhu, F. What Contributes to Serotonin–Norepinephrine Reuptake Inhibitors’ Dual-Targeting Mechanism? The Key Role of Transmembrane Domain 6 in Human Serotonin and Norepinephrine Transporters Revealed by Molecular Dynamics Simulation. ACS Chem. Neurosci. 2018, 9, 1128–1140. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Wang, P.; Tu, G.; Yang, F.; Zheng, G.; Li, X.; Li, X.; Chen, Y.; Yao, X.; Zhu, F. Computational identification of the binding mechanism of a triple reuptake inhibitor amitifadine for the treatment of major depressive disorder. Phys. Chem. Chem. Phys. 2018, 20, 6606–6616. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Yang, W.; Zhao, L.; Hu, G. Conformations of KRAS4B Affected by Its Partner Binding and G12C Mutation: Insights from GaMD Trajectory-Image Transformation-Based Deep Learning. J. Chem. Inf. Model. 2024, 64, 6880–6898. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; Feher, V.A.; McCammon, J.A. Gaussian Accelerated Molecular Dynamics: Unconstrained Enhanced Sampling and Free Energy Calculation. J. Chem. Theory Comput. 2015, 11, 3584–3595. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Arantes, P.R.; Bhattarai, A.; Hsu, R.V.; Pawnikar, S.; Huang, Y.-M.M.; Palermo, G.; Miao, Y. Gaussian accelerated molecular dynamics: Principles and applications. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, 11, e1521. [Google Scholar] [CrossRef]
- Wang, J.; Miao, Y. Ligand Gaussian Accelerated Molecular Dynamics 2 (LiGaMD2): Improved Calculations of Ligand Binding Thermodynamics and Kinetics with Closed Protein Pocket. J. Chem. Theory Comput. 2023, 19, 733–745. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; McCammon, J.A. Graded activation and free energy landscapes of a muscarinic G-protein–coupled receptor. Proc. Natl. Acad. Sci. USA 2016, 113, 12162–12167. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Miao, Y. Mechanistic Insights into Specific G Protein Interactions with Adenosine Receptors. J. Phys. Chem. B 2019, 123, 6462–6473. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, Q.; Wang, W.; Sun, H.; Hu, G. Decoding the Identification Mechanism of an SAM-III Riboswitch on Ligands through Multiple Independent Gaussian-Accelerated Molecular Dynamics Simulations. J. Chem. Inf. Model. 2022, 62, 6118–6132. [Google Scholar] [CrossRef]
- Wang, J.; Miao, Y. Ligand Gaussian Accelerated Molecular Dynamics 3 (LiGaMD3): Improved Calculations of Binding Thermodynamics and Kinetics of Both Small Molecules and Flexible Peptides. J. Chem. Theory Comput. 2024, 20, 5829–5841. [Google Scholar] [CrossRef]
- Chen, J.; Wang, W.; Sun, H.; He, W. Roles of Accelerated Molecular Dynamics Simulations in Predictions of Binding Kinetic Parameters. Mini-Rev. Med. Chem. 2024, 24, 1323–1333. [Google Scholar] [CrossRef]
- Yang, W.; Wang, J.; Zhao, L.; Chen, J. Insights into the Interaction Mechanisms of Peptide and Non-Peptide Inhibitors with MDM2 Using Gaussian-Accelerated Molecular Dynamics Simulations and Deep Learning. Molecules 2024, 29, 3377. [Google Scholar] [CrossRef]
- Pathak, R.K.; Kim, W.-I.; Kim, J.-M. Targeting the PEDV 3CL protease for identification of small molecule inhibitors: An insight from virtual screening, ADMET prediction, molecular dynamics, free energy landscape, and binding energy calculations. J. Biol. Eng. 2023, 17, 29. [Google Scholar] [CrossRef]
- Umar, A.K.; Zothantluanga, J.H.; Aswin, K.; Maulana, S.; Sulaiman Zubair, M.; Lalhlenmawia, H.; Rudrapal, M.; Chetia, D. Antiviral phytocompounds “ellagic acid” and “(+)-sesamin” of Bridelia retusa identified as potential inhibitors of SARS-CoV-2 3CLpro using extensive molecular docking, molecular dynamics simulation studies, binding free energy calculations, and bioactivity prediction. Struct. Chem. 2022, 33, 1445–1465. [Google Scholar] [PubMed]
- Khamto, N.; Utama, K.; Tateing, S.; Sangthong, P.; Rithchumpon, P.; Cheechana, N.; Saiai, A.; Semakul, N.; Punyodom, W.; Meepowpan, P. Discovery of Natural Bisbenzylisoquinoline Analogs from the Library of Thai Traditional Plants as SARS-CoV-2 3CLPro Inhibitors: In Silico Molecular Docking, Molecular Dynamics, and In Vitro Enzymatic Activity. J. Chem. Inf. Model. 2023, 63, 2104–2121. [Google Scholar] [CrossRef]
- Alamri, M.A.; Afzal, O.; Akhtar, M.J.; Karim, S.; Husain, M.; Alossaimi, M.A.; Riadi, Y. Synthesis, in silico and in vitro studies of novel quinazolinone derivatives as potential SARS-CoV-2 3CLpro inhibitors. Arab. J. Chem. 2024, 17, 105384. [Google Scholar] [CrossRef]
- Kumar, S.; Sharma, P.P.; Shankar, U.; Kumar, D.; Joshi, S.K.; Pena, L.; Durvasula, R.; Kumar, A.; Kempaiah, P.; Poonam; et al. Discovery of New Hydroxyethylamine Analogs against 3CLpro Protein Target of SARS-CoV-2: Molecular Docking, Molecular Dynamics Simulation, and Structure–Activity Relationship Studies. J. Chem. Inf. Model. 2020, 60, 5754–5770. [Google Scholar] [CrossRef]
- Soukaina, E.; Wissal, L.; Yassine, K.; Achraf, E.A.; Guenoun, F.; Bouachrine, M. Design of new dipeptide inhibitors against SARS-CoV 3CLpro: 3D-QSAR, molecular docking, MD simulation, ADMET studies and retrosynthesis strategy. Arab. J. Chem. 2024, 17, 105584. [Google Scholar] [CrossRef]
- Moritsugu, K.; Ekimoto, T.; Ikeguchi, M.; Kidera, A. Binding and Unbinding Pathways of Peptide Substrates on the SARS-CoV-2 3CL Protease. J. Chem. Inf. Model. 2023, 63, 240–250. [Google Scholar] [CrossRef]
- Han, S.H.; Goins, C.M.; Arya, T.; Shin, W.-J.; Maw, J.; Hooper, A.; Sonawane, D.P.; Porter, M.R.; Bannister, B.E.; Crouch, R.D.; et al. Structure-Based Optimization of ML300-Derived, Noncovalent Inhibitors Targeting the Severe Acute Respiratory Syndrome Coronavirus 3CL Protease (SARS-CoV-2 3CLpro). J. Med. Chem. 2022, 65, 2880–2904. [Google Scholar] [CrossRef]
- Skjaerven, L.; Martinez, A.; Reuter, N. Principal component and normal mode analysis of proteins; a quantitative comparison using the GroEL subunit. Proteins 2011, 79, 232–243. [Google Scholar] [CrossRef] [PubMed]
- Amadei, A.; Linssen, A.B.M.; Berendsen, H.J.C. Essential dynamics of proteins. Proteins 1993, 17, 412–425. [Google Scholar] [CrossRef] [PubMed]
- Ichiye, T.; Karplus, M. Collective motions in proteins: A covariance analysis of atomic fluctuations in molecular dynamics and normal mode simulations. Proteins 1991, 11, 205–217. [Google Scholar] [CrossRef]
- Bao, H.; Wang, W.; Sun, H.; Chen, J. Probing mutation-induced conformational transformation of the GTP/M-RAS complex through Gaussian accelerated molecular dynamics simulations. J. Enzym. Inhib. Med. Chem. 2023, 38, 2195995. [Google Scholar] [CrossRef]
- Skjærven, L.; Yao, X.-Q.; Scarabelli, G.; Grant, B.J. Integrating protein structural dynamics and evolutionary analysis with Bio3D. BMC Bioinform. 2014, 15, 399. [Google Scholar] [CrossRef]
- Grant, B.J.; Rodrigues, A.P.C.; ElSawy, K.M.; McCammon, J.A.; Caves, L.S.D. Bio3d: An R package for the comparative analysis of protein structures. Bioinformatics 2006, 22, 2695–2696. [Google Scholar] [CrossRef] [PubMed]
- Grant, B.J.; Skjærven, L.; Yao, X.-Q. The Bio3D packages for structural bioinformatics. Protein Sci. 2021, 30, 20–30. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Morin, P.; Wang, W.; Kollman, P.A. Use of MM-PBSA in Reproducing the Binding Free Energies to HIV-1 RT of TIBO Derivatives and Predicting the Binding Mode to HIV-1 RT of Efavirenz by Docking and MM-PBSA. J. Am. Chem. Soc. 2001, 123, 5221–5230. [Google Scholar] [CrossRef]
- Wang, C.; Greene, D.A.; Xiao, L.; Qi, R.; Luo, R. Recent Developments and Applications of the MMPBSA Method. Front. Mol. Biosci. 2018, 4, 87. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Kollman, P.A. Free energy calculations on dimer stability of the HIV protease using molecular dynamics and a continuum solvent model. J. Mol. Biol. 2000, 303, 567–582. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, J.; Yang, W.; Zhao, K.; Sun, Q.; Chen, J. Unveiling Conformational States of CDK6 Caused by Binding of Vcyclin Protein and Inhibitor by Combining Gaussian Accelerated Molecular Dynamics and Deep Learning. Molecules 2024, 29, 2681. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, J.; Zhang, Q.; Chen, K.; Zhu, W. Probing Origin of Binding Difference of inhibitors to MDM2 and MDMX by Polarizable Molecular Dynamics Simulation and QM/MM-GBSA Calculation. Sci. Rep. 2015, 5, 17421. [Google Scholar] [CrossRef]
- Xiong, D.; Zhao, X.; Luo, S.; Zhang, J.Z.H.; Duan, L. Molecular Mechanism of the Non-Covalent Orally Targeted SARS-CoV-2 Mpro Inhibitor S-217622 and Computational Assessment of Its Effectiveness against Mainstream Variants. J. Phys. Chem. Lett. 2022, 13, 8893–8901. [Google Scholar] [CrossRef]
- Liang, S.; Liu, X.; Zhang, S.; Li, M.; Zhang, Q.; Chen, J. Binding mechanism of inhibitors to SARS-CoV-2 main protease deciphered by multiple replica molecular dynamics simulations. Phys. Chem. Chem. Phys. 2022, 24, 1743–1759. [Google Scholar] [CrossRef] [PubMed]
- Jawarkar, R.D.; Bakal, R.L.; Zaki, M.E.A.; Al-Hussain, S.; Ghosh, A.; Gandhi, A.; Mukerjee, N.; Samad, A.; Masand, V.H.; Lewaa, I. QSAR based virtual screening derived identification of a novel hit as a SARS CoV-229E 3CLpro Inhibitor: GA-MLR QSAR modeling supported by molecular Docking, molecular dynamics simulation and MMGBSA calculation approaches. Arab. J. Chem. 2022, 15, 103499. [Google Scholar] [CrossRef]
- Scarabelli, G.; Grant, B.J. Mapping the Structural and Dynamical Features of Kinesin Motor Domains. PLOS Comput. Biol. 2013, 9, e1003329. [Google Scholar] [CrossRef]
- Gasper, P.M.; Fuglestad, B.; Komives, E.A.; Markwick, P.R.L.; McCammon, J.A. Allosteric networks in thrombin distinguish procoagulant vs. anticoagulant activities. Proc. Natl. Acad. Sci. USA 2012, 109, 21216–21222. [Google Scholar] [CrossRef]
- Scarabelli, G.; Grant, B.J. Kinesin-5 Allosteric Inhibitors Uncouple the Dynamics of Nucleotide, Microtubule, and Neck-Linker Binding Sites. Biophys. J. 2014, 107, 2204–2213. [Google Scholar] [CrossRef]
- Samanta, P.N.; Majumdar, D.; Leszczynski, J. Elucidating Atomistic Insight into the Dynamical Responses of the SARS-CoV-2 Main Protease for the Binding of Remdesivir Analogues: Leveraging Molecular Mechanics to Decode the Inhibition Mechanism. J. Chem. Inf. Model. 2023, 63, 3404–3422. [Google Scholar] [CrossRef]
- Webb, B.; Sali, A. Comparative protein structure modeling using MODELLER. Curr. Protoc. Bioinform. 2016, 54, 5.6.1–5.6.37. [Google Scholar] [CrossRef]
- Case, D.A.; Cheatham, T.E., III; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [PubMed]
- Anandakrishnan, R.; Aguilar, B.; Onufriev, A.V. H++ 3.0: Automating pK prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulations. Nucleic Acids Res. 2012, 40, W537–W541. [Google Scholar] [CrossRef] [PubMed]
- Arafet, K.; Serrano-Aparicio, N.; Lodola, A.; Mulholland, A.J.; González, F.V.; Świderek, K.; Moliner, V. Mechanism of inhibition of SARS-CoV-2 Mpro by N3 peptidyl Michael acceptor explained by QM/MM simulations and design of new derivatives with tunable chemical reactivity. Chem. Sci. 2021, 12, 1433–1444. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Man, V.H.; Yang, W.; Lee, T.-S.; Wang, J. A fast and high-quality charge model for the next generation general AMBER force field. J. Chem. Phys. 2020, 153, 114502. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Jakalian, A.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef]
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Cerutti, D.S.; Cisneros, G.A.; Cruzeiro, V.W.D.; Forouzesh, N.; Giese, T.J.; Götz, A.W.; Gohlke, H.; et al. AmberTools. J. Chem. Inf. Model. 2023, 63, 6183–6191. [Google Scholar] [CrossRef] [PubMed]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Joung, I.S.; Cheatham, T.E., III. Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef]
- Joung, I.S.; Cheatham, T.E., III. Molecular Dynamics Simulations of the Dynamic and Energetic Properties of Alkali and Halide Ions Using Water-Model-Specific Ion Parameters. J. Phys. Chem. B 2009, 113, 13279–13290. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Miao, Y.; Sinko, W.; Pierce, L.; Bucher, D.; Walker, R.C.; McCammon, J.A. Improved Reweighting of Accelerated Molecular Dynamics Simulations for Free Energy Calculation. J. Chem. Theory Comput. 2014, 10, 2677–2689. [Google Scholar] [CrossRef] [PubMed]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Izaguirre, J.A.; Catarello, D.P.; Wozniak, J.M.; Skeel, R.D. Langevin stabilization of molecular dynamics. J. Chem. Phys. 2001, 114, 2090–2098. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Götz, A.W.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef]
- Götz, A.W.; Williamson, M.J.; Xu, D.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput. 2012, 8, 1542–1555. [Google Scholar] [CrossRef] [PubMed]
- Roe, D.R.; Cheatham, T.E., III. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Li, Y.; Shen, M.; Tian, S.; Xu, L.; Pan, P.; Guan, Y.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 5. Improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring. Phys. Chem. Chem. Phys. 2014, 16, 22035–22045. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Li, Y.; Tian, S.; Xu, L.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set. Phys. Chem. Chem. Phys. 2014, 16, 16719–16729. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Sun, H.; Li, Y.; Wang, J.; Hou, T. Assessing the Performance of MM/PBSA and MM/GBSA Methods. 3. The Impact of Force Fields and Ligand Charge Models. J. Phys. Chem. B 2013, 117, 8408–8421. [Google Scholar] [CrossRef] [PubMed]
- Weng, G.; Wang, E.; Chen, F.; Sun, H.; Wang, Z.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 9. Prediction reliability of binding affinities and binding poses for protein–peptide complexes. Phys. Chem. Chem. Phys. 2019, 21, 10135–10145. [Google Scholar] [CrossRef] [PubMed]
- Miller, B.R., III; McGee, T.D., Jr.; Swails, J.M.; Homeyer, N.; Gohlke, H.; Roitberg, A.E. MMPBSA.py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. [Google Scholar] [CrossRef] [PubMed]
- Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins 2004, 55, 383–394. [Google Scholar] [CrossRef]
- Gohlke, H.; Kiel, C.; Case, D.A. Insights into Protein–Protein Binding by Binding Free Energy Calculation and Free Energy Decomposition for the Ras–Raf and Ras–RalGDS Complexes. J. Mol. Biol. 2003, 330, 891–913. [Google Scholar] [CrossRef] [PubMed]
- Lange, O.F.; Grubmüller, H. Generalized correlation for biomolecular dynamics. Proteins 2006, 62, 1053–1061. [Google Scholar] [CrossRef] [PubMed]
- Sethi, A.; Eargle, J.; Black, A.A.; Luthey-Schulten, Z. Dynamical networks in tRNA:protein complexes. Proc. Natl. Acad. Sci. USA 2009, 106, 6620–6625. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef] [PubMed]
- Doerr, S.; Harvey, M.J.; Noé, F.; De Fabritiis, G. HTMD: High-Throughput Molecular Dynamics for Molecular Discovery. J. Chem. Theory Comput. 2016, 12, 1845–1852. [Google Scholar] [CrossRef] [PubMed]


| a Components | 7YY-3CLpro | 7XB-3CLpro | Y6G-3CLpro | |||
|---|---|---|---|---|---|---|
| Average | Std | Average | Std | Average | Std | |
| −53.29 | 0.31 | −47.67 | 0.43 | −51.21 | 0.16 | |
| −37.05 | 0.38 | −34.43 | 0.51 | −23.48 | 0.30 | |
| 54.39 | 0.29 | 50.08 | 0.44 | 40.12 | 0.35 | |
| −5.76 | 0.02 | −6.51 | 0.04 | −5.72 | 0.02 | |
| b | −41.71 | 0.27 | −41.52 | 0.45 | −40.29 | 0.26 |
| 27.05 | 0.74 | 27.63 | 0.71 | 26.02 | 1.00 | |
| c | −14.66 | 0.33 | −13.89 | 0.41 | −14.27 | 0.54 |
| d | −10.78 | −6.92 | −9.34 | |||
| a Components | 7YY-3CLpro | 7XB-3CLpro | Y6G-3CLpro | |||
|---|---|---|---|---|---|---|
| Average | Std | Average | Std | Average | Std | |
| −49.28 | 0.24 | −47.13 | 0.43 | −50.89 | 0.23 | |
| −0.1 | 0.01 | −0.05 | 0.01 | −0.06 | 0.01 | |
| 59.39 | 0.29 | 49.92 | 0.48 | 51.55 | 0.26 | |
| −5.75 | 0.02 | −5.69 | 0.04 | −5.78 | 0.04 | |
| −44.75 | 0.32 | −35.56 | 0.55 | −32.67 | 0.34 | |
| b | −40.5 | 0.22 | −39.31 | 0.55 | −37.85 | 0.21 |
| 27.05 | 1.00 | 27.63 | 0.71 | 26.02 | 1.00 | |
| c | −13.45 | 0.21 | −11.68 | 0.30 | −11.83 | 0.22 |
| d | −10.78 | −6.92 | −9.34 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Wang, J.; Yang, W.; Zhao, L.; Xu, X. Identifying Inhibitor-SARS-CoV2-3CLpro Binding Mechanism Through Molecular Docking, GaMD Simulations, Correlation Network Analysis and MM-GBSA Calculations. Molecules 2025, 30, 805. https://doi.org/10.3390/molecules30040805
Chen J, Wang J, Yang W, Zhao L, Xu X. Identifying Inhibitor-SARS-CoV2-3CLpro Binding Mechanism Through Molecular Docking, GaMD Simulations, Correlation Network Analysis and MM-GBSA Calculations. Molecules. 2025; 30(4):805. https://doi.org/10.3390/molecules30040805
Chicago/Turabian StyleChen, Jianzhong, Jian Wang, Wanchun Yang, Lu Zhao, and Xiaoyan Xu. 2025. "Identifying Inhibitor-SARS-CoV2-3CLpro Binding Mechanism Through Molecular Docking, GaMD Simulations, Correlation Network Analysis and MM-GBSA Calculations" Molecules 30, no. 4: 805. https://doi.org/10.3390/molecules30040805
APA StyleChen, J., Wang, J., Yang, W., Zhao, L., & Xu, X. (2025). Identifying Inhibitor-SARS-CoV2-3CLpro Binding Mechanism Through Molecular Docking, GaMD Simulations, Correlation Network Analysis and MM-GBSA Calculations. Molecules, 30(4), 805. https://doi.org/10.3390/molecules30040805





