Theoretical Examination on the Chiral Separation Mechanism of Ibuprofen on Cellulose Tris(4-methylbenzoate)
Abstract
1. Introduction
2. Results and Discussion
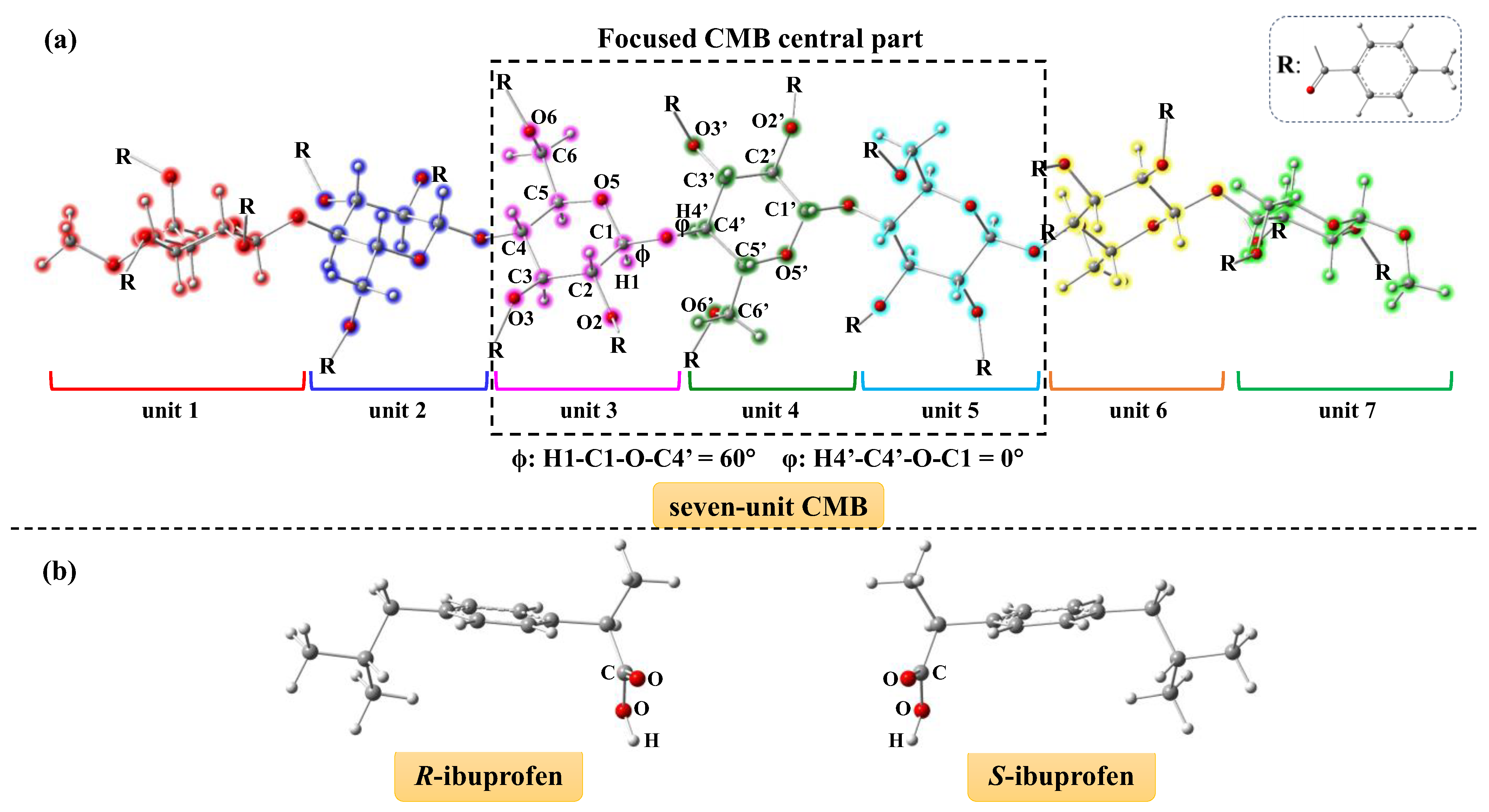
2.1. Binding Structures of Ibuprofen with CMB Based on Docking Simulation
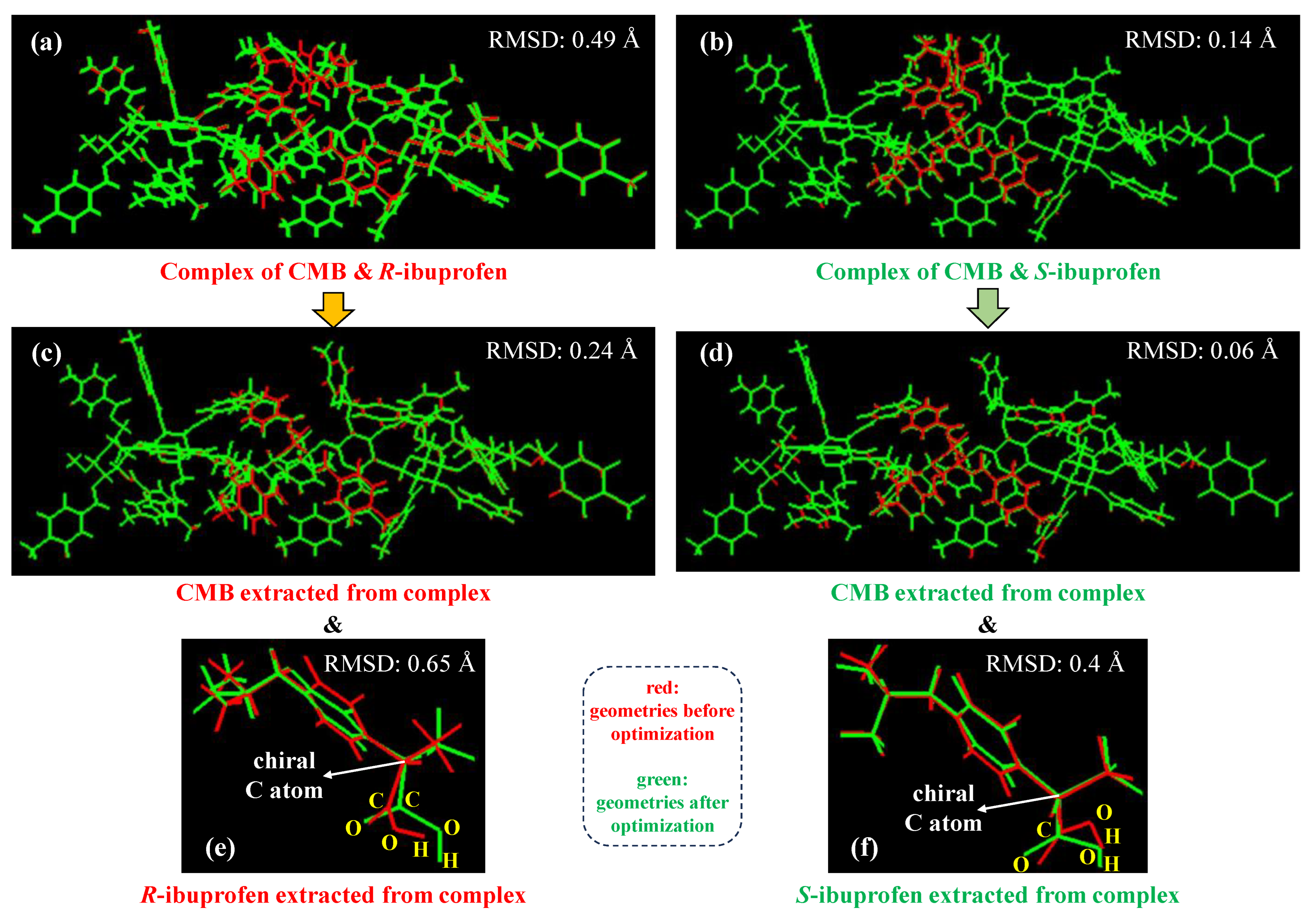
2.2. Comparison of Geometries Before and After Geometry Optimization
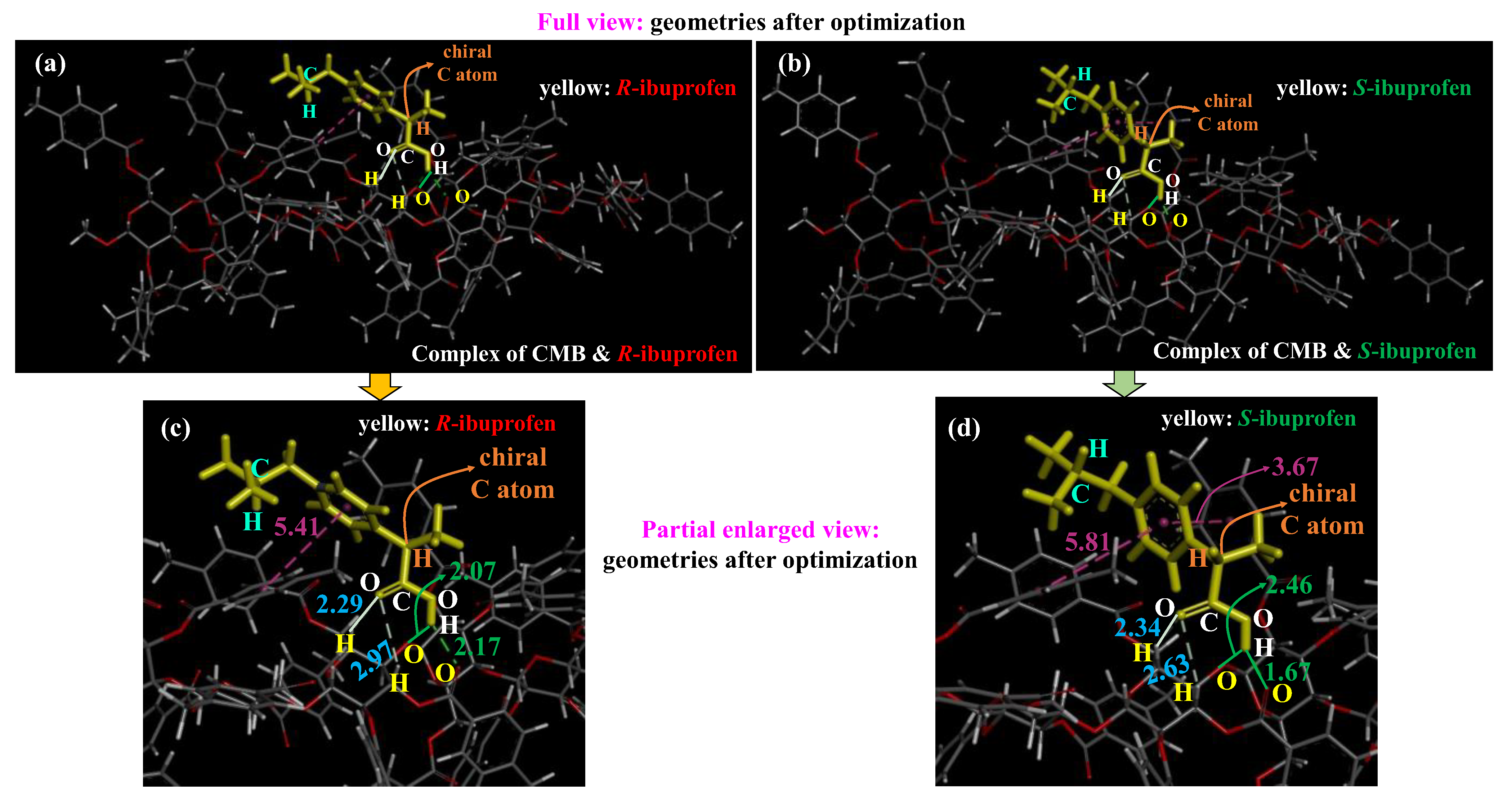
2.3. Analysis of Interactions Between CMB and Ibuprofen
3. Method and Computational Details
3.1. Method
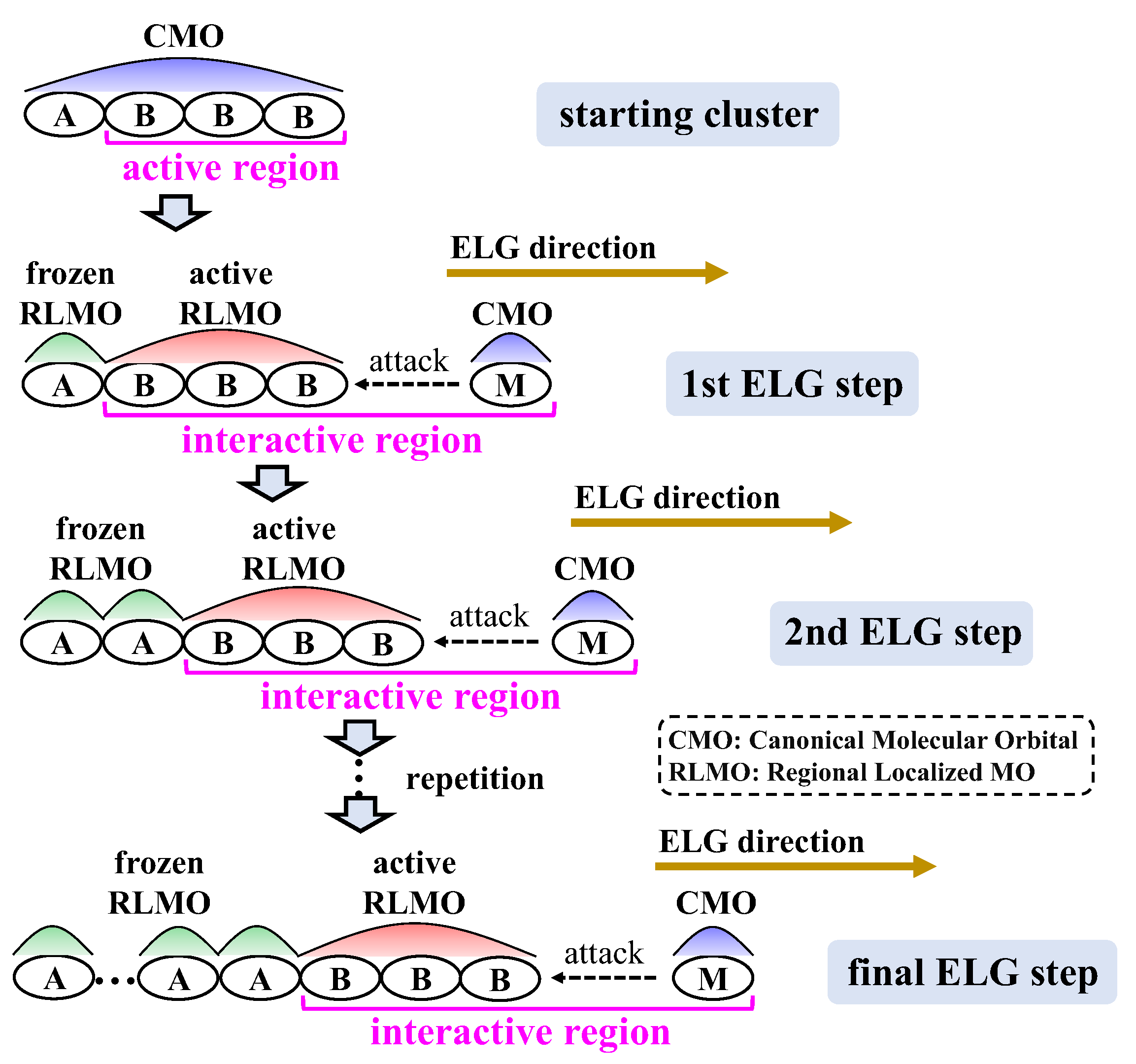
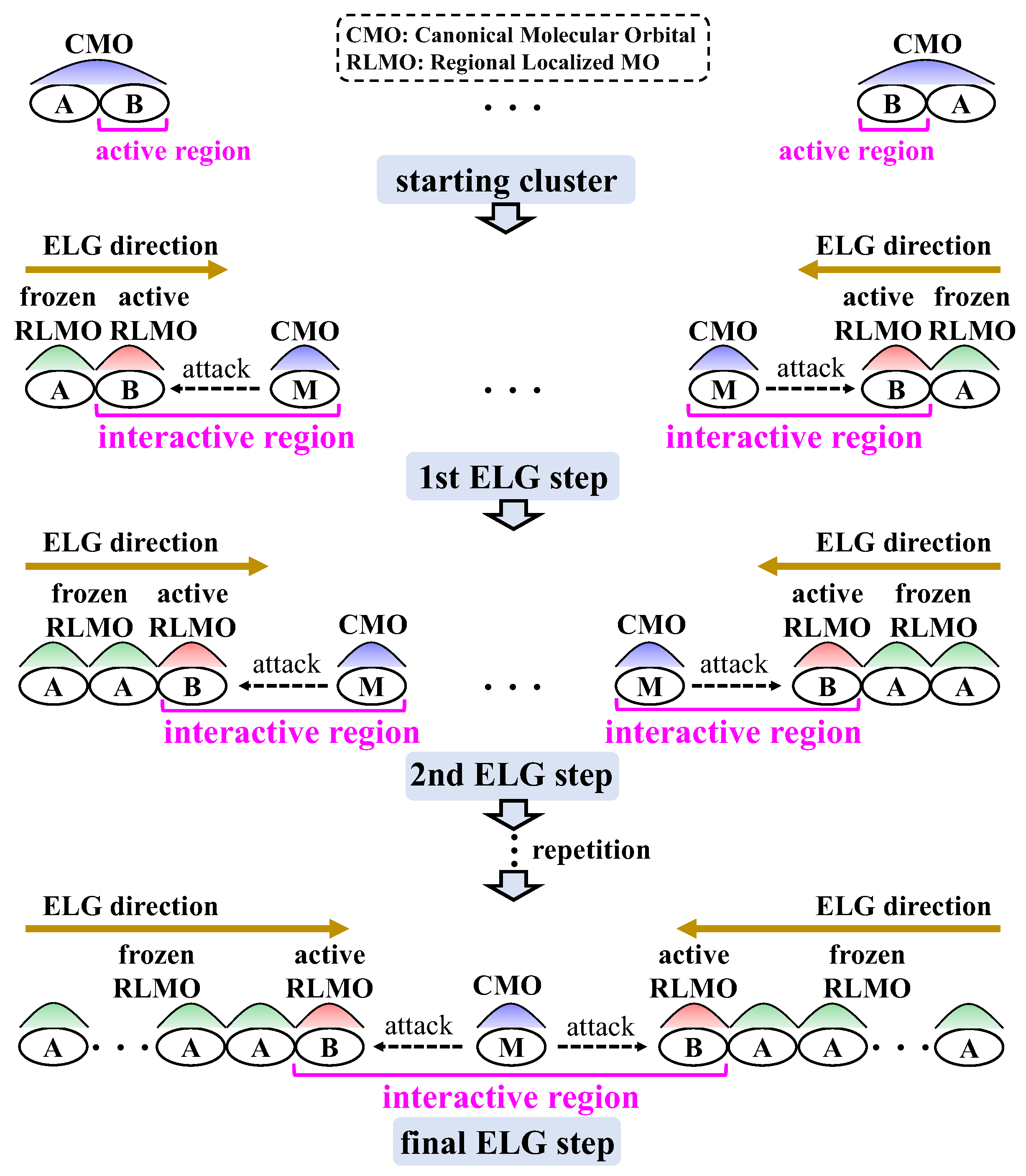
3.1.1. ELG Method
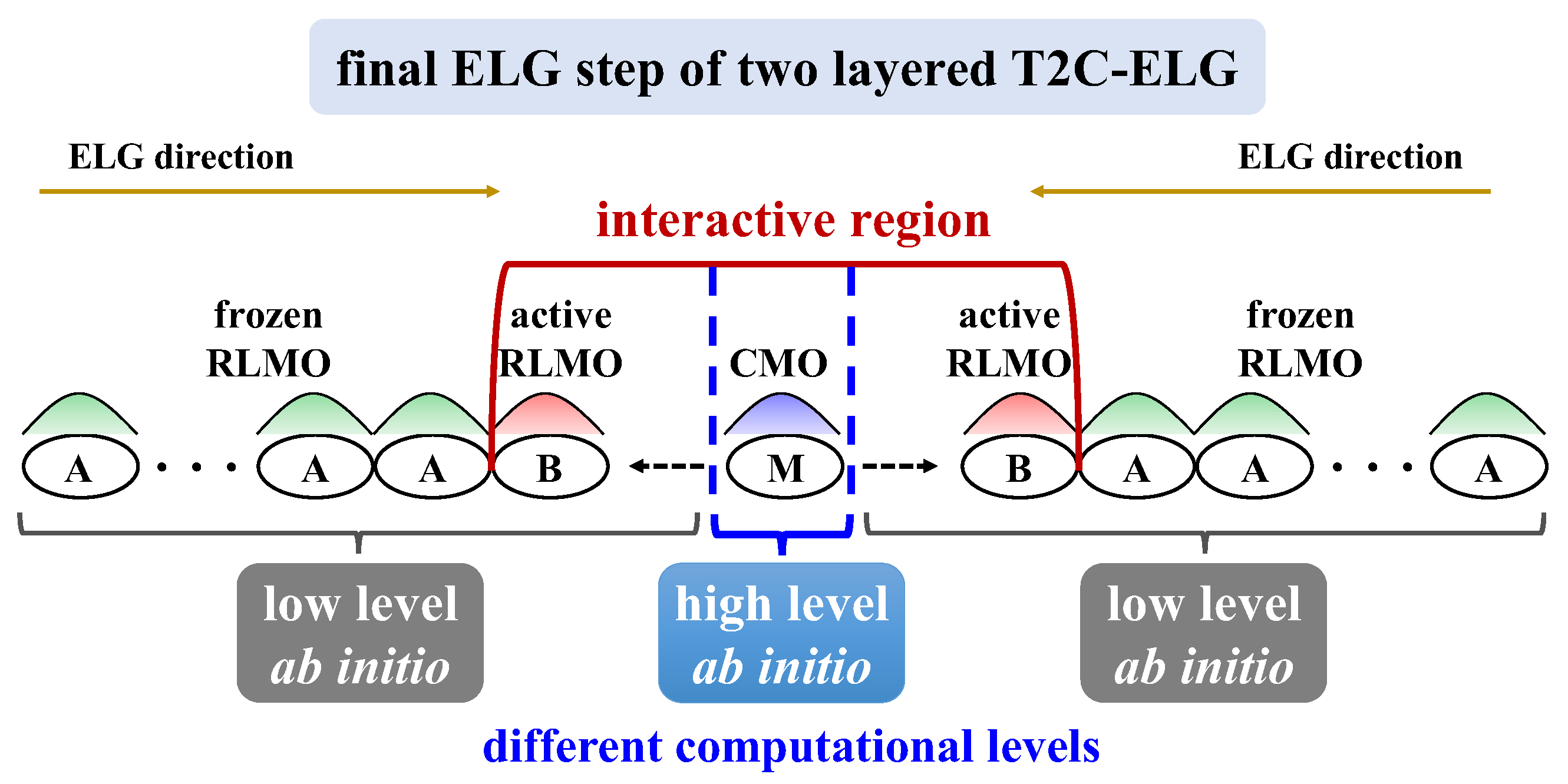
3.1.2. T2C-ELG Method
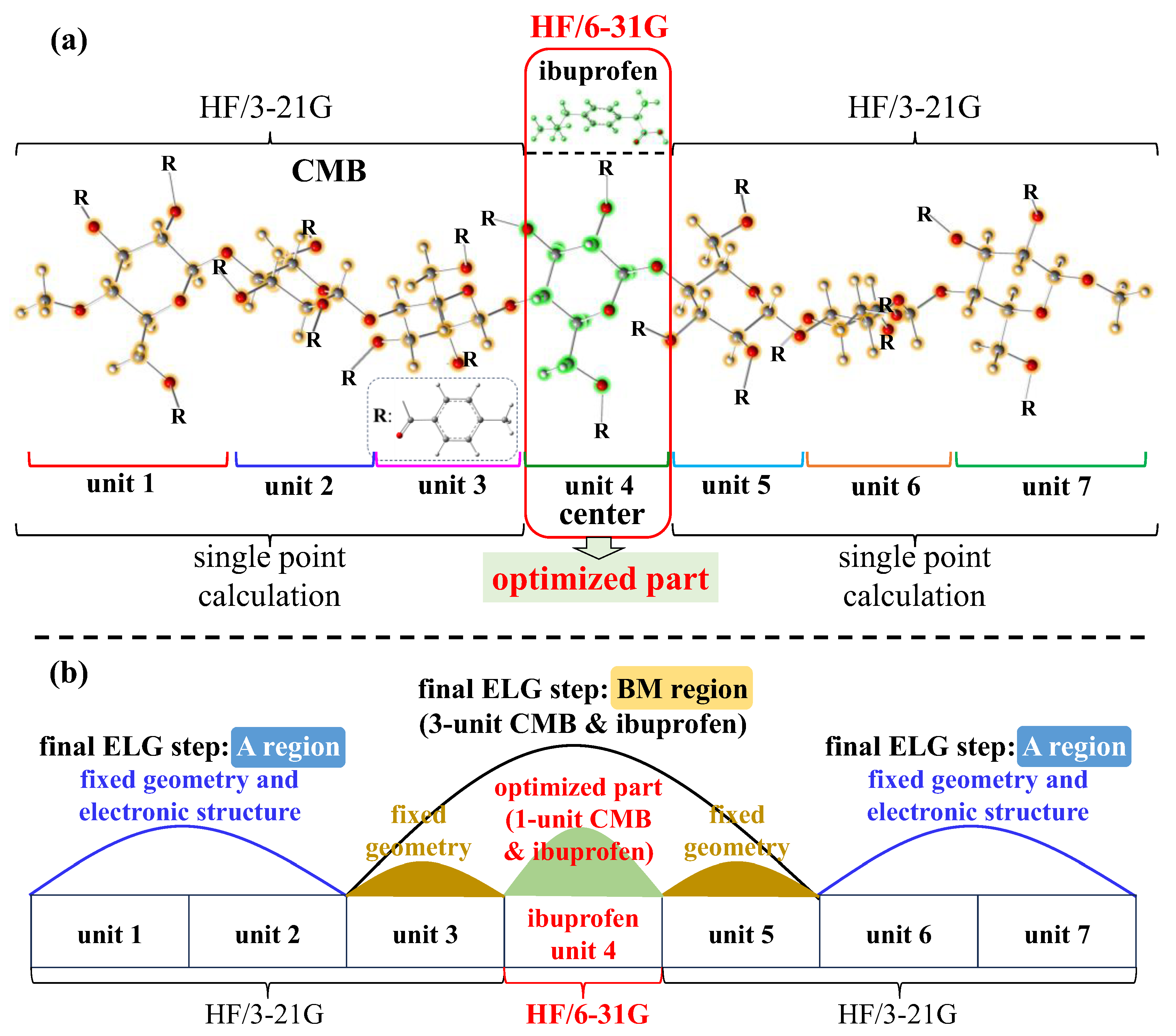
3.1.3. ML-T2C-ELG Method
3.2. Computational Details
3.2.1. Docking Simulation
3.2.2. Geometry Optimization
3.2.3. Complexation Energy Calculation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CMB | cellulose tris(4-methylbenzoate) |
| ELG | elongation |
| T2C-ELG | terminal-to-center elongation |
| ML-T2C-ELG | multi-level layered terminal-to-center elongation |
| HPLC | high-performance liquid chromatography |
| 2-APA | 2-arylpropionic acid |
| PGs | prostaglandins |
| COX-1 | cyclooxygenase-1 |
| COX-2 | cyclooxygenase-2 |
| CSPs | chiral stationary phases |
| MD | molecular dynamics |
| QC | quantum chemical |
| DFT | density functional theory |
| RMSD | root mean square deviation |
| BSSE | basis set superposition error |
| CMOs | canonical molecular orbitals |
| RLMOs | regional localized molecular orbitals |
| M | monomer |
| MM | molecular mechanics |
References
- Vashistha, V.K.; Kumar, T.; Yadav, S.; Das, D.K. Enantioselective Separation and Determination of Ibuprofen: Stereoselective Pharmacokinetics, Pharmacodynamics and Analytical Methods. Chirality 2024, 36, e23647. [Google Scholar] [CrossRef]
- Davies, N.M. Clinical Pharmacokinetics of Ibuprofen. The first 30 years. Clin. Pharmacokinet. 1998, 34, 101–154. [Google Scholar] [CrossRef]
- Evans, A.M. Comparative Pharmacology of S(+)-ibuprofen and (RS)-ibuprofen. Clin. Rheumatol. 2001, 20, 9–14. [Google Scholar] [CrossRef]
- Cheng, H.; Rogers, J.D.; Demetriades, J.L.; Holland, S.D.; Seibold, J.R.; Depuy, E. Pharmacokinetics and Bioinversion of Ibuprofen Enantiomers in Humans. Pharm. Res. 1994, 11, 824–830. [Google Scholar] [CrossRef]
- Geisslinger, G.; Schuster, O.; Stock, K.P.; Loew, D.; Bach, G.L.; Brune, K. Pharmacokinetics of S(+)- and R(−)-ibuprofen in Volunteers and First Clinical Experience of S(+)-ibuprofen in Rheumatoid Arthritis. Eur. J. Clin. Pharmacol. 1990, 38, 493–497. [Google Scholar] [CrossRef]
- Brooks, W.H.; Guida, W.C.; Daniel, K.G. The Significance of Chirality in Drug Design and Development. Curr. Top. Med. Chem. 2011, 11, 760–770. [Google Scholar] [CrossRef]
- Foroughbakhshfasaei, M.; Szabó, Z.I.; Mirzahosseini, A.; Horváth, P.; Tóth, G. Enantiomeric Quality Control of R-Tofisopam by HPLC using Polysaccharide-Type Chiral Stationary Phases in Polar Organic Mode. Electrophoresis 2018, 39, 2566–2574. [Google Scholar] [CrossRef]
- Calcaterra, A.; D’Acquarica, I. The Market of Chiral Drugs: Chiral Switches versus de novo Enantiomerically Pure Compounds. J. Pharmaceut. Biomed. Anal. 2018, 147, 323–340. [Google Scholar] [CrossRef]
- Przejczowska-Pomierny, K.; Włodyka, M.; Cios, A.; Wyska, E. Enantioselective Analysis of Ibuprofen Enantiomers in Mice Plasma and Tissues by High-Performance Liquid Chromatography with Fluorescence Detection: Application to a Pharmacokinetic Study. Chirality 2017, 29, 500–511. [Google Scholar] [CrossRef]
- Cao, S.; Zhou, Y.; Ma, Q.; Zhang, J.; Wang, Z. Experimental and Computational Studies of Enantioseparation of Three Profen Enantiomers with a Focus on Quantification of the Enantiomeric Impurities Present in the Corresponding Enantiopure S-profen Drugs. J. Chromatogr. A 2022, 1673, 463095. [Google Scholar] [CrossRef]
- Dallocchio, R.; Dessì, A.; Sechi, B.; Chankvetadze, B.; Jibuti, G.; Cossu, S.; Mamane, V.; Peluso, P. Enantioseparation of Planar Chiral Ferrocenes on Cellulose-Based Chiral Stationary Phases: Benzoate versus Carbamate Pendant Groups. Electrophoresis 2023, 44, 203–216. [Google Scholar] [CrossRef]
- Dallocchio, R.; Dessì, A.; Sechi, B.; Peluso, P. Molecular Dynamics Simulations of Amylose- and Cellulose-Based Selectors and Related Enantioseparations in Liquid Phase Chromatography. Molecules 2023, 28, 7419. [Google Scholar] [CrossRef]
- Cao, S.; Xie, C.; Ma, Q.; Wang, S.; Zhang, J.; Wang, Z. Enantioselective Separation of Nonsteroidal Anti-Inflammatory Drugs with Amylose Tris(3-chloro-5-methylphenylcarbamate) Stationary Phase in HPLC with a Focus on Enantiomeric Quality Control in Six Pharmaceutical Formulations Containing Racemic Mixtures or Single Stereoisomers. Chirality 2021, 33, 938–950. [Google Scholar] [CrossRef]
- Okamoto, Y.; Kawashima, M.; Yamamoto, K.; Hatada, K. Useful Chiral Packing Materials for High-Performance Liquid Chromatographic Resolution. Cellulose Triacetate and Tribenzoate Coated on Macroporous Silica Gel. Chem. Lett. 1984, 13, 739–742. [Google Scholar] [CrossRef]
- Okamoto, Y.; Aburatani, R.; Hatada, K. Chromatographic Chiral Resolution: XIV. Cellulose Tribenzoate Derivatives as Chiral Stationary Phases for High-Performance Liquid Chromatography. J. Chromatogr. A 1987, 389, 95–102. [Google Scholar] [CrossRef]
- Chankvetadze, B.; Yashima, E.; Okamoto, Y. Dimethyl-, Dichloro- and Chloromethylphenylcarbamates of Amylose as Chiral Stationary Phases for High-Performance Liquid Chromatography. J. Chromatogr. A 1995, 694, 101–109. [Google Scholar] [CrossRef]
- Okamoto, Y.; Yashima, E. Polysaccharide Derivatives for Chromatographic Separation of Enantiomers. Angew. Chem. Int. Ed. 1998, 37, 1020–1043. [Google Scholar] [CrossRef]
- Peluso, P.; Chankvetadze, B. Recognition in the Domain of Molecular Chirality: From Noncovalent Interactions to Separation of Enantiomers. Chem. Rev. 2022, 122, 13235–13400. [Google Scholar] [CrossRef]
- O’Brien, T.; Crocker, L.; Thompson, R.; Thompson, K.; Toma, P.H.; Conlon, D.A.; Feibush, B.; Moeder, C.; Bicker, G.; Grinberg, N. Mechanistic Aspects of Chiral Discrimination Modified Cellulose. Anal. Chem. 1997, 69, 1999–2007. [Google Scholar] [CrossRef]
- Murakami, Y.; Shibata, T.; Ueda, K. Discrimination between Naphthacene and Triphenylene using Cellulose Tris(4-methylbenzoate) and Cellulose Tribenzoate: A Computational Study. Carbohydr. Res. 2017, 439, 35–43. [Google Scholar] [CrossRef]
- Peluso, P.; Chankvetadze, B. The Molecular Bases of Chiral Recognition in 2-(Benzylsulfinyl)benzamide Enantioseparation. Anal. Chim. Acta 2021, 1141, 194–205. [Google Scholar] [CrossRef]
- Veljković, D.Ž.; Đunović, A.B.; Zarić, S.D. Significant Differences in the Energy of X-H/Pt Interactions between Cisplatin and Transplatin Molecules. ChemistrySelect 2019, 4, 12909–12914. [Google Scholar] [CrossRef]
- Imamura, A.; Aoki, Y.; Maekawa, K. A Theoretical Synthesis of Polymers by using Uniform Localization of Molecular Orbitals: Proposal of an Elongation Method. J. Chem. Phys. 1991, 95, 5419–5431. [Google Scholar] [CrossRef]
- Aoki, Y.; Gu, F.L. An Elongation Method for Large Systems toward Bio-Systems. Phys. Chem. Chem. Phys. 2012, 14, 7640–7668. [Google Scholar] [CrossRef]
- Liu, K.; Inerbaev, T.; Korchowiec, J.; Gu, F.L.; Aoki, Y. Geometry Optimization for Large Systems by the Elongation Method. Theor. Chem. Acc. 2012, 131, 1277. [Google Scholar] [CrossRef]
- Hisama, K.; Orimoto, Y.; Pomogaeva, A.; Nakatani, K.; Aoki, Y. Ab Initio Multi-Level Layered Elongation Method and Its Application to Local Interaction Analysis between DNA Bulge and Ligand Molecules. J. Chem. Phys. 2021, 155, 044110. [Google Scholar] [CrossRef]
- Yashima, E.; Yamada, M.; Kaida, Y.; Okamoto, Y. Computational Studies on Chiral Discrimination Mechanism of Cellulose Trisphenylcarbamate. J. Chromatogr. A 1995, 694, 347–354. [Google Scholar] [CrossRef]
- Steinmeier, H.; Zugenmaier, P. “Homogeneous” and “Heterogeneous” Cellulose Tri-esters and a Cellulose Triurethane: Synthesis and Structural Investigations of the Crystalline State. Carbohydr. Res. 1987, 164, 97–105. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhu, B.; Zhao, F.; Yu, J.; Wang, Z.; Song, Y.; Li, Q. Chiral Separation and a Molecular Modeling Study of Eight Azole Antifungals on the Cellulose Tris(3, 5-dichlorophenylcarbamate) Chiral Stationary Phase. New J. Chem. 2018, 42, 13421–13429. [Google Scholar] [CrossRef]
- Yamamoto, C.; Yamada, K.; Motoya, K.; Kamiya, Y.; Kamigaito, M.; Okamoto, Y.; Aratani, T. Preparation of HPLC Chiral Packing Materials using Cellulose Tris(4-methylbenzoate) for the Separation of Chrysanthemate Isomers. J. Polym. Sci. Part A Polym. Chem. 2006, 44, 5087–5097. [Google Scholar] [CrossRef]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization, and Multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, Version 6; Semichem Inc.: Shawnee Mission, KS, USA, 2016.
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B Condens. Matter Mater. Phys. 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H. Results Obtained with the Correlation Energy Density Functionals of Becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200–206. [Google Scholar] [CrossRef]
- Delle Piane, M.; Corno, M.; Pedone, A.; Dovesi, R.; Ugliengo, P. Large-Scale B3LYP Simulations of Ibuprofen Adsorbed in MCM-41 Mesoporous Silica as Drug Delivery System. J. Phys. Chem. C 2014, 118, 26737–26749. [Google Scholar] [CrossRef]
- Sa’adeh, H.; Maris, A.; Prince, K.C.; Plekan, O.; Grazioli, C.; Coreno, M.; Richter, R. Insights into the Electronic Structure of Non-steroidal Anti-Inflammatory Drugs: Soft X-ray Study of Fenoprofen, Ketoprofen and Methyl Salicylate in the Gas Phase. Phys. Chem. Chem. Phys. 2024, 26, 29082–29094. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A Visualization System for Exploratory Research and Analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef]
- Morris, G.M.; Huey, R.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. AutoDock4 and AutoDockTools4: Automated Docking with Selective Receptor Flexibility. J. Comput. Chem. 2009, 30, 2785–2791. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Su, P.; Liang, H.; Li, Y.; Ke, Z. Insight into Roles of Rare-Earth Metals in Heterobimetallic Ni–Y Bifunctional Catalysis for Alkyne Semihydrogenation. ACS Catal. 2024, 14, 18278–18291. [Google Scholar] [CrossRef]
- Guzmán, J.; Urriolabeitia, A.; Padilla, M.; García-Orduña, P.; Polo, V.; Fernández-Alvarez, F.J. Mechanism Insights into the Iridium (III)-and B(C6F5)3-Catalyzed Reduction of CO2 to the Formaldehyde Level with Tertiary Silanes. Inorg. Chem. 2022, 61, 20216–20221. [Google Scholar] [CrossRef]


| Ligand | E_Total (Complex) a | E_Total (CMB) b | E_Total (Ligand) c | E (BSSE) | Complexation Energy d |
|---|---|---|---|---|---|
| (a.u.) | (a.u.) | (a.u.) | (kcal/mol) | (kcal/mol) | |
| R-ibuprofen | −13,149.2976297 | −12,492.3431564 | −656.8938190 | 7.9 | −30.2 |
| S-ibuprofen | −13,149.2949832 | −12,492.3403913 | −656.8883585 | 8.5 | −33.0 |
| Atom Pairs | Interaction Type | Distance (Å) | Angle (°) Between Two Phenyl Rings | |||
|---|---|---|---|---|---|---|
| Ibuprofen | CMB | R-Ibuprofen | S-Ibuprofen | R-Ibuprofen | S-Ibuprofen | |
| (C=O) O | H-C | O···H-C | 2.29 | 2.34 | ||
| (C=O) O | H-C | O···H-C | 2.97 | 2.63 | ||
| O-H | O (pyranose) | O-H···O | 2.07 | 2.46 | ||
| O-H | O (O=C) | O-H···O | 2.17 | 1.67 | ||
| phenyl | phenyl | T-shaped π-π | 5.41 | 5.81 | 122.2 | 90 |
| phenyl | phenyl | parallel π-π | — a | 3.67 | — b | 165.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Orimoto, Y.; Aoki, Y. Theoretical Examination on the Chiral Separation Mechanism of Ibuprofen on Cellulose Tris(4-methylbenzoate). Molecules 2025, 30, 3503. https://doi.org/10.3390/molecules30173503
Huang X, Orimoto Y, Aoki Y. Theoretical Examination on the Chiral Separation Mechanism of Ibuprofen on Cellulose Tris(4-methylbenzoate). Molecules. 2025; 30(17):3503. https://doi.org/10.3390/molecules30173503
Chicago/Turabian StyleHuang, Xiao, Yuuichi Orimoto, and Yuriko Aoki. 2025. "Theoretical Examination on the Chiral Separation Mechanism of Ibuprofen on Cellulose Tris(4-methylbenzoate)" Molecules 30, no. 17: 3503. https://doi.org/10.3390/molecules30173503
APA StyleHuang, X., Orimoto, Y., & Aoki, Y. (2025). Theoretical Examination on the Chiral Separation Mechanism of Ibuprofen on Cellulose Tris(4-methylbenzoate). Molecules, 30(17), 3503. https://doi.org/10.3390/molecules30173503







