Hydrophobicity of Benzene-Based Surfactants and Its Effect on Bubble Coalescence Inhibition
Abstract
1. Introduction
2. Results and Discussion
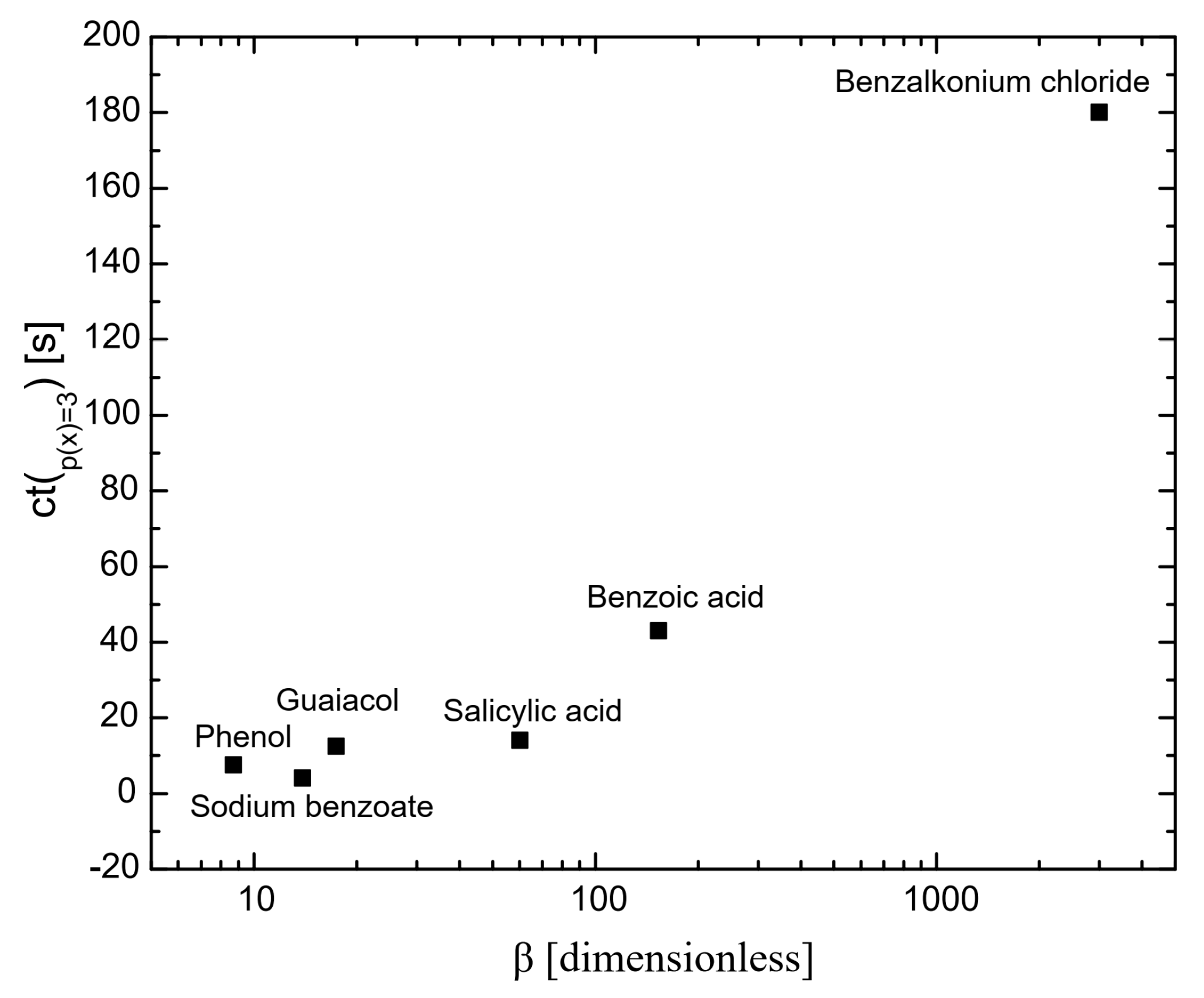
2.1. Coalescence Time

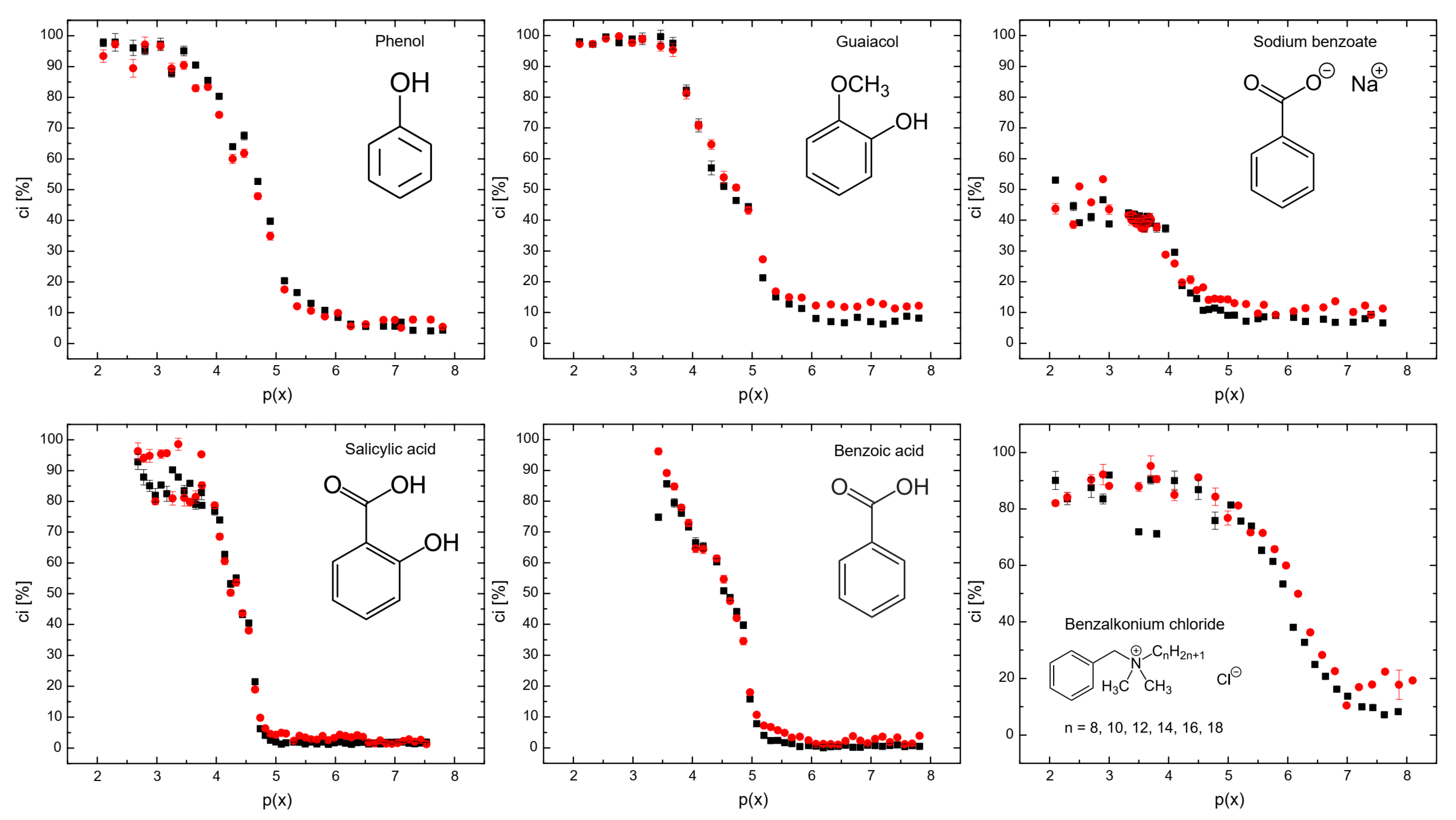
2.2. Coalescence Inhibition
| Surfactant | Upper Detector | Lower Detector |
|---|---|---|
| p(x0) A | p(x0) B | |
| Phenol | 4.66 | 4.59 |
| Guaiacol | 4.58 | 4.56 |
| Sodium Benzoate | 4.16 | 4.03 |
| Salicylic acid | 4.50 | 4.41 |
| Benzoic acid | 4.86 | 4.81 |
| Benzalkonium chloride | 6.02 | 6.19 |

2.3. The Relationship Between Bubble Size and Hydrophobicity
3. Materials and Methods
3.1. Materials
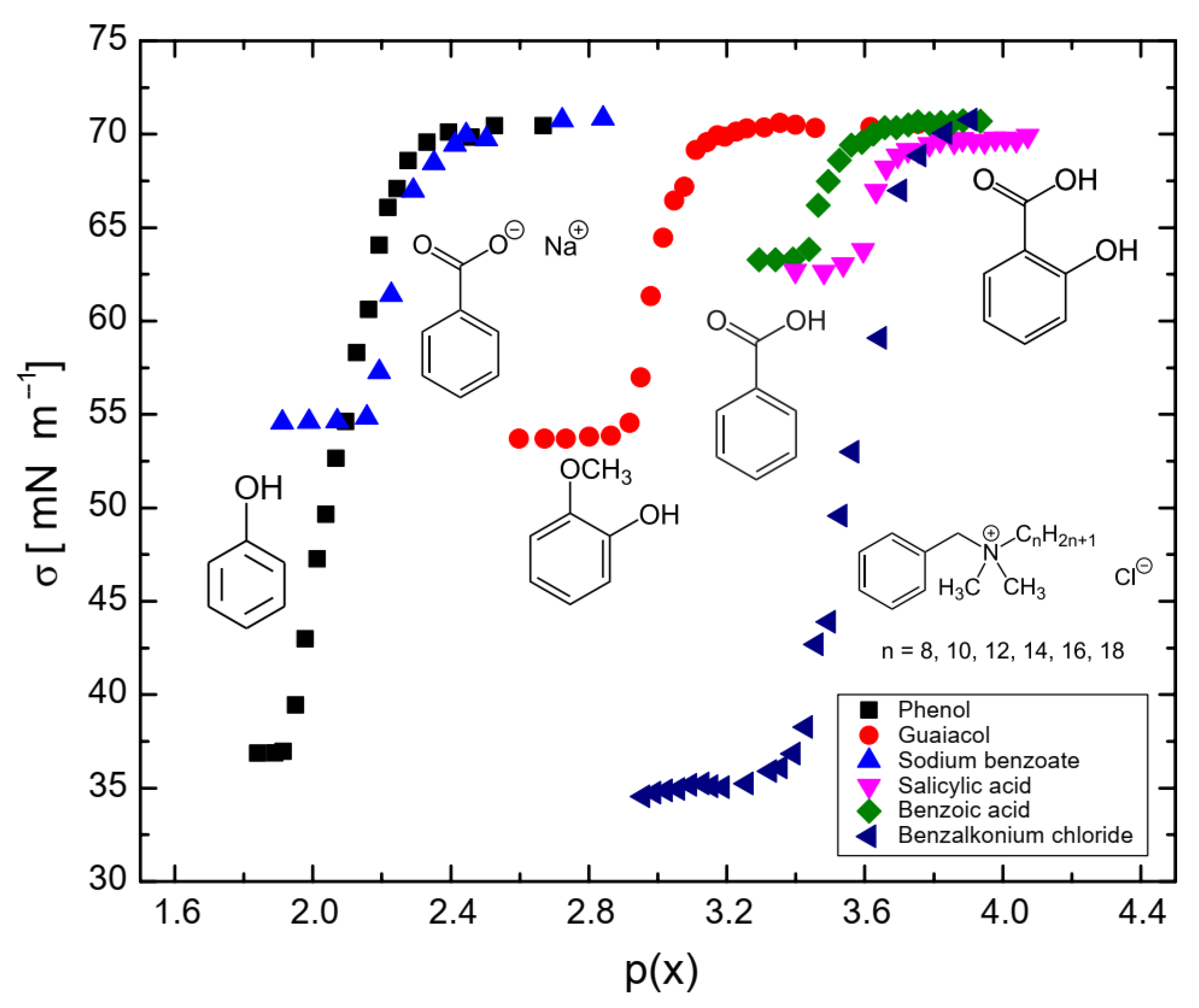
3.2. Surface Tension Measurements
| Surfactant | β | ΓsRT [mmol/m2] |
|---|---|---|
| Phenol | 7.8 ± 3.2 | 17 ± 2.6 |
| Guaiacol | 11.3 ± 1.5 | 16 ± 3.7 |
| Sodium benzoate | 19.4 ± 4.1 | 15 ± 1.8 |
| Salicylic acid | 55.5 ± 10.6 | 17 ± 2.2 |
| Benzoic acid | 125.9 ± 31.8 | 10 ± 1.3 |
| Benzalkonium chloride | 3001 ± 365.9 | 20 ± 1.7 |
3.3. Coalescence Measurements
3.3.1. Coalescence Time Measurements

3.3.2. Coalescence Inhibition Measurements

3.4. Bubble Size Measurements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Langevin, D. Recent Advances on Emulsion and Foam Stability. Langmuir 2023, 39, 3821–3828. [Google Scholar] [CrossRef] [PubMed]
- Carter, B.O.; Wang, W.; Adams, D.J.; Cooper, A.I. Gas storage in “Dry Water” and “Dry Gel” clathrates. Langmuir 2010, 26, 3186–3193. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Pereira, J.-M.; Gan, Y. Effect of Wetting Transition during Multiphase Displacement in Porous Media. Langmuir 2020, 36, 2449–2458. [Google Scholar] [CrossRef] [PubMed]
- Wisløff, U.; Richardson, R.S.; Brubakk, A.O. Exercise and nitric oxide prevent bubble formation: A novel approach to the prevention of decompression sickness? J. Physiol. 2004, 555, 825–829. [Google Scholar] [CrossRef]
- Mathavan, A.; Jones, K.; Ataya, A. Systemic capillary leak syndrome secondary to decompression sickness. BMJ Case Rep. 2023, 16, e253045. [Google Scholar] [CrossRef]
- Velázquez-Wallraf, A.; Caballero, M.J.; Fernández, A.; Betancor, M.B.; Saavedra, P.; Hemingway, H.W.; de Quirós, Y.B. Biomarkers related to gas embolism: Gas score, pathology, and gene expression in a gas bubble disease model. PLoS ONE 2023, 18, e0288659. [Google Scholar] [CrossRef]
- Little, T.; Butler, B.D. Pharmacological Intervention to the Inflammatory Response from Decompression Sickness in Rats. Aviat. Space Environ. Med. 2008, 79, 87–93. [Google Scholar] [CrossRef]
- Schwarz, W.J.; Martin, A.R.; Davis, R.C. The Influence of Calcium on the Adsorption of Sodium Dodecylbenzenesulfonate of Cottons. Text. Res. J. 1962, 32, 1–8. [Google Scholar] [CrossRef]
- Choi, S.M.; Roh, T.H.; Lim, D.S.; Kacew, S.; Kim, H.S.; Lee, B.-M. Risk assessment of benzalkonium chloride in cosmetic products. J. Toxicol. Environ. Health B 2018, 21, 8–23. [Google Scholar] [CrossRef]
- Pereira, B.M.P.; Tagkopoulos, I. Benzalkonium Chlorides: Uses, Regulatory Status, and Microbial Resistance. Appl. Environ. Microbiol. 2019, 85, e00377-19. [Google Scholar]
- Craig, V.S.J. Bubble coalescence and specific-ion effects. Curr. Opin. Colloid Interface Sci. 2004, 9, 178–184. [Google Scholar] [CrossRef]
- Guo, H.; Liu, Q.; Huang, L.; Liu, J.; Bao, X.; Zhang, F.; Cao, Y.; Gui, X.; Xing, Y.; Xu, M. Microfluidic Investigation of the Ion-Specific Effect on Bubble Coalescence in Salt Solutions. Langmuir 2023, 39, 8234–8243. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, H.; Wang, T. A model of bubble coalescence in the presence of a nonionic surfactant with a low bubble approach velocity. AIChE J. 2022, 68, e17743. [Google Scholar] [CrossRef]
- Yang, Y.M.; Maa, J.R. Bubble coalescence in dilute surfactant solutions. J. Colloid Interface Sci. 1984, 98, 120–125. [Google Scholar] [CrossRef]
- Beneventi, D.; Belgacem, M.N.; Carré, B. Influence of surfactant structure on bubble size and foaming in bubble columns: Focus on flotation de-inking. Nord. Pulp Pap. Res. J. 2006, 21, 702–709. [Google Scholar] [CrossRef]
- Arenas-Quevedo, M.G.; Gracia-Fadrique, J. The Gibbs adsorption isotherm, the total surface pressure and surface pressure of micellar formation. Fluid Ph. Equilibria 2023, 573, 113875. [Google Scholar] [CrossRef]
- Langevin, D. Bubble coalescence in pure liquids and in surfactant solutions. Curr. Opin. Colloid Interface Sci. 2015, 20, 92–97. [Google Scholar] [CrossRef]
- Doe, P.H.; El-Emary, M.; Wade, W.H.; Schechter, R.S. Surfactants for producing low interfacial tensions I: Linear alkyl benzene sulfonates. J. Am. Oil Chem. Soc. 1977, 54, 570–577. [Google Scholar] [CrossRef]
- García-Figueroa, A.A.; López-Cervantes, J.L.; Gracia-Fadrique, J. Phase equilibrium with a two-phase system with surface area. Fluid Ph. Equilibria 2023, 564, 113616. [Google Scholar] [CrossRef]
- Li, P.; Huang, H.; Fang, Y.; Wang, Y.; No, D.S.; Bhatnagar, R.S.; Abbaspourrad, A. Interfacial engineering of clear emulsions: Surfactant hydrophobicity and the hidden role of chain structure. Colloids Surf. A 2023, 676, 132242. [Google Scholar] [CrossRef]
- Kristen, N.; Vüllings, A.; Laschewsky, A.; Miller, R.; von Klitzing, R. Foam Films from Oppositely Charged Polyelectolyte/Surfactant Mixtures: Effect of Polyelectrolyte and Surfactant Hydrophobicity on Film Stability. Langmuir 2010, 26, 9321–9327. [Google Scholar] [CrossRef] [PubMed]
- Sharipova, A.; Aidarova, S.; Cernoch, P.; Miller, R. Effect of surfactant hydrophobicity on the interfacial properties of polyallylamine hydrochloride/sodium alkylsulphate at water/hexane interface. Colloids Surf. A 2013, 438, 141–147. [Google Scholar] [CrossRef]
- Politova, N.I.; Tcholakova, S.; Tsibranska, S.; Denkov, N.D.; Muelheims, K. Coalescence stability of water-in-oil drops: Effects of drop size and surfactant concentration. Colloids Surf. A 2017, 531, 32–39. [Google Scholar] [CrossRef]
- Nowak, E.; Kovalchuk, N.M.; Che, Z.; Simmons, M.J.H. Effect of surfactant concentration and viscosity of outer phase during the coalescence of a surfactant-laden drop with a surfactant-free drop. Colloids Surf. A 2016, 505, 124–131. [Google Scholar] [CrossRef]
- Berg, J.M.; Eriksson, L.G.T.; Claesson, P.M.; Borve, K.G.N. Three-Component Langmuir-Blodgett Films with a Controllable Degree of Polarity. Langmuir 1994, 10, 1225–1234. [Google Scholar] [CrossRef]
- Tilton, R.D.; Robertson, C.R.; Gast, A.P. Manipulation of hydrophobic interactions in protein adsorption. Langmuir 1991, 7, 2710–2718. [Google Scholar] [CrossRef]
- Kaur, J.; Farzeen, R.; Singh, M.; Thakur, N.; Lal, M.; Upadhyaya, S.K.; Walia, Y.K.; Kishore, K. Overview of Surfactants, Properties, Types, and Role in Chemistry. In Advances in Surfactant Biosensor and Sensor Technologies; Manjunatha, J.G., Ed.; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Henry, C.L.; Craig, V.S.J. Inhibition of Bubble Coalescence by Osmolytes: Sucrose, Other Sugars, and Urea. Langmuir 2009, 25, 11406–11412. [Google Scholar] [CrossRef]
- Doble, M. Perry’s Chemical Engineers’ Handbook; McGraw-Hill: New York, NY, USA, 1984. [Google Scholar]
- Pesci, C.; Weiner, A.; Marschall, H.; Bothe, D. Computational analysis of single rising bubbles influenced by soluble surfactant. J. Fluid Mech. 2018, 856, 709–763. [Google Scholar] [CrossRef]
- Parhizkar, M.; Edirisinghe, M.; Stride, E. The effect of surfactant type and concentration on the size and stability of microbubbles produced in a capillary embedded T-junction device. RSC Adv. 2015, 5, 10751–10762. [Google Scholar] [CrossRef]
- Pardo-Cervantes, A.; Viades-Trejo, J.; Gracia-Fadrique, J. Activity coefficients at infinite dilution and critical micelle concentrations of poly(oxy-1,2-ethanedyil), α-tridecyl-ω-hydroxy ethers (c13ei = 6, 10, 18) in aqueous media by the Volmer surface equation of state and group contributions. J. Chem. Eng. Data 2011, 56, 2812–2817. [Google Scholar] [CrossRef]
- Leo, A.; Hansch, C.; Elkins, D. Partition coefficients and their uses. Chem. Rev. 1971, 71, 525–674. [Google Scholar] [CrossRef]
- Viades-Trejo, J.; Amigo, A.; Gracia-Fadrique, J. Activity coefficients at infinite dilution for surfactants. Fluid Ph. Equilib. 2006, 250, 158–164. [Google Scholar] [CrossRef]
- Ghosh, P. Coalescence of bubbles in liquid. Bubble Sci. Eng. Technol. 2016, 1, 75–87. [Google Scholar] [CrossRef]
- Oolman, T.O.; Blanch, H.W. Bubble coalescence in stagnant liquids. Chem. Eng. Commun. 2007, 43, 237–261. [Google Scholar] [CrossRef]
- Henry, C.L.; Dalton, C.N.; Scruton, L.; Craig, V.S.J. Ion-Specific Coalescence of Bubbles in Mixed Electrolyte Solutions. J. Phys. Chem. C 2007, 111, 1015–1023. [Google Scholar] [CrossRef]

| Surfactant | d32 [mm] |
|---|---|
| Phenol | 0.49 ± 0.06 |
| Salicylic acid | 0.65 ± 0.12 |
| Benzalkonium chloride | 0.73 ± 0.23 |
| Guaiacol | 0.88 ± 0.19 |
| Benzoic acid | 1.17 ± 0.32 |
| Sodium benzoate | 1.87 ± 0.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Río-Arrillaga, R.; García-Figueroa, A.A.; López-Cervantes, J.L.; Albijanic, B.; Gracia-Fadrique, J. Hydrophobicity of Benzene-Based Surfactants and Its Effect on Bubble Coalescence Inhibition. Molecules 2024, 29, 5042. https://doi.org/10.3390/molecules29215042
Del Río-Arrillaga R, García-Figueroa AA, López-Cervantes JL, Albijanic B, Gracia-Fadrique J. Hydrophobicity of Benzene-Based Surfactants and Its Effect on Bubble Coalescence Inhibition. Molecules. 2024; 29(21):5042. https://doi.org/10.3390/molecules29215042
Chicago/Turabian StyleDel Río-Arrillaga, Rafael, Arturo A. García-Figueroa, José L. López-Cervantes, Boris Albijanic, and Jesús Gracia-Fadrique. 2024. "Hydrophobicity of Benzene-Based Surfactants and Its Effect on Bubble Coalescence Inhibition" Molecules 29, no. 21: 5042. https://doi.org/10.3390/molecules29215042
APA StyleDel Río-Arrillaga, R., García-Figueroa, A. A., López-Cervantes, J. L., Albijanic, B., & Gracia-Fadrique, J. (2024). Hydrophobicity of Benzene-Based Surfactants and Its Effect on Bubble Coalescence Inhibition. Molecules, 29(21), 5042. https://doi.org/10.3390/molecules29215042






