Competitive Adsorptive Mechanism of H2/N2 in LTA/FAU Zeolites by Molecular Simulations and Experiments
Abstract
1. Introduction
2. Results and Discussion
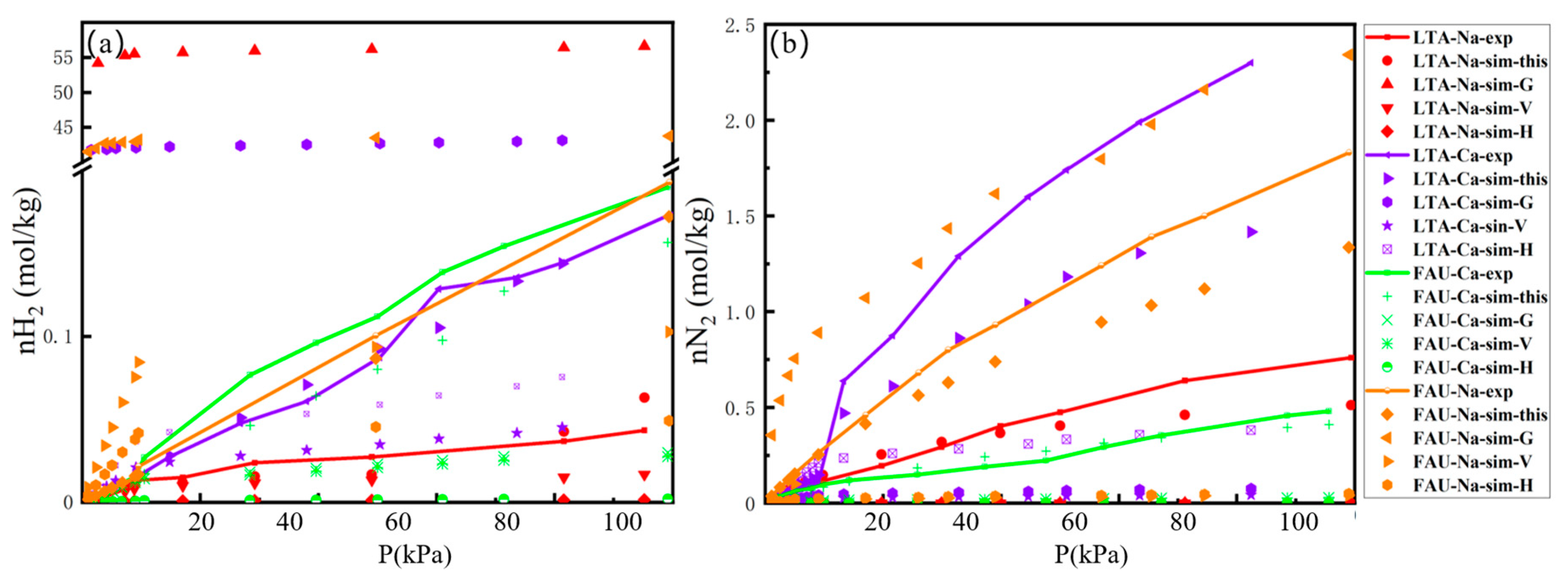
2.1. Adsorption Isotherm
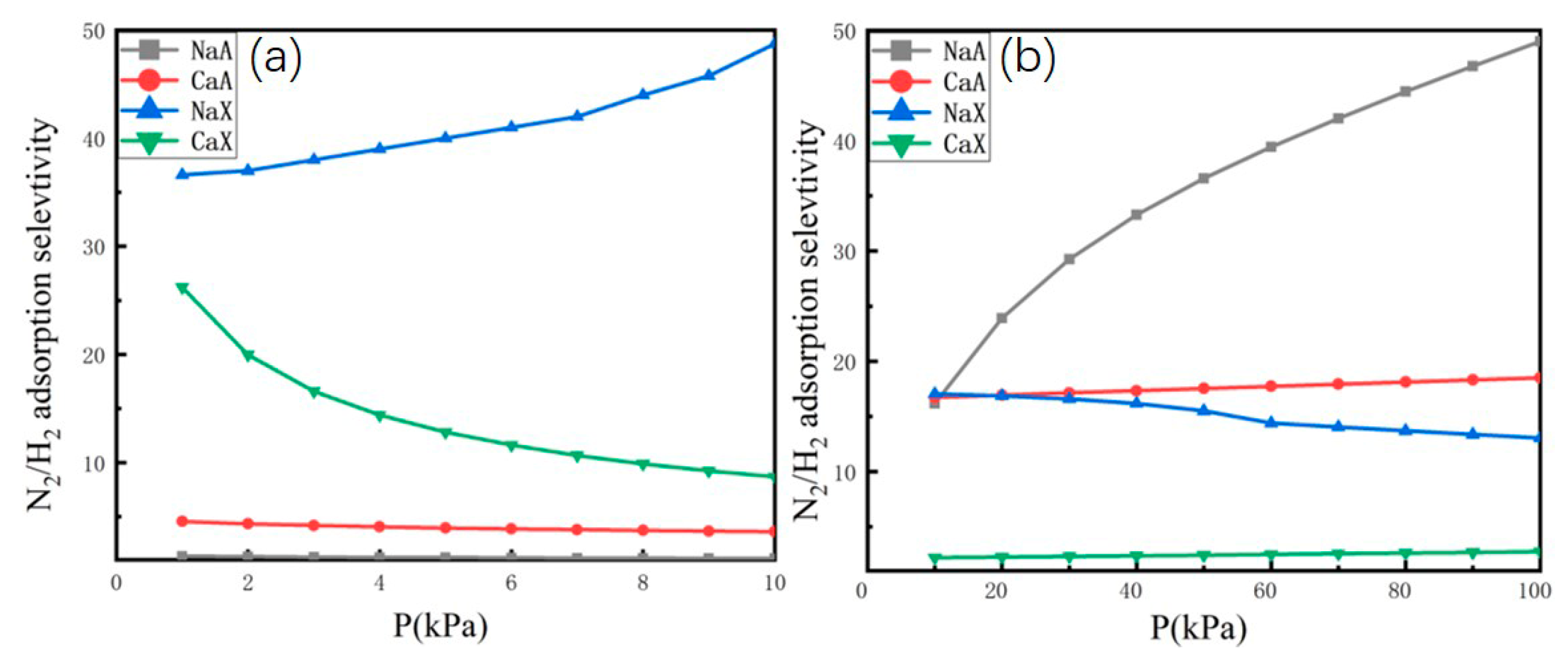
2.2. Adsorption Selectivity and Heat
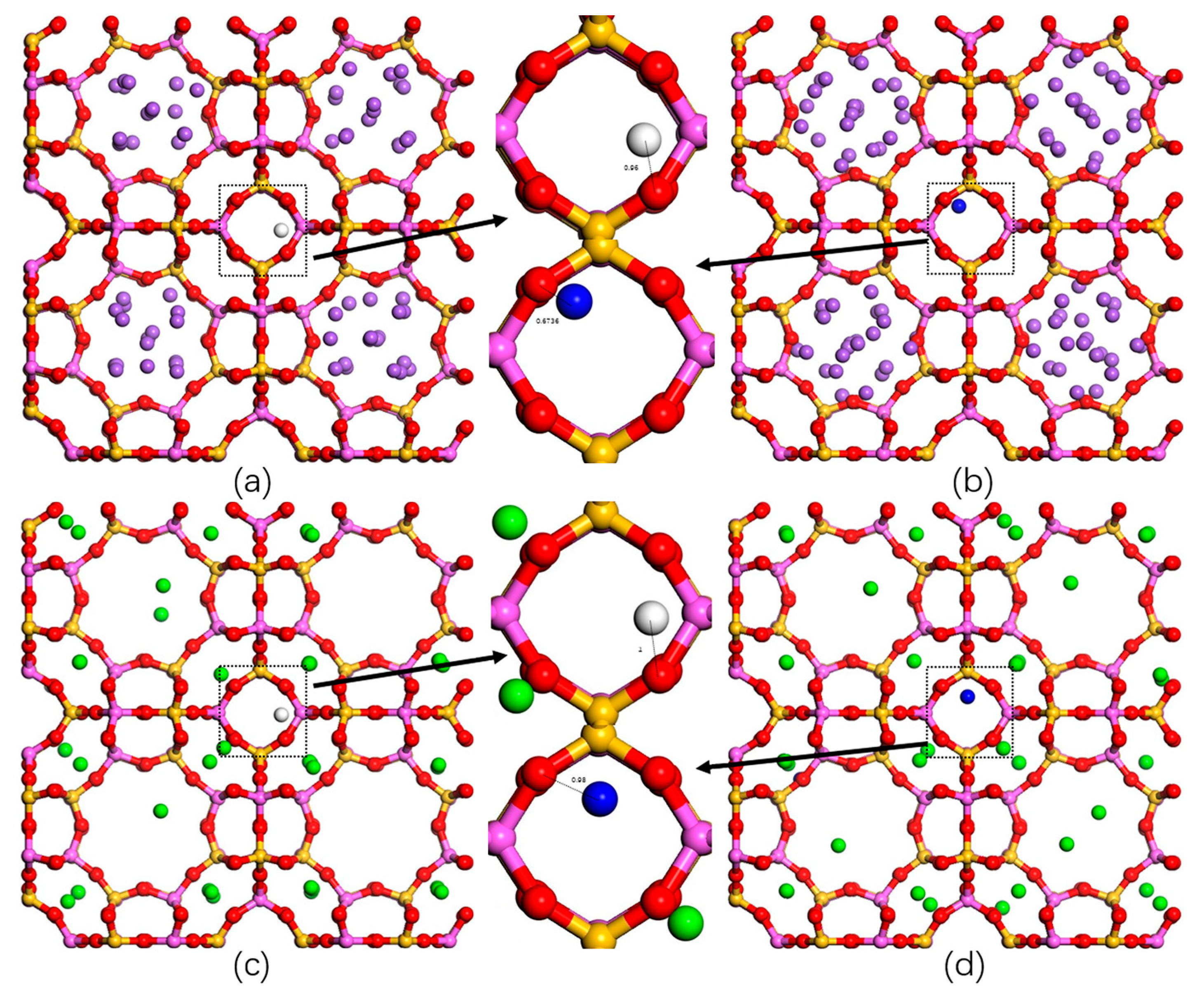
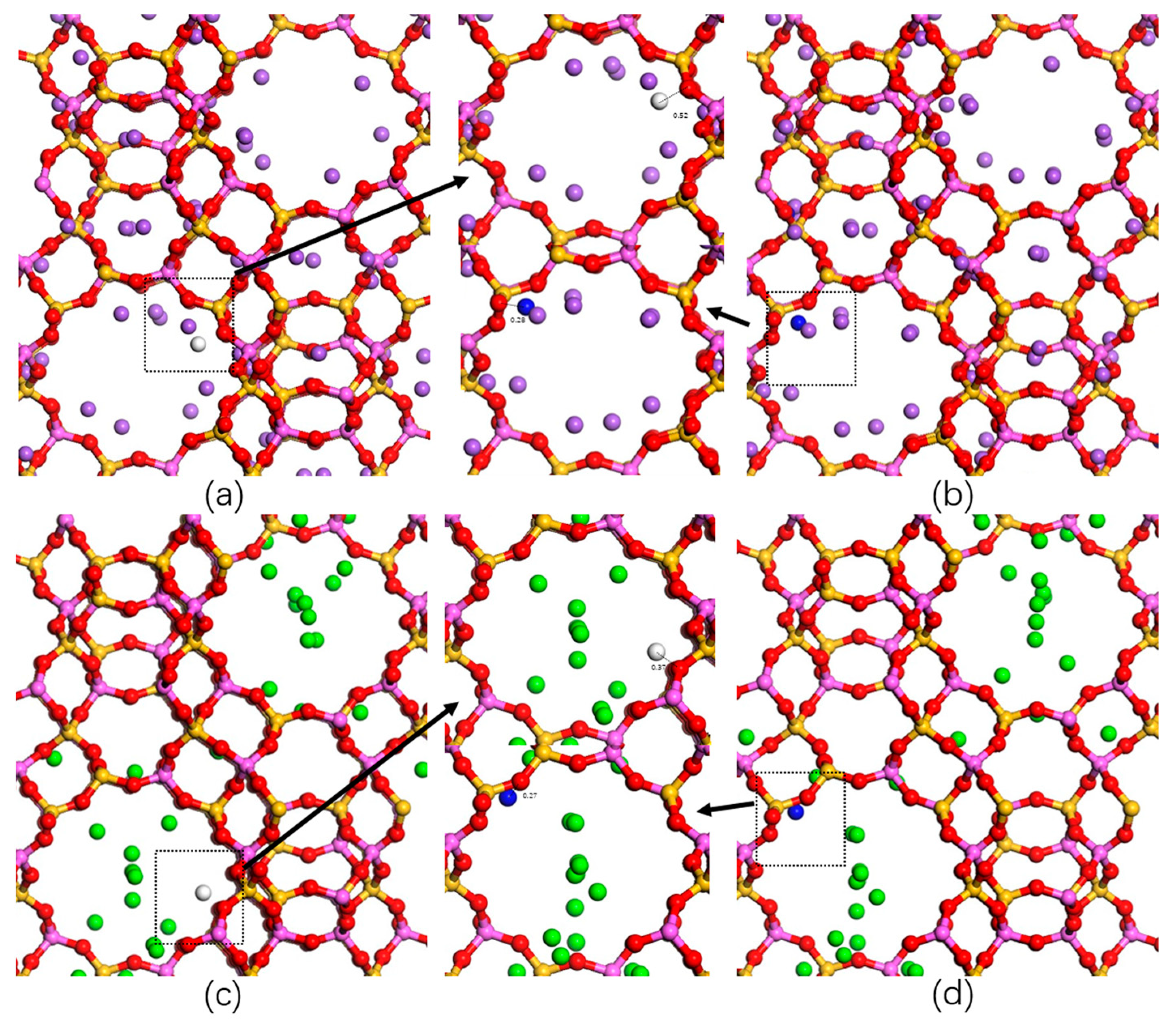
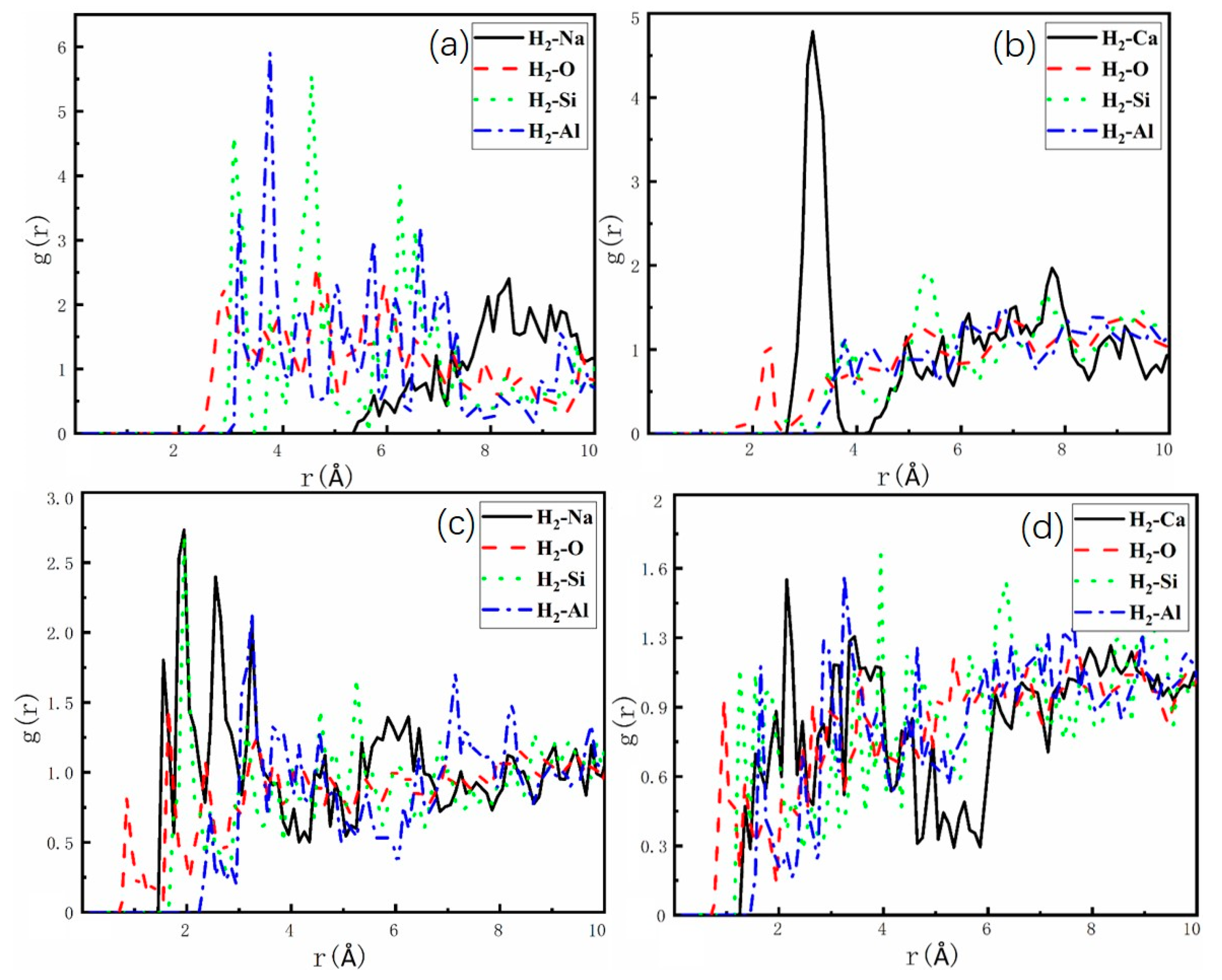
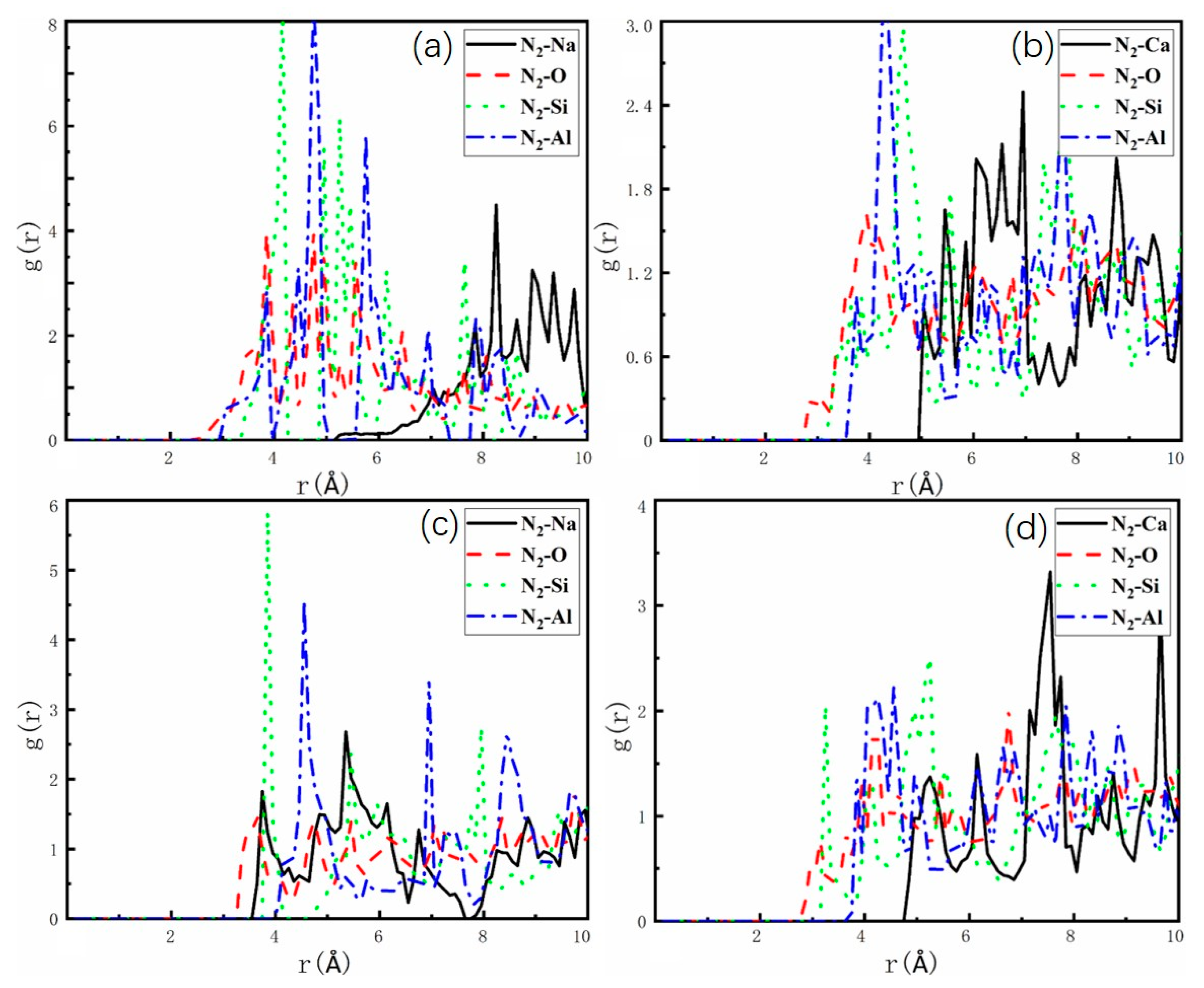
2.3. Adsorption Sites
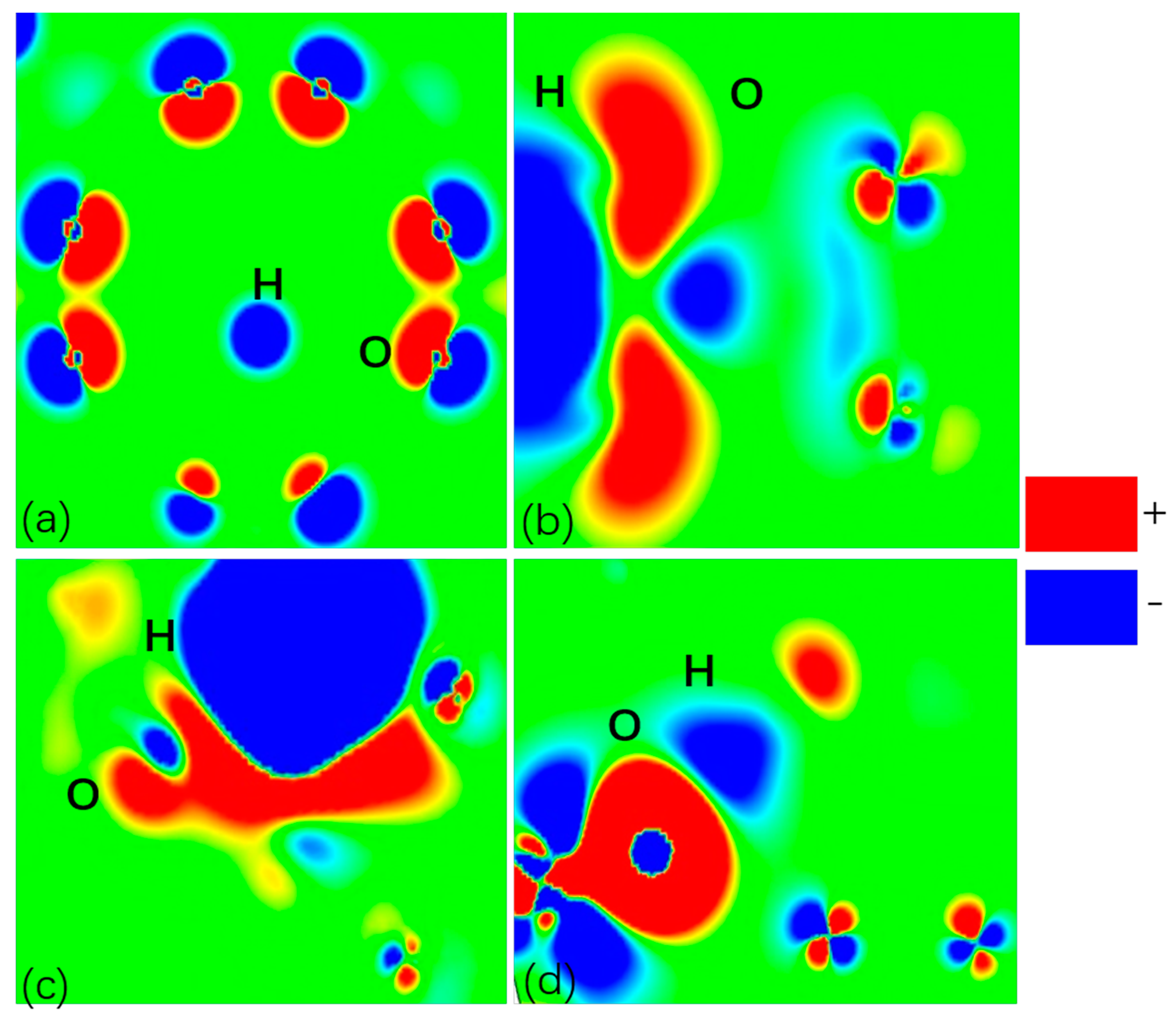
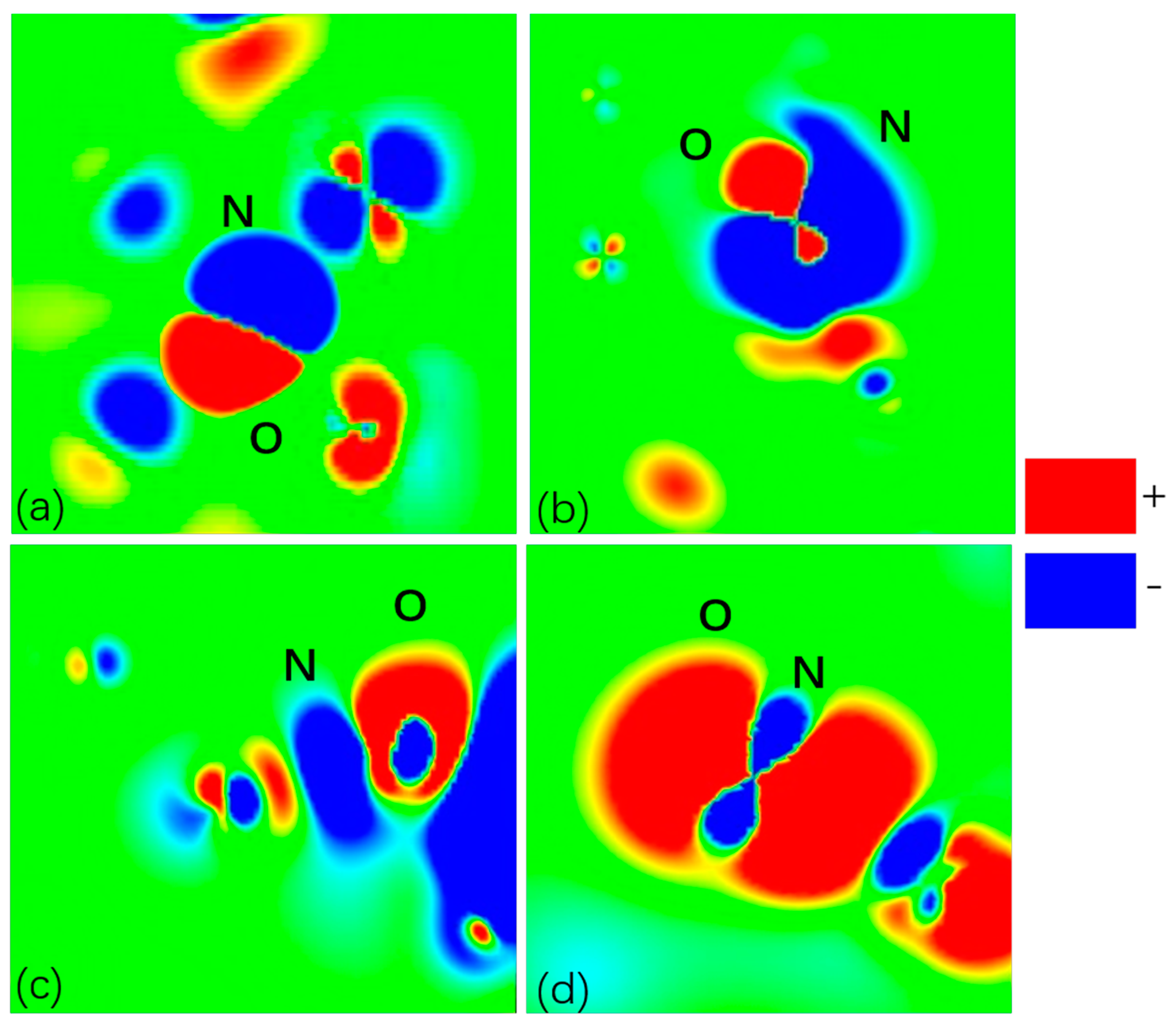
2.4. Investigation of Charge Density
3. Methods
3.1. Framework and Adsorbate: Models and Force Fields
3.2. Simulation Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yusaf, T.; Fernandes, L.; Abu Talib, A.R.; Altarazi, Y.S.; Alrefae, W.; Kadirgama, K.; Ramasamy, D.; Jayasuriya, A.; Brown, G.; Mamat, R.; et al. Sustainable aviation—Hydrogen is the future. Sustainability 2022, 14, 548. [Google Scholar] [CrossRef]
- Ranjekar, A.M.; Yadav, G.D. Steam reforming of methanol for hydrogen production: A critical analysis of catalysis, processes, and scope. Ind. Eng. Chem. Res. 2021, 60, 89–113. [Google Scholar] [CrossRef]
- Amin, A.M.; Croiset, E.; Epling, W. Review of methane catalytic cracking for hydrogen production. Int. J. Hydrogen Energy 2011, 36, 2904–2935. [Google Scholar] [CrossRef]
- Noussan, M.; Raimondi, P.P.; Scita, R.; Hafner, M. The role of green and blue hydrogen in the energy transition—A technological and geopolitical perspective. Sustainability 2021, 13, 298. [Google Scholar] [CrossRef]
- Howarth, R.W.; Jacobson, M.Z. How green is blue hydrogen? Energy Sci. Eng. 2021, 9, 1676–1687. [Google Scholar] [CrossRef]
- Oliveira, A.M.; Beswick, R.R.; Yan, Y. A green hydrogen economy for a renewable energy society. Curr. Opin. Chem. Eng. 2021, 33, 100701–100707. [Google Scholar] [CrossRef]
- Fu, Q.; Wang, D.; Li, X.; Yang, Q.; Xu, Q.; Ni, B.J.; Wang, Q.; Liu, X. Towards hydrogen production from waste activated sludge: Principles, challenges and perspectives. Renew. Sustain. Energy Rev. 2021, 135, 110283–110295. [Google Scholar] [CrossRef]
- Aziz, M.; Darmawan, A.; Juangsa, F.B. Hydrogen production from biomasses and wastes: A technological review. Int. J. Hydrog. Energy 2021, 46, 33756–33781. [Google Scholar] [CrossRef]
- Bartlett, J.; Krupnick, A. Investment Tax Credits for Hydrogen Storage. 2020. Available online: https://www.rff.org/publications/issue-briefs/investment-tax-credits-hydrogen-storage (accessed on 1 August 2023).
- Lopes, F.V.S.; Grande, C.A.; Ribeiro, A.M.; Loureiro, J.M.; Evaggelos, O.; Nikolakis, V.; Rodrigues, A.E. Adsorption of H2, CO2, CH4, CO, N2 and H2O in activated carbon and zeolite for hydrogen production. Sep. Sci. Technol. 2009, 44, 1045–1073. [Google Scholar] [CrossRef]
- Schmitt, N.; Apfelbacher, A.; Jäger, N.; Daschner, R.; Stenzel, F.; Hornung, A. Thermo-chemical conversion of biomass and upgrading to biofuel: The thermo-catalytic reforming process—A review. Biofuels Bioprod. Bioref. 2019, 13, 822–837. [Google Scholar] [CrossRef]
- Rouwenhorst KH, R.; Krzywda, P.M.; Benes, N.E.; Mul, G.; Lefferts, L. Ammonia production technologies. Techno-Econ. Chall. Green Ammon. Energy Vector 2021, 4, 41–83. [Google Scholar]
- Delgado, J.A.; Agueda, V.I.; Uguina, M.A.; Sotelo, J.L.; Brea, P. Hydrogen recovery from off-gases with nitrogen-rich impurity by pressure swing adsorption using CaX and 5A zeolites. Adsorption 2015, 21, 107–123. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, Z.; Jiang, J. Sorption-induced structural transition of zeolitic imidazolate framework-8: A hybrid molecular simulation study. J. Am. Chem. Soc. 2013, 135, 3722–3728. [Google Scholar] [CrossRef] [PubMed]
- Perez-Carbajo, J.; Gómez-Álvarez, P.; Bueno-Perez, R.; Merkling, P.J.; Calero, S. Optimisation of the Fischer–Tropsch process using zeolites for tail gas separation. Phys. Chem. Chem. Phys. 2014, 16, 5678–5688. [Google Scholar] [CrossRef] [PubMed]
- Yaremov, P.S.; Scherban, N.D.; Ilyin, V.G. Adsorption of nitrogen, hydrogen, methane, and carbon oxides on micro- and mesoporous molecular sieves of different nature. Theor. Exp. Chem. 2013, 48, 394–400. [Google Scholar] [CrossRef]
- Wang, Z.M.; Zhang, Y.J.; Liu, T.; Kurmoo, M.; Gao, S. [Fe3(HCOO)6]: A permanent porous diamond framework displaying H2/N2 adsorption, guest inclusion, and guest-dependent magnetism. Adv. Funct. Mater. 2007, 17, 1523–1536. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, X.; Li, J.; Wang, N.; Wang, Z.; Zhou, Y. Synthesis of ordered mesoporous carbon molecular sieve and its adsorption capacity for H2, N2, O2, CH4 and CO2. Chem. Phys. Lett. 2005, 413, 6–9. [Google Scholar] [CrossRef]
- Peng, X.; Jain, S.K.; Singh, J.K. Adsorption and separation of N2/CH4/CO2/SO2 gases in disordered carbons obtained using hybrid reverse Monte Carlo simulations. J. Phys. Chem. C 2017, 121, 13457–13473. [Google Scholar] [CrossRef]
- Ötvös, Z.; Onyestyák, G.; Valyon, J.; Kiricsi, I.; Kónya, Z.; Rees LV, C. The dynamics of H2 and N2 sorption in carbon nanotubes. Appl. Surf. Sci. 2004, 238, 73–76. [Google Scholar] [CrossRef]
- Chisholm, N.O.; Anderson, G.C.; McNally, J.F.; Funke, H.H.; Noble, R.D.; Falconer, J.L. Increasing H2/N2 separation selectivity in CHA zeolite membranes by adding a third gas. J. Membr. Sci. 2015, 496, 118–124. [Google Scholar] [CrossRef]
- Jung, K.Y.; So, J.H.; Park, S.B.; Yang, S.M. Hydrogen separation from the H2/N2 mixture by using a single and multi-stage inorganic membrane. Korean J. Chem. Eng. 1999, 16, 193–201. [Google Scholar] [CrossRef]
- Barrer, R.M. Transient flow of gases in sorbents providing uniform capillary networks of molecular dimensions. Trans. Faraday Soc. 1949, 45, 358–373. [Google Scholar] [CrossRef]
- John, K. Selectivity of Clinoptilolite Towards Heavy Metals from Industrial Wastewater: Equilibrium, Kinetic, Thermodynamic and Elution Studies. Eng. Lett. 2021, 29, 158–167. [Google Scholar]
- Li, G.; Wang, Q.; Jiang, T.; Luo, J.; Rao, M.; Peng, Z. Roll-up effect of sulfur dioxide adsorption on zeolites FAU 13X and LTA 5A. Adsorption 2017, 23, 699–710. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101–014108. [Google Scholar] [CrossRef] [PubMed]
- Kotoh, K.; Takashima, S.; Sakamoto, T.; Tsuge, T. Multi-component behaviors of hydrogen isotopes adsorbed on synthetic zeolites 4A and 5A at 77.4K and 87.3K. Fusion Eng. Des. 2010, 85, 1928–1934. [Google Scholar] [CrossRef]
- Du, X.; Wu, E. Application of the adsorption potential theory to hydrogen adsorption on zeolites above critical temperature. Acta Phys.-Chim. Sin. 2007, 23, 813–819. [Google Scholar] [CrossRef]
- Langmi, H.W.; Book, D.; Walton, A.; Johnson, S.R.; Al-Mamouri, M.M.; Speight, J.D.; Edwards, P.P.; Harris, I.R.; Anderson, P.A. Hydrogen storage in ion-exchanged zeolites. J. Alloys Compd. 2005, 404–406, 637–642. [Google Scholar] [CrossRef]
- Kazansky, V.B.; Borovkov, V.Y.; Serich, A.; Karge, H.G. Low temperature hydrogen adsorption on sodium forms of faujasites: Barometric measurements and drift spectra. Microporous Mesoporous Mater. 1998, 22, 251–259. [Google Scholar] [CrossRef]
- Sircar, A.; Devi, V.G.; Yadav, D.; Mishra, J.; Ranjana, G.; Gayathry, J.M.; Tomar, R.; Pragnesh, D.; Dave, P. Study and characterization of potential adsorbent materials for the design of the hydrogen isotopes extraction and analysis system. Fusion Eng. Des. 2021, 166, 112308. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Liu, Y.; Yang, X.; Li, Z.; Jiang, L.; Zhang, C.; Wang, H.; Yang, R.T. Thermodynamic analysis of molecular simulations of N2 and O2 adsorption on zeolites under plateau special conditions. Appl. Surf. Sci. 2019, 480, 868–875. [Google Scholar] [CrossRef]
- Simon, C.M.; Smit, B.; Maciej, H. pyIAST: Ideal adsorbed solution theory (IAST) Python package. Comput. Phys. Commun. 2016, 200, 364–380. [Google Scholar] [CrossRef]
- Muhtaseb, S.A.; Ritter, J.A. New virial-type model for predicting single-and multicomponent isosteric heats of adsorption. Ind. Eng. Chem. Res. 1998, 37, 684–696. [Google Scholar] [CrossRef]
- Bär, N.K.; Ernst, H.; Jobic, H.; Kärger, J. Combined quasi-elastic neutron scattering and NMR study of hydrogen diffusion in zeolites. Magn. Reson. Chem. 1999, 37, 79–83. [Google Scholar] [CrossRef]
- García-Pérez, E.; Parra, J.B.; Ania, C.O.; Dubbeldam, D.; Vlugt, T.J.H.; Castillo, J.M.; Merkling, P.J.; Calero, S. Unraveling the argon adsorption processes in MFI-Type zeolite. J. Phys. Chem. C 2008, 112, 9976–9979. [Google Scholar] [CrossRef]
- Vlugt, T.J.H.; Schenk, M. Influence of framework flexibility on the adsorption properties of hydrocarbons in the zeolite silicalite. J. Phys. Chem. B 2002, 106, 12757–12763. [Google Scholar] [CrossRef]
- Baerlocher, C.; McCusker, L.B. Database of Zeolite Structures. Available online: www.iza-structure.org (accessed on 1 August 2023).
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. cp2k: Atomistic simulations of condensed matter systems. WIREs Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104–154123. [Google Scholar] [CrossRef]
- Vujić, B.; Lyubartsev, A.P. Transferable force-field for modelling of CO2, N2, O2 and Ar in all silica and Na+ exchanged zeolites. Model. Simul. Mater. Sci. Eng. 2016, 24, 045002–045028. [Google Scholar] [CrossRef]
- Pantatosaki, E.; Papadopoulos, G.K. On the computation of long-range interactions in fluids under confinement: Application to pore systems with various types of spatial periodicity. J. Chem. Phys. 2007, 127, 164723–164733. [Google Scholar] [CrossRef] [PubMed]
- Kowsari, M.H.; Naderlou, S. Understanding the dynamics, self-diffusion, and microscopic structure of hydrogen inside the nanoporous Li-LSX zeolite. Microporous Mesoporous Mater. 2017, 240, 39–49. [Google Scholar] [CrossRef]
- Du, X. Molecular dynamics study of hydrogen on Alkali-Earth metal cations exchanged X zeolites. Int. J. Chem. Eng. 2014, 2014, 701057. [Google Scholar]
- Pantatosaki, E.; Papadopoulos, G.K.; Jobic, H.; Theodorou, D.N. Combined atomistic simulation and quasielastic neutron scattering study of the low-temperature dynamics of hydrogen and deuterium confined in NaX zeolite. J. Phys. Chem. B 2008, 112, 11708–11715. [Google Scholar] [CrossRef]
- Huang, X.; Martín-Calvo, A.; Mulder MJ, J.; van Acht SC, J.; Gutiérrez-Sevillano, J.J.; García-Navarro, J.C.; Calero, S. Effect of zeolitic imidazolate framework topology on the purification of hydrogen from coke oven gas. ACS Sustain. Chem. Eng. 2023, 11, 8020–8034. [Google Scholar] [CrossRef]
- da Silva, G.C.Q.; Simon, J.M.; Salazar, J.M. Role of electrical charges on the adsorption of hydrogen: Something old, something new. J. Chem. Phys. 2022, in press; hal-03822161f. [Google Scholar]
- Peng, X.; Cao, D.; Wang, W. Computational characterization of hexagonally ordered carbon nanopipes CMK-5 and structural optimization for H2 storage. Langmuir 2009, 25, 10863–10872. [Google Scholar] [CrossRef]
- Darkrim, F.; Aoufi, A.; Malbrunot, P.; Levesque, D. Hydrogen adsorption in the NaA zeolite: A comparison between numerical simulations and experiments. J. Chem. Phys. 2000, 112, 5991–5999. [Google Scholar] [CrossRef]
- van Duijnen, P.T.; Swart, M. Molecular and atomic polarizabilities: Thole’s Model revisited. J. Phys. Chem. A 1998, 102, 2399–2407. [Google Scholar] [CrossRef]
- Shannon, R.D. Dielectric polarizabilities of ions in oxides and fluorides. J. Appl. Phys. 1993, 73, 348–366. [Google Scholar] [CrossRef]
- Dubbeldam, D.; Calero, S.; Ellis, D.E.; Snurr, R.Q. RASPA: Molecular simulation software for adsorption and diffusion in flexible nanoporous materials. Mol. Simul. 2016, 42, 81–101. [Google Scholar] [CrossRef]
- Dubbeldam, D.; Torres-Knoop, A.; Walton, K.S. On the inner workings of Monte Carlo codes. Mol. Simul. 2013, 39, 1253–1292. [Google Scholar] [CrossRef]
- Erdős, M.; Geerdink, D.F.; Martin-Calvo, A.; Pidko, E.A.; Broeke, L.J.P.v.D.; Calero, S.; Vlugt, T.J.H.; Moultos, O.A. In silico screening of zeolites for high-pressure hydrogen drying. Appl. Mater. Interfaces 2021, 13, 8383–8394. [Google Scholar] [CrossRef]
- Düren, T.; Sarkisov, L.; Yaghi, O.M.; Snurr, R.Q. Design of new materials for methane storage. Langmuir 2004, 20, 2683–2689. [Google Scholar] [CrossRef]
- Lee, Y.; Poloni, R.; Kim, J. Probing Gas Adsorption in MOFs Using an Efficient Ab Initio Widom Insertion Monte Carlo Method. J. Comput. Chem. 2016, 37, 2808–2815. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, D.; Smit, B.; Tobochnik, J.; McKay, S.R.; Christian, W. Understanding molecular simulation. Comput. Phys. 1997, 11, 351–354. [Google Scholar] [CrossRef]
- Schnabel, T.; Vrabec, J.; Hasse, H. Unlike Lennard–Jones parameters for vapor–liquid equilibria. J. Mol. Liq. 2007, 135, 170–178. [Google Scholar] [CrossRef]
- Toukmaji, A.Y.; Board, J.A. Ewald summation techniques in perspective: A survey. Comput. Phys. Commun. 1996, 95, 73–92. [Google Scholar] [CrossRef]
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2011, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- VandeVondele, J.; Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105–114114. [Google Scholar] [CrossRef] [PubMed]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef] [PubMed]



| Molecular | Kinetic Diameter (Å) | Polarizability (Å) | Dipole Moment (D) | Quadruple Moment (D Å) |
|---|---|---|---|---|
| H2 | 2.89 | 0.8 | 0 | 0 |
| N2 | 3.6 | 1.74 | 0 | 1.18 |
| Molecular | Zeolite | Experiment Adsorption Heat (kJ/mol) | Simulation Adsorption Heat (kJ/mol) | ||
|---|---|---|---|---|---|
| 77 K | 298 K | 77 K | 298 K | ||
| H2 | NaA | −10.59 | −4.47 | −9.23 | −4.50 |
| CaA | −7.40 | −4.32 | −8.12 | −5.51 | |
| NaX | −10.54 | −4.30 | −9.47 | −4.94 | |
| CaX | −6.39 | −4.51 | −5.25 | −5.99 | |
| N2 | NaA | −17.07 | −16.71 | −17.16 | −18.65 |
| CaA | −18.06 | −15.01 | −21.87 | −17.23 | |
| NaX | −18.98 | −14.19 | −17.29 | −15.07 | |
| CaX | −11.73 | −11.05 | −15.51 | −11.69 | |
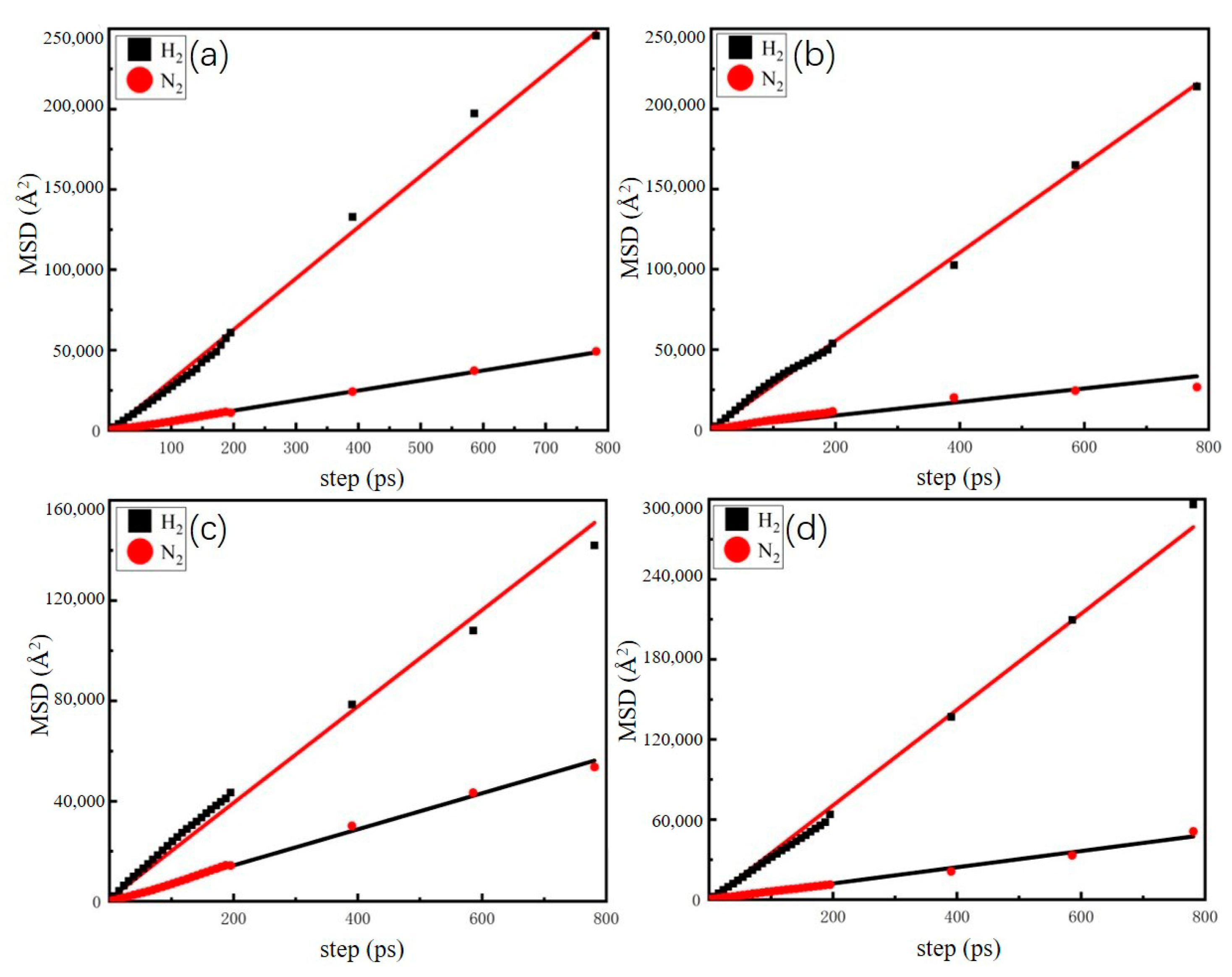
| Zeolites | NaA | CaA | NaX | CaX |
|---|---|---|---|---|
| H2 (Å2/ps) | 10.1 | 19.6 | 20.3 | 19.3 |
| N2 (Å2/ps) | 3.8 | 2.8 | 2.7 | 3.0 |
| H2/N2 | 2.6 | 7.0 | 7.6 | 6.4 |
| Zeolites | NaA | CaA | NaX | CaX |
|---|---|---|---|---|
| H2 (Å2/ps) | 52.8 | 46.0 | 32.2 | 57.9 |
| N2 (Å2/ps) | 10.4 | 7.0 | 12.2 | 10.1 |
| H2/N2 | 5.1 | 6.5 | 2.7 | 5.7 |
| NaA | CaA | NaX | CaX | |
|---|---|---|---|---|
| Accessible pore volume (cm3/g) | 0.28 | 0.3 | 0.261 | 0.31 |
| Supercage pore size (Å) | 4 | 5 | 7.4 | 8 |
| Cation | Na | Ca | Na | Ca |
| Number of cations (N) | 96 | 48 | 88 | 44 |
| Si/Al | 1 | 1 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Wang, Z.; Zhang, L.; Fu, Q.; Wang, M. Competitive Adsorptive Mechanism of H2/N2 in LTA/FAU Zeolites by Molecular Simulations and Experiments. Molecules 2024, 29, 3686. https://doi.org/10.3390/molecules29153686
Dong Z, Wang Z, Zhang L, Fu Q, Wang M. Competitive Adsorptive Mechanism of H2/N2 in LTA/FAU Zeolites by Molecular Simulations and Experiments. Molecules. 2024; 29(15):3686. https://doi.org/10.3390/molecules29153686
Chicago/Turabian StyleDong, Zixu, Zhilu Wang, Lina Zhang, Qiang Fu, and Ming Wang. 2024. "Competitive Adsorptive Mechanism of H2/N2 in LTA/FAU Zeolites by Molecular Simulations and Experiments" Molecules 29, no. 15: 3686. https://doi.org/10.3390/molecules29153686
APA StyleDong, Z., Wang, Z., Zhang, L., Fu, Q., & Wang, M. (2024). Competitive Adsorptive Mechanism of H2/N2 in LTA/FAU Zeolites by Molecular Simulations and Experiments. Molecules, 29(15), 3686. https://doi.org/10.3390/molecules29153686







