Ab Initio Electronic, Magnetic, and Optical Properties of Fe Phthalocyanine on Cr2O3(0001)
Abstract
1. Introduction
2. Results
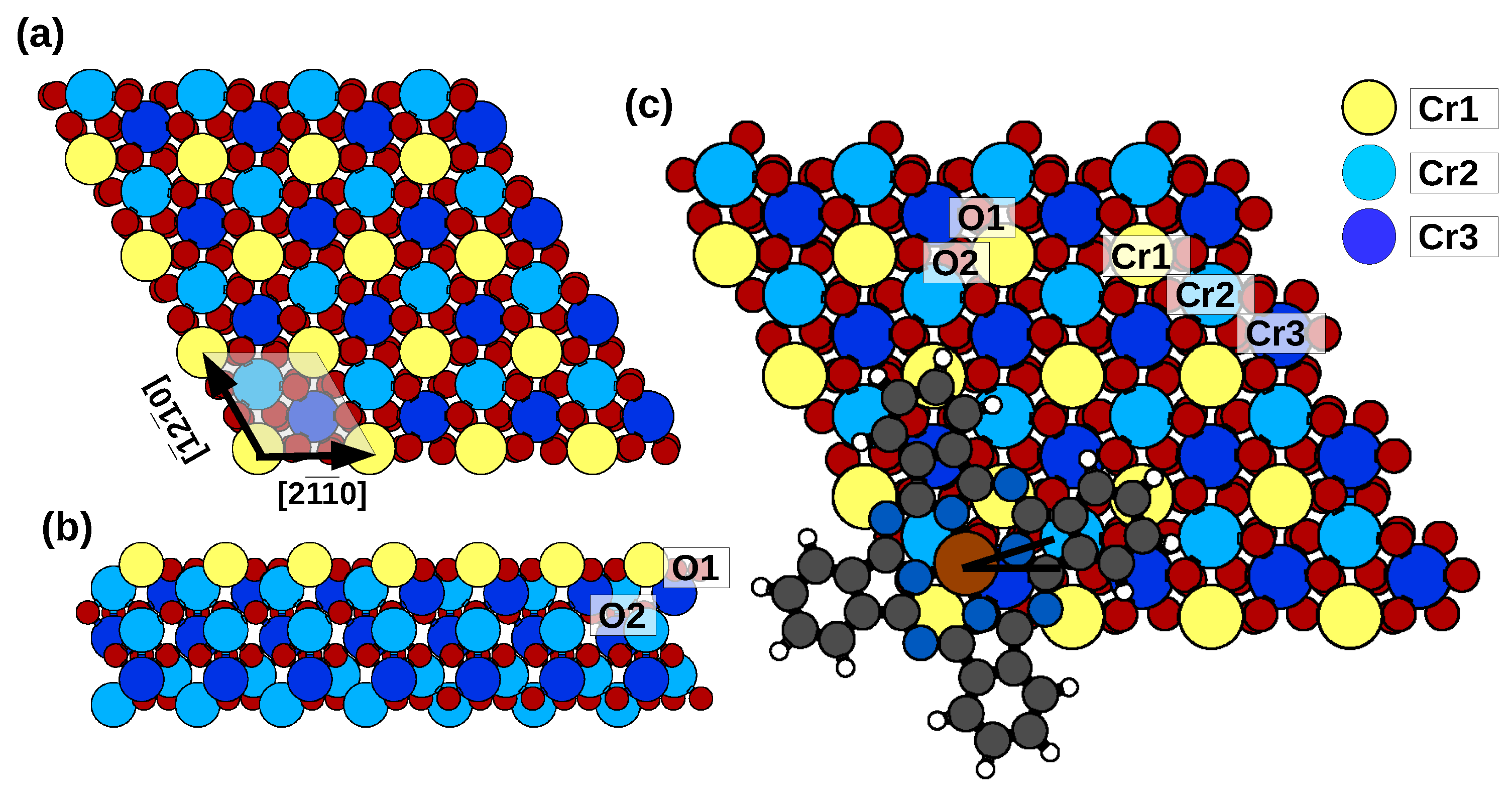
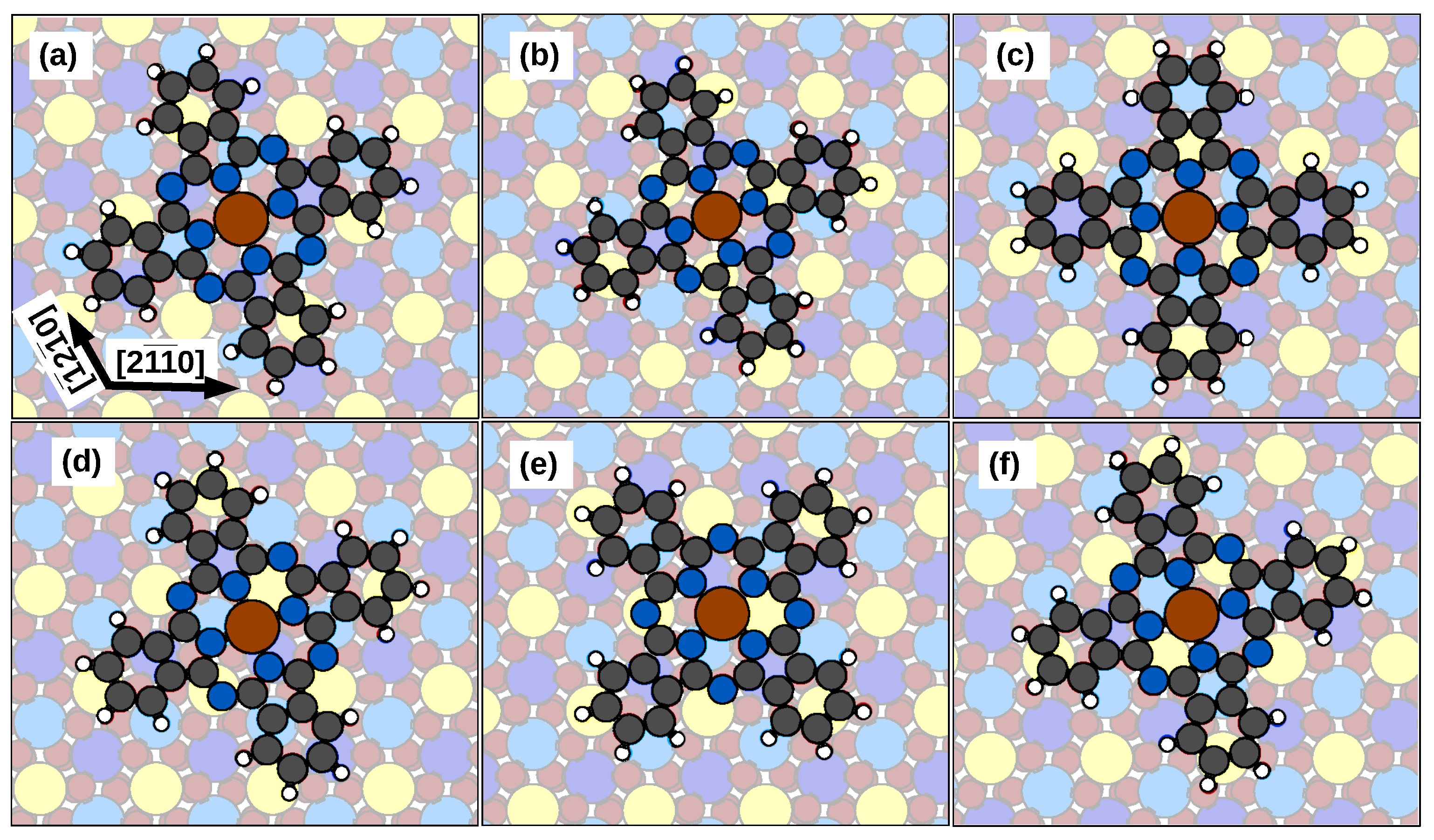
2.1. Adsorption Configurations
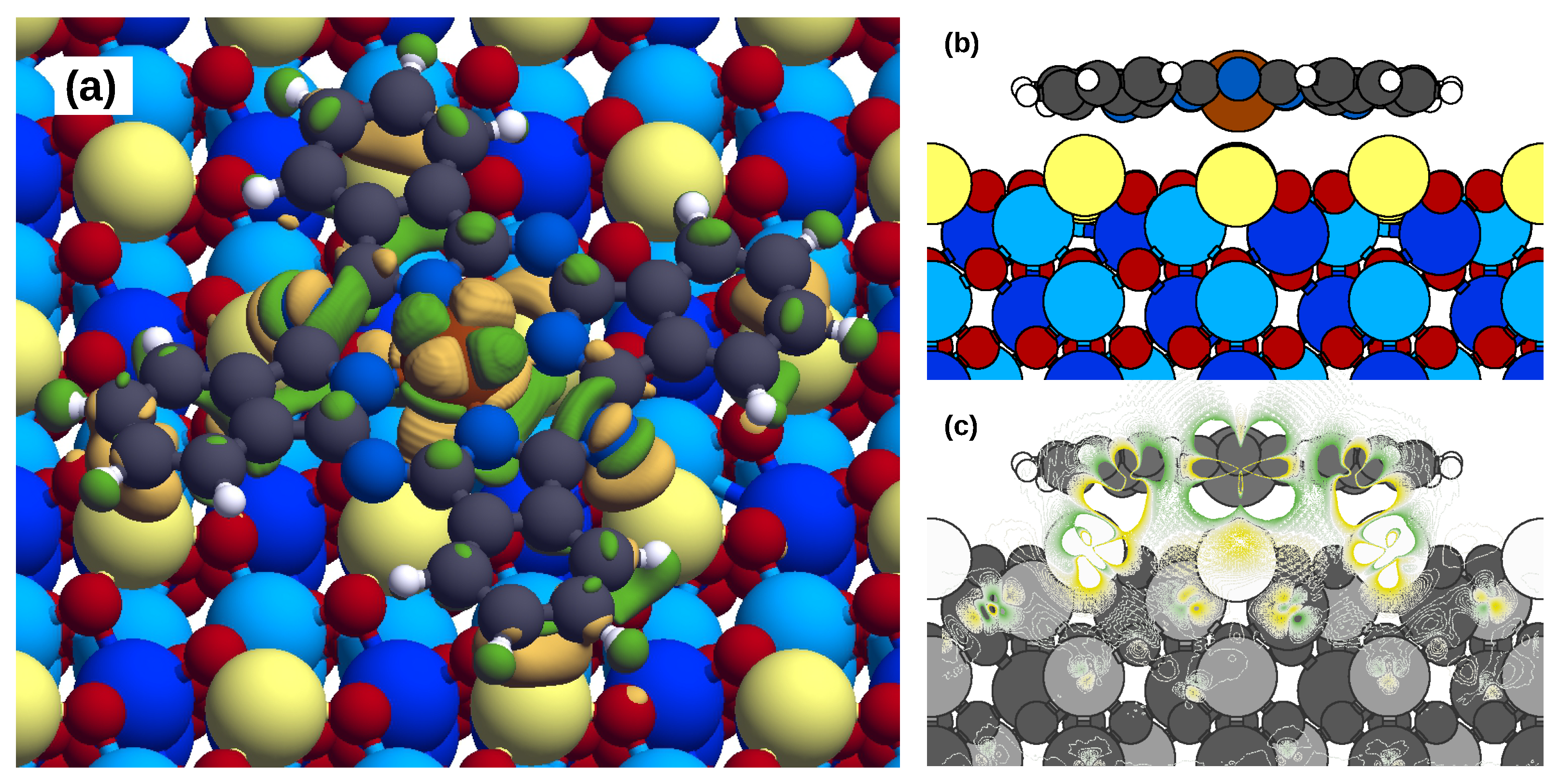
2.2. Electronic Properties
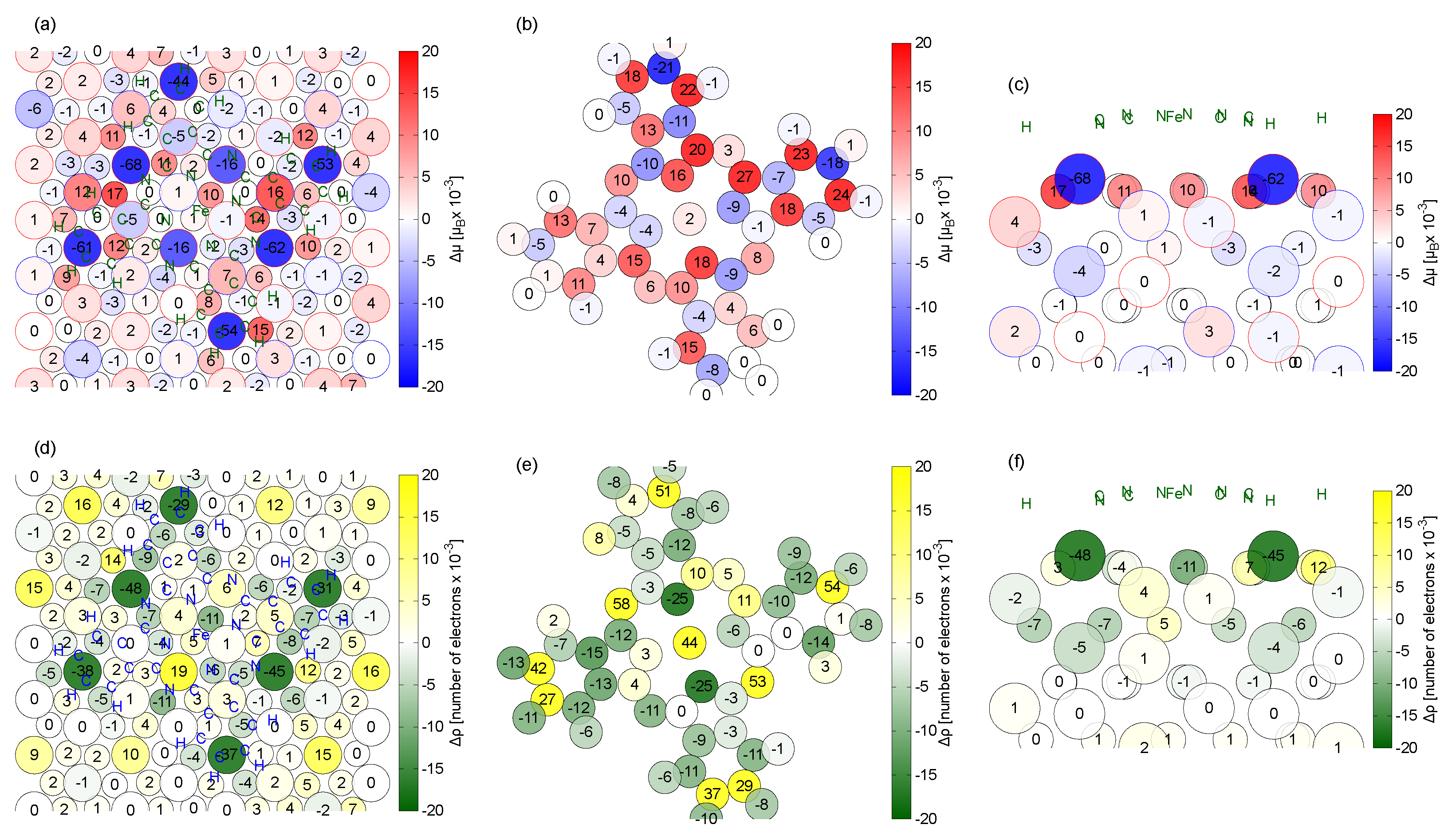
2.3. Magnetic Properties
2.4. Optical Properties
3. Computational Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Joshi, V.K. Spintronics: A contemporary review of emerging electronics devices. Eng. Sci. Technol. Int. J. 2016, 19, 1503–1513. [Google Scholar] [CrossRef]
- Žutić, I.; Fabian, J.; Das Sarma, S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323–410. [Google Scholar] [CrossRef]
- Naber, W.; Faez, S.; van der Wiel, W. Organic spintronics. J. Phys. D Appl. Phys. 2007, 24, R205. [Google Scholar] [CrossRef]
- Xiong, Z.H.; Wu, D.; Vardeny, Z.V.; Shi, J. Giant magnetoresistance in organic spin-valves. Nature 2004, 427, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Devkota, J.; Geng, R.; Subedi, R.C.; Nguyen, T.D. Organic spin valves: A review. Adv. Funct. Mater. 2016, 26, 3881–3898. [Google Scholar] [CrossRef]
- Shao, Y.; Pang, R.; Pan, H.; Shi, X. Fullerene/layered antiferromagnetic reconstructed spinterface: Subsurface layer dominates molecular orbitals’ spin-split and large induced magnetic moment. J. Chem. Phys. 2018, 148, 114704. [Google Scholar] [CrossRef] [PubMed]
- Sanvito, S. Molecular spintronics. Chem. Soc. Rev. 2011, 40, 3336–3355. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Yu, G. Innovation of Materials, Devices, and Functionalized Interfaces in Organic Spintronics. Adv. Funct. Mater. 2021, 31, 2100550. [Google Scholar] [CrossRef]
- Delprat, S.; Galbiati, M.; Tatay, S.; Quinard, B.; Barraud, C.; Petroff, F.; Seneor, P.; Mattana, R. Molecular spintronics: The role of spin-dependent hybridization. J. Phys. D Appl. Phys. 2018, 51, 473001. [Google Scholar] [CrossRef]
- Bergenti, I.; Dediu, V. Spinterface: A new platform for spintronics. Nano Mater. Sci. 2019, 1, 149–155. [Google Scholar] [CrossRef]
- Baltz, V.; Manchon, A.; Tsoi, M.; Moriyama, T.; Ono, T.; Tserkovnyak, Y. Antiferromagnetic spintronics. Rev. Mod. Phys. 2018, 90, 015005. [Google Scholar] [CrossRef]
- Kipgen, L.; Bernien, M.; Tuczek, F.; Kuch, W. Spin-Crossover Molecules on Surfaces: From Isolated Molecules to Ultrathin Films. Adv. Mater. 2021, 33, 2008141. [Google Scholar] [CrossRef]
- Wagner, M.; Calcinelli, F.; Jeindl, A.; Schmid, M.; Hofmann, O.T.; Diebold, U. Adsorption configurations of Co-phthalocyanine on In2O3(111). Surf. Sci. 2022, 722, 122065. [Google Scholar] [CrossRef]
- Karstens, R.; Chassé, T.; Peisert, H. Interface interaction of transition metal phthalocyanines with strontium titanate (100). Beilstein J. Nanotechnol. 2021, 12, 485–496. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, W.; Guo, P.; Wang, K.; Wang, J.; Qian, H.; Kurash, I.; Wang, C.H.; Yang, Y.W.; Xu, F. A direct Fe–O coordination at the FePc/MoOx interface investigated by XPS and NEXAFS spectroscopies. Phys. Chem. Chem. Phys. 2015, 17, 3463–3469. [Google Scholar] [CrossRef]
- Schmitt, T.; Ferstl, P.; Hammer, L.; Schneider, M.A.; Redinger, J. Adsorption and Intermolecular Interaction of Cobalt Phthalocyanine on CoO(111) Ultrathin Films: An STM and DFT Study. J. Phys. Chem. C 2017, 121, 2889–2895. [Google Scholar] [CrossRef]
- Glaser, M.; Peisert, H.; Adler, H.; Polek, M.; Uihlein, J.; Nagel, P.; Merz, M.; Schuppler, S.; Chassé, T. Transition-Metal Phthalocyanines on Transition-Metal Oxides: Iron and Cobalt Phthalocyanine on Epitaxial MnO and TiOx Films. J. Phys. Chem. C 2015, 119, 27569–27579. [Google Scholar] [CrossRef]
- Marino, M.; Molteni, E.; Achilli, S.; Fratesi, G. Ab-initio electronic, magnetic, and optical properties of Fe-phthalocyanine on NiO(001). Inorganica Chim. Acta 2024, 562, 121877. [Google Scholar] [CrossRef]
- Franco-Cañellas, A.; Duhm, S.; Gerlach, A.; Schreiber, F. Binding and electronic level alignment of π-conjugated systems on metals. Rep. Prog. Phys. 2020, 83, 066501. [Google Scholar] [CrossRef]
- Shen, K.; Narsu, B.; Ji, G.; Sun, H.; Hu, J.; Liang, Z.; Gao, X.; Li, H.; Li, Z.; Song, B.; et al. On-surface manipulation of atom substitution between cobalt phthalocyanine and the Cu(111) substrate. RSC Adv. 2017, 7, 13827–13835. [Google Scholar] [CrossRef]
- Peisert, H.; Uihlein, J.; Petraki, F.; Chassé, T. Charge transfer between transition metal phthalocyanines and metal substrates: The role of the transition metal. J. Electron Spectrosc. Relat. Phenom. 2015, 204, 49–60. [Google Scholar] [CrossRef]
- Catti, M.; Sandrone, G.; Valerio, G.; Dovesi, R. Electronic, magnetic and crystal structure of Cr2O3 by theoretical methods. J. Phys. Chem. Solids 1996, 57, 1735–1741. [Google Scholar] [CrossRef]
- Brumboiu, I.E.; Haldar, S.; Lüder, J.; Eriksson, O.; Herper, H.C.; Brena, B.; Sanyal, B. Influence of Electron Correlation on the Electronic Structure and Magnetism of Transition-Metal Phthalocyanines. J. Chem. Theory Comput. 2016, 12, 1772–1785. [Google Scholar] [CrossRef]
- Liao, M.S.; Scheiner, S. Electronic structure and bonding in metal porphyrins, metal = Fe, Co, Ni, Cu, Zn. J. Chem. Phys. 2002, 117, 205–219. [Google Scholar] [CrossRef]
- Gottfried, J.M. Surface chemistry of porphyrins and phthalocyanines. Surf. Sci. Rep. 2015, 70, 259–379. [Google Scholar] [CrossRef]
- Avvisati, G.; Cardoso, C.; Varsano, D.; Ferretti, A.; Gargiani, P.; Betti, M.G. Ferromagnetic and Antiferromagnetic Coupling of Spin Molecular Interfaces with High Thermal Stability. Nano Lett. 2018, 18, 2268–2273. [Google Scholar] [CrossRef] [PubMed]
- Gruber, M.; Ibrahim, F.; Boukari, S.; Isshiki, H.; Joly, L.; Peter, M.; Studniarek, M.; Costa, V.D.; Jabbar, H.; Davesne, V.; et al. Exchange bias and room-temperature magnetic order in molecular layers. Nat. Mater. 2015, 14, 981–984. [Google Scholar] [CrossRef]
- Baffou, G.; Mayne, A.J.; Comtet, G.; Dujardin, G.; Stauffer, L.; Sonnet, P. SiC(0001) 3 × 3 Heterochirality Revealed by Single-Molecule STM Imaging. J. Am. Chem. Soc. 2009, 131, 3210–3215. [Google Scholar] [CrossRef] [PubMed]
- Baby, A.; Marcaud, G.; Dappe, Y.J.; D’Angelo, M.; Cantin, J.L.; Silly, M.G.; Fratesi, G. Phthalocyanine reactivity and interaction on the 6H-SiC(0001)-(3 × 3) surface investigated by core-level experiments and simulations. Phys. Chem. Chem. Phys. 2022, 24, 14937–14946. [Google Scholar] [CrossRef]
- Rohrbach, A.; Hafner, J.; Kresse, G. Ab initio study of the (0001) surfaces of hematite and chromia: Influence of strong electronic correlations. Phys. Rev. B 2004, 70, 125426. [Google Scholar] [CrossRef]
- Rehbein, C.; Harrison, N.; Wander, A. Structure of the α-Cr2O3 (0001) surface: An ab initio total-energy study. Phys. Rev. B 1996, 54, 14066. [Google Scholar] [CrossRef]
- Rohr, F.; Bäumer, M.; Freund, H.J.; Mejias, J.; Staemmler, V.; Müller, S.; Hammer, L.; Heinz, K. Strong relaxations at the Cr2O3(0001) surface as determined via low-energy electron diffraction and molecular dynamics simulations. Surf. Sci. 1997, 372, L291–L297. [Google Scholar] [CrossRef]
- Maurice, V.; Cadot, S.; Marcus, P. XPS, LEED and STM study of thin oxide films formed on Cr(110). Surf. Sci. 2000, 458, 195–215. [Google Scholar] [CrossRef]
- Fratesi, G.; Paoloni, D.; Persichetti, L.; Camilli, L.; Caporale, A.; Baby, A.; Cvetko, D.; Kladnik, G.; Morgante, A.; Ruocco, A. Spontaneous transmetalation at the ZnPc/Al(100) interface. Inorganica Chim. Acta 2024, 559, 121790. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with QUANTUM ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Cooper, V. Van der Waals density functional: An appropriate exchange functional. Phys. Rev. B 2010, 81, 161104. [Google Scholar] [CrossRef]
- Lee, K.; Murray, E.D.; Kong, L.; Lundqvist, B.I.; Langreth, D.C. Higher-accuracy van der Waals density functional. Phys. Rev. B 2010, 82, 081101. [Google Scholar] [CrossRef]
- Garrity, K.F.; Bennett, J.W.; Rabe, K.M.; Vanderbilt, D. Pseudopotentials for high-throughput DFT calculations. Comput. Mater. Sci. 2014, 81, 446–452. [Google Scholar] [CrossRef]
- Sangalli, D.; Ferretti, A.; Miranda, H.; Attaccalite, C.; Marri, I.; Cannuccia, E.; Melo, P.; Marsili, M.; Paleari, F.; Marrazzo, A.; et al. Many-body perturbation theory calculations using the yambo code. J. Phys. Condens. Matter 2019, 31, 325902. [Google Scholar] [CrossRef]
- van Setten, M.J.; Giantomassi, M.; Bousquet, E.; Verstraete, M.; Hamann, D.R.; Gonze, X.; Rignanese, G.M. The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 2018, 226, 39–54. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]


| Site | Angle | |||
|---|---|---|---|---|
| Cr1 (up) | −3.793 | −3.710 | 0.082 | |
| −3.453 | −3.860 | −0.407 | ||
| Cr2 (up) | −3.436 | −3.519 | −0.083 | |
| −3.533 | −3.541 | −0.009 | ||
| Cr3 (down) | −3.493 | −3.438 | 0.055 | |
| O-up | −4.100 | −4.165 | −0.065 | |
| −4.202 | −4.203 | −0.001 | ||
| −3.558 | −3.575 | −0.017 | ||
| O-dn | −3.444 | −3.454 | −0.010 | |
| −4.233 | −4.234 | 0.000 | ||
| B | −4.316 | −4.252 | 0.065 | |
| −4.169 | −4.234 | −0.065 | ||
| −3.444 | −3.460 | −0.016 | ||
| −3.494 | −3.511 | −0.016 | ||
| −3.410 | −3.394 | 0.016 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marino, M.; Molteni, E.; Achilli, S.; Onida, G.; Fratesi, G. Ab Initio Electronic, Magnetic, and Optical Properties of Fe Phthalocyanine on Cr2O3(0001). Molecules 2024, 29, 2889. https://doi.org/10.3390/molecules29122889
Marino M, Molteni E, Achilli S, Onida G, Fratesi G. Ab Initio Electronic, Magnetic, and Optical Properties of Fe Phthalocyanine on Cr2O3(0001). Molecules. 2024; 29(12):2889. https://doi.org/10.3390/molecules29122889
Chicago/Turabian StyleMarino, Marco, Elena Molteni, Simona Achilli, Giovanni Onida, and Guido Fratesi. 2024. "Ab Initio Electronic, Magnetic, and Optical Properties of Fe Phthalocyanine on Cr2O3(0001)" Molecules 29, no. 12: 2889. https://doi.org/10.3390/molecules29122889
APA StyleMarino, M., Molteni, E., Achilli, S., Onida, G., & Fratesi, G. (2024). Ab Initio Electronic, Magnetic, and Optical Properties of Fe Phthalocyanine on Cr2O3(0001). Molecules, 29(12), 2889. https://doi.org/10.3390/molecules29122889









