3.1. H-Bonding in Diatomic Hydrides
As simplest cases of AH···B hydrogen bonding, we consider the self- and cross-interactions of elementary hydrogen halides (XH, X = F, Cl, Br) and the related (X = H) diatomic H
2 that
lacks a dipole moment and corresponds to the weakest limit of recognizable H-bonding.
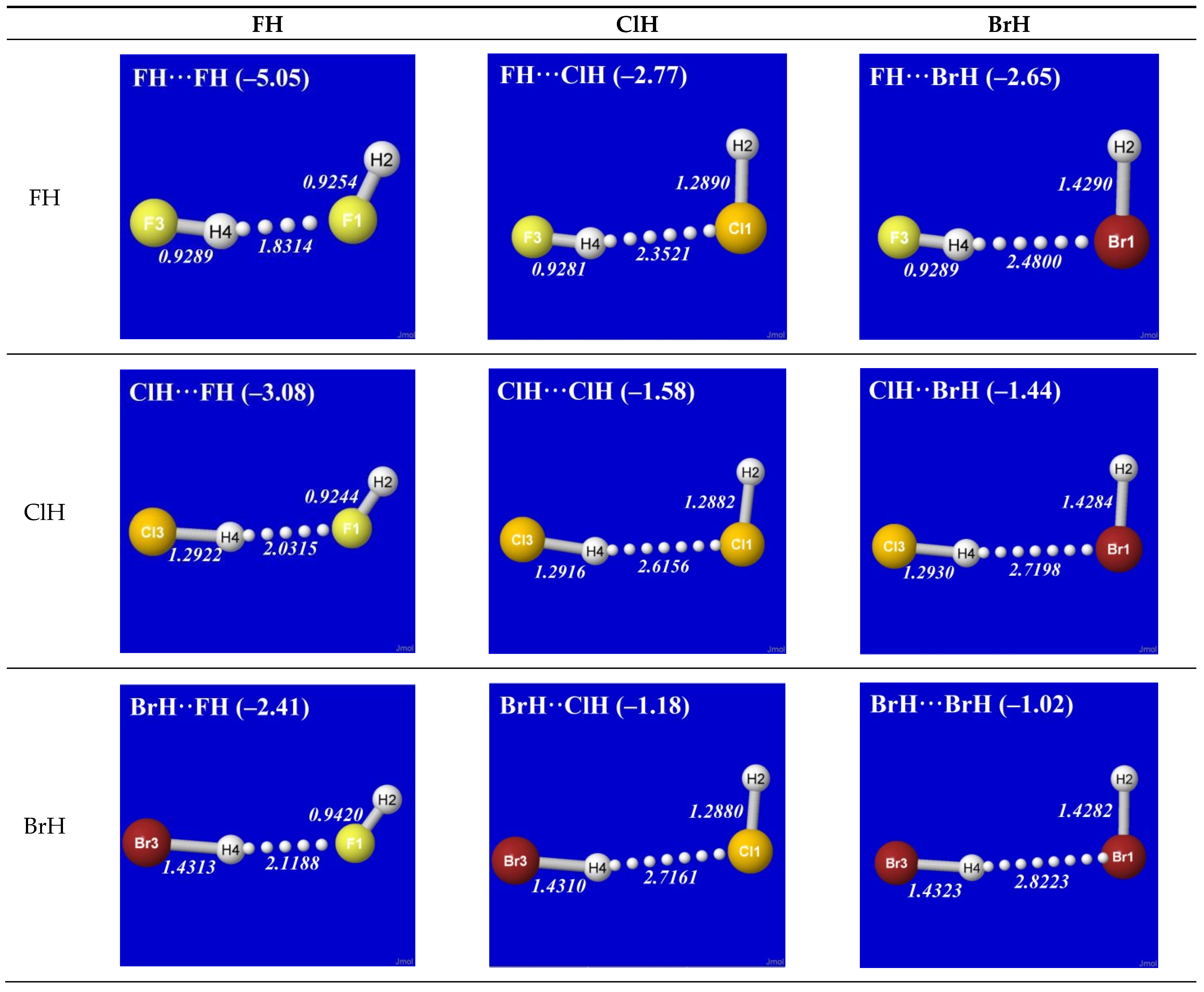
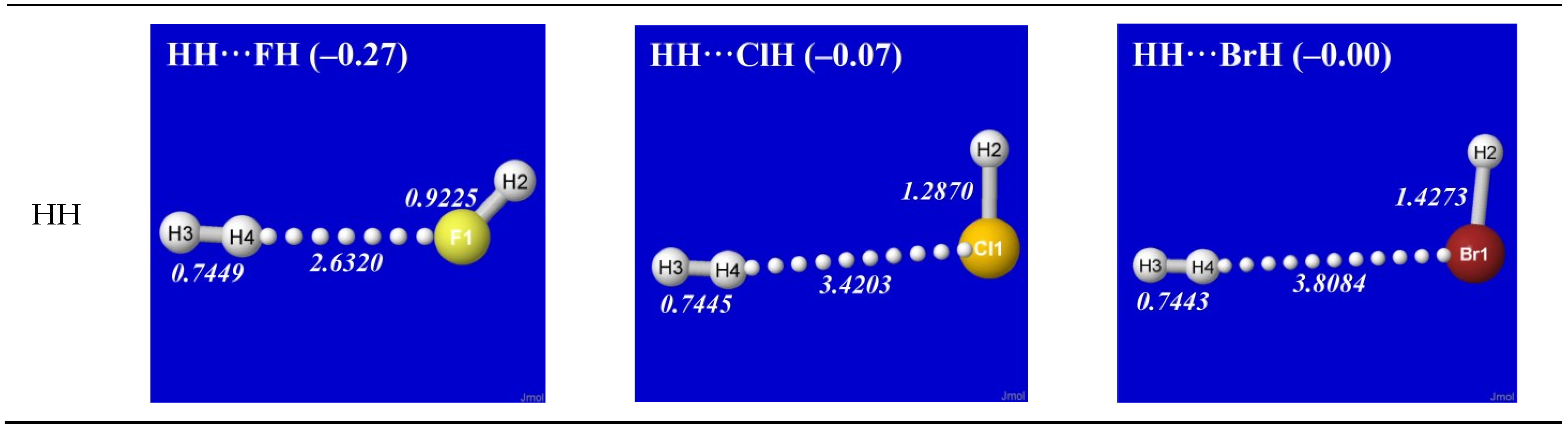
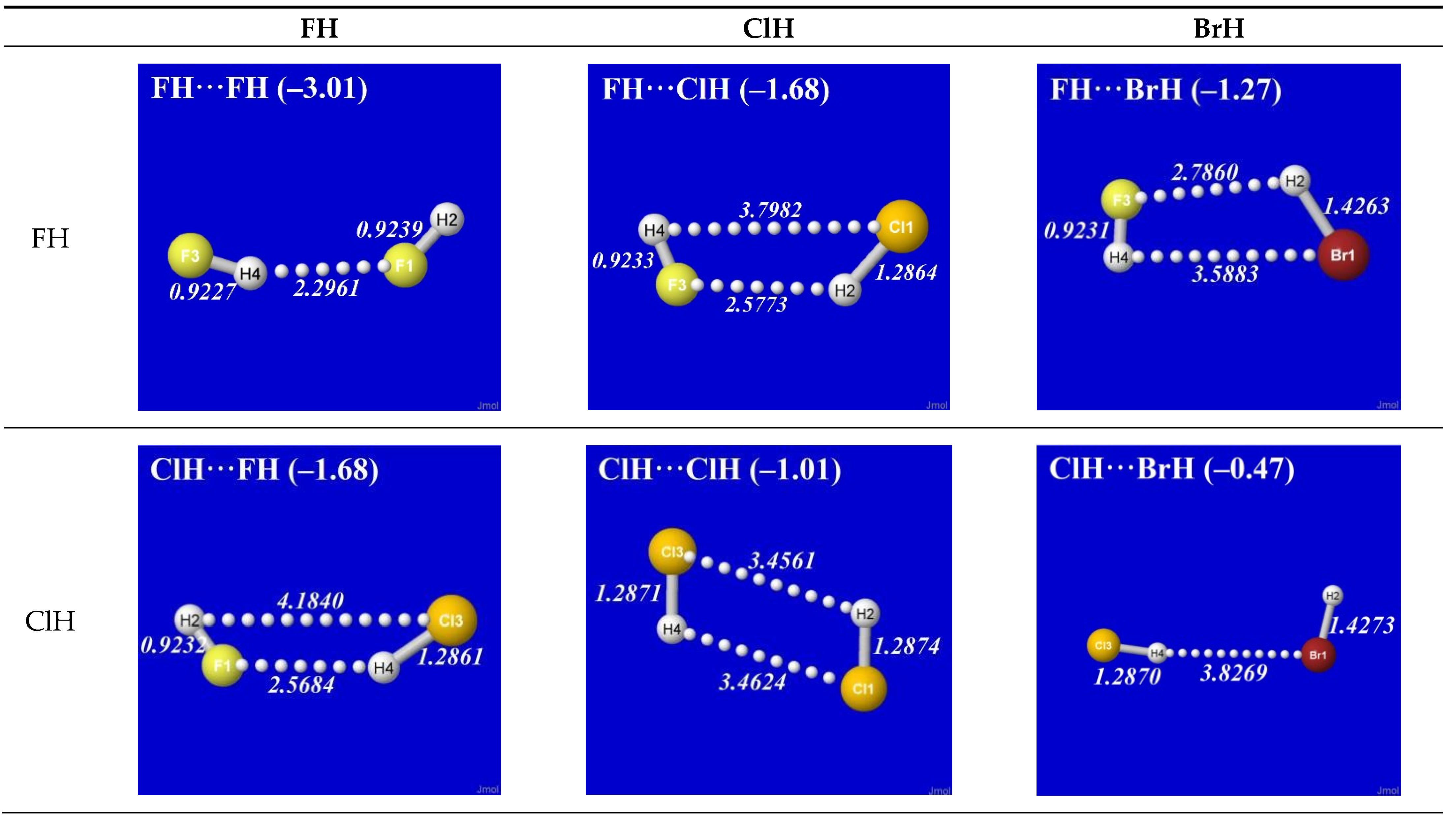
Figure 1 shows the optimized equilibrium geometry (and parenthesized net binding energy in kcal/mol) for all twelve possible supramolecular complexes from these precursors. All these complexes are seen to exhibit severely bent (L-shaped) geometry, with more-or-less linear X-H···Y alignment along the long axis between two halogens,
the characteristic structural signatures of H-bonding.
Other features of this family of complexes are immediately evident. From the strong (near-perpendicular) deviations from overall linear geometry, one also sees that these complexes deviate
as strongly as possible from the expected doggie-magnet alignment geometry of classical dipole–dipole interactions. Moreover, with the exception of X = Y = H, each XH···YH complex shown in the “XH” row and “YH” column of
Figure 1 is complemented by a
related YH···XH complex shown in the “YH” row and “XH” column. Thus, each diatomic XH monomer has the ability (even with near-
equal propensity) to serve either as the H-donor or H-acceptor in the H-bonding geometry. This indicates that we are not looking at “competition for the H-atom” (as conventional terminology might suggest) but rather that the H atom serves to “bridge” the resonance-type bonding character with one terminal halogen or the other, viz. (in conventional resonance structural symbolism),
Indeed, if we include an additional bond on each side of the resonance arrow, we can see obvious resemblance to, e.g., the resonance-type representation of the peptide group by a protein chemist, viz.,
or the analogous representations of allyl-type resonance by an organic chemist, viz.,
In each case, what is being “donated” or “accepted” is not a hydrogen atom but rather a
shared electron-pair bond, the essential change of perspective from original Brønsted–Lowry to the more prescient Lewis formulation of acid–base interactions [
3]. All such “covalency”-type conceptions appear deeply in conflict with classical electrostatics. The
electrons (not the protons) are the dominant “quantum particles” in chemistry.
As we learn from Bohr theory, description of electronic phenomena must always involve the available
orbitals in which electrons may be “found” (with probability distribution as detected experimentally). In the case of a diatomic hydride HX, the bonding orbital for a shared
e-pair (denoted σ
HX) may be expressed as the
in-phase linear combination of hybrid atomic orbitals (denoted
hH,
hX), viz.,
where
The linear combination (Equation (3a)) expresses the superposition [
18] of atomic orbitals
hH,
hX to form a new “bond orbital” σ
HX, thereby putting into mathematical form what the chemist describes as the “sharing” (equal or unequal, according to values of
cH,
cX) of the
e-pair between atoms—the essence of covalent bonding.
Equation (3b) also expresses an important conservation principle of orbital construction. In a certain sense, each starting hybrid atomic orbital hH, hX in Equation (3a) is like an axis of a many-dimensional Cartesian space, and the coefficients cH, cX serve as components of the σHX orbital in each spatial direction. Whether the σHX orbital is “tilted” more into the hH or the hX direction, the sum of squared components (Equation (3b)) must always remain constant (the orbital remains “normalized”). Since the probability of detecting an electron “in” σHX (i.e., in the spatial region where σHX has finite amplitude) is related to the square of the orbital amplitude (|σHX|2), the conservation condition (Equation (3b)) guarantees that the total probability for finding the e-pair in σHX is independent of its equal or unequal sharing between hH, hX hybrids. This merely assures the unitary condition that the total number of electrons undergoes neither gain nor loss in the domain of chemical transformations.
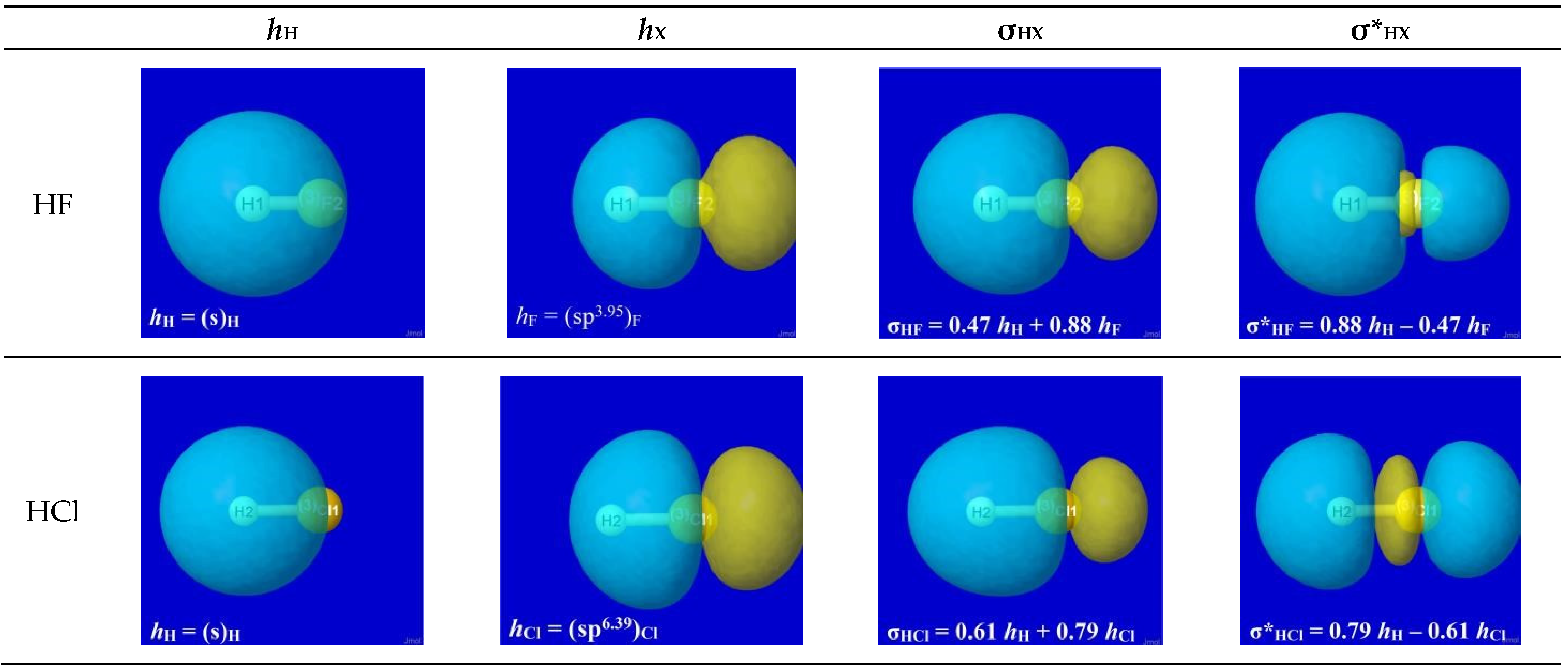
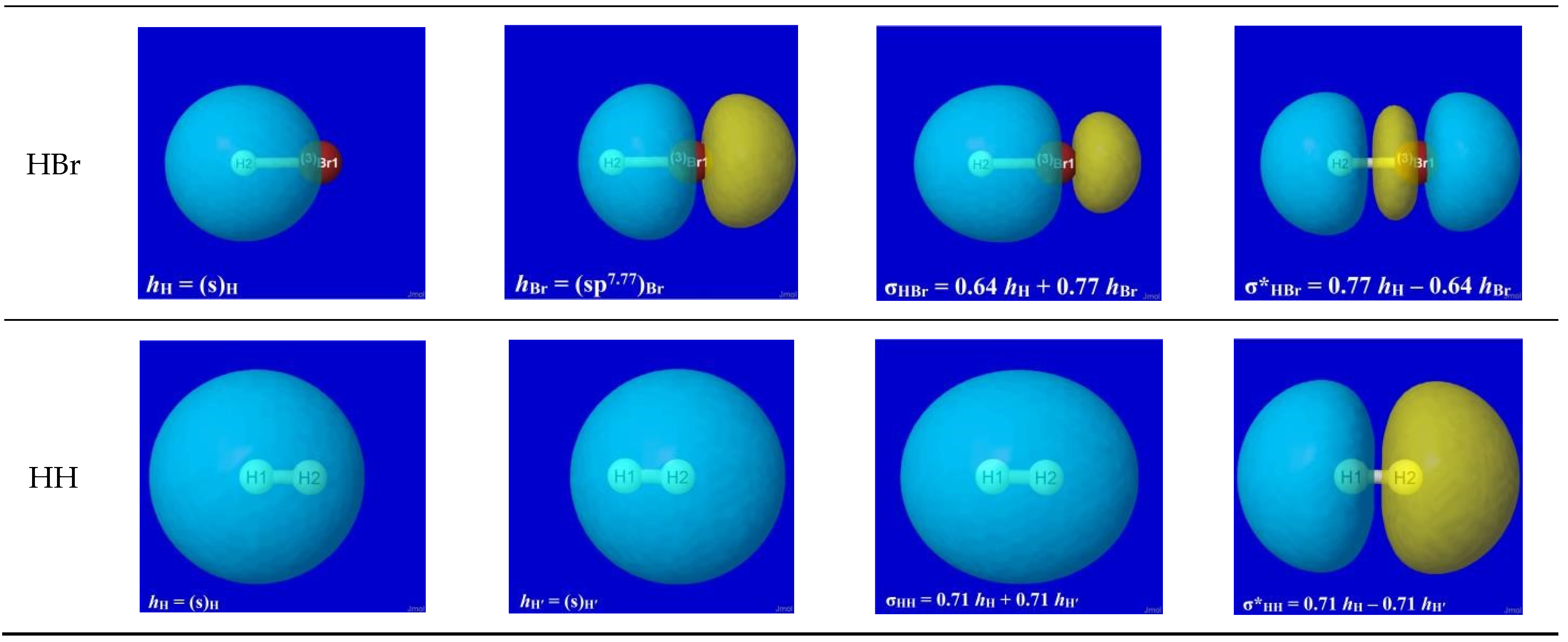
The specific forms of natural hybrid orbitals (NHOs)
hH,
hX and the resultant bonding NBO σ
HX are readily obtained from NBO analysis output of the quantum chemical calculation for each HX.
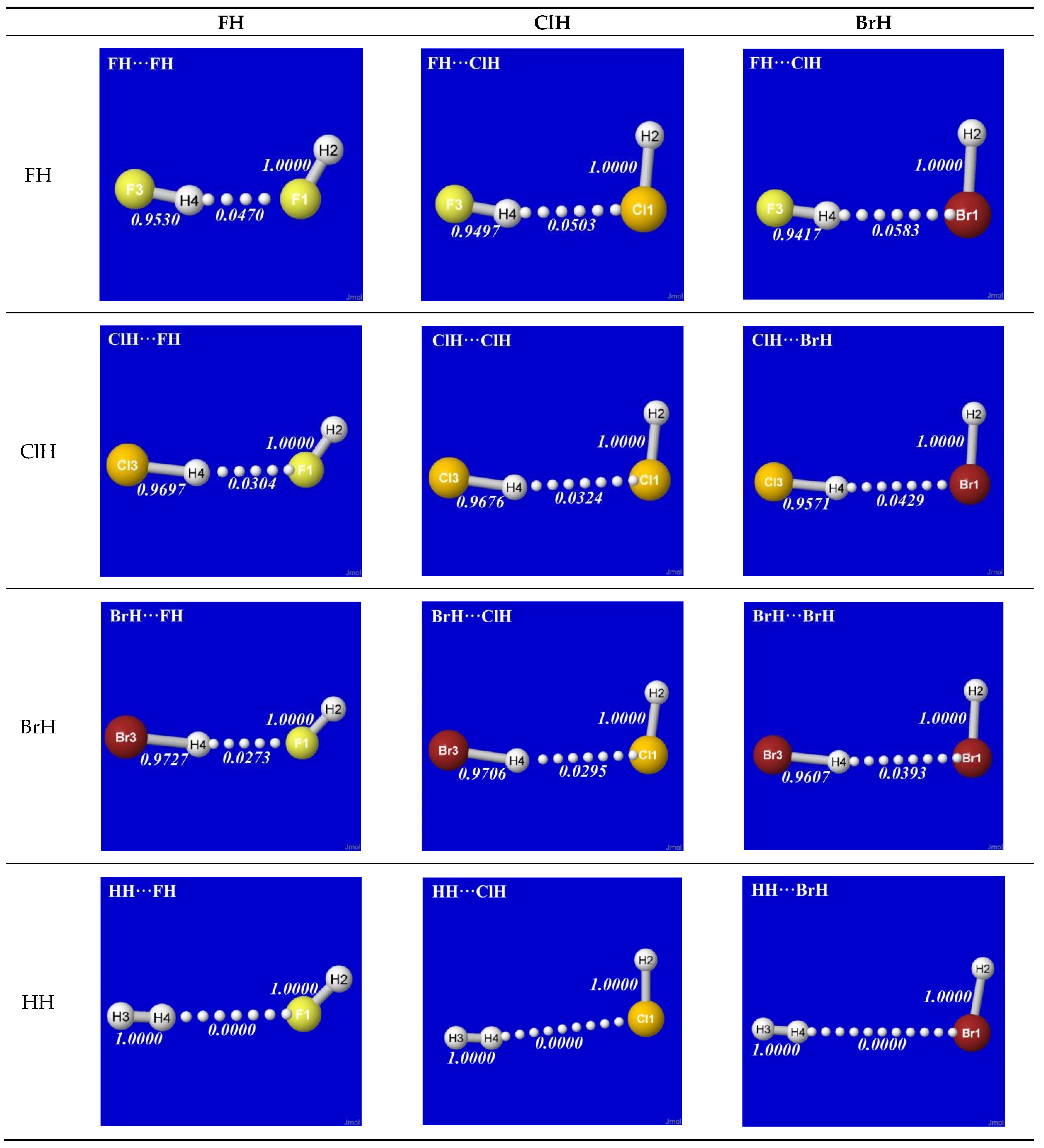
Figure 2 displays the 3D shapes of these orbitals and the composition (Equation (3a)) of each bonding σ
HX in the left three panels of each row. The chosen orbital surface contour approximates the “van der Waals contact” limit (discussed below) at which interatomic interactions become comparable to ambient thermal energies. The exponentially steep decline of orbital density beyond this limit (as depicted in a following section) ensures that chemically significant NBO interactions remain essentially
localized (2- or 3-center) and highly recognizable rather than “completely delocalized” as suggested by the florid graphical imagery of canonical molecular orbitals. The latter are merely one of
infinitely many alternative ways of choosing idealized doubly occupied orbital “axes” to describe a DFT calculation (with no effect on the density or other measurable property), thereby disguising the nuances of localized electronic-pair sharing between
proximal atomic centers that is the essence of covalent bonding.
The σ
HX bonding orbitals shown in the third column of
Figure 2 might seem to be the end of the covalency story, but they are not. As mentioned near Equation (3a), each component of an orbital superposition acts like an independent axis of a Cartesian coordinate system and the coefficients of each superposition satisfy a conservation relation (3b), ensuring that the resultant orbital also preserves such axis-like character in a
rotated Cartesian axis system. This can be made explicit by formally defining a rotation angle (θ
HX) such that
cH ≡ cos(θ
HX) and
cX ≡ sin(θ
HX). Equation (3a,b) can then be rewritten as
Equation (4b) is a well-known trigonometric identity that is true for
all rotation angles θ
HX (all possible physical values of bond polarity) so that the conservation property (Equation (3b)) is automatically maintained in such a geometrical picture of the superposition. However, the elementary geometry of rigid-body rotations tells us that Equation (4a) can represent only
one axis of the rotated Cartesian system, whereas the second axis (which ensures conservation of dimensionality under rotations) must be the corresponding
out-of-phase superposition, denoted σ*
HX (“antibonding”), viz.,
A little vector algebra then establishes that if orbitals
hH,
hX are mutually perpendicular (such as the axes of a Cartesian system), then so are the orbitals σ
HX and σ*
HX. In effect, the σ*
HX orbital must
always be created in synchrony with the σ
HX orbital, “completing the space” of the orbital superposition. The inexorable logic of quantum theory (based on the Cartesian-like qualities of many-dimensional Hilbert space) demands that σ
HX and σ*
HX are inextricably linked in the domain of covalency.
But what can be the physical meaning of such an
antibonding (out-of-phase) NBO? To answer this, we recall one other aspect of quantum covalency, namely, the
Pauli exclusion principle, a consequence of the exchange antisymmetry property of many-electron wavefunctions. This principle restricts the maximum electronic occupancy of any orbital to one
pair of electrons: one with spin angular momentum “up” and the other with spin angular momentum “down”. However, the complementary σ*
HX orbital provides the
capacity for change in electronic bond shifts, i.e., for receiving the electronic charge “transfer” (CT) from one closed-shell molecule to another (or from another filled bond orbital in the same molecule). Analogous to atoms of the periodic table, which remain chemically
inert unless one or more valence-shell orbitals are vacant, so does a diatomic HX molecule require a σ*
HX “acceptor” NBO to enjoy the benefits of CT-type bond–antibond interactions with a doubly occupied “donor” NBO of a nearby HY molecule. As shown by a simple second-order perturbation theory argument [
18,
19], each such “donor–acceptor” interaction is intrinsically
stabilizing because its magnitude (
Ed-a(2)) depends only on the
square (|
hd,a|
2) of the
hd,a transition amplitude and the non-negative energy difference (ε
a–ε
d) between acceptor and donor NBOs no matter what combination of kinetic and potential energy contributes to the total energy of the system.
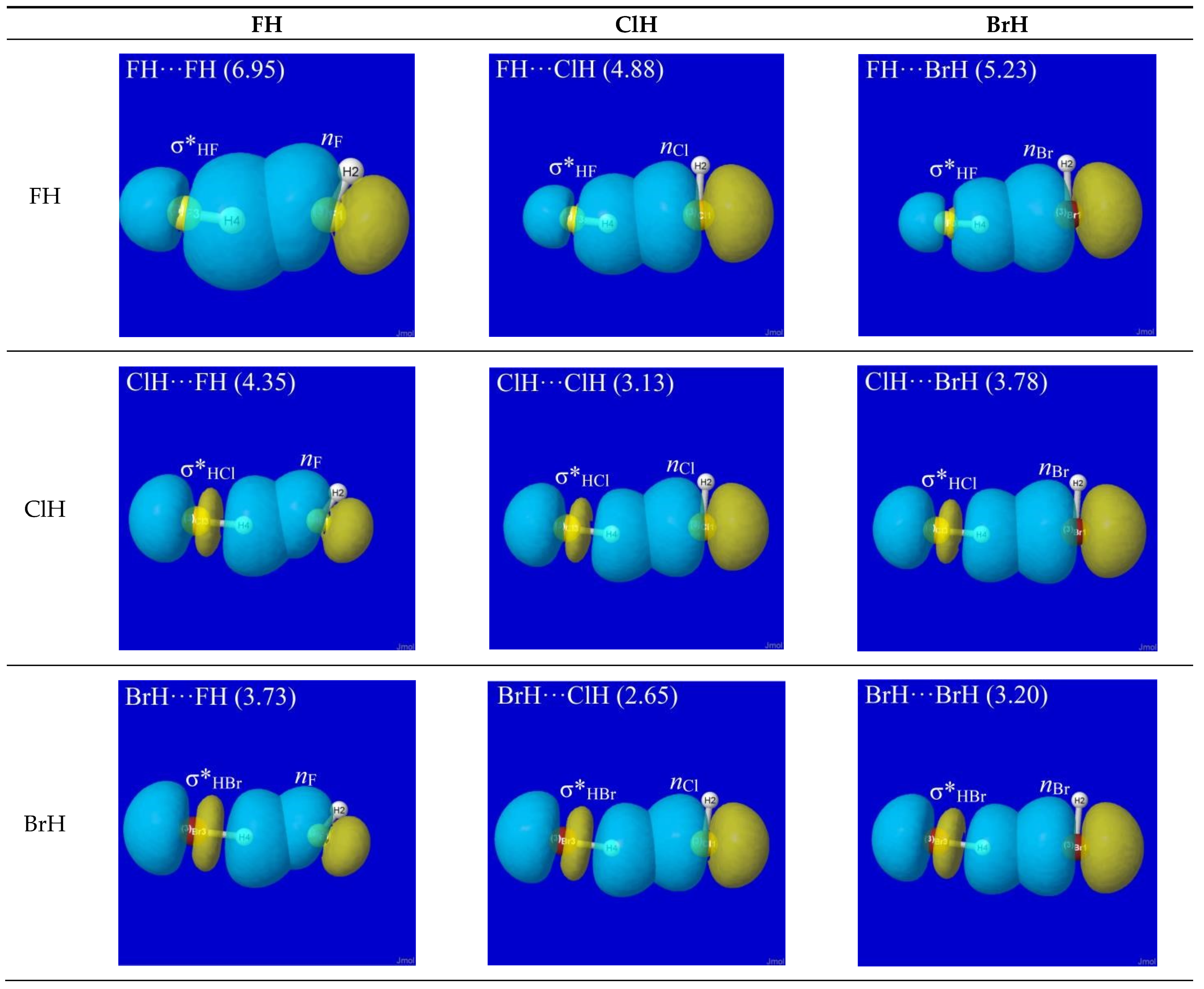
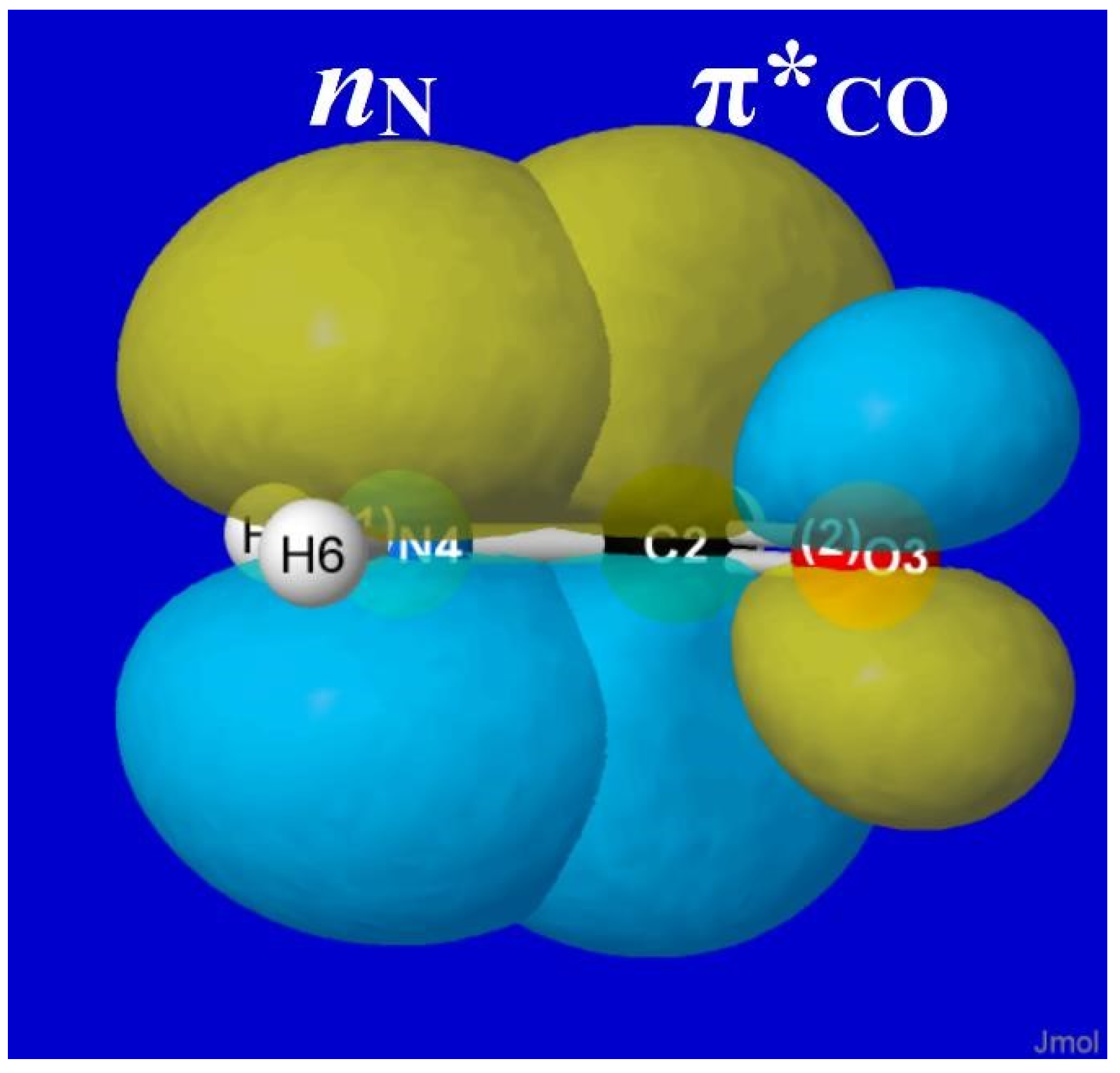
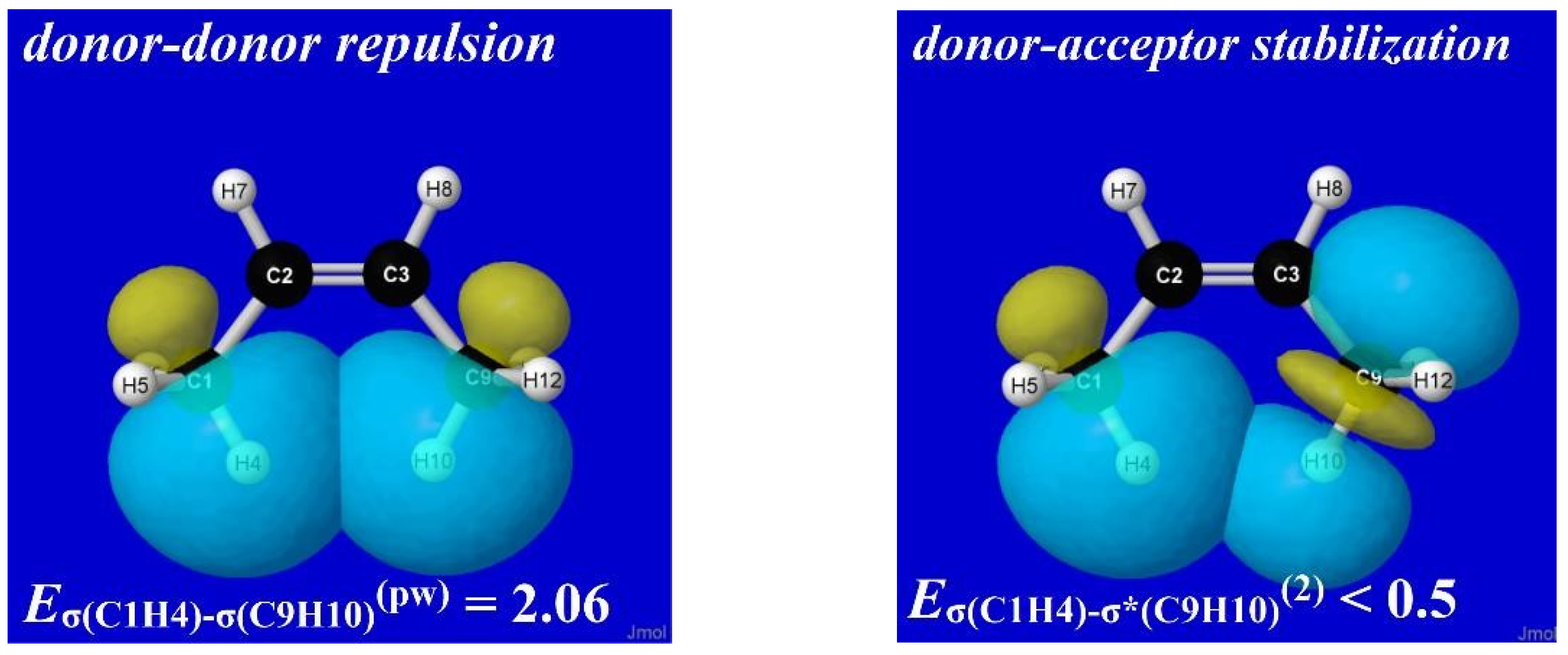
NBO analysis provides a read-out of leading donor–acceptor interactions for each XH···YH complex. Invariably, the leading acceptor orbital is the σ*
HX valence antibond (“BD*” in NBO output) of the HX monomer that lies along the H-bond axis. The leading donor orbital is generally an off-axis lone pair
nY (“LP” in NBO output, generally of high p-character) on the YH monomer. Each such
nY- σ*
HX interaction leads to the corresponding second-order perturbative estimate of stabilization (
En-σ*(2)).
Figure 3 depicts the leading
nY -σ*
HX donor–acceptor interaction (and parenthesized
En-σ*(2) estimate; kcal/mol) for each HX···YH complex in
Figure 1.
The high transferability [
20] of NBOs and consistency of
nY-σ*
HX near-alignment in XH···YH complexes is evident throughout
Figure 3. Overall, one can see that
all these clusters prefer the L-shaped geometry that is dictated by
nY-σ*
HX co-alignment, which is directly opposed to any plausible “dipole–dipole” logic. The left-hand column of
Figure 3 shows that HF generally prefers a slightly more open angle between the two arms of the L-shape (perhaps reflecting a residual dipole–dipole tendency toward overall linearity), but the strong dominance of
nY-σ*
HX orbital interaction over any presumed dipole–dipole driving force of H-bonding is evident throughout the series.
Additional questions may remain about the small deviations from idealized linearity of H-bonding, as reflected in the apparent failure of
nY and σ*
HX NBOs to achieve the perfectly collinear “maximum overlap” geometry that their shapes suggest. Other questions concern the differences between
En-σ*(2) estimates (
Figure 3) vs. the actual net binding energies Δ
E (
Figure 1) of the complexes. Both types of deviations largely reflect the role of
steric repulsions, which will be discussed below as an integral feature of the total quantum covalency picture.
3.2. NBO-Deletions Analysis of H-Bonding
In the former section we argued from first principles that bonding (σ
HX) and antibonding (σ*
HX) orbitals are inseparable aspects of covalent bonding, and the latter are
unique prerequisites for the
nY-σ*
HX donor–acceptor interactions that consistently appear in NBO analysis of H-bonding in the studied XH···YH complexes (as well as all other known H-bonded species). The species chosen for study generally lie toward the weak limit of H-bonding, in contrast to a previous study [
21] where progressively stronger H-bonds were found whose NRT bond orders ranged continuously upward toward full integer values.
The consistent importance of charge transfer (CT) from donor
nY to acceptor σ*
HX NBOs in H-bonded X–H···:Y species draws a sharp distinction between NBO-based and “HOMO-LUMO”-based analyses of supramolecular interactions. The σ*
HX NBO (valence antibond, “BD*” in NBO output) may superficially appear equivalent to a “virtual” orbital in MO theory or, more specifically, to the lowest unoccupied (LUMO) orbital of canonical SCF-MO or DFT calculations. By definition, however, any virtual MO has
zero occupancy and makes
no contribution to H-bonding or any other observable property. Similarly, for multi-center molecules of appreciable complexity, the highest-energy doubly occupied molecular orbital (HOMO) often differs unrecognizably from the relevant (proximal!)
nY NBO of the critical
nY-σ*
HX donor–acceptor interaction. The CMO keyword [
22] of NBO analysis provides quantitative details of the relationship between NBOs and MOs that allows any confusion between HOMO-LUMO and
nY-σ*
HX involvement in X–H···:Y hydrogen bonding to be quickly resolved.
A more direct and dramatic demonstration of the
necessity for σ*
HX involvement in H-bonding can be given for the current data set of XH···YH complexes. For any MO/DFT method (with well-defined Fock/Kohn-Sham 1-electron energy operator), the NBO program allows the user (with
$DEL…
$END keylist input [
23]) to
delete one or more low-occupancy (“non-Lewis”) NBOs (or any of their specific donor–acceptor interactions) and
recalculate the new (
E(DEL)) potential energy surface and its altered equilibrium geometry, vibrational, and reactive features. Deleting the σ*
HX NBO removes the capacity for
nY-σ*
HX stabilization and thereby
raises the variational energy (
E(DEL) >
E(full)) by an amount that approximates the corresponding
En-σ*(2) perturbative estimate. However, the variational
E(DEL) recalculation also allows one to quantify the many additional structural and vibrational effects of σ*
HX participation in terms of associated
differences between
E(DEL) and
E(full) potential energy features. For the present XH···YH complexes, we specifically removed
both σ*
HX and σ*
HY NBOs because removing only σ*
HX would merely cause the XH···YH complex to rearrange to the alternative YH···XH coordination.
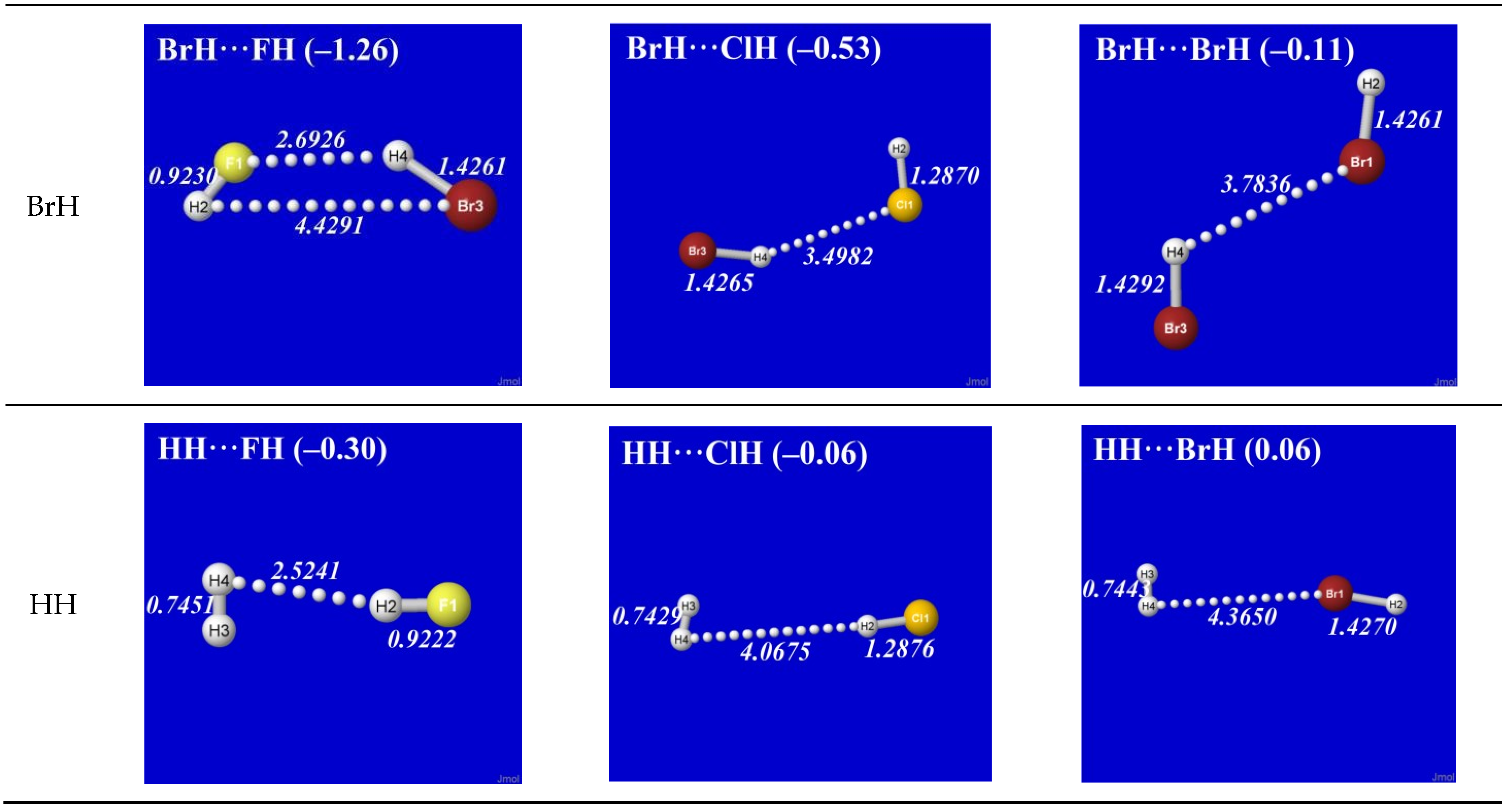
Figure 4 displays the reoptimized
E(DEL) structure in a way that allows direct comparisons with the corresponding panels of
Figure 1. One can see that the
E(DEL) structures differ unrecognizably from the orderly H-bond patterns of
Figure 1. Even where some distant similarity remains to the
E(full) structure of
Figure 1 (as, e.g., for FH···FH or ClH···BrH), the inter-monomer separation is significantly increased (up to or beyond the formal distance of van der Waals contact), the net binding energy is significantly reduced (often to the much weaker range of dispersion and other near-ambient thermal effects), and the characteristic structural signatures of H-bonding are
absent (with
RF(3)H(4) shorter than
RF(1)H(2) and so forth). In short, one concludes that removal of σ*
HX and σ*
HY NBOs
annihilates recognizable H-bonding features in these complexes. Logically, this serves as definitive proof that
presence of the hydride antibonds is a
necessary condition for realistic H-bonding.
More specific deletions of individual nY-σ*HX matrix elements further confirm the unique dependence of realistic H-bond properties on this particular donor–acceptor interaction in all XH···YH complexes. In this connection, it should also be noted that deletion of the σ*HX NBO has no effect on any property of the isolated HX monomer, because the numerical occupancy of the σ*HX NBO is automatically vanishing in any such diatomic species. Thus, the E(DEL) calculation can be said to exactly preserve the dipole moments and other steric and electrostatic properties of isolated monomers but with failure to preserve realistic vestiges of H-bonding.
3.4. Consistent Correlations with Experimental Signatures of H-Bonding
Do the structural features exhibited in
Figure 1 (and annihilated by
E(DEL) deletions in
Figure 4) constitute authentic H-bonding? Although the answer seems obvious “by inspection”, we can apply the operational criteria as recently adopted in the IUPAC
Gold Book definition of the hydrogen bond [
25] to address the question. Similar criteria were applied in previous studies [
26] of much stronger H-bonds, including bifluoride anions (FHF
−) and Zundel cations (H
5O
2+) with binding energies roughly an order of magnitude greater than those of the present study.
In short, the IUPAC definition identifies well-established experimental signatures of XH···Y H-bonding (such as νHX vibrational red-shifting, RHX covalent bond elongation, sub-van der Waals RH···Y approach distance, anomalously high proton-NMR shielding, etc.) and requires that as many of these criteria as possible be verified for their consistent correlations with trends exhibited by consensus examples of H-bonding. Theoretical descriptors of H-bonding (such as NRT bond orders bHX, bH···Y) or new experimental technologies can similarly be tested for mutually consistent correlations with established experimental criteria of H-bonding, thereby building a more stringent and comprehensive characterization of H-bonding as experimental and theoretical methodologies progress.
In particular, inclusion of NRT bond orders makes explicit the deep connection of H-bonding to resonance covalency, confirming the apparent parallels noted in Equations (1) and (2a,b) above. The present species all lie toward the lower end of recognizable H-bonding, where BOBL correlations must eventually
deviate from linearity (because
RH···Y finally increases without limit as
bH···Y → 0). The idea of
fractional bond orders (particularly in the sub-integer range) may seem puzzling when first introduced, but such
continuously variable descriptors of chemical bonding merely reflect the ubiquity of resonance-type phenomena throughout the chemical domain, further extending the obligatory invocation of resonance in discussions of aromaticity or peptide chemistry. Chemical teaching based on the perception of disjoint “covalent” and “noncovalent” domains serves only to obscure the broader role of resonance-type superposition [
18]. Such pedagogical misconceptions must eventually yield to current rapid advances in understanding supramolecular phenomena [
27,
28].
Table 1 summarizes calculated values for a variety of experimentally measurable and theoretical descriptors of H-bonding in the XH···YH complexes of
Figure 1, ordered by net binding energy (Δ
EHB, kcal/mol) in column one. The successive columns present numerical values for the shift in IR stretching frequency (Δν
XH, cm
−1), bond length (Δ
RXH, Å), and NRT bond order (Δ
bXH) of the covalent HX bond, followed by the net charge transfer (
QCT,
e) and perturbative estimate of
nY-σ*
HX stabilization (
Enσ*(2), kcal/mol) in complex formation. These descriptors still neglect steric effects on net binding energy Δ
EHB, but their ordering according to this property allows one to directly see expected types of correlations with other properties.
Correlations between experimental and theoretical descriptors of H-bonding are exhibited more explicitly in
Table 2, which presents values of the Pearson correlation coefficient (χ) for each pair of descriptors in
Table 1. The χ-values exhibit the expected sign of the correlation in all cases. The magnitude |χ| is in the range 0.6–0.9 for correlations with net Δ
EHB, but it is significantly stronger (0.8 or higher) among the various measurable descriptors of the acceptor HX monomer or NBO/NRT characterizations of
nY-σ*
HX interactions. All these correlations suggest that the experimentally measurable (Δν
XH, Δ
RXH) and NBO/NRT-based (Δ
bAH,
QCT,
Enσ*(2)) descriptors of H-bonding are mutually complementary and consistent for the entire data set of XH···YH complexes, including the case X = H where “dipole” character is absent in the XH acceptor (Lewis acid) monomer.
The foregoing pedagogical examples were chosen for clarity and simplicity, but analogous results are reliably predictable for any H-bonded species of the reader’s choice. All such results focus attention on the importance of σ*HX valence antibond orbitals as the “missing link” (Equation (4c)) of covalent bond formation that ties H-bonding (and other supramolecular complexation phenomena) to the same basic quantum superposition principles that underlie other aspects of covalency throughout the molecular sciences. Merely introducing σ*HX as the necessary complement of σHX bond formation (at the same time the latter is introduced) can smoothly provide the firm foundation for the later introduction to H-bonding, sparing students the (ultimately futile) digressions into classical multipole electrostatics.
As the name implies, the “non-Lewis” orbitals represent the capacity for change from the basic Lewis-structural bonding pattern to alternative resonance-structural patterns, which is the essence of resonance conceptions in chemistry. Expected complementary shifts in the shapes of bonding σHX and antibonding σ*HX NBOs with changes in polarity are expected to modulate the primary nY-σ*HX interaction, similar to the manner in which heteroatomic substitutions shift the nuances of resonance-type aromaticity, but the primary focus of introductory chemical pedagogy should be to emphasize the covalent aspects of H-bonding, deprecating usage of “noncovalent” terminology.
3.5. “Sigma-Hole” Picture of H/X-Bonding
A Reviewer has requested consideration of alternative “σ-Hole” nomenclature and conceptions of H-bonded and general X-ogen (X = halogen, pnictogen, etc.) bonded species [
29,
30,
31,
32]. This approach builds on the use of the electrostatic potential (ESP) V(
r),
whose value at a chosen point
r (e.g.,
rLB of a nearby Lewis base) depends on the locations (
RA) of charged nuclei (Z
A) and the Coulombically averaged electron density (ρ) of the chosen molecule (e.g., a hydridic Lewis acid). The strength and sign of a Lewis acid–base interaction is thereby considered to be electrostatically driven [
30] if a point (
rσ) of reduced electron density (“σ-hole”) near the hydride terminus leads to V(
rσ) of
opposite sign (in the “intuitive” classical picture of Coulombic attraction) to that of the corresponding V(
rLB) of the Lewis base. The
rσ depletion point is chosen along a particular contour (0.001 a.u.) for rendering the V(
r) surface plot in color-coded gradations, leading to the colorful “bulls-eye” graphical images of σ-holes that are commonly featured in ESP-based analyses.
The “σ-hole” terminology appears less biased than “noncovalent” for expressing its relationship to covalency conceptions as taught elsewhere in the chemistry curriculum. However, the theoretical foundation for ESP-based interpretations is claimed to be the Hellmann–Feynman theorem, as paraphrased in a form (“The force exerted upon any nucleus in a molecule is entirely classically Coulombic” [
30]) that leads to still stronger denial of the role of resonance covalency in supramolecular bonding (e.g., “
There is no need to invoke charge transfer” [
29]). Stated in summary form, it is claimed that the ESP-based framework provides “quick and easy qualitative interpretation” [
29] and “supports the interpretation of these σ-, π-hole interactions as Coulombic in nature, which is consistent with the rigorous Hellmann-Feynman theorem” [
31].
However, the rigor of the Hellmann–Feynman theorem is two-edged. The formal theorem is known to be valid if (and only if) expressed in terms of the
exact electron density ρ, which in turn must be strictly related to the exact quantum-mechanical wavefunction (unobtainable from classical electrostatics alone) [
33]. Unlike other theorems of quantum chemistry, the Hellmann–Feynman theorem has
no underlying stationary or variational properties to guarantee its stability with respect to small errors in the assumed form of ρ. Indeed, it was recognized long ago that apparently insignificant errors in ρ(
r) can lead to grossly
unphysical Hellmann–Feynman predictions of physical properties [
34].
In practice, ESP-based description of intermolecular binding energies is based not on the Hellmann–Feynman theorem or other theorems of quantum chemistry but rather on
correlations (regression fits) for varying numbers of “electrostatics-related” properties [beyond basic V(
rσ), V(
rLB) values]. As statisticians often remind us, correlation is not causation. The presented correlations [
31,
32] typically involve different numbers, identities, and numerical coefficients in fits for different data sets of Lewis acid–base interactions. Examples include a four-term fit [with added dependence on electric field ℇ(R) and dipole polarizability α values] and a five-term fit [with added dependence on V(R) along the line R of acid–base separation] for tabulated σ-hole interactions but a
different four-term fit for π-hole interactions and still other fits for other data sets in which basic V(
rσ) or V(
rLB) dependence is omitted [
31]. Despite their relatively unconstrained forms, the best such fits are marked by significant “outlier” error (ca. 8 kcal/mol, 36% of Δ
E) that is attributed to neglected contributions of “secondary interactions”.
All such features of ESP-based interpretations of H/X-bonding may be compared with corresponding NBO/NRT-based graphical and numerical descriptors of resonance-type charge-transfer interactions in
Section 3.1,
Section 3.2,
Section 3.3 and
Section 3.4. The latter appear in consistent and unified fashion in
all known H-bonded and X-bonded species. Indeed, if we consider the changes in shape of the hydride σ*
AX NBO (automatically coupled to those of the corresponding σ
AX NBO) under changes of polarization coefficients
cA,
cX [cf. Equation (4a–c)], the similarity to the changes in electron density polarized by a unit charge near the sigma-hole becomes apparent (Figure 2 of Ref. [
29]). Such similarities assure that the same NBO/NRT picture of resonance covalency will apply consistently to all the species mentioned in Refs. [
29,
30,
31,
32].