Vertical Stress Induced Anomalous Spectral Shift of 13.17° Moiré Superlattice in Twist Bilayer Graphene
Abstract
1. Introduction
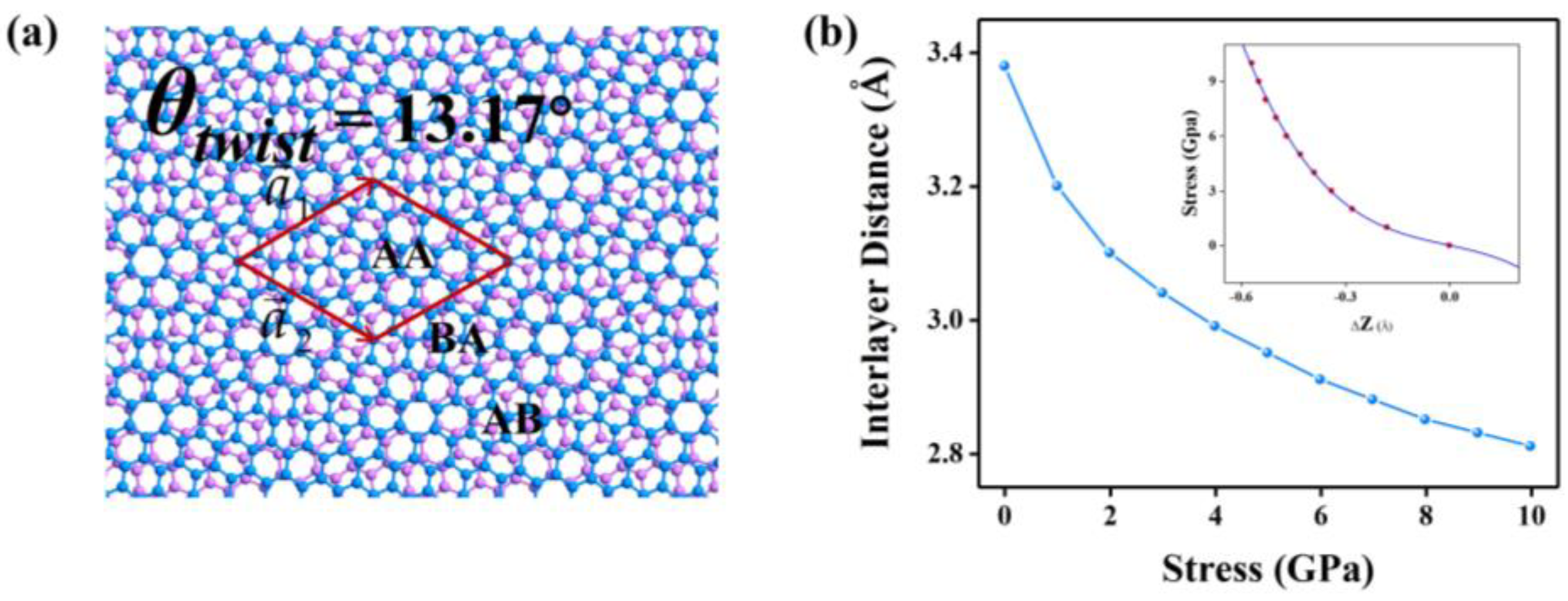
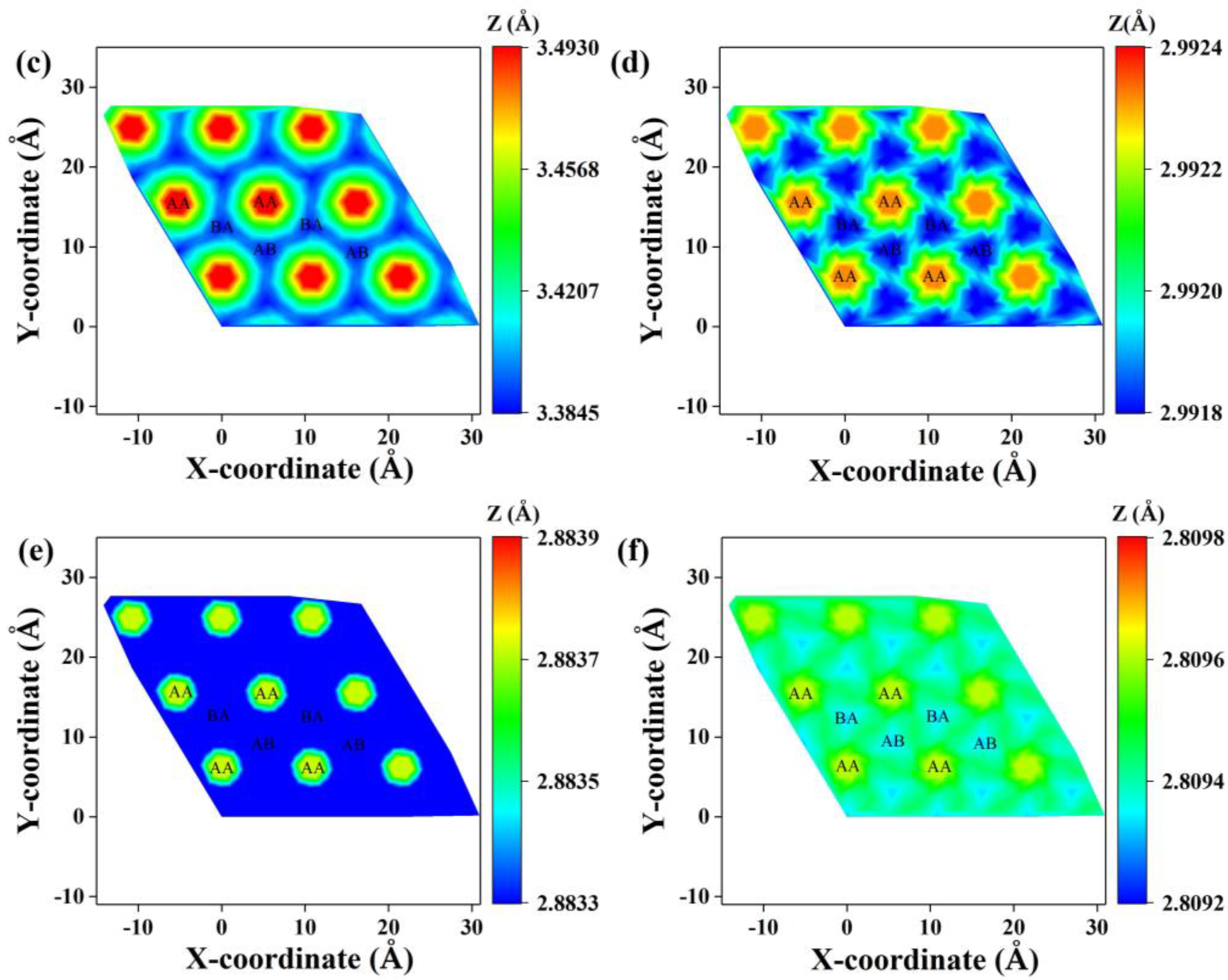
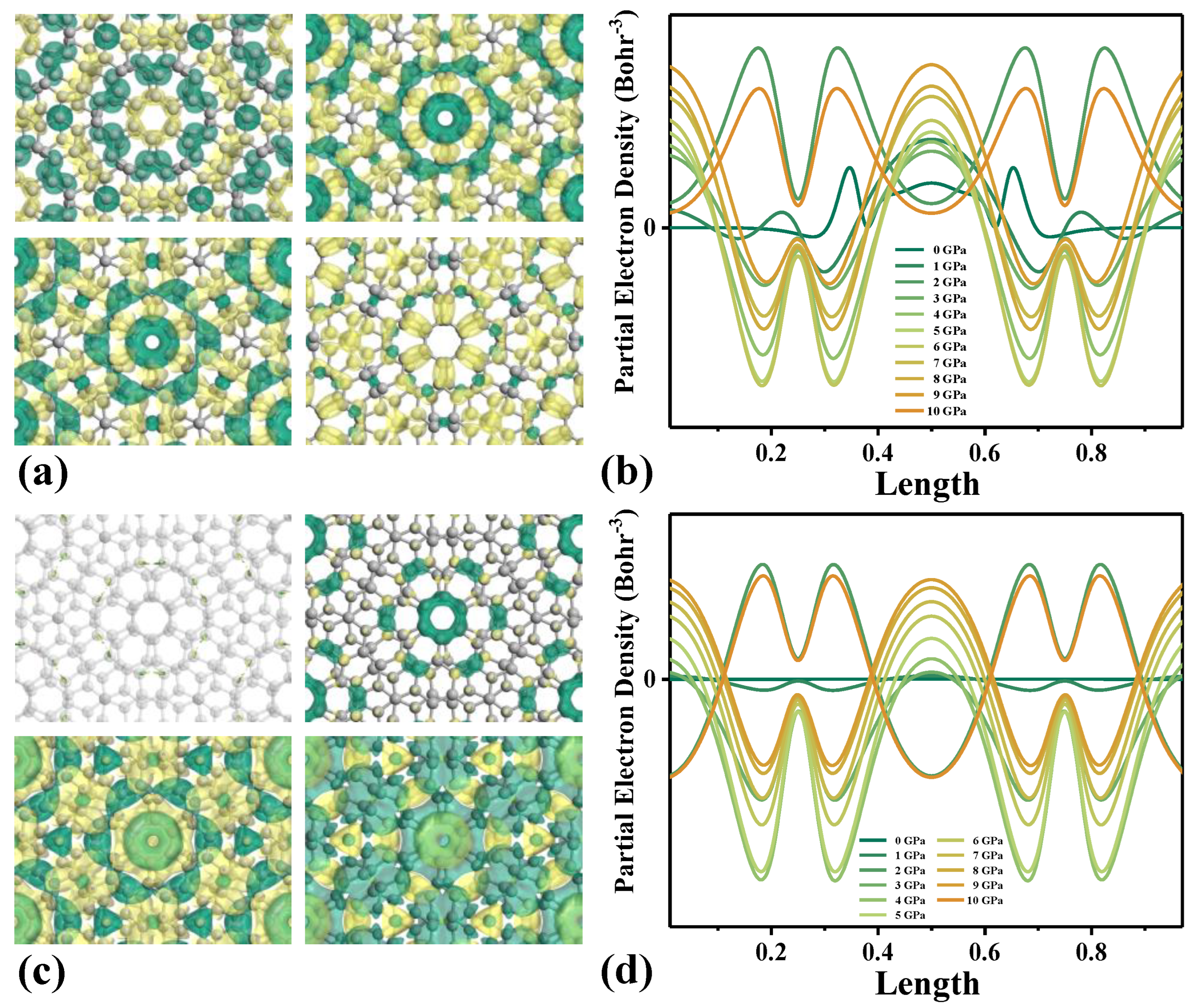
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Mele, E.J. Novel electronic states seen in graphene. Nature 2018, 556, 37–38. [Google Scholar] [CrossRef] [PubMed]
- Marchenko, D.; Evtushinsky, D.V.; Golias, E.; Varykhalov, A.; Rader, O. Extremely flat band in bilayer graphene. Sci. Adv. 2018, 4, eaau0059. [Google Scholar] [CrossRef]
- Ramires, A.; Lado, J.L. Electrically Tunable Gauge Fields in Tiny-Angle Twisted Bilayer Graphene. Phys. Rev. Lett. 2018, 121, 146801. [Google Scholar] [CrossRef] [PubMed]
- Yuan, C.; Fatemi, V.; Demir, A.; Fang, S.; Tomarken, S.L.; Luo, J.Y.; Sanchezyamagishi, J.D.; Watanabe, K.; Taniguchi, T.; Kaxiras, E. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 2018, 556, 80–84. [Google Scholar]
- Kim, Y.; Herlinger, P.; Moon, P.; Koshino, M.; Taniguchi, T.; Watanabe, K.; Smet, J.H. Charge Inversion and Topological Phase Transition at a Twist Angle Induced van Hove Singularity of Bilayer Graphene. Nano Lett. 2016, 16, 5053–5059. [Google Scholar] [CrossRef]
- Kort-Kamp, W.J.M. Topological Phase Transitions in the Photonic Spin Hall Effect. Phys. Rev. Lett. 2017, 119, 147401. [Google Scholar] [CrossRef]
- Huang, S.; Kim, K.; Efimkin, D.K.; Lovorn, T.; Taniguchi, T.; Watanabe, K.; MacDonald, A.H.; Tutuc, E.; LeRoy, B.J. Topologically Protected Helical States in Minimally Twisted Bilayer Graphene. Phys. Rev. Lett. 2018, 121, 037702. [Google Scholar] [CrossRef]
- Alex, T.; Shubhayu, C.; Subir, S.; Mathias, S.S. Triangular antiferromagnetism on the honeycomb lattice of twisted bilayer graphene. Phys. Rev. B 2018, 98, 075109. [Google Scholar]
- Pant, D.; Aryal, S.; Mandal, S.; Pati, R. Emergence of ferromagnetism due to spontaneous symmetry breaking in a twisted bilayer graphene nanoflex. Nano Lett. 2021, 21, 7548–7554. [Google Scholar] [CrossRef]
- Nick, B.; Shubhayu, C.; Michael, P.Z. Mechanism for Anomalous Hall Ferromagnetism in Twisted Bilayer Graphene. Phys. Rev. Lett. 2020, 124, 166601. [Google Scholar]
- Lin, X.; Chen, B.B.; Li, W.; Meng, Z.Y.; Shi, T. Exciton Proliferation and Fate of the Topological Mott Insulator in a Twisted Bilayer Graphene Lattice Model. Phys. Rev. Lett. 2022, 128, 157201. [Google Scholar] [CrossRef]
- Andrea, B.; Michele, F. Local Kekulé distortion turns twisted bilayer graphene into topological Mott insulators and superconductors. Phys. Rev. B 2022, 106, 235112. [Google Scholar]
- Huang, T.; Zhang, L.; Ma, T. Antiferromagnetically ordered mott insulator and d+id superconductivity in twisted bilayer graphene: A quantum monte carlo study. Sci. Bull. 2019, 64, 310–314. [Google Scholar] [CrossRef]
- Kou, A.; Feldman, B.E.; Levin, A.J.; Halperin, B.I.; Watanabe, K.; Taniguchi, T.; Yacoby, A. Electron-hole asymmetric integer and fractional quantum hall effect in bilayer graphene. Science 2014, 345, 55–57. [Google Scholar] [CrossRef]
- Lee, D.S.; Riedl, C.; Beringer, T.; Neto, A.C.; von Klitzing, K.; Starke, U.; Smet, J.H. Quantum hall effect in twisted bilayer graphene. Phys. Rev. Lett. 2011, 107, 216602. [Google Scholar] [CrossRef]
- Liu, Z.; Shi, W.; Yang, T.; Zhang, Z. Magic angles and flat Chern bands in alternating-twist multilayer graphene system. J. Mater. Sci. Technol. 2022, 111, 28–34. [Google Scholar] [CrossRef]
- Sharpe, A.L.; Fox, E.J.; Barnard, A.W.; Finney, J.; Watanabe, K.; Taniguchi, T.; Kastner, M.A.; Goldhaber-Gordon, D. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 2019, 365, 605–608. [Google Scholar] [CrossRef] [PubMed]
- Serlin, M.; Tschirhart, C.L.; Polshyn, H.; Zhang, Y.; Zhu, J.; Watanabe, K.; Taniguchi, T.; Balents, L.; Young, A.F. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 2020, 367, 900–903. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.F.; Liu, F.; Chou, M.Y. Fractal Landau-Level Spectra in Twisted Bilayer Graphene. Nano Lett. 2012, 12, 3833–3838. [Google Scholar] [CrossRef] [PubMed]
- Yin, L.J.; Qiao, J.B.; Wang, W.X.; Zuo, W.J.; Yan, W.; Xu, R.; Dou, R.F.; Nie, J.C.; He, L. Landau quantization and Fermi velocity renormalization in twisted graphene bilayers. Phys. Rev. B 2015, 92, 201408. [Google Scholar] [CrossRef]
- Hicks, J.; Sprinkle, M.; Shepperd, K.; Wang, F.; Tejeda, A.; Taleb-Ibrahimi, A.; Bertran, F.; Le Fèvre, P.; de Heer, W.A.; Berger, C.; et al. Symmetry breaking in commensurate graphene rotational stacking: Comparison of theory and experiment. Phys. Rev. B 2011, 82, 205403. [Google Scholar] [CrossRef]
- Ni, Z.; Wang, Y.; Yu, T.; You, Y.; Shen, Z. Reduction of Fermi velocity in folded graphene observed by resonance Raman spectroscopy. Phys. Rev. B 2008, 77, 235403. [Google Scholar] [CrossRef]
- Sunku, S.S.; McLeod, A.S.; Stauber, T.; Yoo, H.; HalbertaL, D.; Ni, G.; Sternbach, A.; Jiang, B.Y.; Taniguchi, T.; Watanabe, K.; et al. Nano-photocurrent mapping of local electronicstructure in twisted bilayer graphene. Nano Lett. 2020, 20, 2958–2964. [Google Scholar] [CrossRef] [PubMed]
- Xiong, L.; Forsythe, C.; Jung, M.; McLeod, A.S.; Sunku, S.S.; Shao, Y.M.; Ni, G.X.; Sternbach, A.J.; Liu, S.; Edgar, J.H.; et al. Photonic crystal for graphene plasmons. Nat. Commun. 2019, 10, 4780. [Google Scholar] [CrossRef]
- Yoo, H.; Engelke, R.; Carr, S.; Fang, S.; Zhang, K.; Cazeaux, P.; Sung, S.H.; Hovden, R.; Tsen, A.W.; Taniguchi, T.; et al. Atomic and electronic reconstruction at the van der Waals interface in twisted bilayer graphene. Nat. Phys. 2019, 18, 448–453. [Google Scholar] [CrossRef]
- Patel, H.; Huang, L.; Kim, C.J.; Park, J.; Graham, M.W. Stacking angle-tunable photoluminescence from interlayer exciton states in twisted bilayer graphene. Nat. Commun. 2019, 10, 1445. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Hao, H.; Huang, J.; Zhao, Y.; Yang, T.; Zhang, J.; Tong, L. Twist-Induced New Phonon Scattering Pathways in Bilayer Graphene Probed by Helicity-Resolved Raman Spectroscopy. J. Phys. Chem. C 2022, 126, 10487–10493. [Google Scholar] [CrossRef]
- Liao, L.; Wang, H.; Peng, H.; Ying, J.; Koh, A.L.; Chen, Y.; Xie, Q.; Peng, H.; Liu, Z. van Hove Singularity Enhanced Photochemical Reactivity of Twisted Bilayer Graphene. Nano Lett. 2015, 15, 5585–5589. [Google Scholar] [CrossRef]
- Lu, X.; Stepanov, P.; Yang, W.; Xie, M.; Efetov, D.K. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 2019, 574, 653–657. [Google Scholar] [CrossRef]
- Stepanov, P.; Das, I.; Lu, X.; Fahimniya, A.; Watanabe, K.; Taniguchi, T.; Koppens, F.H.; Lischner, J.; Levitov, L.; Efetov, D.K. Untying the insulating and superconducting orders in magic-angle graphene. Nature 2020, 583, 375–378. [Google Scholar] [CrossRef]
- Koshino, M.; Yuan, N.F.Q.; Koretsune, T.; Ochi, M.; Kuroki, K.; Fu, L. Maximally localized wannier orbitals and the extended hubbard model for twisted bilayer graphene. Phys. Rev. X 2018, 8, 031087. [Google Scholar] [CrossRef]
- Salman, S.; Rekik, N.; Abuzir, A.; Alshoaibi, A.; Suleiman, J. The effect of an external electric Öeld on the electronic properties of defective CBNnanotubes: A density functional theory approach. Crystals 2022, 12, 321. [Google Scholar] [CrossRef]
- Salman, S.; Rekik, N.; Abuzir, A.; Suleiman, J. Electronic properties tuning of defective heterostructured CBN nanotubes by uniaxial pressure: A density functional study. Appl. Phys. A 2021, 127, 914. [Google Scholar] [CrossRef]
- Hidalgo, F.; Rubio-Ponce, A.; Noguez, C. Cysteine Adsorption on Twisted-Bilayer Graphene. J. Phys. Chem. C 2021, 125, 27314–27322. [Google Scholar] [CrossRef]
- Hidalgo, F.; Rubio-Ponce, A.; Noguez, C. Tuning Adsorption of Methylamine and Methanethiol on Twisted-Bilayer Graphene. J. Phys. Chem. C 2019, 123, 15273–15283. [Google Scholar] [CrossRef]
- Yankowitz, M.; Chen, S.; Polshyn, H.; Zhang, Y.; Watanabe, K.; Taniguchi, T.; Graf, D.; Young, A.F.; Dean, C.R. Tuning superconductivity in twisted bilayer graphene. Science 2019, 363, 1059–1064. [Google Scholar] [CrossRef]
- Tap, P.; Guo, H.; Yang, T.; Zhang, Z. Stacking stability of MoS2 bilayer: An ab initio study. Chin. Phys. B 2014, 23, 106801. [Google Scholar]
- Tan, P.; Cong, X. Raman Spectroscopy of Graphene-Based Materials; East China University of Technology Press: Shanghai, China, 2021; p. 202. [Google Scholar]
- Smidstrup, S.; Markussen, T.; Vancraeyveld, P.; Wellendorff, J.; Schneider, J.; Gunst, T.; Verstichel, B.; Stradi, D.; Khomyakov, P.A.; Vej-Hansen, U.G.; et al. QuantumATK: An integrated platform of electronic and atomic-scale modelling tools. J. Phys.-Condens. Matter 2019, 32, 015901. [Google Scholar] [CrossRef]
- van Setten, M.J.; Giantomassi, M.; Bousquet, E.; Verstraete, M.J.; Hamann, D.R.; Gonze, X.; Rignanese, G.M. The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 2018, 226, 39–54. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, W.; Sheng, H.; Wang, J. Vertical Stress Induced Anomalous Spectral Shift of 13.17° Moiré Superlattice in Twist Bilayer Graphene. Molecules 2023, 28, 3015. https://doi.org/10.3390/molecules28073015
Miao W, Sheng H, Wang J. Vertical Stress Induced Anomalous Spectral Shift of 13.17° Moiré Superlattice in Twist Bilayer Graphene. Molecules. 2023; 28(7):3015. https://doi.org/10.3390/molecules28073015
Chicago/Turabian StyleMiao, Wenjing, Hao Sheng, and Jingang Wang. 2023. "Vertical Stress Induced Anomalous Spectral Shift of 13.17° Moiré Superlattice in Twist Bilayer Graphene" Molecules 28, no. 7: 3015. https://doi.org/10.3390/molecules28073015
APA StyleMiao, W., Sheng, H., & Wang, J. (2023). Vertical Stress Induced Anomalous Spectral Shift of 13.17° Moiré Superlattice in Twist Bilayer Graphene. Molecules, 28(7), 3015. https://doi.org/10.3390/molecules28073015






