Next Article in Journal
Chitosan and Chitosan Nanoparticles: Parameters Enhancing Antifungal Activity
Next Article in Special Issue
Theoretical–Computational Modeling of CD Spectra of Aqueous Monosaccharides by Means of Molecular Dynamics Simulations and Perturbed Matrix Method
Previous Article in Journal
Pt2CeO2 Heterojunction Supported on Multiwalled Carbon Nanotubes for Robust Electrocatalytic Oxidation of Methanol
Previous Article in Special Issue
Aromatic Character and Relative Stability of Pyrazoloporphyrin Tautomers and Related Protonated Species: Insights into How Pyrazole Changes the Properties of Carbaporphyrinoid Systems
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 7
10.3390/molecules28072993
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Influence of the Solvent on the Stability of Aminopurine Tautomers and Properties of the Amino Group

by
Anna Jezuita
1,
Paweł A. Wieczorkiewicz
2,*,
Tadeusz M. Krygowski
3 and
Halina Szatylowicz
2,*
1
Faculty of Science and Technology, Jan Dlugosz University in Czestochowa, Al. Armii Krajowej 13/15, 42-200 Czestochowa, Poland
2
Faculty of Chemistry, Warsaw University of Technology, Noakowskiego 3, 00-664 Warsaw, Poland
3
Department of Chemistry, Warsaw University, Pasteura 1, 02-093 Warsaw, Poland
*
Authors to whom correspondence should be addressed.
Molecules 2023, 28(7), 2993; https://doi.org/10.3390/molecules28072993
Submission received: 27 February 2023 / Revised: 23 March 2023 / Accepted: 24 March 2023 / Published: 27 March 2023
(This article belongs to the Special Issue Computational and Theoretical Studies on Isomeric Organic Compounds)
Browse Figures
Versions Notes

Abstract

:
Amino derivatives of purine (2-, 6-, 8-, and N-NH2) have found many applications in biochemistry. This paper presents the results of a systematic computational study of the substituent and solvent effects in these systems. The issues considered are the electron-donating properties of NH2, its geometry, π-electron delocalization in purine rings and tautomeric stability. Calculations were performed in ten environments, with 1 < ε < 109, using the polarizable continuum model of solvation. Electron-donating properties were quantitatively described by cSAR (charge of the substituent active region) parameter and π-electron delocalization by using the HOMA (harmonic oscillator model of aromaticity) index. In aminopurines, NH2 proximity interactions depend on its position and the tautomer. The results show that they are the main factor determining how solvation affects the electron-donating strength and geometry of NH2. Proximity with the NH∙∙∙HN repulsive interaction between the NH2 and endocyclic NH group results in stronger solvent effects than the proximity with two attractive NH∙∙∙N interactions. The effect of amino and nitro (previously studied) substitution on aromaticity was compared; these two groups have, in most cases, the opposite effect, with the largest being in N1H and N3H purine tautomers. The amino group has a smaller effect on the tautomeric preferences of purine than the nitro group. Only in 8-aminopurine do tautomeric preferences change: N7H is more stable than N9H in H2O.

1. Introduction

Purine derivatives are important in many biological processes. They are, among others, components of nucleic acids (e.g., adenine and guanine) and many co-factors recognized by proteins. Apart from them, adenine (6-aminopurine) is a building block of energy storage units in living cells, ATP and ADP (adenosine 5′-triphosphate and diphosphate, respectively), of the second intracellular messenger cAMP (3′-5′-cyclic adenosine monophosphate) and of coenzyme NAD+ (nicotinamide adenine dinucleotide), which is involved in redox reactions within many metabolic pathways [1,2]. Furthermore, several well-known alkaloids, such as theophylline, theobromine, and caffeine, are purine derivatives. Purine derivatives exhibit diverse biological activity and are components of some medicines [3,4].
Purine can exist in the form of nine prototropic tautomers: four NH tautomers with the labile proton at the N atom (N1H, N3H, N7H, or N9H) and five CH tautomers with the labile proton at the C atom (C2H, C4H, C5H, C6H, or C8H; see Scheme 1).
The NH forms are much more stable, with a difference between the least stable NH form and the most stable CH form of 27 kcal/mol. The amount of individual tautomers in a mixture strongly depends on the environment [5,6]. In both the gas phase (GP) and the aqueous phase, the N9H tautomer is the most stable, with energy of 4.0 (GP) and 0.2 (H2O) kcal/mol below the N7H tautomer, according to calculations [5]. Due to this small energy difference in polar solvents, the coexistence of N9H and N7H tautomers in similar amounts is observed in experimental studies (UV [7], NMR [8], and Raman spectra [9]), while, according to the IR matrix isolation study, in the gas phase, the N9H tautomer highly dominates [10,11]. Oxidation or reduction of purine also affects the tautomeric equilibrium. For oxidized species, the N1H tautomer is preferred over N9H. Thus, it clearly indicates that the purine structure is sensitive to the environment and electron-transfer reactions [5]. Other factors influencing the purine tautomerism are the presence of substituent(s) [12,13] and metal complexation [8,14,15].
The unique reactivity of purine allows its structure to be modified in many ways. Positions 2, 6, and 8 are susceptible to attack by nucleophiles, whereas 3 and 7 by electrophiles [16]. Both carbon and nitrogen can be used as anchoring points for attaching various types of functional groups, such as dyes or binding molecules. For nucleosides/nucleotides of purine, C6 is the most common carbon anchoring position, while nitrogen positions are N1 and N7. Different strategies used in the modification of purine nucleosides and nucleotides are presented in the review by Kore et al. [17]. The modification or substitution at C2, C6, C8, or N positions of purine allows to acquire specific properties and functions of the molecule. For example, the fluorination of the C2, C6, and C8 position in purines and purine nucleosides has been studied due to the potential antitumor and antiviral activities of such compounds [18]; examples of anticancer drugs are 6-mercaptopurine [4], cladribine and fludarabine [19]. Moreover, the synthetic variability is needed for implementing drug-like properties [20] and selective protein binding [21] into the purine skeleton. Substituted purines have been shown to form hydrophobic contacts, including π-interactions, and various pairs and triplets of hydrogen bonding, which supports enzyme molecular recognition and/or inhibitory activity [22,23]. Some structurally modified bases are being studied as genetic probes for the study of higher eukaryotic organisms. The adenine analog 2-aminopurine (2AP) is a mutagen which mimics the natural base [24,25]. It has good qualities as a probe: The DNA structure is minimally perturbed by the replacement of adenine by 2-aminopurine; the latter has high fluorescence quantum yield in contrast to the natural nucleic acid bases [26]. It is also used in mutagenesis research, as it forms base pairs with both thymine and cytosine residues. The incorporation of 2AP into the nucleic acids of E. coli and other eukaryotic organisms has been well studied [27,28]. The presence of the amino group in the C2 position of purine and the hydroxyl amino group at the C6 position gives one of the most potent mutagen-AHAs (2-amino-6-hydroxylaminopurine); it easily replaces adenine and causes mutations by mispairing with cytosine, being active at relatively low concentrations [29]. In turn, 8-substituted purines have been studied as, for example, kinase inhibitors [30]. The importance of 8-substituted purine derivatives in nucleoside and nucleotide chemistry is also significant. For example, some S-substituted 8-sulfanylpurine derivatives exhibit important biological activities; 8-(benzylsulfanyl)purines are known as irreversible inhibitors of xanthine oxidase [31], and 8[(phenoxyalkyl)sulfanyl]adenosines have hypolipidemic activity [32]. Similarly, N9-substituted analogs of natural purine nucleosides have been widely studied due to their biological activity [33]. N7-nucleoside analogs have been studied less frequently [34], often in the context of N7/N9-glycosyl transfer [35,36]. In addition, purine analogs with the N3 nitrogen replaced by another group (3-deazapurines) are also being studied; such an exchange is biologically important, and alters interactions with proteins, water, and other molecules (see [37] and references therein).
As already mentioned above, the solvent affects the stability of purine tautomers. The same applies to the properties of their derivatives. For example, the solvent effects on the stability of tautomers and π-electron delocalization in 6-amino derivative of purine, adenine, have already been computationally studied by Raczyńska and Makowski [38], taking into account all 23 tautomers. The environment also plays a significant role in the emissive properties of 2-aminopurine: its fluorescence yield increases dramatically with solvent polarity [26]. However, it should be emphasized that most of the theoretical research concerning the nucleic acid base derivatives have been performed in the gas phase [39,40], while theoretical studies on the solvated systems are still limited. Continuum solvation models [41,42,43] are mainly used to account for solvent effects.
The substituent effect (SE) is one of the most useful terms in organic chemistry, describing how group rearrangements or substituent changes in a molecule affect its chemical, physical, and biochemical properties. For its description, substituent constants, σ, are mainly used, which were obtained from the dissociation constants of unsubstituted and p-/m-substituted benzoic acids according to the Hammett equations [44,45]. The σ values characterize the electron-withdrawing/donating properties of the substituents. However, the properties of the substituents depend on the character of the reaction center and the nature of intramolecular interactions, as is reflected in many different scales of substituent constants that have been introduced [46,47], for example, different values of substituent constant for the para and meta positions. Undoubtedly, the use of quantum chemistry methods turned out to be very helpful in the study of the substituent effect. This resulted in the introduction of many concepts (proposed and tested) to its description, for example, MESP (molecular electrostatic potentials) [48], SESE (substituent effect stabilization energy) [49], and cSAR (charge of the substituent active region) [50,51]. The latter substituent effect descriptor seems to be the simplest and is very useful. It can be used to characterize the properties of substituents regardless of the system under consideration, both in the gas phase and in any solvent. Thus, cSAR allows for the comparison of changes in the electronic properties of the substituent (X) and the reaction center (Y) on the same scale. It should be emphasized that the substituent effect can be considered from different points of view, e.g., the classical and reverse substituent effect. For systems presented as X-R-Y (R is a transmitting moiety), the classical substituent effect describes the influence of X on chemical or physicochemical properties of the Y reaction site. Its strength is described by the reaction constant, ρ, of the Hammett equation: P = ρ∙σ + b, where P is some physicochemical property on which a series of substituents, each of them described by σ, is acting. The reverse substituent effect describes changes in the properties of the substituent X depending on the position in R or the nature of reaction site Y [52]; in other words, it is the effective σ in a given system. Further aspects of the substituent effect are the influence of X on the properties of the transmitting moiety, R, and the effect of the substituent X on the structural fragments of reaction site Y, leading to their mutual correlations [53].
Generally, changes in the strength of substituent effects and substituent properties can result from various factors, e.g., intra- and intermolecular interactions [54] or solvation [55]. An interesting example of the influence of intramolecular interactions on the properties of a substituent is when steric or attractive interactions between neighboring groups cause the rotation of one of them. For example, the rotation of the nitro group, as observed in some compounds [56,57], can decrease the strength of the substituent effect by ~45% in the case of 90° rotation [58].
Recent research on nitro derivatives of purine [59], using the polarizable continuum model (PCM), revealed that solvation generally increases the electron-withdrawing properties of the NO2 group. The extent of this increase depends on the through-space proximity interactions experienced by the group—the largest changes were observed in derivatives, in which NO2 participated in two repulsive NO···N interactions. Moreover, both the nitro substitution and the solvent have been shown to have a substantial effect on the tautomeric equilibrium. The C6-NO2 N7H tautomer (Scheme 1 with X = NO2) is more stable than the N9H tautomer in all solvents considered (by about 4 kcal/mol in the gas phase), while the C2-substituted N7H tautomer becomes slightly more stable than the N9H form in more polar solvents. In C8-substituted systems, the least stable N-tautomer of the unsubstituted purine, N1H, becomes the most stable, but the differences between energies of the N9H, N7H, and N1H tautomers are lower than 1 kcal/mol. Interestingly, in C8-nitroadenine, the most stable tautomer in water solution is 3H [60]; thus, it is possible to tune the tautomeric properties of purine derivatives by substitution.
In this paper, we show how the NH2 substitution at the C (C2, C6, or C8) or N (N1, N3, N7, or N9) positions of purine affects the electron-donating properties of the amino group, its geometry, the π-electron structure of the purine rings, and the tautomeric preferences of aminopurines (Scheme 1). For all studied systems, DFT calculations were performed in nine solvents (PCM, 1 < ɛ < 109) and in the gas phase in order to describe the solvent effects in different environments in which biological processes take place.

2. Results

The presentation of the results is divided into four parts concerning: electronic properties of the amino group, geometry and proximity interactions, π-electron delocalization in five- and six-membered rings of purine, and the stability of tautomers of aminopurines. All obtained characteristics of the studied systems are collected in Supplementary Tables S2–S11. In this section, the shortened tautomer notation is used, i.e., 9H, 7H, 3H, and 1H, instead of N9H, N7H, N3H, and N1H, respectively.
First, it should be mentioned that the proximity interactions in nucleic acid base derivatives can be somewhat complicated due to the existence of the endocyclic N or NH groups in various positions. In these systems, the NH2 group can be a hydrogen bond donor and can engage in attractive interactions with endocyclic N atoms (NH···N). Moreover, when the NH group is present in the proximity, a repulsive (NH···HN) interaction occurs. In the N-NH2 substitution, the amino group can also interact with neighboring CH groups, which (in this case) is also a repulsive interaction (NH···HC). Therefore, throughout this paper, the proximity effects will be classified into three types: attractive, mixed, and repulsive, shown in Scheme 2. In the 2× attractive proximity, NH2 engages in two attractive interactions (2× NH···N). In the mixed proximity, NH2 experiences one attractive (NH···N) and one repulsive interaction (NH···HN or NH···HC), whereas, in the 2× repulsive proximity, only two repulsive (NH···HC) interactions are present.

2.1. Electronic Properties of the Amino Group

In order to evaluate and compare the electron-donating strength of the NH2 group in studied aminopurines, the cSAR parameter of the NH2 group was calculated for each system. Taking into account all systems, the values of cSAR(NH2) range from 0.133 to 0.375. Thus, the electron-donating power of the NH2 group may change by as much as 0.242e due to the factors considered in this study: substitution position, tautomeric form of aminopurine, and solvent effects. For comparison, the cSAR(NO2) values of the NO2 group in nitropurines indicate that this group changes its electron-withdrawing ability by 0.142e, due to similar factors [59]. Thus, for substituted purine derivatives, the reverse substituent effect of the amino group is much greater than that of the nitro group.
The cSAR values of the amino group, cSAR(NH2), presented in Figure 1, indicate its electron-donating properties in each system. First, it can be noticed that the values in the N-NH2 systems are, on average, lower than in the C NH2. Moreover, when comparing the substitution positions and tautomeric forms, we can see that the properties of the NH2 group differ. Considering the gas phase, for each substitution position, the NH2 group is slightly more electron donating in 1H and 3H tautomeric forms of aminopurine (NH group in the six-membered ring) than in 7H and 9H (NH group in the five-membered ring). No statistically significant differences were found between cSAR(NH2) values in the gas phase for different proximity types (t-test). The differences between the cSAR(NH2) values calculated in the gas and water phases indicate that solvation is another factor affecting the ED properties of the amino group. An increase in the polarity of the solvent increases its ED properties, except for the two systems with the weakest solvent effects: C2 7H and C8 1H. Additionally, the strength of the solvent effects (extent of changes in the substituent properties induced by solvation) depends on the proximity effects experienced by the NH2 group. Systems with at least one repulsive interaction of the NH2 (mixed and 2× repulsive proximity) experience much stronger solvent effects than the systems with two attractive interactions. In N-NH2 systems, the difference in cSAR(NH2) between the gas phase and H2O is slightly higher in 2× repulsive systems than in the mixed ones. Among them, the least sensitive position to the solvent effect is the N9 position–the place of bonding between saccharide and nucleobase via the N-glycosidic bond. Differences in cSAR(NH2) variability due to solvation between the two proximity effects types in C-NH2 systems are statistically significant (t-test; p-value = 2.27 × 10−6); only two values per proximity type in N-NH2 systems do not allow us to perform such an analysis.
It should be mentioned that the reciprocal of the solvent dielectric constant (1/ε, Table 1) and cSAR(NH2) can be correlated linearly with, in most cases, large determination coefficients, R2. Therefore, the values of slopes (a) of the obtained cSAR(NH2) = a∙(1/ε) + b relations allow to quantitatively compare the sensitivities to the solvent effect of different aminopurines. Appropriate data for all studied systems are presented in Table 2. Additionally, the linear character of the cSAR(NH2) vs. 1/ε relation means that most changes in cSAR(NH2) occur in the solvents with ε < 10, and only minor changes occur in more polar solvents (Supplementary Table S2). Two systems with small R2 values, C2 7H and C8 1H, are the only ones in which the electron-donating properties slightly decrease in polar solvents, as evidenced by small and negative Δ (positive a) values (Table 2). Clearly, the greatest differences between the sensitivities occur in the C2- and C8-NH2 purines, which are tautomers with mixed and 2× attractive proximity. In these cases, mixed proximity systems are, on average, 20 and 16 times more sensitive to the solvent effect, respectively, whereas, in C6-NH2 systems (adenine), only a 3.3-fold difference between these two proximity types is computed. Regarding the N-NH2 systems, those with 2× repulsive proximity experience slightly stronger solvent effects than mixed ones. In this case, the ratio between average values of a for the two 2× repulsive and the two mixed tautomers is 1.5. Thus, it appears that the existence of repulsive interactions increases the sensitivity of the electronic properties of the NH2 group to the solvent effect; moreover, two repulsive interactions further increase it.
In the study, which concerned the nitro derivatives of purine [59], a higher sensitivity to the solvent effect was found in systems with 2× repulsive proximity (2× NO∙∙∙N) contacts than with the mixed one (1× NO∙∙∙N and 1× NO∙∙∙HN). The sensitivity in tautomers with 2× repulsive proximity was, on average, 3.2 times higher in C8 derivatives, 3.6 in C6, and 5.6 in C2 than in mixed-type systems.

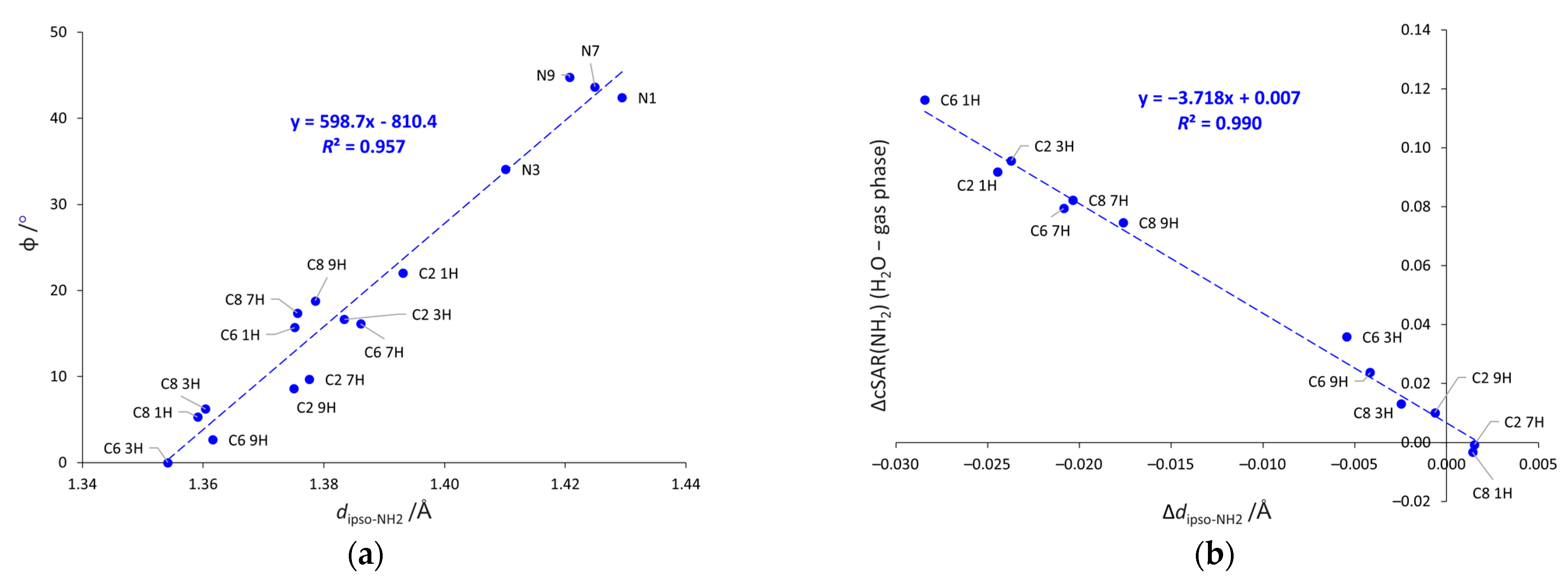
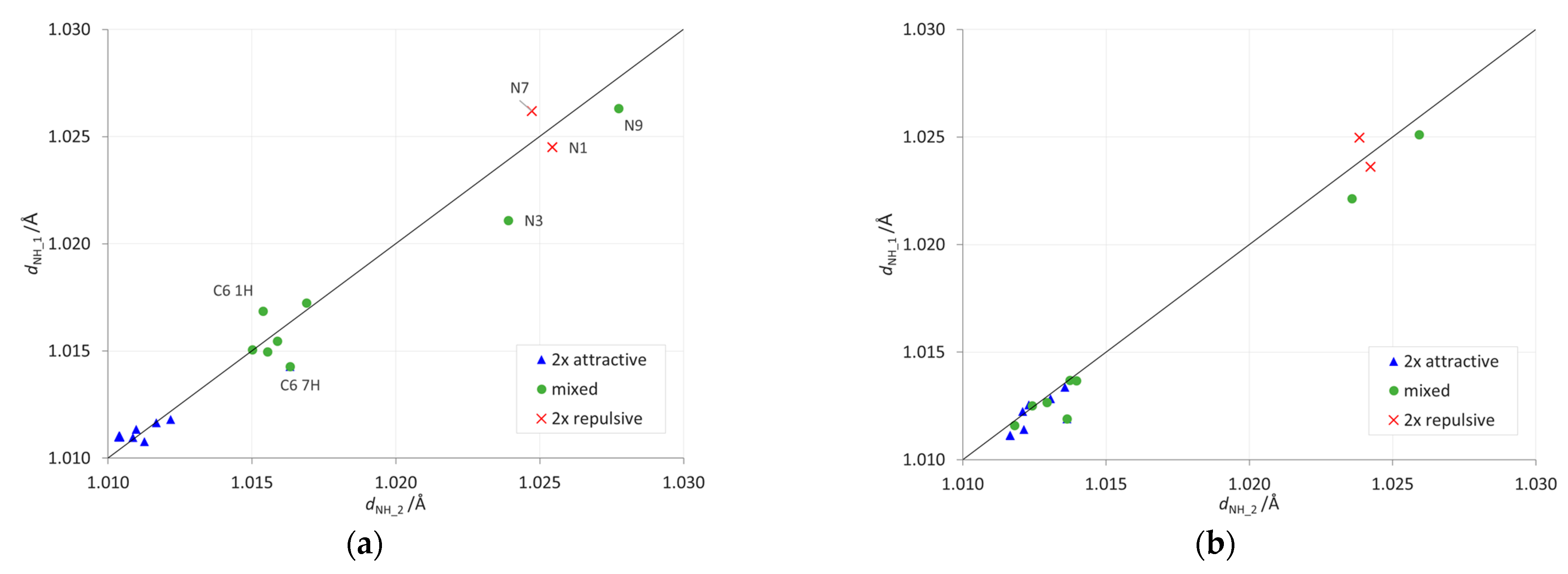
2.2. Geometric Parameters of the Amino Group

The amino group can be characterized by its structural parameters, such as the bond lengths and angles (Scheme 3). A particularly important parameter for the interactions of the NH2 group is its pyramidalization (φ). It can be calculated as 360° minus a sum of all valence angles at the N atom (Figure 2). Larger pyramidalization indicates the greater sp3 character of the hybrid orbitals at the N atom and more of a tetrahedral shape for the amino group. Such a group has a highly localized lone electron pair (Lewis basic site), which can be easily accessed by Lewis acidic centers to form an intermolecular interaction. On the other hand, small pyramidalization indicates a more planar shape, where the central N atom is sp2 hybridized. Such a shape indicates a substantial delocalization of the lone electron pair onto the rest of the substituted system. Studies of aniline derivatives show that the shape of the NH2 group (its pyramidalization) depends on the substituent effects (intramolecular interaction), as well as on intermolecular interaction by H-bonding [54]. For example, a decrease in the pyramidalization of the NH2 group may be related to an increase in the π-electron-accepting power of the para-substituent (substituent effect quantified by σp−) or the formation of a NH···B (B–Lewis base) hydrogen bond by the NH2 group. On the contrary, an increase is computed when the NH2 group is involved in the N···HB interaction (HB-Brønsted acid).
Comparing the different tautomeric forms of the C2-, C6-, and C8-substituted aminopurines in the gas phase, we can see that the 2× attractive proximity type systems have lower values of pyramidalization than the mixed ones (Figure 2). Thus, the presence of two attractive NH∙∙∙N interactions promotes more of a planar shape for the NH2 group. In the C6 3H system, the amino group is completely planar (φ = 0°), while in C6 9H, it is almost planar (φ = 2.7°). This probably comes from the relatively strong NH∙∙∙N interactions in these systems, one of which (with the N7 atom, Scheme 2) has a favorable geometry for the five-membered ring. Interestingly, the solvation effects act oppositely in 2× attractive and mixed-type systems; namely, the values of φ increase in the former and decrease in the latter. The decreases in the mixed-type systems are so substantial that, in some cases, they become more planar than their 2× attractive counterparts for a given substitution. There may be two reasons for this. First, the solvation of polar fragments of molecules—for example the repulsive NH∙∙∙HN interaction between two partially positively charged hydrogen atoms or the attractive NH∙∙∙N interaction between positively charged hydrogen and negatively charged nitrogen—decreases the strength of such interactions (all proximity interactions between partially charged fragments are weakened). Thus, in the polar environment, less planarization coming from NH∙∙∙N interactions and less pyramidalization due to NH∙∙∙HN repulsion is predicted by the calculations. The second reason can be a change in the electronic properties of the NH2 group in polar solvents. Relatively large increases in the electron-donating strength of substituents due to solvation in mixed-type systems (Figure 1) suggest an increase in resonance between the NH2 and the purine moiety, which increases the sp2 character of the hybrid orbital at the N atom and planarizes the amino group. On the contrary, in 2×-attractive-type systems, solvation only slightly increases its electron-donating properties; thus, the changes in pyramidalization should be much smaller. Values of φ in the N-NH2 systems are noticeably larger than in the C-NH2 systems, probably due to the different character of the NN bond than the CN bond between the NH2 and substituted atom of purine.
Another parameter worth considering is the bond length between the NH2 nitrogen atom and substituted atom of purine (C or N), herein called dipso-NH2 (illustrated in Scheme 3). It indicates the strength of interaction of the NH2 group with the substituted system. In the gas phase, the bonds in mixed and 2×-repulsive-type systems for particular substitution are longer than in water, as shown in Figure 3.
As mentioned earlier, solvation weakens the through-space proximity interactions. Accordingly, in systems with at least one repulsive interaction (mixed and 2× repulsive) that “forces” the bond to be longer in the gas phase, solvation allows it to be shortened. In the solvent environment, dipso-NH2 becomes shorter in some mixed-type systems than in 2× attractive systems. The length differences in H2O and in the gas phase (Supplementary Table S4) indicate that, in mixed-type systems, the CN bonds are clearly shortened with an increase in solvent polarity (by 0.018–0.029 Å), whereas, in 2× attractive systems, the changes are slight (from −0.005 to +0.002 Å). These differences result from how the weakening of through-space interactions by solvation affects both systems. In mixed-proximity systems, the NH∙∙∙HN interaction in the gas phase seems to be strong enough to dictate the CN bond length; however, solvation of the two positively charged NH hydrogen atoms weakens their repulsion. It follows that, in the polar environment, the CN bond can be shortened. In systems with 2× attractive interactions, there is no steric hindrance for the CN bond to obtain its shorter “optimal” length; hence, solvation does not change its length as much.
Both the geometric parameters discussed above, φ and dipso-NH2, are mutually correlated (see Figure 4a). Shorter bonds are present in systems with more planar NH2 group, in line with changes in hybridization and the rules of valence bond theory. It is worth noting that the points corresponding to the systems with the NH2 group attached to the five-membered ring are grouped above the trendline, whereas the analogous points for the six-membered substituted systems are below it (except C6 1H). This suggests that the NH2 group has generally slightly more tetrahedral shape when substituted to the five-membered ring than to the six-membered one. In addition, the strengths of the solvent effects on electronic properties and geometry are also well-correlated, as shown in Figure 4b. The increase in the electron-donating properties of the NH2 group due to solvation is closely related to the shortening of the Cipso-NH2 bond.
The proximity interactions of the NH2 group can be detected by plotting the lengths of its two NH bonds against each other (Figure 5 and Supplementary Table S5). Deviation from the y = x line in such a plot indicates that the group interacts stronger on one side than on the other. Here, the strongest deviations are detected for the gas phase (Figure 5a) in the C6 1H and 7H systems, as well as in the N-NH2 systems. Interestingly, the same plot created for the data in formamide (Figure 5b) confirms that solvation weakens repulsive through-space proximity interactions, because the points for mixed-type and 2×-attractive-type systems group together.
Analysis of the proximity effects, using the NCI method, only reveals weak NH∙∙∙N interactions classified as van der Waals interactions in C6 1H, N-NH2 3H, and N-NH2 9H aminopurines (Supplementary Figure S1). Additionally, the AIM analysis detects no bond critical points corresponding to these interactions; thus, they are too weak to be called hydrogen bonds. The reason for that is probably the large distance between N and H atoms, together with the low value of the NH∙∙∙N angle (2.6–2.7 Å and ~100° in systems where the interaction has five-membered ring geometry and 2.4–2.5 Å, ~70° in other (Table S6). On the other hand, the bulkier NO2 group can engage in a stronger intramolecular interaction with the endocyclic NH groups in heterocycles [61], which sometimes meet the criteria for the hydrogen-bond formation [62].

2.3. π-Electron Delocalization in Aminopurine Tautomers

One of the aspects of the substituent effect is its influence on the π-electron structure of the transmitting moiety. Before discussing these effects, it is important to mention that, in purine, the π-electron structure depends on the tautomeric form considered. This is because the endocyclic NH group has two 2pz electrons, which can be delocalized within the rings, whereas the endocyclic N atom provides just one π-delocalizable electron. Therefore, 9H and 7H tautomers with the NH group in the five-membered ring consist of imidazole and pyrimidine rings, both of which have 6π delocalizable electrons, and hence are aromatic according to the Hückel 4n + 2 rule. However, in 1H and 3H tautomers with the NH group in the six-membered ring, the six-membered ring contains 7π electrons, while the five-membered ring has 5π electrons. Consequently, the 9H and 7H tautomers of unsubstituted purine have higher aromaticity, as evidenced by aromaticity indices, e.g., HOMA (Figure 6 and Supplementary Table S7).
The NH2 group in the C8 and C2 positions reduces the aromaticity of both purine rings in all tautomers, except for the five-membered ring in C2 3H and 7H systems (Figure 7a). However, in the C6 and N-NH2 derivatives, the aromaticity of both rings increases, except for the six-membered ring in N-NH2 9H and 7H. Changes in the aromaticity are more pronounced in the 1H and 3H tautomers than in the 7H and 9H ones. Thus, the π-electron structure in “aromatic” tautomers tends to be preserved, whereas, in “nonaromatic” ones, it can change significantly due to the substituent effect. Interestingly, the aromaticity of the six-membered ring in C6 3H (so, the 3H tautomer of adenine) increases so much that its aromaticity is noticeably higher than in the C6 7H tautomer (a decrease of aromaticity of the latter also assists this exchange).
Larger changes in the aromaticity of the 1H and 3H tautomers were also found for the NO2 substitution of purine (Figure 7b and Supplementary Table S8). Importantly, the electron-donating NH2 and electron-withdrawing NO2 groups have the opposite effect on aromaticity in several cases. This is easiest to see in C6 derivatives, where NH2 increases aromaticity of the 1H and 3H tautomers substantially (by ~0.1–0.2 HOMA units), while NO2 decreases it (by ~0.20–0.25). A similar effect happens for the 9H tautomer, but in 7H, the effects of these two groups are reversed. This is probably due to the distortion of geometry by a relatively strong NH/NO∙∙∙HN interaction, repulsive and attractive, respectively, with a six-membered ring geometry present in these systems. In C8 derivatives, apart from the six-membered ring in the 7H and 9H tautomers, NO2 increases aromaticity, whereas the NH2 group decreases it.
The differences between the HOMA values in amino and nitro derivatives of purine are shown in Figure 8a. They are clearly most pronounced for the C6 substitution, but also in the C2 3H and C8 3H and 1H systems. Plotting changes in HOMA due to substitution (with respect to unsubstituted purine) in the five-membered ring against the corresponding value for the six-membered ring (Figure 8b) reveals that, in NH2 derivatives, changes in the aromaticity of the five-membered ring are statistically 40% larger than those in the six-membered ring (slope value, a = 1.404). Thus, the substituent effect of the NH2 group is acting stronger on the five-membered ring. On the other hand, the NO2 substitution gives a slope value lower than 1 (a = 0.886). Thus, statistically, the substituent effect of the NO2 group changes the π-electron structure of the six-membered ring to a greater extent than the five-membered one. The opposite effects for the electron-donating NH2 and electron-withdrawing NO2 groups most likely come from the fact that, in the “nonaromatic” 1H and 3H tautomers, the 6-membered ring has an excess of π electrons (7), whereas the 5-membered is deficit (5), compared to the 6π electrons needed for the Hückel aromaticity.
The π-electron structure can also change due to solvation. Figure 9 presents the differences in HOMA aromaticity indices calculated for the geometry in the most polar solvent and in the gas phase. In most cases, aromaticity increases in polar solvents. Moreover, the increases of HOMA are much more pronounced than the decreases; the maximum decrease is 0.015, while the increase can be as high as 0.120. This applies to both NH2 (Figure 9a) and NO2 (Figure 9b) substitutions. By far, the largest changes occur in the 1H tautomers (least aromatic in the gas phase, Figure 6) for all substitution positions. Moreover, the six-membered rings of the 1H amino derivatives are more sensitive to solvation than the five-membered ones (Figure 9a), and generally the same is true for all amine systems (Supplementary Figure S2a). Nonaromatic 1H and 3H tautomers are more prone to changes in aromaticity due to solvation (Figure 9) and, as shown earlier, by substitution. It should be added that relatively similar results were obtained by using the Harmonic Oscillator Model of Electron Delocalization (HOMED) index [63] (see Supplementary Figures S2b, S3, and S4).

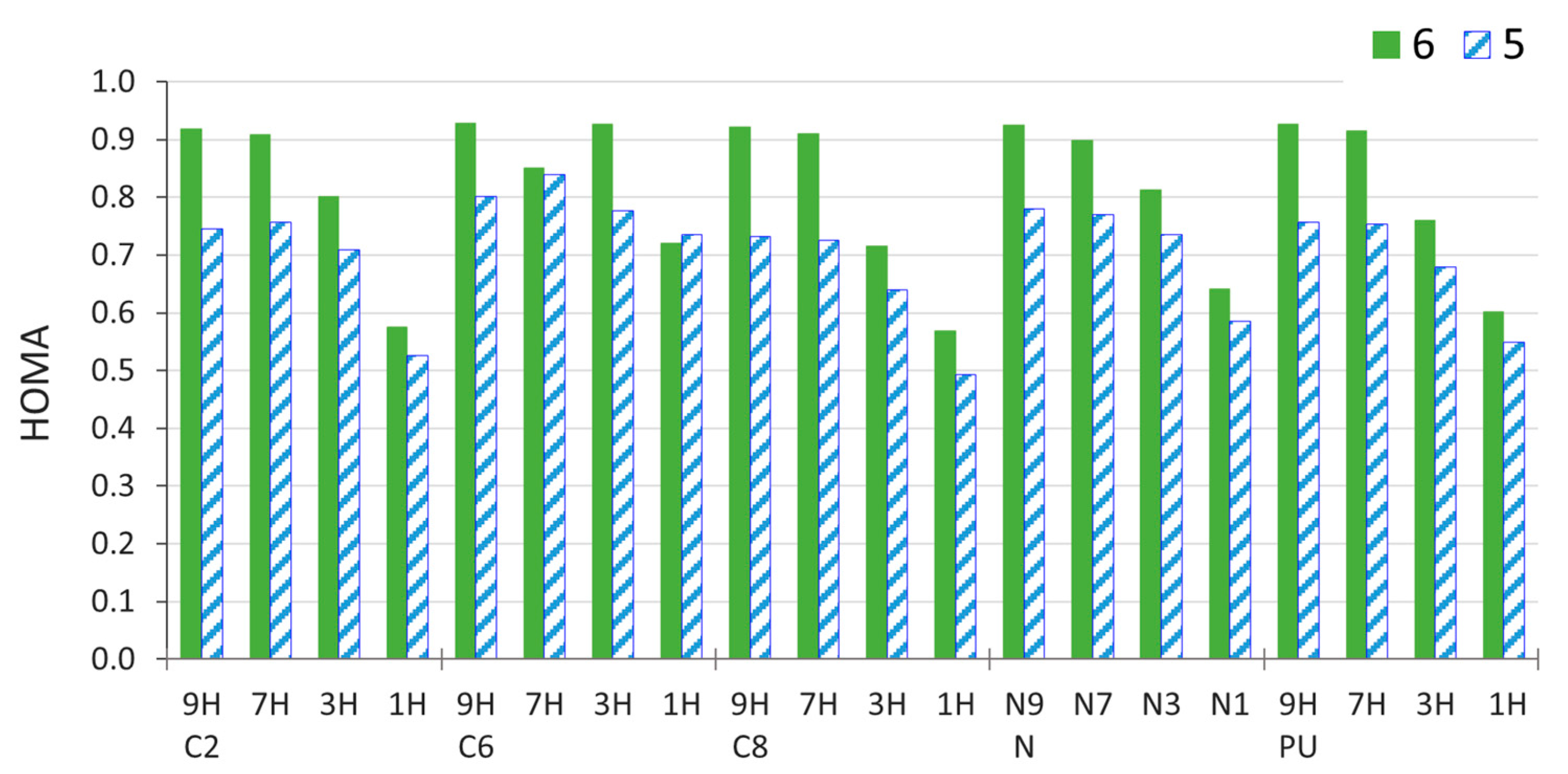
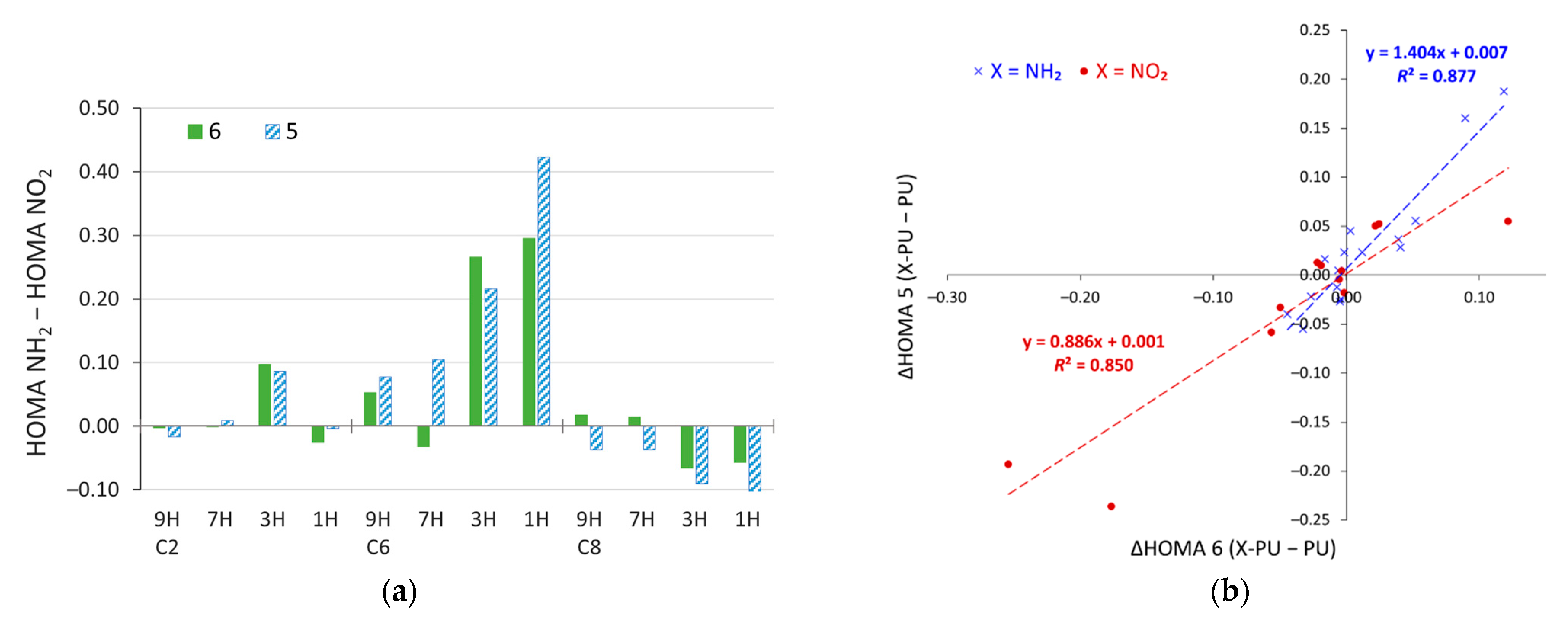
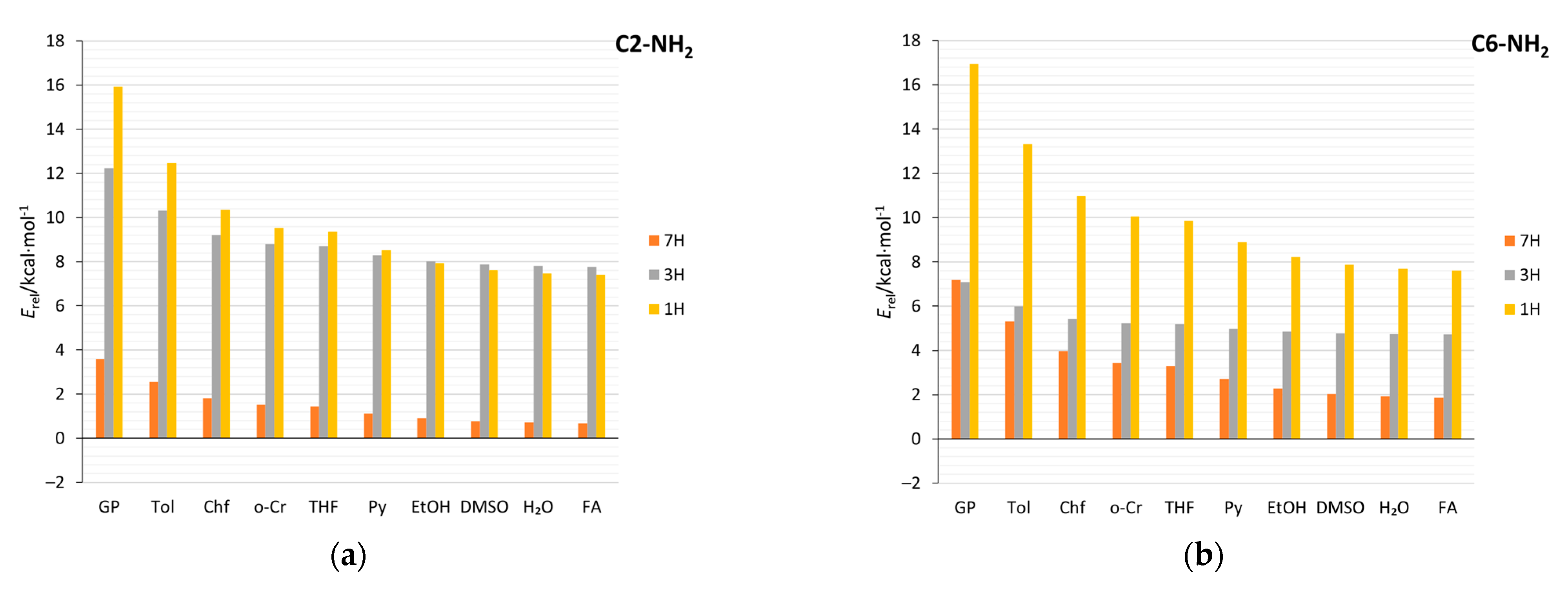
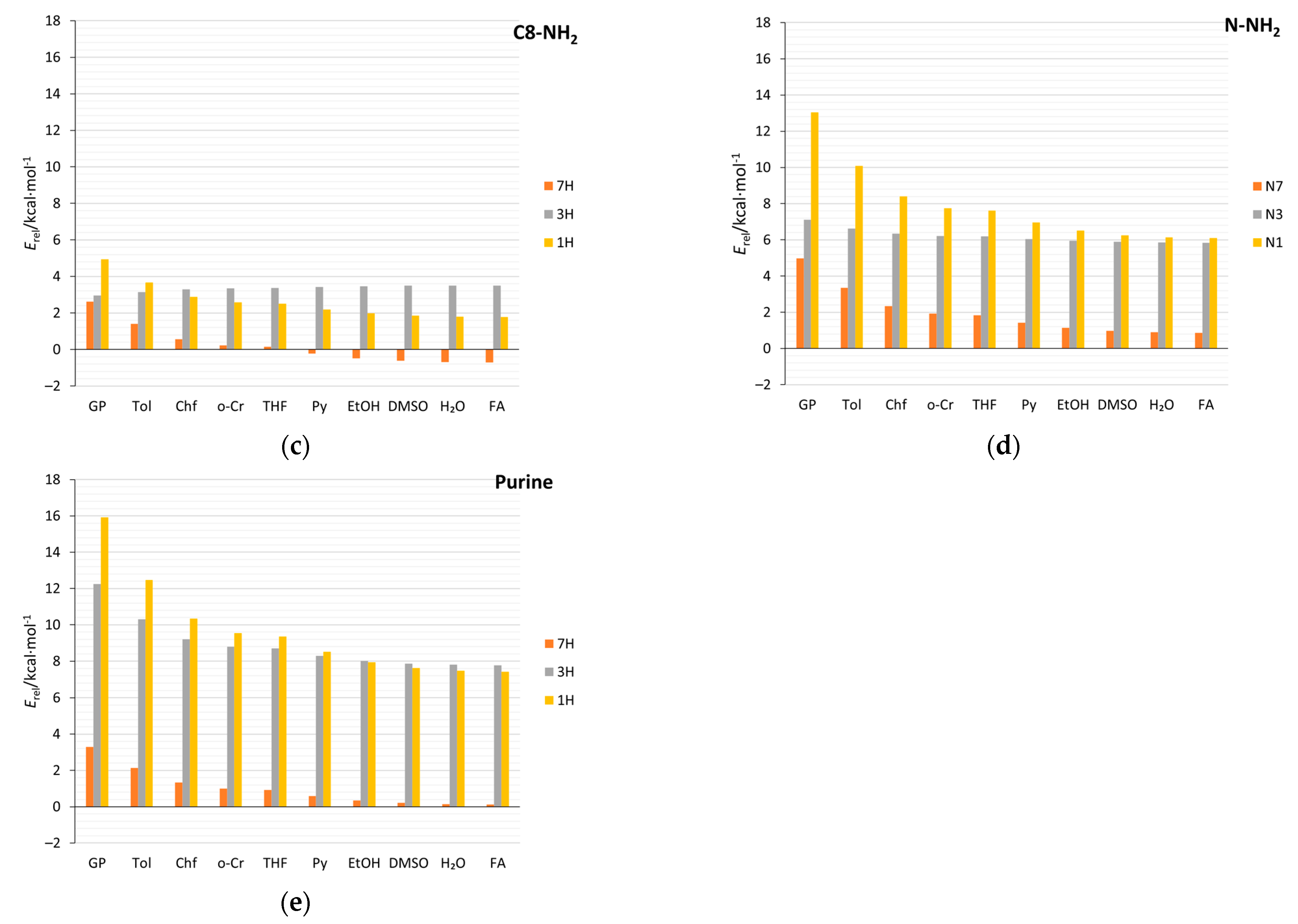
2.4. Stability of Aminopurine Tautomers in Various Solvents

Solvation, as well as the substitution of N-heterocyclic compounds, can affect the relative stabilities of tautomers and, in some cases, change the tautomeric preferences [11,64]. Data in Table 3 and Supplementary Table S9 cover both substituent and solvent effects on the relative energy of tautomers (Erel) in studied aminopurines. For comparison, the relative stabilities of the unsubstituted and nitro-substituted purine tautomers are also included. Regarding the aminopurines, in the gas phase, the 9H tautomer is the most stable for all types of substitutions. For C2-, C8-, and N-NH2-substituted purines, the stability decreases in order from the most stable tautomer, 9H, through 7H, 3H, to 1H, similar to the unsubstituted purine tautomers. However, in C8-NH2 derivatives, in solvents with ɛ > 10, tautomeric preferences change: The 7H tautomer is more stable than the 9H (Figure 10c). In C2- and C8-NH2, like in the unsubstituted purine, solvation highly stabilizes the 1H tautomer, so that it becomes more stable than the 3H. This is not found for the C6- and N-NH2 tautomers. In C6 derivatives (adenine), in the gas phase, the 3H tautomer is more stable than the 7H tautomer, and the stability sequence is 9H, 3H, 7H, and 1H, while in water, it changes to 9H, 7H, 3H, and 1H.
In all cases, an increase in the solvent polarity decreases the differences in energy between the most and least stable tautomers. For all amino derivatives, except for the C8-NH2 systems, and the unsubstituted purine, this difference decreases by about 50%. As indicated by the ∆ values in Table 3, the relative energies of the 1H tautomer derivatives are the most sensitive to the solvent effect—the greatest stabilizations are predicted. In an aqueous environment, the differences between the energies (Erel) of the 9H and 7H tautomers are small. This means that both tautomers can coexist in the solution, just as it was computed for unsubstituted purine [5]. In the NO2 derivatives, more interesting things happen; for example, the 7H C6-NO2 tautomer is much more stable (due to intramolecular hydrogen bonding) than 9H in both the gas phase and water (by more than 4 and 2 kcal/mol, respectively). Additionally, in C8-NO2, 1H becomes the most stable tautomer in polar environments due to its exceptional stabilization by the solvent (∆ = −11.6 kcal/mol).
In order to explain why some systems are stabilized better than others, the solvation energies (Supplementary Table S10) and their dependence on 1/ε of solvent were analyzed (Table 4). Considering the tautomers of the C-NH2 derivatives, it can be noticed that the substitutions which cause the mixed-type proximity effect have higher dipole moments than the 2× attractive ones. Rather, this is due not to the proximity effects but to the fact that when NH and NH2 are close to each other (like in mixed-type systems), the vectors of their contributions to the molecular dipole moment add up in a way that the overall dipole moment increases. This leads to higher solvation energies in mixed-type systems. Additionally, the dipole moments increase with the polarity of the solvent in these systems to a greater extent (Supplementary Table S11), as indicated by Δμ. For this reason, the solvation energies increase more in mixed than in 2× attractive systems, as evidenced by the values of a (Table 4). Here, the possible cause might be that cSAR(NH2) in mixed-type systems increases substantially due to solvation, and, as the electron-donating properties of NH2 increase, this contributes to the overall increase in the polarity of charge distribution in the molecule. Moreover, 1H tautomers have the highest dipole moments and the highest increases of them due to solvation. This is the reason for the predicted largest solvation energies and changes in relative energies (Table 3, Figure 10, and Supplementary Figure S5) for 1H tautomers of unsubstituted, as well as amino-substituted, purine.

3. Methodology

The research objects were monosubstituted C- and N-NH2 purines in the four most stable tautomeric forms. For studied systems, optimization was carried out without any symmetry constraints (in the gas phase and solution), with the use of the Gaussian09 package [66]. Calculations were performed using the DFT method at B97D3 functional [67], with Dunning’s aug-cc-pVDZ basis set [68]. The choice of this computational level was based on its ability to characterize stacking interactions in adenine dimers, with both the energetic and geometric criteria considered [69]. In the case of the N-NH2 substitution, the conformation in which the NH2 group is perpendicular to the plane of the purine ring is the most stable (see Supplementary Materials Table S1). In these systems, an optimization constraint was added to forbid the rotation of the NH2 group around the N-N bond and to force “coplanar” conformation. This way, the types of proximity effect in the N-NH2 systems can be classified along with the C-NH2 systems, and the comparison between them is easier. However, the values of energy and dipole moments in the manuscript are given for the most stable (perpendicular) conformation. To confirm that presented structures correspond to the minima on the potential energy surface, the vibrational frequencies were calculated at the same level of theory. No imaginary frequencies were found in the C-NH2 systems and N-NH2 systems with the perpendicular conformation of the NH2; in N-NH2 systems with a forced “coplanar” NH2 group, one imaginary frequency associated with rotation was found.
The PCM model of solvation [41] was used to study the effect of selected solvents (with dielectric constants, ɛ, from 1 to 109, Table 1) on various properties of aminopurines.
The amino group was characterized by both geometric (bond lengths and angles) and electronic parameters. As for the geometric parameters (Scheme 3), lengths of bonds between the NH2 and ipso atom of purine (C or N) (dipso-NH2), and NH bonds in amino group (dNH) and pyramidalization (φ) of the NH2 group were investigated.
Electronic properties of the amino group were quantitatively described by the cSAR (charge of the substituent active region) parameter [50,51]. The cSAR(X) of the amino group was calculated as the sum of the charges at all atoms of the NH2 group and the charge at the ipso carbon or nitrogen atom, Equation (1).
cSAR ( NH 2 ) = q ( NH 2 ) + q ( C   or   N ) ipso
The values of cSAR are positive for electron-donating groups; the higher the values, the more electron-donating the substituent is in a given system. Oppositely, for electron-withdrawing groups, cSAR has negative values, which are more negative with an increase of electron-withdrawing ability. Hirshfeld atomic charges were used in the calculation of cSAR [70].
Changes in π-electron delocalization in both purine rings were assessed using the geometry-based HOMA (Harmonic Oscillator Model of Aromaticity) index [71]. It is defined in Equation (2):
HOMA = 1 − 1 n ∑ i n α j ( d opt , j − d j , i ) 2 ,
where n is the number of bonds taken into account when carrying out the summation, i means the type of bond (CC or CN), αj is an empirical normalization constant (for CC and CN bonds, αCC = 257.7 and αCN = 93.52 from Ref. [72]), dopt,j is the optimal length of a given bond assumed to be realized in fully aromatic systems with HOMA = 1 (for CC and CN bonds, dopt,CC = 1.388 Å and dopt,CN = 1.334 Å), and dj,i is an actual bond length in the studied system. The NCI (non-covalent interaction index) method was used to detect possible noncovalent intramolecular interactions [73]; their nature was determined on the basis of the value of sgn(λ2)·ρ(r), where λ2 is the second eigenvalue of the Hessian matrix of electron density (ρ(r)). NCI analyses were performed in Multiwfn [74] and visualization in VMD program [75].

4. Conclusions

The aim of the work was to investigate changes in the properties of the amino group attached to the C2, C6, C8, or N (N1, N3, N7, or N9) position in the four most stable purine tautomers in various solvents, as well as the effect of substitution on the tautomer stability and π-electron structure of the purine rings. It was shown that, due to the position of substitution, tautomeric form, and solvent effect, changes in the electron-donating power of the NH2 group are significant; its cSAR (charge of the substituent active region) value ranges from 0.133 to 0.375. Thus, for substituted purine derivatives, the reverse substituent effect of the amino group is much greater than previously found for the electron-accepting nitro group [59].
It was found that the solvent effect’s strength depends on the proximity interactions of the amino group present in the given tautomeric form of aminopurine. In systems with repulsive proximity interactions (NH∙∙∙HN), a much stronger solvent effect is found than for derivatives with two attractive interactions (NH∙∙∙N). This is evidenced by appropriate changes in the electronic and geometric parameters of the amino group.
Substitution and solvation also affect π-electron delocalization in aminopurine rings, and the effect varies depending on the substitution position and tautomer; larger changes in aromaticity occur in the N1H and N3H tautomers than in N7H and N9H. In most cases, the aromatic character increases with the solvent polarity. Substitution with the amino group has a distinctly opposite effect on aromaticity than with the nitro group.
In 2-, 6-, and N-aminopurines, an increase in solvent polarity significantly reduces the differences in stability between the most and least stable tautomers; however, the tautomeric preferences do not change compared to unsubstituted purine. In 8-aminopurines, the difference in water is only 4 kcal/mol; additionally, the sequence of stability changes from N9H > N7H > N3H > N1H (gas phase) to N7H > N9H > N1H > N3H (water).

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/molecules28072993/s1, Table S1: Energy values and the difference between the coplanar and perpendicular conformations of NH2 in N-NH2 derivatives of purine; Table S2: The cSAR(NH2) values for C2-, C6-, C8-, and N-NH2-substituted purine tautomers; Table S3: The valence angles at the N atom and pyramidalization of the NH2 group in the gas phase and water, their difference, and type of proximity for C2-, C6-, C8-, and N-NH2-substituted purine tautomers; Table S4: dipso-NH2 bond lengths in the gas phase and water, their difference, and type of proximity for C2-, C6-, C8-, and N-NH2-substituted purine tautomers; Table S5: dNH bond lengths in the gas phase and formamide, their difference, and type of proximity for C2-, C6-, C8-, and N-NH2-substituted purine tautomers; Table S6: Distance between H atom from NH2 and N atom from the purine ring, H···N, in the gas phase and formamide, their difference, and type of proximity for C2-, C6-, C8-, and N-NH2-substituted purine tautomers; Table S7: HOMA values of five- and six-membered rings in gas phase and formamide, their difference, and ∆HOMANH2PU-PU for purine and analyzed NH2-substituted derivatives of purine tautomers; Table S8: HOMA values of five- and six-membered rings (5MR, 6MR) in gas phase and formamide, their difference, and ∆HOMANO2PU-PU for analyzed NO2-substituted derivatives of purine tautomers; Table S9: Relative energies of C2-, C6-, C8-, and N-NH2-substituted purines; Table S10: Solvation energies of C2-, C6-, C8-, and N-NH2 coplanar-substituted purines; Table S11: Dipole moments, μ, of C2-, C6-, C8-, and N-NH2-substituted purines. Figure S1: NCI analysis for selected systems. Visualization of reduced density gradient isosurfaces; Figure S2: Change in (a) HOMA and (b) HOMED of 6- and 5-membered rings between the formamide and the gas phase plotted against the HOMA (HOMED) value for the respective ring of aminopurines in the gas phase; Figure S3: Values of HOMED index for 6- and 5-membered rings of C2, C6, C8, and N amino-substituted derivatives of purine in four tautomeric forms, calculated for the gas phase geometry; Figure S4: Changes in HOMED index due to (a) solvation and (b) substitution; Figure S5: Solvation energies of tautomers, Esolv, for (a) C2-NH2, (b) C6-NH2 (c) C8-NH2 (d) N-NH2, and (e) unsubstituted purines.

Author Contributions

Conceptualization, T.M.K. and H.S.; Methodology, A.J. and P.A.W.; Formal analysis, A.J. and P.A.W.; Investigation, A.J. and P.A.W.; Writing— original draft, A.J. and P.A.W.; Writing—review & editing, T.M.K. and H.S.; Supervision, H.S.; Funding acquisition, H.S. All authors have read and agreed to the published version of the manuscript.

Funding

H.S. and P.A.W. thank the Warsaw University of Technology for financial support.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All data generated in this study are presented in the Manuscript and its Supplementary Materials.

Acknowledgments

The authors would like to thank the Wrocław Centre for Networking and Supercomputing and the Interdisciplinary Center for Mathematical and Computational Modeling (Warsaw, Poland) for providing computer time and facilities.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

All calculation files are available from the authors.

References

  1. Rosemeyer, H. The Chemodiversity of Purine as a Constituent of Natural Products. Chem. Biodivers. 2004, 1, 361–401. [Google Scholar] [CrossRef] [PubMed]
  2. Covarrubias, A.J.; Perrone, R.; Grozio, A.; Verdin, E. NAD+ metabolism and its roles in cellular processes during ageing. Nat. Rev. Mol. Cell Biol. 2021, 22, 119–141. [Google Scholar] [CrossRef]
  3. Legraverend, M.; Grierson, D.S. The purines: Potent and versatile small molecule inhibitors and modulators of key biological targets. Bioorganic Med. Chem. 2006, 14, 3987–4006. [Google Scholar] [CrossRef]
  4. Pozharskiĭ, A.F.; Soldatenkov, A.T.; Katritzky, A.R. Heterocycles in Life and Society: An Introduction to Heterocyclic Chemistry, Biochemistry, and Applications, 2nd ed.; Wiley: Chichester, UK, 2011. [Google Scholar]
  5. Raczyńska, E.D.; Kamińska, B. Variations of the tautomeric preferences and π-electron delocalization for the neutral and redox forms of purine when proceeding from the gas phase (DFT) to water (PCM). J. Mol. Model. 2013, 19, 3947–3960. [Google Scholar] [CrossRef] [Green Version]
  6. Raczyńska, E.D.; Kamińska, B. Prototropy and π-electron delocalization for purine and its radical ions—DFT studies. J. Phys. Org. Chem. 2010, 23, 828–835. [Google Scholar] [CrossRef]
  7. Peral, F.; Gallego, E. A study by ultraviolet spectroscopy on self-association of purine, 6-methylpurine, benzimidazole, and imidazo [1,2-a]pyridine in aqueous solution. Spectrochim. Acta 2000, 56, 747–759. [Google Scholar] [CrossRef]
  8. Gonnella, N.C.; Roberts, J.D. Studies of the tautomerism of purine and the protonation of purine, and its 7- and 9-methyl derivatives, by nitrogen-15 nuclear magnetic resonance spectroscopy. J. Am. Chem. Soc. 1982, 104, 3162–3164. [Google Scholar] [CrossRef]
  9. Burova, T.G.; Ten, G.N.; Kucherova, V.V. Investigations of Tautomeric Purine Forms by the Methods of Vibrational Spectroscopy and Resonance Raman Scattering. II. Quantum-Mechanical Calculations of the Resonance Raman Scattering Spectra of Purine Tautomers. Russ. Phys. J. 2004, 47, 721–725. [Google Scholar] [CrossRef]
  10. Nowak, M.J.; Lapinski, L.; Kwiatkowski, J.S. An infrared matrix isolation study of tautomerism in purine and adenine. Chem. Phys. Lett. 1989, 157, 14–18. [Google Scholar] [CrossRef]
  11. Nowak, M.J.; Rostkowska, H.; Lapinski, L.; Kwiatkowski, J.S.; Leszczynski, J. Tautomerism N(9)H .dblharw. N(7)H of Purine, Adenine, and 2-Chloroadenine: Combined Experimental IR Matrix Isolation and Ab Initio Quantum Mechanical Studies. J. Phys. Chem. 1994, 98, 2813–2816. [Google Scholar] [CrossRef]
  12. Chenon, M.T.; Pugmire, R.J.; Grant, D.M.; Panzica, R.P.; Townsend, L.B. Carbon-13 magnetic resonance. XXVI. Quantitative determination of the tautomeric populations of certain purines. J. Am. Chem. Soc. 1975, 97, 4636–4642. [Google Scholar] [CrossRef] [PubMed]
  13. Sečkářová, P.; Marek, R.; Maliňáková, K.; Kolehmainen, E.; Hocková, D.; Hocek, M.; Sklenář, V. Direct determination of tautomerism in purine derivatives by low-temperature NMR spectroscopy. Tetrahedron Lett. 2004, 45, 6259–6263. [Google Scholar] [CrossRef]
  14. Lippert, B.; Gupta, D. Promotion of rare nucleobase tautomers by metal binding. Dalton Trans. 2009, 4619–4634. [Google Scholar] [CrossRef] [PubMed]
  15. Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C.; Kamińska, B.; Igielska, M.; Kurpiewski, J.; Juras, W. Purine tautomeric preferences and bond-length alternation in relation with protonation-deprotonation and alkali metal cationization. J. Mol. Model. 2020, 26, 93. [Google Scholar] [CrossRef] [Green Version]
  16. Ouellette, R.J.; Rawn, J.D. Nucleosides, Nucleotides, and Nucleic Acids. In Organic Chemistry: Structure, Mechanism, Syn-Thesis; Elsevier: San Diego, CA, USA, 2018; pp. 973–1000. ISBN 978-0-12-812838-1. [Google Scholar]
  17. Yang, B.; Srinivasan, B. Recent Developments in the Synthesis of Substituted Purine Nucleosides and Nucleotides. Curr. Org. Chem. 2014, 18, 2072–2107. [Google Scholar] [CrossRef]
  18. Ratsep, P.C.; Robins, R.K.; Vaghefi, M.M. Introduction of Fluorine Into the C8 Position of Purine Nucleosides. Nucleosides Nucleotides 1990, 9, 197–204. [Google Scholar] [CrossRef]
  19. Galmarini, C.M.; Mackey, J.R.; Dumontet, C. Nucleoside analogues and nucleobases in cancer treatment. Lancet Oncol. 2002, 3, 415–424. [Google Scholar] [CrossRef]
  20. Walters, W.P.; Murcko, M.A. Library Filtering Systems and Prediction of Drug-Like Properties. In Methods and Principles in Medicinal Chemistry; Böhm, H., Schneider, G., Eds.; Wiley: New York, NY, USA, 2000; pp. 15–32. ISBN 978-3-527-30153-9. [Google Scholar]
  21. Naumann, T.; Matter, H. Structural Classification of Protein Kinases Using 3D Molecular Interaction Field Analysis of Their Ligand Binding Sites: Target Family Landscapes. J. Med. Chem. 2002, 45, 2366–2378. [Google Scholar] [CrossRef]
  22. Schulze-Gahmen, U.; Brandsen, J.; Jones, H.D.; Morgan, D.; Meijer, L.; Vesely, J.; Kim, S.-H. Multiple modes of ligand recognition: Crystal structures of cyclin-dependent protein kinase 2 in complex with ATP and two inhibitors, olomoucine and isopentenyladenine. Proteins: Struct. Funct. Genet. 1995, 22, 378–391. [Google Scholar] [CrossRef]
  23. Donohue, J.; Trueblood, K.N. Base pairing in deoxyribonucleic acid. J. Mol. Biol. 1960, 2, 363–371. [Google Scholar] [CrossRef]
  24. Freese, E. The specific mutagenic effect of base analogues on Phage T4. J. Mol. Biol. 1959, 1, 87–105. [Google Scholar] [CrossRef]
  25. Drake, J.W. The Molecular Basis of Mutation; Holden-Day: San Francisco, CA, USA, 1970; ISBN 978-0-816-22450-0. [Google Scholar]
  26. Ludwig, V.; Amaral, M.S.D.; da Costa, Z.M.; Borin, A.C.; Canuto, S.; Serrano-Andrés, L. 2-Aminopurine non-radiative decay and emission in aqueous solution: A theoretical study. Chem. Phys. Lett. 2008, 463, 201–205. [Google Scholar] [CrossRef]
  27. Glickman, B.W. 2-Aminopurine Mutagenesis in Escherichia coli. In Genetic Consequences of Nucleotide Pool Imbalance, Basic Life Sciences; de Serres, F.J., Ed.; Springer: Boston, MA, USA, 1985; Volume 31, pp. 353–379. ISBN 978-1-4612-9488-7. [Google Scholar]
  28. Ronen, A. 2-Aminopurine. Mutat. Res./Rev. Mutat. Res. 1980, 75, 1–47. [Google Scholar] [CrossRef]
  29. de Serres, F.J.; Brockman, H.E.; Hung, C.Y.; Overton, L.K. Mutagenicity of 2-aminopurine, 6-N-hydroxylaminopurine, and 2-amino-N6-hydroxyadenine in Neurospora crassa. In Genetic Consequences of Nucleotide Pool Imbalance, Basic Life Sciences; de Serres, F.J., Ed.; Springer: Boston, MA, USA, 1985; Volume 31, pp. 381–389. ISBN 978-1-4612-9488-7. [Google Scholar]
  30. Laufer, S.A.; Domeyer, D.M.; Scior, T.R.F.; Albrecht, W.; Hauser, D.R.J. Synthesis and Biological Testing of Purine Derivatives as Potential ATP-Competitive Kinase Inhibitors. J. Med. Chem. 2005, 48, 710–722. [Google Scholar] [CrossRef]
  31. Baker, B.; Hendrickson, J. Irreversible enzyme inhibitors XCII. Inhibition of xanthine oxidase by some purines and pyr midines. J. Pharm. Sci. 1967, 56, 955–959. [Google Scholar] [CrossRef]
  32. Vanotti, E.; Bani, M.; Favara, D.; Gobetti, M.; Lombroso, M.; Magnetti, S.; Olgiati, V.; Palladino, M.; Tonon, G. 8-Substituted purine derivatives: A new class of lipid-lowering agents. Eur. J. Med. Chem. 1994, 29, 287–294. [Google Scholar] [CrossRef]
  33. Huryn, D.M.; Okabe, M. AIDS-driven nucleoside chemistry. Chem. Rev. 1992, 92, 1745–1768. [Google Scholar] [CrossRef]
  34. Seela, F.; Winter, H. N7-DNA: Synthesis and Base Pairing of Oligonucleotides containing 7-(2-Deoxy-D-erythro-pentofuranosyl)adenine (N7Ad). Helv. Chim. Acta 1994, 77, 597–607. [Google Scholar] [CrossRef]
  35. Boryski, J. Transglycosylation Reactions of Purine Nucleosides. A Review. Nucleosides Nucleotides 1996, 15, 771–791. [Google Scholar] [CrossRef]
  36. Marek, R.; Brus, J.; Toušek, J.; Kovács, L.; Hocková, D. N7- and N9-substituted purine derivatives: A 15n NMR study. Org. Magn. Reson. 2002, 40, 353–360. [Google Scholar] [CrossRef]
  37. Arico, J.W. 3-Substituted Purines: Methodology, Synthesis, and Studies of DNA Hydration in the Minor Groove. Ph.D. Thesis, Department of Chemistry, The Graduate School of Arts and Sciences, Boston College, Boston, MA, USA, 2010. Available online: http://hdl.handle.net/2345/1824 (accessed on 20 March 2023).
  38. Raczyńska, E.D.; Makowski, M. Geometric consequences of electron delocalization for adenine tautomers in aqueous solution. J. Mol. Model. 2014, 20, 2234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  39. Mburu, E.; Matsika, S. An Ab Initio Study of Substituent Effects on the Excited States of Purine Derivatives. J. Phys. Chem. A 2008, 112, 12485–12491. [Google Scholar] [CrossRef] [PubMed]
  40. Palamarchuk, G.V.; Shishkin, O.V.; Gorb, L.; Leszczynski, J. Nucleic Acid Bases in Anionic 2′-Deoxyribonucleotides: A DFT/B3LYP Study of Structures, Relative Stability, and Proton Affinities. J. Phys. Chem. B 2013, 117, 2841–2849. [Google Scholar] [CrossRef] [PubMed]
  41. Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
  42. Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum. A direct utilizaion of AB initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
  43. Miertuš, S.; Tomasi, J. Approximate evaluations of the electrostatic free energy and internal energy changes in solution processes. Chem. Phys. 1982, 65, 239–245. [Google Scholar] [CrossRef]
  44. Hammett, L.P. Physical Organic Chemistry, Table II; McGraw–Hill: New York, NY, USA, 1940; p. 189. [Google Scholar]
  45. Hammett, L.P. The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives. J. Am. Chem. Soc. 1937, 59, 96–103. [Google Scholar] [CrossRef]
  46. Hansch, C.; Leo, A.; Taft, R.W. A survey of Hammett substituent constants and resonance and field parameters. Chem. Rev. 1991, 91, 165–195. [Google Scholar] [CrossRef]
  47. Exner, O. Theory of Substituent Effects: Recent Advances. Curr. Org. Chem. 2006, 10, 763–778. [Google Scholar] [CrossRef]
  48. Galabov, B.; Ilieva, S.; Schaefer, I.H.F. An Efficient Computational Approach for the Evaluation of Substituent Constants. J. Org. Chem. 2006, 71, 6382–6387. [Google Scholar] [CrossRef]
  49. Krygowski, T.M.; Zachara, J.E.; Szatylowicz, H. Molecular Geometry as a Source of Chemical Information. 3. How H-Bonding Affects Aromaticity of the Ring in the Case of Phenol and p-Nitrophenol Complexes: A B3LYP/6-311+G** Study. J. Org. Chem. 2004, 69, 7038–7043. [Google Scholar] [CrossRef] [PubMed]
  50. Sadlej-Sosnowska, N. On the way to physical interpretation of Hammett constants: How substituent active space impacts on acidity and electron distribution in p-substituted benzoic acid molecules. Polish J. Chem. 2007, 81, 1123–1134. [Google Scholar]
  51. Sadlej-Sosnowska, N. Substituent active region—A gate for communication of substituent charge with the rest of a molecule: Monosubstituted benzenes. Chem. Phys. Lett. 2007, 447, 192–196. [Google Scholar] [CrossRef]
  52. Stasyuk, O.A.; Szatylowicz, H.; Guerra, C.F.; Krygowski, T.M. Theoretical study of electron-attracting ability of the nitro group: Classical and reverse substituent effects. Struct. Chem. 2015, 26, 905–913. [Google Scholar] [CrossRef] [Green Version]
  53. Szatylowicz, H.; Siodla, T.; Stasyuk, O.A.; Krygowski, T.M. Towards physical interpretation of substituent effects: The case of meta- and para-substituted anilines. Phys. Chem. Chem. Phys. 2015, 18, 11711–11721. [Google Scholar] [CrossRef] [PubMed]
  54. Szatyłowicz, H.; Krygowski, T.M.; Hobza, P. How the Shape of the NH2 Group Depends on the Substituent Effect and H-Bond Formation in Derivatives of Aniline. J. Phys. Chem. A 2006, 111, 170–175. [Google Scholar] [CrossRef]
  55. Szatylowicz, H.; Jezuita, A.; Siodła, T.; Varaksin, K.S.; Ejsmont, K.; Madura, I.D.; Krygowski, T.M. Dependence of the Substituent Effect on Solvent Properties. J. Phys. Chem. A 2018, 122, 1896–1904. [Google Scholar] [CrossRef]
  56. Iii, G.L.D.; Je, L.; Tanski, J.M. Crystallographic and spectroscopic characterization of 4-nitro-2-(trifluoromethyl)benzoic acid and 4-nitro-3-(trifluoromethyl)benzoic acid. Acta Crystallogr. Sect. E Crystallogr. Commun. 2019, 75, 524–528. [Google Scholar] [CrossRef] [Green Version]
  57. Hanson, J.R.; Hitchcock, P.B.; Toche, F. The Rotation of the Nitro and Formyl Groups Relative to the Aromatic Ring in Some ortho-nitroarylaldehydes. J. Chem. Res. 2008, 2008, 476–478. [Google Scholar] [CrossRef]
  58. Dobrowolski, M.A.; Krygowski, T.M.; Cyrański, M.K. Substituent Constants (σp−) of the Rotated Nitro Group. The In-terplay Between the Substituent Effect of a Rotated−NO2 Group and H-Bonds Affecting π-Electron Delocalization in 4-Nitrophenol and 4-Nitrophenolate Complexes: A B3LYP/6-311+ G** Study. Croat. Chem. Acta 2009, 82, 139–147. [Google Scholar]
  59. Jezuita, A.; Wieczorkiewicz, P.; Szatylowicz, H.; Krygowski, T. Solvent Effect on the Stability and Reverse Substituent Effect in Nitropurine Tautomers. Symmetry 2021, 13, 1223. [Google Scholar] [CrossRef]
  60. Jezuita, A.; Wieczorkiewicz, P.A.; Szatylowicz, H.; Krygowski, T.M. Effect of the Solvent and Substituent on Tautomeric Preferences of Amine-Adenine Tautomers. ACS Omega 2021, 6, 18890–18903. [Google Scholar] [CrossRef] [PubMed]
  61. Wieczorkiewicz, P.A. Relationships between the Substituent and Solvent Effects in Selected Pyrimidine and Purine Derivatives. Master’s Thesis, Faculty of Chemistry, Warsaw University of Technology,, Warsaw, Poland, 2022. Available online: https://repo.pw.edu.pl/info/master/WUTbdff88096cd14b41a128a1d9253761b7/ (accessed on 20 March 2023).
  62. Desiraju, G.R. A Bond by Any Other Name. Angew. Chem. Int. Ed. 2010, 50, 52–59. [Google Scholar] [CrossRef] [PubMed]
  63. Raczyńska, E.D.; Hallman, M.; Kolczynska, K.; Stępniewski, T.M. On the Harmonic Oscillator Model of Electron Delocalization (HOMED) Index and its Application to Heteroatomic π-Electron Systems. Symmetry 2010, 2, 1485–1509. [Google Scholar] [CrossRef] [Green Version]
  64. Szczȩśniak, M.; Nowak, M.; Szczepaniak, K. Infrared matrix isolation studies on tautomerism of cytosine and isocytosine methyl-derivatives. J. Mol. Struct. 1984, 115, 221–224. [Google Scholar] [CrossRef]
  65. Jezuita, A.; Szatylowicz, H.; Marek, P.H.; Krygowski, T.M. Aromaticity of the most stable adenine and purine tautomers in terms of Hückel’s 4n+2 principle. Tetrahedron 2019, 75, 130474. [Google Scholar] [CrossRef]
  66. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
  67. Grimme, S.; Antony, J.; Schwabe, T.; Mück-Lichtenfeld, C. Density functional theory with dispersion corrections for supramolecular structures, aggregates, and complexes of (bio)organic molecules. Org. Biomol. Chem. 2007, 5, 741–758. [Google Scholar] [CrossRef]
  68. Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
  69. Marek, P.H.; Szatylowicz, H.; Krygowski, T.M. Stacking of nucleic acid bases: Optimization of the computational approach—the case of adenine dimers. Struct. Chem. 2018, 30, 351–359. [Google Scholar] [CrossRef] [Green Version]
  70. Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
  71. Kruszewski, J.; Krygowski, T. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
  72. Krygowski, T.M. Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of .pi.-electron systems. J. Chem. Inf. Comput. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
  73. Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  74. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  75. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
Molecules 28 02993 sch001 550
Scheme 1. Structures of nine prototropic purine tautomers. Mono-NH2-substituted derivatives of four N tautomers are the subject of this study. Substitution positions (C2-, C6-, C8-, and N-) are marked in red.
Scheme 1. Structures of nine prototropic purine tautomers. Mono-NH2-substituted derivatives of four N tautomers are the subject of this study. Substitution positions (C2-, C6-, C8-, and N-) are marked in red.
Molecules 28 02993 sch001
Molecules 28 02993 sch002 550
Scheme 2. Classification of the proximity interactions into three types used throughout this paper, along with the systems belonging to each type. The presented color-coding scheme is maintained in all Figures.
Scheme 2. Classification of the proximity interactions into three types used throughout this paper, along with the systems belonging to each type. The presented color-coding scheme is maintained in all Figures.
Molecules 28 02993 sch002
Molecules 28 02993 g001 550
Figure 1. Values of cSAR(NH2) in 9H, 7H, 3H, and 1H tautomeric forms of C- and N-NH2 derivatives of purine, calculated in the gaseous and aqueous phases. The color coding of each bar indicates the proximity interactions present in each system.
Figure 1. Values of cSAR(NH2) in 9H, 7H, 3H, and 1H tautomeric forms of C- and N-NH2 derivatives of purine, calculated in the gaseous and aqueous phases. The color coding of each bar indicates the proximity interactions present in each system.
Molecules 28 02993 g001
Molecules 28 02993 sch003 550
Scheme 3. Geometric parameters of the amino group.
Scheme 3. Geometric parameters of the amino group.
Molecules 28 02993 sch003
Molecules 28 02993 g002 550
Figure 2. Values of pyramidalization of the NH2 group (φ = 360° − sum of valence angles at the N atom) in all studied aminopurines calculated in the gas phase and water (H2O).
Figure 2. Values of pyramidalization of the NH2 group (φ = 360° − sum of valence angles at the N atom) in all studied aminopurines calculated in the gas phase and water (H2O).
Molecules 28 02993 g002
Molecules 28 02993 g003 550
Figure 3. Lengths of bonds connecting the NH2 with substituted C or N atom of purine moiety, dipso-NH2, in all studied aminopurines calculated in the gas phase and water (H2O).
Figure 3. Lengths of bonds connecting the NH2 with substituted C or N atom of purine moiety, dipso-NH2, in all studied aminopurines calculated in the gas phase and water (H2O).
Molecules 28 02993 g003
Molecules 28 02993 g004 550
Figure 4. Dependences between (a) the pyramidalization, angle φ, and dipso-NH2, and (b) differences, Δ, in cSAR(NH2) and dipso-NH2 values calculated in water and in the gas phase (Δ = 0 means that the same values of a given parameter were obtained in water and in gas phase). N-NH2 systems not included in (b).
Figure 4. Dependences between (a) the pyramidalization, angle φ, and dipso-NH2, and (b) differences, Δ, in cSAR(NH2) and dipso-NH2 values calculated in water and in the gas phase (Δ = 0 means that the same values of a given parameter were obtained in water and in gas phase). N-NH2 systems not included in (b).
Molecules 28 02993 g004
Molecules 28 02993 g005 550
Figure 5. Dependences between the lengths of two NH bonds of the NH2 group. The y = x line indicates a situation when both have the same length. Data for (a) the gas phase and (b) the most polar solvent considered, formamide.
Figure 5. Dependences between the lengths of two NH bonds of the NH2 group. The y = x line indicates a situation when both have the same length. Data for (a) the gas phase and (b) the most polar solvent considered, formamide.
Molecules 28 02993 g005
Molecules 28 02993 g006 550
Figure 6. Values of HOMA index for 6- and 5-membered rings of C2-, C6-, C8-, and N-amino-substituted derivatives of purine in four tautomeric forms, calculated for the gas-phase geometry. PU is the values for unsubstituted purine.
Figure 6. Values of HOMA index for 6- and 5-membered rings of C2-, C6-, C8-, and N-amino-substituted derivatives of purine in four tautomeric forms, calculated for the gas-phase geometry. PU is the values for unsubstituted purine.
Molecules 28 02993 g006
Molecules 28 02993 g007 550
Figure 7. Changes in HOMA index due to substitution, ΔHOMA, calculated by subtracting the value for unsubstituted purine (PU) from the value for substituted purine (NH2PU or NO2PU). Data for the (a) amino and, for comparison, (b) nitro derivatives [59].
Figure 7. Changes in HOMA index due to substitution, ΔHOMA, calculated by subtracting the value for unsubstituted purine (PU) from the value for substituted purine (NH2PU or NO2PU). Data for the (a) amino and, for comparison, (b) nitro derivatives [59].
Molecules 28 02993 g007
Molecules 28 02993 g008 550
Figure 8. (a) Differences in the values of HOMA for amino and nitro derivatives of purine and (b) changes in HOMA due to substitution for 5- and 6-membered rings plotted against each other.
Figure 8. (a) Differences in the values of HOMA for amino and nitro derivatives of purine and (b) changes in HOMA due to substitution for 5- and 6-membered rings plotted against each other.
Molecules 28 02993 g008
Molecules 28 02993 g009 550
Figure 9. Changes in HOMA index due to solvation ΔHOMA (FA–GP), calculated by subtracting the value in the gas phase from the value in the most polar solvent considered, formamide. Data for the (a) amino and, for comparison, (b) nitro derivatives [59].
Figure 9. Changes in HOMA index due to solvation ΔHOMA (FA–GP), calculated by subtracting the value in the gas phase from the value in the most polar solvent considered, formamide. Data for the (a) amino and, for comparison, (b) nitro derivatives [59].
Molecules 28 02993 g009
Molecules 28 02993 g010a 550Molecules 28 02993 g010b 550
Figure 10. Relative energies of tautomers (Erel) in various solvents (abbreviations and dielectric constants in Table 1), with respect to the 9H tautomer, for (a) C2-NH2, (b) C6-NH2 (c) C8-NH2 (d) N-NH2, and (e) unsubstituted purines.
Figure 10. Relative energies of tautomers (Erel) in various solvents (abbreviations and dielectric constants in Table 1), with respect to the 9H tautomer, for (a) C2-NH2, (b) C6-NH2 (c) C8-NH2 (d) N-NH2, and (e) unsubstituted purines.
Molecules 28 02993 g010aMolecules 28 02993 g010b
Table
Table 1. Values of dielectric constants (ε) of studied solvents.
Table 1. Values of dielectric constants (ε) of studied solvents.
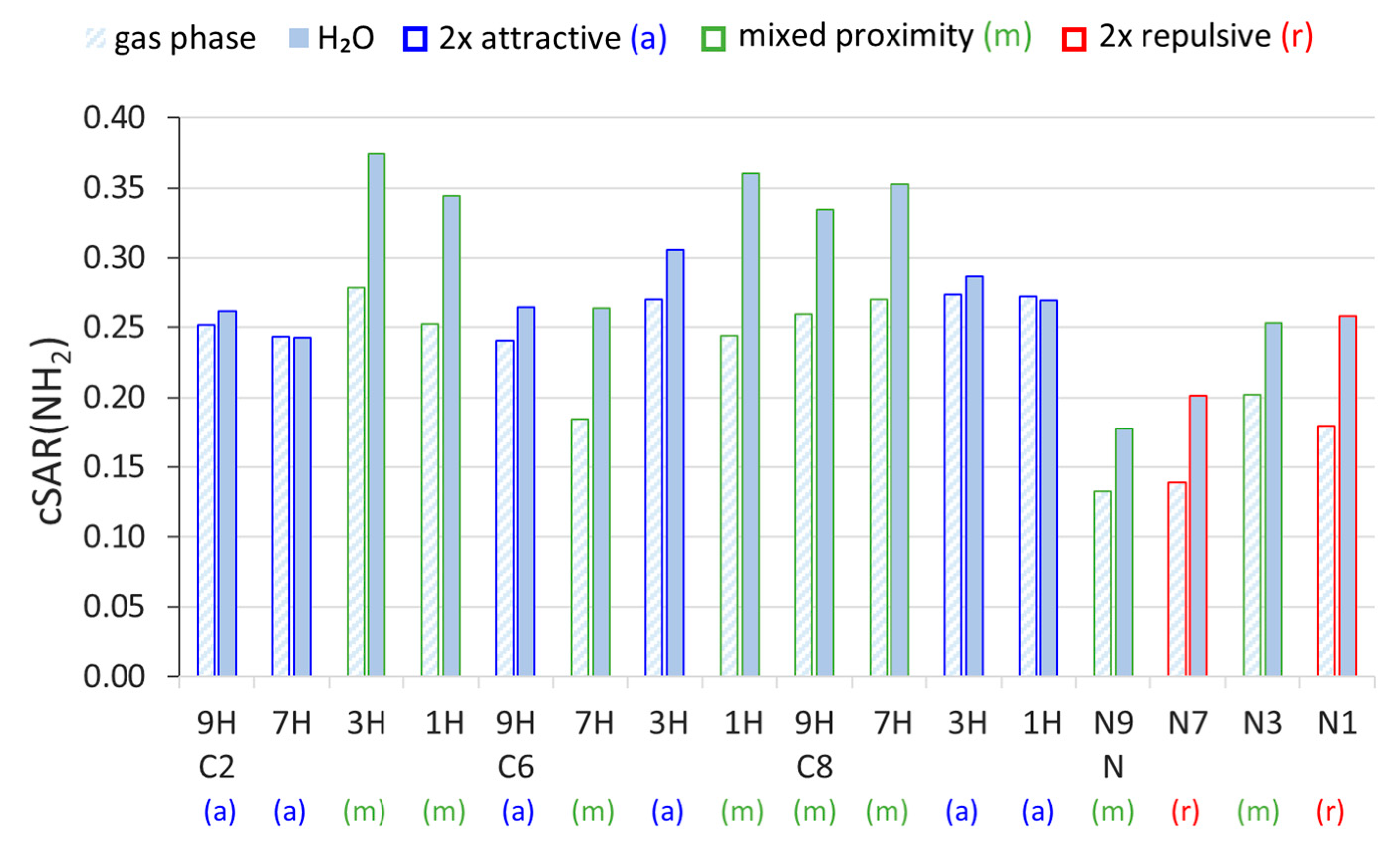
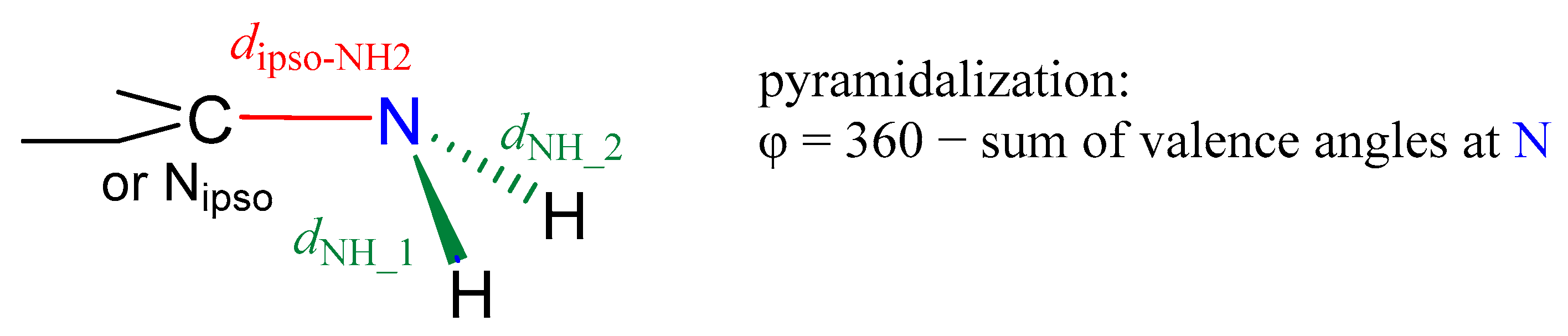
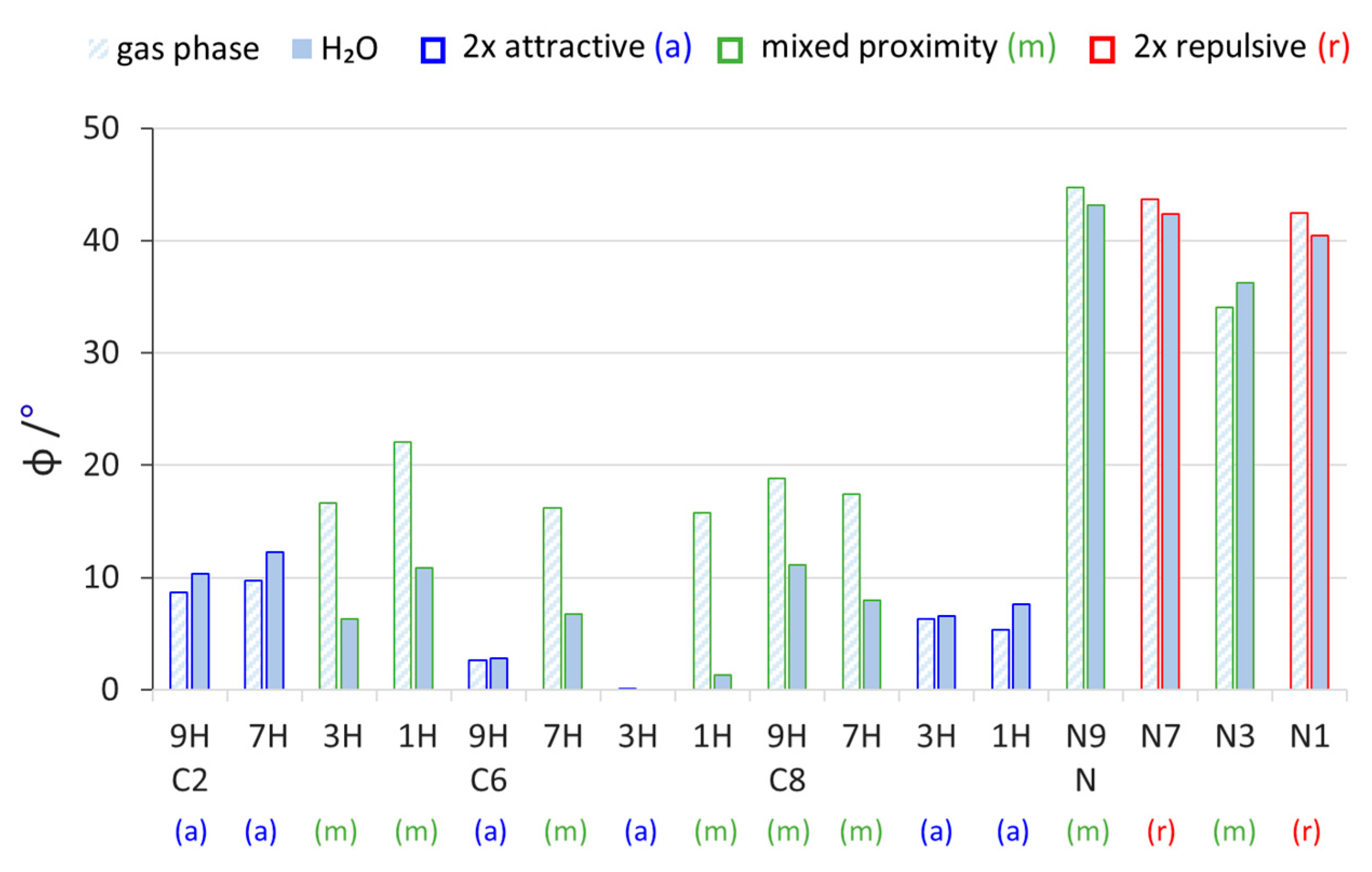
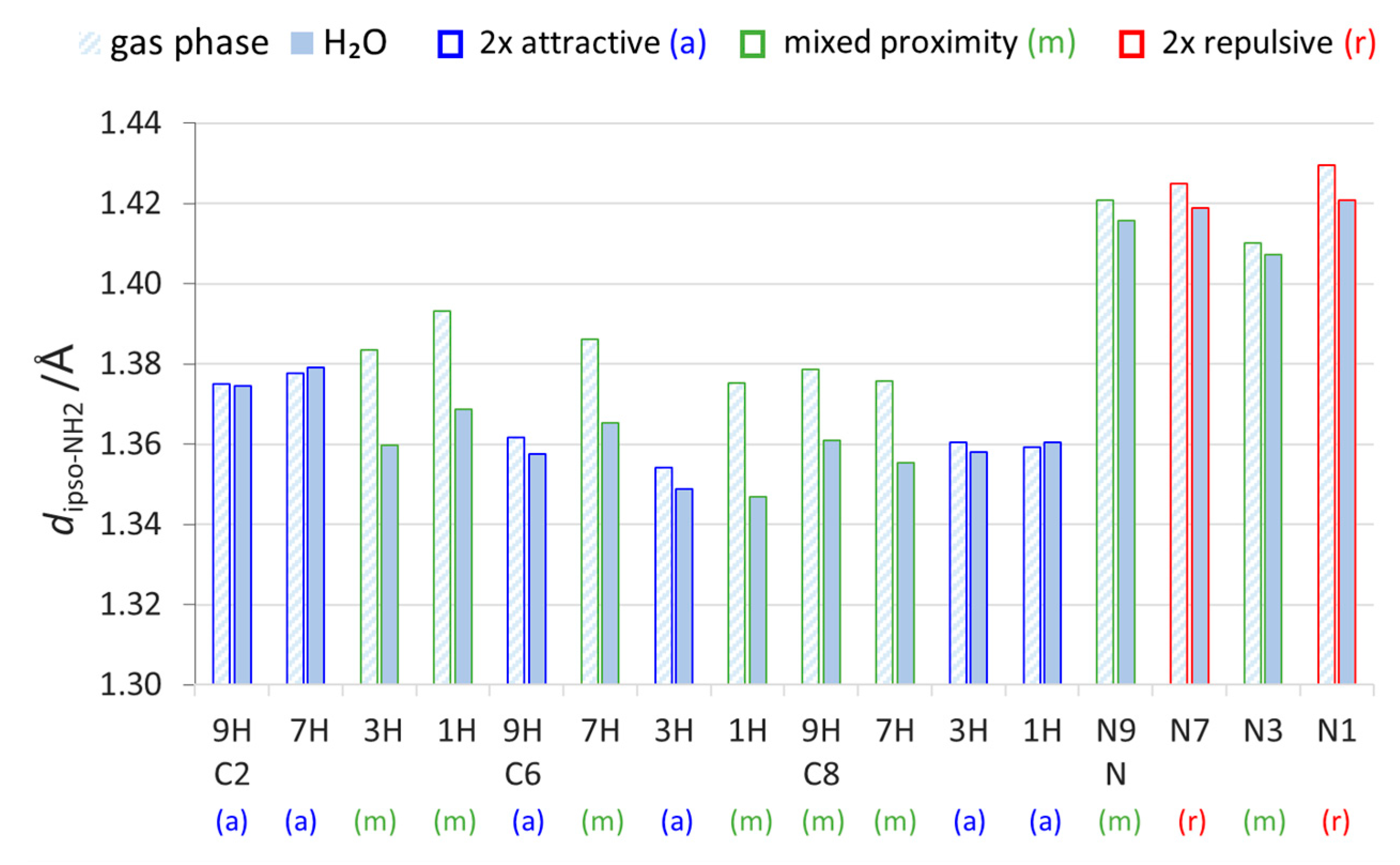
Solvent/MediumAcronymε1/ε
FormamideFA108.940.0092
WaterH2O78.360.0128
Dimethyl sulfoxideDMSO46.830.0214
EthanolEtOH24.850.0402
PyridinePy12.980.0771
TetrahydrofuranTHF7.430.1347
o-cresolo-Cr6.760.1479
ChloroformChf4.710.2123
TolueneTol2.370.4212
Gas phaseGP1.001.00
Table
Table 2. Statistical data on cSAR(NH2) = a∙(1/ε) + b linear fitting equations for C2-, C6-, C8-, and N-NH2-substituted 9H, 7H, 3H, and 1H purine tautomers; Δ is the difference between the value of cSAR(NH2) in H2O and the gas phase. Mixed-proximity systems in bold.
Table 2. Statistical data on cSAR(NH2) = a∙(1/ε) + b linear fitting equations for C2-, C6-, C8-, and N-NH2-substituted 9H, 7H, 3H, and 1H purine tautomers; Δ is the difference between the value of cSAR(NH2) in H2O and the gas phase. Mixed-proximity systems in bold.
ΔcSAR(NH2)aR2Proximity Type
C29H0.0102−0.01040.99642× att
7H−0.00070.00080.05852× att
3H0.0956−0.09790.9744mix
1H0.0919−0.09470.9691mix
C69H0.0238−0.02440.99892× att
7H0.0795−0.08180.9415mix
3H0.0359−0.03670.98772× att
1H0.1163−0.11890.9668mix
C89H0.0747−0.07660.9703mix
7H0.0823−0.08460.9692mix
3H0.0132−0.01340.99472× att
1H−0.00320.00350.30252× att
NN90.0449−0.04600.9780mix
N70.0623−0.06380.97252× rep
N30.0510−0.05230.9795mix
N10.0789−0.08080.91212× rep
Table
Table 3. Tautomer energies (in kcal/mol), relative to the 9H (Erel), for all considered substitution positions of purines (X = NH2, H, and NO2) in the gas (GP) and aqueous (H2O) phases. Values of ∆ indicate the change due to solvation, ∆ = Erel(H2O)–Erel(GP).
Table 3. Tautomer energies (in kcal/mol), relative to the 9H (Erel), for all considered substitution positions of purines (X = NH2, H, and NO2) in the gas (GP) and aqueous (H2O) phases. Values of ∆ indicate the change due to solvation, ∆ = Erel(H2O)–Erel(GP).
X = NH2 X = NO2 *
GPH2O∆GPH2O∆
C29H0.000.000.000.000.000.00
7H3.590.71−2.883.33−0.31−3.64
3H12.257.80−4.458.1711.603.43
1H15.927.47−8.459.699.36−0.33
C69H0.000.000.000.000.000.00
7H7.181.91−5.27−4.06−2.121.94
3H7.094.74−2.3510.167.99−2.17
1H16.947.69−9.2510.349.81−0.53
C89H0.000.000.000.000.000.00
7H2.62−0.69−3.313.670.90−2.77
3H2.953.500.558.962.10−6.86
1H4.931.80−3.1311.55−0.08−11.63
NN90.000.000.00
N74.980.90−4.07
N37.115.86−1.25
N113.036.14−6.89
PU9H0.00 **0.000.00
7H3.29 **0.15−3.14
3H8.69 **6.70−1.99
1H11.50 **4.98−6.52
* Data taken from [59]. ** Data taken from [65].
Table
Table 4. Statistical data (a and R2) of Esolv = a∙(1/ε) + b linear fitting equations, where 1/ε is the reciprocal of solvent dielectric constant (Table 1). Dipole moments for geometry in the gas phase, μ, and their changes due to solvation, ∆μ = μ(FA) – E(GP). All data concern NH2 derivatives of purine. C-NH2 systems with mixed proximity type are marked in bold.
Table 4. Statistical data (a and R2) of Esolv = a∙(1/ε) + b linear fitting equations, where 1/ε is the reciprocal of solvent dielectric constant (Table 1). Dipole moments for geometry in the gas phase, μ, and their changes due to solvation, ∆μ = μ(FA) – E(GP). All data concern NH2 derivatives of purine. C-NH2 systems with mixed proximity type are marked in bold.
aR2μ/DΔμ/DProximity Type
9HC28.9050.9793.21.32× att
C68.9490.9812.41.02× att
C811.2110.9765.42.8mix
N97.5850.9823.11.2mix
7HC211.8690.9704.12.02× att
C614.3640.9646.83.6mix
C814.6110.9686.93.6mix
N711.7650.9736.22.42× rep
3HC213.4660.9766.03.3mix
C611.3530.9813.91.82× att
C810.6450.9783.01.32× att
N38.8550.9773.12.4mix
1HC217.5810.9697.74.5mix
C618.4530.9678.24.8mix
C814.4320.9724.12.42× att
N114.6500.9747.03.12× rep
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Jezuita, A.; Wieczorkiewicz, P.A.; Krygowski, T.M.; Szatylowicz, H. Influence of the Solvent on the Stability of Aminopurine Tautomers and Properties of the Amino Group. Molecules 2023, 28, 2993. https://doi.org/10.3390/molecules28072993

AMA Style

Jezuita A, Wieczorkiewicz PA, Krygowski TM, Szatylowicz H. Influence of the Solvent on the Stability of Aminopurine Tautomers and Properties of the Amino Group. Molecules. 2023; 28(7):2993. https://doi.org/10.3390/molecules28072993

Chicago/Turabian Style

Jezuita, Anna, Paweł A. Wieczorkiewicz, Tadeusz M. Krygowski, and Halina Szatylowicz. 2023. "Influence of the Solvent on the Stability of Aminopurine Tautomers and Properties of the Amino Group" Molecules 28, no. 7: 2993. https://doi.org/10.3390/molecules28072993

APA Style

Jezuita, A., Wieczorkiewicz, P. A., Krygowski, T. M., & Szatylowicz, H. (2023). Influence of the Solvent on the Stability of Aminopurine Tautomers and Properties of the Amino Group. Molecules, 28(7), 2993. https://doi.org/10.3390/molecules28072993

Article Metrics

Back to TopTop