Molecular Dynamics Study of Clathrate-like Ordering of Water in Supersaturated Methane Solution at Low Pressure
Abstract
1. Introduction
2. Results and Discussion
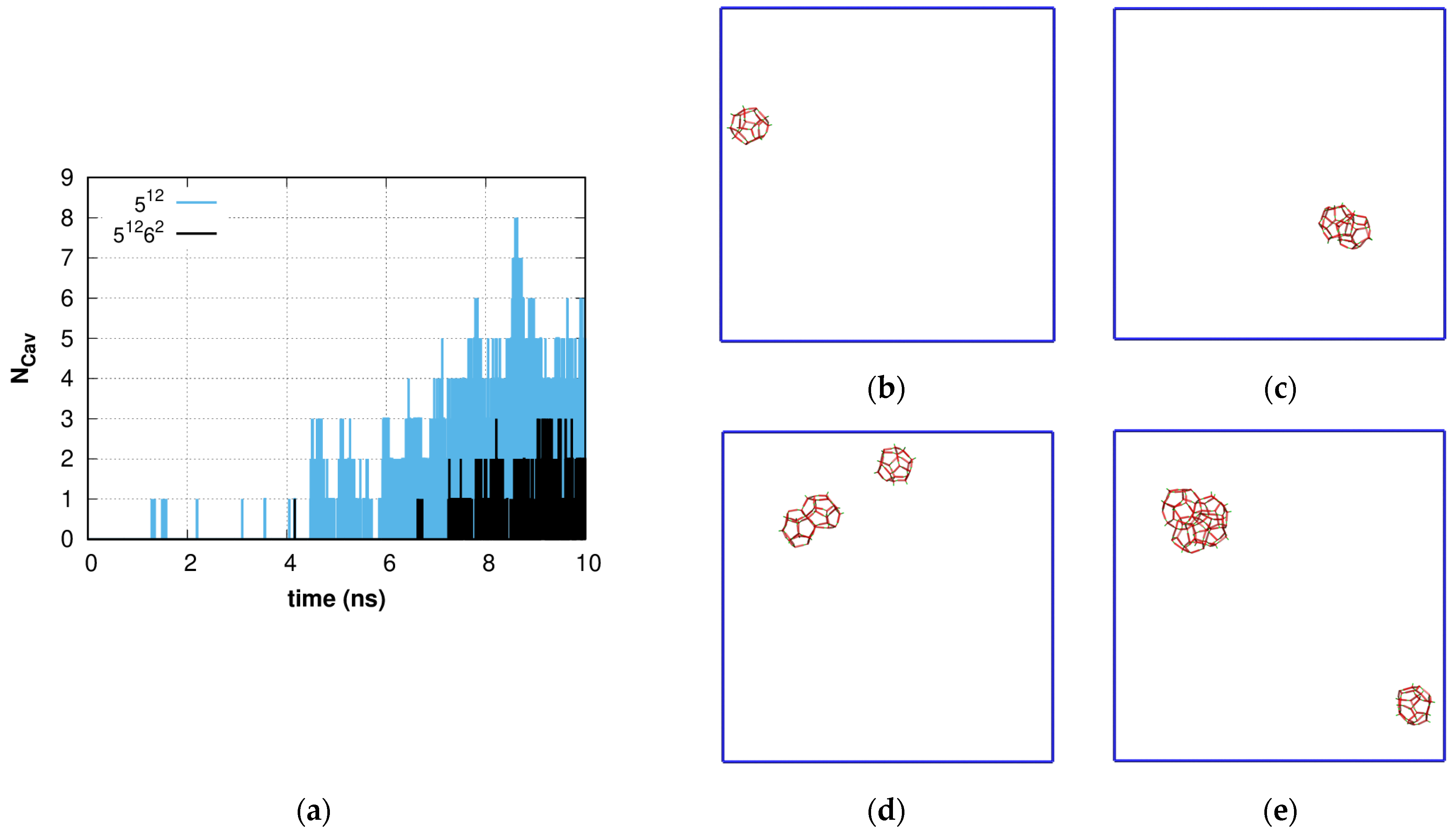
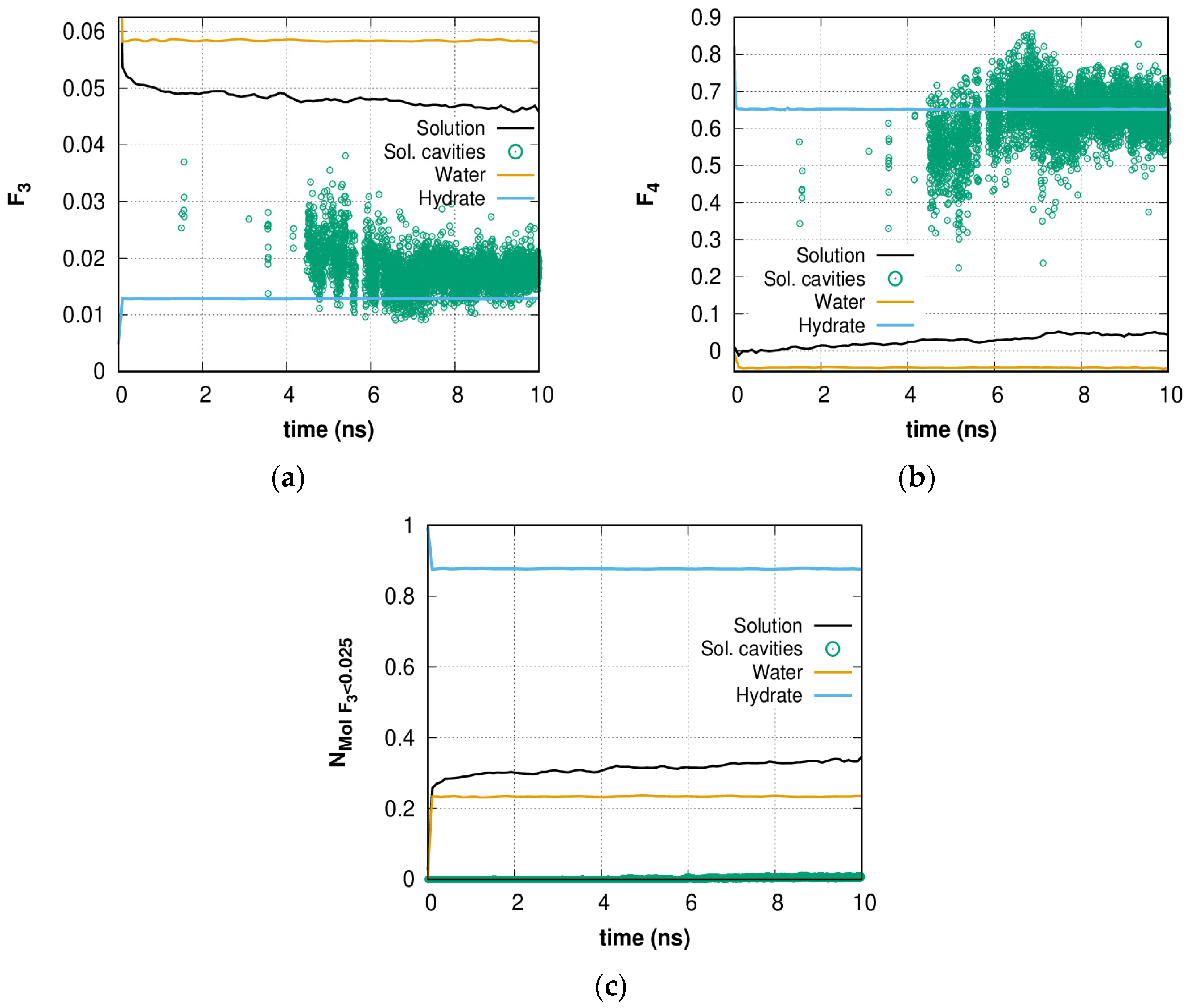
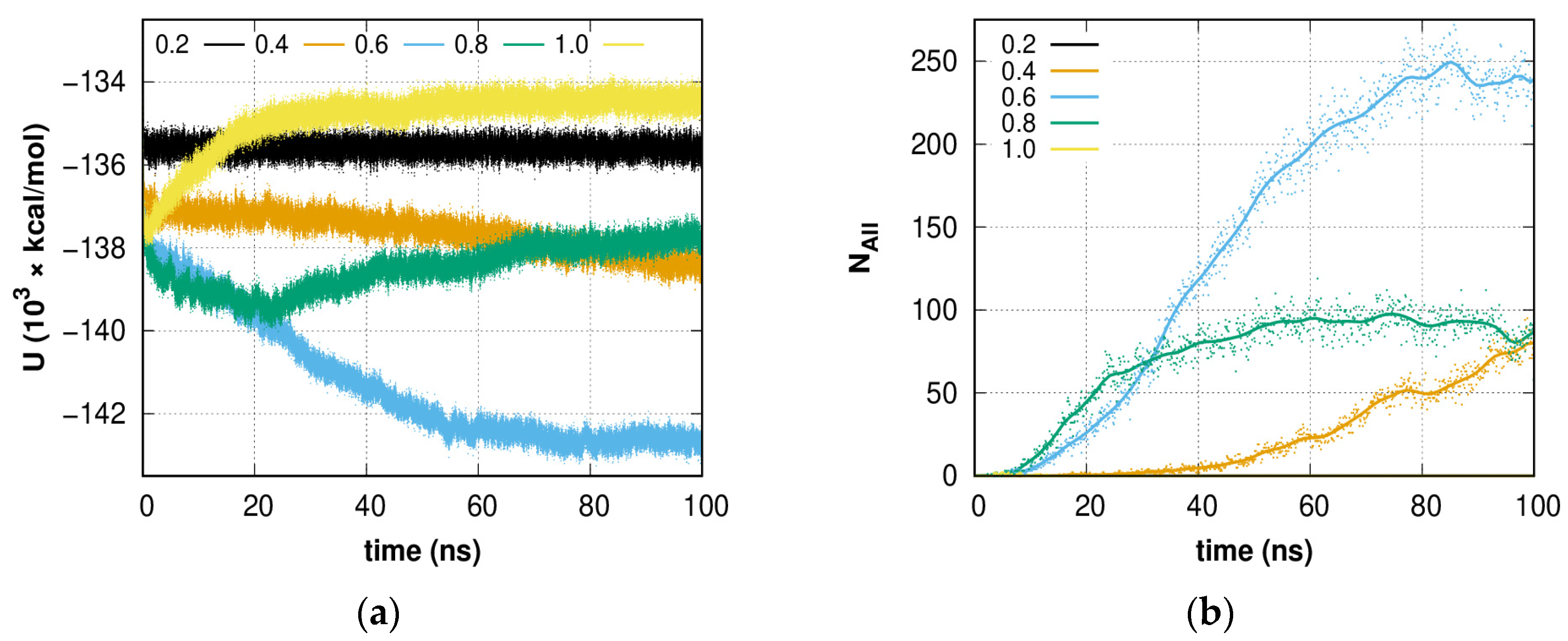
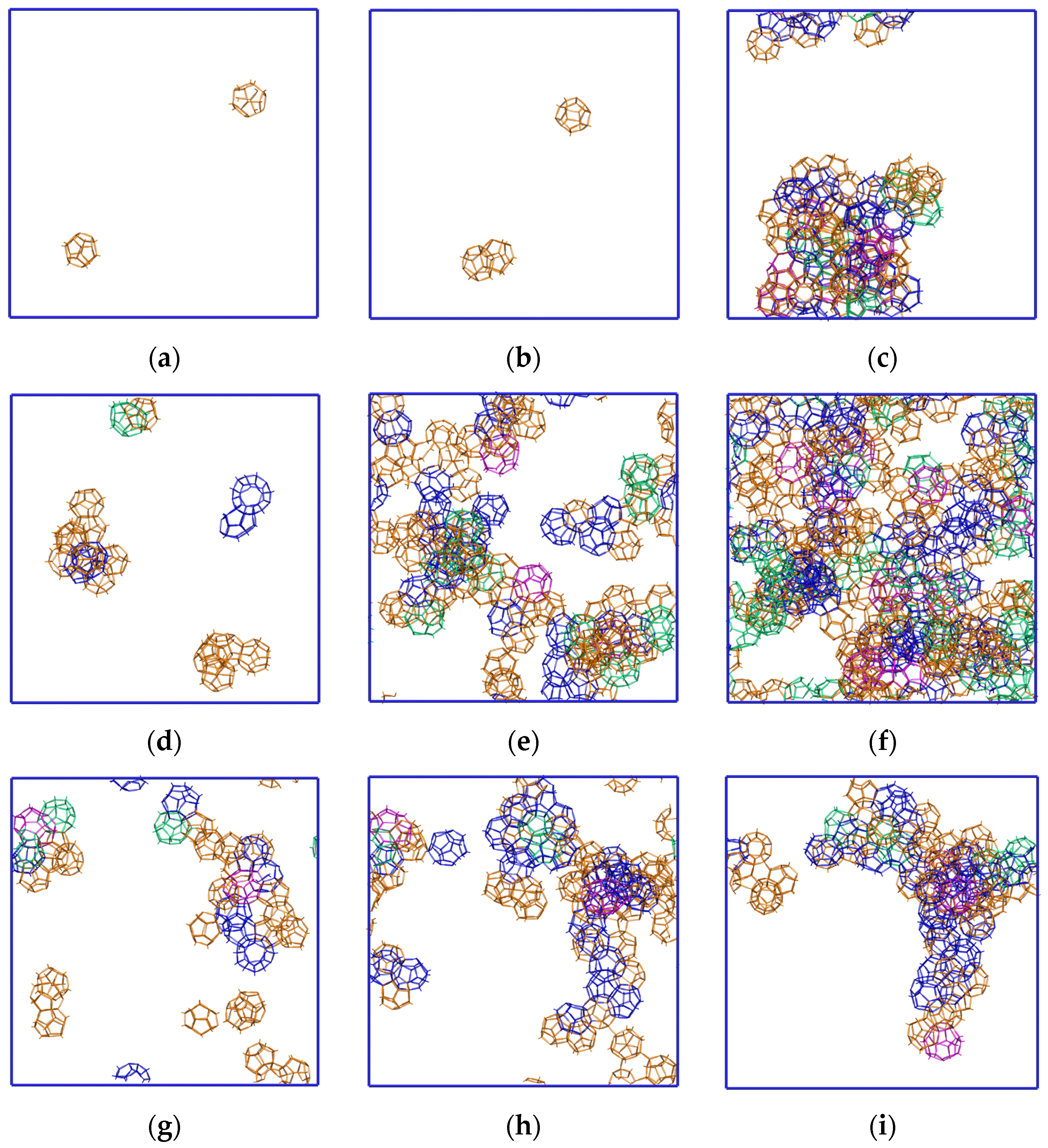
2.1. Fluctuation Character of the H-Bond Network Structure at the Hydrate-like Structure Pre-Nucleation Interval
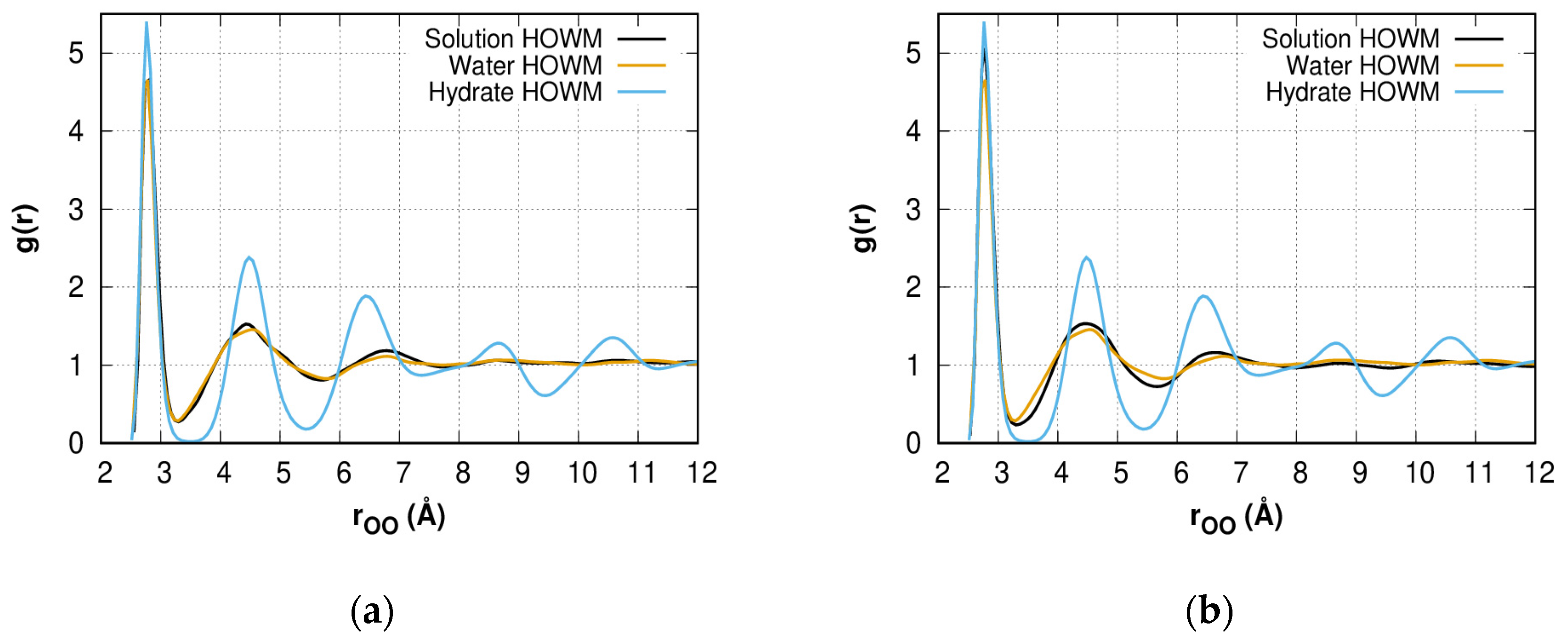
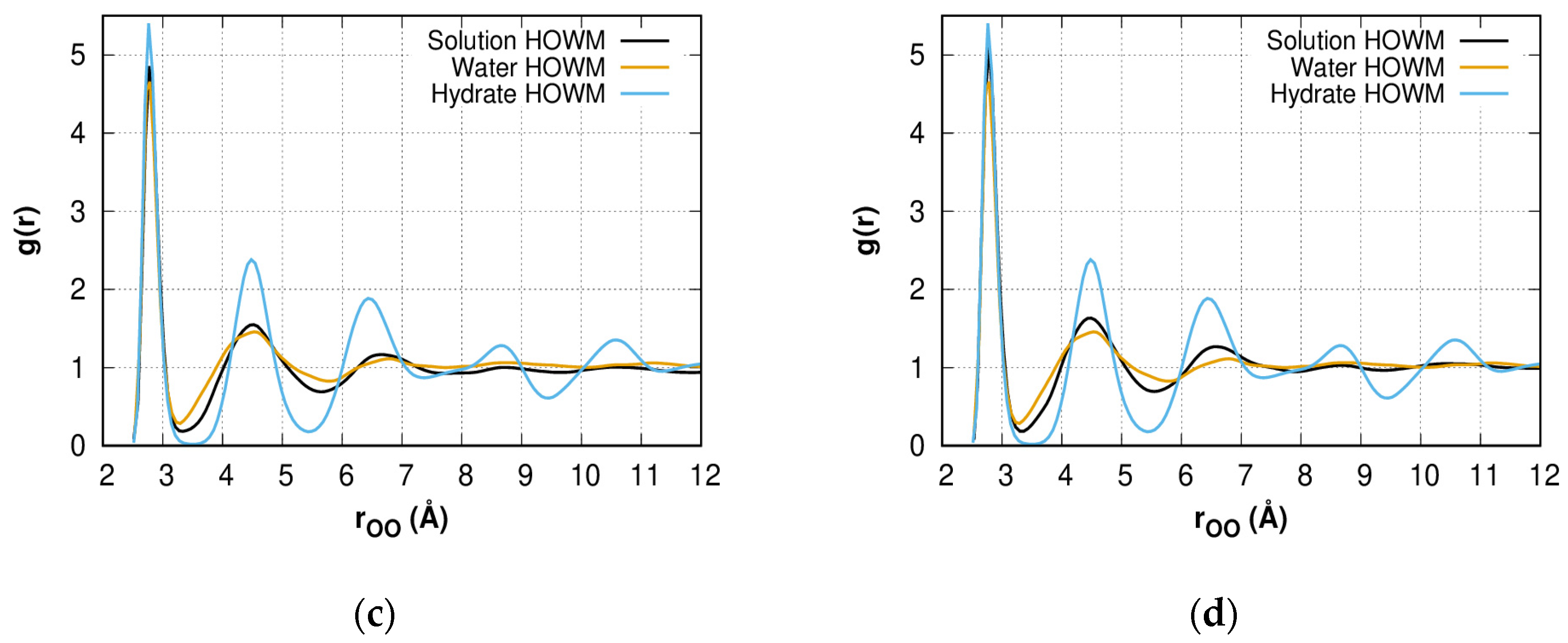
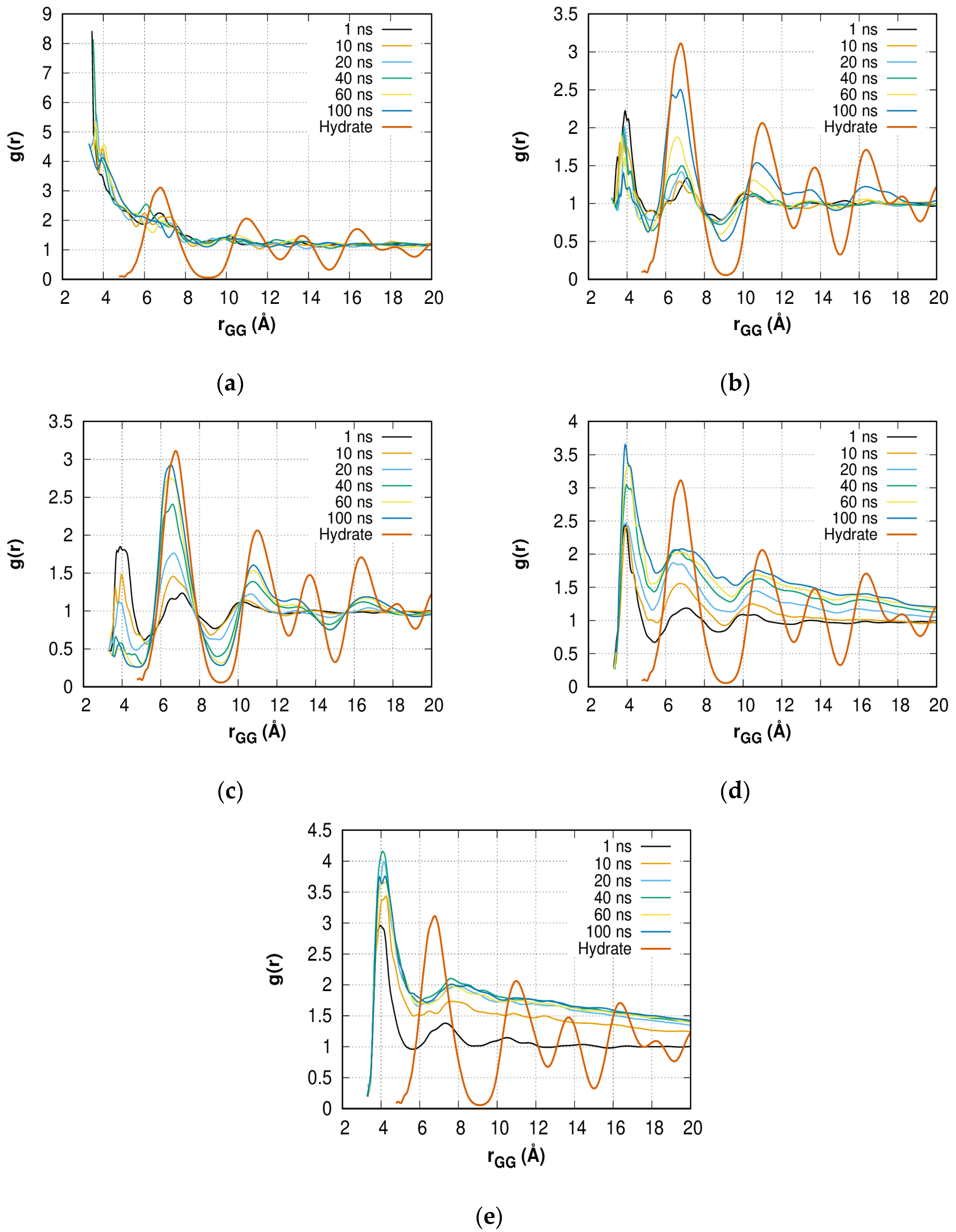
2.2. Radial Distribution Function of HOWMs
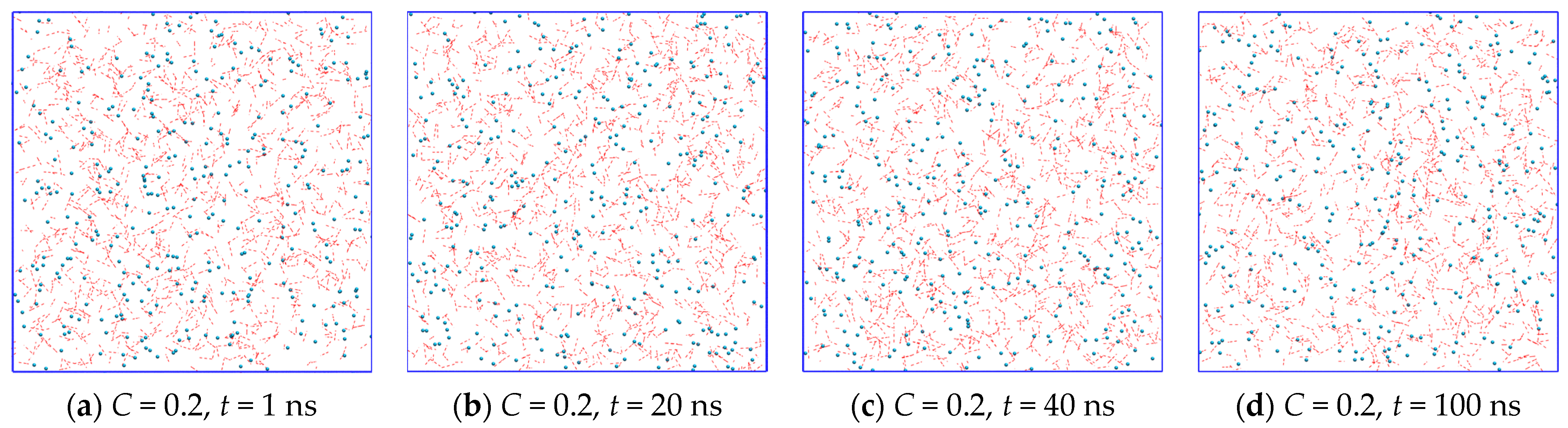
2.3. Growth Outside the Stability Region
3. Calculation Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Sloan, E.D., Jr.; Koh, C.A. Clathrate Hydrates of Natural Gases, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2007; p. 752. [Google Scholar] [CrossRef]
- Khurana, M.; Yin, Z.; Linga, P. A Review of Clathrate Hydrate Nucleation. ACS Sustain. Chem. Eng. 2017, 5, 11176–11203. [Google Scholar] [CrossRef]
- Bosio, L.; Teixeira, J.; Stanley, H.E. Enhanced density fuctuations in supercooled H2O, D2O, and ethanol-water solutions: Evidence from small-angle x-ray scattering. Phys. Rev. Lett. 1981, 46, 597–600. [Google Scholar] [CrossRef]
- Geiger, A.; Mausbach, P.; Schnitker, J.; Blumberg, R.L.; Stanley, H.E. Structure and dynamics of the hydrogen bond network in water by computer simulations. J. Phys. Colloq. 1984, 45, C7-13–C7-30. [Google Scholar] [CrossRef]
- Belosludov, V.; Gets, K.; Zhdanov, R.; Malinovsky, V.; Bozhko, Y.; Belosludov, R.; Surovtsev, N.; Subbotin, O.; Kawazoe, Y. The nano-structural inhomogeneity of dynamic hydrogen bond network of TIP4P/2005 water. Sci. Rep. 2020, 10, 7323. [Google Scholar] [CrossRef]
- Sosso, G.C.; Chen, J.; Cox, S.J.; Fitzner, M.; Pedevilla, P.; Zen, A.; Michaelides, A. Crystal Nucleation in Liquids: Open Questions and Future Challenges in Molecular Dynamics Simulations. Chem. Rev. 2016, 116, 7078–7116. [Google Scholar] [CrossRef] [PubMed]
- English, N.J.; MacElroy, J.M.D. Perspectives on molecular simulation of clathrate hydrates: Progress, prospects and challenges. Chem. Eng. Sci. 2015, 121, 133–156. [Google Scholar] [CrossRef]
- Owicki, J.C.; Scheraga, H.A. Monte Carlo calculation in isothermal-isobaric ensemble.2. Dilute aqueous solution of methane. J. Am. Chem. Soc. 1977, 99, 7413–7418. [Google Scholar] [CrossRef]
- Swaminathan, S.; Harrison, S.W.; Beveridge, D.L. Monte Carlo studies on the structure of dilute aqueous solution of methane. J. Am. Chem. Soc. 1978, 100, 5705–5712. [Google Scholar] [CrossRef]
- Geiger, A.; Rahman, A.; Stillinger, F.H. Molecular dynamics study of the hydration of Lennard-Jones solutes. J. Chem. Phys. 1979, 70, 263–276. [Google Scholar] [CrossRef]
- Guillot, B.; Guissani, Y. A computer simulation study of the temperature dependence of the hydrophobic hydration. J. Chem. Phys. 1993, 99, 8075–8094. [Google Scholar] [CrossRef]
- Chau, P.L.; Mancera, R.L. Computer simulation of structural effect of pressure on the hydrophobic hydration of methane. Mol. Phys. 1999, 96, 109–122. [Google Scholar] [CrossRef]
- Long, J.; Sloan, E.D. Quantized water cluster around apolar molecules. Mol. Simul. 1993, 11, 145–161. [Google Scholar] [CrossRef]
- Skipper, N.T. Computer simulation of methane-water solutions. Evidence for a temperature-dependent hydrophobic attraction. Chem. Phys. Lett. 1993, 207, 424–429. [Google Scholar] [CrossRef]
- Mancera, R.L.; Buckingham, A.D.; Skipper, N.T. The aggregation of methane in aqueous solution. J. Chem. Soc. Faraday Trans. 1997, 93, 2263–2267. [Google Scholar] [CrossRef]
- Silverstein, K.A.T.; Haymet, A.D.J.; Dill, K.A. Molecular model of hydrophobic solvation. J. Chem. Phys. 1999, 111, 8000–8009. [Google Scholar] [CrossRef]
- Silverstein, K.A.T.; Haymet, A.D.J.; Dill, K.A. A simple model of water and the hydrophobic effect. J. Am. Chem. Soc. 1998, 120, 3166–3175. [Google Scholar] [CrossRef]
- Mancera, R.L. Computer simulation of effect of salt on the hydrophobic effect. J. Chem. Soc. Faraday Trans. 1998, 94, 3549–3559. [Google Scholar] [CrossRef]
- Lazaridis, T. Solvent reorganization energy and entropy in hydrophobic hydration. J. Phys. Chem. B 2000, 104, 4964–4979. [Google Scholar] [CrossRef]
- Lederhos, J.P.; Long, J.P.; Sum, A.; Christiansen, R.L.; Sloan, E.D. Effective kinetic inhibitors for natural gas hydrates. Chem. Eng. Sci. 1996, 51, 1221–1229. [Google Scholar] [CrossRef]
- Arjun Berendsen, T.A.; Bolhuis, P.G. Unbiased atomistic insight in the competing nucleation mechanisms of methane hydrates. Proc. Natl. Acad. Sci. USA 2019, 116, 19305–19310. [Google Scholar] [CrossRef]
- Meng, E.C.; Kollman, P.A. Molecular dynamics studies of the properties of water around simple organic solutes. J. Phys. Chem. 1996, 100, 11460–11470. [Google Scholar] [CrossRef]
- Hernandez-Cobos, J.; Mackie, A.D.; Vega, L.F. The hydrophobic hydration of methane as a function of temperature from histogram reweighting Monte Carlo simulations. J. Chem. Phys. 2001, 114, 7527–7535. [Google Scholar] [CrossRef]
- Broadbent, R.D.; Neilson, G.W. The interatomic structure of argon in water. J. Chem. Phys. 1994, 100, 7543–7547. [Google Scholar] [CrossRef]
- De Jong, P.H.K.; Wilson, J.E.; Neilson, G.W.; Buckingham, A.D. Hydrophobic hydration of methane. Mol. Phys. 1997, 91, 99–104. [Google Scholar] [CrossRef]
- Koh, C.A.; Wisbey, R.P.; Wu, X.; Westacott, R.E.; Scoper, A.K. Water ordering around methane during hydrate formation. J. Chem. Phys. 2000, 113, 6390–6397. [Google Scholar] [CrossRef]
- Filipponi, A.; Bowron, D.T.; Lobban, C.; Finney, J.L. Structural determination of hydrophobic hydration shell of Kr. Phys. Rev. Lett. 1997, 79, 1293–1296. [Google Scholar] [CrossRef]
- Bowron, D.T.; Filipponi, A.; Roberts, M.A.; Finney, J.L. Hydrophobic hydration and the formation of a clathrate hydrate. Phys. Rev. Lett. 1998, 81, 4164–4167. [Google Scholar] [CrossRef]
- Gao, S.; Chapman, W.G.; House, W. NMR and Viscosity Investigation of Clathrate Hydrate Formation and Dissociation. Ind. Eng. Chem. Res. 2005, 44, 7373–7379. [Google Scholar] [CrossRef]
- Sloan, E.D.; Fleyfel, F.A. A molecular mechanism for gas hydrate nucleation from ice. AIChE J. 1991, 37, 1281–1292. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Trout, B.L. A new approach for studying nucleation phenomena using molecular simulations: Application to CO2 hydrate clathrates. J. Chem. Phys. 2002, 117, 1786–1796. [Google Scholar] [CrossRef]
- Moon, C.; Taylor, P.C.; Rodger, P.M. Molecular Dynamics Study of Gas Hydrate Formation. J. Am. Chem. Soc. 2003, 125, 4706–4707. [Google Scholar] [CrossRef] [PubMed]
- Hawtin, R.W.; Quigley, D.; Rodger, P.M. Gas hydrate nucleation and cage formation at a water/methane interface. Phys. Chem. Chem. Phys. 2008, 10, 4853–4864. [Google Scholar] [CrossRef]
- Jacobson, L.C.; Hujo, W.; Molinero, V. Amorphous Precursors in the Nucleation of Clathrate Hydrates. J. Am. Chem. Soc. 2010, 132, 11806–11811. [Google Scholar] [CrossRef]
- Vatamanu, J.; Kusalik, P.G. Observation of two-step nucleation in methane hydrates. Phys. Chem. Chem. Phys. 2010, 12, 15065–15072. [Google Scholar] [CrossRef] [PubMed]
- Guo, G.-J.; Zhang, Y.-G.; Liu, C.-J.; Li, K.-H. Using the face-saturated incomplete cage analysis to quantify the cage compositions and cage linking structures of amorphous phase hydrates. Phys. Chem. Chem. Phys. 2011, 13, 12048–12057. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, L.C.; Hujo, W.; Molinero, V. Nucleation pathways of clathrate hydrates: Effect of guest size and solubility. J. Phys. Chem. B 2010, 114, 13796–13807. [Google Scholar] [CrossRef]
- Walsh, M.R.; Koh, C.A.; Sloan, E.D.; Sum, A.K.; Wu, D.T. Microsecond simulations of spontaneous methane hydrate nucleation and growth. Science 2009, 326, 1095–1098. [Google Scholar] [CrossRef] [PubMed]
- Guo, G.-J.; Rodger, P.M. Solubility of Aqueous Methane under Metastable Conditions: Implications for Gas Hydrate Nucleation. J. Phys. Chem. B 2013, 117, 6498–6504. [Google Scholar] [CrossRef]
- Rodger, P. Methane hydrate: Melting and memory. Ann. N. Y. Acad. Sci. 2000, 912, 474–482. [Google Scholar] [CrossRef]
- Hallbrucker, A.; Mayer, E. Unexpectedly stable nitrogen, oxygen, carbon monoxide and argon clathrate hydrates from vapour-deposited amorphous solid water: An X-ray and two-step differential scanning calorimetry study. J. Chem. Soc. Faraday Trans. 1990, 86, 3785–3792. [Google Scholar] [CrossRef]
- Hallbrucker, A.; Mayer, E. Unexpectedly stable clathrate hydrates formed from microporous vapor-deposited amorphous solid water at low “external” guest pressures and their astrophysical implications. Icarus 1991, 90, 176–180. [Google Scholar] [CrossRef]
- Guo, G.-J.; Zhang, Y.-G.; Liu, H. Effect of Methane Adsorption on the Lifetime of a Dodecahedral Water Cluster Immersed in Liquid Water: A Molecular Dynamics Study on the Hydrate Nucleation Mechanisms. J. Phys. Chem. C 2007, 111, 2595–2606. [Google Scholar] [CrossRef]
- Guo, G.-J.; Li, M.; Zhang, Y.-G.; Wu, C.-H. Why can water cages adsorb aqueous methane? A potential of mean force calculation on hydrate nucleation mechanisms. Phys. Chem. Chem. Phys. 2009, 11, 10427–10437. [Google Scholar] [CrossRef] [PubMed]
- Baez, L.A.; Clancy, P. Computer Simulation of the Crystal Growth and Dissolution of Natural Gas Hydrates. Ann. N. Y. Acad. Sci. 1994, 715, 177–186. [Google Scholar] [CrossRef]
- Rodger, P.M.; Forester, T.R.; Smith, W. Simulations of the methane hydrate/methane gas interface near hydrate forming conditions conditions. Fluid Ph. Equilib. 1996, 116, 326–332. [Google Scholar] [CrossRef]
- Yagasaki, T.; Matsumoto, M.; Andoh, Y.; Okazaki, S.; Tanaka, H. Effect of bubble formation on the dissociation of methane hydrate in water: A molecular dynamics study. J. Phys. Chem. B 2014, 118, 1900–1906. [Google Scholar] [CrossRef]
- Bagherzadeh, S.A.; Alavi, S.; Ripmeester, J.A.; Englezos, P. Formation of methane nano-bubbles during hydrate decomposition and their effect on hydrate growth. J. Chem. Phys. 2015, 142, 214701. [Google Scholar] [CrossRef] [PubMed]
- Knott, B.C.; LaRue, J.L.; Wodtke, A.M.; Doherty, M.F.; Peters, B. Communication: Bubbles, crystals, and laser-induced nucleation. J. Chem. Phys. 2011, 134, 171102. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, M.; Wada, Y.; Oonaka, A.; Onoe, K. Polymorph control of glycine by antisolvent crystallization using nitrogen minute-bubbles. J. Cryst. Growth 2013, 373, 73–77. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, L.; Deng, S.; Zhao, R.; Nie, X.; Liu, Y. Effect of Nanobubble Evolution on Hydrate Process: A Review. J. Therm. Sci. 2019, 28, 948–961. [Google Scholar] [CrossRef]
- Uchida, T.; Yamazaki, K.; Gohara, K. Generation of micro-and nano-bubbles in water by dissociation of gas hydrates. Korean J. Chem. Eng. 2016, 33, 1749–1755. [Google Scholar] [CrossRef]
- Uchida, T.; Yamazaki, K.; Gohara, K. Gas nanobubbles as nucleation acceleration in the gas-hydrate memory effect. J. Phys. Chem. C 2016, 120, 26620–26629. [Google Scholar] [CrossRef]
- Ripmeester, J.A.; Alavi, S. Some current challenges in clathrate hydrate science: Nucleation, decomposition and the memory effect. Curr. Opin. Solid State Mater. Sci. 2016, 20, 344–351. [Google Scholar] [CrossRef]
- Walsh, M.R.; Beckham, G.T.; Koh, C.A.; Sloan, E.D.; Wu, D.T.; Sum, A.K. Methane Hydrate Nucleation Rates from Molecular Dynamics Simulations: Effects of Aqueous Methane Concentration, Interfacial Curvature, and System Size. J. Phys. Chem. C 2011, 115, 21241–21248. [Google Scholar] [CrossRef]
- Walsh, M.R.; Rainey, J.D.; Lafond, P.G.; Park, D.H.; Beckham, G.T.; Jones, M.D.; Lee, K.-H.; Koh, C.A.; Sloan, E.D.; Wu, D.T.; et al. The Cages, Dynamics, and Structuring of Incipient Methane Clathrate Hydrates. Phys. Chem. Chem. Phys. 2011, 13, 19951–19959. [Google Scholar] [CrossRef]
- Liang, S.; Kusalik, P.G. Crystal growth simulations of H2S hydrate. J. Phys. Chem. B 2010, 114, 9563–9571. [Google Scholar] [CrossRef]
- Liang, S.; Kusalik, P.G. Exploring nucleation of H2S hydrates. Chem. Sci. 2011, 2, 1286–1292. [Google Scholar] [CrossRef]
- Sarupria, S.; Debenedetti, P.G. Homogeneous Nucleation of Methane Hydrate in Microsecond Molecular Dynamics Simulations. J. Phys. Chem. Lett. 2012, 3, 2942–2947. [Google Scholar] [CrossRef]
- Jimenez-Angeles, F.; Firoozabadi, A. Nucleation of methane hydrates at moderate subcooling by molecular dynamics simulations. J. Phys. Chem. C 2014, 118, 11310–11318. [Google Scholar] [CrossRef]
- Choudhary, N.; Kushwaha, O.S.; Bhattacharjee, G.; Chakrabarty, S.; Kumar, R. Macro and Molecular Level Insights on Gas Hydrate Growth in the Presence of Hofmeister Salts. Ind. Eng. Chem. Res. 2020, 59, 20591–20600. [Google Scholar] [CrossRef]
- Lauricella, M.; Meloni, S.; English, N.J.; Peters, B.; Ciccotti, G. Methane clathrate hydrate nucleation mechanism by advanced molecular simulations. J. Phys. Chem. C 2014, 118, 22847–22857. [Google Scholar] [CrossRef]
- Jiménez-Ángeles, F.; Firoozabadi, A. Nucleation pathways of gas hydrates from molecular dynamics simulations. In Proceedings of the 8th International Conference on Gas Hydrates (ICGH8), Beijing, China, 28 July–1 August 2014. [Google Scholar] [CrossRef]
- Barnes, B.C.; Sum, A.K. Advances in molecular simulations of clathrate hydrates. Curr. Opin. Chem. Eng. 2013, 2, 184–190. [Google Scholar] [CrossRef]
- Wu, J.Y.; Chen, L.J.; Chen, Y.P.; Lin, S.T. Molecular dynamics study on the growth mechanism of methane plus tetrahydrofuran mixed hydrates. J. Phys. Chem. C 2015, 119, 19883–19890. [Google Scholar] [CrossRef]
- Wu, J.Y.; Chen, L.J.; Chen, Y.P.; Lin, S.T. Molecular dynamics study on the nucleation of methane+ tetrahydrofuran mixed guest hydrate. Phys. Chem. Chem. Phys. 2016, 18, 9935–9947. [Google Scholar] [CrossRef]
- Gets, K.; Belosludov, V.; Zhdanov, R.; Bozhko, Y.; Belosludov, R.; Subbotin, O.; Marasanov, N.; Kawazoe, Y. Transformation of hydrogen bond network during CO2 clathrate hydrate dissociation. Appl. Surf. Sci. 2020, 499, 143644. [Google Scholar] [CrossRef]
- Belosludov, V.R.; Gets, K.V.; Zhdanov, R.K.; Bozhko, Y.Y.; Belosludov, R.V.; Chen, L.J. Collective Effect of Transformation of a Hydrogen Bond Network at the Initial State of Growth of Methane Hydrate. JETP Lett. 2022, 115, 124–129. [Google Scholar] [CrossRef]
- Parui, S.; Jana, B. Factors promoting the formation of clathrate-like ordering of water in biomolecular structure at ambient temperature and pressure. J. Phys. Chem. B 2019, 123, 811–824. [Google Scholar] [CrossRef]
- Lauricella, M.; Ciccotti, G.; English, N.J.; Peters, B.; Meloni, S. Mechanisms and nucleation rate of methane hydrate by dynamical nonequilibrium molecular dynamics. J. Phys. Chem. C 2017, 121, 24223–24234. [Google Scholar] [CrossRef]
- Uchida, T.; Miyoshi, H.; Sugibuchi, R.; Suzuta, A.; Yamazaki, K.; Gohara, K. Contribution of ultra-fine bubbles to promoting effect on propane hydrate formation. Front. Chem. 2020, 8, 480. [Google Scholar] [CrossRef]
- Belosludov, V.R.; Subbotin, O.S.; Krupskii, D.S.; Belosludov, R.V.; Kawazoe, Y.; Kudoh, J.I. Physical and chemical properties of gas hydrates: Theoretical aspects of energy storage application. Mater. Trans. 2007, 48, 704–710. [Google Scholar] [CrossRef]
- Das, S.; Tadepalli, K.M.; Roy, S.; Kumar, R. A review of clathrate hydrate nucleation, growth and decomposition studied using molecular dynamics simulation. J. Mol. Liquid. 2022, 348, 118025. [Google Scholar] [CrossRef]
- Lehmkühler, F.; Paulus, M.; Sternemann, C.; Lietz, D.; Venturini, F.; Gutt, C.; Tolan, M. The carbon dioxide−water interface at conditions of gas hydrate formation. J. Am. Chem. Soc. 2009, 131, 585–589. [Google Scholar] [CrossRef] [PubMed]
- Both, A.K.; Gao, Y.; Zeng, X.C.; Cheung, C.L. Gas hydrates in confined space of nanoporous materials: New frontier in gas storage technology. Nanoscale 2021, 13, 7447–7470. [Google Scholar] [CrossRef] [PubMed]
- Casco, M.E.; Silvestre-Albero, J.; Ramírez-Cuesta, A.J.; Rey, F.; Jordá, J.L.; Bansode, A.; Urakawa, A.; Peral, I.; Martínez-Escandell, M.; Kaneko, K.; et al. Methane hydrate formation in confined nanospace can surpass nature. Nat. Commun. 2015, 6, 6432. [Google Scholar] [CrossRef] [PubMed]
- Yu, K.B.; Yazaydin, A.O. Does confinement enable methane hydrate growth at low pressures? Insights from molecular dynamics simulations. J. Phys. Chem. C 2020, 124, 11015–11022. [Google Scholar] [CrossRef] [PubMed]
- Makogon, T.Y.; Sloan, E.D.J. Phase equilibrium for methane hydrate from 190 to 262K. J. Chem. Eng. Data 1994, 39, 351–353. [Google Scholar] [CrossRef]
- Hirai, S.; Okazaki, K.; Tabe, Y.; Kawamura, K. CO2 clathrate-hydrate formation and its mechanism by molecular dynamics simulation. Energy Convers. Manag. 1997, 38, S301–S306. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles, 1st ed.; CRC Press: Boca Raton, FL, USA, 1988; p. 540. [Google Scholar]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Abascal, J.L.F.; Sanz, E.; Fernández, R.G.; Vega, C. A potential model for the study of ices and amorphous water: TIP4P/Ice. J. Chem. Phys. 2005, 122, 234511. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable Potentials for Phase Equilibria. 1. United-atom Description of n-Alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Kang, K.C.; Hong, S.Y.; Cho, S.J.; Kim, D.H.; Lee, J.D. Evaluation of desalination by nanostructured hydrate formation and pellet production process. J. Nanosci. Nanotechnol. 2017, 17, 4059–4062. [Google Scholar] [CrossRef]
- Mi, F.; He, Z.; Fang, B.; Ning, F.; Jiang, G. Molecular insights into the effects of surface property and pore size of non-swelling clay on methane hydrate formation. Fuel 2022, 311, 122607. [Google Scholar] [CrossRef]
- Tung, Y.T.; Chen, L.J.; Chen, Y.P.; Lin, S.T. Molecular dynamics study on the growth of structure I methane hydrate in aqueous solution of sodium chloride. J. Phys. Chem. B 2012, 116, 14115–14125. [Google Scholar] [CrossRef]
- DeFever, R.S.; Sarupria, S. Nucleation mechanism of clathrate hydrates of water-soluble guest molecules. J. Chem. Phys. 2017, 147, 204503. [Google Scholar] [CrossRef]
- English, N.J.; John, S.T.; Carey, D.J. Mechanisms for thermal conduction in various polymorphs of methane hydrate. Phys. Rev. B 2009, 80, 134306. [Google Scholar] [CrossRef]
- Conde, M.M.; Rovere, M.; Gallo, P. High precision determination of the melting points of water TIP4P/2005 and water TIP4P/Ice models by the direct coexistence technique. J. Chem. Phys. 2017, 147, 244506. [Google Scholar] [CrossRef]


| C | NM | NW | xM |
|---|---|---|---|
| 0.2 | 348 | 10,001 | 3.36 mol% |
| 0.4 | 696 | 10,001 | 6.5 mol% |
| 0.6 | 1043 | 10,001 | 9.45 mol% |
| 0.8 | 1391 | 10,001 | 12.2 mol% |
| 1.0 | 1739 | 10,001 | 14.8 mol% |
| 0.6-small | 125 | 1200 | 9.43 mol% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belosludov, R.V.; Gets, K.V.; Zhdanov, R.K.; Bozhko, Y.Y.; Belosludov, V.R.; Chen, L.-J.; Kawazoe, Y. Molecular Dynamics Study of Clathrate-like Ordering of Water in Supersaturated Methane Solution at Low Pressure. Molecules 2023, 28, 2960. https://doi.org/10.3390/molecules28072960
Belosludov RV, Gets KV, Zhdanov RK, Bozhko YY, Belosludov VR, Chen L-J, Kawazoe Y. Molecular Dynamics Study of Clathrate-like Ordering of Water in Supersaturated Methane Solution at Low Pressure. Molecules. 2023; 28(7):2960. https://doi.org/10.3390/molecules28072960
Chicago/Turabian StyleBelosludov, Rodion V., Kirill V. Gets, Ravil K. Zhdanov, Yulia Y. Bozhko, Vladimir R. Belosludov, Li-Jen Chen, and Yoshiyuki Kawazoe. 2023. "Molecular Dynamics Study of Clathrate-like Ordering of Water in Supersaturated Methane Solution at Low Pressure" Molecules 28, no. 7: 2960. https://doi.org/10.3390/molecules28072960
APA StyleBelosludov, R. V., Gets, K. V., Zhdanov, R. K., Bozhko, Y. Y., Belosludov, V. R., Chen, L.-J., & Kawazoe, Y. (2023). Molecular Dynamics Study of Clathrate-like Ordering of Water in Supersaturated Methane Solution at Low Pressure. Molecules, 28(7), 2960. https://doi.org/10.3390/molecules28072960






