Machine Learning Scoring Functions for Drug Discovery from Experimental and Computer-Generated Protein–Ligand Structures: Towards Per-Target Scoring Functions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Database
2.2. Computer-Generated Database
2.3. Complex Representation
2.4. Target Values
2.5. Regression Model and Training Protocol
3. Results
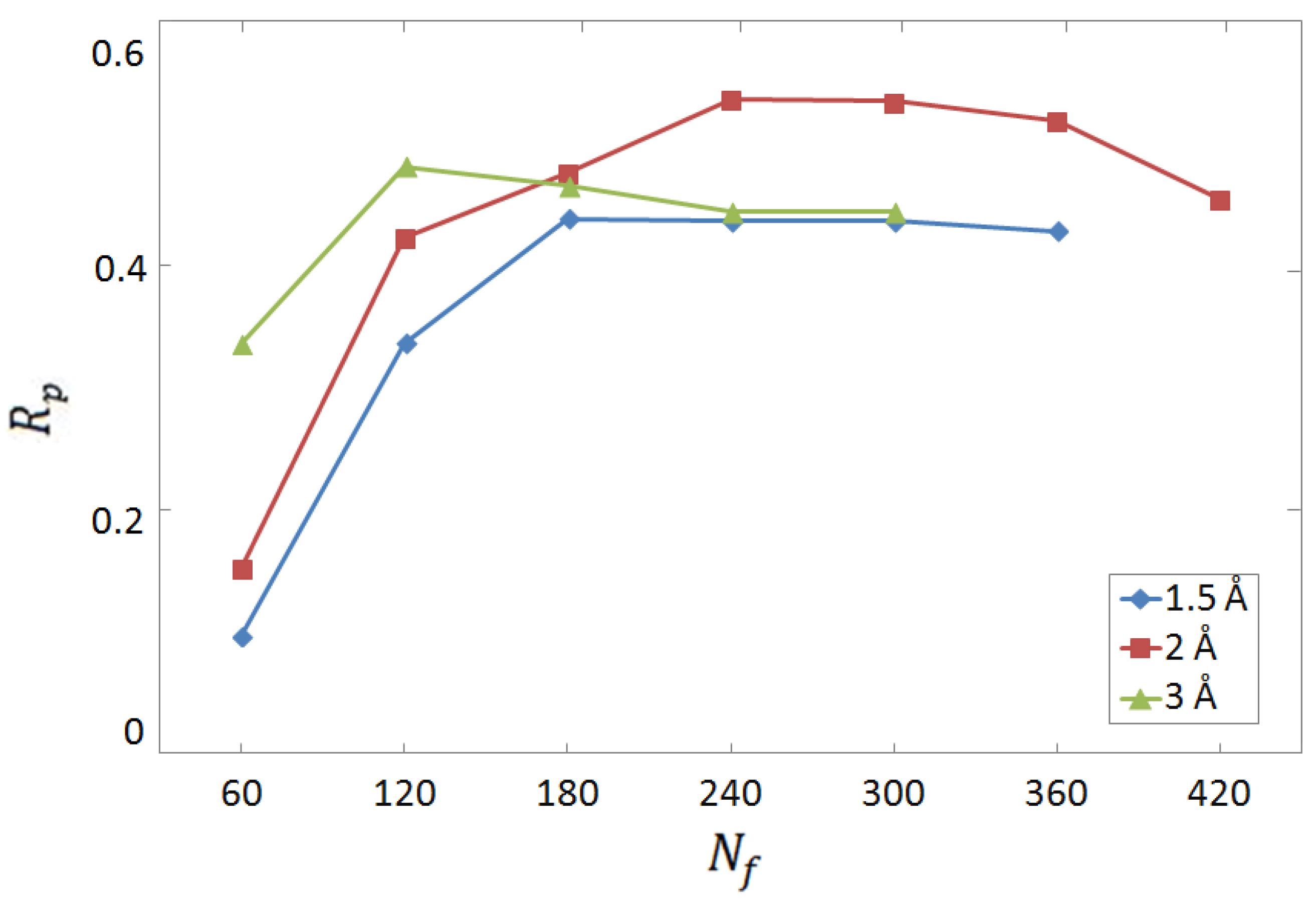
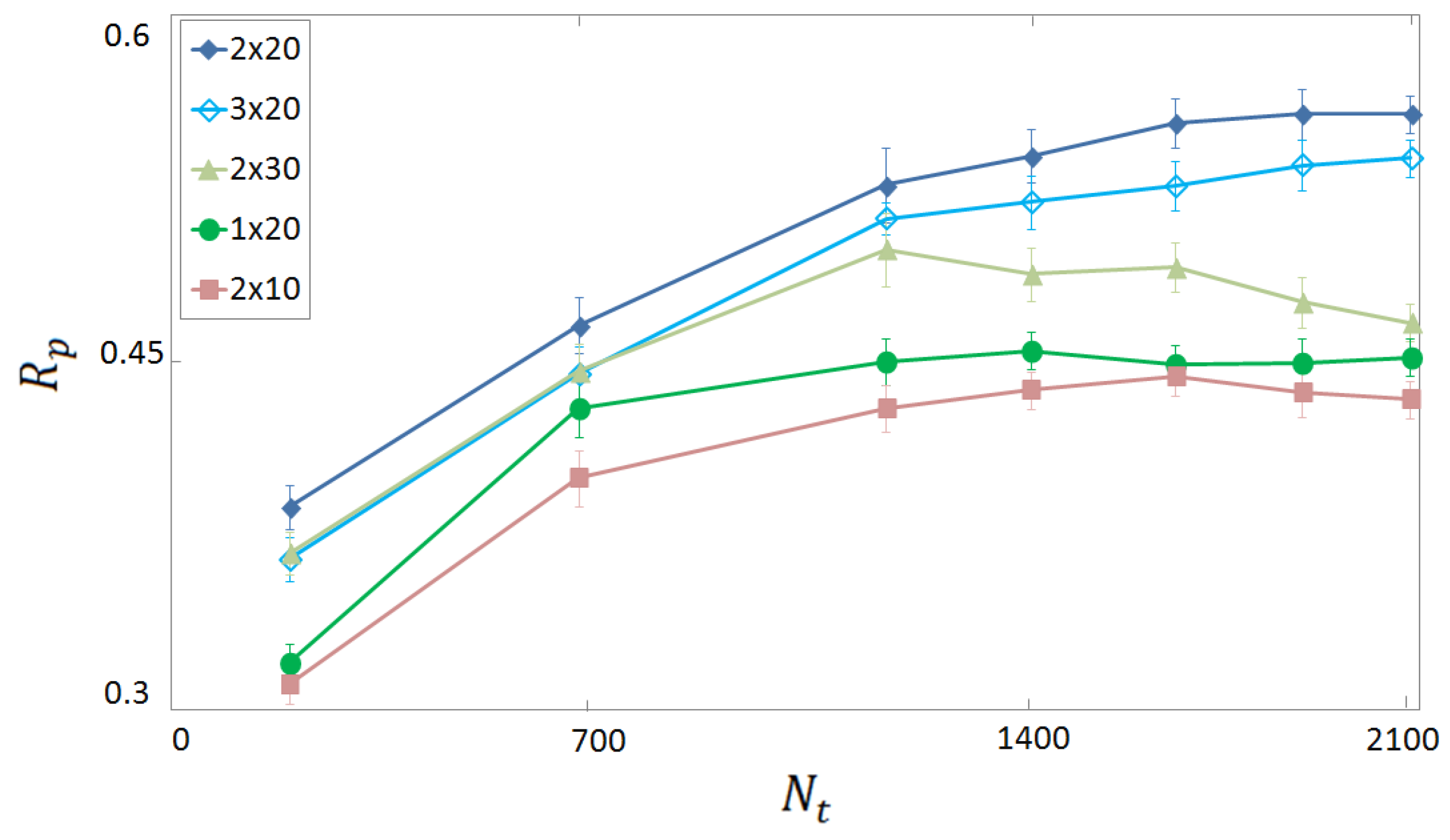
3.1. Selection of Descriptors and Network Structure
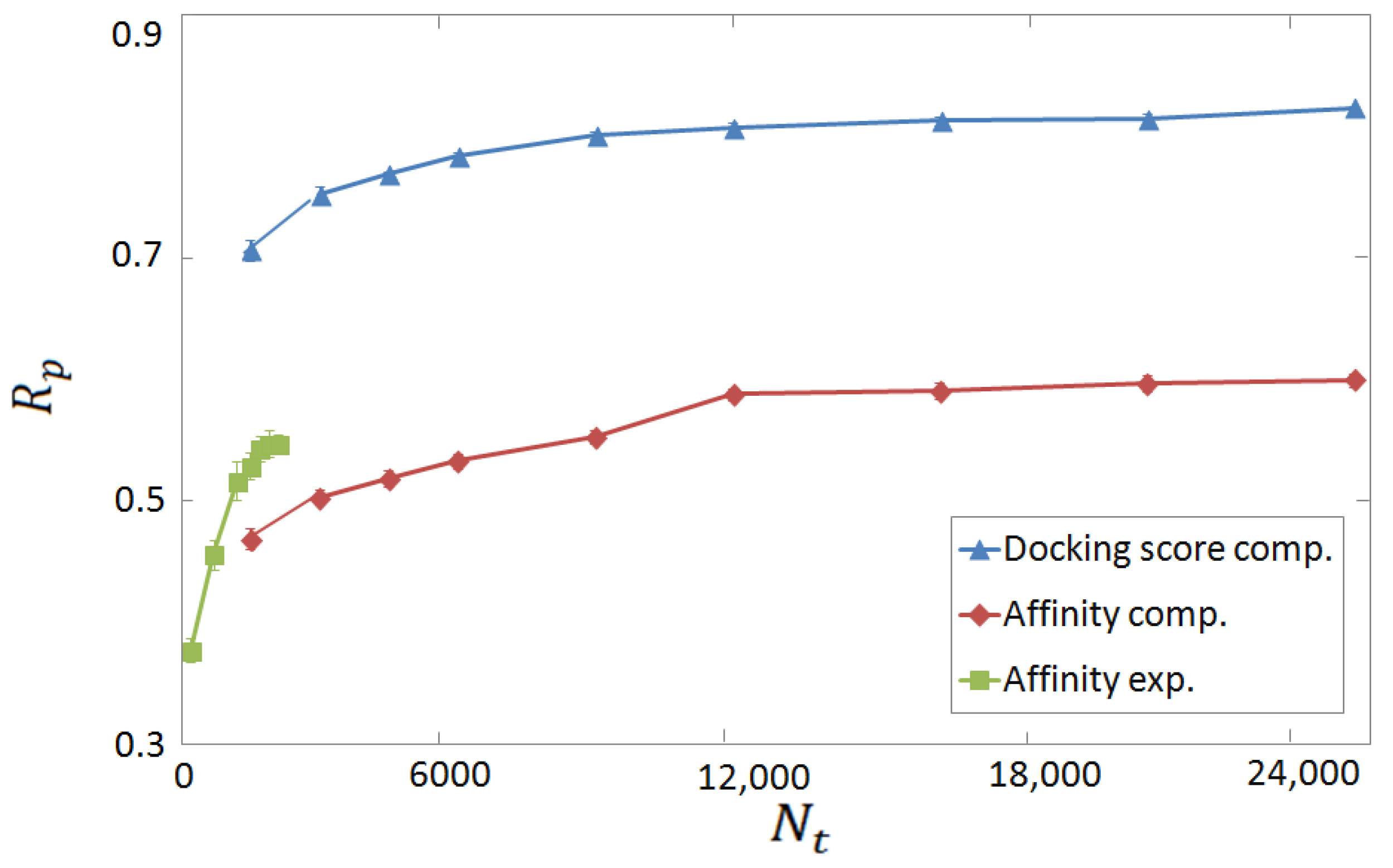
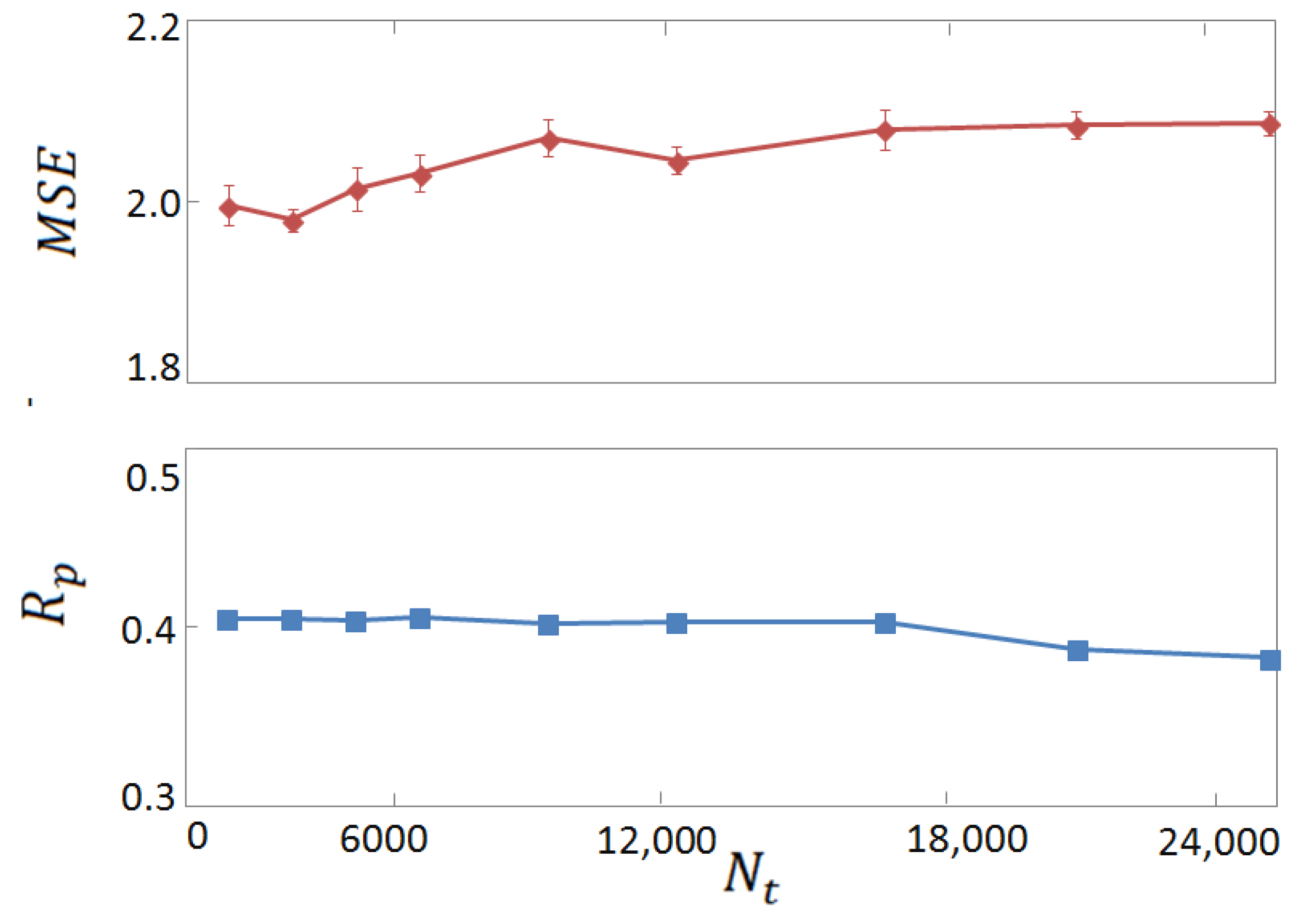
3.2. Horizontal Tests on Experimental and Computer-Generated Structures
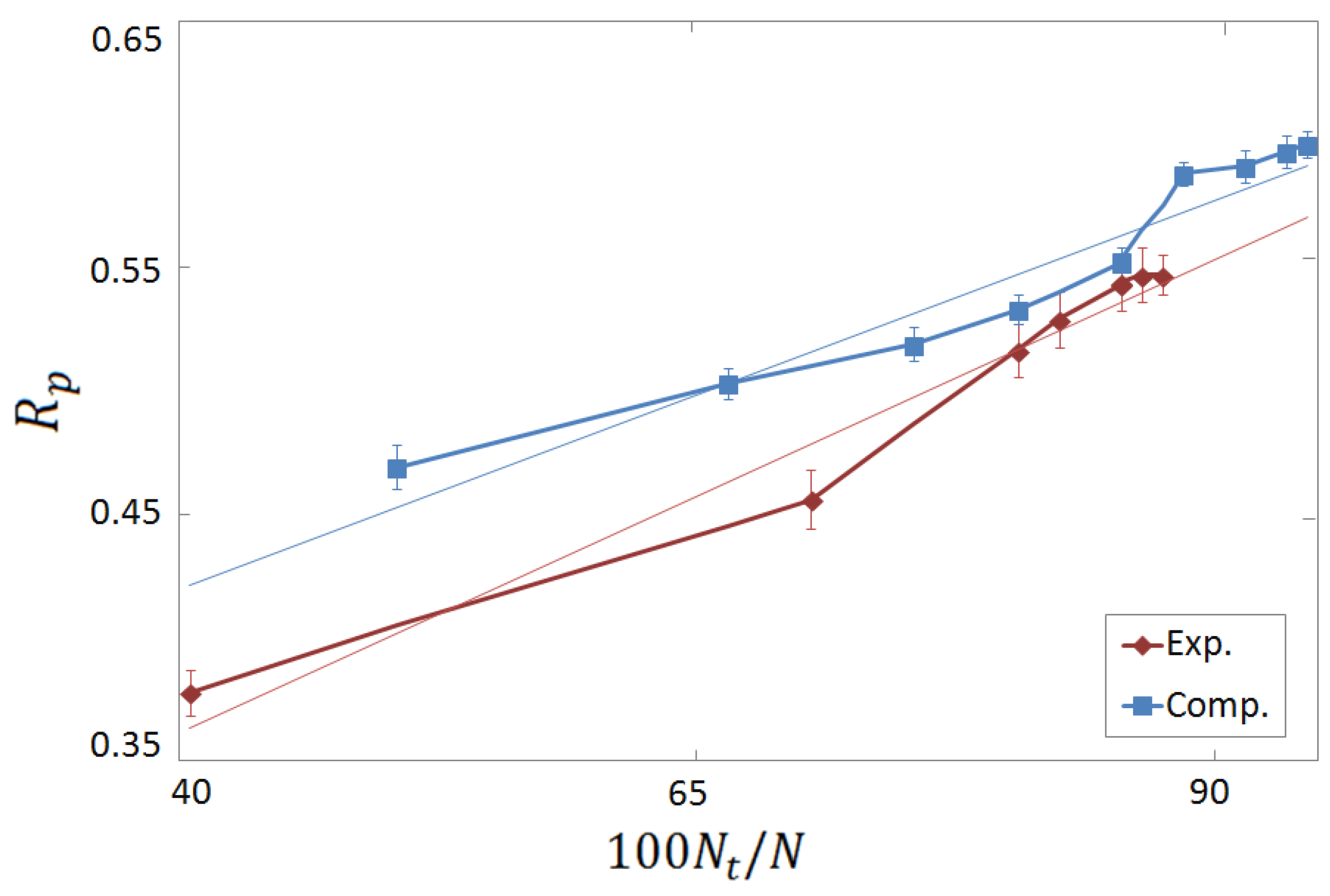
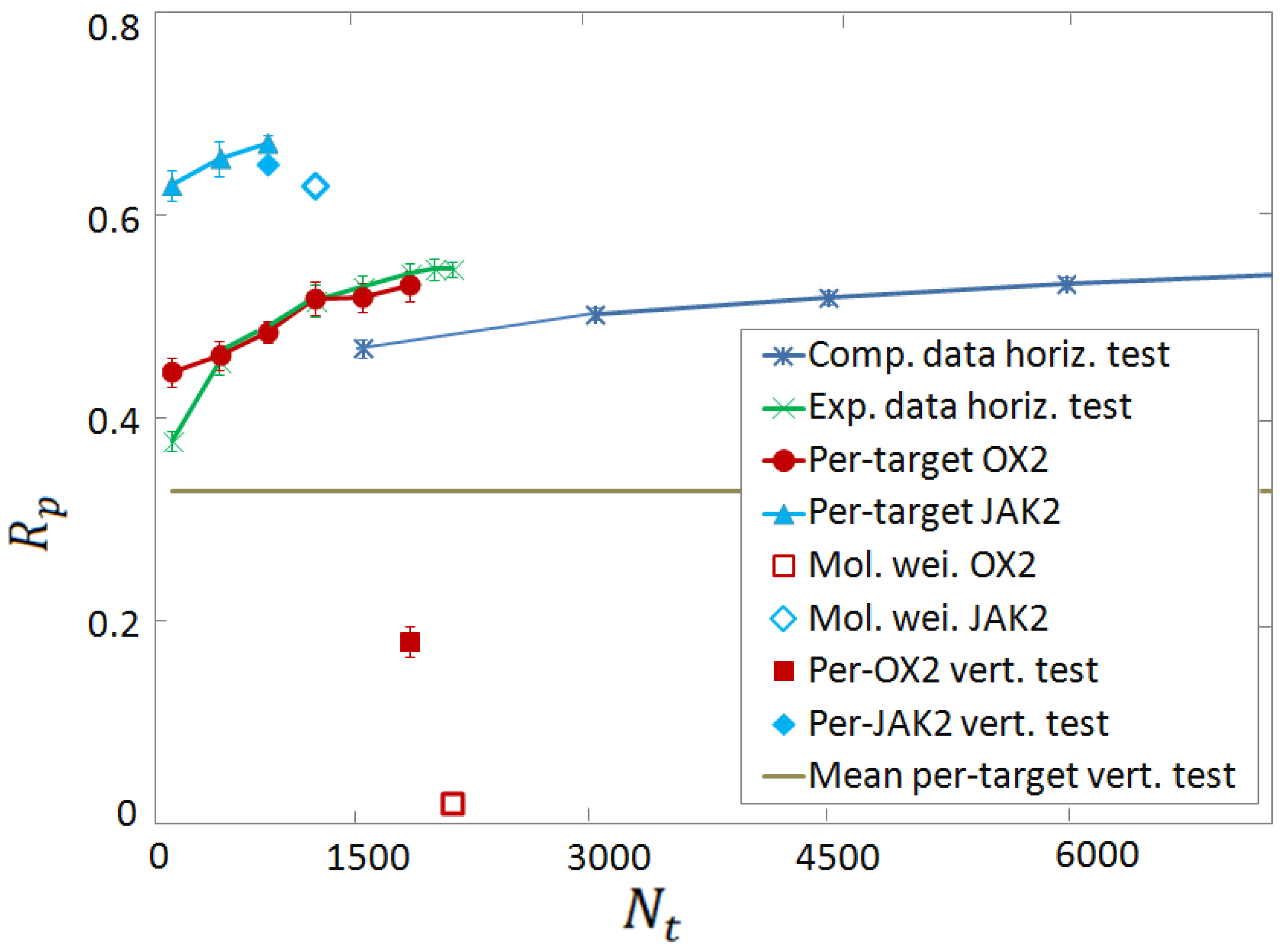
3.3. Vertical Tests
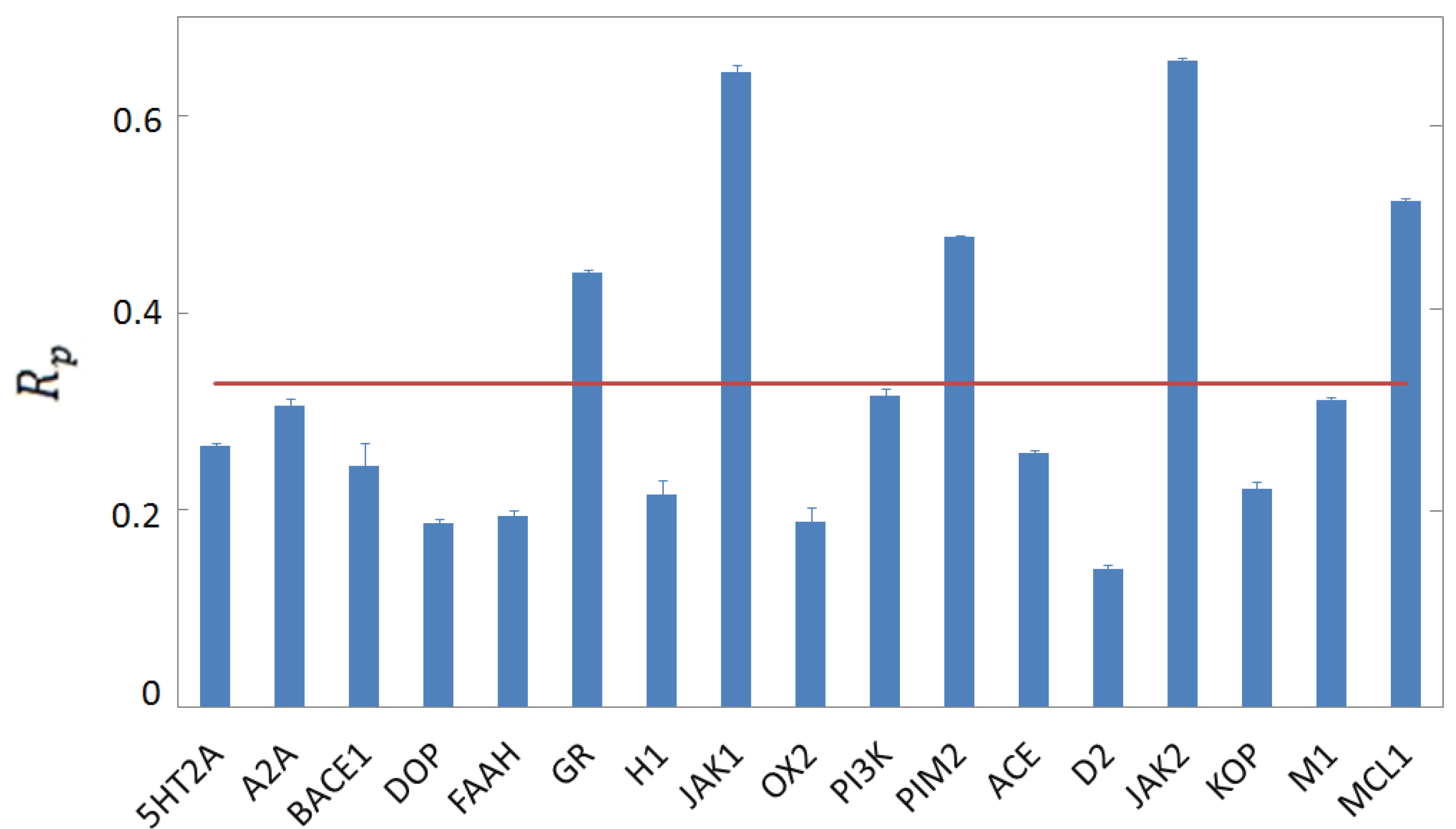
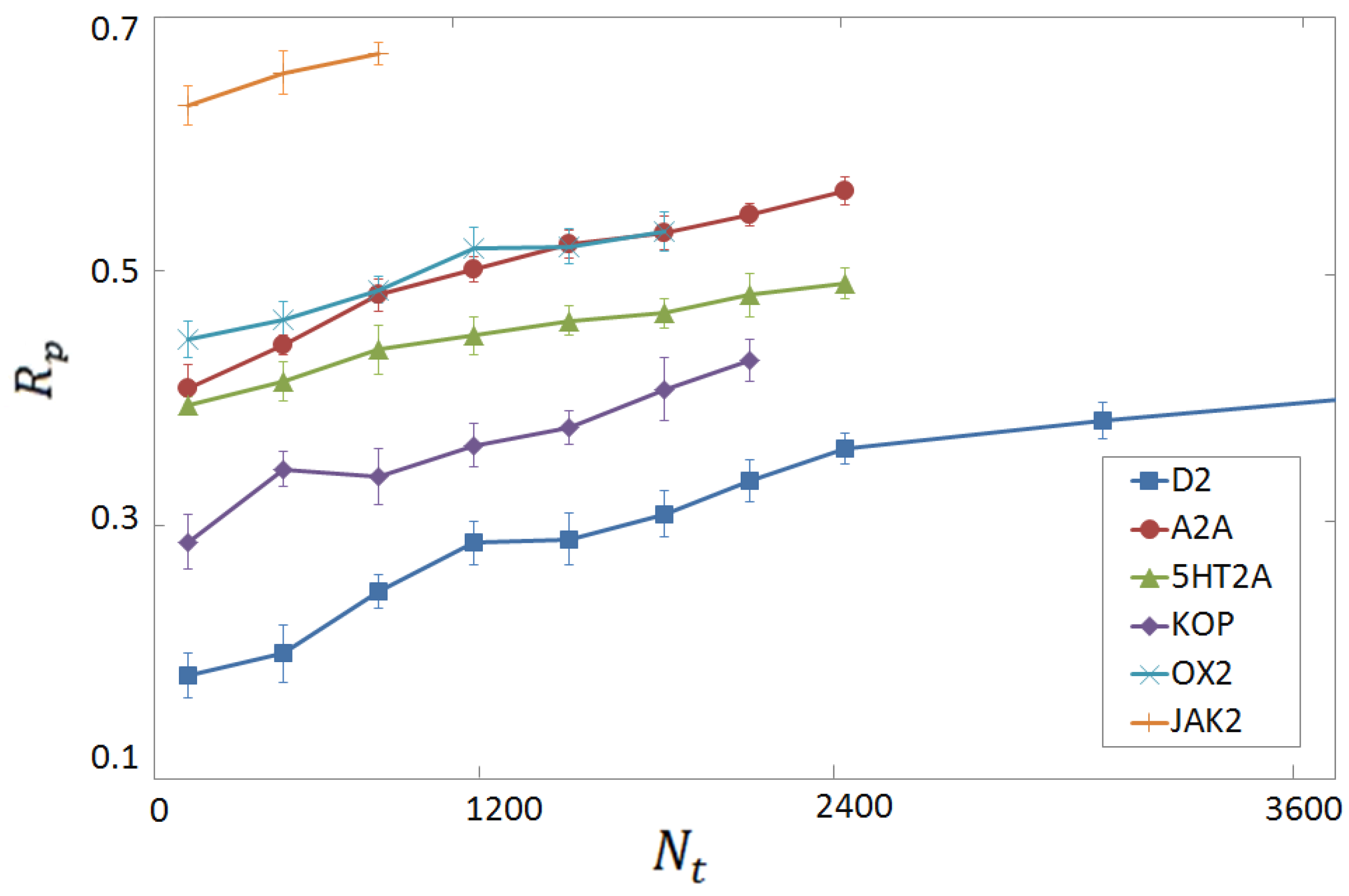
3.4. Per-Target Scoring Functions
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kulharia, M.; Goody, R.S.; Jackson, R.M. Information Theory-Based Scoring Function for the Structure-Based Prediction of Protein- Ligand Binding Affinity. J. Chem. Inf. Model. 2008, 48, 1990–1998. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.N. Scoring functions for protein–ligand docking. Curr. Protein Pept. Sci. 2006, 7, 407–420. [Google Scholar] [CrossRef] [PubMed]
- Walters, W.P.; Stahl, M.T.; Murcko, M.A. Virtual screening—An overview. Drug Discov. Today 1998, 3, 160–178. [Google Scholar] [CrossRef]
- Wienkers, L.C.; Heath, T.G. Predicting in vivo drug interactions from in vitro drug discovery data. Nat. Rev. Drug Discov. 2005, 4, 825–833. [Google Scholar] [CrossRef] [PubMed]
- Drews, J. Drug discovery: A historical perspective. Science 2000, 287, 1960–1964. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wang, R. Classification of current scoring functions. J. Chem. Inf. Model. 2015, 55, 475–482. [Google Scholar] [CrossRef]
- Gohlke, H.; Klebe, G. Statistical potentials and scoring functions applied to protein–ligand binding. Curr. Opin. Struct. Biol. 2001, 11, 231–235. [Google Scholar] [CrossRef]
- Gohlke, H.; Hendlich, M.; Klebe, G. Knowledge-based scoring function to predict protein–ligand interactions. J. Mol. Biol. 2000, 295, 337–356. [Google Scholar] [CrossRef]
- Yin, S.; Biedermannova, L.; Vondrasek, J.; Dokholyan, N.V. MedusaScore: An accurate force field-based scoring function for virtual drug screening. J. Chem. Inf. Model. 2008, 48, 1656–1662. [Google Scholar] [CrossRef]
- Ain, Q.U.; Aleksandrova, A.; Roessler, F.D.; Ballester, P.J. Machine-learning scoring functions to improve structure-based binding affinity prediction and virtual screening. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 405–424. [Google Scholar] [CrossRef]
- Li, H.; Sze, K.H.; Lu, G.; Ballester, P.J. Machine-learning scoring functions for structure-based drug lead optimization. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020, 10, e1465. [Google Scholar] [CrossRef]
- Li, H.; Sze, K.H.; Lu, G.; Ballester, P.J. Machine-learning scoring functions for structure-based virtual screening. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, 11, e1478. [Google Scholar] [CrossRef]
- Palmer, R.A.; Niwa, H. X-ray crystallographic studies of protein–ligand interactions. Biochem. Soc. Trans. 2003, 31, 973–979. [Google Scholar] [CrossRef]
- Ballester, P.J.; Mitchell, J.B.O. A machine learning approach to predicting protein–ligand binding affinity with applications to molecular docking. Bioinformatics 2010, 26, 1169–1175. [Google Scholar] [CrossRef] [PubMed]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Fang, X.; Lu, Y.; Wang, S. The PDBbind database: Collection of binding affinities for protein- ligand complexes with known three-dimensional structures. J. Med. Chem. 2004, 47, 2977–2980. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Fang, X.; Lu, Y.; Yang, C.Y.; Wang, S. The PDBbind database: Methodologies and updates. J. Med. Chem. 2005, 48, 4111–4119. [Google Scholar] [CrossRef]
- Liu, Z.; Su, M.; Han, L.; Liu, J.; Yang, Q.; Li, Y.; Wang, R. Forging the basis for developing protein–ligand interaction scoring functions. Accounts Chem. Res. 2017, 50, 302–309. [Google Scholar] [CrossRef]
- Gabel, J.; Desaphy, J.; Rognan, D. Beware of Machine Learning-Based Scoring Functions: On the Danger of Developing Black Boxes. J. Chem. Inf. Model. 2014, 54, 2807–2815. [Google Scholar] [CrossRef]
- Zhu, F.; Zhang, X.; Allen, J.E.; Jones, D.; Lightstone, F.C. Binding affinity prediction by pairwise function based on neural network. J. Chem. Inf. Model. 2020, 60, 2766–2772. [Google Scholar] [CrossRef]
- Jiménez, J.; Skalic, M.; Martinez-Rosell, G.; De Fabritiis, G. Kdeep: Protein–ligand absolute binding affinity prediction via 3d-convolutional neural networks. J. Chem. Inf. Model. 2018, 58, 287–296. [Google Scholar] [CrossRef]
- Gomes, J.; Ramsundar, B.; Feinberg, E.N.; Pande, V.S. Atomic convolutional networks for predicting protein–ligand binding affinity. arXiv 2017, arXiv:1703.10603. [Google Scholar]
- Seo, S.; Choi, J.; Park, S.; Ahn, J. Binding affinity prediction for protein–ligand complex using deep attention mechanism based on intermolecular interactions. BMC Bioinform. 2021, 22, 542. [Google Scholar] [CrossRef] [PubMed]
- Stepniewska-Dziubinska, M.M.; Zielenkiewicz, P.; Siedlecki, P. Development and evaluation of a deep learning model for protein–ligand binding affinity prediction. Bioinformatics 2018, 34, 3666–3674. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhou, J.; Xu, T.; Huang, L.; Wang, F.; Xiong, H.; Huang, W.; Dou, D.; Xiong, H. Structure-aware interactive graph neural networks for the prediction of protein–ligand binding affinity. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual Event, 14–18 August 2021; pp. 975–985. [Google Scholar] [CrossRef]
- Emmert-Streib, F.; Yang, Z.; Feng, H.; Tripathi, S.; Dehmer, M. An Introductory Review of Deep Learning for Prediction Models With Big Data. Front. Artif. Intell. 2020, 3, 4. [Google Scholar] [CrossRef]
- Wójcikowski, M.; Ballester, P.J.; Siedlecki, P. Performance of machine-learning scoring functions in structure-based virtual screening. Sci. Rep. 2017, 7, 46710. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Shen, C.; Huang, N. Predicting or pretending: Artificial intelligence for protein–ligand interactions lack of sufficiently large and unbiased datasets. Front. Pharmacol. 2020, 11, 69. [Google Scholar] [CrossRef]
- Warren, G.L.; Do, T.D.; Kelley, B.P.; Nicholls, A.; Warren, S.D. Essential considerations for using protein–ligand structures in drug discovery. Drug Discov. Today 2012, 17, 1270–1281. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef]
- Jia, X.; Lynch, A.; Huang, Y.; Danielson, M.; Lang’at, I.; Milder, A.; Ruby, A.E.; Wang, H.; Friedler, S.A.; Norquist, A.J.; et al. Anthropogenic biases in chemical reaction data hinder exploratory inorganic synthesis. Nature 2019, 573, 251–255. [Google Scholar] [CrossRef]
- Molecular Operating Environment (MOE), 2022.02 Chemical Computing Group ULC, 1010 Sherbooke St. West, Suite #910, Montreal, QC, Canada, H3A 2R7. 2023. Available online: https://www.chemcomp.com/index.htm (accessed on 1 February 2020).
- Jones, G.; Willett, P.; Glen, R.C.; Leach, A.R.; Taylor, R. Development and validation of a genetic algorithm for flexible docking. J. Mol. Biol. 1997, 267, 727–748. [Google Scholar] [CrossRef]
- Greenidge, P.A.; Lewis, R.A.; Ertl, P. Boosting Pose Ranking Performance via Rescoring with MM-GBSA. Chem. Biol. Drug Des. 2016, 88, 317–328. [Google Scholar] [CrossRef]
- Drenth, J. Principles of Protein X-ray Crystallography; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef]
- The Protein Data Bank. Available online: https://www.rcsb.org/ (accessed on 1 February 2020).
- Pellicani, F.; Dal Ben, D.; Perali, A.; Pilati, S. Data for “Machine Learning Scoring Functions for Drug Discovery from Experimental and Computer-Generated Protein–Ligand Structures: Towards Per-Target Scoring Functions”. Available online: https://zenodo.org/record/7514055#.Y-SpBn1BxD9 (accessed on 1 December 2022).
- Chen, X.; Liu, M.; Gilson, M.K. BindingDB: A web-accessible molecular recognition database. Comb. Chem. High Throughput Screen. 2001, 4, 719–725. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Lin, Y.; Liu, M.; Gilson, M.K. The Binding Database: Data management and interface design. Bioinformatics 2002, 18, 130–139. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Lin, Y.; Wen, X.; Jorissen, R.N.; Gilson, M.K. BindingDB: A web-accessible database of experimentally determined protein–ligand binding affinities. Nucleic Acids Res. 2007, 35, D198–D201. [Google Scholar] [CrossRef] [PubMed]
- Falsini, M.; Catarzi, D.; Varano, F.; Dal Ben, D.; Marucci, G.; Buccioni, M.; Volpini, R.; Di Cesare Mannelli, L.; Ghelardini, C.; Colotta, V. Novel 8-amino-1,2,4-triazolo[4,3-a]pyrazin-3-one derivatives as potent human adenosine A1 and A2A receptor antagonists. Evaluation of their protective effect against β-amyloid-induced neurotoxicity in SH-SY5Y cells. Bioorganic Chem. 2019, 87, 380–394. [Google Scholar] [CrossRef]
- Ceni, C.; Catarzi, D.; Varano, F.; Ben, D.D.; Marucci, G.; Buccioni, M.; Volpini, R.; Angeli, A.; Nocentini, A.; Gratteri, P.; et al. Discovery of first-in-class multi-target adenosine A2A receptor antagonists-carbonic anhydrase IX and XII inhibitors. 8-Amino-6-aryl-2-phenyl-1,2,4-triazolo [4,3-a]pyrazin-3-one derivatives as new potential antitumor agents. Eur. J. Med. Chem. 2020, 201, 112478. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 1 June 2020).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014. [Google Scholar] [CrossRef]
- Brown, N.; Cambruzzi, J.; Cox, P.J.; Davies, M.; Dunbar, J.; Plumbley, D.; Sellwood, M.A.; Sim, A.; Williams-Jones, B.I.; Zwierzyna, M.; et al. Big Data in Drug Discovery. Prog. Med. Chem. 2018, 57, 277–356. [Google Scholar] [CrossRef]
- Brown, N.; Fiscato, M.; Segler, M.H.; Vaucher, A.C. GuacaMol: Benchmarking Models for de Novo Molecular Design. J. Chem. Inf. Model. 2019, 59, 1096–1108. [Google Scholar] [CrossRef]
| Database | Number of Complexes | Mean Affinity | Mean Docking Score (*) |
|---|---|---|---|
| Experimental | 2408 | 5.98 () | |
| Computer generated | 28,200 | 7.48 () | 11.43 |
| Protein | 5HT2A | A2A | BACE1 | DOP | FAAH | GR | H1 | JAK1 | PI3K |
| N. of complexes | 2763 | 2914 | 1413 | 1243 | 508 | 843 | 1070 | 1213 | 1064 |
| Protein | PIM2 | ACE | KOP | M1 | MCL1 | JAK2 | OX2 | D2 | |
| N. of complexes | 384 | 488 | 2431 | 1056 | 688 | 1394 | 2160 | 6568 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pellicani, F.; Dal Ben, D.; Perali, A.; Pilati, S. Machine Learning Scoring Functions for Drug Discovery from Experimental and Computer-Generated Protein–Ligand Structures: Towards Per-Target Scoring Functions. Molecules 2023, 28, 1661. https://doi.org/10.3390/molecules28041661
Pellicani F, Dal Ben D, Perali A, Pilati S. Machine Learning Scoring Functions for Drug Discovery from Experimental and Computer-Generated Protein–Ligand Structures: Towards Per-Target Scoring Functions. Molecules. 2023; 28(4):1661. https://doi.org/10.3390/molecules28041661
Chicago/Turabian StylePellicani, Francesco, Diego Dal Ben, Andrea Perali, and Sebastiano Pilati. 2023. "Machine Learning Scoring Functions for Drug Discovery from Experimental and Computer-Generated Protein–Ligand Structures: Towards Per-Target Scoring Functions" Molecules 28, no. 4: 1661. https://doi.org/10.3390/molecules28041661
APA StylePellicani, F., Dal Ben, D., Perali, A., & Pilati, S. (2023). Machine Learning Scoring Functions for Drug Discovery from Experimental and Computer-Generated Protein–Ligand Structures: Towards Per-Target Scoring Functions. Molecules, 28(4), 1661. https://doi.org/10.3390/molecules28041661









