Conformational Dynamics and Stability of Bilayers Formed by Mycolic Acids from the Mycobacterium tuberculosis Outer Membrane
Abstract
1. Introduction
2. Results and Discussion
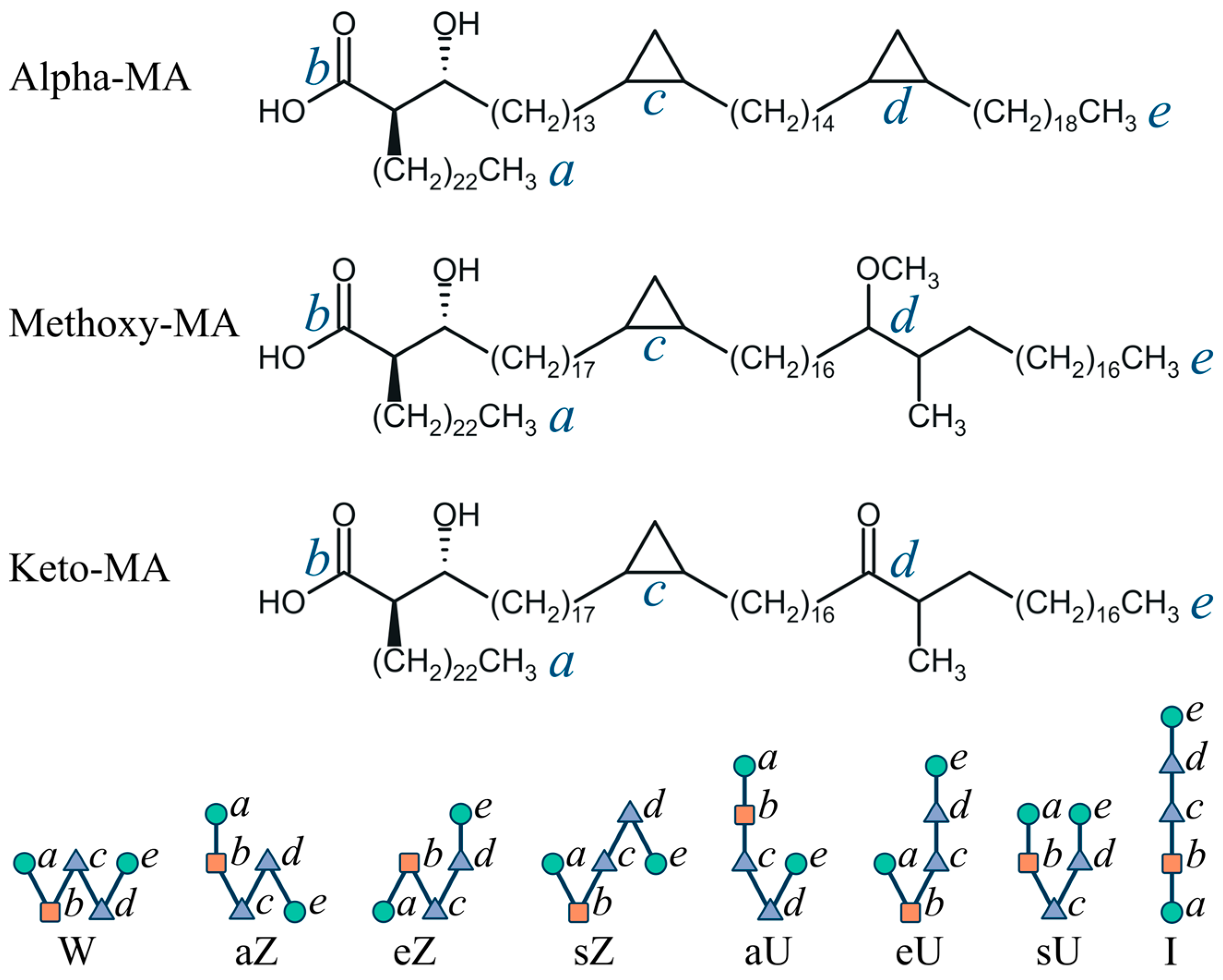
2.1. General Modeling Assumptions
2.2. Dynamic Conformational Diversity in Single-Component Membranes
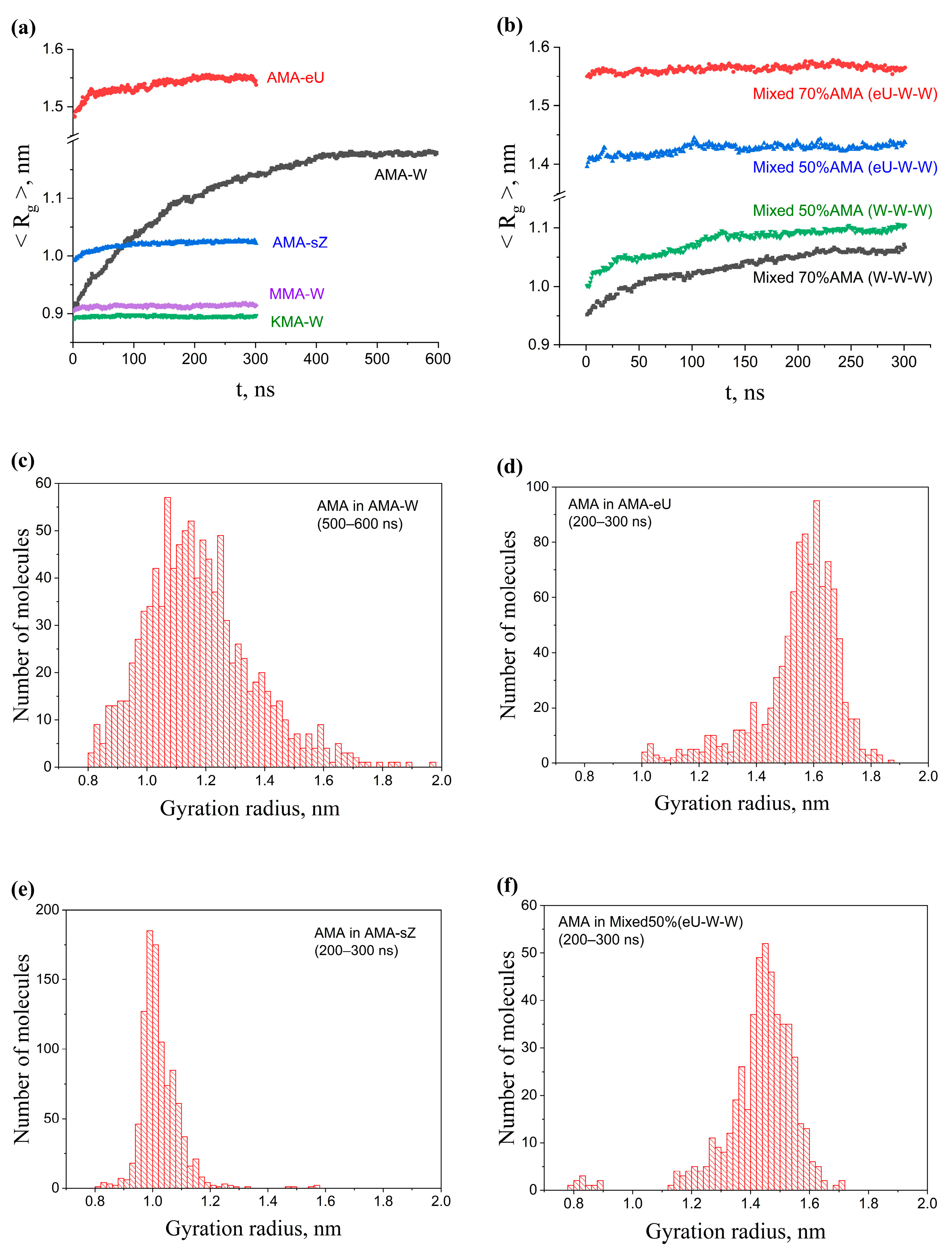
2.3. Influence of Composition and Initial Packing of Membranes on Gyration Radii of Molecules
2.4. Distribution of Molecular Shape Parameters
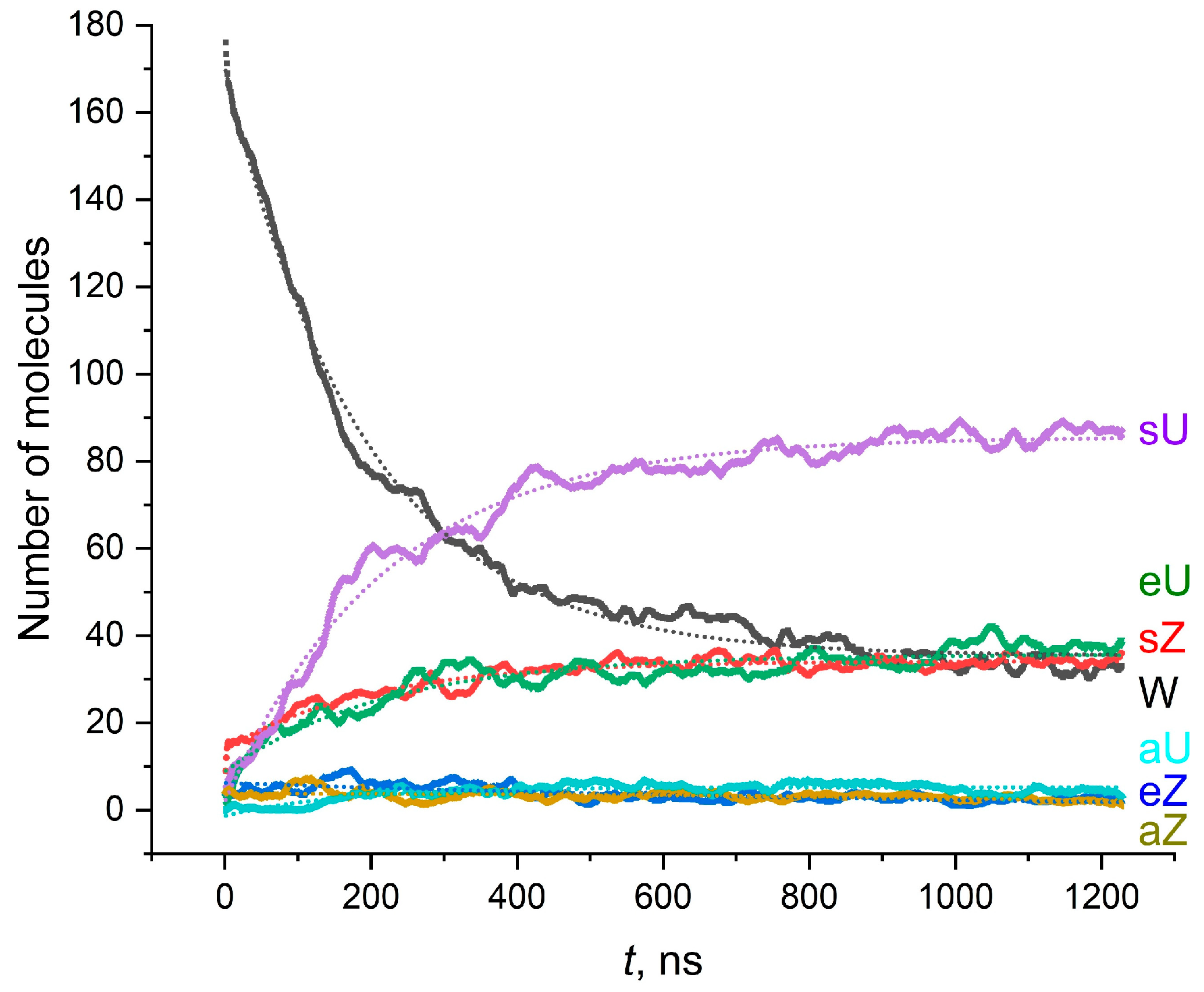
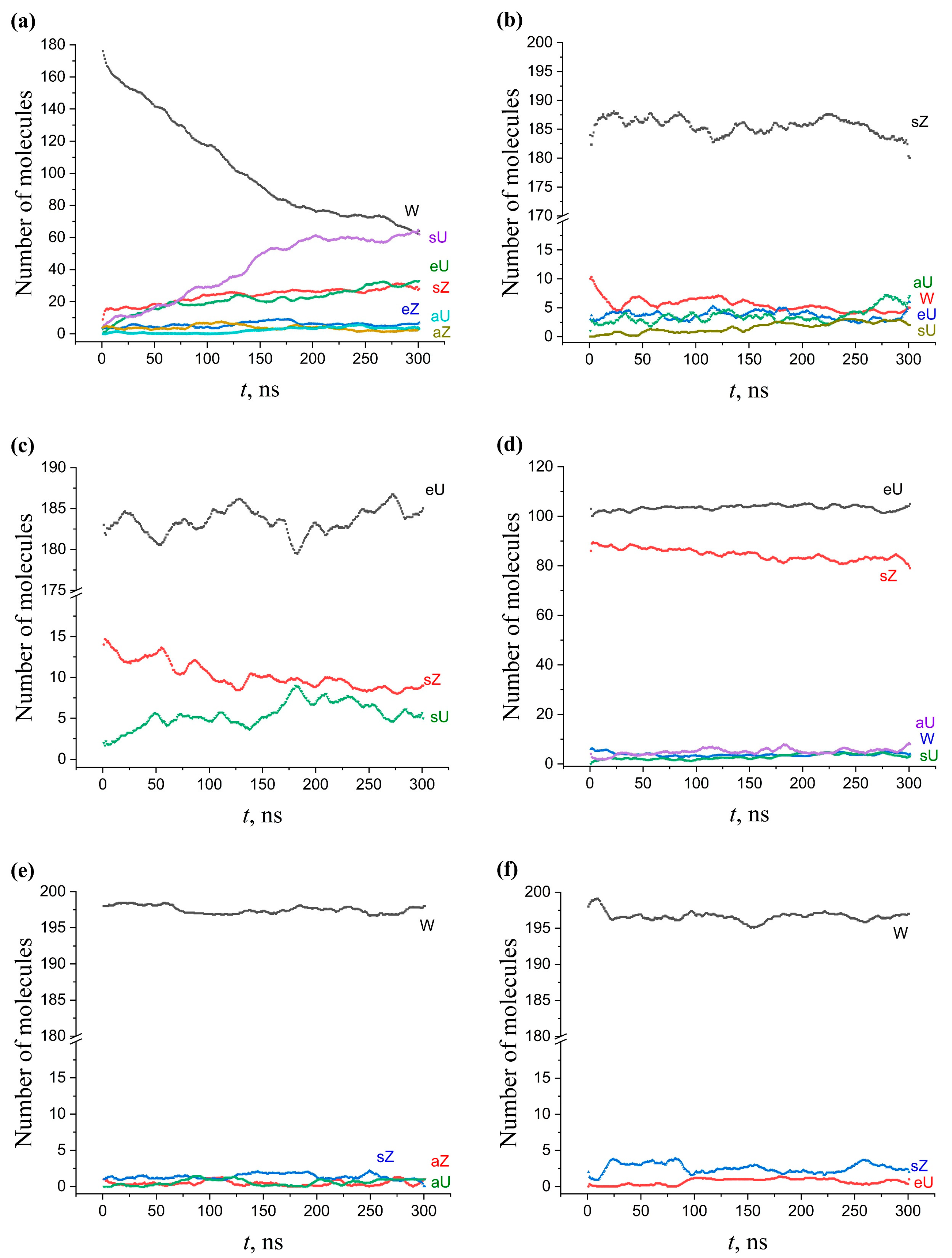
2.5. Kinetics of Conformation Changes in Membranes
2.5.1. Single-Component AMA Membranes
2.5.2. Single-Component KMA and MMA Membranes
2.5.3. Multicomponent Membranes
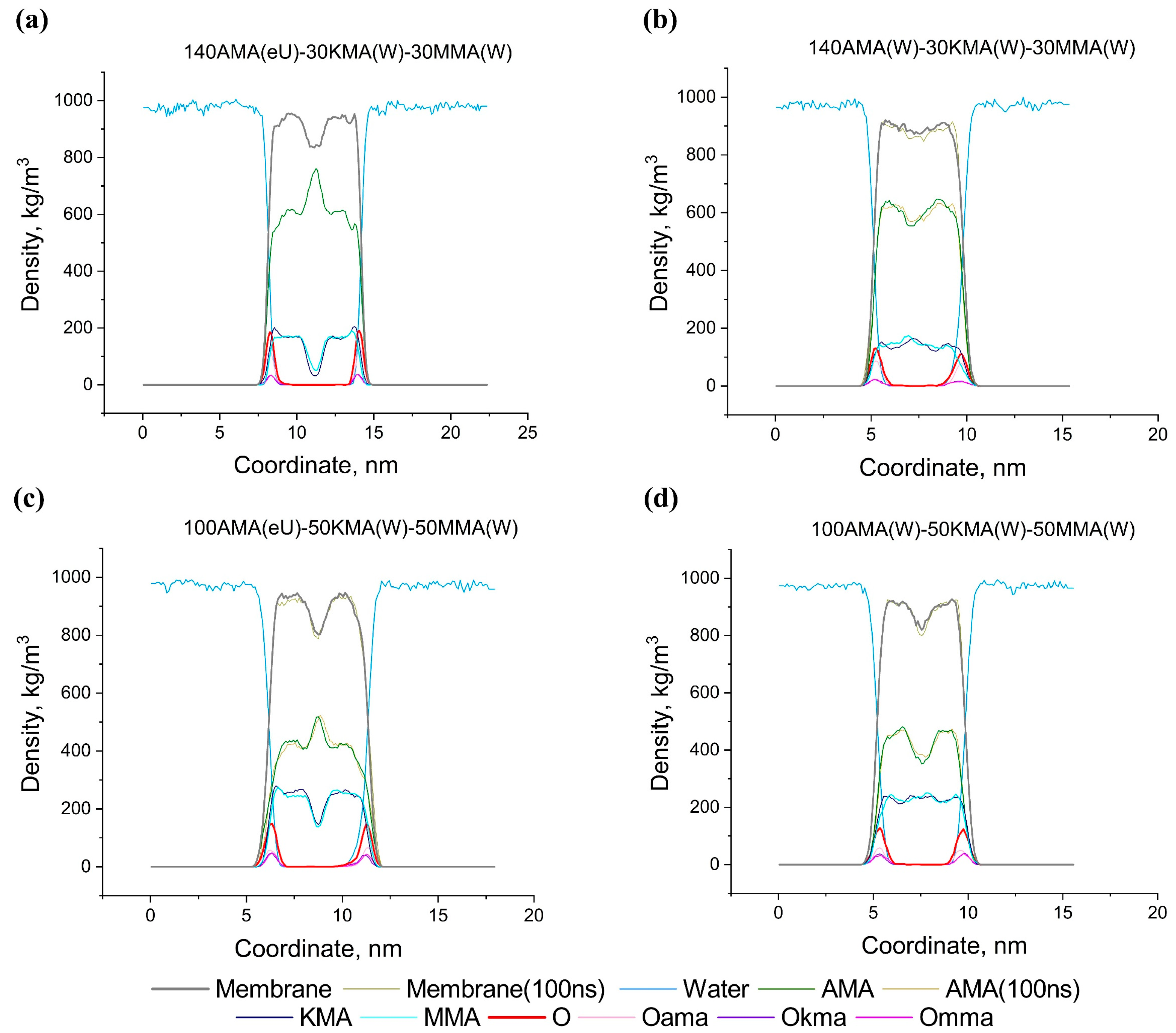
2.6. Effect of Structural Composition on the Thickness and Density of MA Membranes
3. Materials and Methods
3.1. Initial Membrane Structures
3.2. MD Simulation Protocols
3.3. Conformations of Mycolic Acids
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Friedrich, M.J. Tuberculosis Update 2017. JAMA 2017, 318, 2287. [Google Scholar] [CrossRef] [PubMed]
- Friedman, L.N.; Dedicoat, M.; Davies, P.D.O. (Eds.) Clinical Tuberculosis, 6th ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2020; ISBN 978-1-351-24998-0. [Google Scholar]
- Sharma, S.K.; Mohan, A. Textbook of Tuberculosis and Nontuberculous Mycobacterial Diseases; Third Edition; Jaypee Brothers Medical Publishers: New Delhi, India, 2020; ISBN 978-93-89129-21-2. [Google Scholar]
- World Health Organization. Global Tuberculosis Report 2022; World Health Organization: Geneva, Switerland, 2022; ISBN 978-92-4-006172-9. [Google Scholar]
- Chai, Q.; Zhang, Y.; Liu, C.H. Mycobacterium tuberculosis: An adaptable pathogen associated with multiple human diseases. Front. Cell. Infect. Microbiol. 2018, 8, 158. [Google Scholar] [CrossRef] [PubMed]
- Vincent, A.T.; Nyongesa, S.; Morneau, I.; Reed, M.B.; Tocheva, E.I.; Veyrier, F.J. The mycobacterial cell envelope: A relict from the past or the result of recent evolution? Front. Microbiol. 2018, 9, 2341. [Google Scholar] [CrossRef]
- Craggs, P.D.; de Carvalho, L.P.S. Bottlenecks and opportunities in antibiotic discovery against Mycobacterium tuberculosis. Curr. Opin. Microbiol. 2022, 69, 102191. [Google Scholar] [CrossRef] [PubMed]
- Bhat, Z.S.; Rather, M.A.; Maqbool, M.; Lah, H.U.; Yousuf, S.K.; Ahmad, Z. Cell wall: A versatile fountain of drug targets in Mycobacterium tuberculosis. Biomed. Pharmacother. 2017, 95, 1520–1534. [Google Scholar] [CrossRef]
- Dulberger, C.L.; Rubin, E.J.; Boutte, C.C. The mycobacterial cell envelope – a moving target. Nat. Rev. Microbiol. 2020, 18, 47–59. [Google Scholar] [CrossRef]
- Abrahams, K.A.; Besra, G.S. Synthesis and recycling of the mycobacterial cell envelope. Curr. Opin. Microbiol. 2021, 60, 58–65. [Google Scholar] [CrossRef]
- Kuang, W.; Zhang, H.; Wang, X.; Yang, P. Overcoming Mycobacterium tuberculosis through small molecule inhibitors to break down cell wall synthesis. Acta Pharm. Sin. B 2022, 12, 3201–3214. [Google Scholar] [CrossRef]
- Modak, B.; Girkar, S.; Narayan, R.; Kapoor, S. Mycobacterial membranes as actionable targets for lipid-centric therapy in tuberculosis. J. Med. Chem. 2022, 65, 3046–3065. [Google Scholar] [CrossRef]
- Batt, S.M.; Minnikin, D.E.; Besra, G.S. The thick waxy coat of mycobacteria, a protective layer against antibiotics and the host’s immune system. Biochem. J. 2020, 477, 1983–2006. [Google Scholar] [CrossRef]
- Marrakchi, H.; Lanéelle, M.-A.; Daffé, M. Mycolic acids: Structures, biosynthesis, and beyond. Chem. Biol. 2014, 21, 67–85. [Google Scholar] [CrossRef] [PubMed]
- Holzheimer, M.; Buter, J.; Minnaard, A.J. Chemical synthesis of cell wall constituents of Mycobacterium tuberculosis. Chem. Rev. 2021, 121, 9554–9643. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, M.; Aoyagi, Y.; Ridell, M.; Minnikin, D.E. Separation and characterization of individual mycolic acids in representative mycobacteria. Microbiology (Reading) 2001, 147, 1825–1837. [Google Scholar] [CrossRef]
- Takayama, K.; Wang, C.; Besra, G.S. Pathway to synthesis and processing of mycolic acids in Mycobacterium tuberculosis. Clin. Microbiol. Rev. 2005, 18, 81–101. [Google Scholar] [CrossRef] [PubMed]
- Villeneuve, M.; Kawai, M.; Watanabe, M.; Aoyagi, Y.; Hitotsuyanagi, Y.; Takeya, K.; Gouda, H.; Hirono, S.; Minnikin, D.E.; Nakahara, H. Differential conformational behaviors of α-mycolic acids in Langmuir monolayers and computer simulations. Chem. Phys. Lipids 2010, 163, 569–579. [Google Scholar] [CrossRef]
- Groenewald, W.; Bulacu, M.; Croft, A.; Marrink, S.-J. Molecular Dynamics of Mycolic Acid Monolayers. Available online: https://chemrxiv.org/engage/chemrxiv/article-details/60c740edbdbb897f9aa3823d (accessed on 8 January 2023).
- Groenewald, W.; Parra-Cruz, R.A.; Jäger, C.M.; Croft, A.K. Revealing solvent-dependent folding behavior of mycolic acids from Mycobacterium tuberculosis by advanced simulation analysis. J. Mol. Model. 2019, 25, 68. [Google Scholar] [CrossRef]
- Touchette, M.H.; Seeliger, J.C. Transport of outer membrane lipids in mycobacteria. Biochim. Biophys. Acta Mol. Cell. Biol. Lipids 2017, 1862, 1340–1354. [Google Scholar] [CrossRef] [PubMed]
- Radchenko, E.V.; Antonyan, G.V.; Ignatov, S.K.; Palyulin, V.A. Machine learning prediction of mycobacterial cell wall permeability of drugs and drug-like compounds. Molecules 2023, 28, 633. [Google Scholar] [CrossRef]
- Hoffmann, C.; Leis, A.; Niederweis, M.; Plitzko, J.M.; Engelhardt, H. Disclosure of the mycobacterial outer membrane: Cryo-electron tomography and vitreous sections reveal the lipid bilayer structure. Proc. Natl. Acad. Sci. USA 2008, 105, 3963–3967. [Google Scholar] [CrossRef]
- Zuber, B.; Chami, M.; Houssin, C.; Dubochet, J.; Griffiths, G.; Daffé, M. Direct visualization of the outer membrane of mycobacteria and corynebacteria in their native state. J. Bacteriol. 2008, 190, 5672–5680. [Google Scholar] [CrossRef]
- Nikaido, H.; Kim, S.H.; Rosenberg, E.Y. Physical organization of lipids in the cell wall of Mycobacterium chelonae. Mol. Microbiol. 1993, 8, 1025–1030. [Google Scholar] [CrossRef] [PubMed]
- Villeneuve, M.; Kawai, M.; Horiuchi, K.; Watanabe, M.; Aoyagi, Y.; Hitotsuyanagi, Y.; Takeya, K.; Gouda, H.; Hirono, S.; Minnikin, D.E. Conformational folding of mycobacterial methoxy- and ketomycolic acids facilitated by α-methyl trans-cyclopropane groups rather than cis-cyclopropane units. Microbiology 2013, 159, 2405–2415. [Google Scholar] [CrossRef] [PubMed]
- Hong, X.; Hopfinger, A.J. Construction, molecular modeling, and simulation of Mycobacterium tuberculosis cell walls. Biomacromolecules 2004, 5, 1052–1065. [Google Scholar] [CrossRef]
- Rawdon, E.J.; Kern, J.C.; Piatek, M.; Plunkett, P.; Stasiak, A.; Millett, K.C. Effect of knotting on the shape of polymers. Macromolecules 2008, 41, 8281–8287. [Google Scholar] [CrossRef]
- des Cloizeaux, J.; Jannink, G. Polymers in Solution: Their Modelling and Structure; Reprint edition; Oxford University Press: Oxford, UK, 1991; ISBN 0-19-852036-0. [Google Scholar]
- Huang, J.; MacKerell, A.D. CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. J. Comput. Chem. 2013, 34, 2135–2145. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Corradi, V.; Souza, P.C.T.; Ingólfsson, H.I.; Tieleman, D.P.; Sansom, M.S.P. Computational modeling of realistic cell membranes. Chem. Rev. 2019, 119, 6184–6226. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Cheng, X.; Swails, J.M.; Yeom, M.S.; Eastman, P.K.; Lemkul, J.A.; Wei, S.; Buckner, J.; Jeong, J.C.; Qi, Y.; et al. CHARMM-GUI input generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM simulations using the CHARMM36 additive force field. J. Chem. Theory Comput. 2016, 12, 405–413. [Google Scholar] [CrossRef]
- Jo, S.; Cheng, X.; Lee, J.; Kim, S.; Park, S.-J.; Patel, D.S.; Beaven, A.H.; Lee, K.I.; Rui, H.; Park, S.; et al. CHARMM-GUI 10 years for biomolecular modeling and simulation. J. Comput. Chem. 2017, 38, 1114–1124. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Tribello, G.A.; Bonomi, M.; Branduardi, D.; Camilloni, C.; Bussi, G. PLUMED 2: New feathers for an old bird. Comput. Phys. Commun. 2014, 185, 604–613. [Google Scholar] [CrossRef]
- PLUMED consortium Promoting transparency and reproducibility in enhanced molecular simulations. Nat. Methods 2019, 16, 670–673. [CrossRef] [PubMed]
- Avdoshin, A.A. Membrane Creation and Analysis. Available online: https://github.com/hydrazine114/membrana (accessed on 15 January 2023).


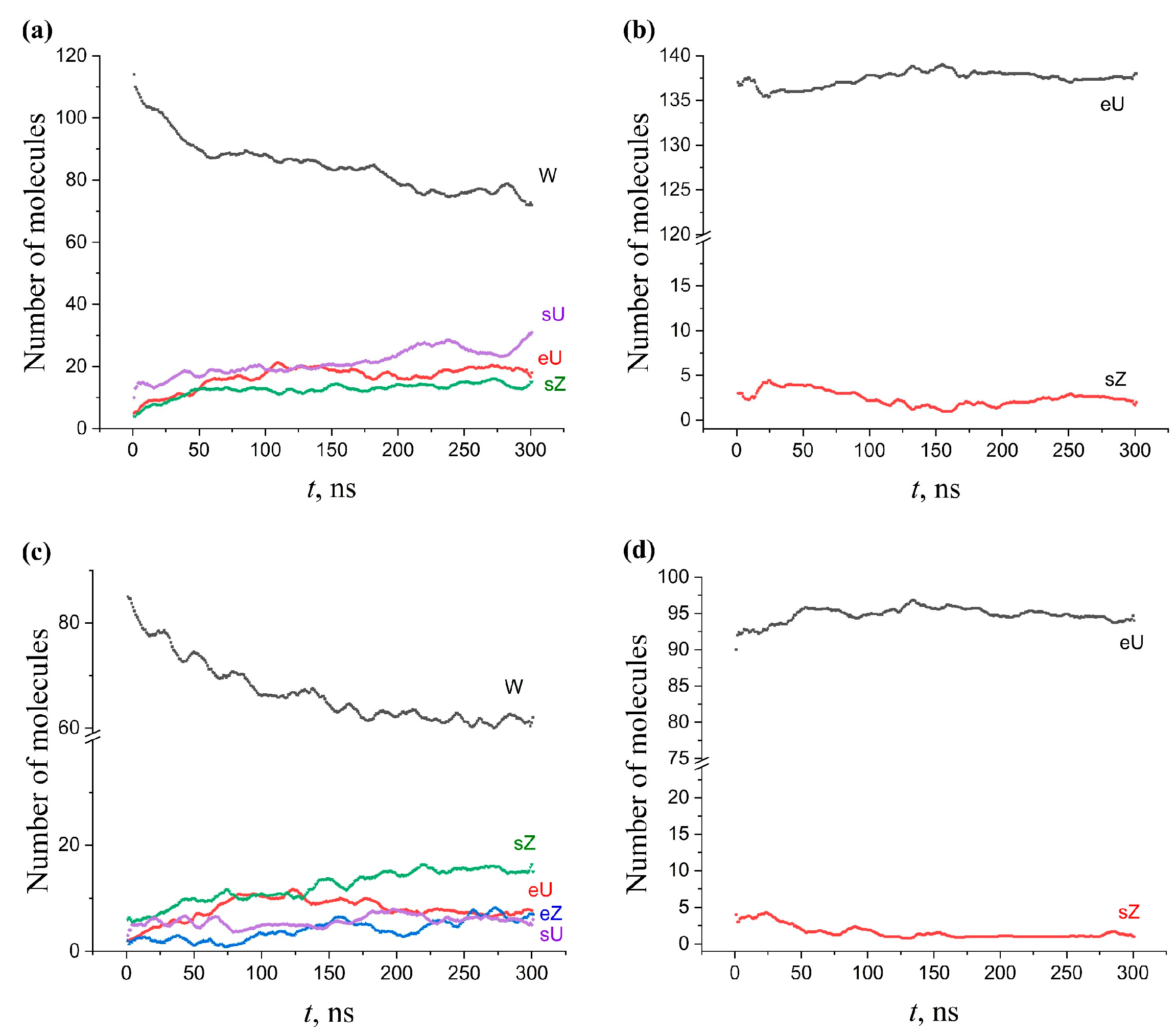


| Most Abundant Conformations * | |||||
|---|---|---|---|---|---|
| W | sZ | eU | sU | aU | |
| Final number of molecules | 33 | 36 | 38 | 87 | 3 |
| Equilibrium number of molecules | 35.3 ± 0.1 | 34.2 ± 0.1 | 35.6 ± 0.1 | 85.6 ± 0.1 | 5.25 ± 0.04 |
| Equilibrium fraction of molecules | 0.177 | 0.171 | 0.178 | 0.428 | 0.027 |
| Characteristic time of accumulation/decay , ns | 192 ± 0.1 | 198.5 ± 3.6 | 222.6 ± 5.8 | 220.1 ± 2.1 | 160.7 ± 6.6 |
| Pre-exponential coefficient | 135.0 ± 0.4 | −20.2 ± 0.2 | −26.8 ± 0.3 | −83.6 ± 0.4 | −6.6 ± 0.2 |
| Rate constant of accumulation/decay , s–1 | 5.20 | 5.04 | 4.49 | 4.54 | 6.22 |
| Coefficient of determination | 0.991 | 0.924 | 0.863 | 0.979 | 0.684 |
| Membrane | Thickness, nm | Density, kg/m3 | Surface Density, Molecules/nm2 |
|---|---|---|---|
| AMA-W | 4.4 | 857.5 | 2.16 |
| AMA-W (1200 ns) | 4.4 | 862.7 | 2.16 |
| AMA-eU | 7.8 | 907.3 | 3.84 |
| AMA-sZ | 5.9 | 891.5 | 2.93 |
| AMA-(sZ+eU) | 5.6 | 865.6 | 2.69 |
| KMA-W | 5.1 | 901.3 | 2.31 |
| MMA-W | 5.3 | 893.9 | 2.40 |
| 140eU–30W–30W 1 | 5.9 | 898.2 | 2.86 |
| 140W–30W–30W 1 | 4.6 | 861.8 | 2.17 |
| 100eU–50W–50W 1 | 5.0 | 876.8 | 2.38 |
| 100W–50W–50W 1 | 4.5 | 865.6 | 2.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savintseva, L.A.; Steshin, I.S.; Avdoshin, A.A.; Panteleev, S.V.; Rozhkov, A.V.; Shirokova, E.A.; Livshits, G.D.; Vasyankin, A.V.; Radchenko, E.V.; Ignatov, S.K.; et al. Conformational Dynamics and Stability of Bilayers Formed by Mycolic Acids from the Mycobacterium tuberculosis Outer Membrane. Molecules 2023, 28, 1347. https://doi.org/10.3390/molecules28031347
Savintseva LA, Steshin IS, Avdoshin AA, Panteleev SV, Rozhkov AV, Shirokova EA, Livshits GD, Vasyankin AV, Radchenko EV, Ignatov SK, et al. Conformational Dynamics and Stability of Bilayers Formed by Mycolic Acids from the Mycobacterium tuberculosis Outer Membrane. Molecules. 2023; 28(3):1347. https://doi.org/10.3390/molecules28031347
Chicago/Turabian StyleSavintseva, Liana A., Ilya S. Steshin, Alexander A. Avdoshin, Sergey V. Panteleev, Alexey V. Rozhkov, Ekaterina A. Shirokova, Grigory D. Livshits, Alexander V. Vasyankin, Eugene V. Radchenko, Stanislav K. Ignatov, and et al. 2023. "Conformational Dynamics and Stability of Bilayers Formed by Mycolic Acids from the Mycobacterium tuberculosis Outer Membrane" Molecules 28, no. 3: 1347. https://doi.org/10.3390/molecules28031347
APA StyleSavintseva, L. A., Steshin, I. S., Avdoshin, A. A., Panteleev, S. V., Rozhkov, A. V., Shirokova, E. A., Livshits, G. D., Vasyankin, A. V., Radchenko, E. V., Ignatov, S. K., & Palyulin, V. A. (2023). Conformational Dynamics and Stability of Bilayers Formed by Mycolic Acids from the Mycobacterium tuberculosis Outer Membrane. Molecules, 28(3), 1347. https://doi.org/10.3390/molecules28031347






