Ternary Mixtures of Hard Spheres and Their Multiple Separated Phases
Abstract
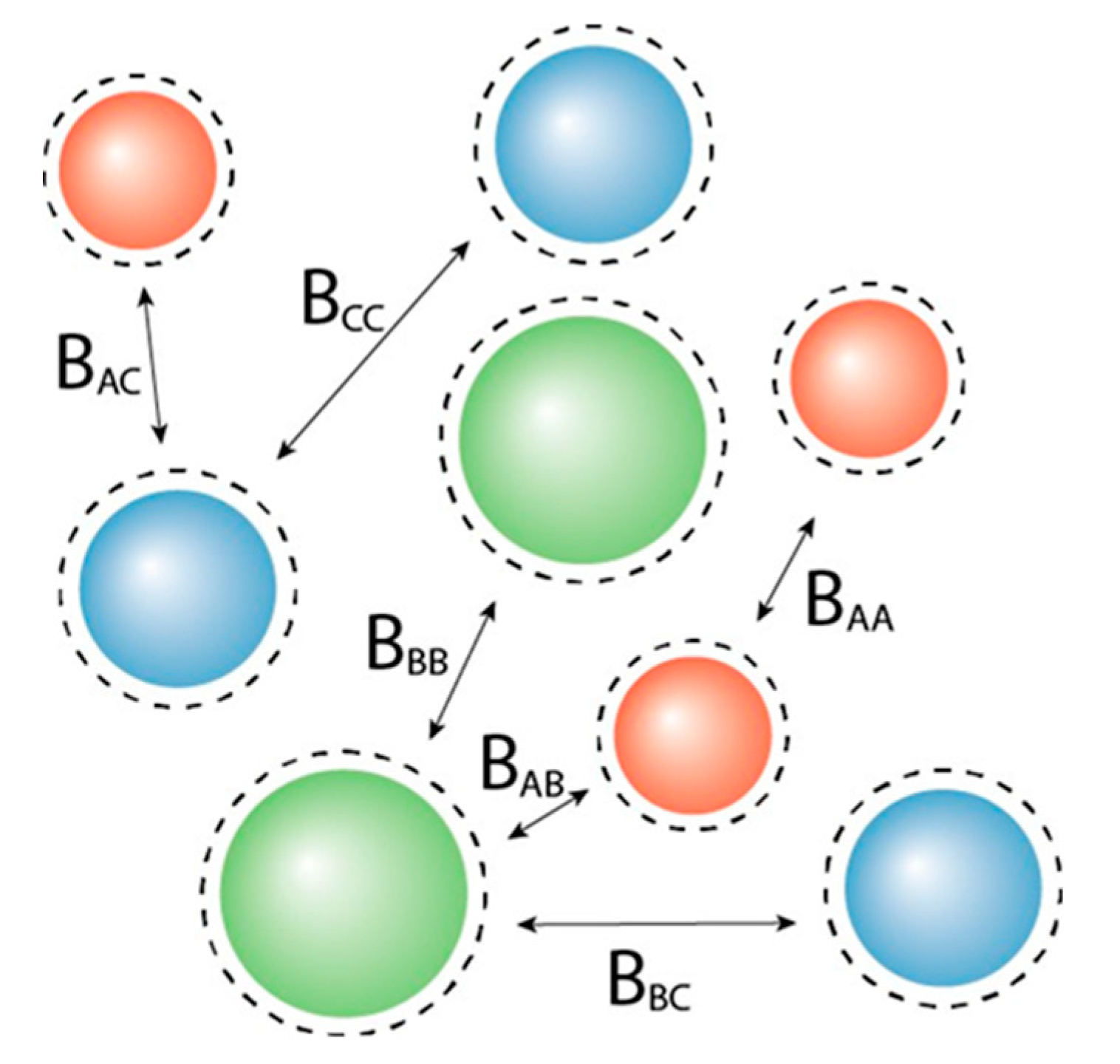
1. Introduction
2. Theory
2.1. Osmotic Virial Coefficient
2.2. Stability of a Mixture
2.3. Plait Points
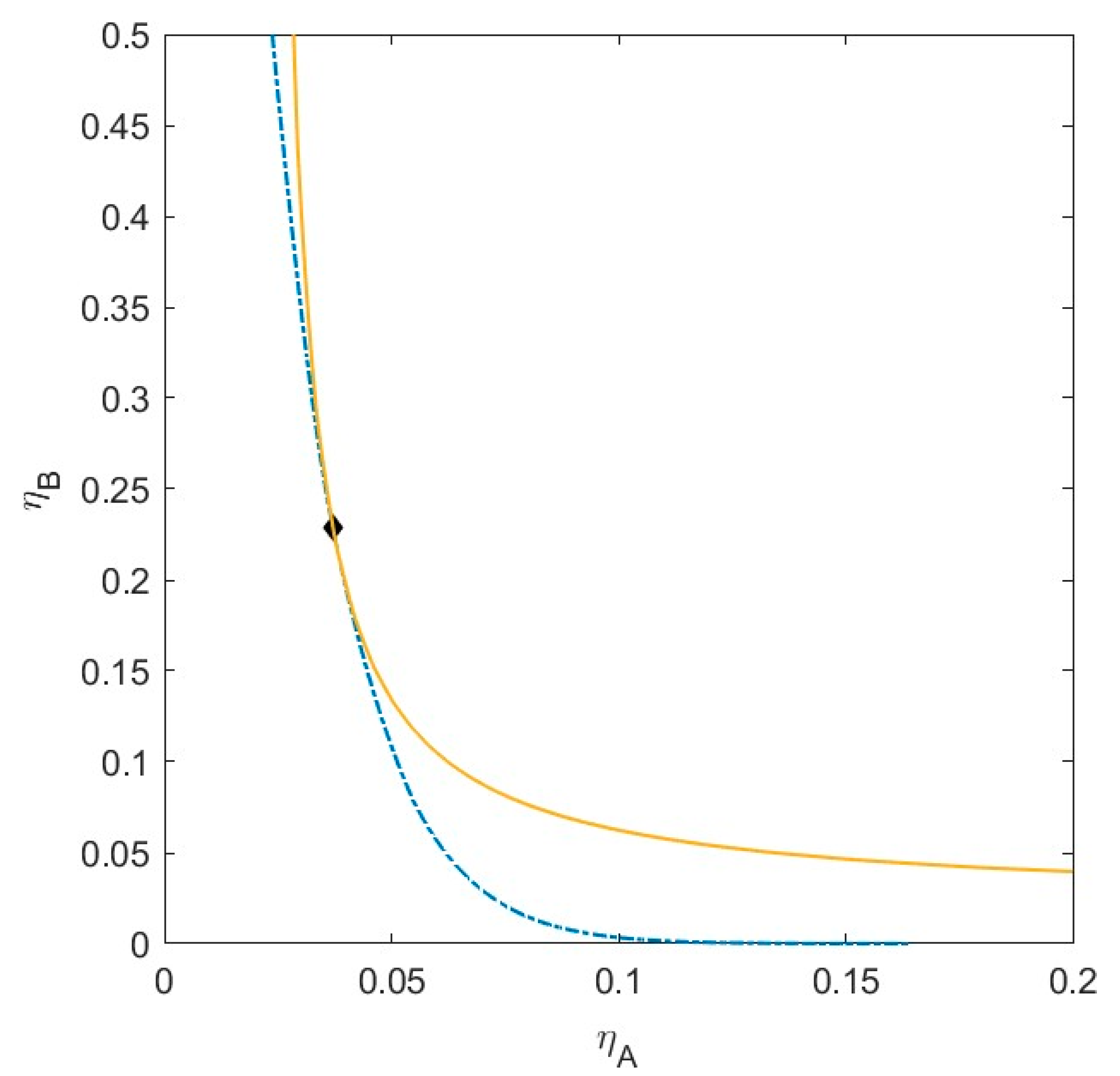
2.4. Phase Boundary
3. Results and Discussion
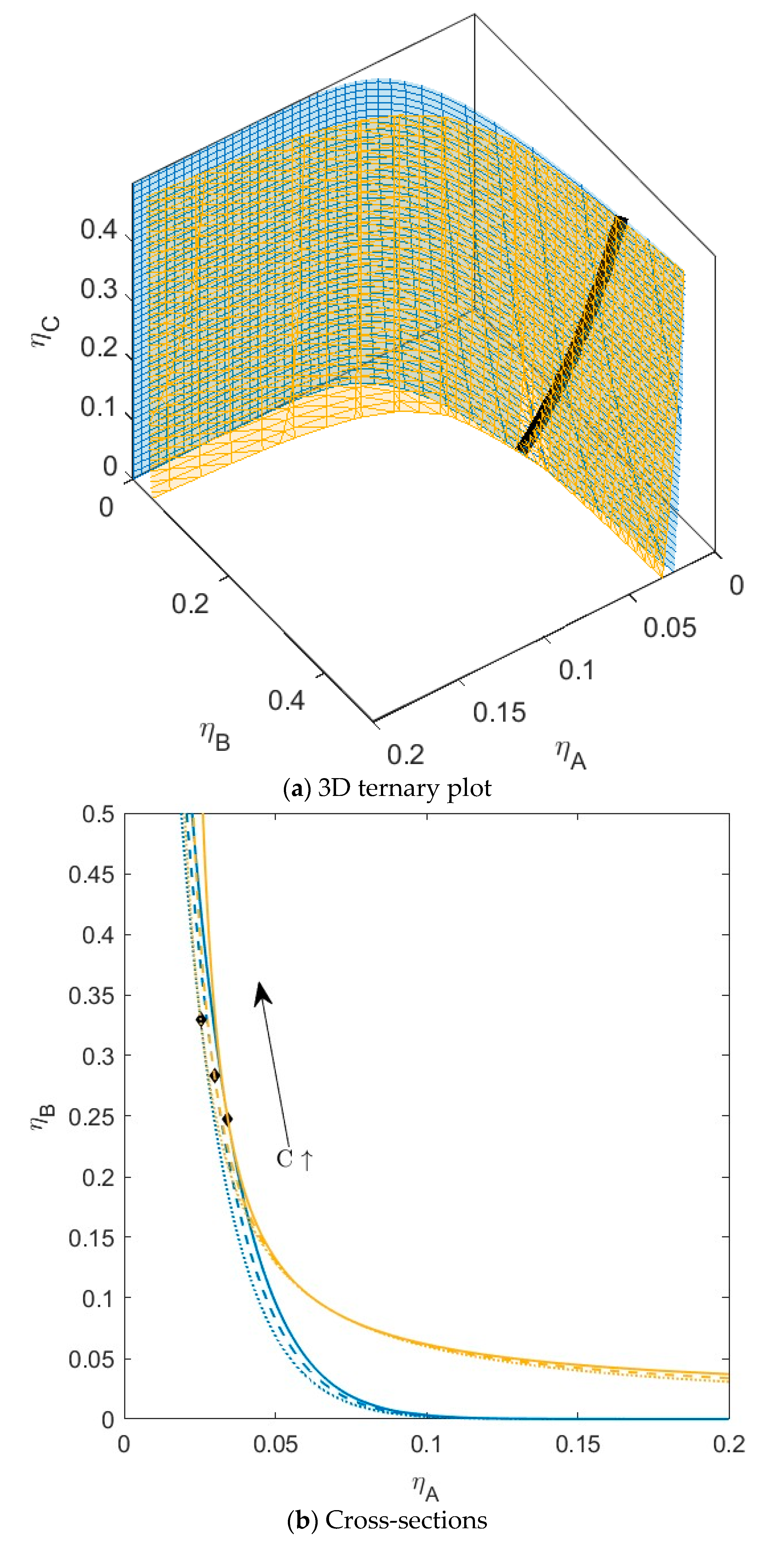
3.1. C Compatible with Both A and B
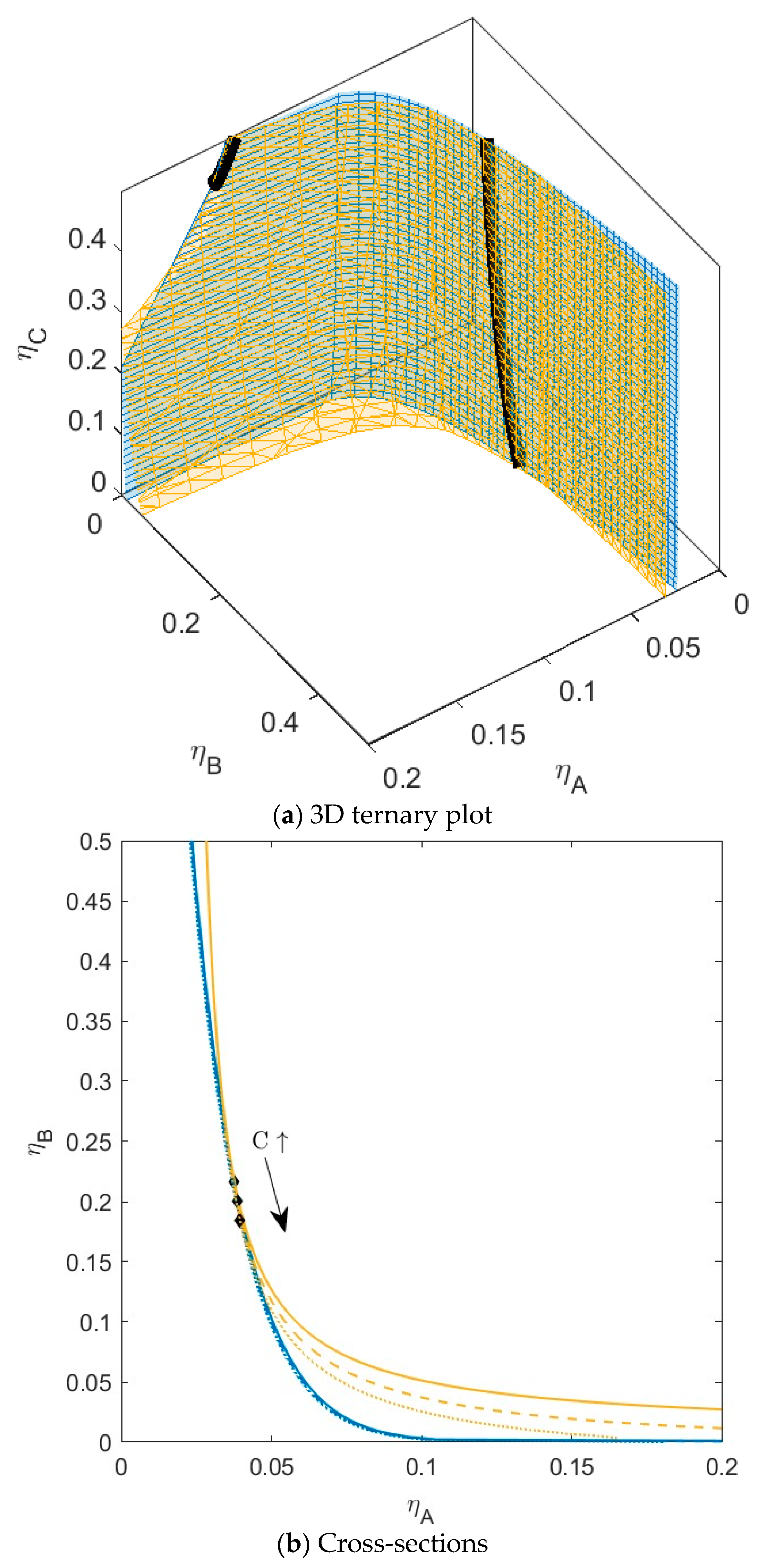
3.2. C Compatible with A or B and Incompatible with the Other One
3.3. C Incompatible with Both A and B
3.4. Fractionation
4. Three-Phase Systems
5. Conclusions
Supplementary Materials
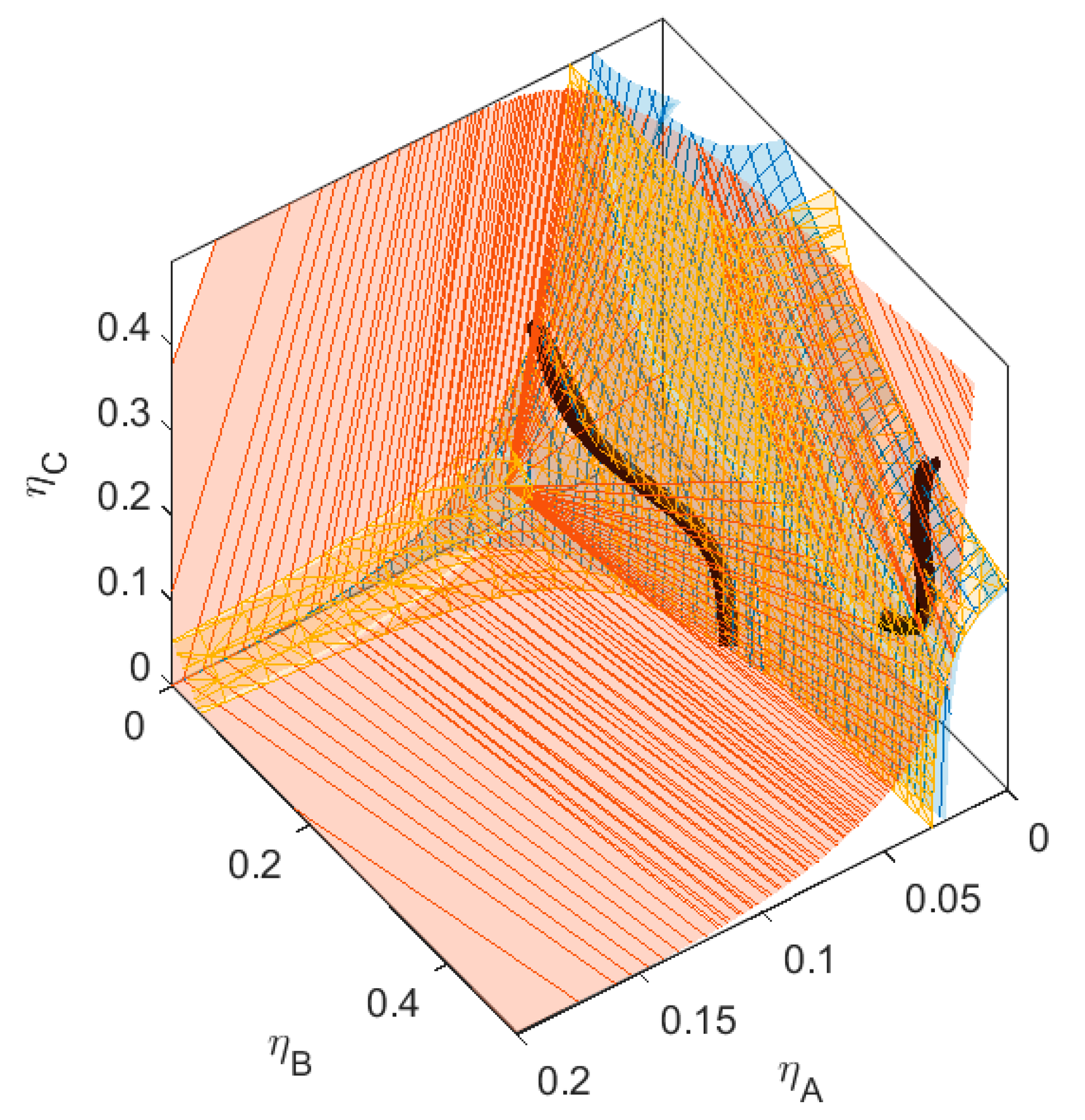
 A is red,
A is red,  B is green,
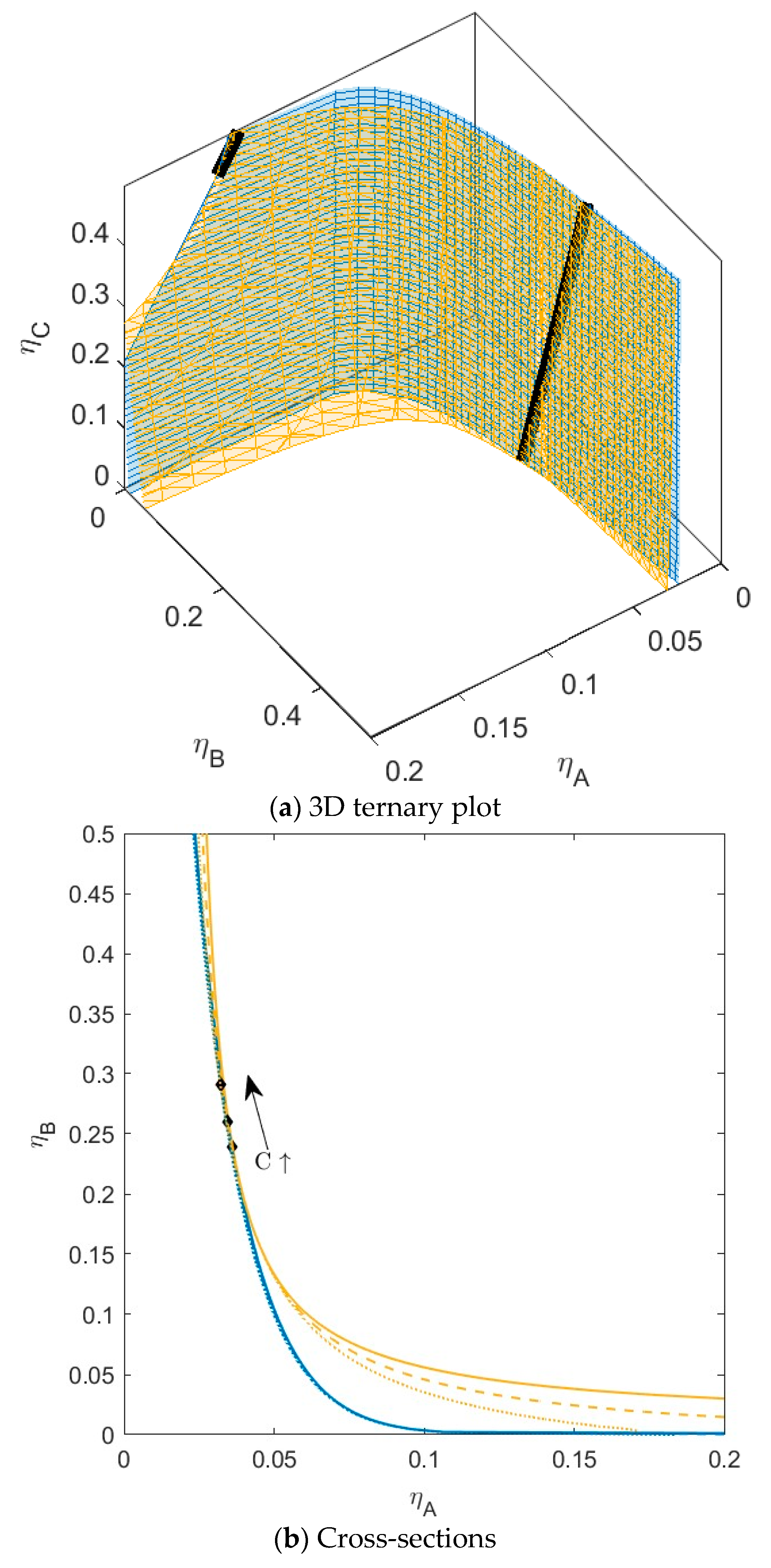
B is green,  C is blue. Figure S2: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = −0.1, and ∆BC = 0, fixed parent phase: η(0.05, 0.20, 0.10),
C is blue. Figure S2: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = −0.1, and ∆BC = 0, fixed parent phase: η(0.05, 0.20, 0.10),  A is red,
A is red,  B is green,
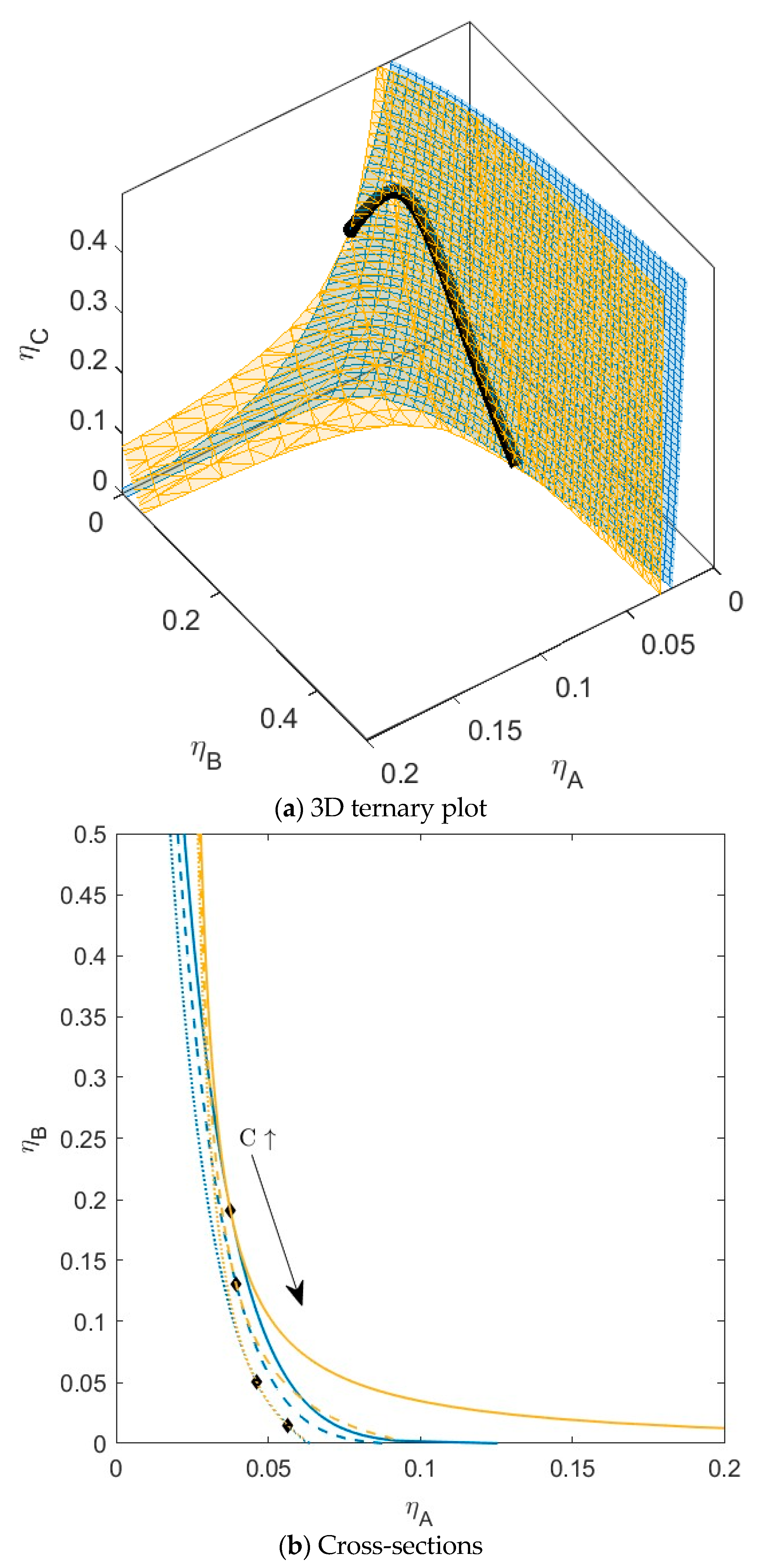
B is green,  C is blue. Figure S3: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = 0, and ∆BC = −0.1, fixed parent phase: η(0.05, 0.20, 0.10),
C is blue. Figure S3: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = 0, and ∆BC = −0.1, fixed parent phase: η(0.05, 0.20, 0.10),  A is red,
A is red,  B is green,
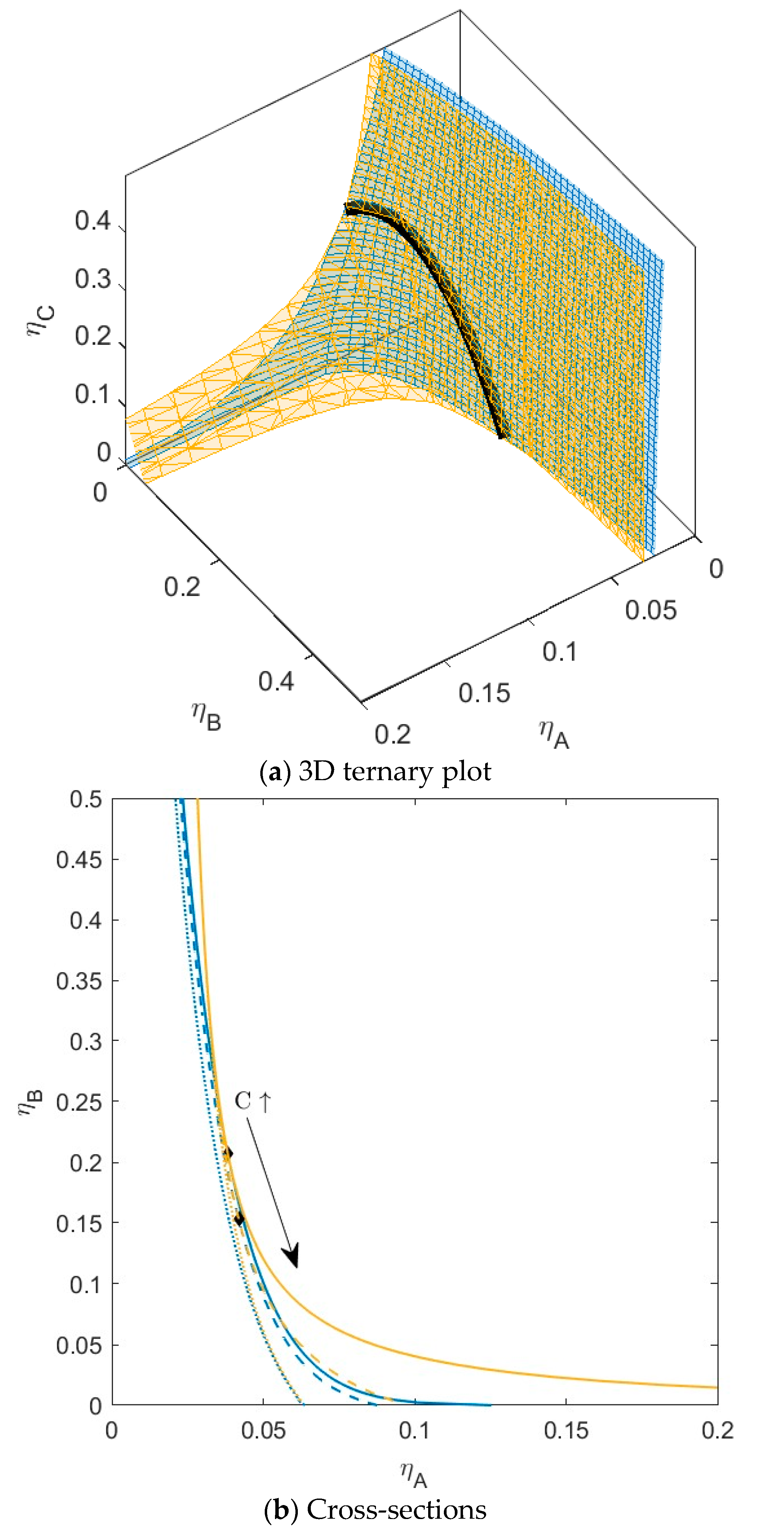
B is green,  C is blue. Figure S4: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = 0, and ∆BC = 0, fixed parent phase: η(0.05, 0.20, 0.10), adjusting A, B, resp. C with η = 0.01,
C is blue. Figure S4: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = 0, and ∆BC = 0, fixed parent phase: η(0.05, 0.20, 0.10), adjusting A, B, resp. C with η = 0.01,  A is red,
A is red,  B is green, and
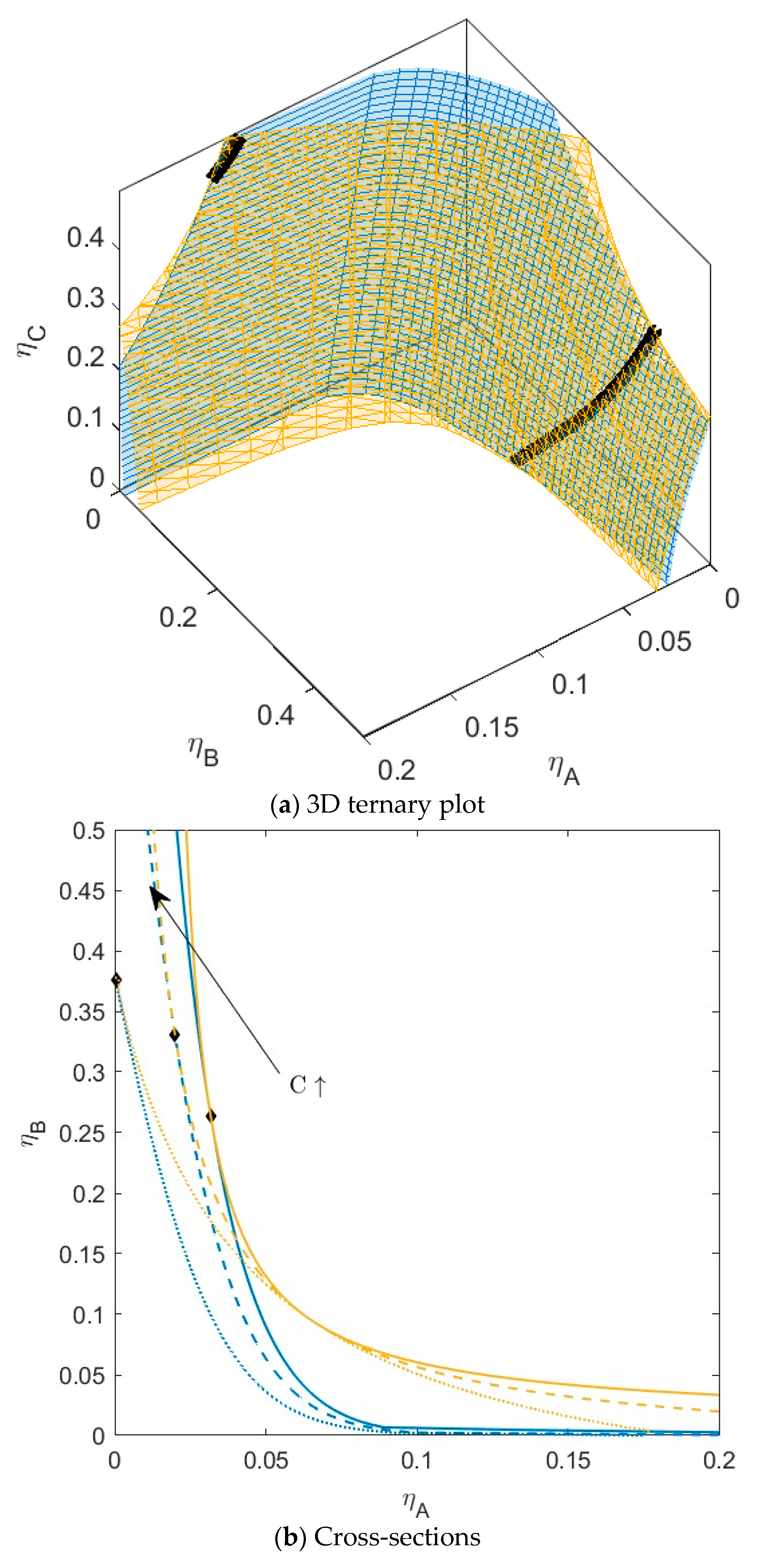
B is green, and  C is blue. Figure S5: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = 0.1, and ∆BC = −0.1, fixed parent phase: η(0.05, 0.20, 0.10), adjusting A, B, resp. C with η = 0.01,
C is blue. Figure S5: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = 0.1, and ∆BC = −0.1, fixed parent phase: η(0.05, 0.20, 0.10), adjusting A, B, resp. C with η = 0.01,  A is red,
A is red,  B is green, and
B is green, and  C is blue. Figure S6: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard spheremixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = 0.1, and ∆BC = 0, fixed parent phase: η(0.05, 0.20, 0.10), adjusting A, B, resp. C with η = 0.01,
C is blue. Figure S6: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard spheremixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = 0.1, and ∆BC = 0, fixed parent phase: η(0.05, 0.20, 0.10), adjusting A, B, resp. C with η = 0.01,  A is red,
A is red,  B is green, and
B is green, and  C is blue. Figure S7: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = −0.1, and ∆BC = 0.1, fixed parent phase: η(0.05, 0.20, 0.10), adjusting A, B, resp. C with η = 0.01,
C is blue. Figure S7: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = −0.1, and ∆BC = 0.1, fixed parent phase: η(0.05, 0.20, 0.10), adjusting A, B, resp. C with η = 0.01,  A is red,
A is red,  B is green, and
B is green, and  C is blue. Figure S8: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = 0, and ∆BC = 0.1, fixed parent phase: η(0.05, 0.20, 0.10), adjusting A, B, resp. C with η = 0.01,
C is blue. Figure S8: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = 0, and ∆BC = 0.1, fixed parent phase: η(0.05, 0.20, 0.10), adjusting A, B, resp. C with η = 0.01,  A is red,
A is red,  B is green, and
B is green, and  C is blue. Figure S9: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = 0.1, and ∆BC = 0.1, fixed parent phase: η(0.05, 0.20, 0.10), adjusting A, B, resp. C with η = 0.01,
C is blue. Figure S9: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixture with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC = 0.1, and ∆BC = 0.1, fixed parent phase: η(0.05, 0.20, 0.10), adjusting A, B, resp. C with η = 0.01,  A is red,
A is red,  B is green, and
B is green, and  C is blue. Table S1: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixtures with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC and ∆BC varying from −0.1 to 0.1, label referring to Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, fixed parent phase: η(0.05, 0.20, 0.10), see also Figure 12a. Table S2: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixtures with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC and ∆BC variying from −0.1 to 0.1, label refering to Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, fixed parent phase: η(0.05, 0.20, 0.25), see also Figure 12b. Table S3: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixtures with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC and ∆BC variying from −0.1 to 0.1, label refering to Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, fixed parent phase: η(0.10, 0.20, 0.10), see also Figure 13a. Table S4: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixtures with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC and ∆BC variying from −0.1 to 0.1, label refering to Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, fixed parent phase: η(0.05, 0.10, 0.10), see also Figure 13b.
C is blue. Table S1: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixtures with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC and ∆BC varying from −0.1 to 0.1, label referring to Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, fixed parent phase: η(0.05, 0.20, 0.10), see also Figure 12a. Table S2: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixtures with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC and ∆BC variying from −0.1 to 0.1, label refering to Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, fixed parent phase: η(0.05, 0.20, 0.25), see also Figure 12b. Table S3: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixtures with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC and ∆BC variying from −0.1 to 0.1, label refering to Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, fixed parent phase: η(0.10, 0.20, 0.10), see also Figure 13a. Table S4: Fractionation of monodisperse ternary (component A, B, and C) non-additive hard sphere mixtures with size ratio qAB = σA/σB = 1/4 and qAC = σA/σC = 1/3, with non-additivity parameters: ∆AB = 0.1, ∆AC and ∆BC variying from −0.1 to 0.1, label refering to Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, fixed parent phase: η(0.05, 0.10, 0.10), see also Figure 13b.Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chu, X.L.; Nikolov, A.D.; Wasan, D.T. Effects of Particle Size and Polydispersity on the Depletion and Structural Forces in Colloidal Dispersions. Langmuir 1996, 12, 5004–5010. [Google Scholar] [CrossRef]
- Edelman, M.W.; van der Linden, E.; de Hoog, E.; Tromp, R.H. Compatibility of Gelatin and Dextran in Aqueous Solution. Biomacromolecules 2001, 2, 1148–1154. [Google Scholar] [CrossRef] [PubMed]
- Edelman, M.W.; van der Linden, E.; Tromp, R.H. Phase Separation of Aqueous Mixtures of Poly(ethylene oxide) and Dextran. Macromolecules 2003, 36, 7783–7790. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Q.; Ji, X.; Dimova, R.; Lipowsky, R.; Liu, Y. Molar mass fractionation in aqueous two-phase polymer solutions of dextran and poly(ethylene glycol). J. Chromatogr. A 2016, 1452, 107–115. [Google Scholar] [CrossRef] [PubMed]
- Ji, S.; Walz, J.Y. Interaction potentials between two colloidal particles surrounded by an extremely bidisperse particle suspension. J. Colloid Interface Sci. 2013, 394, 611–618. [Google Scholar] [CrossRef] [PubMed]
- Park, N.; Conrad, J.C. Phase behavior of colloid–polymer depletion mixtures with unary or binary depletants. Soft Matter 2017, 13, 2781–2792. [Google Scholar] [CrossRef]
- Albertsson, P.; Birkenmeier, G. Affinity separation of proteins in aqueous three-phase systems. Anal. Biochem. 1988, 175, 154–161. [Google Scholar] [CrossRef]
- Hartman, A.; Johansson, G.; Albertsson, P.-A. Partition of Proteins in a Three-Phase System. JBIC J. Biol. Inorg. Chem. 1974, 46, 75–81. [Google Scholar] [CrossRef]
- Ruan, K.; Wang, B.; Xiao, J.; Tang, J. Interfacial Tension of Aqueous Three? Phase Systems Formed by Triton X?100/PEG/Dextran. J. Dispers. Sci. Technol. 2006, 27, 927–930. [Google Scholar] [CrossRef]
- Mace, C.R.; Akbulut, O.; Kumar, A.A.; Shapiro, N.D.; Derda, R.; Patton, M.R.; Mace, C.R.; Akbulut, O.; Kumar, A.A.; Shapiro, N.D.; et al. Aqueous Multiphase Systems of Polymers and Surfactants Provide Self-Assembling Step-Gradients in Density. J. Am. Chem. Soc. 2012, 134, 9094–9097. [Google Scholar] [CrossRef]
- Beck-Candanedo, S.; Viet, D.; Gray, D.G. Triphase Equilibria in Cellulose Nanocrystal Suspensions Containing Neutral and Charged Macromolecules. Macromolecules 2007, 40, 3429–3436. [Google Scholar] [CrossRef]
- Harmon, T.S.; Holehouse, A.S.; Pappu, R.V. To Mix, or To Demix, That Is the Question. Biophys. J. 2017, 112, 565–567. [Google Scholar] [CrossRef] [PubMed]
- Sear, R.P.; Cuesta, J.A. Instabilities in Complex Mixtures with a Large Number of Components. Phys. Rev. Lett. 2003, 91, 245701. [Google Scholar] [CrossRef] [PubMed]
- Sturtewagen, L. Predicting phase behavior of multi-component and polydisperse aqueous mixtures using a virial approach. Ph.D. Thesis, Wageningen University, Droevendaalsesteeg, The Netherlands, 2020. [Google Scholar]
- Sturtewagen, L.; van der Linden, E. Towards Predicting Partitioning of Enzymes between Macromolecular Phases: Effects of Polydispersity on the Phase Behavior of Nonadditive Hard Spheres in Solution. Molecules 2022, 27, 6354. [Google Scholar] [CrossRef] [PubMed]
- Dijkstra, M. Phase behavior of nonadditive hard-sphere mixtures. Phys. Rev. E 1998, 58, 7523–7528. [Google Scholar] [CrossRef]
- Hopkins, P.; Schmidt, M. Binary non-additive hard sphere mixtures: Fluid demixing, asymptotic decay of correlations and free fluid interfaces. J. Phys. Condens. Matter 2010, 22, 325108. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Schmidt, M. Density functional for ternary non-additive hard sphere mixtures. J. Phys. Condens. Matter 2011, 23, 415101. [Google Scholar] [CrossRef][Green Version]
- Sturtewagen, L.; van der Linden, E. Effect of polydispersity on the phase behavior of additive hard spheres in solution, part I. Molecules 2021, 26, 1543. [Google Scholar] [CrossRef]
- Hill, T.L.; Gillis, J. An Introduction to Statistical Thermodynamics. Phys. Today 1961, 14, 62–64. [Google Scholar] [CrossRef]
- Lekkerkerker, H.N.; Tuinier, R. Colloids and the Depletion Interaction; Metzler, J.B., Ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Roth, R.; Evans, R.; Louis, A.A. Theory of asymmetric nonadditive binary hard-sphere mixtures. Phys. Rev. E 2001, 64, 051202. [Google Scholar] [CrossRef]
- Solokhin, M.A.; Solokhin, A.V.; Timofeev, V.S. Phase-Equilibrium Stability Criterion in Terms of the Eigenvalues of the Hessian Matrix of the Gibbs Potential. Theor. Found. Chem. Eng. 2002, 36, 444–446. [Google Scholar] [CrossRef]
- Heidemann, R.A.; Khalil, A.M. The calculation of critical points. AIChE J. 1980, 26, 769–779. [Google Scholar] [CrossRef]
- Heidemann, R.A. The criteria for thermodynamic stability. AIChE J. 1975, 21, 824–826. [Google Scholar] [CrossRef]
- Heidemann, R.A. The Classical Theory of Critical Points. In Supercritical Fluids; Springer: Berlin/Heidelberg, Germany, 1994; p. 39. [Google Scholar]
- Beegle, B.L.; Modell, M.; Reid, R.C. Thermodynamic stability criterion for pure substances and mixtures. AIChE J. 1974, 20, 1200–1206. [Google Scholar] [CrossRef]
- Reid, R.C.; Beegle, B.L. Critical point criteria in legendre transform notation. AIChE J. 1977, 23, 726–732. [Google Scholar] [CrossRef]
- Ersch, C.; van der Linden, E.; Martin, A.; Venema, P. Interactions in protein mixtures. Part II: A virial approach to predict phase behavior. Food Hydrocoll. 2016, 52, 991–1002. [Google Scholar] [CrossRef]
- Johansson, G.; Walter, H. Partitioning and concentrating biomaterials in aqueous phase systems. Int. Rev. Cytol. 1896, 192, 33–60. [Google Scholar] [CrossRef]


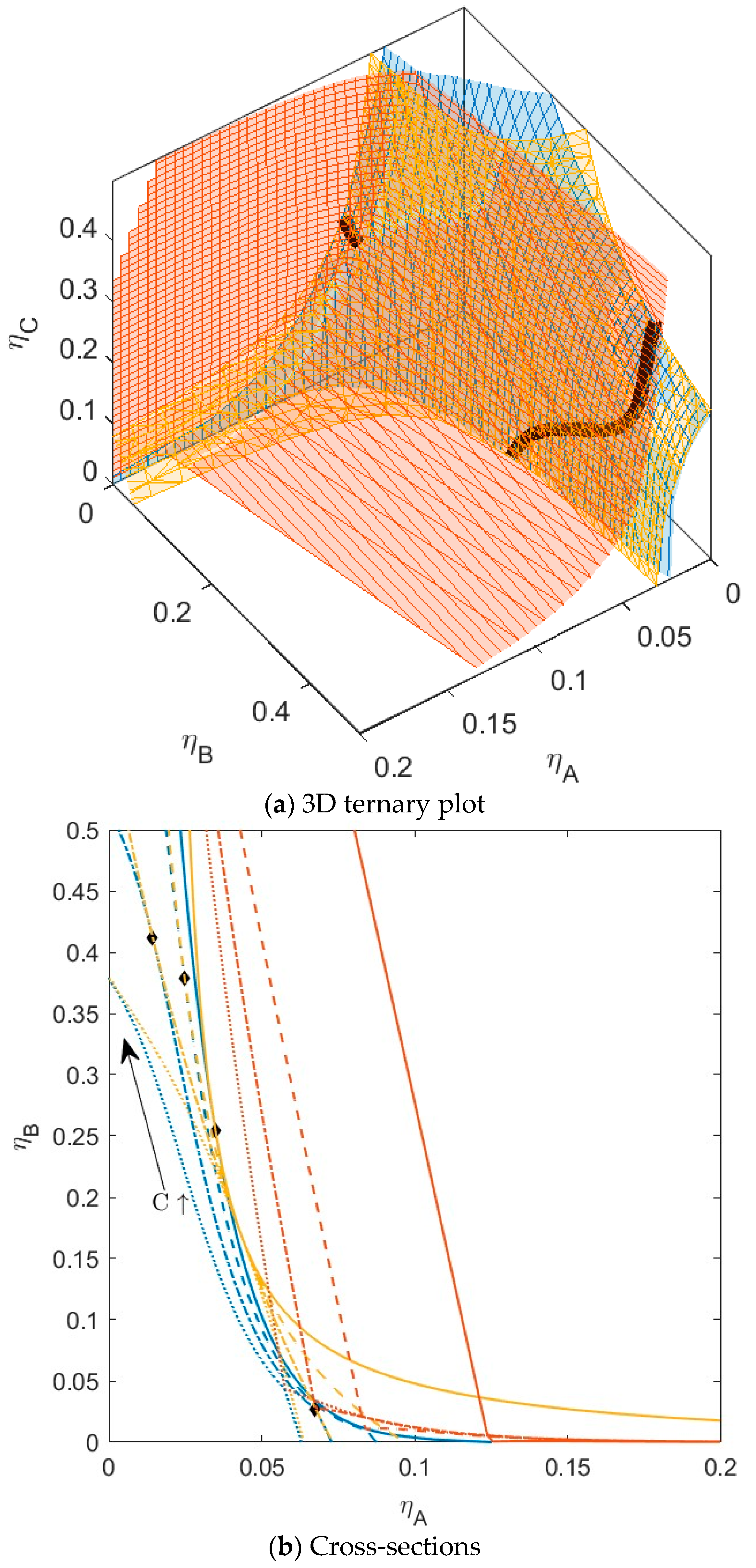
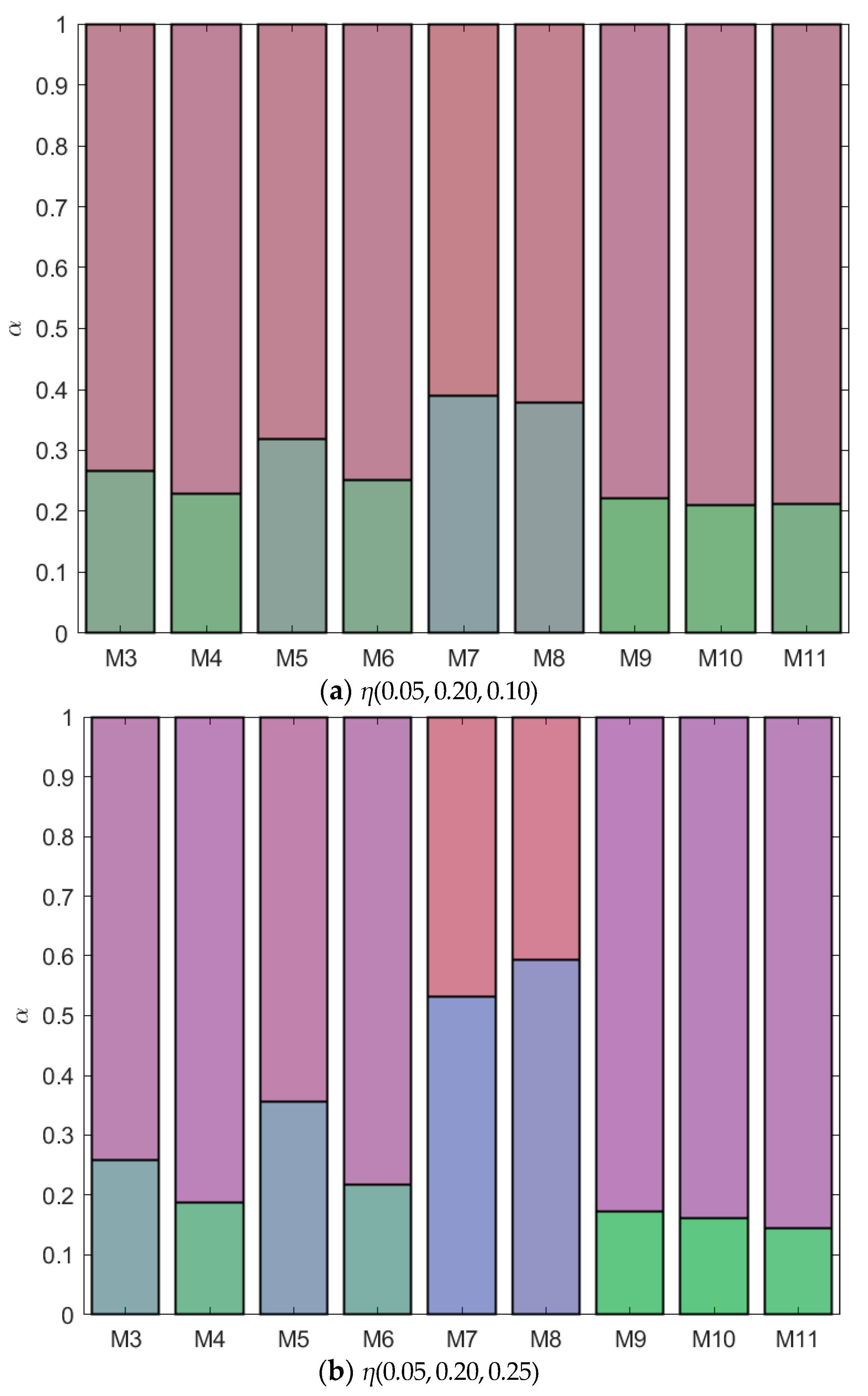
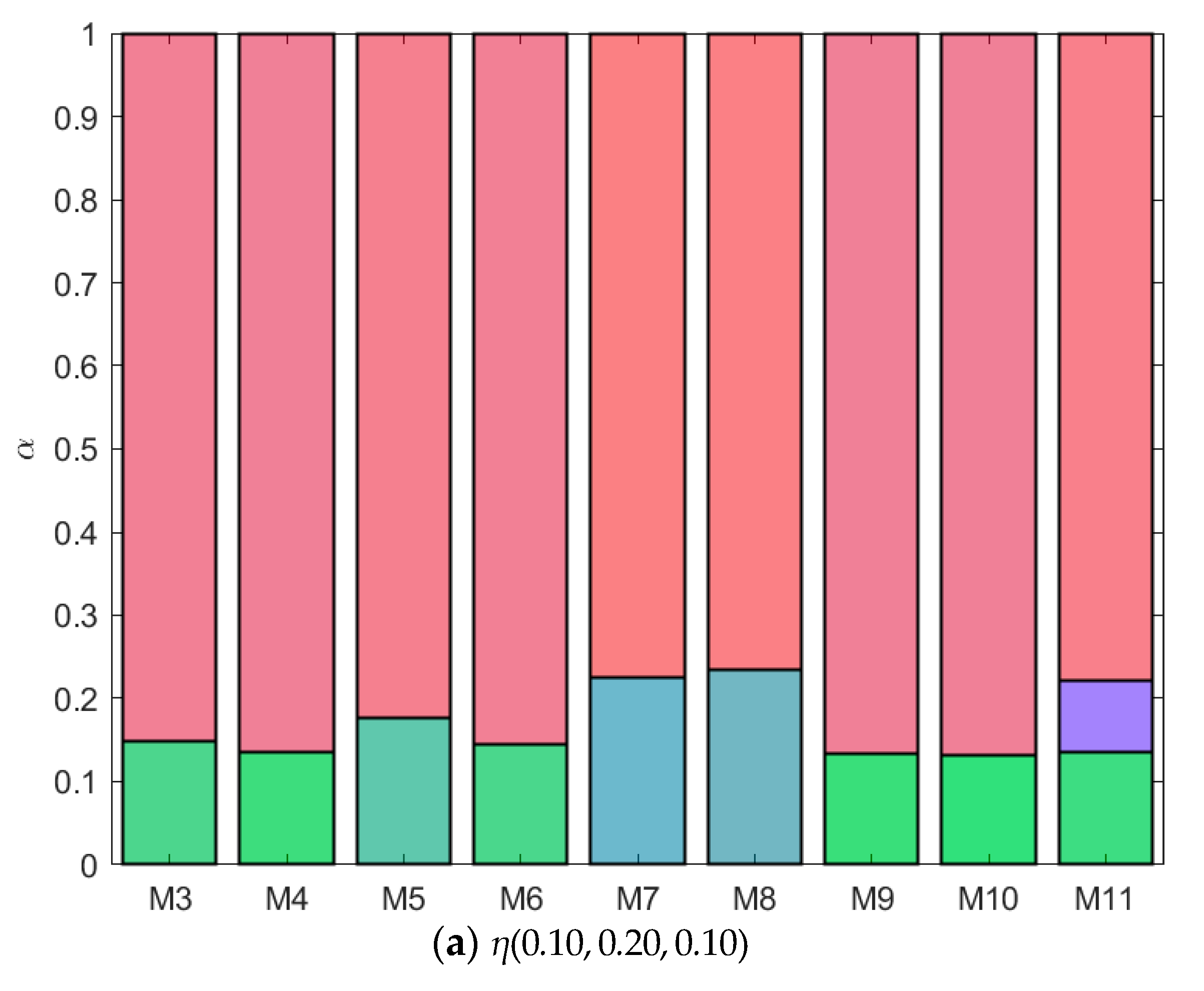

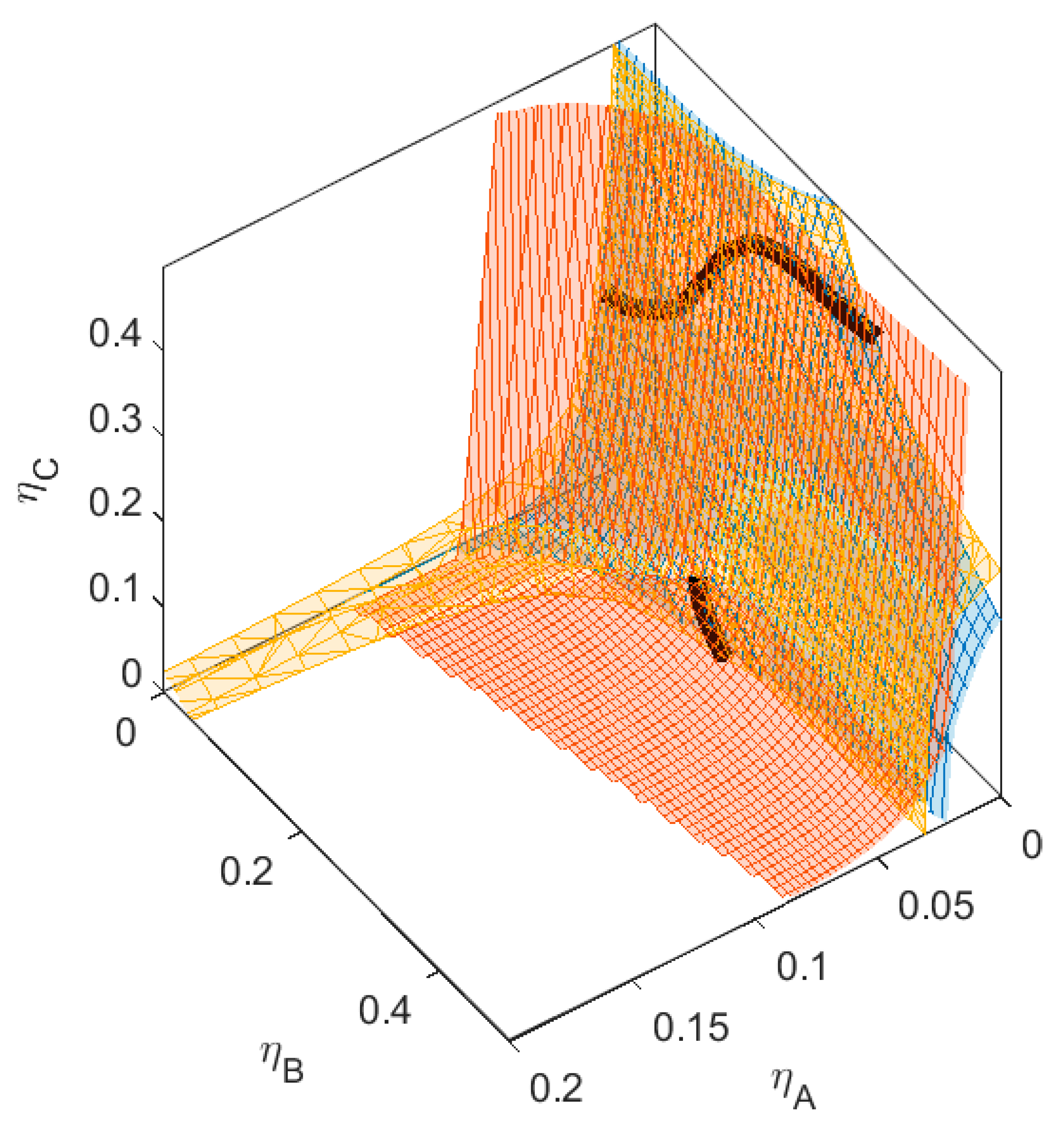
| Mixture | ∆AC | BcritAC | ηcritAC | ∆BC | BcritBC | ηcritBC |
|---|---|---|---|---|---|---|
| 3 | −0.10 | 1.26 | −0.10 | 0.57 | ||
| 4 | −0.10 | 1.26 | 0 | 1.06 | ||
| 5 | 0 | 2.37 | (0.147, 0.442) | −0.10 | 0.57 | |
| 6 | 0 | 2.37 | (0.147, 0.442) | 0 | 1.06 | |
| 7 | 0.10 | 4.20 | (0.069, 0.253) | −0.10 | 0.57 | |
| 8 | 0.10 | 4.20 | (0.069, 0.253) | 0 | 1.06 | |
| 9 | −0.10 | 1.26 | 0.10 | 1.88 | (0.386, 0.295) | |
| 10 | 0 | 2.37 | (0.147, 0.442) | 0.10 | 1.88 | (0.386, 0.295) |
| 11 | 0.10 | 4.20 | (0.069, 0.253) | 0.10 | 1.88 | (0.386, 0.295) |
| Mixture | qAC | ∆AC | BcritAC | ηcritAC | ∆BC | BcritBC | ηcritBC |
|---|---|---|---|---|---|---|---|
| 11 | 1/3 | 0.10 | 4.20 | (0.069, 0.253) | 0.10 | 1.88 | (0.386, 0.295) |
| 14 | 1/5 | 0.10 | 10.33 | (0.022, 0.219) | 0.10 | 1.84 | (0.318, 0.391) |
| 15 | 1/3 | 0.15 | 5.48 | (0.052, 0.208) | 0.10 | 1.88 | (0.386, 0.295) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sturtewagen, L.; van der Linden, E. Ternary Mixtures of Hard Spheres and Their Multiple Separated Phases. Molecules 2023, 28, 7817. https://doi.org/10.3390/molecules28237817
Sturtewagen L, van der Linden E. Ternary Mixtures of Hard Spheres and Their Multiple Separated Phases. Molecules. 2023; 28(23):7817. https://doi.org/10.3390/molecules28237817
Chicago/Turabian StyleSturtewagen, Luka, and Erik van der Linden. 2023. "Ternary Mixtures of Hard Spheres and Their Multiple Separated Phases" Molecules 28, no. 23: 7817. https://doi.org/10.3390/molecules28237817
APA StyleSturtewagen, L., & van der Linden, E. (2023). Ternary Mixtures of Hard Spheres and Their Multiple Separated Phases. Molecules, 28(23), 7817. https://doi.org/10.3390/molecules28237817




