AlphaFold Blindness to Topological Barriers Affects Its Ability to Correctly Predict Proteins’ Topology
Abstract
:1. Introduction
2. Results
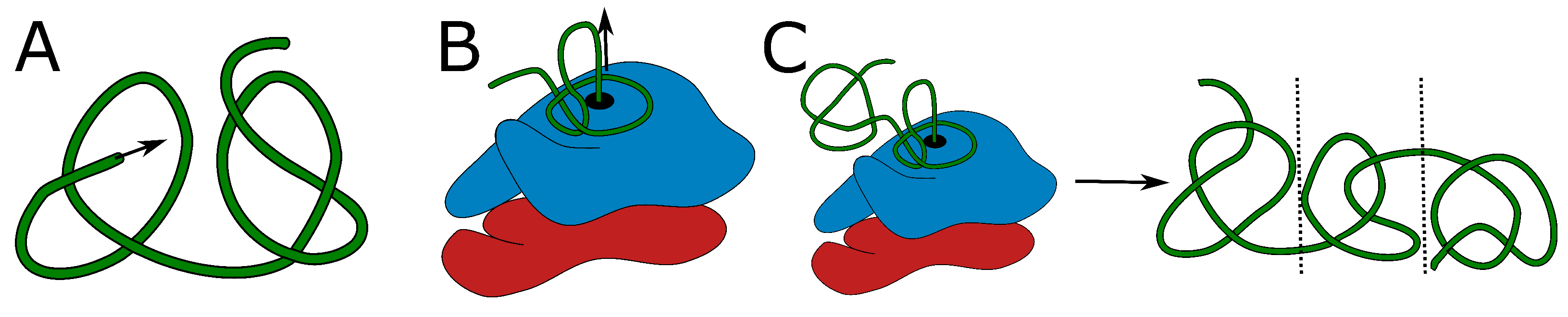
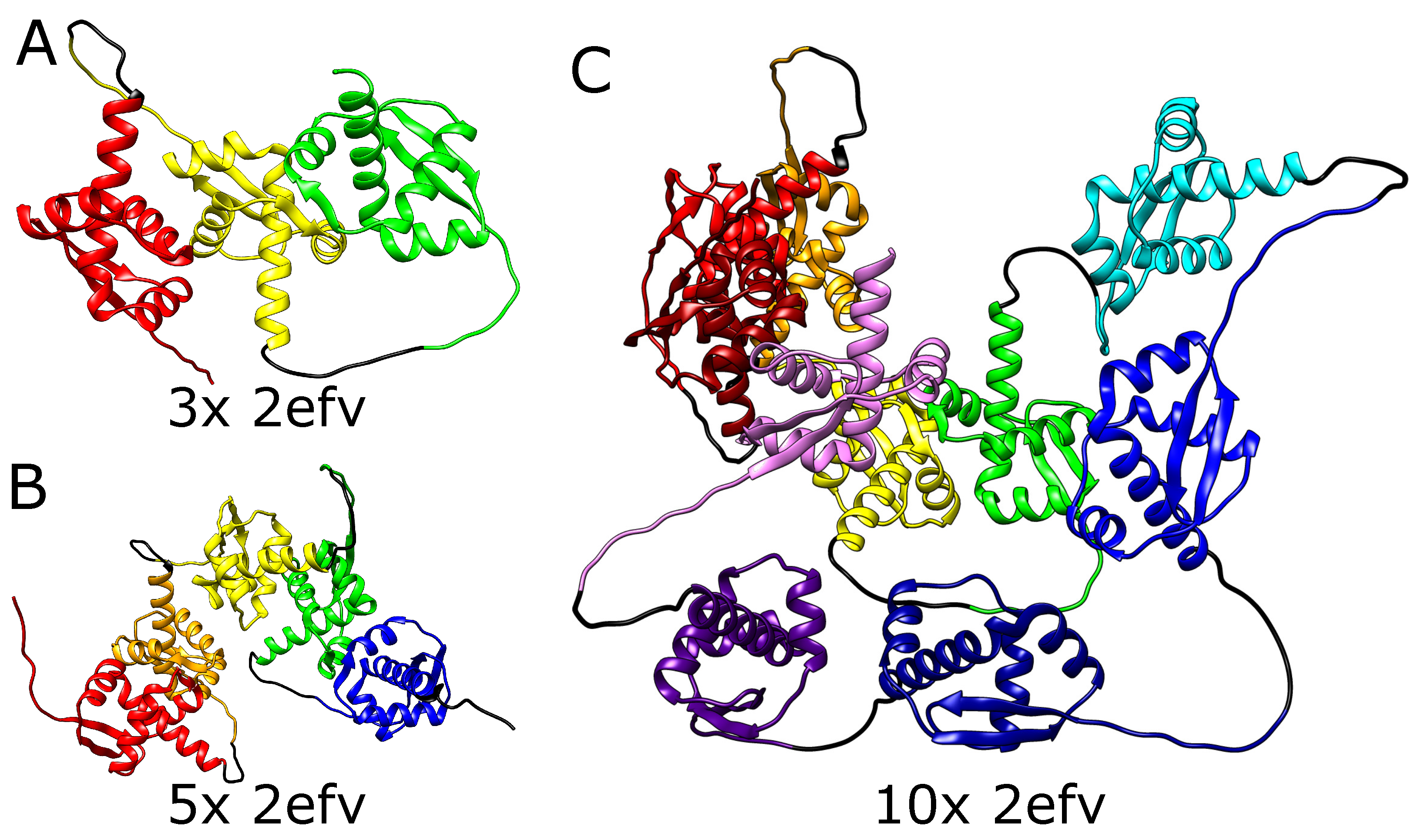
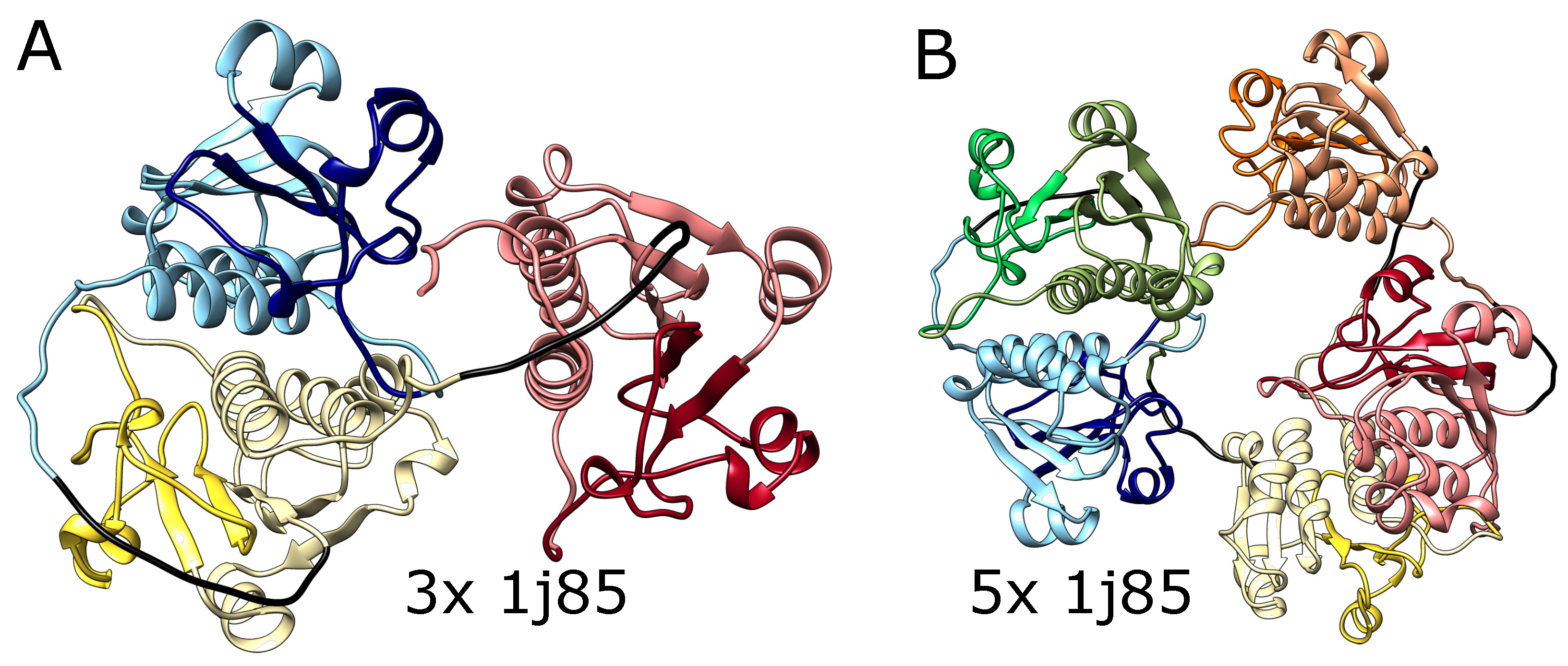
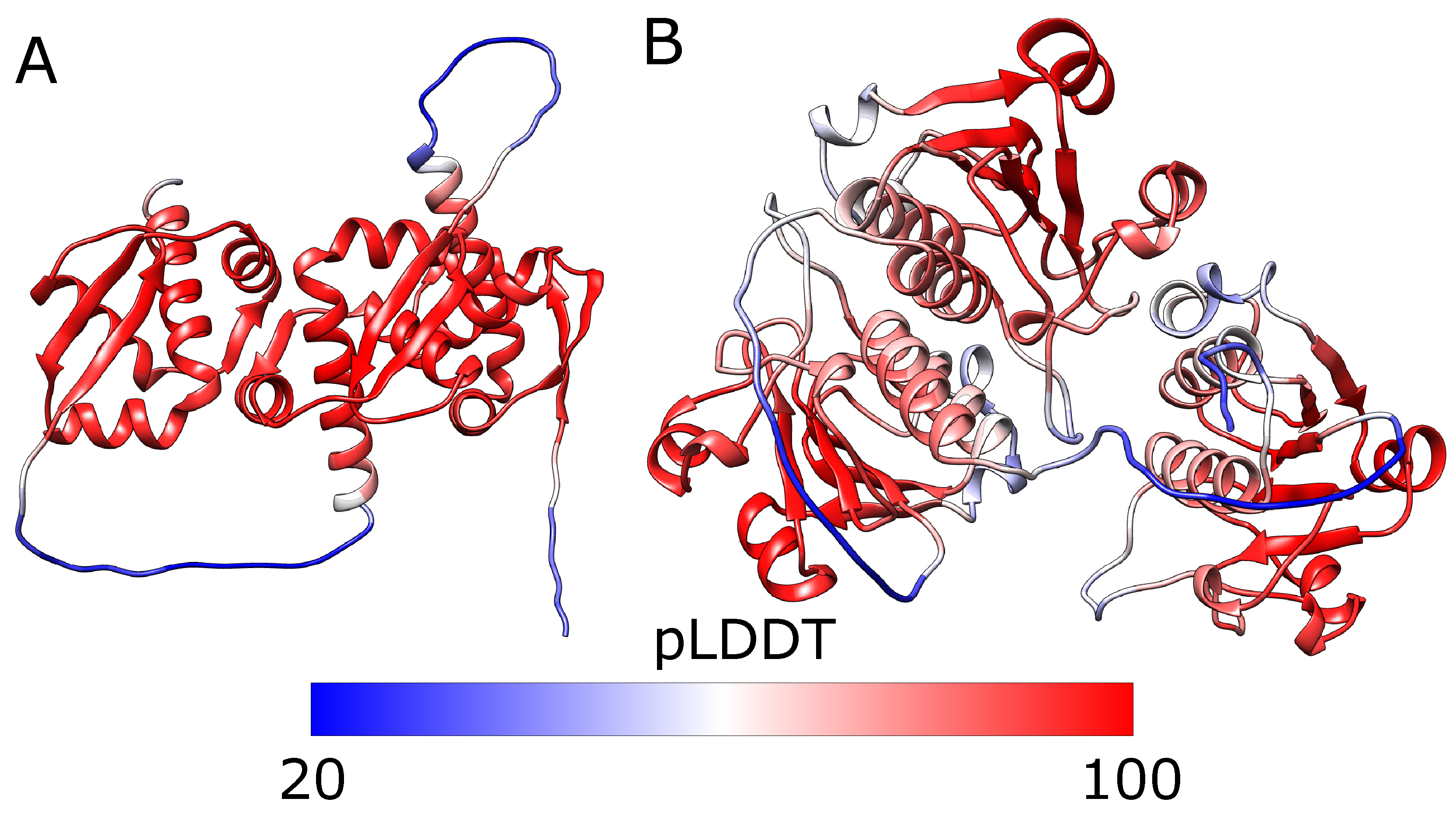
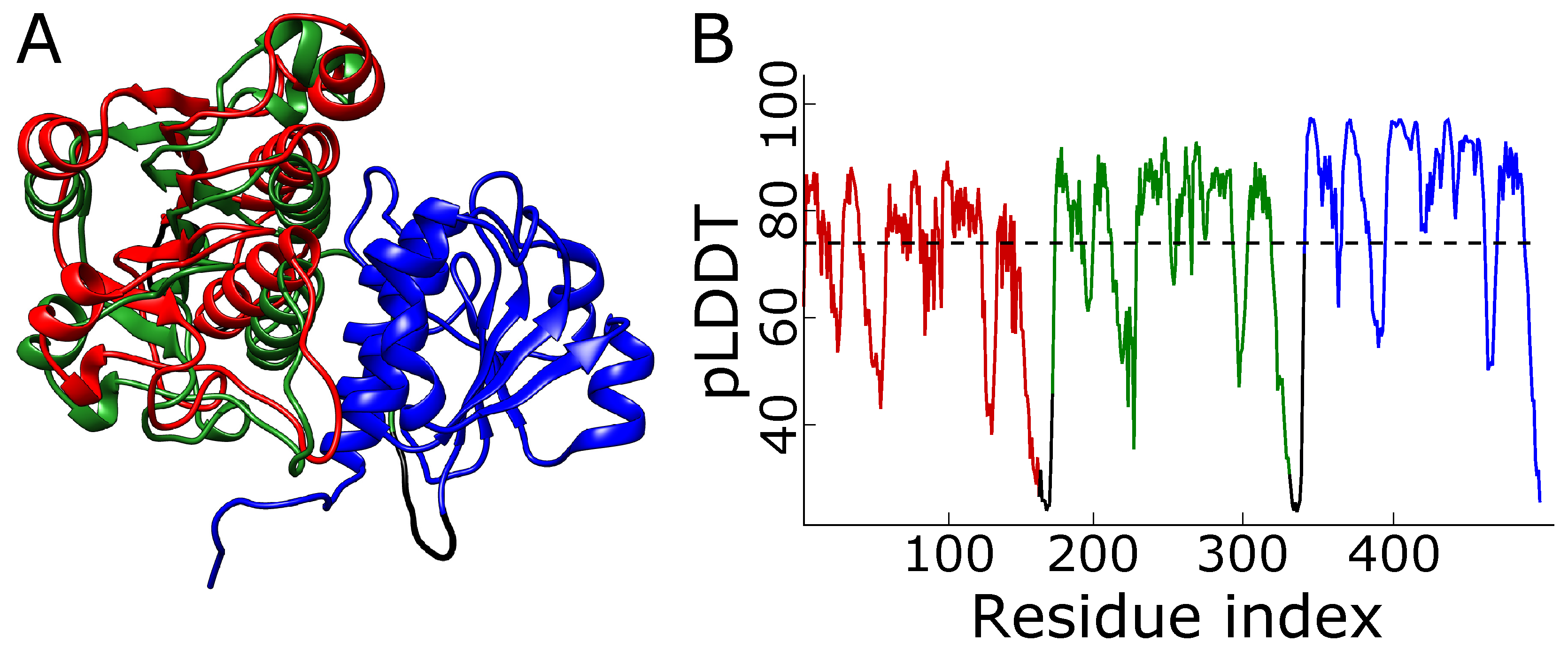
2.1. Alphafold Builds Protein Structures Forming Arbitrary Complex Knots
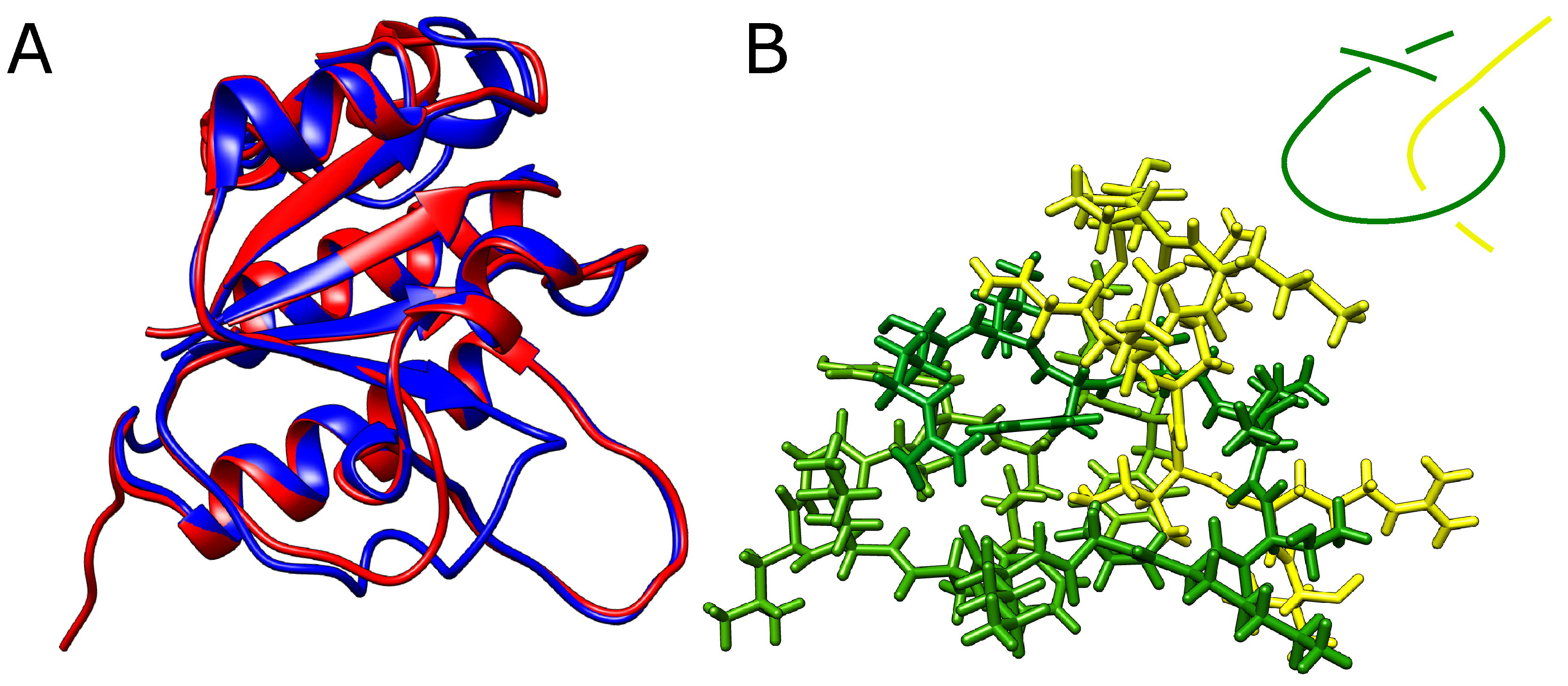
2.2. Alphafold Predicts Impossibly Densely Packed Structures
3. Discussion
4. Materials and Methods
4.1. Software and Hardware
4.2. Structures and Sequences
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.; Bridgland, A.; et al. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.; Bridgland, A.; et al. Protein structure prediction using multiple deep neural networks in the 13th Critical Assessment of Protein Structure Prediction (CASP13). Proteins Struct. Funct. Bioinform. 2019, 87, 1141–1148. [Google Scholar] [CrossRef]
- Kryshtafovych, A.; Schwede, T.; Topf, M.; Fidelis, K.; Moult, J. Critical assessment of methods of protein structure prediction (CASP)—Round XIII. Proteins Struct. Funct. Bioinform. 2019, 87, 1011–1020. [Google Scholar] [CrossRef]
- Kryshtafovych, A.; Schwede, T.; Topf, M.; Fidelis, K.; Moult, J. Critical assessment of methods of protein structure prediction (CASP)—Round XIV. Proteins Struct. Funct. Bioinform. 2021, 89, 1607–1617. [Google Scholar] [CrossRef]
- Mirdita, M.; Schütze, K.; Moriwaki, Y.; Heo, L.; Ovchinnikov, S.; Steinegger, M. ColabFold: Making protein folding accessible to all. Nat. Methods 2022, 19, 679–682. [Google Scholar] [CrossRef] [PubMed]
- Luebbert, L.; Pachter, L. Efficient querying of genomic reference databases with gget. Bioinformatics 2023, 39, btac836. [Google Scholar] [CrossRef]
- Evans, R.; O’Neill, M.; Pritzel, A.; Antropova, N.; Senior, A.; Green, T.; Žídek, A.; Bates, R.; Blackwell, S.; Yim, J.; et al. Protein complex prediction with AlphaFold-Multimer. bioRxiv 2021. [Google Scholar] [CrossRef]
- Baek, M.; Anishchenko, I.; Humphreys, I.; Cong, Q.; Baker, D.; DiMaio, F. Efficient and accurate prediction of protein structure using RoseTTAFold2. bioRxiv 2023. [Google Scholar] [CrossRef]
- Baek, M.; Baker, D. Deep learning and protein structure modeling. Nat. Methods 2022, 19, 13–14. [Google Scholar] [CrossRef]
- Baek, M.; DiMaio, F.; Anishchenko, I.; Dauparas, J.; Ovchinnikov, S.; Lee, G.R.; Wang, J.; Cong, Q.; Kinch, L.N.; Schaeffer, R.D.; et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science 2021, 373, 871–876. [Google Scholar] [CrossRef] [PubMed]
- Hekkelman, M.L.; de Vries, I.; Joosten, R.P.; Perrakis, A. AlphaFill: Enriching AlphaFold models with ligands and cofactors. Nat. Methods 2023, 20, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Terwilliger, T.C.; Poon, B.K.; Afonine, P.V.; Schlicksup, C.J.; Croll, T.I.; Millán, C.; Richardson, J.S.; Read, R.J.; Adams, P.D. Improved AlphaFold modeling with implicit experimental information. Nat. Methods 2022, 19, 1376–1382. [Google Scholar] [CrossRef]
- Ahdritz, G.; Bouatta, N.; Kadyan, S.; Xia, Q.; Gerecke, W.; O’Donnell, T.J.; Berenberg, D.; Fisk, I.; Zanichelli, N.; Zhang, B.; et al. OpenFold: Retraining AlphaFold2 yields new insights into its learning mechanisms and capacity for generalization. bioRxiv 2022. [Google Scholar] [CrossRef]
- Tunyasuvunakool, K.; Adler, J.; Wu, Z.; Green, T.; Zielinski, M.; Žídek, A.; Bridgland, A.; Cowie, A.; Meyer, C.; Laydon, A.; et al. Highly accurate protein structure prediction for the human proteome. Nature 2021, 596, 590–596. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Sulkowska, J.I. To tie or not to tie? That is the question. Polymers 2017, 9, 454. [Google Scholar] [CrossRef]
- Flapan, E.; Heller, G. Topological complexity in protein structures. Comput. Math. Biophys. 2015, 3, 23–42. [Google Scholar] [CrossRef]
- Jackson, S.E.; Suma, A.; Micheletti, C. How to fold intricately: Using theory and experiments to unravel the properties of knotted proteins. Curr. Opin. Struct. Biol. 2017, 42, 6–14. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Rubach, P.; Goundaroulis, D.; Dorier, J.; Sułkowski, P.; Millett, K.C.; Rawdon, E.J.; Stasiak, A.; Sulkowska, J.I. KnotProt 2.0: A database of proteins with knots and other entangled structures. Nucleic Acids Res. 2019, 47, D367–D375. [Google Scholar] [CrossRef]
- Arsuaga, J.; Vazquez, M.; McGuirk, P.; Trigueros, S.; Sumners, D.W.; Roca, J. DNA knots reveal a chiral organization of DNA in phage capsids. Proc. Natl. Acad. Sci. USA 2005, 102, 9165–9169. [Google Scholar] [CrossRef]
- Marenduzzo, D.; Micheletti, C.; Orlandini, E.; Sumners, D.W. Topological friction strongly affects viral DNA ejection. Proc. Natl. Acad. Sci. USA 2013, 110, 20081–20086. [Google Scholar] [CrossRef]
- Reith, D.; Cifra, P.; Stasiak, A.; Virnau, P. Effective stiffening of DNA due to nematic ordering causes DNA molecules packed in phage capsids to preferentially form torus knots. Nucleic Acids Res. 2012, 40, 5129–5137. [Google Scholar] [CrossRef]
- Bölinger, D.; Sułkowska, J.I.; Hsu, H.P.; Mirny, L.A.; Kardar, M.; Onuchic, J.N.; Virnau, P. A Stevedore’s protein knot. PLoS Comput. Biol. 2010, 6, e1000731. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Stasiak, A.; Sulkowska, J.I. In search of functional advantages of knots in proteins. PLoS ONE 2016, 11, e0165986. [Google Scholar] [CrossRef] [PubMed]
- Faísca, P.F. Knotted proteins: A tangled tale of structural biology. Comput. Struct. Biotechnol. J. 2015, 13, 459–468. [Google Scholar] [CrossRef]
- Brems, M.A.; Runkel, R.; Yeates, T.O.; Virnau, P. AlphaFold predicts the most complex protein knot and composite protein knots. Protein Sci. 2022, 31, e4380. [Google Scholar] [CrossRef]
- Perlinska, A.P.; Niemyska, W.H.; Gren, B.A.; Bukowicki, M.; Nowakowski, S.; Rubach, P.; Sulkowska, J.I. AlphaFold predicts novel human proteins with knots. Protein Sci. 2023, 32, e4631. [Google Scholar] [CrossRef] [PubMed]
- Taylor, W.R. Protein knots and fold complexity: Some new twists. Comput. Biol. Chem. 2007, 31, 151–162. [Google Scholar] [CrossRef]
- Niemyska, W.; Rubach, P.; Gren, B.A.; Nguyen, M.L.; Garstka, W.; Bruno da Silva, F.; Rawdon, E.J.; Sulkowska, J.I. AlphaKnot: Server to analyze entanglement in structures predicted by AlphaFold methods. Nucleic Acids Res. 2022, 50, W44–W50. [Google Scholar] [CrossRef]
- a Beccara, S.; Škrbić, T.; Covino, R.; Micheletti, C.; Faccioli, P. Folding pathways of a knotted protein with a realistic atomistic force field. PLoS Comput. Biol. 2013, 9, e1003002. [Google Scholar] [CrossRef]
- Chwastyk, M.; Cieplak, M. Multiple folding pathways of proteins with shallow knots and co-translational folding. J. Chem. Phys. 2015, 143, 045101. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Jarmolinska, A.; Sulkowska, J. Prediction of the optimal set of contacts to fold the smallest knotted protein. J. Phys. Condens. Matter 2015, 27, 354109. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Dabrowski-Tumanski, P.; Niewieczerzal, S.; Sulkowska, J.I. The exclusive effects of chaperonin on the behavior of proteins with 52 knot. PLoS Comput. Biol. 2018, 14, e1005970. [Google Scholar] [CrossRef]
- Lim, N.C.; Jackson, S.E. Molecular knots in biology and chemistry. J. Phys. Condens. Matter 2015, 27, 354101. [Google Scholar] [CrossRef]
- King, N.P.; Jacobitz, A.W.; Sawaya, M.R.; Goldschmidt, L.; Yeates, T.O. Structure and folding of a designed knotted protein. Proc. Natl. Acad. Sci. USA 2010, 107, 20732–20737. [Google Scholar] [CrossRef]
- Chwastyk, M.; Cieplak, M. Cotranslational folding of deeply knotted proteins. J. Phys. Condens. Matter 2015, 27, 354105. [Google Scholar] [CrossRef] [PubMed]
- Mallam, A.L.; Onuoha, S.C.; Grossmann, J.G.; Jackson, S.E. Knotted fusion proteins reveal unexpected possibilities in protein folding. Mol. Cell 2008, 30, 642–648. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Piejko, M.; Niewieczerzal, S.; Stasiak, A.; Sulkowska, J.I. Protein knotting by active threading of nascent polypeptide chain exiting from the ribosome exit channel. J. Phys. Chem. B 2018, 122, 11616–11625. [Google Scholar] [CrossRef]
- Taylor, W.R. A deeply knotted protein structure and how it might fold. Nature 2000, 406, 916–919. [Google Scholar] [CrossRef]
- Mariani, V.; Biasini, M.; Barbato, A.; Schwede, T. lDDT: A local superposition-free score for comparing protein structures and models using distance difference tests. Bioinformatics 2013, 29, 2722–2728. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Rubach, P.; Niemyska, W.; Gren, B.A.; Sulkowska, J.I. Topoly: Python package to analyze topology of polymers. Briefings Bioinform. 2021, 22, bbaa196. [Google Scholar] [CrossRef] [PubMed]
- Sulkowska, J.I.; Rawdon, E.J.; Millet, K.C.; Onuchic, J.N.; Stasiak, A. Conservation of complex knotting and slipknotting patterns in proteins. Proc. Natl. Acad. Sci. USA 2012, 109, E1715–E1723. [Google Scholar] [CrossRef] [PubMed]
- Prlić, A.; Bliven, S.; Rose, P.W.; Bluhm, W.F.; Bizon, C.; Godzik, A.; Bourne, P.E. Pre-calculated protein structure alignments at the RCSB PDB website. Bioinformatics 2010, 26, 2983–2985. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Godzik, A. Flexible structure alignment by chaining aligned fragment pairs allowing twists. Bioinformatics 2003, 19, ii246–ii255. [Google Scholar] [CrossRef]
- Buel, G.R.; Walters, K.J. Can AlphaFold2 predict the impact of missense mutations on structure? Nat. Struct. Mol. Biol. 2022, 29, 1–2. [Google Scholar] [CrossRef]
- Pak, M.A.; Markhieva, K.A.; Novikova, M.S.; Petrov, D.S.; Vorobyev, I.S.; Maksimova, E.S.; Kondrashov, F.A.; Ivankov, D.N. Using AlphaFold to predict the impact of single mutations on protein stability and function. PLoS ONE 2023, 18, e0282689. [Google Scholar] [CrossRef] [PubMed]
- Niemyska, W.; Dabrowski-Tumanski, P.; Kadlof, M.; Haglund, E.; Sułkowski, P.; Sulkowska, J.I. Complex lasso: New entangled motifs in proteins. Sci. Rep. 2016, 6, 36895. [Google Scholar] [CrossRef] [PubMed]
- Haglund, E.; Sulkowska, J.I.; Noel, J.K.; Lammert, H.; Onuchic, J.N.; Jennings, P.A. Pierced lasso bundles are a new class of knot-like motifs. PLoS Comput. Biol. 2014, 10, e1003613. [Google Scholar] [CrossRef]
- Doyle, L.A.; Takushi, B.; Kibler, R.D.; Milles, L.F.; Orozco, C.T.; Jones, J.D.; Jackson, S.E.; Stoddard, B.L.; Bradley, P. De novo design of knotted tandem repeat proteins. Nat. Commun. 2023, 14, 6746. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dabrowski-Tumanski, P.; Stasiak, A. AlphaFold Blindness to Topological Barriers Affects Its Ability to Correctly Predict Proteins’ Topology. Molecules 2023, 28, 7462. https://doi.org/10.3390/molecules28227462
Dabrowski-Tumanski P, Stasiak A. AlphaFold Blindness to Topological Barriers Affects Its Ability to Correctly Predict Proteins’ Topology. Molecules. 2023; 28(22):7462. https://doi.org/10.3390/molecules28227462
Chicago/Turabian StyleDabrowski-Tumanski, Pawel, and Andrzej Stasiak. 2023. "AlphaFold Blindness to Topological Barriers Affects Its Ability to Correctly Predict Proteins’ Topology" Molecules 28, no. 22: 7462. https://doi.org/10.3390/molecules28227462
APA StyleDabrowski-Tumanski, P., & Stasiak, A. (2023). AlphaFold Blindness to Topological Barriers Affects Its Ability to Correctly Predict Proteins’ Topology. Molecules, 28(22), 7462. https://doi.org/10.3390/molecules28227462







