Interaction of Hoechst 33342 with POPC Membranes at Different pH Values
Abstract
1. Introduction
2. Results and Discussion
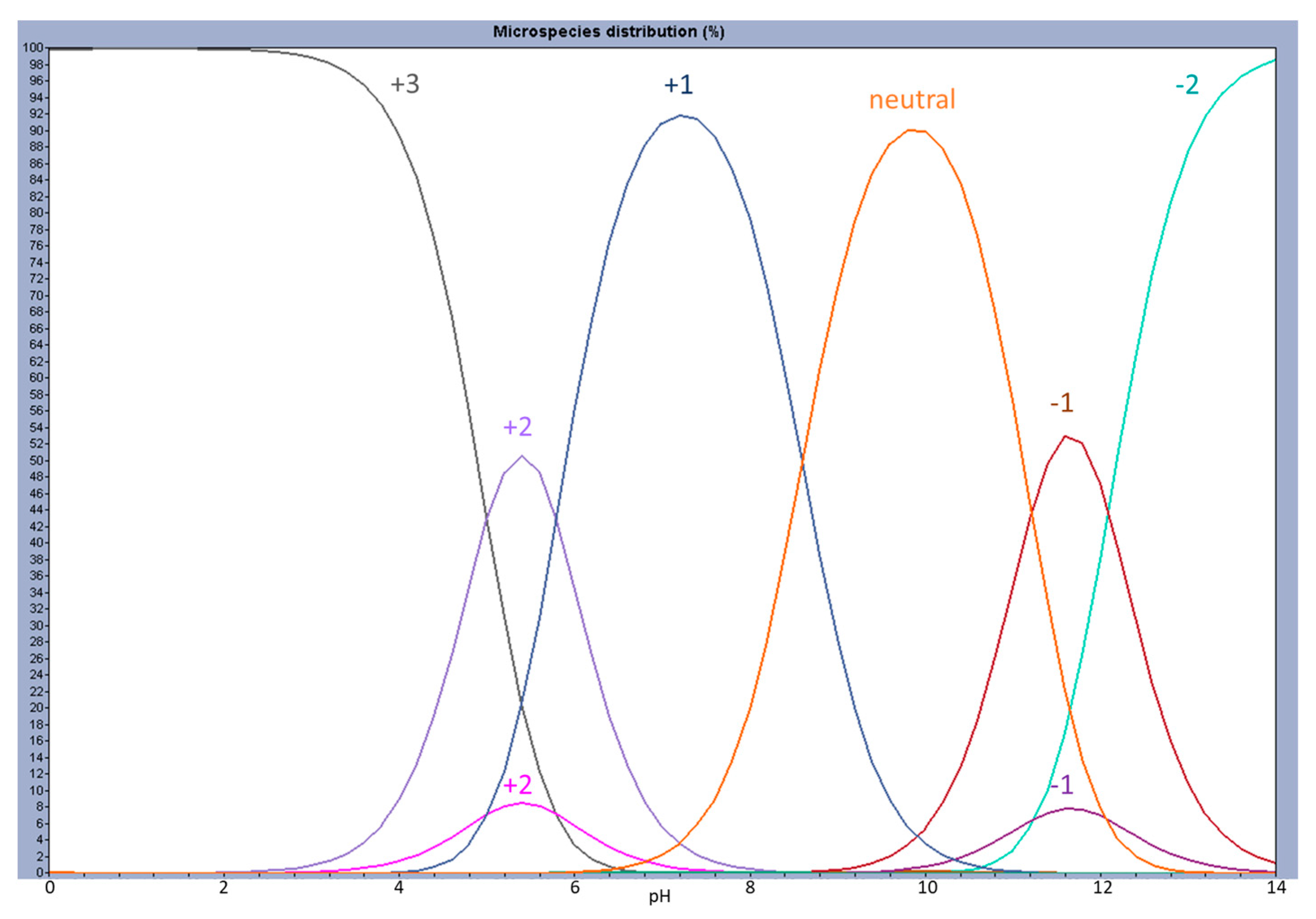
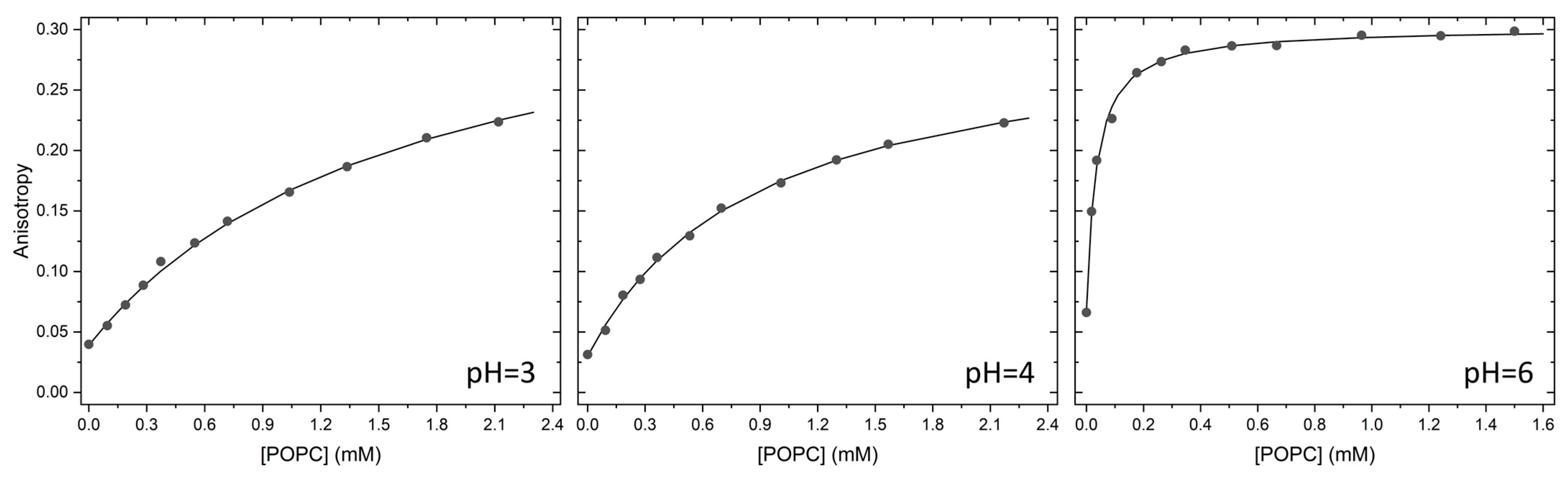
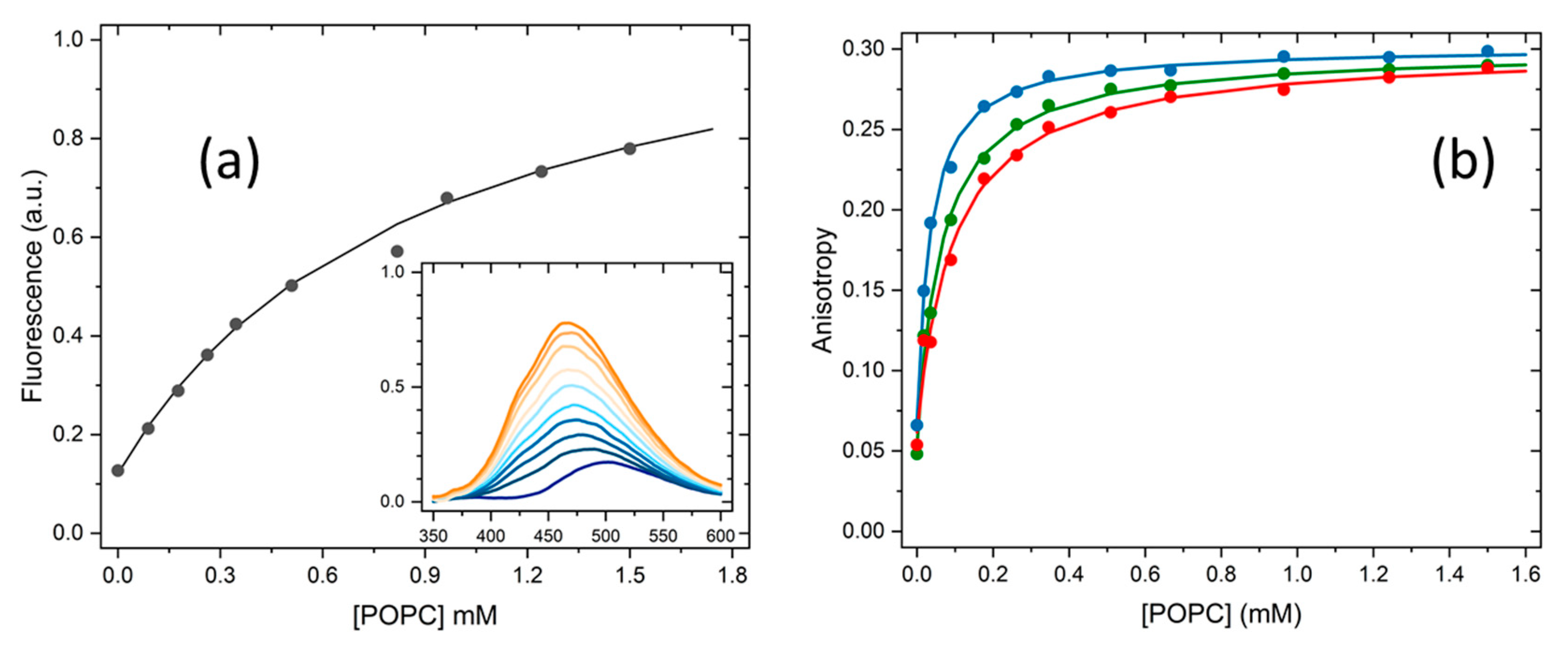
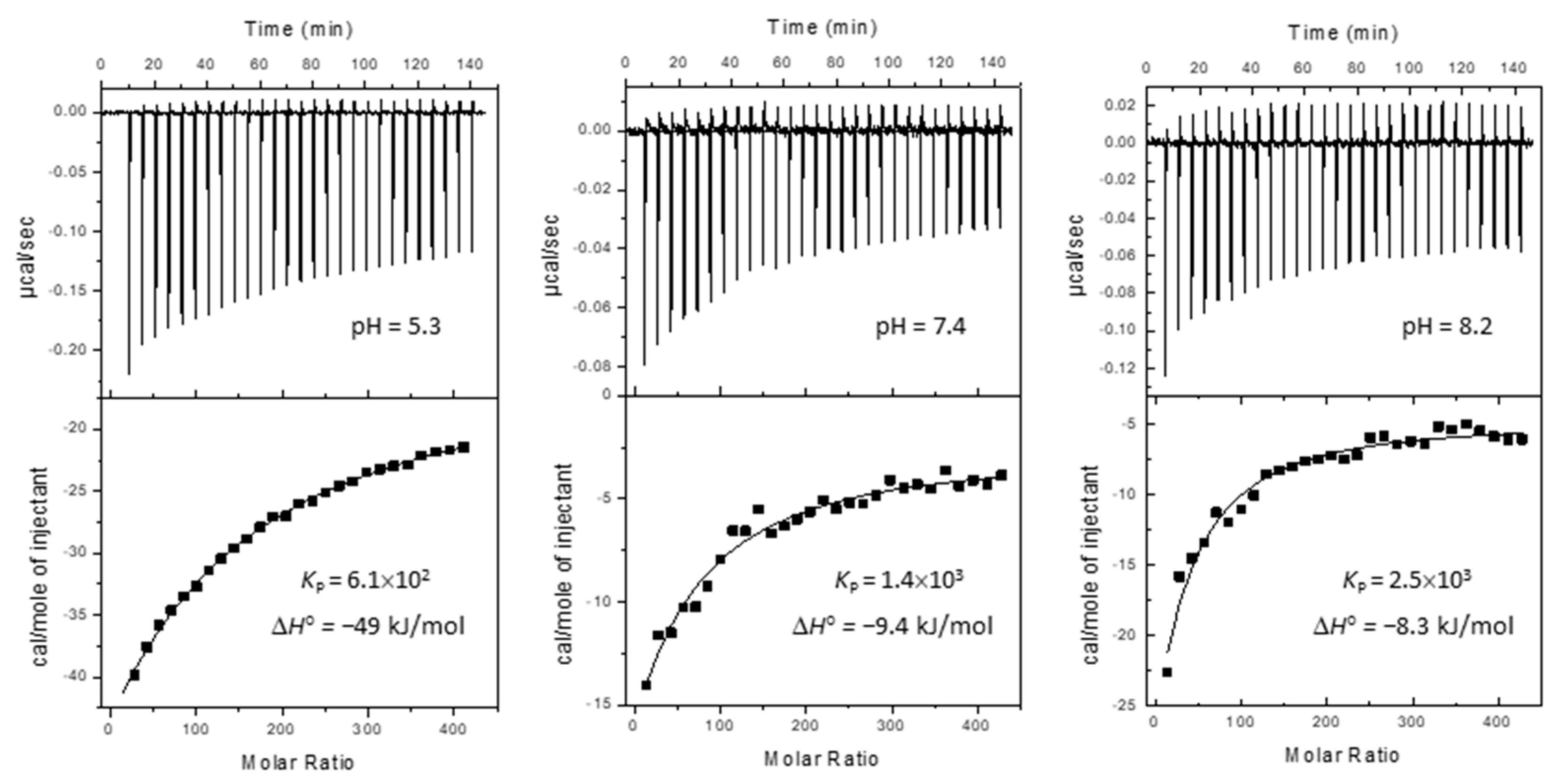
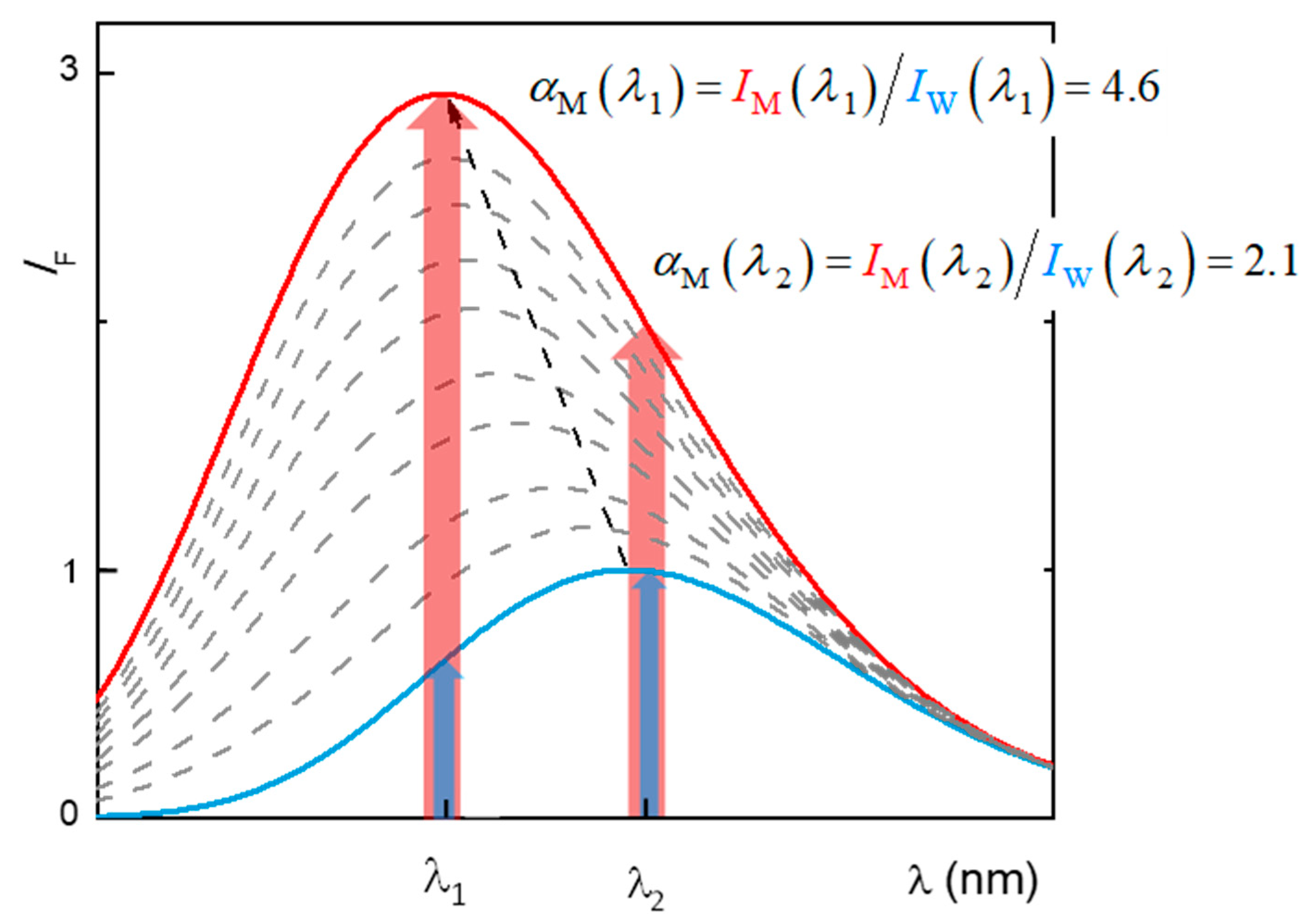
2.1. Partition to POPC LUVs
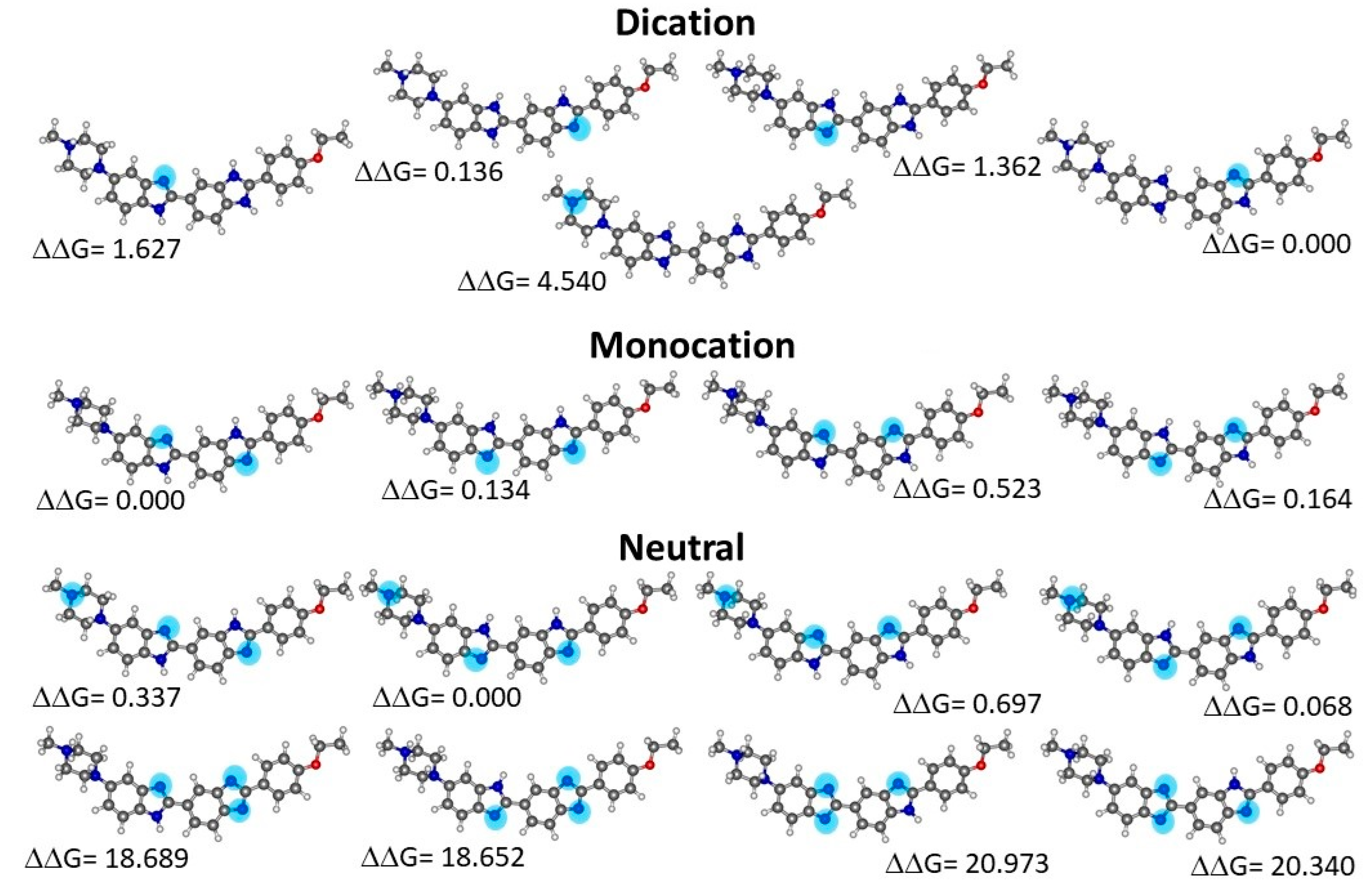
2.2. Quantum Chemical Determinations of Isomer Relative Stability
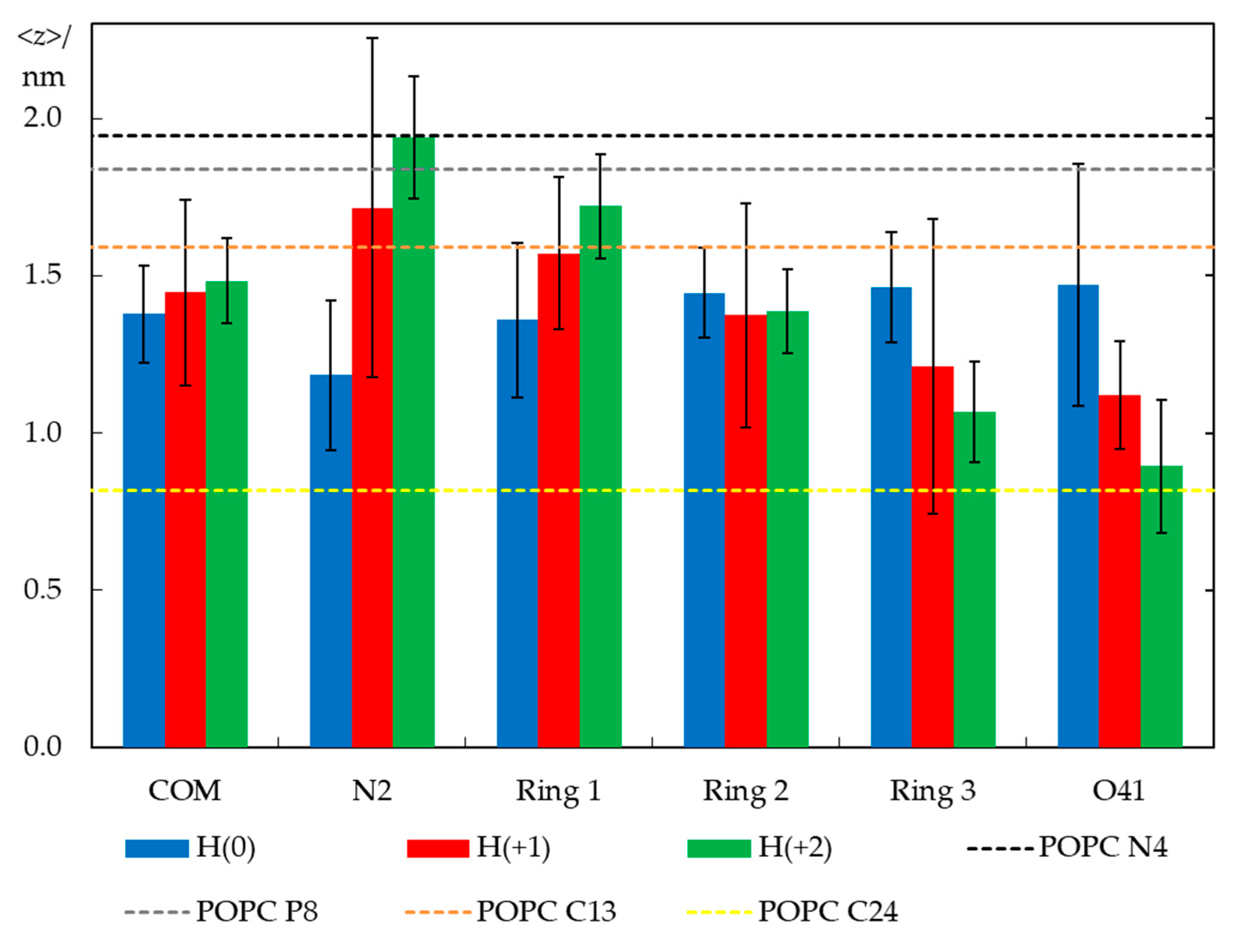
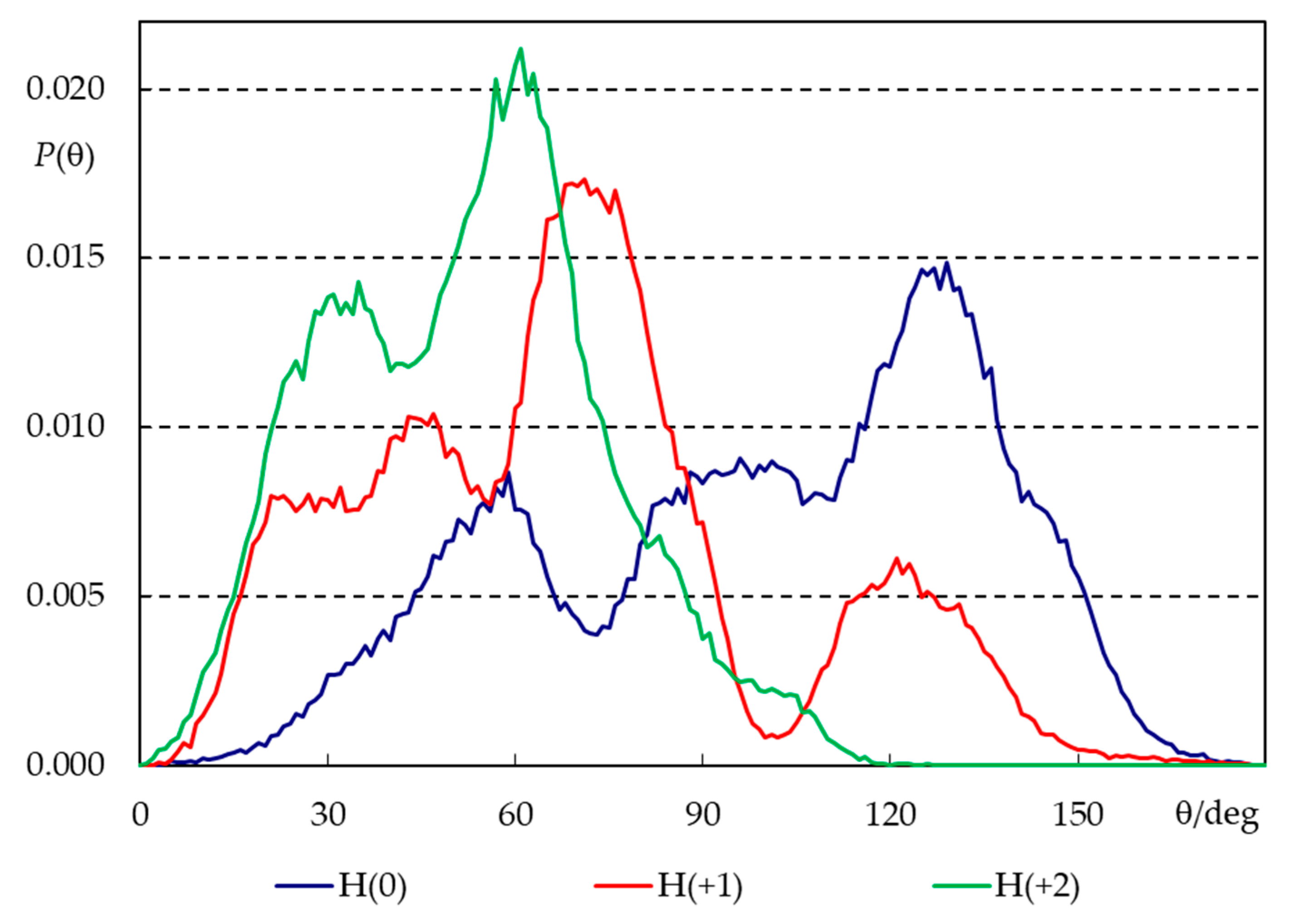
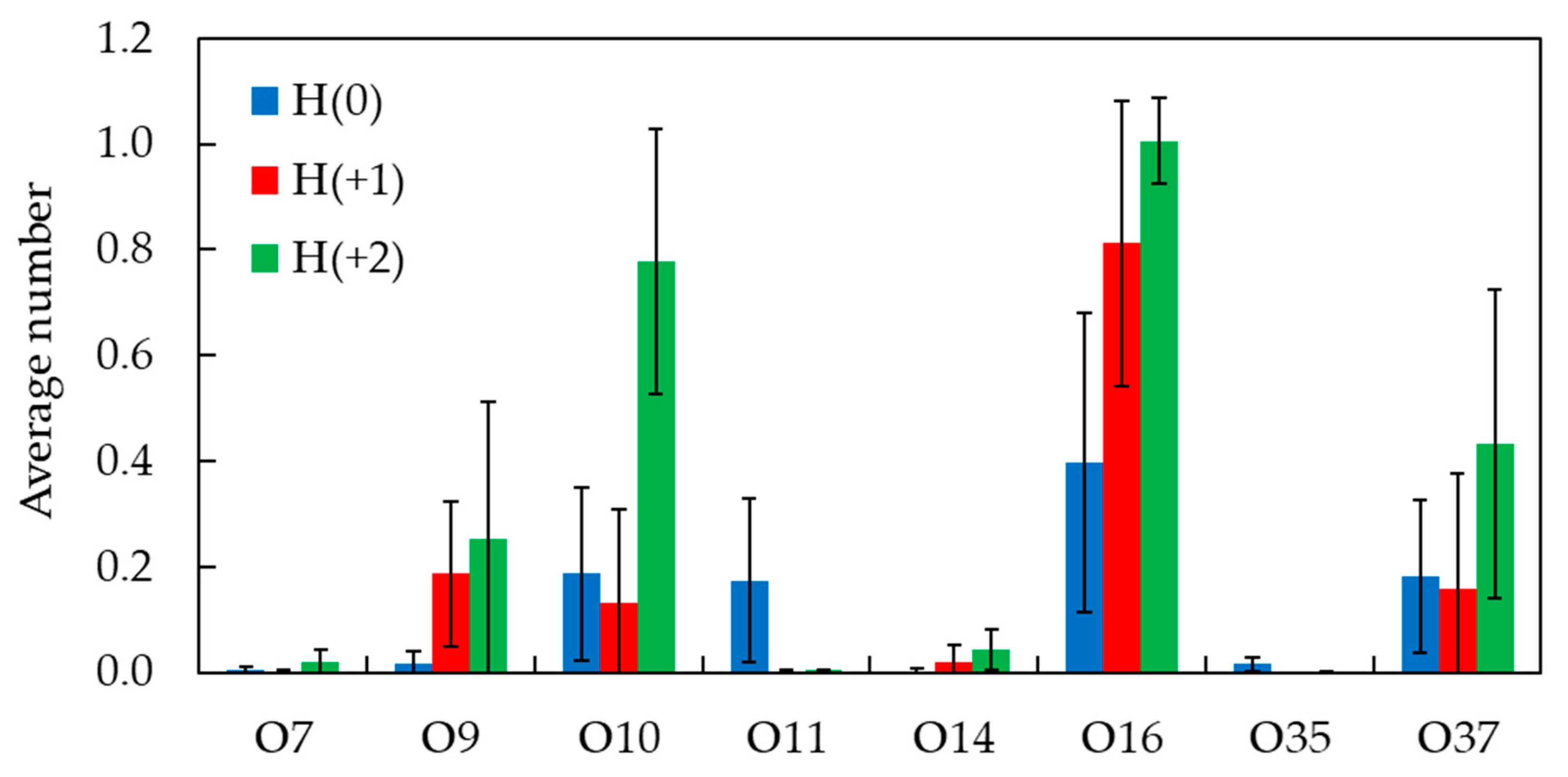
2.3. Unrestrained MD Simulations
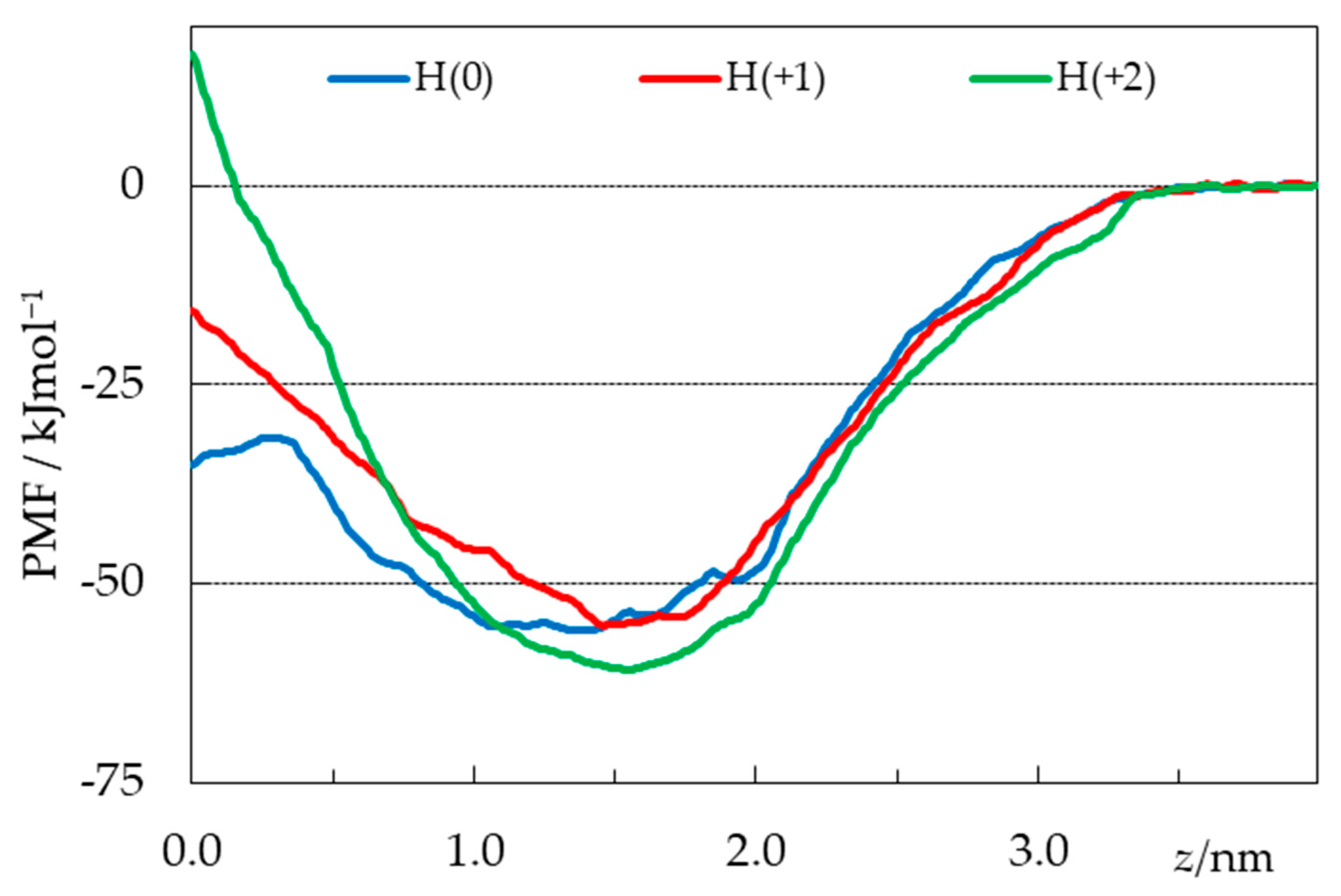
2.4. Free Energy Profiles from Umbrella Sampling MD
3. Materials and Methods
3.1. Materials
3.2. Preparation of Large Unilamellar Vesicles (LUVs)
3.3. Partition of Hoechst 33342 to POPC LUVs
3.4. Quantum Chemical Calculations
3.5. MD Simulation Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Appendix A

References
- Bazhulina, N.P.; Nikitin, A.M.; Rodin, S.A.; Surovaya, A.N.; Kravatsky, Y.V.; Pismensky, V.F.; Archipova, V.S.; Martin, R.; Gursky, G. V Binding of Hoechst 33258 and Its Derivatives to DNA. J. Biomol. Struct. Dyn. 2009, 26, 701–718. [Google Scholar] [CrossRef] [PubMed]
- Karlsson, H.J.; Bergqvist, M.H.; Lincoln, P.; Westman, G. Syntheses and DNA-Binding Studies of a Series of Unsymmetrical Cyanine Dyes: Structural Influence on the Degree of Minor Groove Binding to Natural DNA. Bioorg. Med. Chem. 2004, 12, 2369–2384. [Google Scholar] [CrossRef] [PubMed]
- Nogueira, J.J.; Oppel, M.; González, L. Enhancing Intersystem Crossing in Phenotiazinium Dyes by Intercalation into DNA. Angew. Chem. Int. Ed. 2015, 54, 4375–4378. [Google Scholar] [CrossRef] [PubMed]
- Berdnikova, D.V.; Sosnin, N.I.; Fedorova, O.A.; Ihmels, H. Governing the DNA-Binding Mode of Styryl Dyes by the Length of Their Alkyl Substituents—From Intercalation to Major Groove Binding. Org. Biomol. Chem. 2018, 16, 545–554. [Google Scholar] [CrossRef] [PubMed]
- Abeywickrama, C.S.; Wijesinghe, K.J.; Plescia, C.B.; Fisher, L.S.; Goodson, T., III; Stahelin, R.V.; Pang, Y. A Pyrene-Based Two-Photon Excitable Fluorescent Probe to Visualize Nuclei in Live Cells. Photochem. Photobiol. Sci. 2020, 19, 1152–1159. [Google Scholar] [CrossRef] [PubMed]
- Weisenfeld, R.B. Mass Transport Kinetics of the DNA-Binding Dye Hoechst-33342 into Bovine Spermatozoa. Bioorg. Med. Chem. 2007, 15, 6361–6366. [Google Scholar] [CrossRef]
- Lalande, M.E.; Ling, V.; Miller, R.G. Hoechst 33342 Dye Uptake as a Probe of Membrane Permeability Changes in Mammalian Cells. Proc. Natl. Acad. Sci. USA 1981, 78, 363–367. [Google Scholar] [CrossRef]
- Neuberger, A.; van Veen, H.W. Hoechst 33342 Is a Hidden “Janus” amongst Substrates for the Multidrug Efflux Pump LmrP. PLoS ONE 2015, 10, e0141991. [Google Scholar] [CrossRef]
- Tang, F.; Ouyang, H.; Yang, J.Z.; Borchardt, R.T. Bidirectional Transport of Rhodamine 123 and Hoechst 33342, Fluorescence Probes of the Binding Sites on P-Glycoprotein, across MDCK–MDR1 Cell Monolayers. J. Pharm. Sci. 2004, 93, 1185–1194. [Google Scholar] [CrossRef]
- Clay, A.T.; Sharom, F.J. Lipid Bilayer Properties Control Membrane Partitioning, Binding, and Transport of P-Glycoprotein Substrates. Biochemistry 2013, 52, 343–354. [Google Scholar] [CrossRef]
- Bucevičius, J.; Lukinavičius, G.; Gerasimaitė, R. The Use of Hoechst Dyes for DNA Staining and Beyond. Chemosensors 2018, 6, 18. [Google Scholar] [CrossRef]
- Alemán, C.; Namba, A.M.; Casanovas, J. Acid-Base and Electronic Structure-Dependent Properties of Hoechst 33342. J. Biomol. Struct. Dyn. 2005, 23, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, A.B.; Corder, A.B.; Ling, V. P-Glycoprotein-Mediated Hoechst 33342 Transport Out of the Lipid Bilayer. Eur. J. Biochem. 1997, 250, 115–121. [Google Scholar] [CrossRef] [PubMed]
- Eckford, P.D.W.; Sharom, F.J. ABC Efflux Pump-Based Resistance to Chemotherapy Drugs. Chem. Rev. 2009, 109, 2989–3011. [Google Scholar] [CrossRef] [PubMed]
- Chufan, E.E.; Sim, H.-M.; Ambudkar, S. V Chapter Three—Molecular Basis of the Polyspecificity of P-Glycoprotein (ABCB1): Recent Biochemical and Structural Studies. Adv. Cancer Res. 2015, 125, 71–96. [Google Scholar] [PubMed]
- Benzimidazole Derivatives—Drugbank Online. Available online: https://www.drugbank.ca/categories/DBCAT002403 (accessed on 12 June 2023).
- Imidazole Derivatives—Drugbank Online. Available online: https://www.drugbank.ca/categories/DBCAT002246 (accessed on 12 June 2023).
- Alghamdi, S.S.; Suliman, R.S.; Almutairi, K.; Kahtani, K.; Aljatli, D. Imidazole as a Promising Medicinal Scaffold: Current Status and future Direction. Drug Des. Devel. Ther. 2021, 15, 3289–3312. [Google Scholar] [CrossRef]
- Rezai, T.; Bock, J.E.; Zhou, M.V.; Kalyanaraman, C.; Lokey, R.S.; Jacobson, M.P. Conformational Flexibility, Internal Hydrogen Bonding, and Passive Membrane Permeability: Successful in Silico Prediction of the Relative Permeabilities of Cyclic Peptides. J. Am. Chem. Soc. 2006, 128, 14073–14080. [Google Scholar] [CrossRef]
- Andersen, P.S.; Fuchs, M. Potential Energy Barriers to Ion Transport within Lipid Bilayers. Studies with Tetraphenylborate. Biophys. J. 1975, 15, 795–830. [Google Scholar] [CrossRef]
- Deamer, D.W.; Bramhall, J. Permeability of Lipid Bilayers to Water and Ionic Solutes. Chem. Phys. Lipids 1986, 40, 167–188. [Google Scholar] [CrossRef]
- Flewelling, R.F.; Hubbell, W.L. Hydrophobic Ion Interactions with Membranes. Thermodynamic Analysis of Tetraphenylphosphonium Binding to Vesicles. Biophys. J. 1986, 49, 531–540. [Google Scholar] [CrossRef]
- Gaohua, L.; Miao, X.; Dou, L. Crosstalk of Physiological PH and Chemical PKa under the Umbrella of Physiologically Based Pharmacokinetic Modeling of Drug Absorption, Distribution, Metabolism, Excretion, and Toxicity. Expert Opin. Drug Metab. Toxicol. 2021, 17, 1103–1124. [Google Scholar] [CrossRef] [PubMed]
- MarvinSketch Version 22.9.0. Available online: http://www.chemaxon.com (accessed on 24 May 2023).
- Pradas, I.; Huynh, K.; Cabré, R.; Ayala, V.; Meikle, P.J.; Jové, M.; Pamplona, R. Lipidomics Reveals a Tissue-Specific Fingerprint. Front. Physiol. 2018, 9, 1165. [Google Scholar] [CrossRef]
- Aviram, R.; Manella, G.; Kopelman, N.; Neufeld-Cohen, A.; Zwighaft, Z.; Elimelech, M.; Adamovich, Y.; Golik, M.; Wang, C.; Han, X.; et al. Lipidomics Analyses Reveal Temporal and Spatial Lipid Organization and Uncover Daily Oscillations in Intracellular Organelles. Mol. Cell 2016, 62, 636–648. [Google Scholar] [CrossRef] [PubMed]
- Gerl, M.J.; Sampaio, J.L.; Urban, S.; Kalvodova, L.; Verbavatz, J.-M.; Binnington, B.; Lindemann, D.; Lingwood, C.A.; Shevchenko, A.; Schroeder, C.; et al. Quantitative Analysis of the Lipidomes of the Influenza Virus Envelope and MDCK Cell Apical Membrane. J. Cell Biol. 2012, 196, 213–221. [Google Scholar] [CrossRef] [PubMed]
- Leidl, K.; Liebisch, G.; Richter, D.; Schmitz, G. Mass Spectrometric Analysis of Lipid Species of Human Circulating Blood Cells. Biochim. Et Biophys. Acta (BBA) Mol. Cell Biol. Lipids 2008, 1781, 655–664. [Google Scholar] [CrossRef]
- Moreno, M.J.; Teles Martins, P.A.; Bernardino, E.F.; Abel, B.; Ambudkar, S. V Characterization of the Lipidome and Biophysical Properties of Membranes from High Five Insect Cells Expressing Mouse P-Glycoprotein. Biomolecules 2021, 11, 426. [Google Scholar] [CrossRef] [PubMed]
- Klose, C.; Surma, M.A.; Simons, K. Organellar Lipidomics—Background and Perspectives. Curr. Opin. Cell Biol. 2013, 25, 406–413. [Google Scholar] [CrossRef]
- Martins, P.T.; Velazquez-Campoy, A.; Vaz, W.L.C.; Cardoso, R.M.S.; Valério, J.; Moreno, M.J. Kinetics and Thermodynamics of Chlorpromazine Interaction with Lipid Bilayers: Effect of Charge and Cholesterol. J. Am. Chem. Soc. 2012, 134, 4184–4195. [Google Scholar] [CrossRef]
- Coreta-Gomes, F.M.; Martins, P.A.T.; Velazquez-Campoy, A.; Vaz, W.L.C.; Geraldes, C.F.G.; Moreno, M.J. Interaction of Bile Salts with Model Membranes Mimicking the Gastrointestinal Epithelium: A Study by Isothermal Titration Calorimetry. Langmuir 2015, 31, 9097–9104. [Google Scholar] [CrossRef]
- Rowe, E.S.; Zhang, F.; Leung, T.W.; Parr, J.S.; Guy, P.T. Thermodynamics of Membrane Partitioning for a Series of N-Alcohols Determined by Titration Calorimetry: Role of Hydrophobic Effects. Biochemistry 1998, 37, 2430–2440. [Google Scholar] [CrossRef]
- Martins, P.A.T.; Domingues, N.; Pires, C.; Alves, A.M.; Palmeira, T.; Samelo, J.; Cardoso, R.; Velazquez-Campoy, A.; Moreno, M.J. Molecular Crowding Effects on the Distribution of Amphiphiles in Biological Media. Colloids Surf. B Biointerfaces 2019, 180, 319–325. [Google Scholar] [CrossRef] [PubMed]
- Beschiaschvili, G.; Seelig, J. Peptide Binding to Lipid Bilayers. Nonclassical Hydrophobic Effect and Membrane-Induced PK Shifts. Biochemistry 1992, 31, 10044–10053. [Google Scholar] [CrossRef] [PubMed]
- Loura, L.M.S.; Prates Ramalho, J.P. Fluorescent Membrane Probes’ Behavior in Lipid Bilayers: Insights from Molecular Dynamics Simulations. Biophys. Rev. 2009, 1, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Loura, L.M.S.; Ramalho, J.P.P. Recent Developments in Molecular Dynamics Simulations of Fluorescent Membrane Probes. Molecules 2011, 16, 5437–5452. [Google Scholar] [CrossRef] [PubMed]
- Filipe, H.A.L.; Moreno, M.J.; Loura, L.M.S. The Secret Lives of Fluorescent Membrane Probes as Revealed by Molecular Dynamics Simulations. Molecules 2020, 25, 3424. [Google Scholar] [CrossRef]
- Debruycker, V.; Hutchin, A.; Masureel, M.; Ficici, E.; Martens, C.; Legrand, P.; Stein, R.A.; Mchaourab, H.S.; Faraldo-Gómez, J.D.; Remaut, H.; et al. An Embedded Lipid in the Multidrug Transporter LmrP Suggests a Mechanism for Polyspecificity. Nat. Struct. Mol. Biol. 2020, 27, 829–835. [Google Scholar] [CrossRef]
- Thaker, T.M.; Mishra, S.; Zhou, W.; Mohan, M.; Tang, Q.; Faraldo-Goméz, J.D.; Mchaourab, H.S.; Tomasiak, T.M. Asymmetric Drug Binding in an ATP-Loaded Inward-Facing State of an ABC Transporter. Nat. Chem. Biol. 2022, 18, 226–235. [Google Scholar] [CrossRef]
- Thai, N.Q.; Tseng, N.-H.; Vu, M.T.; Nguyen, T.T.; Linh, H.Q.; Hu, C.-K.; Chen, Y.-R.; Li, M.S. Discovery of DNA Dyes Hoechst 34580 and 33342 as Good Candidates for Inhibiting Amyloid Beta Formation: In Silico and in Vitro Study. J. Comput. Aided Mol. Des. 2016, 30, 639–650. [Google Scholar] [CrossRef]
- Subramanian, N.; Schumann-Gillett, A.; Mark, A.E.; O’Mara, M.L. Probing the Pharmacological Binding Sites of P-Glycoprotein Using Umbrella Sampling Simulations. J. Chem. Inf. Model 2019, 59, 2287–2298. [Google Scholar] [CrossRef]
- Singh, M.; Sur, S.; Rastogi, G.K.; Jayaram, B.; Tandon, V. Bi and Tri-Substituted Phenyl Rings Containing Bisbenzimidazoles Bind Differentially with DNA Duplexes: A Biophysical and Molecular Simulation Study. Mol. Biosyst. 2013, 9, 2541–2553. [Google Scholar] [CrossRef]
- Putman, M.; Koole, L.A.; van Veen, H.W.; Konings, W.N. The Secondary Multidrug Transporter LmrP Contains Multiple Drug Interaction Sites. Biochemistry 1999, 38, 13900–13905. [Google Scholar] [CrossRef] [PubMed]
- Ladinig, M.; Leupin, W.; Meuwly, M.; Respondek, M.; Wirz, J.; Zoete, V. Protonation Equilibria of Hoechst 33258 in Aqueous Solution. Helv. Chim. Acta 2005, 88, 53–67. [Google Scholar] [CrossRef]
- Swain, B.M.; Guo, D.; Singh, H.; Rawlins, P.B.; McAlister, M.; van Veen, H.W. Complexities of a Protonatable Substrate in Measurements of Hoechst 33342 Transport by Multidrug Transporter LmrP. Sci. Rep. 2020, 10, 20026. [Google Scholar] [CrossRef] [PubMed]
- Austin, R.P.; Barton, P.; Davis, A.M.; Fessey, R.E.; Wenlock, M.C. The Thermodynamics of the Partitioning of Ionizing Molecules Between Aqueous Buffers and Phospholipid Membranes. Pharm. Res. 2005, 22, 1649–1657. [Google Scholar] [CrossRef]
- Lombardi, D.; Cuenoud, B.; Krämer, S.D. Lipid Membrane Interactions of Indacaterol and Salmeterol: Do They Influence Their Pharmacological Properties? Eur. J. Pharm. Sci. 2009, 38, 533–547. [Google Scholar] [CrossRef]
- Katzer, M.; Stillwell, W. Partitioning of ABA into Bilayers of Di-Saturated Phosphatidylcholines as Measured by DSC. Biophys. J. 2003, 84, 314–325. [Google Scholar] [CrossRef][Green Version]
- Thomae, A.V.; Wunderli-Allenspach, H.; Krämer, S.D. Permeation of Aromatic Carboxylic Acids across Lipid Bilayers: The PH-Partition Hypothesis Revisited. Biophys. J. 2005, 89, 1802–1811. [Google Scholar] [CrossRef]
- Thomae, A.V.; Koch, T.; Panse, C.; Wunderli-Allenspach, H.; Krämer, S.D. Comparing the Lipid Membrane Affinity and Permeation of Drug-like Acids: The Intriguing Effects of Cholesterol and Charged Lipids. Pharm. Res. 2007, 24, 1457–1472. [Google Scholar] [CrossRef]
- Filipe, H.A.L.; Coreta-Gomes, F.M.; Velazquez-Campoy, A.; Almeida, A.R.; Peixoto, A.F.; Pereira, M.M.; Vaz, W.L.C.; Moreno, M.J. Synthesis and Characterization of a Lipidic Alpha Amino Acid: Solubility and Interaction with Serum Albumin and Lipid Bilayers. J. Phys. Chem. B 2013, 117, 3439–3448. [Google Scholar] [CrossRef]
- Heerklotz, H. The Microcalorimetry of Lipid Membranes. J. Phys. Condens. Matter 2004, 16, R441. [Google Scholar] [CrossRef]
- Goldberg, R.N.; Kishore, N.; Lennen, R.M. Thermodynamic Quantities for the Ionization Reactions of Buffers. J. Phys. Chem. Ref. Data 2002, 31, 231–370. [Google Scholar] [CrossRef]
- Elías-Wolff, F.; Lindén, M.; Lyubartsev, A.P.; Brandt, E.G. Computing Curvature Sensitivity of Biomolecules in Membranes by Simulated Buckling. J. Chem. Theory Comput. 2018, 14, 1643–1655. [Google Scholar] [CrossRef]
- Paketurytė, V.; Petrauskas, V.; Zubrienė, A.; Abian, O.; Bastos, M.; Chen, W.-Y.; Moreno, M.J.; Krainer, G.; Linkuvienė, V.; Sedivy, A.; et al. Uncertainty in Protein–Ligand Binding Constants: Asymmetric Confidence Intervals versus Standard Errors. Eur. Biophys. J. 2021, 50, 661–670. [Google Scholar] [CrossRef]
- Filipe, H.A.L.; Moreno, M.J.; Róg, T.; Vattulainen, I.; Loura, L.M.S. How to Tackle the Issues in Free Energy Simulations of Long Amphiphiles Interacting with Lipid Membranes: Convergence and Local Membrane Deformations. J. Phys. Chem. B 2014, 118, 3572–3581. [Google Scholar] [CrossRef] [PubMed]
- Filipe, H.A.L.; Javanainen, M.; Salvador, A.; Galvão, A.M.; Vattulainen, I.; Loura, L.M.S.; Moreno, M.J. Quantitative Assessment of Methods Used To Obtain Rate Constants from Molecular Dynamics Simulations—Translocation of Cholesterol across Lipid Bilayers. J. Chem. Theory Comput. 2018, 14, 3840–3848. [Google Scholar] [CrossRef] [PubMed]
- Magalhães, N.; Simões, G.M.; Ramos, C.; Samelo, J.; Oliveira, A.C.; Filipe, H.A.L.; Ramalho, J.P.P.; Moreno, M.J.; Loura, L.M.S. Interactions between Rhodamine Dyes and Model Membrane Systems—Insights from Molecular Dynamics Simulations. Molecules 2022, 27, 1420. [Google Scholar] [CrossRef]
- Oliveira, A.C.; Filipe, H.A.L.; Loura, L.M.S. Fluorescent Probes Cis- and Trans-Parinaric Acids in Fluid and Gel Lipid Bilayers: A Molecular Dynamics Study. Molecules 2023, 28, 2241. [Google Scholar] [CrossRef]
- Filipe, H.A.L.; Loura, L.M.S.; Moreno, M.J. Permeation of a Homologous Series of NBD-Labeled Fatty Amines through Lipid Bilayers: A Molecular Dynamics Study. Membranes 2023, 13, 551. [Google Scholar] [CrossRef]
- MacCallum, J.L.; Tieleman, D.P. Computer Simulation of the Distribution of Hexane in a Lipid Bilayer: Spatially Resolved Free Energy, Entropy, and Enthalpy Profiles. J. Am. Chem. Soc. 2006, 128, 125–130. [Google Scholar] [CrossRef]
- Paloncýová, M.; DeVane, R.; Murch, B.; Berka, K.; Otyepka, M. Amphiphilic Drug-Like Molecules Accumulate in a Membrane below the Head Group Region. J. Phys. Chem. B 2014, 118, 1030–1039. [Google Scholar] [CrossRef]
- Kiametis, A.S.; Stock, L.; Cirqueira, L.; Treptow, W. Atomistic Model for Simulations of the Sedative Hypnotic Drug 2,2,2-Trichloroethanol. ACS Omega 2018, 3, 15916–15923. [Google Scholar] [CrossRef]
- Tang, P.K.; Chakraborty, K.; Hu, W.; Kang, M.; Loverde, S.M. Interaction of Camptothecin with Model Cellular Membranes. J. Chem. Theory Comput. 2020, 16, 3373–3384. [Google Scholar] [CrossRef] [PubMed]
- Piasentin, N.; Lian, G.; Cai, Q. Evaluation of Constrained and Restrained Molecular Dynamics Simulation Methods for Predicting Skin Lipid Permeability. ACS Omega 2021, 6, 35363–35374. [Google Scholar] [CrossRef] [PubMed]
- Samelo, J.; Mora, M.J.; Granero, G.E.; Moreno, M.J. Partition of Amphiphilic Molecules to Lipid Bilayers by ITC: Low-Affinity Solutes. ACS Omega 2017, 2, 6863–6869. [Google Scholar] [CrossRef]
- Thermo Scientific Instructions—Hoechst 33342. Available online: https://assets.thermofisher.com/TFS-Assets/LSG/manuals/MAN0011717_Hoechst_33342_UG.pdf (accessed on 12 June 2023).
- Moreno, M.J.; Bastos, M.; Velazquez-Campoy, A. Partition of Amphiphilic Molecules to Lipid Bilayers by Isothermal Titration Calorimetry. Anal. Biochem. 2010, 399, 44–47. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Amovilli, C.; Barone, V.; Cammi, R.; Cancès, E.; Cossi, M.; Mennucci, B.; Pomelli, C.S.; Tomasi, J. Recent Advances in the Description of Solvent Effects with the Polarizable Continuum Model. Adv. Quantum Chem. 1998, 32, 227–261. [Google Scholar]
- Cossi, M.; Barone, V. Time-Dependent Density Functional Theory for Molecules in Liquid Solutions. J. Chem. Phys. 2001, 115, 4708–4717. [Google Scholar] [CrossRef]
- Ribeiro, R.F.; Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Use of Solution-Phase Vibrational Frequencies in Continuum Models for the Free Energy of Solvation. J. Phys. Chem. B 2011, 115, 14556–14562. [Google Scholar] [CrossRef]
- Besler, B.H.; Merz, K.M., Jr.; Kollman, P.A. Atomic Charges Derived from Semiempirical Methods. J. Comput. Chem. 1990, 11, 431–439. [Google Scholar] [CrossRef]
- Singh, U.C.; Kollman, P.A. An Approach to Computing Electrostatic Charges for Molecules. J. Comput. Chem. 1984, 5, 129–145. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision, version C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindah, E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef]
- Schmid, N.; Eichenberger, A.P.; Choutko, A.; Riniker, S.; Winger, M.; Mark, A.E.; van Gunsteren, W.F. Definition and Testing of the GROMOS Force-Field Versions 54A7 and 54B7. Eur. Biophys. J. 2011, 40, 843–856. [Google Scholar] [CrossRef]
- Poger, D.; Van Gunsteren, W.F.; Mark, A.E. A New Force Field for Simulating Phosphatidylcholine Bilayers. J. Comput. Chem. 2010, 31, 1117–1125. [Google Scholar] [CrossRef] [PubMed]
- Poger, D.; Mark, A.E. On the Validation of Molecular Dynamics Simulations of Saturated and Cis-Monounsaturated Phosphatidylcholine Lipid Bilayers: A Comparison with Experiment. J. Chem. Theory Comput. 2010, 6, 325–336. [Google Scholar] [CrossRef]
- Malde, A.K.; Zuo, L.; Breeze, M.; Stroet, M.; Poger, D.; Nair, P.C.; Oostenbrink, C.; Mark, A.E. An Automated Force Field Topology Builder (ATB) and Repository: Version 1.0. J. Chem. Theory Comput. 2011, 7, 4026–4037. [Google Scholar] [CrossRef]
- Stroet, M.; Caron, B.; Visscher, K.M.; Geerke, D.P.; Malde, A.K.; Mark, A.E. Automated Topology Builder Version 3.0: Prediction of Solvation Free Enthalpies in Water and Hexane. J. Chem. Theory Comput. 2018, 14, 5834–5845. [Google Scholar] [CrossRef]
- Koziara, K.B.; Stroet, M.; Malde, A.K.; Mark, A.E. Testing and Validation of the Automated Topology Builder (ATB) Version 2.0: Prediction of Hydration Free Enthalpies. J. Comput. Aided Mol. Des. 2014, 28, 221–233. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; Hermans, J. Interaction Models for Water in Relation to Protein Hydration. In Intermolecular Forces; Pullman, B., Ed.; Springer: Dordrecht, The Netherlands, 1981; pp. 331–342. [Google Scholar]
- Filipe, H.A.L.; Santos, L.S.; Prates Ramalho, J.P.; Moreno, M.J.; Loura, L.M.S. Behaviour of NBD-Head Group Labelled Phosphatidylethanolamines in POPC Bilayers: A Molecular Dynamics Study. Phys. Chem. Chem. Phys. 2015, 17, 20066–20079. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical Sampling Distributions in Monte Carlo Free-Energy Estimation: Umbrella Sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Hub, J.S.; De Groot, B.L.; Van Der Spoel, D. G_wham—A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates. J. Chem. Theory Comput. 2010, 6, 3713–3720. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Shore, P.A.; Brodie, B.B.; Hogben, C.A.M. The Gastric Secretion of Drugs: A PH Partition Hypothesis. J. Pharmacol. Exp. Ther. 1957, 119, 361–369. [Google Scholar]
- Moreno, M.J.; Salvador, A. Ligand’s Partition to the Lipid Bilayer Should Be Accounted for When Estimating Their Affinity to Proteins. Molecules 2023, 28, 3136. [Google Scholar] [CrossRef] [PubMed]
- Moreno, M.J.; Filipe, H.A.L.; Cunha, S.V.P.; Ramos, C.V.; Martins, P.A.T.; Abel, B.; Loura, L.M.S.; Ambudkar, S. V Interaction of a Homologous Series of Amphiphiles with P-Glycoprotein in a Membrane Environment—Contributions of Polar and Non-Polar Interactions. Pharmaceutics 2023, 15, 174. [Google Scholar] [CrossRef]



| pH | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|
| N | 4 | 5 | 3 | 6 | 6 | 4 | 2 | 4 | 4 | |
| log KP | µ | 2.8 | 2.8 | 3.3 | 3.3 | 3.6 | 3.6 | 3.7 | 3.8 | 3.6 |
| σ | 0.16 | 0.22 | 0.26 | 0.17 | 0.19 | 0.05 | 0.01 | 0.08 | 0.06 | |
| KP | µ | 5.8 × 102 | 6.1 × 102 | 2.6 × 103 | 2.0 × 103 | 3.8 × 103 | 4.4 × 103 | 4.7 × 103 | 6.3 × 103 | 4.3 × 103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cordeiro, M.M.; Filipe, H.A.L.; Santos, P.d.; Samelo, J.; Ramalho, J.P.P.; Loura, L.M.S.; Moreno, M.J. Interaction of Hoechst 33342 with POPC Membranes at Different pH Values. Molecules 2023, 28, 5640. https://doi.org/10.3390/molecules28155640
Cordeiro MM, Filipe HAL, Santos Pd, Samelo J, Ramalho JPP, Loura LMS, Moreno MJ. Interaction of Hoechst 33342 with POPC Membranes at Different pH Values. Molecules. 2023; 28(15):5640. https://doi.org/10.3390/molecules28155640
Chicago/Turabian StyleCordeiro, Margarida M., Hugo A. L. Filipe, Patrícia dos Santos, Jaime Samelo, João P. Prates Ramalho, Luís M. S. Loura, and Maria J. Moreno. 2023. "Interaction of Hoechst 33342 with POPC Membranes at Different pH Values" Molecules 28, no. 15: 5640. https://doi.org/10.3390/molecules28155640
APA StyleCordeiro, M. M., Filipe, H. A. L., Santos, P. d., Samelo, J., Ramalho, J. P. P., Loura, L. M. S., & Moreno, M. J. (2023). Interaction of Hoechst 33342 with POPC Membranes at Different pH Values. Molecules, 28(15), 5640. https://doi.org/10.3390/molecules28155640












