Prediction and Construction of Energetic Materials Based on Machine Learning Methods
Abstract
1. Introduction
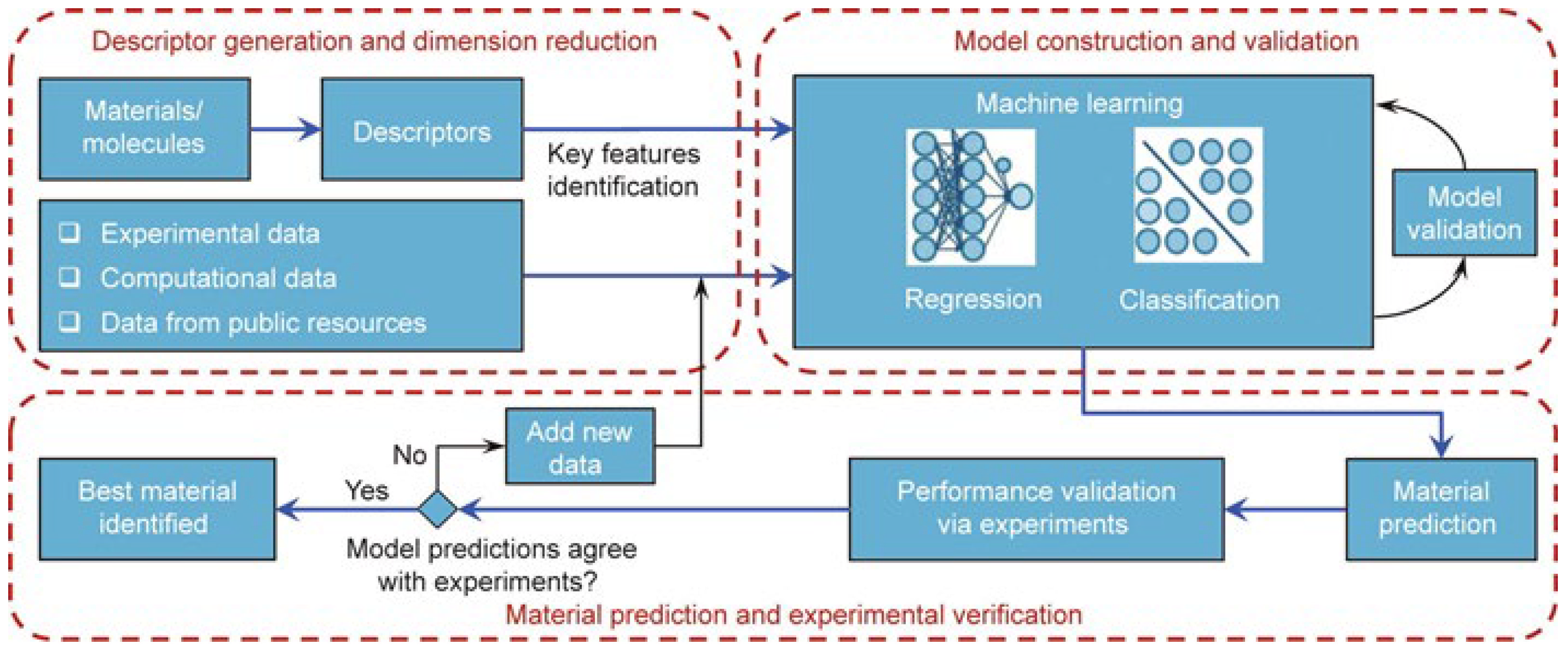
2. ML Workflow
2.1. Data Preparation
2.2. Feature Engineering
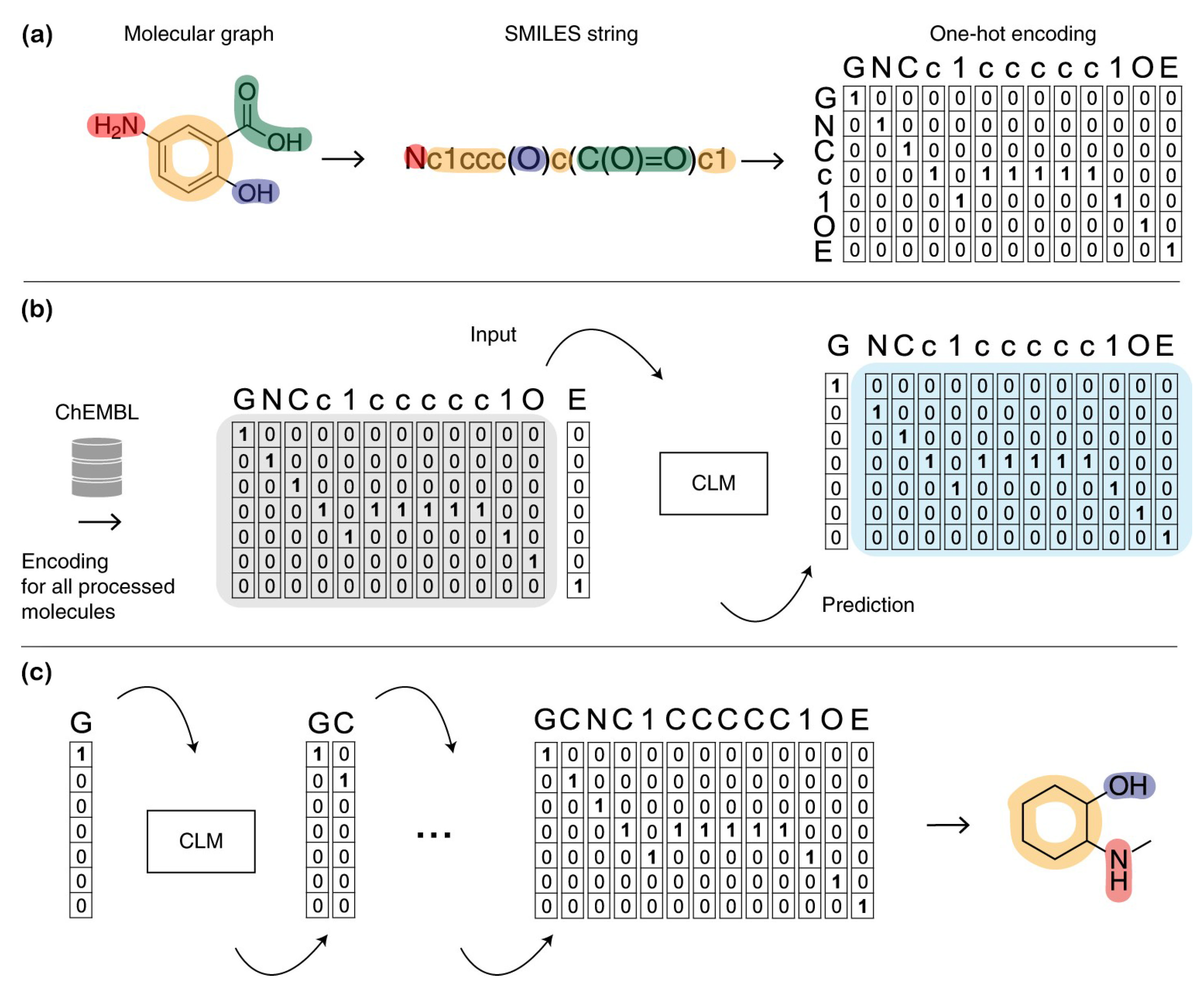
2.2.1. Traditional Class of Molecular Representation
2.2.2. Computer-Learned Representation
2.3. ML Models in EMs Prediction and Construction
2.3.1. The Regression Models
2.3.2. The Classification Models
2.4. Model Performance Evaluation
2.4.1. Model Evaluation in the Regression Model
2.4.2. Model Evaluation in the Classification Model
3. Applications of ML in R&D of EMs
3.1. Single-Compound EMs
3.2. Composite EMs
4. Challenges of Applying ML Methods
5. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EMs | energetic materials |
| R&D | research and development |
| ML | machine learning |
| DFT | density functional theory |
| HE | high explosives |
| CHNO | carbon, hydrogen, nitrogen, and oxygen |
| CSD | Cambridge Structural Database |
| CCDC | Cambridge Crystallographic Data Centre |
| OB | oxygen balance |
| SMILES | simplified molecular input line entry specification |
| RNN | recurrent neural network |
| MF | multi-fidelity |
| CNN | convolutional neural network |
| LSTM | long short-term memory |
| KRR | kernel ridge regression |
| GNN | graph neural network |
| KNN | K-nearest neighbor |
| SVR | Support vector regression |
| RF | Random forests |
| MPNN | Message passing neural network |
| SVM | Support vector machine |
| QSPR | Quantitative structure−property relationship |
| SRNN | RNN model with inclusion of the pretrained knowledge |
| ANN | Artificial Neural Network |
| MLP | Multilayer perceptron |
| PLSR | Partial least-squares regression |
| C−J | Chapman−Jouguet |
| H50 | Values of the drop weight impact height |
| QNO2 | Mulliken net charges of the nitro group |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| R2 | determination coefficient |
| TNT | 2,4,6-trinitrotoluene |
| Pe(TNT) | TNT equivalent power index |
| HNB | Hexanitrobenzene |
| TATB | 1,3,5-triamino-2,4,6-trinitrobenzene |
| HTVS | high-throughput virtual screening |
| ICM-104 | 7,8- dinitropyrazolo[1,5-a][1,3,5]triazine-2,4-diamine |
| LLM-105 | 2,6-diamino-3,5-dinitropyrazine-1-oxide |
| RDX | 1,3,5-trinitro-1,3,5-triazinane |
| CL-20 | Hexanitrohexaazaisowurtzitane |
| SA | synthetic accessibility |
| GAP | glycidyl azide polymer |
References
- Song, S.; Wang, Y.; Chen, F.; Yan, M.; Zhang, Q. Machine learning-assisted high-throughput virtual screening for on-demand customization of advanced energetic materials. Engineering 2022, 10, 99–109. [Google Scholar] [CrossRef]
- Elton, D.C.; Boukouvalas, Z.; Butrico, M.S.; Fuge, M.D.; Chung, P.W. Applying machine learning techniques to predict the properties of energetic materials. Sci. Rep. 2018, 8, 9059. [Google Scholar] [CrossRef] [PubMed]
- Bu, R.; Xiong, Y.; Zhang, C. π–π Stacking Contributing to the Low or Reduced Impact Sensitivity of Energetic Materials. Cryst. Growth Des. 2020, 20, 2824–2841. [Google Scholar] [CrossRef]
- Wang, R.; Liu, J.; He, X.; Xie, W.; Zhang, C. Decoding hexanitrobenzene (HNB) and 1,3,5-triamino-2,4,6-trinitrobenzene (TATB) as two distinctive energetic nitrobenzene compounds by machine learning. Phys. Chem. Chem. Phys. 2022, 24, 9875–9884. [Google Scholar] [CrossRef] [PubMed]
- Tsyshevsky, R.; Pagoria, P.; Zhang, M.; Racoveanu, A.; Parrish, D.A.; Smirnov, A.S.; Kuklja, M.M. Comprehensive End-to-End Design of Novel High Energy Density Materials: I. Synthesis and Characterization of Oxadiazole Based Heterocycles. J. Phys. Chem. C 2017, 121, 23853–23864. [Google Scholar] [CrossRef]
- Yao, W.; Xue, Y.; Qian, L.; Yang, H.; Cheng, G. Combination of 1,2,3-triazole and 1,2,4-triazole frameworks for new high-energy and low-sensitivity compounds. Energetic Mater. Front. 2021, 2, 131–138. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Y.; Feng, Y.; Yang, X.; Zhang, Q. 5,6-Fused bicyclic tetrazolo-pyridazine energetic materials. Chem. Commun. (Camb) 2020, 56, 1493–1496. [Google Scholar] [CrossRef]
- Zohari, N.; Ghiasvand Mohammadkhani, F. Prediction of the Density of Energetic Co-crystals: A Way to Design High Performance Energetic Materials. Cent. Eur. J. Energetic Mater. 2020, 17, 31–48. [Google Scholar] [CrossRef]
- Zhang, J.; Mitchell, L.A.; Parrish, D.A.; Shreeve, J.M. Enforced Layer-by-Layer Stacking of Energetic Salts towards High-Performance Insensitive Energetic Materials. J. Am. Chem. Soc. 2015, 137, 10532–10535. [Google Scholar] [CrossRef]
- Schulze, M.C.; Scott, B.L.; Chavez, D.E. A high density pyrazolo-triazine explosive (PTX). J. Mater. Chem. A 2015, 3, 17963–17965. [Google Scholar] [CrossRef]
- Ma, P.; Jin, Y.T.; Wu, P.H.; Hu, W.; Pan, Y.; Zang, X.W.; Zhu, S.G. Synthesis, molecular dynamic simulation, and density functional theory insight into the cocrystal explosive of 2,4,6-trinitrotoluene/1,3,5-trinitrobenzene. Combust. Explos. Shock. Waves 2017, 53, 596–604. [Google Scholar] [CrossRef]
- Tsyshevsky, R.; Smirnov, A.S.; Kuklja, M.M. Comprehensive End-To-End Design of Novel High Energy Density Materials: III. Fused Heterocyclic Energetic Compounds. J. Phys. Chem. C 2019, 123, 8688–8698. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, Y.; Hu, R.; Lin, X.; Hu, J.; Pu, X. A property-oriented adaptive design framework for rapid discovery of energetic molecules based on small-scale labeled datasets. RSC Adv. 2021, 11, 25764–25776. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Jiang, X.; Rogachev, A.V.; Sun, D.; Zang, X. Growth and characteristics of diamond-like carbon films with titanium and titanium nitride functional layers by cathode arc plasma. Surf. Coat. Technol. 2013, 223, 17–23. [Google Scholar] [CrossRef]
- Avdeeva, A.V.; Zang, X.; Muradova, A.G.; Yurtov, E.V. Formation of Zinc-Oxide Nanorods by the Precipitation Method. Semiconductors 2018, 51, 1724–1727. [Google Scholar] [CrossRef]
- Zhou, T.; Song, Z.; Sundmacher, K. Big Data Creates New Opportunities for Materials Research: A Review on Methods and Applications of Machine Learning for Materials Design. Engineering 2019, 5, 1017–1026. [Google Scholar] [CrossRef]
- Koroleva, M.Y.; Tokarev, A.M.; Yurtov, E.V. Langevin-dynamics simulation of flocculation in water-in-oil emulsions. Colloid. J. 2013, 75, 660–667. [Google Scholar] [CrossRef]
- Koroleva, M.Y.; Plotniece, A. Aggregative Stability of Nanoemulsions in eLiposomes: Analysis of the Results of Mathematical Simulation. Colloid. J. 2022, 84, 162–168. [Google Scholar] [CrossRef]
- Shi, A.; Zheng, H.; Chen, Z.; Zhang, W.; Zhou, X.; Rossi, C.; Shen, R.; Ye, Y. Exploring the Interfacial Reaction of Nano Al/CuO Energetic Films through Thermal Analysis and Ab Initio Molecular Dynamics Simulation. Molecules 2022, 27, 3586. [Google Scholar] [CrossRef]
- Zhou, X.; Torabi, M.; Lu, J.; Shen, R.; Zhang, K. Nanostructured energetic composites: Synthesis, ignition/combustion modeling, and applications. ACS Appl. Mater Interfaces 2014, 6, 3058–3074. [Google Scholar] [CrossRef]
- Ryan, K.; Lengyel, J.; Shatruk, M. Crystal Structure Prediction via Deep Learning. J. Am. Chem. Soc. 2018, 140, 10158–10168. [Google Scholar] [CrossRef] [PubMed]
- Ceriotti, M. Unsupervised machine learning in atomistic simulations, between predictions and understanding. J. Chem. Phys. 2019, 150, 150901. [Google Scholar] [CrossRef] [PubMed]
- Hou, F.; Ma, Y.; Hu, Z.; Ding, S.; Fu, H.; Wang, L.; Zhang, X.; Li, G. Machine Learning Enabled Quickly Predicting of Detonation Properties of N-Containing Molecules for Discovering New Energetic Materials. Adv. Theory Simul. 2021, 4, 2100057. [Google Scholar] [CrossRef]
- Nguyen, P.; Loveland, D.; Kim, J.T.; Karande, P.; Hiszpanski, A.M.; Han, T.Y.-J. Predicting Energetics Materials’ Crystalline Density from Chemical Structure by Machine Learning. J. Chem. Inf. Model. 2021, 61, 2147–2158. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.-C.; Botti, S.; Marques, M.A.L. Predicting stable crystalline compounds using chemical similarity. npj Comput. Mater. 2021, 7, 12. [Google Scholar] [CrossRef]
- Sumita, M.; Yang, X.; Ishihara, S.; Tamura, R.; Tsuda, K. Hunting for Organic Molecules with Artificial Intelligence: Molecules Optimized for Desired Excitation Energies. ACS Cent. Sci. 2018, 4, 1126–1133. [Google Scholar] [CrossRef]
- Kamlet, M.J.; Jacobs, S.J. Chemistry of Detonations. I. A Simple Method for Calculating Detonation Properties of C–H–N–O Explosives. J. Chem. Phys. 1968, 48, 23–35. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Shu, Y.J.; Huang, Y.G.; Zhao, X.D.; Dong, H.S. Investigation of correlation between impact sensitivities and nitro group charges in nitro compounds. J. Phys. Chem. B 2005, 109, 8978–8982. [Google Scholar] [CrossRef]
- Huang, L.; Massa, L. Applications of energetic materials by a theoretical method (discover energetic materials by a theoretical method). Int. J. Energetic Mater. Chem. Propuls. 2013, 12, 197–262. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, K.; Lee, Y. Machine Learning Enabled Tailor-Made Design of Application-Specific Metal-Organic Frameworks. ACS Appl. Mater. Interfaces 2020, 12, 734–743. [Google Scholar] [CrossRef]
- Jennings, P.C.; Lysgaard, S.; Hummelshøj, J.S.; Vegge, T.; Bligaard, T. Genetic algorithms for computational materials discovery accelerated by machine learning. npj Comput. Mater. 2019, 5, 46. [Google Scholar] [CrossRef]
- Bian, H.; Jiang, J.; Zhu, Z.; Dou, Z.; Tang, B. Design and implementation of an early-stage monitoring system for iron sulfides oxidation. Process. Saf. Environ. Prot. 2022, 165, 181–190. [Google Scholar] [CrossRef]
- Wu, R.-T.; Liu, T.-W.; Jahanshahi, M.R.; Semperlotti, F. Design of one-dimensional acoustic metamaterials using machine learning and cell concatenation. Struct. Multidiscip. Optim. 2021, 63, 2399–2423. [Google Scholar] [CrossRef]
- Moret, M.; Friedrich, L.; Grisoni, F.; Merk, D.; Schneider, G. Generative molecular design in low data regimes. Nat. Mach. Intell. 2020, 2, 171–180. [Google Scholar] [CrossRef]
- Hu, W.; Yu, X.; Huang, J.; Li, K.; Liu, Y. Accurate Prediction of the Boiling Point of Organic Molecules by Multi-Component Heterogeneous Learning Model. Acta Chim. Sin. 2022, 80, 714. [Google Scholar] [CrossRef]
- Ziletti, A.; Kumar, D.; Scheffler, M.; Ghiringhelli, L.M. Insightful classification of crystal structures using deep learning. Nat. Commun. 2018, 9, 2775. [Google Scholar] [CrossRef]
- Wang, P.-J.; Fan, J.-Y.; Su, Y.; Zhao, J.-J. Energetic potential of hexogen constructed by machine learning. Acta Physica. Sinica. 2020, 69, 238702. [Google Scholar] [CrossRef]
- Zheng, W.; Zhang, H.; Hu, H.; Liu, Y.; Li, S.; Ding, G.; Zhang, J. Performance prediction of perovskite materials based on different machine learning algorithms. Chin. J. Nonferrous Met. 2019, 29, 803–809. [Google Scholar] [CrossRef]
- Yu, J.; Wang, Y.; Dai, Z.; Yang, F.; Fallahpour, A.; Nasiri-Tabrizi, B. Structural features modeling of substituted hydroxyapatite nanopowders as bone fillers via machine learning. Ceram. Int. 2021, 47, 9034–9047. [Google Scholar] [CrossRef]
- Spannaus, A.; Law, K.J.H.; Luszczek, P.; Nasrin, F.; Micucci, C.P.; Liaw, P.K.; Santodonato, L.J.; Keffer, D.J.; Maroulas, V. Materials Fingerprinting Classification. Comput. Phys. Commun. 2021, 266, 108019. [Google Scholar] [CrossRef]
- Wang, X.; He, Y.; Cao, W.; Guo, W.; Zhang, T.; Zhang, J.; Shu, Q.; Guo, X.; Liu, R.; Yao, Y. Fast explosive performance prediction via small-dose energetic materials based on time-resolved imaging combined with machine learning. J. Mater. Chem. A 2022, 10, 13114–13123. [Google Scholar] [CrossRef]
- Kim, M.; Ha, M.Y.; Jung, W.-B.; Yoon, J.; Shin, E.; Kim, I.-d.; Lee, W.B.; Kim, Y.; Jung, H.-t. Searching for an Optimal Multi-Metallic Alloy Catalyst by Active Learning Combined with Experiments. Adv. Mater. 2022, 34, 2108900. [Google Scholar] [CrossRef]
- Cai, W.; Abudurusuli, A.; Xie, C.; Tikhonov, E.; Li, J.; Pan, S.; Yang, Z. Toward the Rational Design of Mid-Infrared Nonlinear Optical Materials with Targeted Properties via a Multi-Level Data-Driven Approach. Adv. Funct. Mater. 2022, 32, 2200231. [Google Scholar] [CrossRef]
- Cheng, G.; Gong, X.-G.; Yin, W.-J. Crystal structure prediction by combining graph network and optimization algorithm. Nat. Commun. 2022, 13, 1492. [Google Scholar] [CrossRef]
- Leitherer, A.; Ziletti, A.; Ghiringhelli, L.M. Robust recognition and exploratory analysis of crystal structures via Bayesian deep learning. Nat. Commun. 2021, 12, 6234. [Google Scholar] [CrossRef]
- Gubaev, K.; Podryabinkin, E.V.; Hart, G.L.W.; Shapeev, A.V. Accelerating high-throughput searches for new alloys with active learning of interatomic potentials. Comput. Mater. Sci. 2019, 156, 148–156. [Google Scholar] [CrossRef]
- Georgescu, A.B.; Ren, P.; Toland, A.R.; Zhang, S.; Miller, K.D.; Apley, D.W.; Olivetti, E.A.; Wagner, N.; Rondinelli, J.M. Database, Features, and Machine Learning Model to Identify Thermally Driven Metal-Insulator Transition Compounds. Chem. Mater. 2021, 33, 5591–5605. [Google Scholar] [CrossRef]
- Xia, K.; Gao, H.; Liu, C.; Yuan, J.; Sun, J.; Wang, H.-T.; Xing, D. A novel superhard tungsten nitride predicted by machine-learning accelerated crystal structure search. Sci. Bull. 2018, 63, 817–824. [Google Scholar] [CrossRef]
- An, H.; Smith, J.W.; Ji, B.; Cotty, S.; Zhou, S.; Yao, L.; Kalutantirige, F.C.; Chen, W.; Ou, Z.; Su, X.; et al. Mechanism and performance relevance of nanomorphogenesis in polyamide films revealed by quantitative 3D imaging and machine learning. Sci. Adv. 2022, 8. [Google Scholar] [CrossRef]
- Jia, X.; Deng, Y.; Bao, X.; Yao, H.; Li, S.; Li, Z.; Chen, C.; Wang, X.; Mao, J.; Cao, F.; et al. Unsupervised machine learning for discovery of promising half-Heusler thermoelectric materials. npj Comput. Mater. 2022, 8, 34. [Google Scholar] [CrossRef]
- Erhard, L.C.; Rohrer, J.; Albe, K.; Deringer, V.L. A machine-learned interatomic potential for silica and its relation to empirical models. npj Comput. Mater. 2022, 8, 90. [Google Scholar] [CrossRef]
- Chun, S.; Roy, S.; Nguyen, Y.T.; Choi, J.B.; Udaykumar, H.S.; Baek, S.S. Deep learning for synthetic microstructure generation in a materials-by-design framework for heterogeneous energetic materials. Sci. Rep. 2020, 10, 13307. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.-W.; Yang, C.-M.; Liu, J. Exploring novel fused-ring energetic compounds via high-throughput computing and deep learning. Chin. J. Energetic Mater. (Hanneng Cailiao). in press. [CrossRef]
- Lv, C.; Zhou, X.; Zhong, L.; Yan, C.; Srinivasan, M.; Seh, Z.W.; Liu, C.; Pan, H.; Li, S.; Wen, Y.; et al. Machine Learning: An Advanced Platform for Materials Development and State Prediction in Lithium-Ion Batteries. Adv. Mater. 2022, 34, 2101474. [Google Scholar] [CrossRef]
- Jiao, P.; Alavi, A.H. Artificial intelligence-enabled smart mechanical metamaterials: Advent and future trends. Int. Mater. Rev. 2021, 66, 365–393. [Google Scholar] [CrossRef]
- Yang, Z.; Gao, W. Applications of Machine Learning in Alloy Catalysts: Rational Selection and Future Development of Descriptors. Adv. Sci. 2022, 9, 2106043. [Google Scholar] [CrossRef] [PubMed]
- Goldsmith, B.R.; Esterhuizen, J.; Liu, J.-X.; Bartel, C.J.; Sutton, C. Machine learning for heterogeneous catalyst design and discovery. Aiche J. 2018, 64, 2311–2323. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, Y.; Wu, Y.; Chen, C.; Hong, Y.; Yue, Y.; Zhang, J.; Hou, B. Molecular Dynamics and Machine Learning in Catalysts. Catalysts 2021, 11, 1129. [Google Scholar] [CrossRef]
- Woodley, S.M.; Day, G.M.; Catlow, R. Structure prediction of crystals, surfaces and nanoparticles. Philos. Trans. A Math. Phys. Eng. Sci. 2020, 378, 20190600. [Google Scholar] [CrossRef]
- Muravyev, N.V.; Luciano, G.; Ornaghi, H.L., Jr.; Svoboda, R.; Vyazovkin, S. Artificial Neural Networks for Pyrolysis, Thermal Analysis, and Thermokinetic Studies: The Status Quo. Molecules 2021, 26, 3727. [Google Scholar] [CrossRef]
- Wang, L.-L.; Xiong, Y.; Xie, W.-Y.; Niu, L.L.; Zhang, C.Y. Review of crystal density prediction methods for energetic materials. Chin. J. Energetic Mater. (Hanneng Cailiao) 2020, 28, 1–12. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, T.; Ju, W.; Shi, S. Materials discovery and design using machine learning. J. Mater. 2017, 3, 159–177. [Google Scholar] [CrossRef]
- Song, S.; Chen, F.; Wang, Y.; Wang, K.; Yan, M.; Zhang, Q. Accelerating the discovery of energetic melt-castable materials by a high-throughput virtual screening and experimental approach. J. Mater. Chem. A 2021, 9, 21723–21731. [Google Scholar] [CrossRef]
- Chandrasekaran, N.; Oommen, C.; Kumar, V.R.S.; Lukin, A.N.; Abrukov, V.S.; Anufrieva, D.A. Prediction of Detonation Velocity and N-O Composition of High Energy C-H-N-O Explosives by Means of Artificial Neural Networks. Propellants Explos. Pyrotech. 2019, 44, 579–587. [Google Scholar] [CrossRef]
- Casey, A.D.; Son, S.F.; Bilionis, I.; Barnes, B.C. Prediction of energetic material properties from electronic structure using 3D convolutional neural networks. J. Chem. Inf. Model. 2020, 60, 4457–4473. [Google Scholar] [CrossRef] [PubMed]
- Fink, T.; Bruggesser, H.; Reymond, J.L. Virtual exploration of the small-molecule chemical universe below 160 Daltons. Angew. Chem. Int. Ed. Engl. 2005, 44, 1504–1508. [Google Scholar] [CrossRef]
- Ruddigkeit, L.; van Deursen, R.; Blum, L.C.; Reymond, J.L. Enumeration of 166 billion organic small molecules in the chemical universe database GDB-17. J. Chem. Inf. Model. 2012, 52, 2864–2875. [Google Scholar] [CrossRef]
- Walters, D.; Rai, N.; Sen, O.; Lee Perry, W. Toward a machine-guided approach to energetic material discovery. J. Appl. Phys. 2022, 131, 234902. [Google Scholar] [CrossRef]
- Song, S.; Wang, Y.; Wang, K.; Chen, F.; Zhang, Q. Decoding the crystal engineering of graphite-like energetic materials: From theoretical prediction to experimental verification. J. Mater. Chem. A 2020, 8, 5975–5985. [Google Scholar] [CrossRef]
- Yang, C.; Chen, J.; Wang, R.; Zhang, M.; Zhang, C.; Liu, J. Density Prediction Models for Energetic Compounds Merely Using Molecular Topology. J. Chem. Inf. Model. 2021, 61, 2582–2593. [Google Scholar] [CrossRef]
- Lansford, J.L.; Barnes, B.C.; Rice, B.M.; Jensen, K.F. Building Chemical Property Models for Energetic Materials from Small Datasets Using a Transfer Learning Approach. J. Chem. Inf. Model. 2022, 62, 5397–5410. [Google Scholar] [CrossRef]
- Jiang, Y.; Yang, Z.; Guo, J.; Li, H.; Liu, Y.; Guo, Y.; Li, M.; Pu, X. Coupling complementary strategy to flexible graph neural network for quick discovery of coformer in diverse co-crystal materials. Nat. Commun. 2021, 12, 5950. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Liu, D.; Deng, S.; Zhong, L.; Chan, S.H.Y.; Li, S.; Hng, H.H. Accurate machine learning models based on small dataset of energetic materials through spatial matrix featurization methods. J. Energy Chem. 2021, 63, 364–375. [Google Scholar] [CrossRef]
- Deng, Q.; Hu, J.; Wang, L.; Liu, Y.; Guo, Y.; Xu, T.; Pu, X. Probing impact of molecular structure on bulk modulus and impact sensitivity of energetic materials by machine learning methods. Chemom. Intell. Lab. Syst. 2021, 215, 104331. [Google Scholar] [CrossRef]
- Xu, Y.-B.; Sun, S.-J.; Wu, Z. Enthalpy of formation prediction for energetic materials based on deep learning. Chin. J. Energetic Mater. (Hanneng Cailiao) 2021, 29, 20–28. [Google Scholar] [CrossRef]
- Kang, P.; Liu, Z.; Abou-Rachid, H.; Guo, H. Machine-Learning assisted screening of energetic materials. J. Phys. Chem. A 2020, 124, 5341–5351. [Google Scholar] [CrossRef]
- Li, B.; Hou, Y.; Che, W. Data augmentation approaches in natural language processing: A survey. AI Open 2022, 3, 71–90. [Google Scholar] [CrossRef]
- Fortunato, M.E.; Coley, C.W.; Barnes, B.C.; Jensen, K.F. Data Augmentation and Pretraining for Template-Based Retrosynthetic Prediction in Computer-Aided Synthesis Planning. J. Chem. Inf. Model. 2020, 60, 3398–3407. [Google Scholar] [CrossRef]
- Li, C.; Wang, C.; Sun, M.; Zeng, Y.; Yuan, Y.; Gou, Q.; Wang, G.; Guo, Y.; Pu, X. Correlated RNN Framework to Quickly Generate Molecules with Desired Properties for Energetic Materials in the Low Data Regime. J. Chem. Inf. Model. 2022, 62, 4873–4887. [Google Scholar] [CrossRef]
- Arus-Pous, J.; Johansson, S.V.; Prykhodko, O.; Bjerrum, E.J.; Tyrchan, C.; Reymond, J.L.; Chen, H.; Engkvist, O. Randomized SMILES strings improve the quality of molecular generative models. J. Cheminform. 2019, 11, 71. [Google Scholar] [CrossRef]
- Mathieu, D. Sensitivity of Energetic Materials: Theoretical Relationships to Detonation Performance and Molecular Structure. Ind. Eng. Chem. Res. 2017, 56, 8191–8201. [Google Scholar] [CrossRef]
- Batra, R.; Pilania, G.; Uberuaga, B.P.; Ramprasad, R. Multifidelity Information Fusion with Machine Learning: A Case Study of Dopant Formation Energies in Hafnia. ACS Appl. Mater. Interfaces 2019, 11, 24906–24918. [Google Scholar] [CrossRef] [PubMed]
- Pilania, G.; Gubernatis, J.E.; Lookman, T. Multi-fidelity machine learning models for accurate bandgap predictions of solids. Comput. Mater. Sci. 2017, 129, 156–163. [Google Scholar] [CrossRef]
- Patra, A.; Batra, R.; Chandrasekaran, A.; Kim, C.; Huan, T.D.; Ramprasad, R. A multi-fidelity information-fusion approach to machine learn and predict polymer bandgap. Comput. Mater. Sci. 2020, 172. [Google Scholar] [CrossRef]
- Narasimhan, S. A handle on the scandal: Data driven approaches to structure prediction. APL Mater. 2020, 8, 040903. [Google Scholar] [CrossRef]
- Amar, Y.; Schweidtmann, A.; Deutsch, P.; Cao, L.; Lapkin, A. Machine learning and molecular descriptors enable rational solvent selection in asymmetric catalysis. Chem. Sci. 2019, 10, 6697–6706. [Google Scholar] [CrossRef] [PubMed]
- Isayev, O.; Oses, C.; Toher, C.; Gossett, E.; Curtarolo, S.; Tropsha, A. Universal fragment descriptors for predicting properties of inorganic crystals. Nat. Commun. 2017, 8, 15679. [Google Scholar] [CrossRef] [PubMed]
- Axen, S.D.; Huang, X.P.; Caceres, E.L.; Gendelev, L.; Roth, B.L.; Keiser, M.J. A Simple Representation of Three-Dimensional Molecular Structure. J. Med. Chem. 2017, 60, 7393–7409. [Google Scholar] [CrossRef] [PubMed]
- Rogers, D.; Hahn, M. Extended-Connectivity Fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. [Google Scholar] [CrossRef]
- Hall, L.H.; Kier, L.B. Electrotopological state indices for atom types: A novel combination of electronic, topological, and valence state information. J. Chem. Inf. Comput. Sci. 1995, 35, 1039–1045. [Google Scholar] [CrossRef]
- Hall, L.H.; Story, C.T. Boiling point and critical temperature of a heterogeneous data set: QSAR with atom type electrotopological state indices using artificial neural networks. J. Chem. Inf. Comput. Sci. 1996, 36, 1004–1014. [Google Scholar] [CrossRef]
- Landrum, G. RDKit: Open-source cheminformatics from machine learning to chemical registration. Abstr. Pap. Am. Chem. Soc. 2019, 258. [Google Scholar]
- Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-performance deep learning library. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Wigh, D.S.; Goodman, J.M.; Lapkin, A.A. A review of molecular representation in the age of machine learning. WIREs Comput. Mol. Sci. 2022, 12, 1603. [Google Scholar] [CrossRef]
- Barnard, A.S.; Motevatti, B.; Parker, A.J.; Fischer, J.M.; Feigt, C.A.; Opletal, G. Nanoinformatics, and the big challenges for the science of small things. Nanoscale 2019, 11, 19190–19201. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Detonation Performance and Sensitivity: A Quest for Balance. Adv. Quantum Chem. 2014, 69, 1–30. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Huang, H. pi-stacked interactions in explosive crystals: Buffers against external mechanical stimuli. J. Am. Chem. Soc. 2008, 130, 8359–8365. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Gers, F.A.; Schraudolph, N.N.; Schmidhuber, J. Learning precise timing with LSTM recurrent networks. J. Mach. Learn. Res. 2003, 3, 115–143. [Google Scholar] [CrossRef][Green Version]
- Sami, Y.; Richard, N.; Gauchard, D.; Esteve, A.; Rossi, C. Selecting machine learning models to support the design of Al/CuO nanothermites. J. Phys. Chem. A 2022, 126, 1245–1254. [Google Scholar] [CrossRef]
- Chen, D.S.; Wong, D.S.H.; Chen, C.Y. Neural network correlations of detonation properties of high energy explosives. Propellants Explos. Pyrotech. 1998, 23, 296–300. [Google Scholar] [CrossRef]
- Wang, R.; Jiang, J.; Pan, Y.; Cao, H.; Cui, Y. Prediction of impact sensitivity of nitro energetic compounds by neural network based on electrotopological-state indices. J. Hazard. Mater. 2009, 166, 155–186. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Jiang, J.; Pan, Y. Prediction of impact sensitivity of nonheterocyclic nitroenergetic compounds using genetic algorithm and artificial neural network. J. Energetic Mater. 2012, 30, 135–155. [Google Scholar] [CrossRef]
- Keshavarz, M.H.; Jaafari, M. Investigation of the various structure parameters for predicting impact sensitivity of energetic molecules via artificial neural network. Propellants Explos. Pyrotech. 2006, 31, 216–225. [Google Scholar] [CrossRef]
- Nefati, H.; Cense, J.M.; Legendre, J.J. Prediction of the impact sensitivity by neural networks. J. Chem. Inf. Comput. Sci. 1996, 36, 804–810. [Google Scholar] [CrossRef]
- Claussen, N.; Bernevig, B.A.; Regnault, N. Detection of topological materials with machine learning. Phys. Rev. B 2020, 101. [Google Scholar] [CrossRef]
- Acosta, C.M.; Ogoshi, E.; Souza, J.A.; Dalpian, G.M. Machine Learning Study of the Magnetic Ordering in 2D Materials. Acs. Appl. Mater. Interfaces 2022, 14, 9418–9432. [Google Scholar] [CrossRef]
- Freeze, J.G.; Kelly, H.R.; Batista, V.S. Search for Catalysts by Inverse Design: Artificial Intelligence, Mountain Climbers, and Alchemists. Chem. Rev. 2019, 119, 6595–6612. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Q.; Shreeve, J.n.M. Fused heterocycle-based energetic materials (2012–2019). J. Mater. Chem. A 2020, 8, 4193–4216. [Google Scholar] [CrossRef]
- Gani, R.; Brignole, E.A. Molecular design of solvents for liquid extraction based on UNIFAC. Fluid. Phase. Equilibria 1983, 13, 331–340. [Google Scholar] [CrossRef]
- Han, Z.; Jiang, Q.; Du, Z.; Zhang, Y.; Yang, Y. 3-Nitro-4-(tetrazol-5-yl) furazan: Theoretical calculations, synthesis and performance. RSC Adv. 2018, 8, 14589–14596. [Google Scholar] [CrossRef]
- Shao, Y.; Pan, Y.; Wu, Q.; Zhu, W.; Li, J.; Cheng, B.; Xiao, H. Comparative theoretical studies on energetic substituted 1,2,4-triazole molecules and their corresponding ionic salts containing 1,2,4-triazole-based cations or anions. Struct. Chem. 2012, 24, 1429–1442. [Google Scholar] [CrossRef]
- Dalinger, I.L.; Vatsadze, I.A.; Shkineva, T.K.; Kormanov, A.V.; Struchkova, M.I.; Suponitsky, K.Y.; Bragin, A.A.; Monogarov, K.A.; Sinditskii, V.P.; Sheremetev, A.B. Novel Highly Energetic Pyrazoles:N-Trinitromethyl-Substituted Nitropyrazoles. Chem. Asian J. 2015, 10, 1987–1996. [Google Scholar] [CrossRef] [PubMed]
- Li, B.-T.; Li, L.-L.; Li, X. Computational study about the derivatives of pyrrole as high-energy-density compounds. Mol. Simul. 2019, 45, 1459–1464. [Google Scholar] [CrossRef]
- Pepekin, V.I.; Korsunskii, B.L.; Denisaev, A.A. Initiation of Solid Explosives by Mechanical Impact. Combust. Explos. Shock Waves 2008, 44, 586–590. [Google Scholar] [CrossRef]
- Li, X.-H.; Fu, Z.-M.; Zhang, X.-Z. Computational DFT studies on a series of toluene derivatives as potential high energy density compounds. Struct. Chem. 2011, 23, 515–524. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Impact sensitivity and the maximum heat of detonation. J. Mol. Model. 2015, 21, 262. [Google Scholar] [CrossRef]
- Sheibani, N.; Zohari, N.; Fareghi-Alamdari, R. Rational design, synthesis and evaluation of new azido-ester structures as green energetic plasticizers. Dalton. Trans. 2020, 49, 12695–12706. [Google Scholar] [CrossRef]
- Aitipamula, S.; Banerjee, R.; Bansal, A.K.; Biradha, K.; Cheney, M.L.; Choudhury, A.R.; Desiraju, G.R.; Dikundwar, A.G.; Dubey, R.; Duggirala, N.; et al. Polymorphs, Salts, and Cocrystals: What’s in a Name? Cryst. Growth Des. 2012, 12, 2147–2152. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Chen, Y.; Mi, Y.Y.; Hu, G. From data to network structure-Reconstruction of dynamic networks. Sci. Sin. Phys. Mech. Astron. 2019, 50, 010502. [Google Scholar] [CrossRef]
- Paszkowicz, W. Genetic Algorithms, a Nature-Inspired Tool: A Survey of Applications in Materials Science and Related Fields: Part II. Mater. Manuf. Process. 2013, 28, 708–725. [Google Scholar] [CrossRef]
- Casadevall, A.; Steen, R.G.; Fang, F.C. Sources of error in the retracted scientific literature. FASEB J. 2014, 28, 3847–3855. [Google Scholar] [CrossRef] [PubMed]
- Chambers, L.M.; Michener, C.M.; Falcone, T. Plagiarism and data falsification are the most common reasons for retracted publications in obstetrics and gynaecology. Bjog. Int. J. Obstet. Gynaecol. 2019, 126, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Else, H. Major chemical database investigates suspicious structures. Nature 2022, 608, 461. [Google Scholar] [CrossRef] [PubMed]
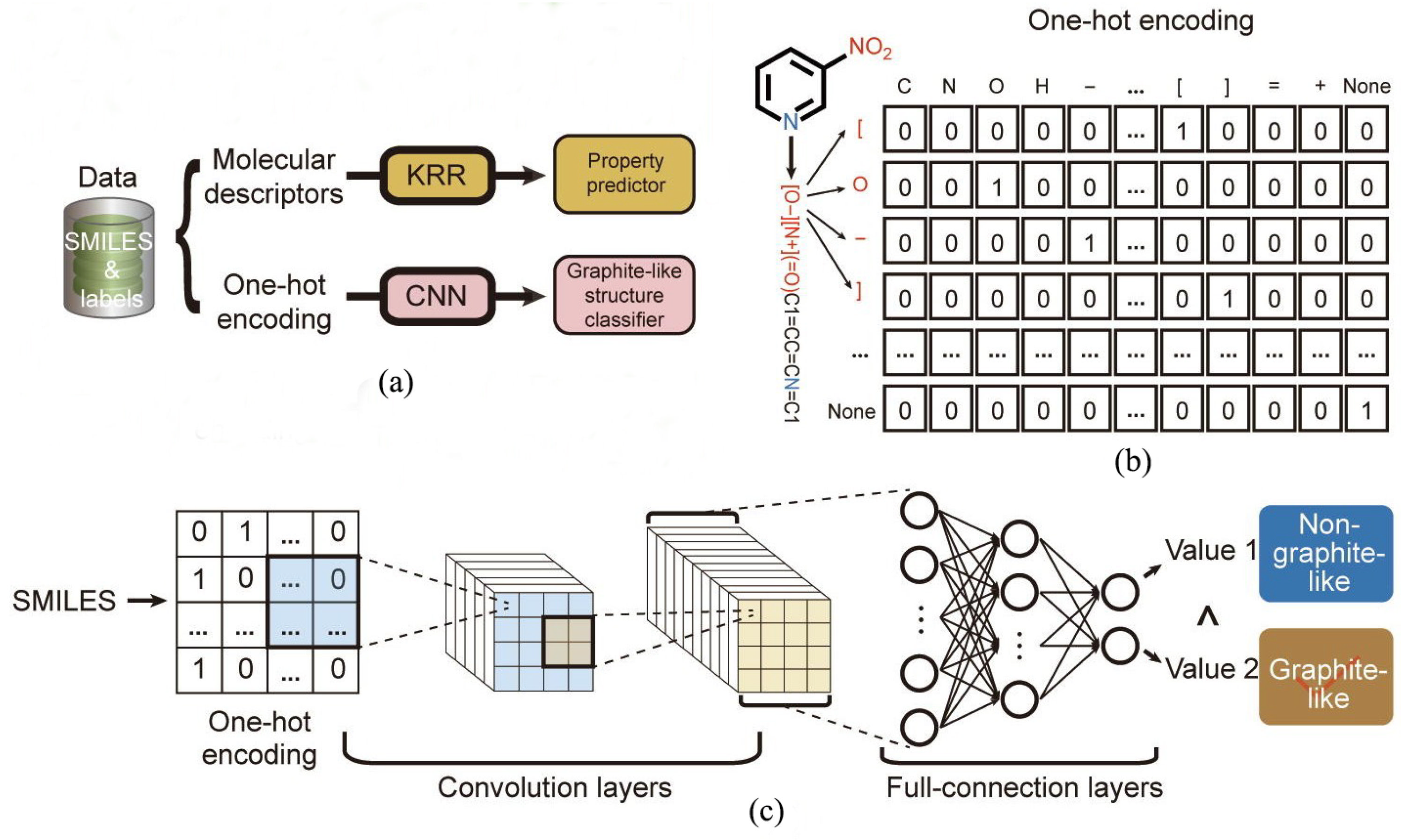
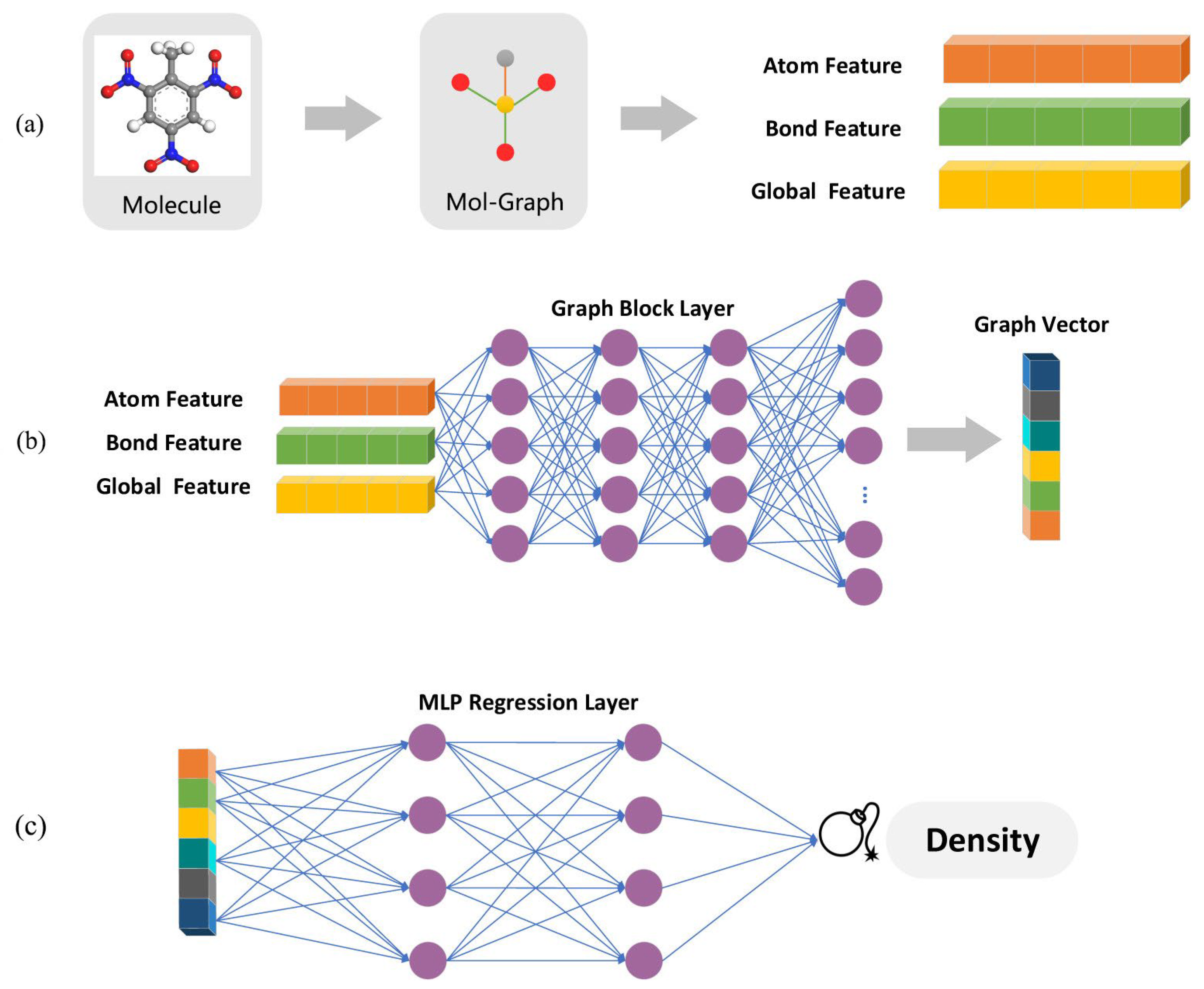
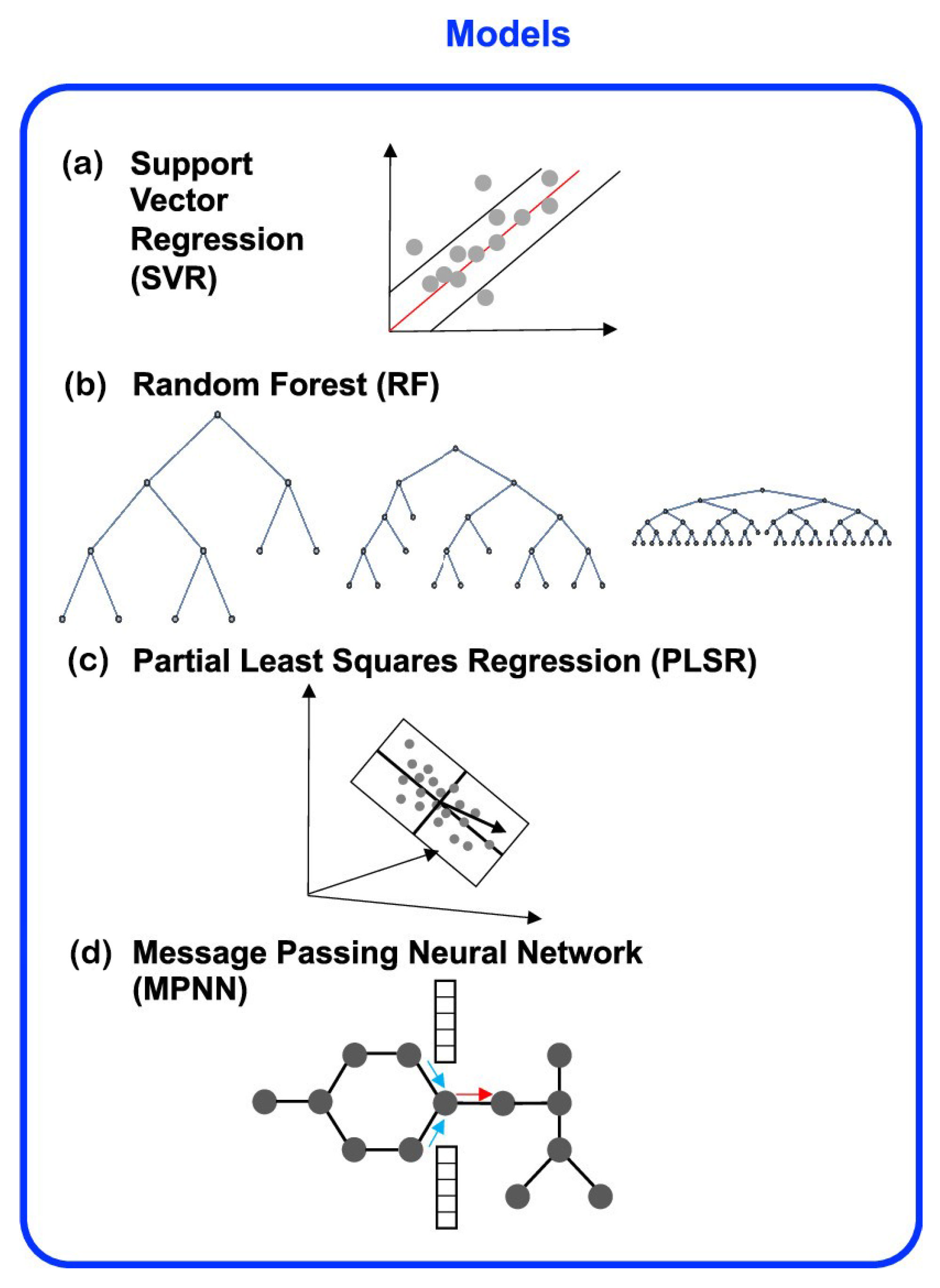
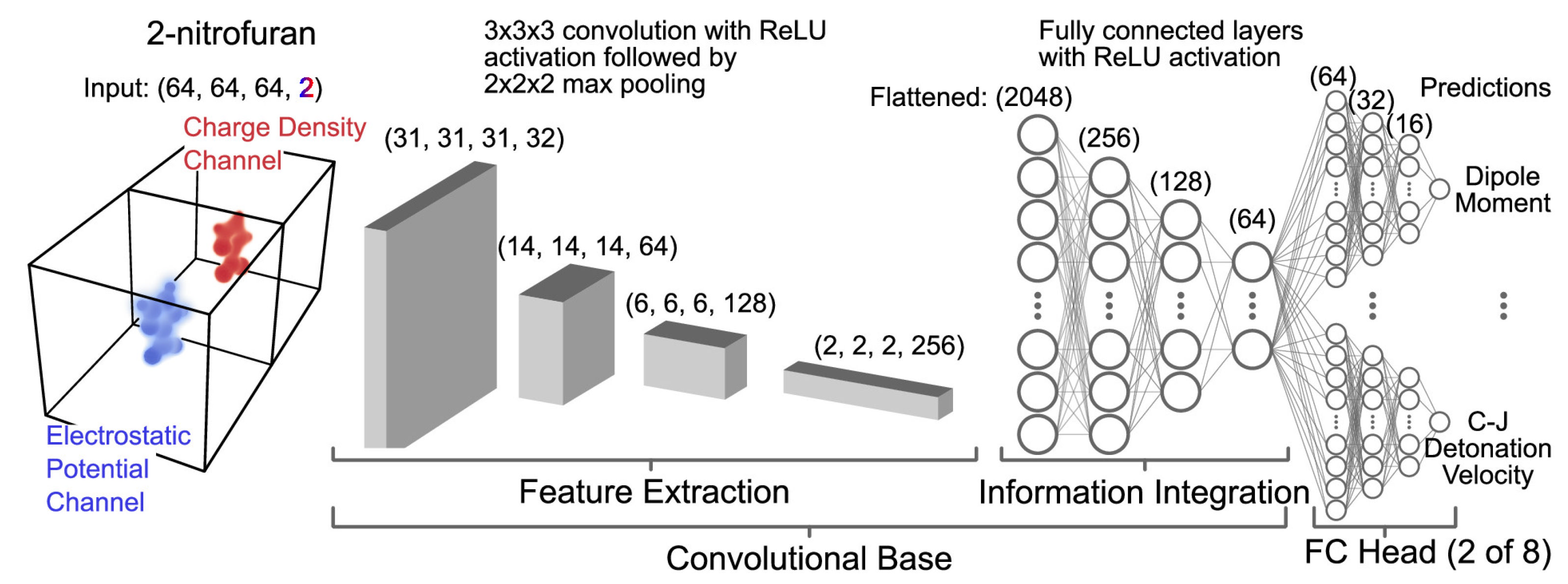
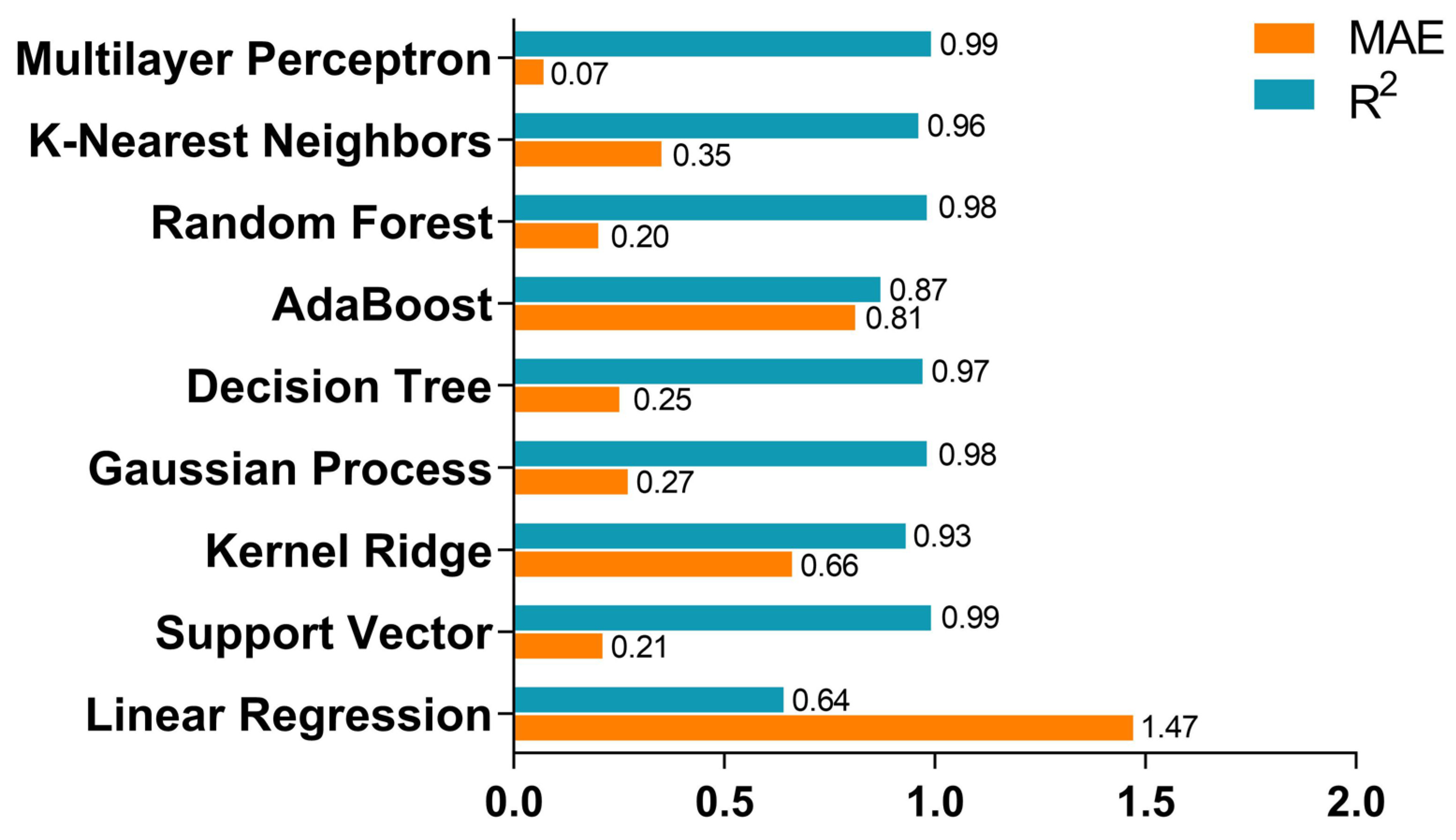
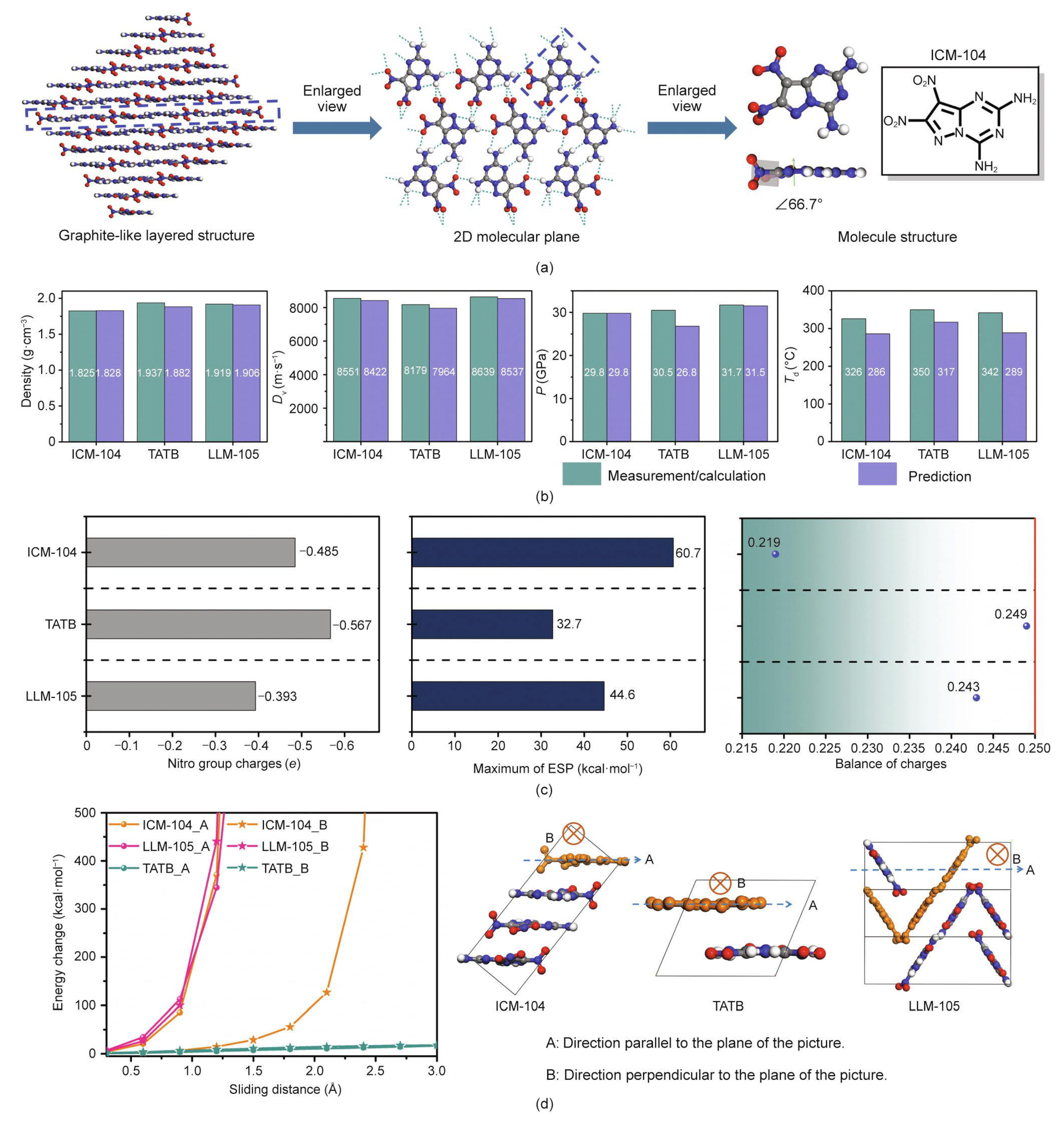


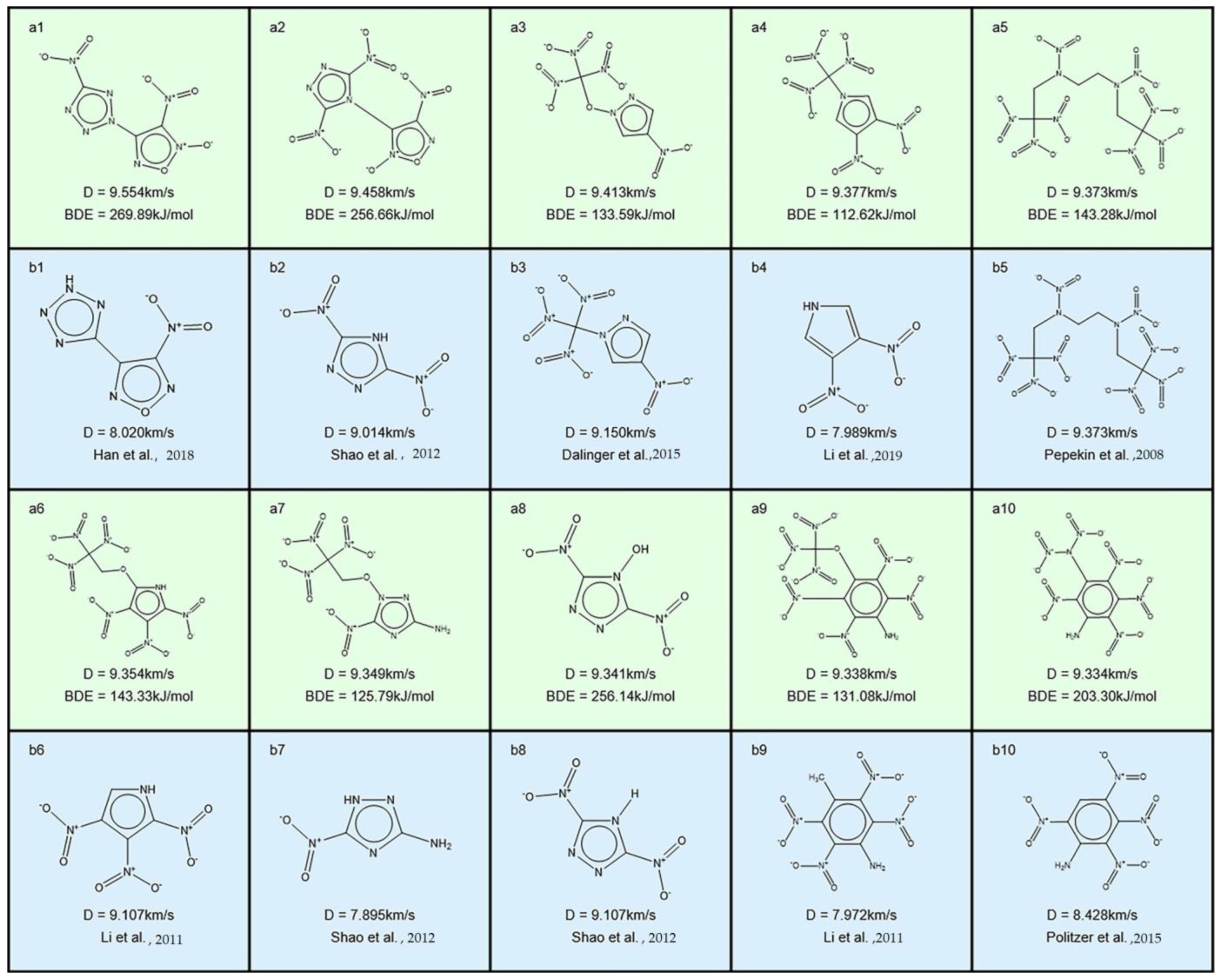
| No. | Database Name | Sources |
|---|---|---|
| 1 | CCDC | [1,53,69,70] |
| 2 | GDB | [65,71] |
| 3 | CSD | [4,24,72,73,74] |
| 4 | PubChem | [72,73,75,76] |
| Model Category | Target EMs | Target Property | Main Method | Accuracy | F1 Score | Mean Absolute Error (MAE) | Root Mean Square Error (RMSE) | Determination Coefficient (R2) | Source |
|---|---|---|---|---|---|---|---|---|---|
| The classification model | Graphite-like layered crystal | Impact sensitivity | CNN | 0.98 | 0.94 | / | / | / | [1] |
| LSTM | 0.93 | 0.78 | / | / | / | ||||
| K-nearest neighbor (KNN) | 0.95 | 0.33 | / | / | / | ||||
| The regression model | HE | Density | Support vector regression (SVR) | / | / | / | 0.085 | 0.683 | [24] |
| Random forests (RF) | / | / | / | 0.053 | 0.878 | ||||
| Partial least-squares regression | / | / | / | 0.048 | 0.9 | ||||
| Message passing neural network (MPNN) | / | / | / | 0.044 | 0.914 | ||||
| The regression model | Nitramines | Density | Group addition method | / | / | 0.092 | 0.12 | 0.686 | [70] |
| Support vector machine (SVM) | / | / | 0.097 | 0.122 | 0.796 | ||||
| RF | / | / | 0.088 | 0.105 | 0.624 | ||||
| Quantitative structure−property relationship based on the DFT (DFT−QSPR) | / | / | 0.041 | 0.057 | 0.941 | ||||
| GNN | / | / | 0.04 | 0.047 | 0.944 | ||||
| The regression model | CHNO-containi-ng energetic molecules | Detonation velocity | RNN | / | / | 0.0968 | 0.1391 | 0.9445 | [79] |
| RNN model with inclusion of the pretrained knowledge (SRNN) | / | / | 0.0801 | 0.1273 | 0.9572 | ||||
| RF | / | / | 0.1812 | 0.2524 | 0.819 |
| Method | Category | Target Property | Source |
|---|---|---|---|
| KRR | Regression | Density, detonation velocity, detonation pressure, decomposition temperature, heat of formation, heat of explosion, enthalpy of formation, burn rate | [1,13,73,101] |
| Least absolute shrinkage and selection operator | Regression | Density, molecular flatness, bond dissociation energy, heat of formation, heat of explosion, enthalpy of formation | [4,13,73] |
| Linear regression model | Regression | Heat of formation, heat of explosion, burn rate | [13,76,101] |
| Logistic regression | Regression | Heat of explosion | [76] |
| Multiple linear regression | Regression | Density, molecular flatness, bond dissociation energy, heat of formation | [4,8] |
| Gaussian process regression model (GPR) | Regression | Heat of formation, heat of explosion, burn rate | [13,101] |
| Artificial neural network (ANN) | Regression, classification | Detonation velocity, density, heat of explosion, bulk modulus, impact sensitivity | [64,74,102,103,104,105] |
| SVM | Regression, classification | Density, molecular flatness, bond dissociation energy, heat of formation, impact sensi-tivity, heat of explosion | [4,13,70,72] |
| SVR | Regression | Density, enthalpy of formation, heat of explosion, burn rate | [73,76,101] |
| CNN | Regression, classification | Graphite-like layered crystal structure, enthalpy of formation | [1,75] |
| RNN | Regression, classification | Detonation velocity | [79] |
| LSTM | Regression, classification | Density, detonation velocity, detonation pressure, decomposition temperature, enthalpy of formation | [1,75] |
| GNN | Regression, classification | Density, impact sensi-tivity, heat of explosion | [70,72] |
| Deep neural network (DNN) | Regression, classification | Impact sensi-tivity, heat of explosion | [72] |
| RF | Regression, classification | Density, molecular flatness, bond dissociation energy, heat of formation, enthalpy of formation, impact sensi-tivity, heat of explosion, burn rate | [4,70,72,73,76,101] |
| KNN | Regression, classification | Density, detonation velocity, detonation pressure, decomposition temperature, enthalpy of formation, burn rate | [1,73,101] |
| Multilayer perceptron (MLP) | Regression, classification | Burn rate | [101] |
| Decision tree | Regression, classification | Burn rate | [101] |
| High-dimensional neural network | Regression, classification | Binding energy, atomic force | [37] |
| Generative adversarial networks | Regression, classification | Porosity distribution | [52] |
| MPNN | Regression, classification | Density, impact sensi-tivity | [24,71] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, X.; Zhou, X.; Bian, H.; Jin, W.; Pan, X.; Jiang, J.; Koroleva, M.Y.; Shen, R. Prediction and Construction of Energetic Materials Based on Machine Learning Methods. Molecules 2023, 28, 322. https://doi.org/10.3390/molecules28010322
Zang X, Zhou X, Bian H, Jin W, Pan X, Jiang J, Koroleva MY, Shen R. Prediction and Construction of Energetic Materials Based on Machine Learning Methods. Molecules. 2023; 28(1):322. https://doi.org/10.3390/molecules28010322
Chicago/Turabian StyleZang, Xiaowei, Xiang Zhou, Haitao Bian, Weiping Jin, Xuhai Pan, Juncheng Jiang, M. Yu. Koroleva, and Ruiqi Shen. 2023. "Prediction and Construction of Energetic Materials Based on Machine Learning Methods" Molecules 28, no. 1: 322. https://doi.org/10.3390/molecules28010322
APA StyleZang, X., Zhou, X., Bian, H., Jin, W., Pan, X., Jiang, J., Koroleva, M. Y., & Shen, R. (2023). Prediction and Construction of Energetic Materials Based on Machine Learning Methods. Molecules, 28(1), 322. https://doi.org/10.3390/molecules28010322







