Parameterization and Application of the General Amber Force Field to Model Fluoro Substituted Furanose Moieties and Nucleosides
Abstract
1. Introduction
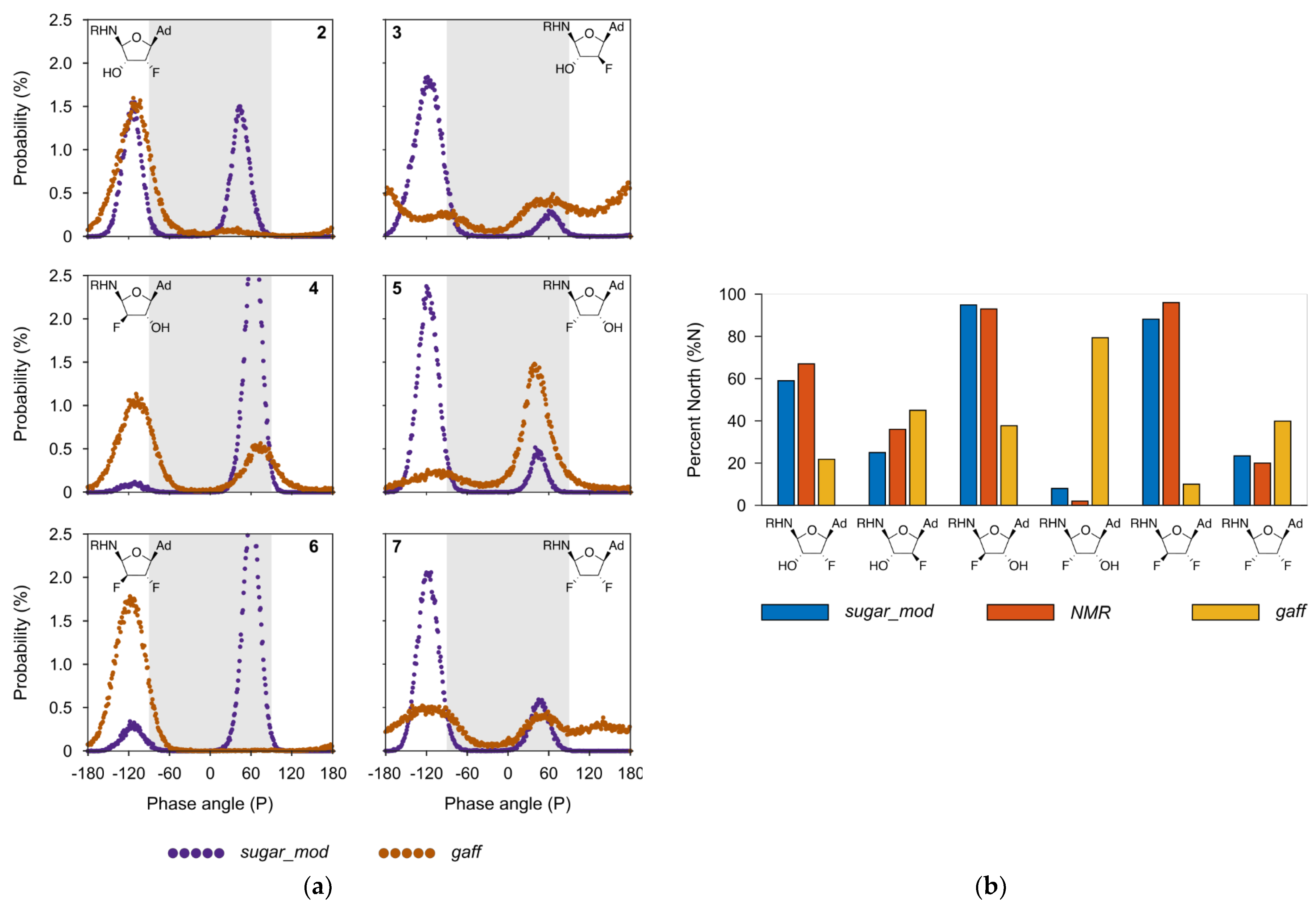
2. Results and Discussion
3. Materials and Methods
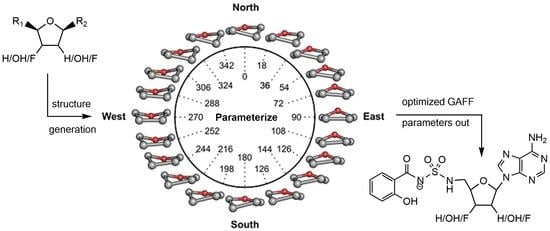
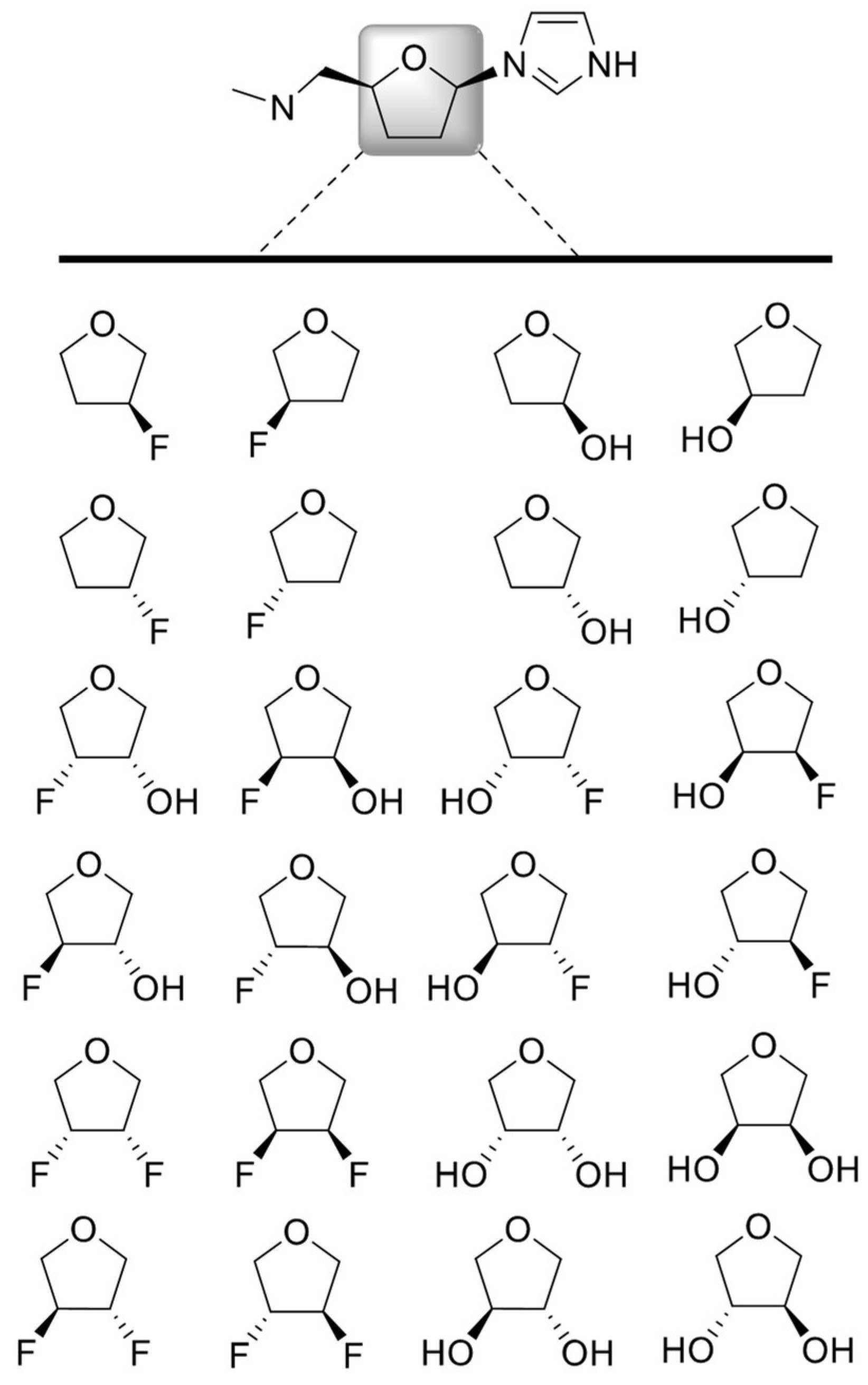
3.1. Structure Generation
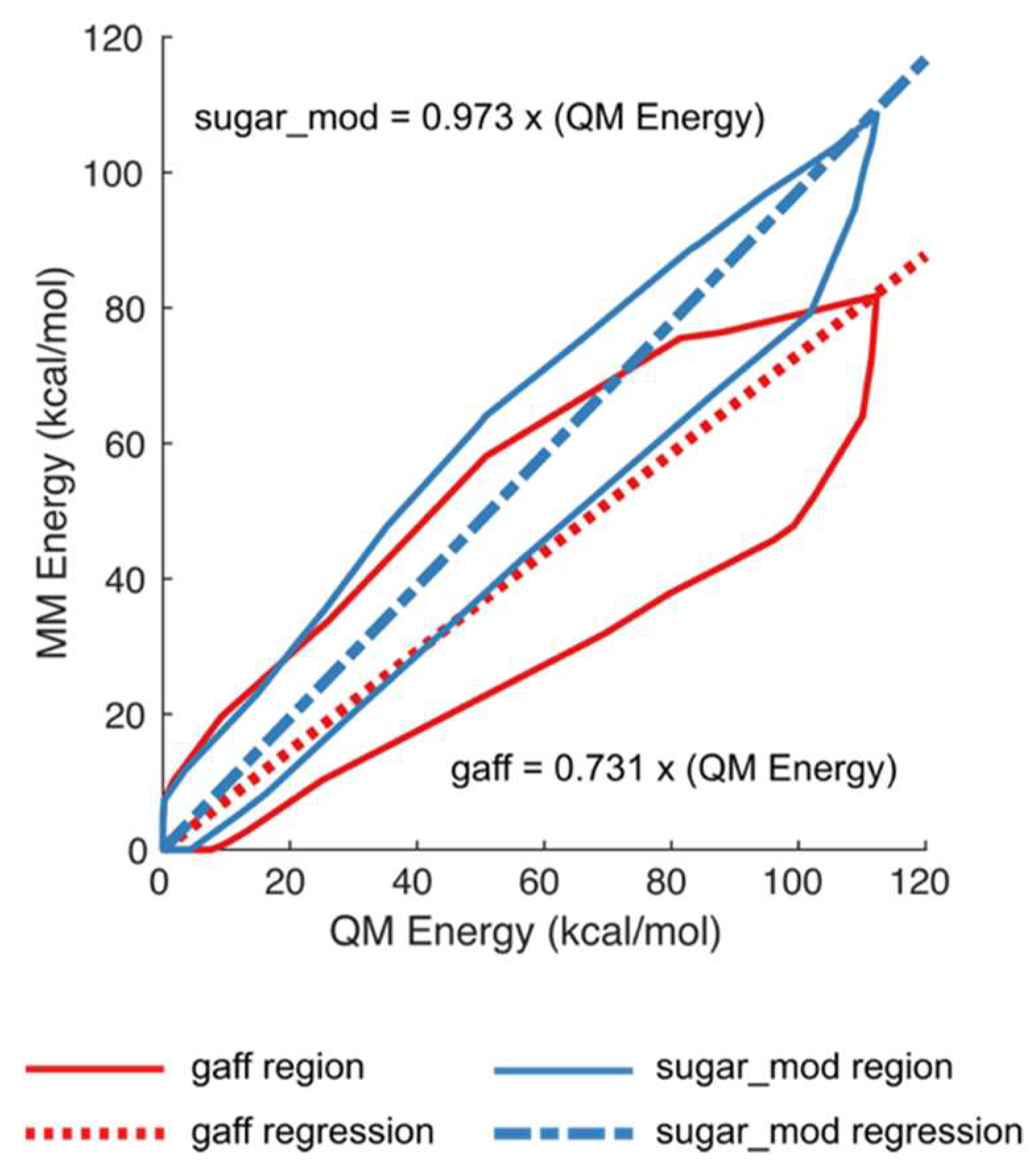
3.2. Calculation of New Parameters
3.2.1. Partial Atomic Charges
3.2.2. Torsional Parameters
3.3. Molecular Dynamic Simulations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Sivets, G.G.; Amblard, F.; Schinazi, R.F. Synthesis of 2-fluoro-substituted and 2, 6-modified purine 2′,3′-dideoxy-2′,3′-difluoro-d-arabinofuranosyl nucleosides from d-xylose. Tetrahedron 2019, 75, 2037–2046. [Google Scholar] [CrossRef]
- Qiu, X.-L.; Xu, X.-H.; Qing, F.-L. Recent advances in the synthesis of fluorinated nucleosides. Tetrahedron 2010, 66, 789–843. [Google Scholar] [CrossRef]
- Liu, P.; Sharon, A.; Chu, C.K. Fluorinated nucleosides: Synthesis and biological implication. J. Fluor. Chem. 2008, 129, 743–766. [Google Scholar] [CrossRef]
- Chong, Y.; Gumina, G.; Mathew, J.S.; Schinazi, R.F.; Chu, C.K. l-2′,3′-Didehydro-2′,3′-dideoxy-3′-fluoronucleosides: Synthesis, Anti-HIV Activity, Chemical and Enzymatic Stability, and Mechanism of Resistance. J. Med. Chem. 2003, 46, 3245–3256. [Google Scholar] [CrossRef]
- Gumina, G.; Schinazi, R.F.; Chu, C.K. Synthesis and potent anti-HIV activity of l-3′-fluoro-2′,3′-unsaturated cytidine. Org. Lett. 2001, 3, 4177–4180. [Google Scholar] [CrossRef]
- Zhou, W.; Gumina, G.; Chong, Y.; Wang, J.; Schinazi, R.F.; Chu, C.K. Synthesis, Structure—Activity Relationships, and Drug Resistance of β-d-3′-Fluoro-2′,3′-Unsaturated Nucleosides as Anti-HIV Agents. J. Med. Chem. 2004, 47, 3399–3408. [Google Scholar] [CrossRef]
- Cushley, R.J.; Codington, J.F.; Fox, J.J. Nucleosides. XLIX. Nuclear magnetic resonance studies of 2′-and 3′-halogeno nucleosides. The conformations of 2′-deoxy-2′-fluorouridine and 3′-deoxy-3′-fluoro-β-d-arabinofuranosyluracil. Can. J. Chem. 1968, 46, 1131–1140. [Google Scholar] [CrossRef]
- Pankiewicz, K.W.; Krzeminski, J.; Ciszewski, L.A.; Ren, W.Y.; Watanabe, K.A. A synthesis of 9-(2-deoxy-2-fluoro-beta-D-arabinofuranosyl) adenine and-hypoxanthine. An effect of C3′-endo to C2′-endo conformational shift on the reaction course of 2′-hydroxyl group with DAST. J. Org. Chem. 1992, 57, 553–559. [Google Scholar] [CrossRef]
- Dawadi, S.; Kawamura, S.; Rubenstein, A.; Remmel, R.; Aldrich, C.C. Synthesis and pharmacological evaluation of nucleoside prodrugs designed to target siderophore biosynthesis in Mycobacterium tuberculosis. Bioorg. Med. Chem. 2016, 24, 1314–1321. [Google Scholar] [CrossRef]
- Dawadi, S.; Viswanathan, K.; Boshoff, H.I.; Barry III, C.E.; Aldrich, C.C. Investigation and conformational analysis of fluorinated nucleoside antibiotics targeting siderophore biosynthesis. J. Org. Chem. 2015, 80, 4835–4850. [Google Scholar] [CrossRef]
- Mikhailopulo, I.A.; Pricota, T.I.; Sivets, G.G.; Altona, C. 2′-Chloro-2′,3′-dideoxy-3′-fluoro-d-ribonucleosides: Synthesis, Stereospecificity, Some Chemical Transformations, and Conformational Analysis. J. Org. Chem. 2003, 68, 5897–5908. [Google Scholar] [CrossRef]
- Marquez, V.E.; Tseng, C.K.; Mitsuya, H.; Aoki, S.; Kelley, J.A.; Ford, H., Jr.; Roth, J.S.; Broder, S.; Johns, D.G.; Driscoll, J.S. Acid-stable 2’-fluoro purine dideoxynucleosides as active agents against HIV. J. Med. Chem. 1990, 33, 978–985. [Google Scholar] [CrossRef]
- Mikhailopulo, I.A.; Sivets, G.G. A Novel route for the synthesis of deoxy fluoro sugars and nucleosides. Helv. Chim. Acta 1999, 82, 2052–2065. [Google Scholar] [CrossRef]
- Schinazi, R.F.; Sivets, G.G.; Detorio, M.A.; McBrayer, T.R.; Whitaker, T.; Coats, S.J.; Amblard, F. Synthesis and antiviral evaluation of 2′,3′-dideoxy-2′,3′-difluoro-D-arabinofuranosyl 2,6-disubstituted purine nucleosides. Heterocycl. Commun. 2015, 21, 315–327. [Google Scholar] [CrossRef]
- Uhrig, M.L.; Lantaño, B.; Postigo, A. Synthetic strategies for fluorination of carbohydrates. Org. Biomol. Chem. 2019, 17, 5173–5189. [Google Scholar] [CrossRef]
- Sapse, A.; Snyder, G. Ab initio studies of the antiviral drug 1-(2-fluoro-2-deoxy-β-d-arabinofuranosyl) thymine. Cancer Investig. 1985, 3, 115–121. [Google Scholar] [CrossRef]
- Garrett, E.C.; Serianni, A.S. Ab initio molecular orbital calculations on furanose sugars: A study with the 6–31G basis set. Carbohydr. Res. 1990, 206, 183–191. [Google Scholar] [CrossRef]
- Ferreras, J.A.; Ryu, J.-S.; Di Lello, F.; Tan, D.S.; Quadri, L.E. Small-molecule inhibition of siderophore biosynthesis in Mycobacterium tuberculosis and Yersinia pestis. Nat. Chem. Biol. 2005, 1, 29–32. [Google Scholar] [CrossRef]
- Miethke, M.; Bisseret, P.; Beckering, C.L.; Vignard, D.; Eustache, J.; Marahiel, M.A. Inhibition of aryl acid adenylation domains involved in bacterial siderophore synthesis. FEBS J. 2006, 273, 409–419. [Google Scholar] [CrossRef]
- Somu, R.V.; Wilson, D.J.; Bennett, E.M.; Boshoff, H.I.; Celia, L.; Beck, B.J.; Barry, C.E.; Aldrich, C.C. Antitubercular nucleosides that inhibit siderophore biosynthesis: SAR of the glycosyl domain. J. Med. Chem. 2006, 49, 7623–7635. [Google Scholar] [CrossRef][Green Version]
- Duckworth, B.P.; Wilson, D.J.; Nelson, K.M.; Boshoff, H.I.; Barry III, C.E.; Aldrich, C.C. Development of a selective activity-based probe for adenylating enzymes: Profiling MbtA involved in siderophore biosynthesis from Mycobacterium tuberculosis. ACS Chem. Biol. 2012, 7, 1653–1658. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L. Efficient drug lead discovery and optimization. Acc. Chem. Res. 2009, 42, 724–733. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Thomas, L.L. Perspective on free-energy perturbation calculations for chemical equilibria. J. Chem. Theory Comput. 2008, 4, 869–876. [Google Scholar] [CrossRef] [PubMed]
- Williams-Noonan, B.J.; Yuriev, E.; Chalmers, D.K. Free energy methods in drug design: Prospects of “alchemical perturbation” in medicinal chemistry: Miniperspective. J. Med. Chem. 2018, 61, 638–649. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L. Free energy calculations: A breakthrough for modeling organic chemistry in solution. Acc. Chem. Res. 1989, 22, 184–189. [Google Scholar] [CrossRef]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef]
- Harder, E.; Damm, W.; Maple, J.; Wu, C.; Reboul, M.; Xiang, J.Y.; Wang, L.; Lupyan, D.; Dahlgren, M.K.; Knight, J.L. OPLS3: A force field providing broad coverage of drug-like small molecules and proteins. J. Chem. Theory Comput. 2016, 12, 281–296. [Google Scholar] [CrossRef]
- Nerenberg, P.S.; Head-Gordon, T. New developments in force fields for biomolecular simulations. Curr. Opin. Struct. Biol. 2018, 49, 129–138. [Google Scholar] [CrossRef]
- Roos, K.; Wu, C.; Damm, W.; Reboul, M.; Stevenson, J.M.; Lu, C.; Dahlgren, M.K.; Mondal, S.; Chen, W.; Wang, L.; et al. OPLS3e: Extending Force Field Coverage for Drug-Like Small Molecules. J. Chem. Theory Comput. 2019, 15, 1863–1874. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wu, Y.; Deng, Y.; Kim, B.; Pierce, L.; Krilov, G.; Lupyan, D.; Robinson, S.; Dahlgren, M.K.; Greenwood, J. Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J. Am. Chem. Soc. 2015, 137, 2695–2703. [Google Scholar] [CrossRef] [PubMed]
- Debiec, K.T.; Cerutti, D.S.; Baker, L.R.; Gronenborn, A.M.; Case, D.A.; Chong, L.T. Further along the Road Less Traveled: AMBER ff15ipq, an Original Protein Force Field Built on a Self-Consistent Physical Model. J. Chem. Theory Comput. 2016, 12, 3926–3947. [Google Scholar] [CrossRef] [PubMed]
- Hendrickx, P.M.; Martins, J.C. A user-friendly Matlab program and GUI for the pseudorotation analysis of saturated five-membered ring systems based on scalar coupling constants. Chem. Cent. J. 2008, 2, 20. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Van Wijk, J.; Huckriede, B.D.; Ippel, J.H.; Altona, C. [15] Furanose sugar conformations in DNA from NMR coupling constants. In Methods in Enzymology; Academic Press: Cambridge, MA, USA, 1992; Volume 211, pp. 286–306. [Google Scholar]
- Barchi, J.J., Jr.; Karki, R.G.; Nicklaus, M.C.; Siddiqui, M.A.; George, C.; Mikhailopulo, I.A.; Marquez, V.E. Comprehensive structural studies of 2′,3′-difluorinated nucleosides: Comparison of theory, solution, and solid state. J. Am. Chem. Soc. 2008, 130, 9048–9057. [Google Scholar] [CrossRef] [PubMed]
- Altona, C.T.; Sundaralingam, M. Conformational analysis of the sugar ring in nucleosides and nucleotides. New description using the concept of pseudorotation. J. Am. Chem. Soc. 1972, 94, 8205–8212. [Google Scholar] [CrossRef]



| Dihedral Angle | |||
|---|---|---|---|
| c3 | c3 | c3 | oh |
| c3 | c3 | c3 | f |
| c3 | c3 | oh | ho |
| f | c3 | c3 | f |
| f | c3 | c3 | oh |
| f | c3 | c3 | os |
| oh | c3 | c3 | oh |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escalante, D.E.; Aldrich, C.C.; Ferguson, D.M. Parameterization and Application of the General Amber Force Field to Model Fluoro Substituted Furanose Moieties and Nucleosides. Molecules 2022, 27, 2616. https://doi.org/10.3390/molecules27092616
Escalante DE, Aldrich CC, Ferguson DM. Parameterization and Application of the General Amber Force Field to Model Fluoro Substituted Furanose Moieties and Nucleosides. Molecules. 2022; 27(9):2616. https://doi.org/10.3390/molecules27092616
Chicago/Turabian StyleEscalante, Diego E., Courtney C. Aldrich, and David M. Ferguson. 2022. "Parameterization and Application of the General Amber Force Field to Model Fluoro Substituted Furanose Moieties and Nucleosides" Molecules 27, no. 9: 2616. https://doi.org/10.3390/molecules27092616
APA StyleEscalante, D. E., Aldrich, C. C., & Ferguson, D. M. (2022). Parameterization and Application of the General Amber Force Field to Model Fluoro Substituted Furanose Moieties and Nucleosides. Molecules, 27(9), 2616. https://doi.org/10.3390/molecules27092616