Preprocessing Strategies for Sparse Infrared Spectroscopy: A Case Study on Cartilage Diagnostics
Abstract
:1. Introduction
2. Results and Discussion
2.1. Histology Reference Data
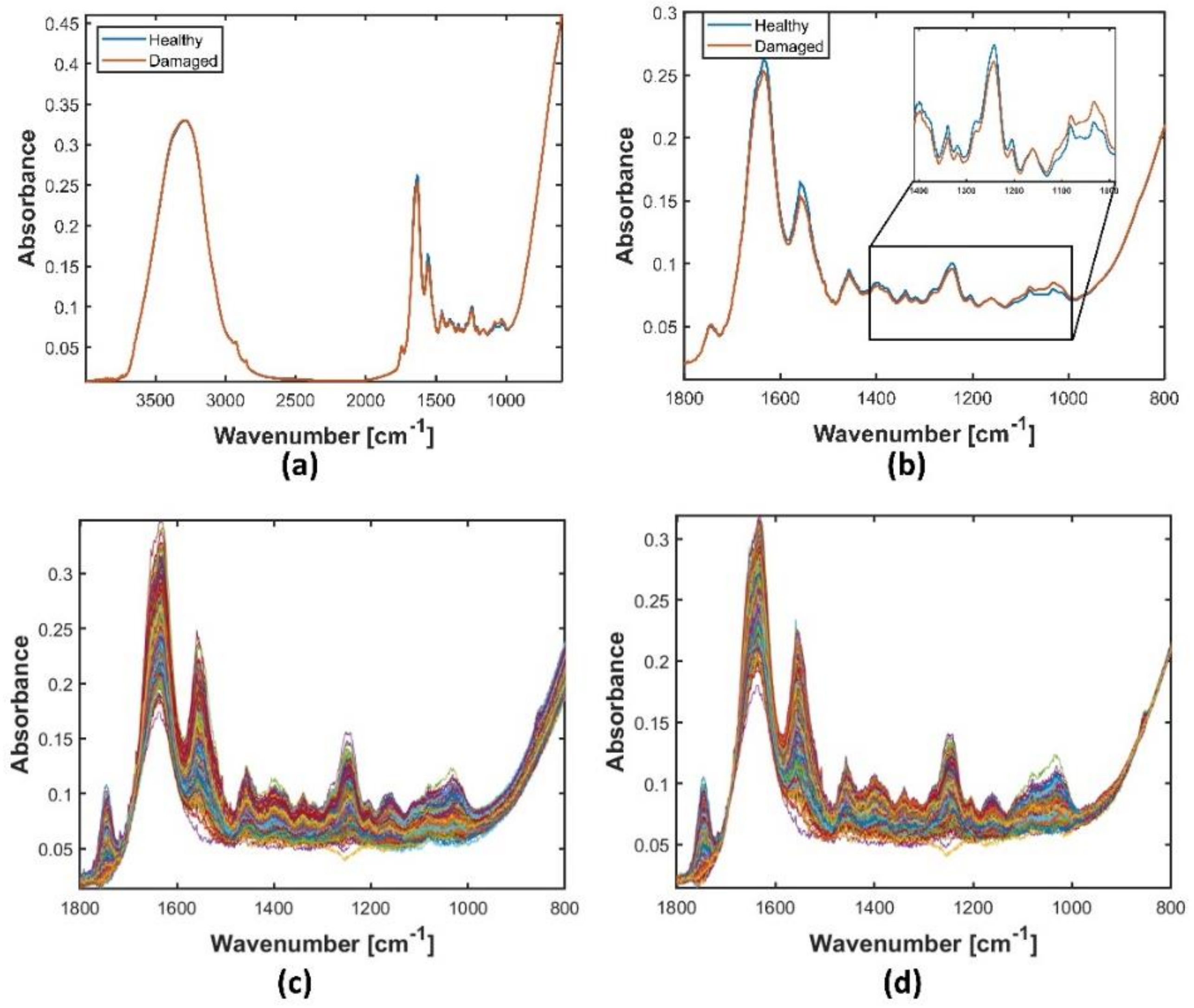
2.2. FTIR Spectral Data
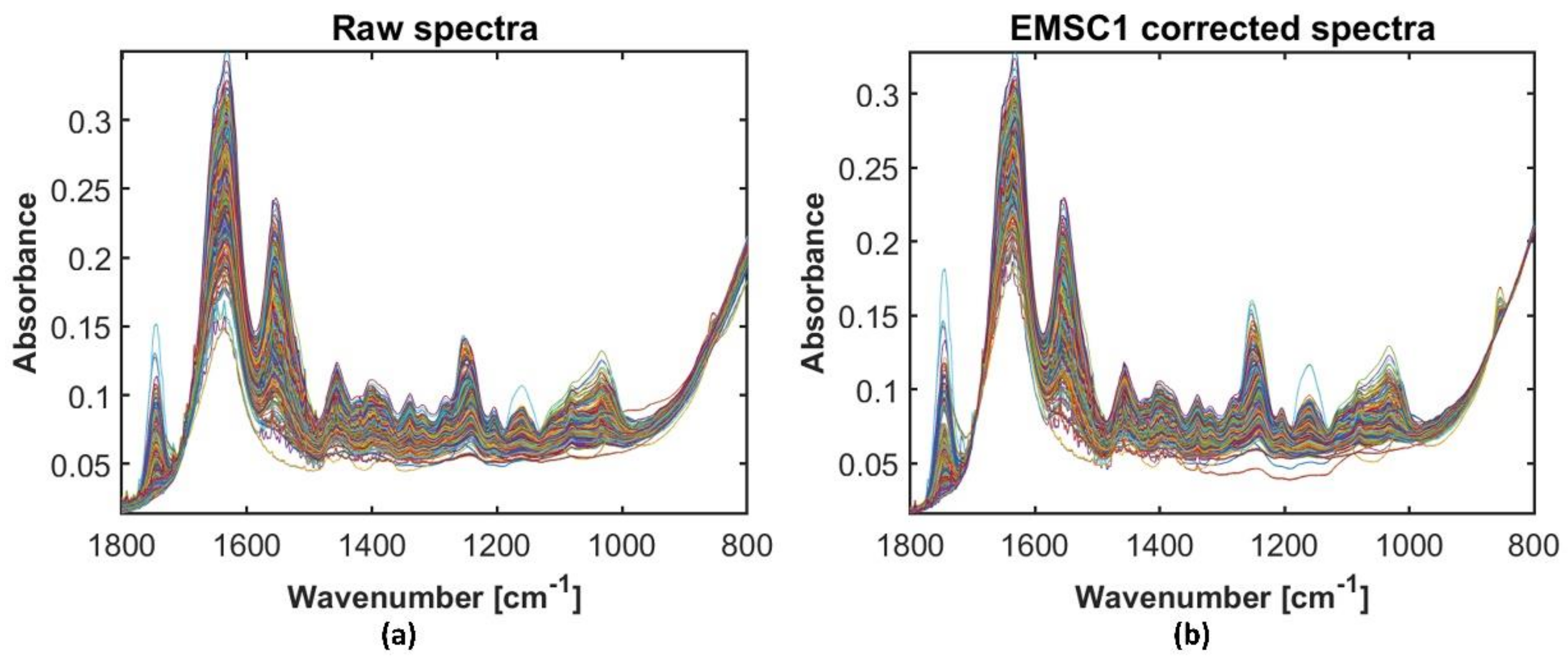
2.3. Preprocessing Strategies for the Broadband Spectra
2.4. Preprocessing Strategies for the Sparse Spectra
3. Methods
3.1. Measured Data
3.1.1. Bovine Broadband Spectra
3.1.2. Human Broadband Spectra
3.1.3. Histology
3.2. Simulated Broadband Spectra
- PCA decomposition of matrix as was done, where are scores and are loadings of matrix .
- Calculation of mean and standard deviation of scores for the chosen number of loadings A.
- New scores were drawn randomly from the respective normal distribution calculated for each score . The random drawing had a feedback loop which was activated if scores higher than the maximum or lower than the minimum obtained in experimental dataset were drawn. This was done to prevent very unrealistic score values being drawn.
- The first set of simulated data were obtained by . These spectra generated for healthy and damaged groups separately were further merged into one dataset and corrected again by the EMSC1 method to avoid creating artificial physical effects by random recombination of loadings in the simulation.The resulting dataset contained the final simulated pure absorbance spectra. To simulate apparent spectra which are “perturbed” by physical effects naturally present in the real data, the following was done.
- Group specific EMSC1 variations were added to simulated pure spectra using parameters drawn from the distributions .
- The spectra were merged into one dataset and white noise vectors w were also added by randomly drawing from a uniform distribution with the level similar to experimental dataset.
3.3. Sparse Spectra
3.4. Spectral Preprocessing and Preclassification Strategies
3.5. Classification Modelling
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Rieppo, L.; Toyras, J.; Saarakkala, S. Vibrational spectroscopy of articular cartilage. Appl. Spectrosc. Rev. 2017, 52, 249–266. [Google Scholar] [CrossRef]
- Kumar, S.; Srinivasan, A.; Nikolajeff, F. Role of Infrared Spectroscopy and Imaging in Cancer Diagnosis. Curr. Med. Chem. 2018, 25, 1055–1072. [Google Scholar] [CrossRef] [PubMed]
- Heraud, P.; Chatchawa, P.; Wongwattanakul, M.; Tippayawat, P.; Doerig, C.; Jearanaikoon, P.; Perez-Guaita, D.; Wood, B.R. Infrared spectroscopy coupled to cloud-based data management as a tool to diagnose malaria: A pilot study in a malaria-endemic country. Malar. J. 2019, 18, 348. [Google Scholar] [CrossRef] [PubMed]
- Figoli, C.B.; Garcea, M.; Bisioli, C.; Tafintseva, V.; Shapaval, V.; Pena, M.G.; Gibbons, L.; Althabe, F.; Yantorno, O.M.; Horton, M.; et al. A robust metabolomics approach for the evaluation of human embryos from in vitro fertilization. Analyst 2021, 146, 6156–6169. [Google Scholar] [CrossRef] [PubMed]
- Boyar, H.; Zorlu, F.; Mut, M.; Severcan, F. The effects of chronic hypoperfusion on rat cranial bone mineral and organic matrix. Anal. Bioanal. Chem. 2004, 379, 433–438. [Google Scholar] [CrossRef]
- Baloglu, F.K.; Garip, S.; Heise, S.; Brockmann, G.; Severcan, F. FTIR imaging of structural changes in visceral and subcutaneous adiposity and brown to white adipocyte transdifferentiation. Analyst 2015, 140, 2205–2214. [Google Scholar] [CrossRef]
- Lacombe, C.; Untereiner, V.; Gobinet, C.; Zater, M.; Sockalingum, G.D.; Garnotel, R. Rapid screening of classic galactosemia patients: A proof-of-concept study using high-throughput FTIR analysis of plasma. Analyst 2015, 140, 2280–2286. [Google Scholar] [CrossRef]
- Isensee, K.; Kröger-Lui, N.; Petrich, W. Biomedical applications of mid-infrared quantum cascade lasers–A review. Analyst 2018, 143, 5888–5911. [Google Scholar] [CrossRef]
- Zimmermann, B.; Tafintseva, V.; Bağcıoğlu, M.; Berdahl, M.H.; Kohler, A. Analysis of allergenic pollen by FTIR microspectroscopy. Anal. Chem. 2016, 88, 803–811. [Google Scholar] [CrossRef]
- Zimmermann, B.; Bagcioglu, M.; Tafinstseva, V.; Kohler, A.; Ohlson, M.; Fjellheim, S. A high-throughput FTIR spectroscopy approach to assess adaptive variation in the chemical composition of pollen. Ecol. Evol. 2017, 7, 10839–10849. [Google Scholar] [CrossRef] [Green Version]
- Kasahara, R.; Kino, S.; Soyama, S.; Matsuura, Y. Noninvasive glucose monitoring using mid-infrared absorption spectroscopy based on a few wavenumbers. J. Biomed. Opt. Express 2018, 9, 289–302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mishra, P.; Woltering, E.J. Identifying key wavenumbers that improve prediction of amylose in rice samples utilizing advanced wavenumber selection techniques. Talanta 2021, 224, 121908. [Google Scholar] [CrossRef]
- Tafintseva, V.; Vigneau, E.; Shapaval, V.; Cariou, V.; Qannari, E.M.; Kohler, A. Hierarchical classification of microorganisms based on high-dimensional phenotypic data. J. Biophotonics 2018, 11, e201700047. [Google Scholar] [CrossRef]
- Baker, M.J.; Trevisan, J.; Bassan, P.; Bhargava, R.; Butler, H.J.; Dorling, K.M.; Fielden, P.R.; Fogarty, S.W.; Fullwood, N.J.; Heys, K.A. Using Fourier transform IR spectroscopy to analyze biological materials. Nat. Protoc. 2014, 9, 1771. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zimmermann, B.; Kohler, A. Optimizing Savitzky-Golay parameters for improving spectral resolution and quantification in infrared spectroscopy. Appl. Spectrosc. 2013, 67, 892–902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kohler, A.; Solheim, J.H.; Tafintseva, V.; Zimmermann, B.; Shapaval, V. Model-Based Preprocessing in Vibrational Spectroscopy. In Comprehensive Chemometrics: Chemical and Biochemical Data Analysis, 2nd ed.; Brown, S., Tauler, R., Walczak, B., Eds.; Elsevier: New York, NY, USA, 2020; pp. 83–100. [Google Scholar]
- Tafintseva, V.; Shapaval, V.; Blazhko, U.; Kohler, A. Correcting replicate variation in spectroscopic data by machine learning and model-based preprocessing. Chemom. Intell. Lab. Syst. 2021, 215, 104350. [Google Scholar] [CrossRef]
- Acquarelli, J.; van Laarhoven, T.; Gerretzen, J.; Tran, T.N.; Buydens, L.M.C.; Marchiori, E. Convolutional neural networks for vibrational spectroscopic data analysis. J. Anal. Chim. Acta 2017, 954, 22–31. [Google Scholar] [CrossRef] [Green Version]
- Lasch, P. Spectral preprocessing for biomedical vibrational spectroscopy and microspectroscopic imaging. Chemom. Intell. Lab. Syst. 2012, 117, 100–114. [Google Scholar] [CrossRef] [Green Version]
- Martens, H.; Stark, E. Extended multiplicative signal correction and spectral interference subtraction: New preprocessing methods for near infrared spectroscopy. J. Pharm. Biomed. Anal. 1991, 9, 625–635. [Google Scholar] [CrossRef]
- Afseth, N.K.; Kohler, A. Extended multiplicative signal correction in vibrational spectroscopy, a tutorial. Chemom. Intell. Lab. Syst. 2012, 117, 92–99. [Google Scholar] [CrossRef]
- Tafintseva, V.; Shapaval, V.; Smirnova, M.; Kohler, A. Extended multiplicative signal correction for FTIR spectral quality test and preprocessing of infrared imaging data. J. Biophotonics 2020, 13, e201960112. [Google Scholar] [CrossRef] [PubMed]
- Diehn, S.; Zimmermann, B.; Tafintseva, V.; Bagcioglu, M.; Kohler, A.; Ohlson, M.; Fjellheim, S.; Kneipp, J. Discrimination of grass pollen of different species by FTIR spectroscopy of individual pollen grains. Anal. Bioanal. Chem. 2020, 412, 6459–6474. [Google Scholar] [CrossRef] [PubMed]
- Solheim, J.H.; Gunko, E.; Petersen, D.; Großerüschkamp, F.; Gerwert, K.; Kohler, A. An open-source code for Mie extinction extended multiplicative signal correction for infrared microscopy spectra of cells and tissues. J. Biophotonics 2019, 12, e201800415. [Google Scholar] [CrossRef] [PubMed]
- Magnussen, E.A.; Solheim, J.H.; Blazhko, U.; Tafintseva, V.; Tøndel, K.; Liland, K.H.; Dzurendova, S.; Shapaval, V.; Sandt, C.; Borondics, F.; et al. Deep convolutional neural network recovers pure absorbance spectra from highly scatter-distorted spectra of cells. J. Biophotonics 2020, 13, e202000204. [Google Scholar] [CrossRef] [PubMed]
- Solheim, J.H.; Borondics, F.; Zimmermann, B.; Sandt, C.; Muthreich, F.; Kohler, A. An automated approach for fringe frequency estimation and removal in infrared spectroscopy and hyperspectral imaging of biological samples. J. Biophotonics 2021, 14, e202100148. [Google Scholar] [CrossRef]
- Wold, S.; Martens, H.; Wold, H. The multivariate calibration problem in chemistry solved by the PLS method. In Matrix Pencils; Springer: Berlin/Heidelberg, Germany, 1983; pp. 286–293. [Google Scholar]
- Martens, H.; Martens, M. Multivariate Analysis of Quality: An Introduction; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Barker, M.; Rayens, W. Partial least squares for discrimination. J. Chemom. 2003, 17, 166–173. [Google Scholar] [CrossRef]
- Querido, W.; Kandel, S.; Pleshko, N. Applications of Vibrational Spectroscopy for Analysis of Connective Tissues. Molecules 2021, 26, 922. [Google Scholar] [CrossRef]
- Hargrave-Thomas, E.; Thambyah, A.; McGlashan, S.R.; Broom, N.D. The bovine patella as a model of early osteoarthritis. J. Anat. 2013, 223, 651–664. [Google Scholar] [CrossRef]
- Virtanen, V.; Nippolainen, E.; Shaikh, R.; Afara, I.O.; Toyras, J.; Solheim, J.; Tafintseva, V.; Zimmermann, B.; Kohler, A.; Saarakkala, S.; et al. Infrared Fiber-Optic Spectroscopy Detects Bovine Articular Cartilage Degeneration. Cartilage 2021, 13, 285S–294S. [Google Scholar] [CrossRef]
- Pritzker, K.P.; Gay, S.; Jimenez, S.A.; Ostergaard, K.; Pelletier, J.P.; Revell, P.A.; Salter, D.; van den Berg, W.B. Osteoarthritis cartilage histopathology: Grading and staging. Osteoarthr. Cartil. 2006, 14, 13–29. [Google Scholar] [CrossRef] [Green Version]
- Ostergaard, K.; Petersen, J.; Andersen, C.B.; Bendtzen, K.; Salter, D.M. Histologic/histochemical grading system for osteoarthritic articular cartilage. Reproducibility and validity. Arthritis Rheum. 1997, 40, 1766–1771. [Google Scholar] [CrossRef]
- Mainil-Varlet, P.; Van Damme, B.; Nesic, D.; Knutsen, G.; Kandel, R.; Roberts, S. A new histology scoring system for the assessment of the quality of human cartilage repair: ICRS II. Am. J. Sports Med. 2010, 38, 880–890. [Google Scholar] [CrossRef] [PubMed]
- Bloomfield, P. Fourier Analysis of Time Series: An Introduction. In Wiley Series in Probability and Statistics, 2nd ed.; Barnett, V., Cressie, N.A.C., Fisher, N.I., Johnstone, I.M., Kadane, J.B., Kendall, G.D., Scott, D.V., Silverman, B.W., Smith, A.F.M., Teugels, J.L., et al., Eds.; John Wiley & Sons: Toronto, ON, Canada, 2000. [Google Scholar]
- Saarakkala, S.; Rieppo, L.; Rieppo, J.; Jurvelin, J.S. Fourier transform infrared (FTIR) microspectroscopy of immature, mature and degenerated articular cartilage. Microscopy 2010, 1, 403–414. [Google Scholar]
- Camacho, N.P.; West, P.; Torzilli, P.A.; Mendelsohn, R. FTIR microscopic imaging of collagen and proteoglycan in bovine cartilage. Biopolymers 2001, 62, 1–8. [Google Scholar] [CrossRef]
- Kohler, A.; Kirschner, C.; Oust, A.; Martens, H. Extended multiplicative signal correction as a tool for separation and characterization of physical and chemical information in Fourier transform infrared microscopy images of cryo-sections of beef loin. Appl. Spectrosc. 2005, 59, 707–716. [Google Scholar] [CrossRef] [PubMed]
- Rehman, H.U.; Tafintseva, V.; Zimmermann, B.; Solheim, J.; Virtanen, V.; Shaikh, R.; Nippolainen, E.; Afara, I.; Saarakkala, S.; Rieppo, L.; et al. Preclassification of broadband and sparse infrared data by multiplicative signal correction approach. Mol. New Wind. Chemom. Theory Appl. 2022. to be submitted. [Google Scholar]
- Martens, H.; Næs, T. Multivariate Calibration; John Wiley & Sons: Chichester, UK, 1992. [Google Scholar]
- Kohler, A.; Hanafi, M.; Bertrand, D.; Quannari, M.; Oust, A.J. Interpreting several types of measurements in bioscience. In Biomedical Vibrational Spectroscopy; Peter Lasch, J.K., Ed.; John Wiley: Hoboken, NJ, USA, 2008; pp. 333–356. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intel. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tafintseva, V.; Lintvedt, T.A.; Solheim, J.H.; Zimmermann, B.; Rehman, H.U.; Virtanen, V.; Shaikh, R.; Nippolainen, E.; Afara, I.; Saarakkala, S.; et al. Preprocessing Strategies for Sparse Infrared Spectroscopy: A Case Study on Cartilage Diagnostics. Molecules 2022, 27, 873. https://doi.org/10.3390/molecules27030873
Tafintseva V, Lintvedt TA, Solheim JH, Zimmermann B, Rehman HU, Virtanen V, Shaikh R, Nippolainen E, Afara I, Saarakkala S, et al. Preprocessing Strategies for Sparse Infrared Spectroscopy: A Case Study on Cartilage Diagnostics. Molecules. 2022; 27(3):873. https://doi.org/10.3390/molecules27030873
Chicago/Turabian StyleTafintseva, Valeria, Tiril Aurora Lintvedt, Johanne Heitmann Solheim, Boris Zimmermann, Hafeez Ur Rehman, Vesa Virtanen, Rubina Shaikh, Ervin Nippolainen, Isaac Afara, Simo Saarakkala, and et al. 2022. "Preprocessing Strategies for Sparse Infrared Spectroscopy: A Case Study on Cartilage Diagnostics" Molecules 27, no. 3: 873. https://doi.org/10.3390/molecules27030873
APA StyleTafintseva, V., Lintvedt, T. A., Solheim, J. H., Zimmermann, B., Rehman, H. U., Virtanen, V., Shaikh, R., Nippolainen, E., Afara, I., Saarakkala, S., Rieppo, L., Krebs, P., Fomina, P., Mizaikoff, B., & Kohler, A. (2022). Preprocessing Strategies for Sparse Infrared Spectroscopy: A Case Study on Cartilage Diagnostics. Molecules, 27(3), 873. https://doi.org/10.3390/molecules27030873






