Reaction Optimization for Greener Chemistry with a Comprehensive Spreadsheet Tool
Abstract
1. Introduction
2. Results
2.1. Reaction Optimisation Spreadsheet Function Tutorial
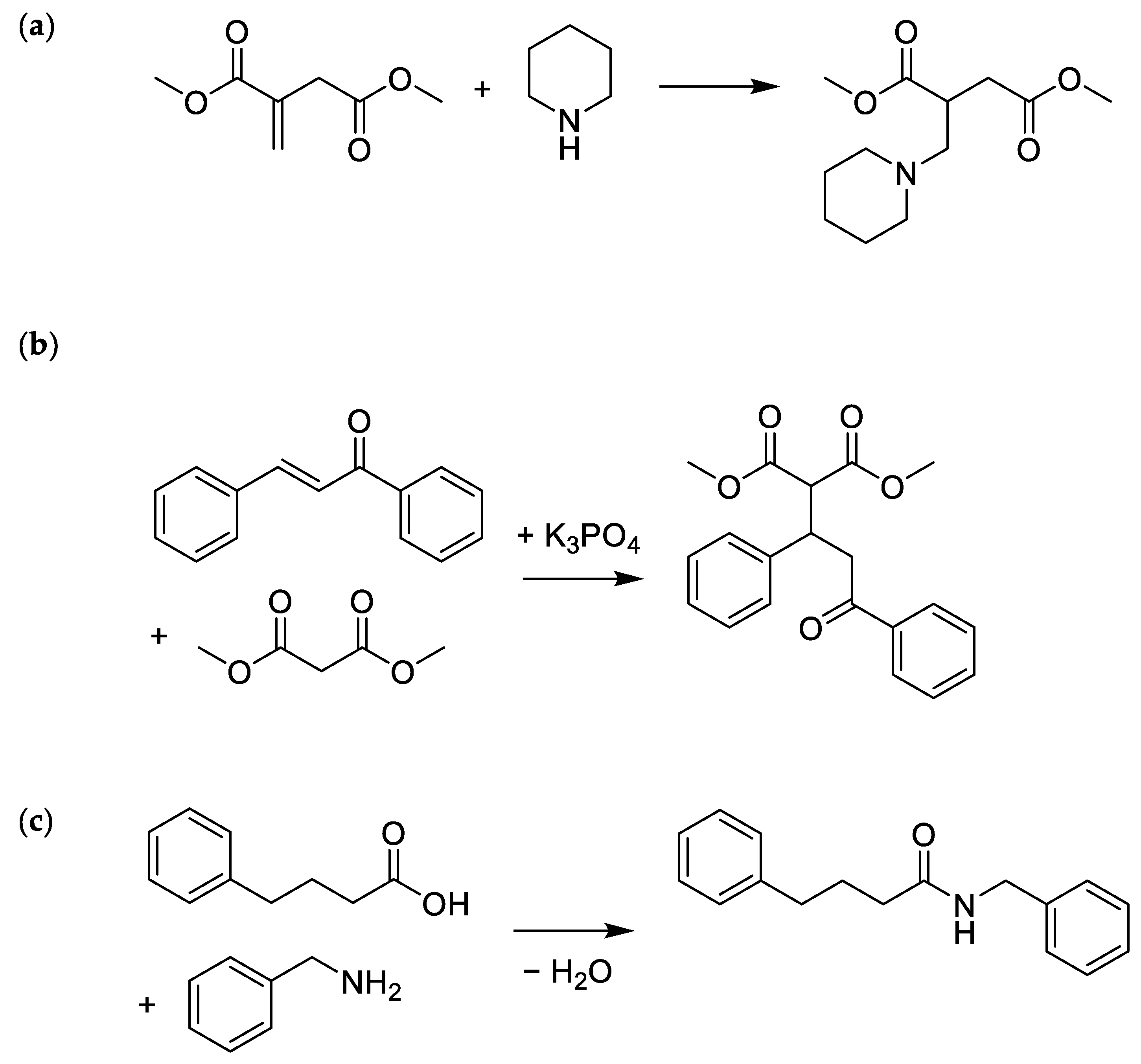
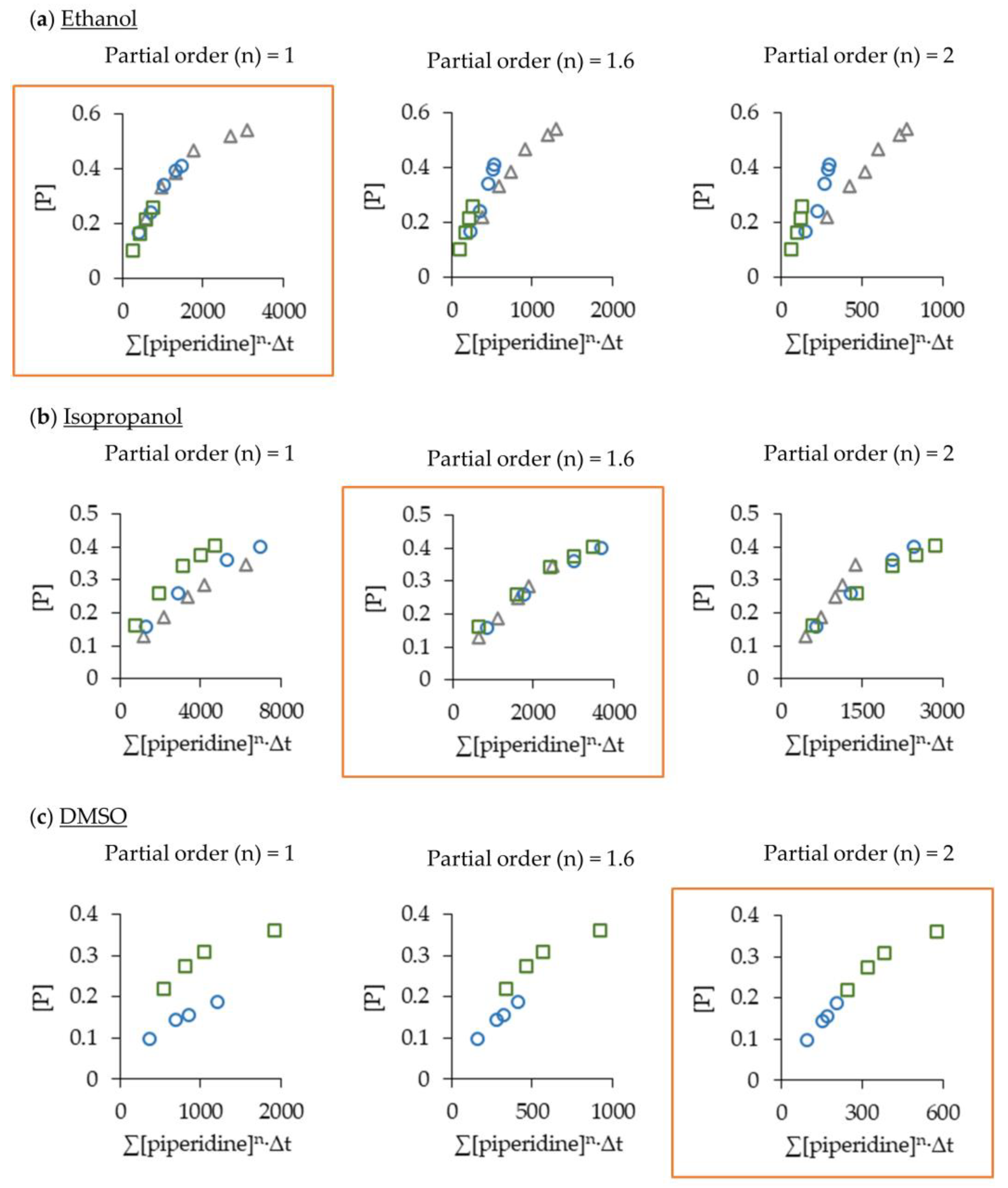
2.2. Optimising the Aza-Michael Reaction
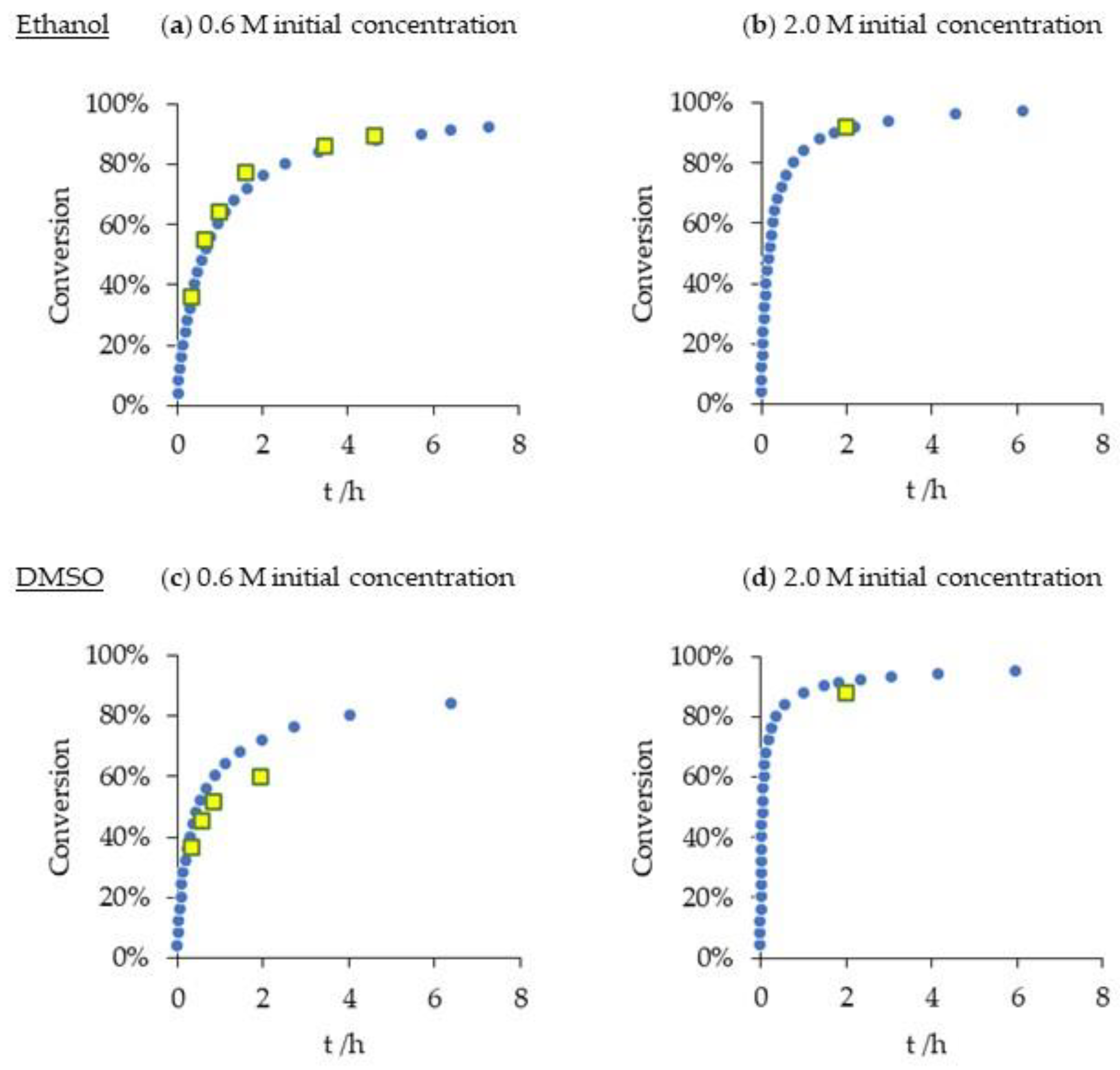
2.3. Green Solvent for the Michael Reaction
2.4. Amidation
3. Discussion
4. Conclusions
5. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- 12 Principles of Green Chemistry. Available online: https://www.acs.org/content/acs/en/greenchemistry/principles/12-principles-of-green-chemistry.html (accessed on 15 October 2022).
- Andraos, J. On using tree analysis to quantify the material, input energy, and cost throughput efficiencies of simple and complex synthesis plans and networks: towards a blueprint for quantitative total synthesis and green chemistry. Org. Process Res. Dev. 2006, 10, 212–240. [Google Scholar] [CrossRef]
- Andraos, J. Safety/hazard indices: Completion of a unified suite of metrics for the assessment of “greenness” for chemical reactions and synthesis plans. Org. Process Res. Dev. 2013, 17, 175–192. [Google Scholar] [CrossRef]
- Rubin, S.J.; Abrams, B. Teaching fundamental skills in Microsoft Excel to first-year students in quantitative analysis. J. Chem. Educ. 2015, 92, 1840–1845. [Google Scholar] [CrossRef]
- Andraos, J.; Sayed, M. On the use of “green” metrics in the undergraduate organic chemistry lecture and lab to assess the mass efficiency of organic reactions. J. Chem. Educ. 2007, 84, 1004–1010. [Google Scholar] [CrossRef]
- McElroy, C.R.; Constantinou, A.; Jones, L.C.; Summerton, L.; Clark, J.H. Towards a holistic approach to metrics for the 21st century pharmaceutical industry. Green Chem. 2015, 17, 3111–3121. [Google Scholar] [CrossRef]
- Lie, Y.; Ortiz, P.; Vendamme, R.; Vanbroekhoven, K.; Farmer, T.J. BioLogicTool: A simple visual tool for assisting in the logical selection of pathways from biomass to products. Ind. Eng. Chem. Res. 2019, 58, 15945–15957. [Google Scholar] [CrossRef]
- Burés, J. Variable Time Normalization Analysis: General graphical elucidation of reaction orders from concentration profiles. Angew. Chem. Ind. Ed. 2016, 55, 16084–16087. [Google Scholar] [CrossRef]
- Burés, J. A simple graphical method to determine the order in catalyst. Angew. Chem. Ind. Ed. 2016, 55, 2028–2031. [Google Scholar] [CrossRef]
- Nielsen, C.D.-T.; Burés, J. Visual kinetic analysis. Chem. Sci. 2019, 10, 348–353. [Google Scholar] [CrossRef]
- Reichardt, C.; Welton, T. Solvents and Solvent Effects in Organic Chemistry, 4th ed.; Wiley-VCH: Weinheim, Germany, 2010; pp. 165–357. [Google Scholar]
- Alder, C.M.; Hayler, J.D.; Henderson, R.K.; Redman, A.M.; Shukla, L.; Shuster, L.E.; Sneddon, H.F. Updating and further expanding GSK’s solvent sustainability guide. Green Chem. 2016, 18, 3879–3890. [Google Scholar] [CrossRef]
- Skowerski, K.; Białecki, J.; Tracz, A.; Olszewski, T.K. An attempt to provide an environmentally friendly solvent selection guide for olefin metathesis. Green Chem. 2014, 16, 1125–1130. [Google Scholar] [CrossRef]
- McGonagle, F.I.; MacMillan, D.S.; Murray, J.; Sneddon, H.F.; Jamieson, C.; Watson, A.J.B. Development of a solvent selection guide for aldehyde-based direct reductive amination processes. Green Chem. 2013, 15, 1159–1165. [Google Scholar] [CrossRef]
- Taft, R.W.; Abboud, J.-L.M.; Kamlet, M.J.; Abraham, M.H. Linear solvation energy relations. J. Solut. Chem. 1985, 14, 153–186. [Google Scholar] [CrossRef]
- Sherwood, J.; Granelli, J.; McElroy, C.R.; Clark, J.H. A method of calculating the Kamlet–Abboud–Taft solvatochromic parameters Using COSMO-RS. Molecules 2019, 24, 2209. [Google Scholar] [CrossRef] [PubMed]
- Day, D.M.; Farmer, T.J.; Sherwood, J.; Clark, J.H. An experimental investigation into the kinetics and mechanism of the aza-Michael additions of dimethyl itaconate. Tetrahedron 2022, 121, 132921. [Google Scholar] [CrossRef]
- Clark, J.H.; Macquarrie, D.J.; Sherwood, J. A quantitative comparison between conventional and bio-derived solvents from citrus waste in esterification and amidation kinetic studies. Green Chem. 2012, 14, 90–93. [Google Scholar] [CrossRef]
- Clark, J.H.; Fitzpatrick, E.M.; Macquarrie, D.J.; Pfaltzgraff, L.A.; Sherwood, J. p-Cymenesulphonic acid: An organic acid synthesised from citrus waste. Catal. Today 2012, 190, 144–149. [Google Scholar] [CrossRef]
- Farmer, T.J.; Macquarrie, D.J.; Comerford, J.W.; Pellis, A.; Clark, J.H. Insights into post-polymerisation modification of bio-based unsaturated itaconate and fumarate polyesters via aza-michael addition: Understanding the effects of C=C isomerisation. J. Polym. Sci. Part A Polym. Chem. 2018, 56, 1935–1945. [Google Scholar] [CrossRef]
- Jessop, P.G.; Jessop, D.A.; Fu, D.; Phan, L. Solvatochromic parameters for solvents of interest in green chemistry. Green Chem. 2012, 14, 1245–1259. [Google Scholar] [CrossRef]
- Prat, D.; Wells, A.; Hayler, J.; Sneddon, H.; McElroy, C.R.; Abou-Shehada, S.; Dunn, P.J. CHEM21 selection guide of classical- and less classical-solvents. Green Chem. 2016, 18, 288–296. [Google Scholar] [CrossRef]
- Capriotti, K.; Capriotti, J.A. Dimethyl sulfoxide: History, chemistry, and clinical utility in dermatology. J. Clin. Aesthet. Dermatol. 2012, 5, 24–26. [Google Scholar] [PubMed]
- Deguchi, Y.; Kono, M.; Koizumi, Y.; Izato, Y.-I.; Miyake, A. Study on autocatalytic decomposition of dimethyl sulfoxide (DMSO). Org. Process Res. Dev. 2020, 24, 1614–1620. [Google Scholar] [CrossRef]
- Pace, V.; Hoyos, P.; Castoldi, L.; Domínguez de María, P.; Alcántara, A.R. 2-Methyltetrahydrofuran (2-MeTHF): A biomass-derived solvent with broad application in organic chemistry. ChemSusChem 2012, 5, 1369–1379. [Google Scholar] [CrossRef]
- Arnold, K.; Davies, B.; Giles, R.L.; Grosjean, C.; Smith, G.E.; Whiting, A. To catalyze or not to catalyze? insight into direct amide bond formation from amines and carboxylic acids under thermal and catalyzed conditions. Adv. Synth. Catal. 2006, 348, 813–820. [Google Scholar] [CrossRef]
- Arkhipenko, S.; Sabatini, M.T.; Batsanov, A.S.; Karaluka, V.; Sheppard, T.D.; Rzepa, H.S.; Whiting, A. Mechanistic insights into boron-catalysed direct amidation reactions. Chem. Sci. 2018, 9, 1058–1072. [Google Scholar] [CrossRef]



| Worksheet | Function |
|---|---|
| Data entry | Kinetic data measurements are added. In the Microsoft 365 compatible spreadsheet (Supplementary Material S1), repeat experiments are automatically combined. |
| Conversions | Product conversion as a function of time is displayed for selected reactions (maximum of five). |
| Kinetics | Orders of reaction are determined using VTNA. Rate constants (k) are calculated for each experiment. |
| Activation parameters | The enthalpy and entropy of activation are calculated for data sets with variable temperatures. |
| Solvent effects | The solvent effect describing the rate of reaction is calculated as a LSER. |
| Solvent selection | High performing solvents are predicted based on the calculated rate constant. |
| Solvent list | Tabulated solvent properties. The greenness of solvents can be calculated on this worksheet also. |
| Metrics | The product conversion at a set time is predicted based on the solvent and temperature and initial concentration of reactants. The green metrics describing the reaction are shown (atom economy, reaction mass efficiency, and optimum efficiency). |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Day, D.M.; Farmer, T.J.; Granelli, J.; Lofthouse, J.H.; Lynch, J.; McElroy, C.R.; Sherwood, J.; Shimizu, S.; Clark, J.H. Reaction Optimization for Greener Chemistry with a Comprehensive Spreadsheet Tool. Molecules 2022, 27, 8427. https://doi.org/10.3390/molecules27238427
Day DM, Farmer TJ, Granelli J, Lofthouse JH, Lynch J, McElroy CR, Sherwood J, Shimizu S, Clark JH. Reaction Optimization for Greener Chemistry with a Comprehensive Spreadsheet Tool. Molecules. 2022; 27(23):8427. https://doi.org/10.3390/molecules27238427
Chicago/Turabian StyleDay, Daniel M., Thomas J. Farmer, Joe Granelli, Janice H. Lofthouse, Julie Lynch, Con R. McElroy, James Sherwood, Seishi Shimizu, and James H. Clark. 2022. "Reaction Optimization for Greener Chemistry with a Comprehensive Spreadsheet Tool" Molecules 27, no. 23: 8427. https://doi.org/10.3390/molecules27238427
APA StyleDay, D. M., Farmer, T. J., Granelli, J., Lofthouse, J. H., Lynch, J., McElroy, C. R., Sherwood, J., Shimizu, S., & Clark, J. H. (2022). Reaction Optimization for Greener Chemistry with a Comprehensive Spreadsheet Tool. Molecules, 27(23), 8427. https://doi.org/10.3390/molecules27238427









