Cu(Proline)2 Complex: A Model of Bio-Copper Structural Ambivalence
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. UV-VIS Optical Activity on Structure and Coordination
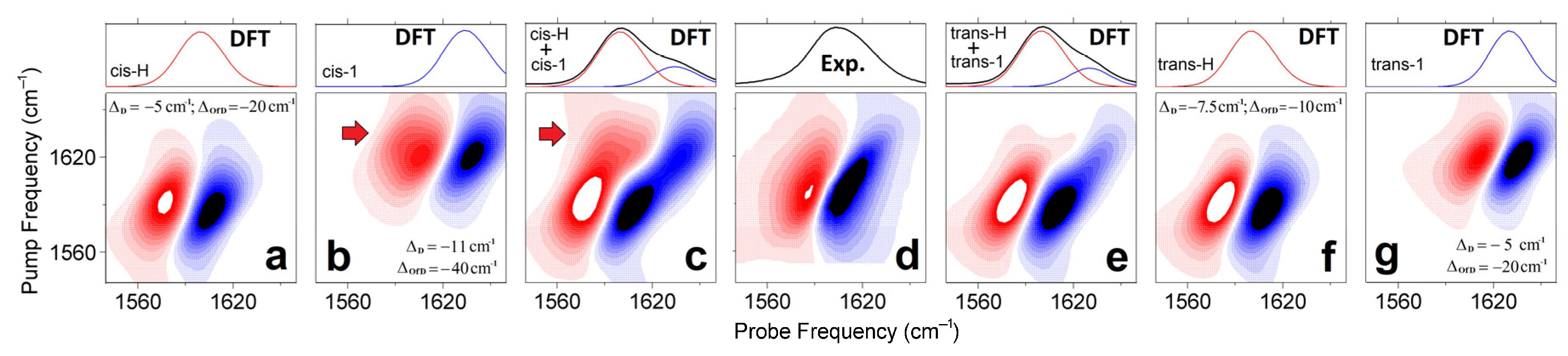
3.2. IR Diagnostics on Intra- and Inter-Molecular Correlations
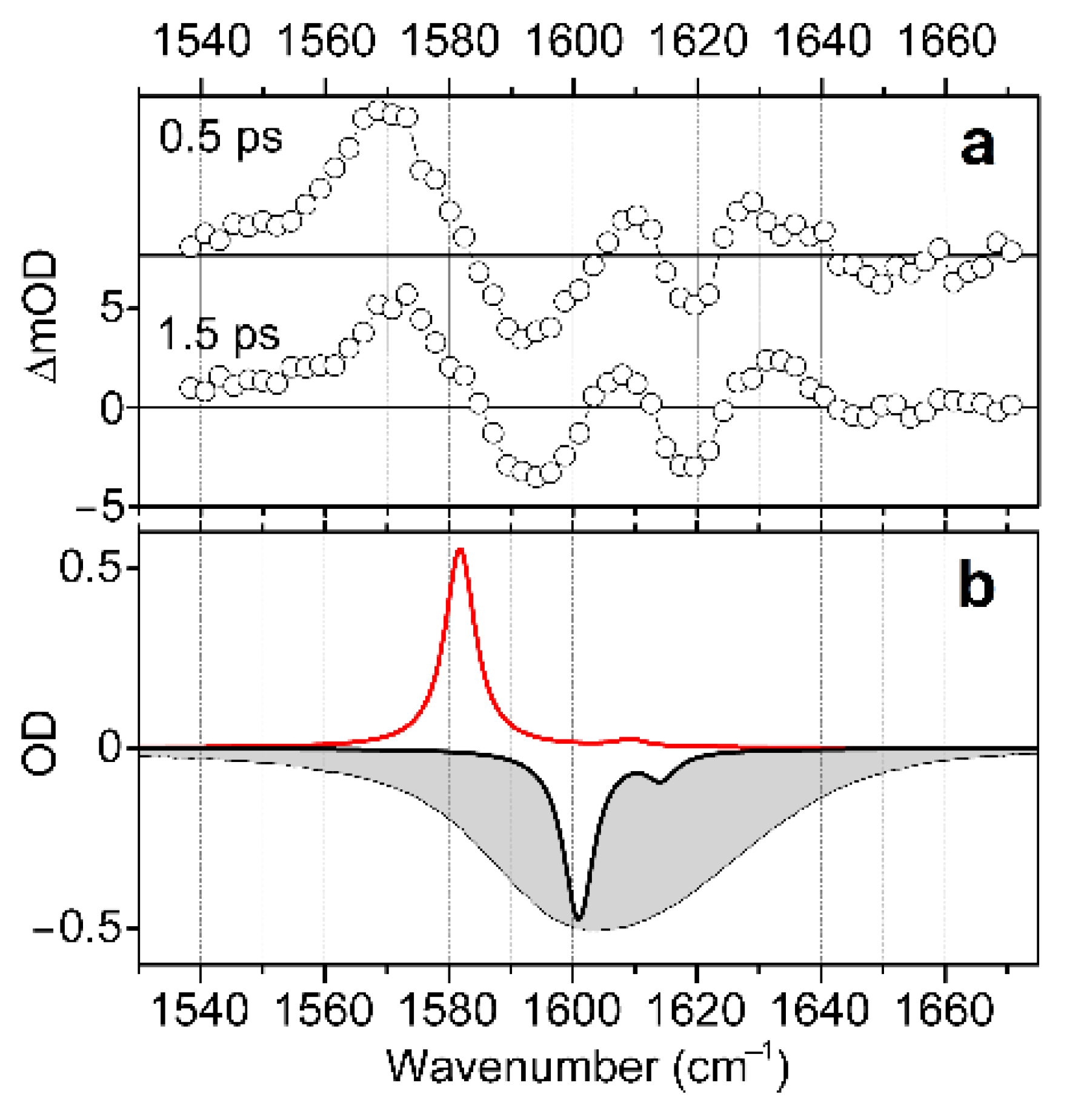
3.3. Photo-Dynamic Perspective of Copper Electronics and Coordination
3.4. Structural Flexibility and Implications
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Haynes, W.M. Abundance of elements in the earth’s crust and in the sea. In CRC Handbook of Chemistry and Physics, 97th ed.; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2017; pp. 14–17. [Google Scholar]
- Cotton, F.A.; Wilkinson, G. Advanced Inorganic Chemistry; John Wiley and Sons Inc.: Hoboken, NJ, USA, 1980; pp. 816–820. [Google Scholar]
- Williams, R.J.P. Energised (entatic) states of groups and of secondary structures in proteins and metalloproteins. Eur. J. Biochem. 1995, 234, 363–381. [Google Scholar] [CrossRef] [PubMed]
- Gaazo, J.; Bersuker, I.B.; Garaj, J.; Kabesova, M.; Kohout, J.; Langfelderova, H.; Melnik, M.; Serator, M.; Valach, F. Plasticity of the coordination sphere of copper(II) complexes, its manifestation and causes. Coord. Chem. Rev. 1976, 19, 253–297. [Google Scholar] [CrossRef]
- Frank, P.; Benfatto, M.; Hedman, B.; Hodgson, K.O. Solution [Cu(amm)]2+ is a Strongly Solvated Square Pyramid: A Full Account of the Copper K-edge XAS Spectrum within Single-Electron Theory. Inorg. Chem. 2008, 47, 4126–4139. [Google Scholar] [CrossRef]
- de Almeida, K.J.; Murugan, N.A.; Rinkevicius, Z.; Hugosson, H.W.; Vahtras, O.; Ågrena, H.; Cesar, A. Conformations, structural transitions and visible near-infrared absorption spectra of four-, five- and six-coordinated Cu(ii) aqua complexes. Phys. Chem. Chem. Phys. 2009, 11, 508–519. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.-E.; Kim, J.; Park, J.W.; Park, K.; Lee, Y. σ-Complexation as a strategy for designing copper-based light emitters. Chem. Commun. 2017, 53, 2858–2861. [Google Scholar] [CrossRef] [PubMed]
- Decaria, L.; Bertini, I.; Williams, R.J.P. Copper proteomes, phylogenetics and evolution. Metallomics 2011, 3, 56–60. [Google Scholar] [CrossRef]
- Roat-Malone, R.M. Bioinorganic Chemistry: A Short Course; John Wiley & Sons Inc.: 111 River Street: Hoboken, NJ, USA, 2020; ISBN 978-1-119-53526-3. [Google Scholar]
- Lanza, V.; Travaglia, A.; Malgieri, G.; Fattorusso, R.; Grasso, G.; Di Natale, G.; Zito, V.; Arena, G.; Milardi, D.; Rizzarelli, E. Ubiquitin Associates with the N-Terminal Domain of Nerve Growth Factor: The Role of Copper(II) Ions. Chem. Eur. J. 2016, 22, 17767–17775. [Google Scholar] [CrossRef]
- Gaucher, J.F.; Reille-Seroussi, M.; Gagey-Eilstein, N.; Broussy, S.; Coric, P.; Seijo, B.; Lascombe, M.B.; Gautier, B.; Liu, W.Q.; Huguenot, F.; et al. Biophysical Studies of the Induced Dimerization of Human VEGF Receptor 1 Binding Domain by Divalent Metals Competing with VEGF-A. PLoS ONE 2016, 11, e0167755. [Google Scholar] [CrossRef]
- Marciniak, A.; Witak, W.; Sabatino, G.; Papini, A.M.; Brasu, J. Detailed Insight into the Interaction of Bicyclic Somatostatin Analogue with Cu(II) Ions. Int. J. Mol. Sci. 2020, 21, 8794. [Google Scholar] [CrossRef]
- Chaka, G.; Sonnenberg, J.L.; Schlegel, H.B.; Heeg, M.J.; Jaeger, G.; Nelson, T.J.; Ochrymowycz, L.A.; Rorabacher, D.B. A Definitive Example of a Geometric “Entatic State” Effect: Electron-Transfer Kinetics for a Copper(II/I) Complex Involving A Quinquedentate Macrocyclic Trithiaether−Bipyridine Ligand. J. Am. Chem. Soc. 2007, 129, 5217–5227. [Google Scholar] [CrossRef]
- Toyama, A.; Takahashi, Y.; Takeuchi, H. Catalytic and Structural Role of a Metal-Free Histidine Residue in Bovine Cu−Zn Superoxide Dismutase. Biochemistry 2004, 43, 4670–4679. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Wu, C.; Cao, Z.; Wang, B. QM/MM MD simulations reveal an asynchronous PCET mechanism for nitrite reduction by copper nitrite reductase. Phys. Chem. Chem. Phys. 2020, 22, 20922–20928. [Google Scholar] [CrossRef] [PubMed]
- Deeth, R.J. Comprehensive Molecular Mechanics Model for Oxidized Type I Copper Proteins: Active Site Structures, Strain Energies, and Entatic Bulging. Inorg. Chem. 2007, 46, 4492–4503. [Google Scholar] [CrossRef] [PubMed]
- Vallee, B.L.; Williams, R.J.P. Metalloenzymes: The entatic nature of their active sites. Proc. Natl. Acad. Sci. USA 1968, 59, 498–505. [Google Scholar] [CrossRef]
- Williams, R.J.P. The entatic state. In Cold Spring Harbour Symposia in Quantitative Biology; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 1972; Volume 36, pp. 53–62. [Google Scholar] [CrossRef]
- Hagen, W.R. Hypothesis: Entatic versus ecstatic states in metalloproteins. Metallomics 2019, 11, 1768–1778. [Google Scholar] [CrossRef]
- Viles, J.H.; Klewpatinond, M.; Nadal, R.C. Copper and the structural biology of the prion protein. Biochem. Soc. Trans. 2008, 36, 1288–1292. [Google Scholar] [CrossRef]
- Streltsov, V.A.; Titmuss, S.J.; Epa, V.C.; Barnham, K.J.; Masters, C.L.; Varghese, J.N. The structure of the amyloid-beta peptide high-affinity copper II binding site in Alzheimer disease. Biophys. J. 2008, 95, 3447–3456. [Google Scholar] [CrossRef]
- Faller, P.; Hureau, C.; Dorlet, O.; Hellwig, P.; Coppel, Y.; Collin, F.; Alies, B. Methods and techniques to study the bioinorganic chemistry of metal–peptide complexes linked to neurodegenerative diseases. Coord. Chem. Rev. 2012, 256, 2381–2396. [Google Scholar] [CrossRef]
- Gray, H.B.; Malmastrom, B.G.; Williams, R.J.P. Copper coordination in blue proteins. J. Biol. Inorg. Chem. 2000, 5, 551–559. [Google Scholar] [CrossRef]
- Volkov, V.; Pfister, R. Cotton Effect in Copper-Proline complexes in the Visible. J. Chem. Educ. 2005, 82, 1663–1666. [Google Scholar] [CrossRef]
- Cotton, A. Absorption inegale des rayons circulaires droit et gauche dans certain corps actifs. C.R.H. Acad. Sci. 1895, 120, 989–991. [Google Scholar]
- Pfeiffer, P.; Christeleit, W. Komplexchemische Methode zur relativen Konfigurationsbestimmung der natürlichen α-Aminosäuren. Hoppe-Seyler’s Z. Für Physiol. Chem. 1937, 245, 197–210. [Google Scholar] [CrossRef]
- Yasui, T.; Hidaka, J.; Shimura, Y. Circular Dichroism of Copper(II) Complexes with Optically Active Amino Acids. J. Am. Chem. Soc. 1965, 87, 2762–2763. [Google Scholar] [CrossRef] [PubMed]
- Gillard, R.D.; Irving, H.M.; Parkins, R.M.; Payne, N.C.; Pettit, L.D. The isomers of complexes of α-amino-acids with Copper(II). J. Chem. Soc. A 1966, 1159–1164. [Google Scholar] [CrossRef]
- Wellman, K.; Mecca, T.; Mungall, W.; Hare, C. Optical rotatory dispersion spectra of bis- and mono(alpha-substituted glycinato)Cu(II) complexes. J. Am. Chem. Soc. 1967, 89, 3646–3647. [Google Scholar] [CrossRef]
- Mathieson, A.; Welsh, H. The crystal structure of Copper proline dihydrate. Acta Cryst. 1952, 5, 599–604. [Google Scholar] [CrossRef]
- Gillard, R.D.; Mason, R.; Payene, N.C.; Robertson, G.B. The isomers of α-amino acids with copper(II). Part II. The crystal and molecular structure of cis-bis-[D-alaninato]copper(II). J. Chem. Soc. A 1969, 1864–1871. [Google Scholar] [CrossRef]
- Goodman, B.; McPhail, D. Electron spin resonance parameters for some copper(II)–bis(amino-acid) complexes. J. Chem. Soc., Dalton Trans. 1985, 8, 1717–1718. [Google Scholar] [CrossRef]
- Kühne, T.D.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package—Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Dunning, T.H.; Hay, P.J. Modern Theoretical Chemistry; Plenum: New York, NY, USA, 1977; Volume 3, pp. 1–28. [Google Scholar]
- Wedig, U.; Dolg, M.; Stoll, H.; Preuss, H. Quantum Chemistry: The Challenge of Transition Metals and Coordination Chemistry; Springer: Berlin/Heidelberg, Germany, 1986; pp. 79–89. [Google Scholar]
- Volkov, V.; Hamm, P. A Two-Dimensional Infrared Study of Localization, Structure, and Dynamics of a Dipeptide in Membrane Environment. Biophys. J. 2004, 87, 4213–4225. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- He, Y.; Cao, X.; Nafie, L.A.; Freedman, T.B. Ab Initio VCD Calculation of a Transition-Metal Containing Molecule and a New Intensity Enhancement Mechanism for VCD. J. Am. Chem. Soc. 2001, 123, 11320–11321. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef] [PubMed]
- Chelli, R.; Volkov, V.; Righini, R. Retrieval of Spectral and Dynamic Properties from Two-Dimensional Infrared Pump-Probe Experiments. J. Comput. Chem. 2008, 29, 1507–1516. [Google Scholar] [CrossRef]
- Califano, S. Vibrational States; John Wiley and Sons: London, UK, 1976. [Google Scholar]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford University Press, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Moscowitz, A. Theoretical aspects of optical activity. Part 1: Small molecules. Adv. Chem. Phys. 1962, 4, 67–112. [Google Scholar] [CrossRef]
- Polavarapu, P. Kramers-Kronig transformation for optical rotatory dispersion studies. J. Phys. Chem. A 2005, 109, 7013–7023. [Google Scholar] [CrossRef]
- Koopmans, T. Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den einzelnen Elektronen eines Atoms. Physica 1934, 1, 104–113. [Google Scholar] [CrossRef]
- Amos, A.T.; Hall, G.G. Single determinant wave functions. Proc. Royal Soc. A 1961, 263, 483–493. [Google Scholar] [CrossRef]
- Martin, R.L. Natural transition orbitals. J. Chem. Phys. 2003, 118, 4775–4777. [Google Scholar] [CrossRef]
- Sartoris, R.P.; Ortigoza, L.; Casado, N.M.C.; Calvo, R.; Castellano, E.E.; Piro, O.E. Structure, Single Crystal EPR Spectra, and Exchange Interactions in [Cu(L-proline)2]2·5H2O and Cu(D,L-proline)2·2H2O. Inorg. Chem. 1999, 38, 3598–3604. [Google Scholar] [CrossRef]
- Hawkins, C.; Wong, C. Circular dichroism spectra of amino acid complexes. III. Copper(II) compounds. Aust. J. Chem. 1970, 23, 2237–2246. [Google Scholar] [CrossRef]
- Solomon, E.; Szilagyi, R.; DeBeer, G.; Basumallick, L. Electronic Structures of Metal Sites in Proteins and Models: Contributions to Function in Blue Copper Proteins. Chem. Rev. 2004, 104, 419–458. [Google Scholar] [CrossRef] [PubMed]
- Wynne, K.; Hochstrasser, R.M. The theory of ultrafast vibrational spectroscopy. Chem. Phys. 1995, 193, 211–236. [Google Scholar] [CrossRef]
- Dong, J.; Atwood, C.S.; Anderson, V.E.; Siedlak, S.L.; Smith, M.A.; Perry, G.; Carey, P.R. Metal Binding and Oxidation of Amyloid-β within Isolated Senile Plaque Cores: Raman Microscopic Evidence. Biochem. 2003, 42, 2768–2773. [Google Scholar] [CrossRef] [PubMed]
- Stellato, F. Copper-zinc cross-modulation in prion protein binding. Eur. Biophys. J. 2014, 43, 631–642. [Google Scholar] [CrossRef]
- Schirer, A.; Khoury, Y.; Faller, P.; Hellwig, P. Similarities and differences of copper and zinc cations binding to biologically relevant peptides studied by vibrational spectroscopies. JBIC J. Bio. Inorg. Chem. 2017, 22, 581–589. [Google Scholar] [CrossRef]
- Rana, M.; Sharma, A.K. Cu and Zn interactions with Aβ peptides: Consequence of coordination on aggregation and formation of neurotoxic soluble Aβ oligomers. Metallomics 2019, 11, 64–84. [Google Scholar] [CrossRef]
- Atrián-Blasco, E.; Gonzalez, P.; Santoro, A.; Alies, B.; Faller, P.; Hureau, C. Cu and Zn coordination to amyloid peptides: From fascinating chemistry to debated pathological relevance. Coord. Chem. Rev. 2018, 375, 38–55. [Google Scholar] [CrossRef]
- Kong, G.K.-W.; Adams, J.J.; Harris, H.H.; Boas, J.F.; Curtain, C.C.; Galatis, D.; Masters, C.L.; Barnham, K.J.; McKinstry, W.J.; Cappai, R.; et al. Structural studies of the Alzheimer’s amyloid precursor protein copper-binding domain reveal how it binds copper ions. J. Mol. Biol. 2007, 367, 148–161. [Google Scholar] [CrossRef]
- Baumkötter, F.; Schmidt, N.; Vargas, C.; Schilling, S.; Weber, R.; Wagner, K.; Fiedler, S.; Klug, W.; Radzimanowski, J.; Nickolaus, S.; et al. Amyloid Precursor Protein Dimerization and Synaptogenic Function Depend on Copper Binding to the Growth Factor-Like Domain. J. Neurosci. 2014, 34, 11159–11172. [Google Scholar] [CrossRef]
- Evans, E.G.B.; Pushie, M.J.; Markham, K.A.; Lee, H.-W.; Millhauser, G.L. Interaction between Prion Protein’s Copper-Bound Octarepeat Domain and a Charged C-Terminal Pocket Suggests a Mechanism for N-Terminal Regulation. Structure 2016, 24, 1057–1067. [Google Scholar] [CrossRef] [PubMed]
- Mufamadi, M.S.; Choonara, Y.E.; Kumar, P.; Modi, G.; Naidoo, D.; Ndesendo, V.M.; du Toit, L.C.; Iyuke, S.E.; Pillay, V. Surface-engineered nanoliposomes by chelating ligands for modulating the neurotoxicity associated with β-amyloid aggregates of Alzheimer’s disease. Pharm. Res. 2012, 29, 3057–3089. [Google Scholar] [CrossRef] [PubMed]
- Summers, K.L.; Roseman, G.P.; Sopasis, G.J.; Millhauser, G.L.; Harris, H.H.; Pickering, I.J.; George, G.N. Copper(II) Binding to PBT2 Differs from That of Other 8-Hydroxyquinoline Chelators: Implications for the Treatment of Neurodegenerative Protein Misfolding Diseases. Inorg. Chem. 2020, 59, 17519–17534. [Google Scholar] [CrossRef] [PubMed]
- Lamberts, K.; Serbb, M.-D.; Englert, U. Unexpected proline coordination in the copper chain polymer [Cu(μ-Cl)2(μ-DL-proline-k2O:O’)]1∞. Acta Cryst. 2015, C71, 271–275. [Google Scholar] [CrossRef]
- VandeVondele, J.; Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M.P. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Hamm, P.; Kaindl, R.A.; Stenger, J. Noise suppression in femtosecond mid-infrared light sources. Opt. Lett. 2000, 25, 1798–1800. [Google Scholar] [CrossRef]
- Thämer, M.; De Marco, L.; Ramasesha, K.; Mandal, A.; Tokmakoff, A. Ultrafast 2D IR spectroscopy of the excess proton in liquid water. Science 2015, 350, 78–82. [Google Scholar] [CrossRef]

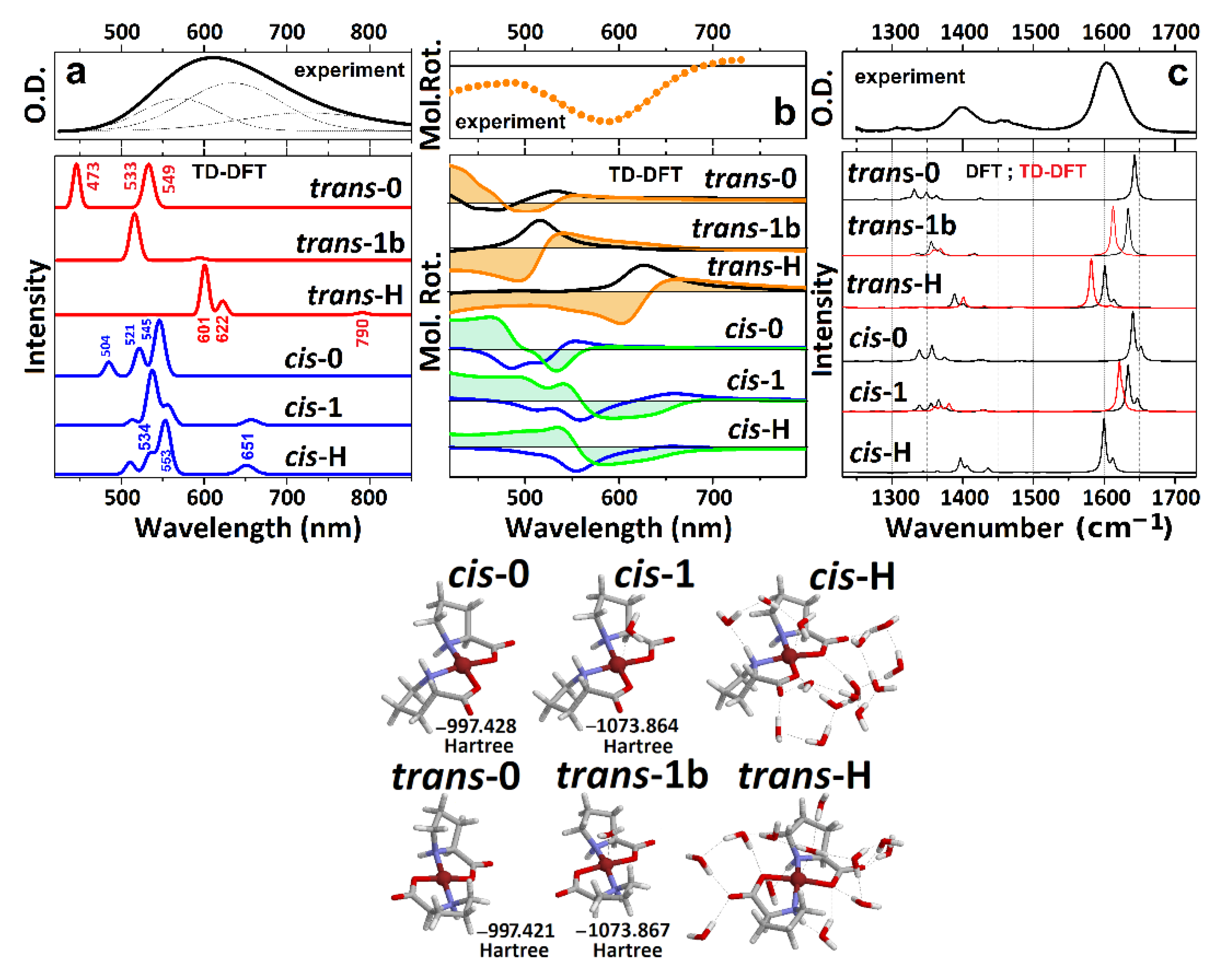


| trans-0 | trans-1b | trans-H | cis-0 | cis-1 | cis-H | |
|---|---|---|---|---|---|---|
| Cu-O/Å | 1.95 (2.00) | 1.97 (2.08) | 2.02 (2.2) | 1.96 (2.04) | 1.97 (2.02) | 2.00 (2.07) |
| Cu-N/Å | 2.03 (2.3) | 2.05 (2.19) | 2.05 (2.15) | 2.1 (2.2) | 2.06 (2.25) | 2.06 (2.21) |
| C=O/Å | 1.238 (1.241) | 1.24 (1.25) | 1.25 (1.26) | 1.239 (1.242) | 1.241 (1.243) | 1.25 (1.26) |
| NCuO′ | 95° (103°) | 95° (97°) | 95° (96°) | 99° (102°) | 98.9° (100°) | 98° (100°) |
| N′CuO′ | 85° (80°) | 85° (81°) | 83° (78°) | 84° (79°) | 84° (81°) | 83.5° (80°) |
| NA′CuB′ | 178° (168°) | 174° (162°) | 157° (142°) | 178° (171°) | 175° (179°) | 179° (178°) |
| Cu-Ow/Å | 2.44 (2.0) | 2.33 (1.96) | 2.47 (2.02) | 2.56 (2.03) | ||
| NCuOw | 97°, 88° (102°, 96°) | 113°, 98° (113°, 106°) | 102°, 91° (104°, 99°) | 103°, 100° (107°, 100°) |
| ω01/cm−1 | ω12/cm−1 | Weight | Δ1/cm−1 | T2*/ps | /ps | γ1/ps−1 | γ2/ps−1 |
|---|---|---|---|---|---|---|---|
| 1595.1(0.1) | 1588.5(0.2) | 0.2 | 8.4(0.1) | 0.80(0.02) | 1.57(0.06) | 1(0.01) | 1.3(0.01) |
| 1604.1(0.1) | 1598.5(0.1) | 0.56 | 8.4(0.1) | 0.96(0.01) | 1.57(0.06) | 0.98(0.01) | 1.3(0.01) |
| 1620.9(0.1) | 1612.3(0.1) | 0.24 | 8.4(0.1) | 0.96(0.01) | 1.57(0.06) | 1(0.01) | 1.3(0.01) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volkov, V.V.; Chelli, R.; Perry, C.C. Cu(Proline)2 Complex: A Model of Bio-Copper Structural Ambivalence. Molecules 2022, 27, 5846. https://doi.org/10.3390/molecules27185846
Volkov VV, Chelli R, Perry CC. Cu(Proline)2 Complex: A Model of Bio-Copper Structural Ambivalence. Molecules. 2022; 27(18):5846. https://doi.org/10.3390/molecules27185846
Chicago/Turabian StyleVolkov, Victor V., Riccardo Chelli, and Carole C. Perry. 2022. "Cu(Proline)2 Complex: A Model of Bio-Copper Structural Ambivalence" Molecules 27, no. 18: 5846. https://doi.org/10.3390/molecules27185846
APA StyleVolkov, V. V., Chelli, R., & Perry, C. C. (2022). Cu(Proline)2 Complex: A Model of Bio-Copper Structural Ambivalence. Molecules, 27(18), 5846. https://doi.org/10.3390/molecules27185846








