Comparison of Multivariate ANOVA-Based Approaches for the Determination of Relevant Variables in Experimentally Designed Metabolomic Studies
Abstract
:1. Introduction
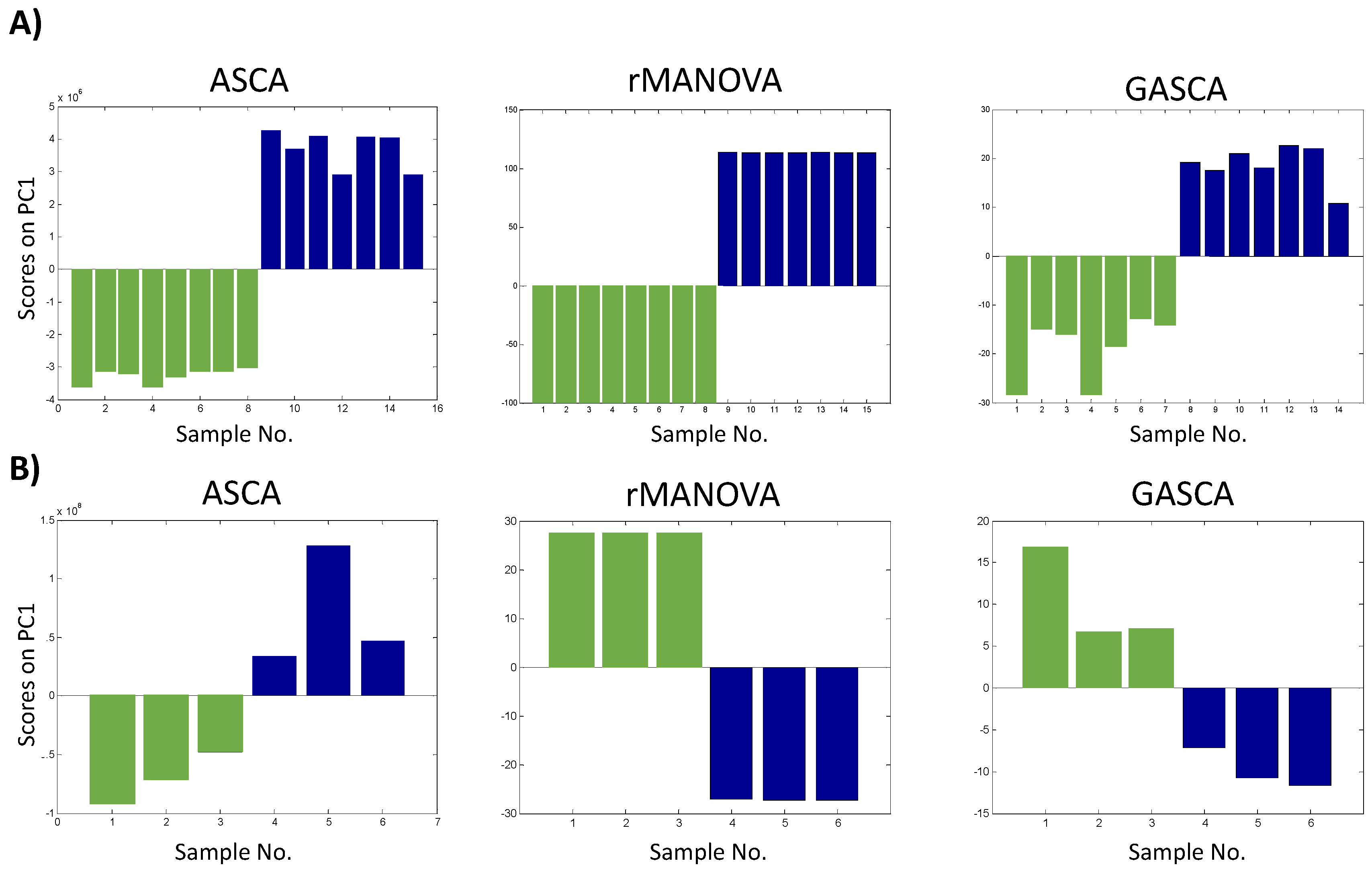
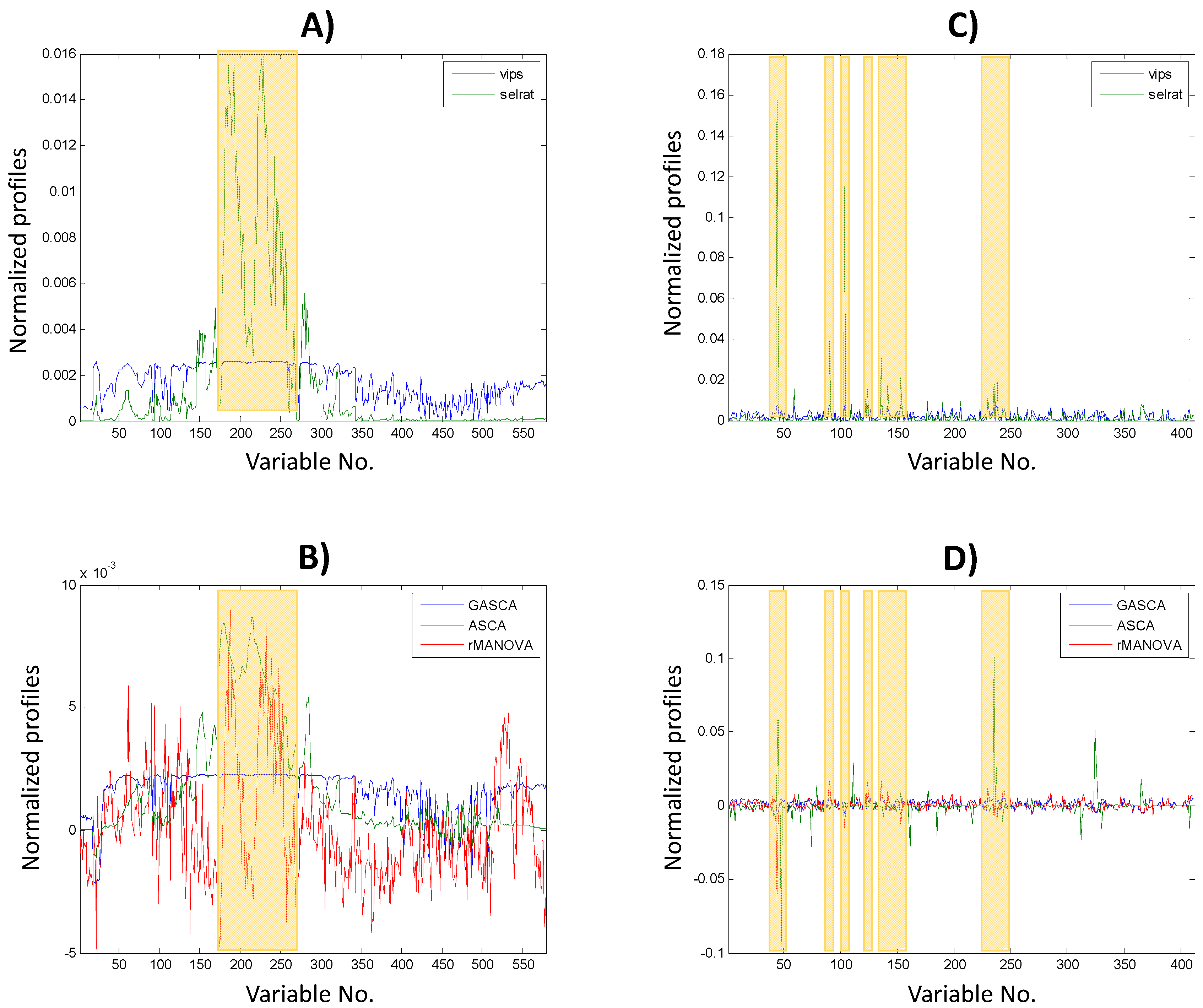
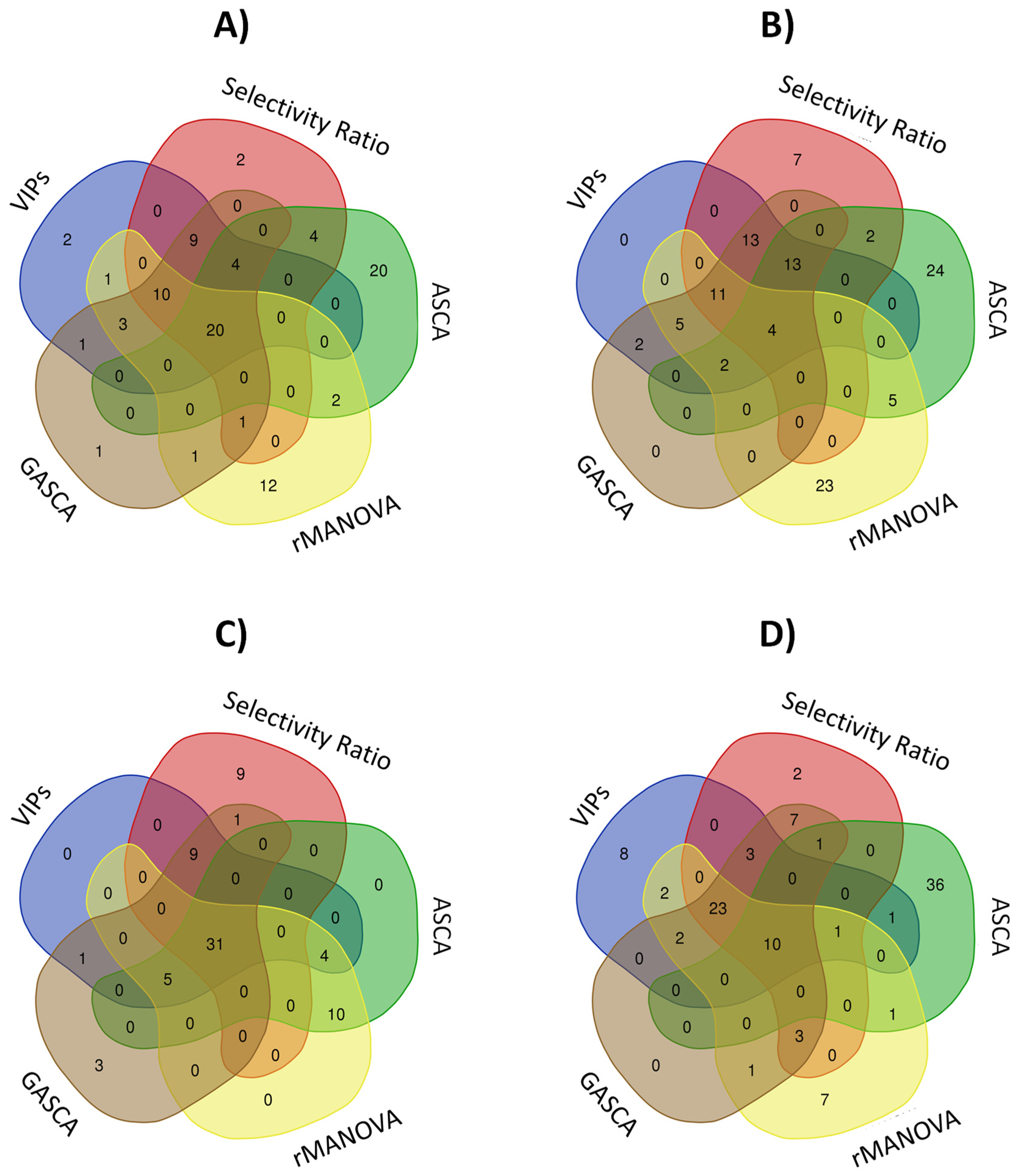
2. Results
2.1. Statistical Assessment of Experimental Factors Effects
2.2. Impact on Variable Selection
3. Materials and Methods
3.1. Chemicals and Reagents
3.2. Yeast Experiments
3.2.1. Culture Growth
3.2.2. Lipid Extractions
3.2.3. LC-MS Analysis
3.3. Zebrafish Embryos Experiments
3.3.1. Zebrafish Maintenance
3.3.2. Exposure Protocols
3.3.3. Metabolite Extraction
3.3.4. LC-MS Analysis
3.4. Data Analysis
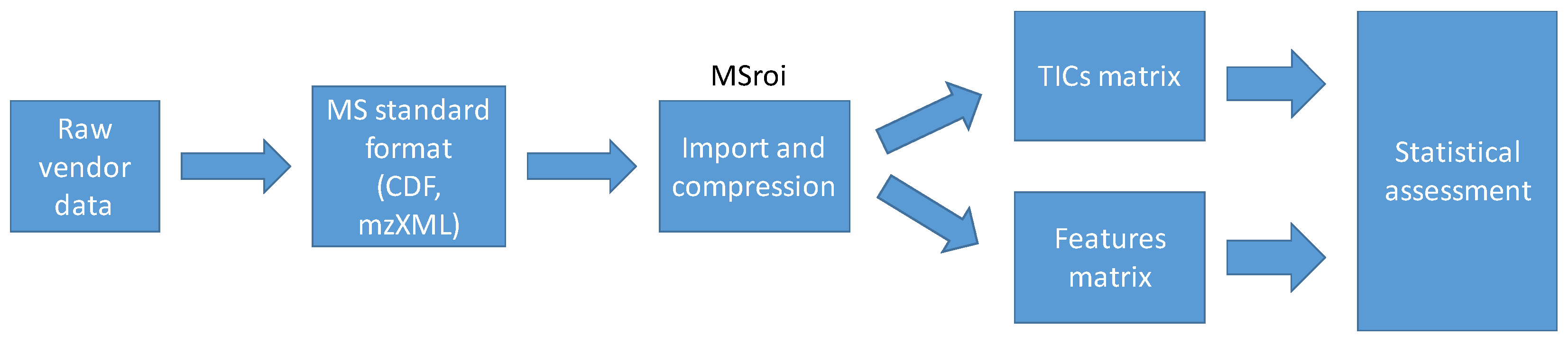
3.4.1. Data Import and Compression
3.4.2. Statistical Assessment
3.4.3. Software Used
3.4.4. Metabolite Identification
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jaumot, J.; Bedia, C. Introduction to Data Analysis in Omics Sciences. In Comprehensive Foodomics, 1st ed.; Cifuentes, A., Ed.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 226–240. [Google Scholar]
- Chong, J.; Wishart, D.S.; Xia, J. Using MetaboAnalyst 4.0 for Comprehensive and Integrative Metabolomics Data Analysis. Curr. Protoc. Bioinform. 2019, 68, e86. [Google Scholar] [CrossRef] [PubMed]
- Oliveri, P. Class-modelling in food analytical chemistry: Development, sampling, optimization and validation issues—A tutorial. Anal. Chim. Acta 2017, 982, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Barker, M.; Rayens, W. Partial least squares for discrimination. J. Chemom. 2003, 17, 166–173. [Google Scholar] [CrossRef]
- Brereton, R.G.; Lloyd, G.R. Partial least squares discriminant analysis: Taking the magic away. J. Chemom. 2014, 28, 213–225. [Google Scholar] [CrossRef]
- Andersen, C.M.; Bro, R. Variable selection in regression-a tutorial. J. Chemom. 2010, 24, 728–737. [Google Scholar] [CrossRef]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Rajalahti, T.; Arneberg, R.; Berven, F.S.; Myhr, K.M.; Ulvik, R.J.; Kvalheim, O.M. Biomarker discovery in mass spectral profiles by means of selectivity ratio plot. Chemom. Intell. Lab. Syst. 2009, 95, 35–48. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Farrés, M.; Platikanov, S.; Tsakovski, S.; Tauler, R. Comparison of the variable importance in projection (VIP) and of the selectivity ratio (SR) methods for variable selection and interpretation. J. Chemom. 2015, 29, 528–536. [Google Scholar] [CrossRef]
- Gromski, P.S.; Muhamadali, H.; Ellis, D.I.; Xu, Y.; Correa, E.; Turner, M.L.; Goodacre, R. A tutorial review: Metabolomics and partial least squares-discriminant analysis—A marriage of convenience or a shotgun wedding. Anal. Chim. Acta 2015, 879, 10–23. [Google Scholar] [CrossRef]
- Ferreira, A.J.; Figueiredo, M.A.T. Efficient feature selection filters for high-dimensional data. Pattern Recognit. Lett. 2012, 33, 1794–1804. [Google Scholar] [CrossRef] [Green Version]
- Jansen, J.; Engel, J. ASCA: The Implementation of Design of Experiments Into Multivariate Modelling in Chemometrics. In Comprehensive Analytical Chemistry, 2nd ed.; Jaumot, J., Bedia, C., Tauler, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 82, pp. 301–335. [Google Scholar] [CrossRef]
- Stahle, L.; Wold, S. Multivariate analysis of variance (MANOVA). Chemom. Intell. Lab. Syst. 1990, 9, 127–141. [Google Scholar] [CrossRef]
- Bertinetto, C.; Engel, J.; Jansen, J. ANOVA simultaneous component analysis: A tutorial review. Anal. Chim. Acta X 2020, 6, 100061. [Google Scholar] [CrossRef] [PubMed]
- Angélina, E.G.; Qannari, E.M.; Moyon, T.; Alexandre-Gouabau, M.C. AoV-PLS: A new method for the analysis of multivariate data depending on several factors. Electron. J. Appl. Stat. Anal. 2015, 8, 214–235. [Google Scholar] [CrossRef]
- Marini, F.; de Beer, D.; Joubert, E.; Walczak, B. Analysis of variance of designed chromatographic data sets: The analysis of variance-target projection approach. J. Chromatogr. A 2015, 1405, 94–102. [Google Scholar] [CrossRef]
- Harrington, P.D.B.; Vieira, N.E.; Espinoza, J.; Nien, J.K.; Romero, R.; Yergey, A.L. Analysis of variance-principal component analysis: A soft tool for proteomic discovery. Anal. Chim. Acta 2005, 544, 118–127. [Google Scholar] [CrossRef]
- Jansen, J.J.; Hoefsloot, H.C.J.; Van Der Greef, J.; Timmerman, M.E.; Westerhuis, J.A.; Smilde, A.K. ASCA: Analysis of multivariate data obtained from an experimental design. J. Chemom. 2005, 19, 469–481. [Google Scholar] [CrossRef]
- Smilde, A.K.; Jansen, J.J.; Hoefsloot, H.C.J.; Lamers, R.J.A.N.; van der Greef, J.; Timmerman, M.E. ANOVA-simultaneous component analysis (ASCA): A new tool for analyzing designed metabolomics data. Bioinformatics 2005, 21, 3043–3048. [Google Scholar] [CrossRef]
- Engel, J.; Blanchet, L.; Bloemen, B.; Van den Heuvel, L.P.; Engelke, U.H.F.; Wevers, R.A.; Buydens, L.M.C. Regularized MANOVA (rMANOVA) in untargeted metabolomics. Anal. Chim. Acta 2015, 899, 1–12. [Google Scholar] [CrossRef]
- Saccenti, E.; Smilde, A.K.; Camacho, J. Group-wise ANOVA simultaneous component analysis for designed omics experiments. Metabolomics 2018, 14, 73. [Google Scholar] [CrossRef] [Green Version]
- Tinnevelt, G.H.; Engelke, U.F.H.; Wevers, R.A.; Veenhuis, S.; Willemsen, M.A.; Coene, K.L.M.; Kulkarni, P.; Jansen, J.J. Variable selection in untargeted metabolomics and the danger of sparsity. Metabolites 2020, 10, 470. [Google Scholar] [CrossRef] [PubMed]
- Martínez, R.; Herrero-Nogareda, L.; Van Antro, M.; Campos, M.P.; Casado, M.; Barata, C.; Piña, B.; Navarro-Martín, L. Morphometric signatures of exposure to endocrine disrupting chemicals in zebrafish eleutheroembryos. Aquat. Toxicol. 2019, 214, 105232. [Google Scholar] [CrossRef] [PubMed]
- Puig-Castellví, F.; Bedia, C.; Alfonso, I.; Piña, B.; Tauler, R. Deciphering the Underlying Metabolomic and Lipidomic Patterns Linked to Thermal Acclimation in Saccharomyces cerevisiae. J. Proteome Res. 2018, 17, 2034–2044. [Google Scholar] [CrossRef] [PubMed]
- Dalmau, N.; Jaumot, J.; Tauler, R.; Bedia, C. Epithelial-to-mesenchymal transition involves triacylglycerol accumulation in DU145 prostate cancer cells. Mol. BioSyst. 2015, 11, 3397–3406. [Google Scholar] [CrossRef] [Green Version]
- Ortiz-Villanueva, E.; Jaumot, J.; Martínez, R.; Navarro-Martín, L.; Piña, B.; Tauler, R. Assessment of endocrine disruptors effects on zebrafish (Danio rerio) embryos by untargeted LC-HRMS metabolomic analysis. Sci. Total Environ. 2018, 635, 156–166. [Google Scholar] [CrossRef]
- Ortiz-Villanueva, E.; Navarro-Martín, L.; Jaumot, J.; Benavente, F.; Sanz-Nebot, V.; Piña, B.; Tauler, R. Metabolic disruption of zebrafish (Danio rerio) embryos by bisphenol A. An integrated metabolomic and transcriptomic approach. Environ. Pollut. 2017, 231, 22–36. [Google Scholar] [CrossRef]
- Chambers, M.C.; MacLean, B.; Burke, R.; Amodei, D.; Ruderman, D.L.; Neumann, S.; Gatto, L.; Fischer, B.; Pratt, B.; Egertson, J.; et al. A cross-platform toolkit for mass spectrometry and proteomics. Nat. Biotechnol. 2012, 30, 918–920. [Google Scholar] [CrossRef]
- Pérez-Cova, M.; Jaumot, J.; Tauler, R. Untangling comprehensive two-dimensional liquid chromatography data sets using regions of interest and multivariate curve resolution approaches. TrAC Trends Anal. Chem. 2021, 137, 116207. [Google Scholar] [CrossRef]
- Gorrochategui, E.; Jaumot, J.; Tauler, R. ROIMCR: A powerful analysis strategy for LC-MS metabolomic datasets. BMC Bioinform. 2019, 20, 256. [Google Scholar] [CrossRef] [Green Version]
- Navarro-Reig, M.; Bedia, C.; Tauler, R.; Jaumot, J. Chemometric Strategies for Peak Detection and Profiling from Multidimensional Chromatography. Proteomics 2018, 18, 1700327. [Google Scholar] [CrossRef]
- Storey, J.D. A direct approach to false discovery rates. J. R. Stat. Soc. Ser. B Stat. Methodol. 2002, 64, 479–498. [Google Scholar] [CrossRef] [Green Version]
- Benjamini, Y.; Hochberg, Y. On the adaptive control of the false discovery rate in multiple testing with independent statistics. J. Educ. Behav. Stat. 2000, 25, 60–83. [Google Scholar] [CrossRef] [Green Version]
- Cocchi, M.; Biancolillo, A.; Marini, F. Chemometric Methods for Classification and Feature Selection. In Comprehensive Analytical Chemistry, 2nd ed.; Jaumot, J., Bedia, C., Tauler, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 82, pp. 265–299. [Google Scholar] [CrossRef]
- Deng, B.C.; Yun, Y.H.; Liang, Y.Z. Model population analysis in chemometrics. Chemom. Intell. Lab. Syst. 2015, 149, 166–176. [Google Scholar] [CrossRef]
- Zwanenburg, G.; Hoefsloot, H.C.J.; Westerhuis, J.A.; Jansen, J.J.; Smilde, A.K. ANOVA–principal component analysis and ANOVA–simultaneous component analysis: A comparison. J. Chemom. 2011, 25, 561–567. [Google Scholar] [CrossRef]
- Ledoit, O.; Wolf, M. Improved estimation of the covariance matrix of stock returns with an application to portfolio selection. J. Empir. Financ. 2003, 10, 603–621. [Google Scholar] [CrossRef] [Green Version]
- Camacho, J.; Rodríguez-Gómez, R.A.; Saccenti, E. Group-Wise Principal Component Analysis for Exploratory Data Analysis. J. Comput. Graph. Stat. 2017, 26, 501–512. [Google Scholar] [CrossRef] [Green Version]
- Tsugawa, H.; Cajka, T.; Kind, T.; Ma, Y.; Higgins, B.; Ikeda, K.; Kanazawa, M.; VanderGheynst, J.; Fiehn, O.; Arita, M. MS-DIAL: Data-independent MS/MS deconvolution for comprehensive metabolome analysis. Nat. Methods 2015, 12, 523–526. [Google Scholar] [CrossRef]
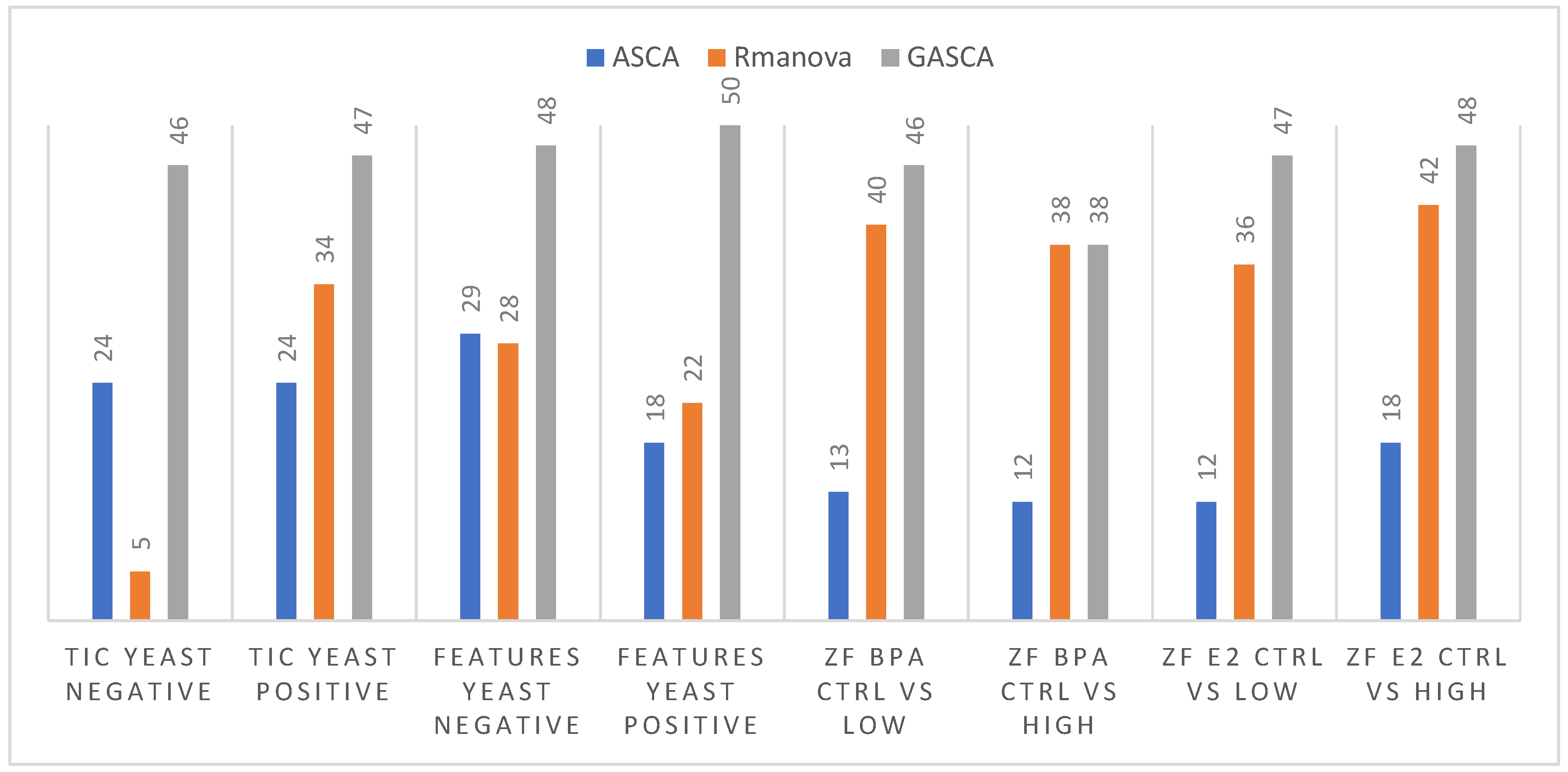
| Dataset | Experimental Factor | ASCA | rMANOVA | GASCA | |
|---|---|---|---|---|---|
| TIC Matrix | Yeast–MS negative ionization mode | Type of lipid extraction | 0.0001 (0.0007 *) | 0.0001 | 0.039 * |
| Yeast–MS positive ionization mode | Type of lipid extraction | 0.0001 (0.0001 *) | 0.0001 | 0.001 * | |
| Features Matrix | Yeast–MS negative ionization mode | Type of lipid extraction | 0.0001 (0.0001 *) | 0.0001 | 0.002 * |
| Yeast–MS positive ionization mode | Type of lipid extraction | 0.0001 (0.0001 *) | 0.0001 | 0.002 * | |
| Zebrafish embryos–BPA exposure | Exposure concentration | ||||
| Control vs. Low | 0.0001 | 0.0001 | 0.09 | ||
| Control vs. High | 0.0001 | 0.0001 | 0.10 | ||
| Control vs. Low vs. High | 0.0001 | 0.0001 | 0.01 | ||
| Zebrafish embryos–E2 exposure | Exposure concentration | ||||
| Control vs. Low | 0.4472 | 0.0001 | 0.47 | ||
| Control vs. High | 0.0001 | 0.0001 | 0.22 | ||
| Control vs. Low vs. High | 0.0093 | 0.0001 | 0.35 | ||
| ASCA | rMANOVA | GASCA | |
|---|---|---|---|
| Advantages | Widespread use in metabolomics (reference multivariate statistical method) Best match between experimental and expected significance | Best of both worlds (model depending on data I MANOVA and ASCA) | A good option for sparse data (i.e., metabolomic datasets) Best match with VIPs from PLS-DA for identifying significant variables |
| Limitations | Most dissimilar matches identifying significant variables compared to VIPs from PLS-DA It assumes metabolites are not correlated and that they all have the same variance. | Dissimilar matches with VIPs from PLS-DA in selection of relevant variables | Very strict for determination of significant factors (only factors with very low p-values in other methods will appear as significant) |
| Opportunities | Good choice when combined with PLS-DA (VIPs) for the determination of the significant variables | Good choice when aiming one method for statistical analysis and selecting relevant variables (but further validation on the variables is desirable) | Good option for assessing the significance of variables and factors when big effects are encountered (very significant factors in the DOE) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Cova, M.; Platikanov, S.; Stoll, D.R.; Tauler, R.; Jaumot, J. Comparison of Multivariate ANOVA-Based Approaches for the Determination of Relevant Variables in Experimentally Designed Metabolomic Studies. Molecules 2022, 27, 3304. https://doi.org/10.3390/molecules27103304
Pérez-Cova M, Platikanov S, Stoll DR, Tauler R, Jaumot J. Comparison of Multivariate ANOVA-Based Approaches for the Determination of Relevant Variables in Experimentally Designed Metabolomic Studies. Molecules. 2022; 27(10):3304. https://doi.org/10.3390/molecules27103304
Chicago/Turabian StylePérez-Cova, Miriam, Stefan Platikanov, Dwight R. Stoll, Romà Tauler, and Joaquim Jaumot. 2022. "Comparison of Multivariate ANOVA-Based Approaches for the Determination of Relevant Variables in Experimentally Designed Metabolomic Studies" Molecules 27, no. 10: 3304. https://doi.org/10.3390/molecules27103304
APA StylePérez-Cova, M., Platikanov, S., Stoll, D. R., Tauler, R., & Jaumot, J. (2022). Comparison of Multivariate ANOVA-Based Approaches for the Determination of Relevant Variables in Experimentally Designed Metabolomic Studies. Molecules, 27(10), 3304. https://doi.org/10.3390/molecules27103304







