An Effective MM/GBSA Protocol for Absolute Binding Free Energy Calculations: A Case Study on SARS-CoV-2 Spike Protein and the Human ACE2 Receptor †
Abstract
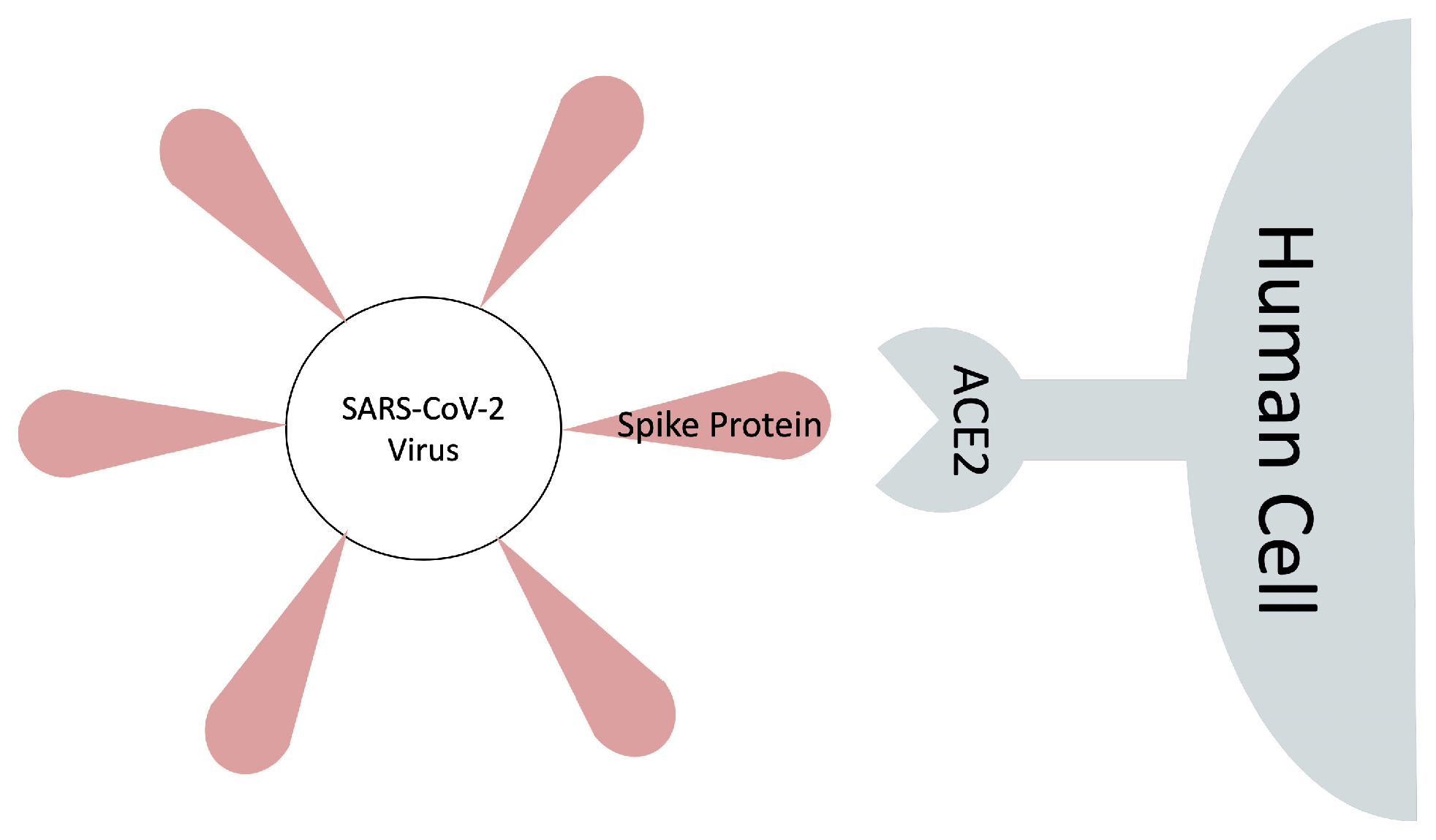
1. Introduction
2. Materials and Methods
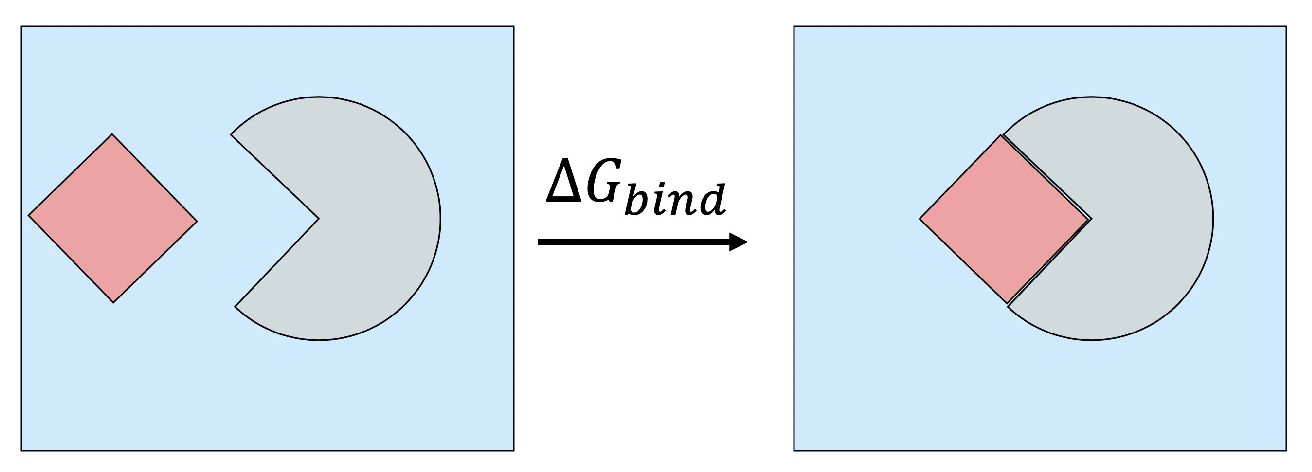
2.1. Binding Free Energy Decomposition
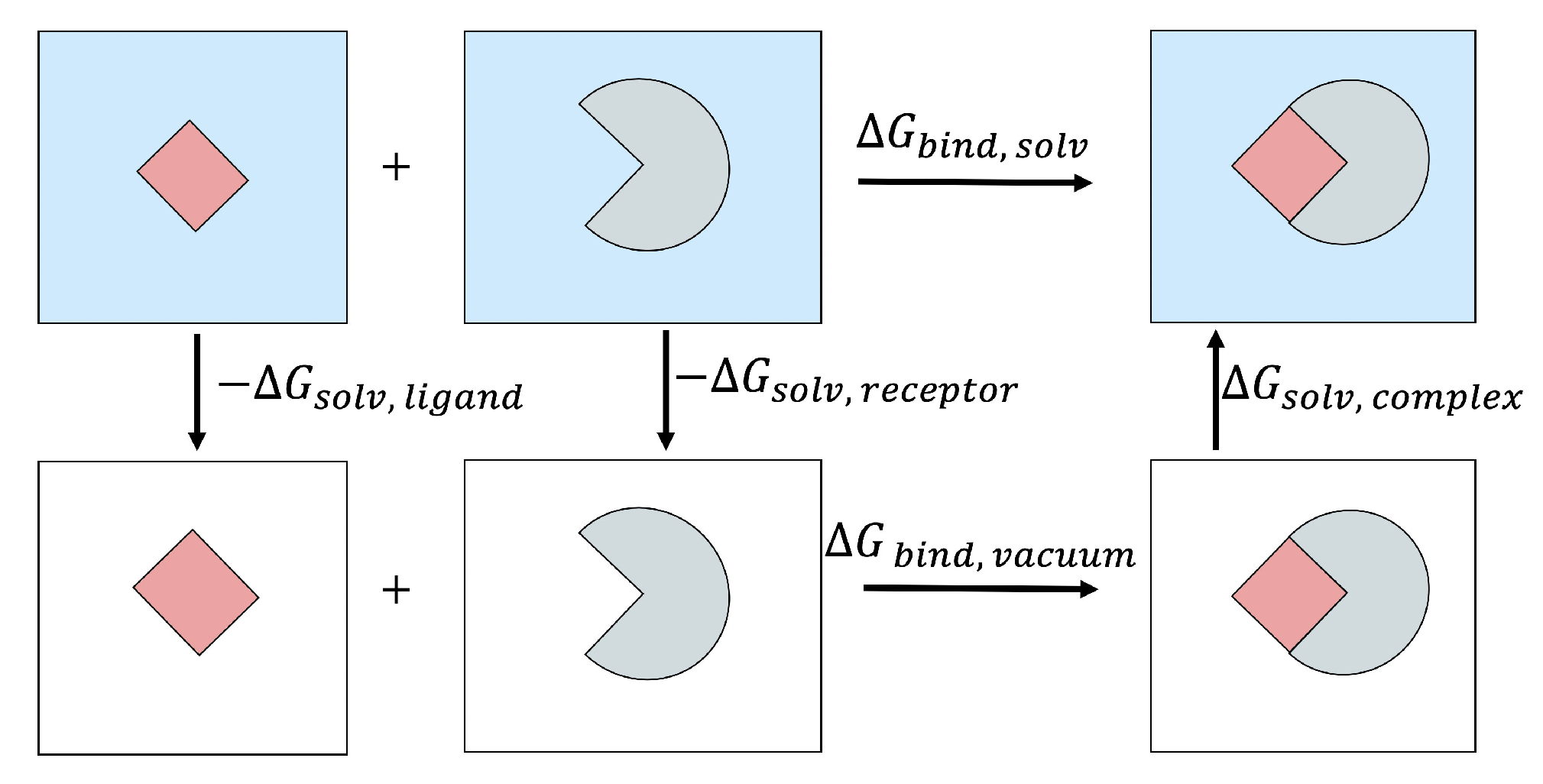
2.2. MM/PB(GB)SA Free Energy Methodology
2.3. Solvation Free Energy
2.3.1. Polar Component
2.3.2. Non-polar Component
2.4. Gas-Phase Energy
2.5. Configurational Entropy
2.6. Structure Preparation
2.6.1. Ras–Raf Complex
2.6.2. SARS-CoV-2 S RBD and ACE2 Complex
2.7. MD Simulation
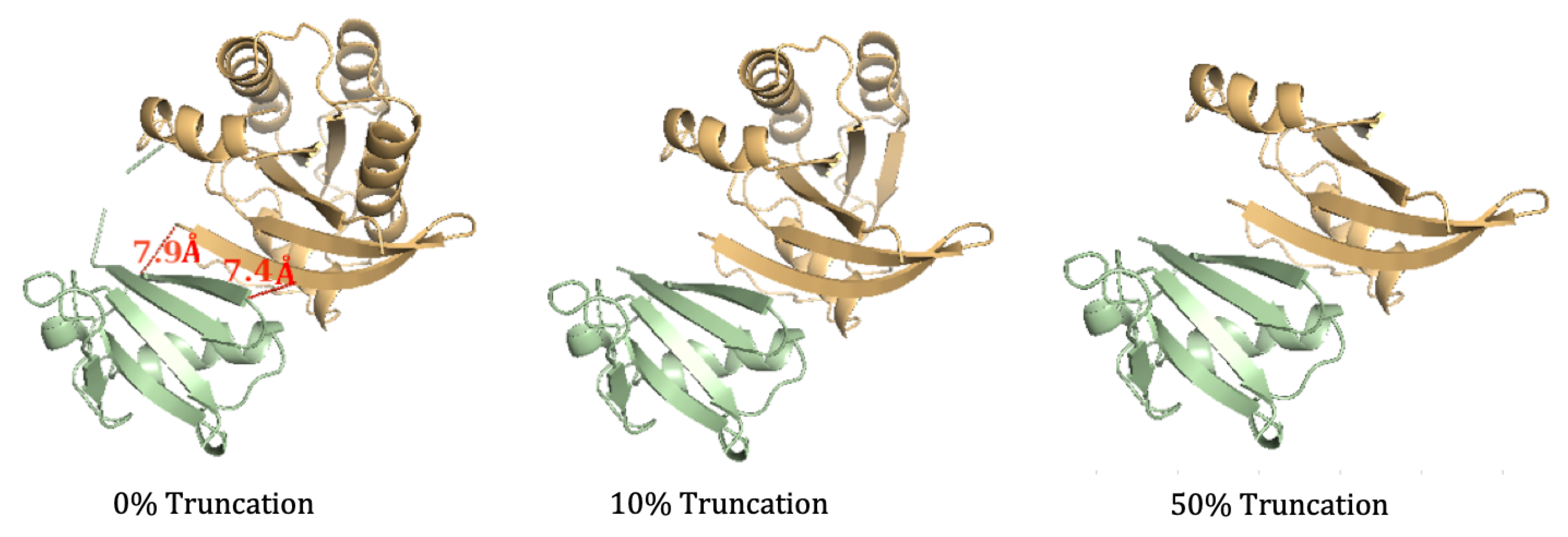
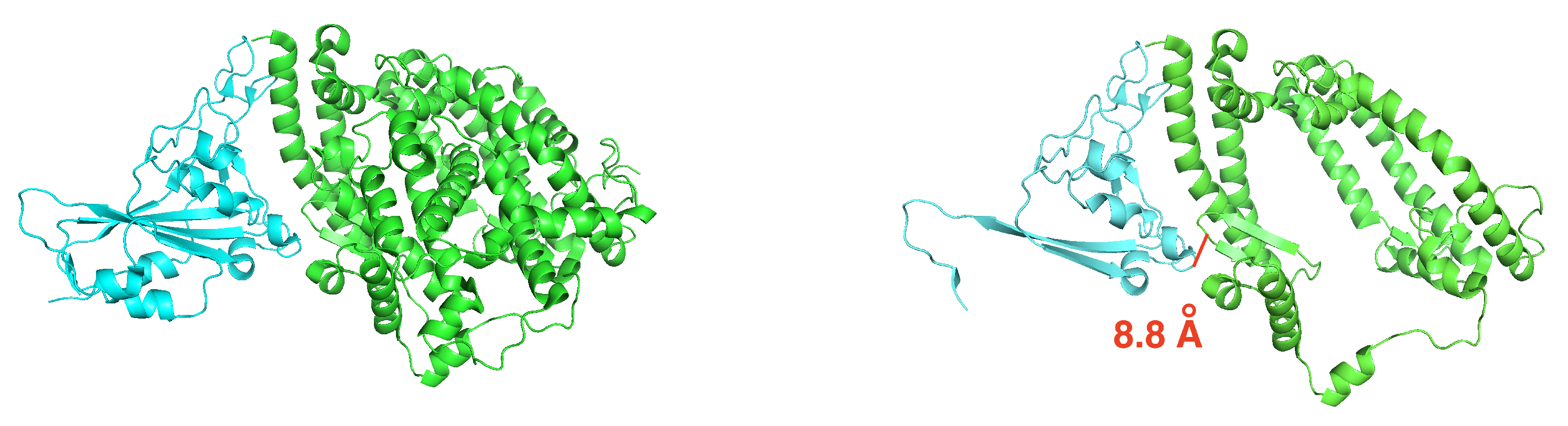
2.8. Proposed Truncation Algorithm
3. Results and Discussion
3.1. Efficient Calculation of Entropy: Continuous Truncation of Protein Structures
3.1.1. NMA on the Truncated Ras–Raf Complex
3.1.2. NMA on the truncated SARS-CoV-2 S RBD and ACE2 Complex
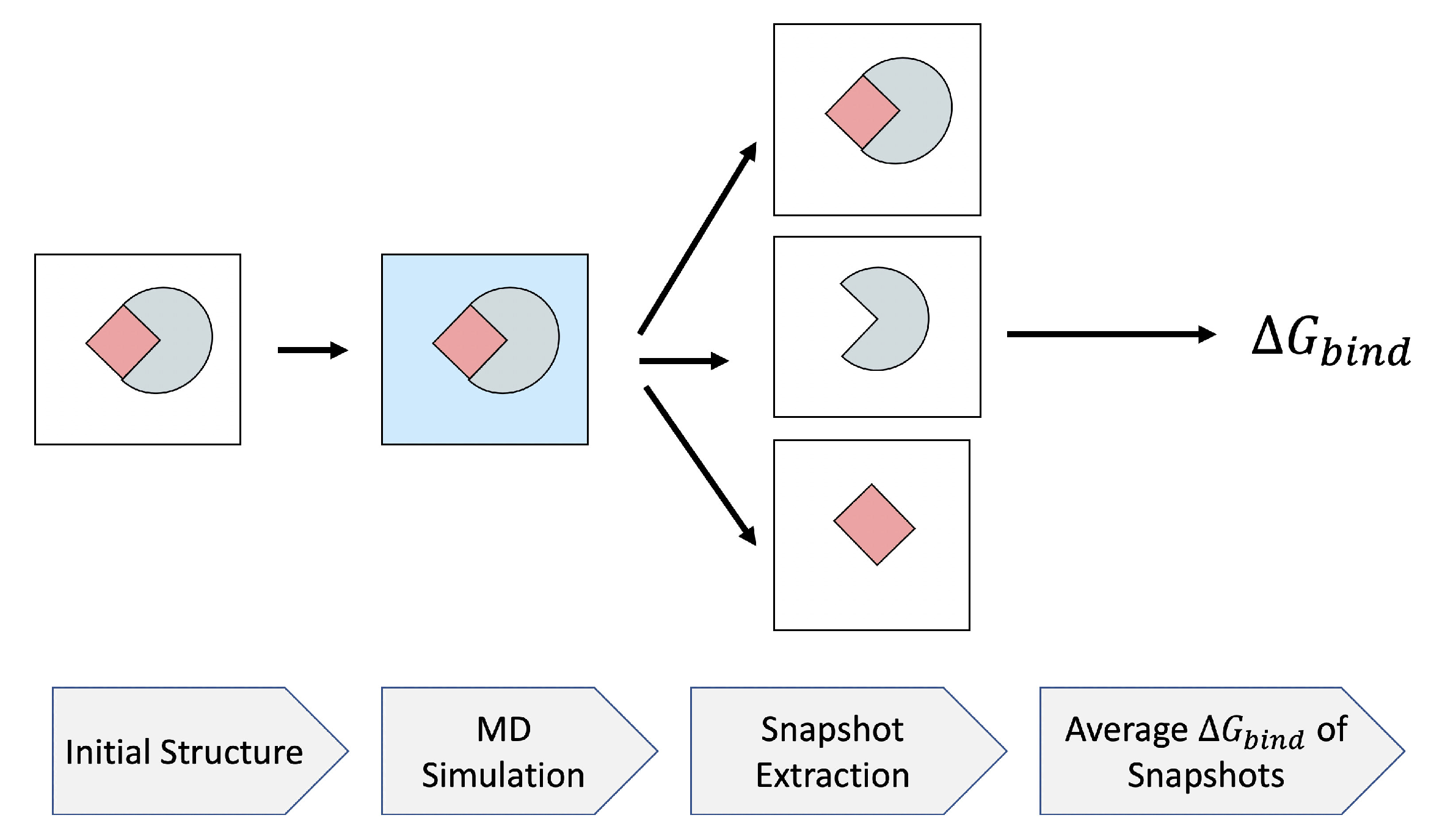
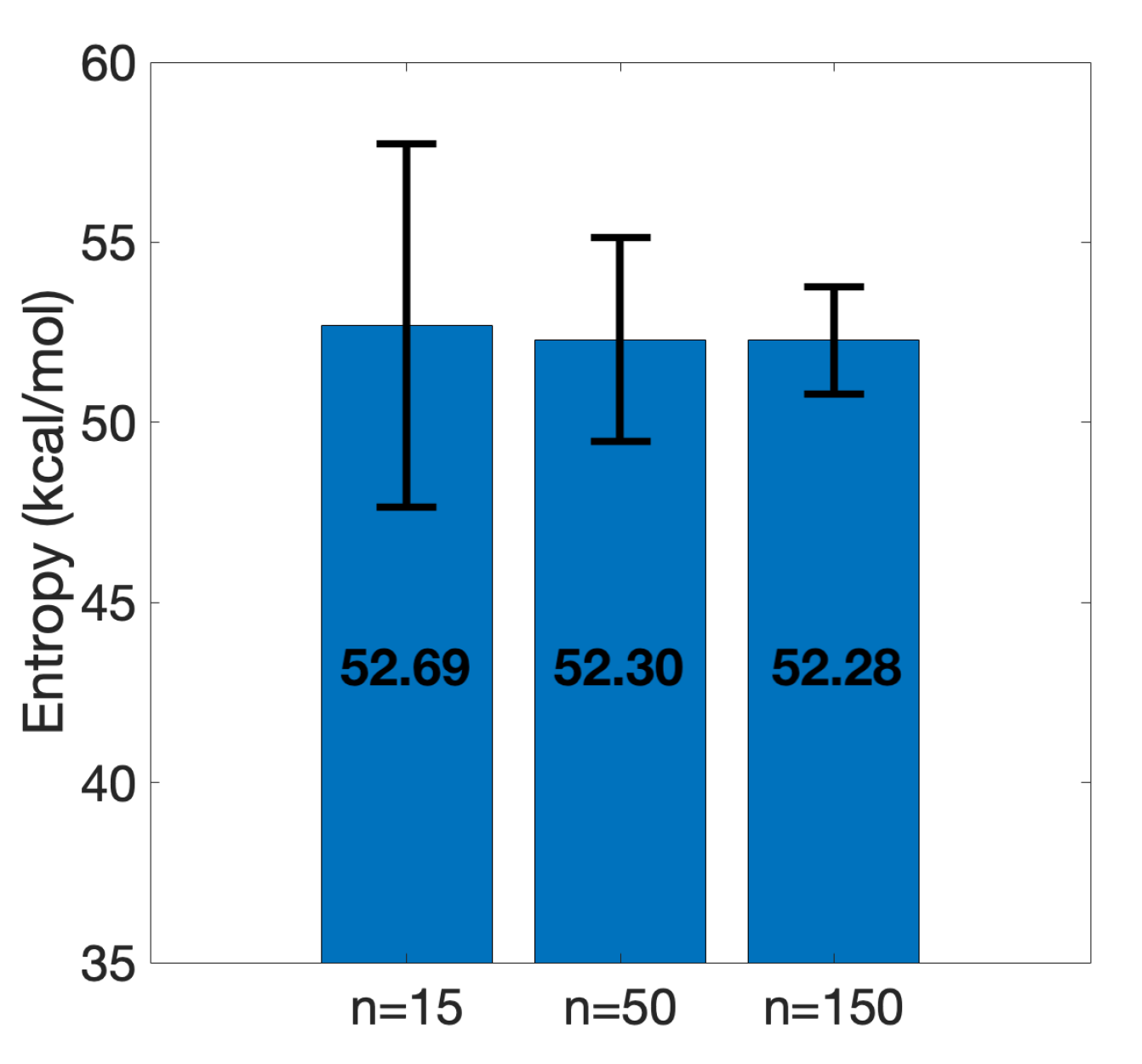
3.2. Efficient Calculation of Entropy: Selection of a Few Snapshots
3.3. MM/GBSA on Ras–Raf
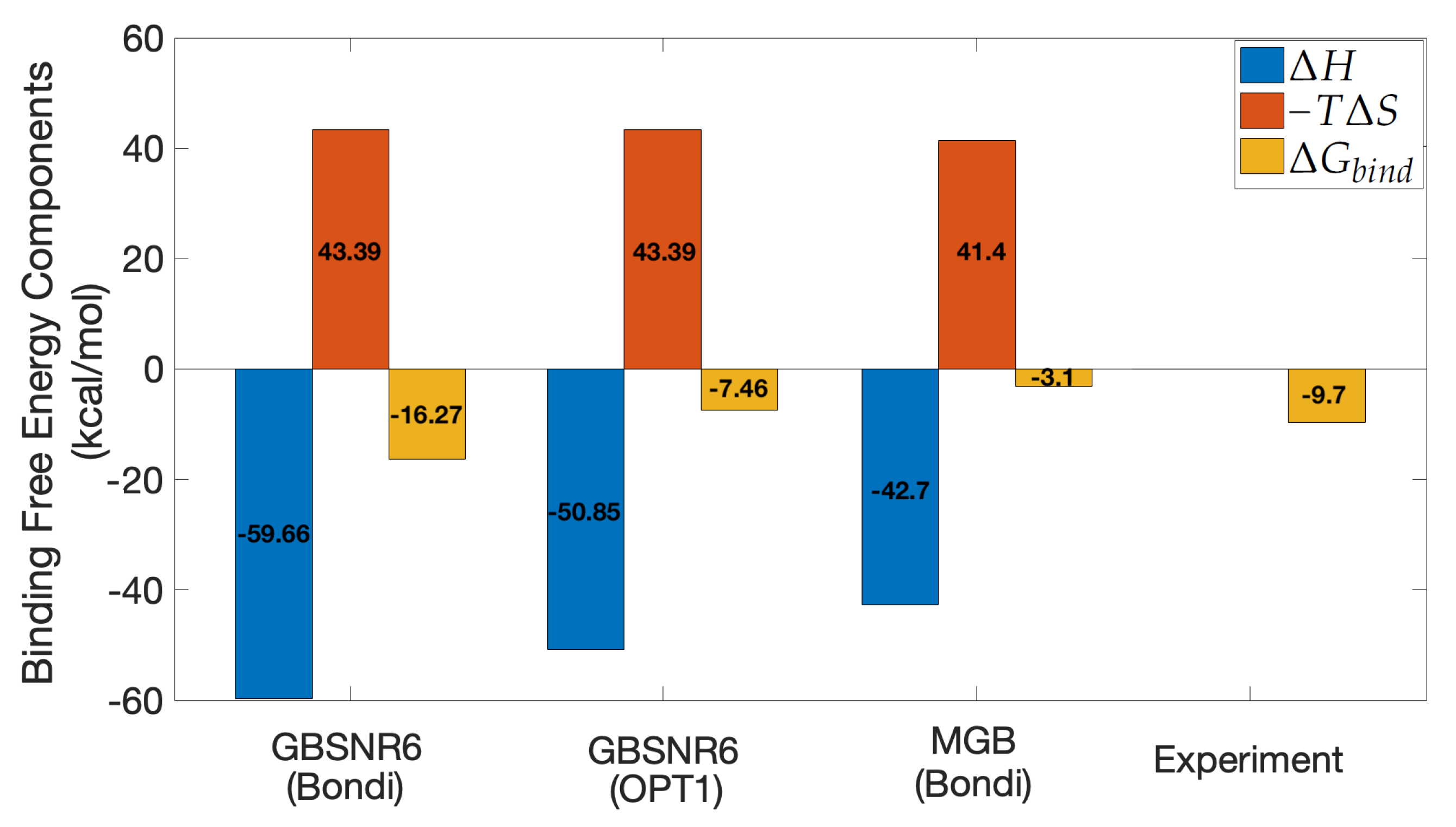
3.4. MM/GBSA on SARS-CoV-2 S RBD and ACE2
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amaro, R.E.; Mulholland, A.J. A Community Letter Regarding Sharing Biomolecular Simulation Data for COVID-19. J. Chem. Inf. Model. 2020, 60, 2653–2656. [Google Scholar] [CrossRef] [PubMed]
- Harrer, S.; Shah, P.; Antony, B.; Hu, J. Artificial intelligence for clinical trial design. Trends Pharmacol. Sci. 2019, 40, 577–591. [Google Scholar] [CrossRef] [PubMed]
- Martínez, M.; Cooper, C.D.; Poma, A.B.; Guzman, H.V. Free energies of the disassembly of viral capsids from a multiscale molecular simulation approach. J. Chem. Inf. Model. 2019, 60, 974–981. [Google Scholar] [CrossRef] [PubMed]
- Giron, C.C.; Laaksonen, A.; Barroso da Silva, F.L. On the interactions of the receptor-binding domain of SARS-CoV-1 and SARS-CoV-2 spike proteins with monoclonal antibodies and the receptor ACE2. Virus Res. 2020, 285, 198021. [Google Scholar] [CrossRef] [PubMed]
- Gao, K.; Wang, R.; Chen, J.; Cheng, L.; Frishcosy, J.; Huzumi, Y.; Qiu, Y.; Schluckbier, T.; Wei, G.W. Methodology-centered review of molecular modeling, simulation, and prediction of SARS-CoV-2. arXiv 2021, arXiv:2102.00971. [Google Scholar]
- Moreira, R.A.; Guzman, H.V.; Boopathi, S.; Baker, J.L.; Poma, A.B. Characterization of Structural and Energetic Differences between Conformations of the SARS-CoV-2 Spike. Materials 2020, 13, 5362. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L. The Many Roles of Computation in Drug Discovery. Science 2004, 303, 1813–1818. [Google Scholar] [CrossRef]
- Gohlke, H.; Kiel, C.; Case, D.A. Insights into protein–protein binding by binding free energy calculation and free energy decomposition for the Ras–Raf and Ras–RalGDS complexes. J. Mol. Biol. 2003, 330, 891–913. [Google Scholar] [CrossRef]
- Zhou, H.X.; Gilson, M.K. Theory of Free Energy and Entropy in Noncovalent Binding. Chem. Rev. 2009, 109, 4092–4107. [Google Scholar] [CrossRef]
- Mobley, D.L.; Dill, K.A. Binding of Small-Molecule Ligands to Proteins: “ What You See” Is Not Always “What You Get”. Structure 2009, 17, 489–498. [Google Scholar] [CrossRef]
- Rizzi, A.; Murkli, S.; McNeill, J.N.; Yao, W.; Sullivan, M.; Gilson, M.K.; Chiu, M.W.; Isaacs, L.; Gibb, B.C.; Mobley, D.L.; et al. Overview of the SAMPL6 Host–Guest Binding Affinity Prediction Challenge. J. Comput.-Aided Mol. Des. 2018, 32, 937–963. [Google Scholar] [CrossRef]
- Zou, J.; Tian, C.; Simmerling, C. Blinded prediction of protein–ligand binding affinity using Amber thermodynamic integration for the 2018 D3R grand challenge 4. J. Comput.-Aided Mol. Des. 2019, 33, 1021–1029. [Google Scholar] [CrossRef]
- Wang, J.; Alekseenko, A.; Kozakov, D.; Miao, Y. Improved Modeling of Peptide–Protein Binding through Global Docking and Accelerated Molecular Dynamics Simulations. Front. Mol. Biosci. 2019, 6, 112. [Google Scholar] [CrossRef]
- Siebenmorgen, T.; Zacharias, M. Computational prediction of protein–protein binding affinities. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020, 10, e1448. [Google Scholar] [CrossRef]
- Straatsma, T.; Berendsen, H.; Postma, J. Free energy of hydrophobic hydration: A molecular dynamics study of noble gases in water. J. Chem. Phys. 1986, 85, 6720–6727. [Google Scholar] [CrossRef]
- Chodera, J.D.; Mobley, D.L.; Shirts, M.R.; Dixon, R.W.; Branson, K.; Pande, V.S. Alchemical free energy methods for drug discovery: Progress and challenges. Curr. Opin. Struct. Biol. 2011, 21, 150–160. [Google Scholar] [CrossRef]
- Abel, R.; Wang, L.; Mobley, D.L.; Friesner, R.A. A critical review of validation, blind testing, and real-world use of alchemical protein-ligand binding free energy calculations. Curr. Top. Med. Chem. 2017, 17, 2577–2585. [Google Scholar] [CrossRef]
- Michel, J.; Foloppe, N.; Essex, J.W. Rigorous free energy calculations in structure-based drug design. Mol. Inform. 2010, 29, 570–578. [Google Scholar] [CrossRef]
- de Ruiter, A.; Oostenbrink, C. Advances in the calculation of binding free energies. Curr. Opin. Struct. Biol. 2020, 61, 207–212. [Google Scholar] [CrossRef]
- Schneider, G.; Böhm, H.J. Virtual screening and fast automated docking methods. Drug Discov. Today 2002, 7, 64–70. [Google Scholar] [CrossRef]
- Wang, E.; Sun, H.; Wang, J.; Wang, Z.; Liu, H.; Zhang, J.Z.; Hou, T. End-point binding free energy calculation with MM/PBSA and MM/GBSA: Strategies and applications in drug design. Chem. Rev. 2019, 119, 9478–9508. [Google Scholar] [CrossRef]
- Genheden, S.; Ryde, U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discov. 2015, 10, 449–461. [Google Scholar] [CrossRef]
- Wang, C.; Greene, D.; Xiao, L.; Qi, R.; Luo, R. Recent developments and applications of the MMPBSA method. Front. Mol. Biosci. 2018, 4, 87. [Google Scholar] [CrossRef]
- Hayes, J.M.; Archontis, G. MM-GB (PB) SA calculations of protein-ligand binding free energies. In Molecular Dynamics - Studies of Synthetic and Biological Macromolecules; Intech Open: London, UK, 2012; pp. 171–190. [Google Scholar]
- Onufriev, A.V.; Izadi, S. Water models for biomolecular simulations. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1347. [Google Scholar] [CrossRef]
- Zhou, H.X.; Pang, X. Electrostatic Interactions in Protein Structure, Folding, Binding, and Condensation. Chem. Rev. 2018, 118, 1691–1741. [Google Scholar] [CrossRef]
- Onufriev, A. Continuum electrostatics solvent modeling with the generalized Born model. Model. Solvent Environ. 2010, 1. [Google Scholar] [CrossRef]
- Gohlke, H.; Case, D.A. Converging free energy estimates: MM-PB (GB) SA studies on the protein–protein complex Ras–Raf. J. Comput. Chem. 2004, 25, 238–250. [Google Scholar] [CrossRef]
- Muddana, H.S.; Fenley, A.T.; Mobley, D.L.; Gilson, M.K. The SAMPL4 host–guest blind prediction challenge: An overview. J. Comput.-Aided Mol. Des. 2014, 28, 305–317. [Google Scholar] [CrossRef]
- Homeyer, N.; Stoll, F.; Hillisch, A.; Gohlke, H. Binding free energy calculations for lead optimization: Assessment of their accuracy in an industrial drug design context. J. Chem. Theory Comput. 2014, 10, 3331–3344. [Google Scholar] [CrossRef]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef]
- Allen, W.J.; Balius, T.E.; Mukherjee, S.; Brozell, S.R.; Moustakas, D.T.; Lang, P.T.; Case, D.A.; Kuntz, I.D.; Rizzo, R.C. DOCK 6: Impact of new features and current docking performance. J. Comput. Chem. 2015, 36, 1132–1156. [Google Scholar] [CrossRef] [PubMed]
- Lyskov, S.; Gray, J.J. The RosettaDock server for local protein–protein docking. Nucleic Acids Res. 2008, 36, W233–W238. [Google Scholar] [CrossRef] [PubMed]
- Grosdidier, A.; Zoete, V.; Michielin, O. SwissDock, a protein-small molecule docking web service based on EADock DSS. Nucleic Acids Res. 2011, 39, W270–W277. [Google Scholar] [CrossRef] [PubMed]
- Sasmal, S.; El Khoury, L.; Mobley, D.L. D3R Grand Challenge 4: Ligand similarity and MM-GBSA-based pose prediction and affinity ranking for BACE-1 inhibitors. J. Comput.-Aided Mol. Des. 2020, 34, 163–177. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Li, Y.; Lei, T.; Wang, E.; Li, D.; Kang, Y.; Zhu, F.; Hou, T. farPPI: A webserver for accurate prediction of protein-ligand binding structures for small-molecule PPI inhibitors by MM/PB (GB) SA methods. Bioinformatics 2019, 35, 1777–1779. [Google Scholar] [CrossRef]
- Sargolzaei, M. Effect of nelfinavir stereoisomers on coronavirus main protease: Molecular docking, molecular dynamics simulation and MM/GBSA study. J. Mol. Graph. Model. 2020, 103, 107803. [Google Scholar] [CrossRef]
- Ben-Shalom, I.Y.; Pfeiffer-Marek, S.; Baringhaus, K.H.; Gohlke, H. Efficient approximation of ligand rotational and translational entropy changes upon binding for use in MM-PBSA calculations. J. Chem. Inf. Model. 2017, 57, 170–189. [Google Scholar] [CrossRef]
- Yamato, T.; Laprévote, O. Normal mode analysis and beyond. Biophys. Physicobiol. 2019, 16, 322–327. [Google Scholar] [CrossRef]
- Genheden, S.; Kuhn, O.; Mikulskis, P.; Hoffmann, D.; Ryde, U. The normal-mode entropy in the MM/GBSA method: Effect of system truncation, buffer region, and dielectric constant. J. Chem. Inf. Model. 2012, 52, 2079–2088. [Google Scholar] [CrossRef]
- Case, D.A.; Brozell, S.; Cerutti, D.; Cheatham, T., III; Cruzeiro, V.; Darden, T.; DG, R.D.; Gilson, M.; Gohlke, H.; Goetz, A.; et al. AMBER 2018; University of California: San Francisco, CA, USA, 2018. [Google Scholar]
- Lan, J.; Ge, J.; Yu, J.; Shan, S.; Zhou, H.; Fan, S.; Zhang, Q.; Shi, X.; Wang, Q.; Zhang, L.; et al. Structure of the SARS-CoV-2 spike receptor-binding domain bound to the ACE2 receptor. Nature 2020, 581, 215–220. [Google Scholar] [CrossRef]
- Forouzesh, N.; Mukhopadhyay, A.; Watson, L.T.; Onufriev, A.V. Multidimensional Global Optimization and Robustness Analysis in the Context of Protein-Ligand Binding. J. Chem. Theory Comput. 2020, 16, 4669–4684. [Google Scholar] [CrossRef]
- Forouzesh, N.; Watson, L.T.; Onufriev, A.V. Robustness of multidimensional optimization outcomes: A general approach and a case study. In Proceedings of the 2020 Spring Simulation Conference, Fairfax, VA, USA, 18–21 May 2020; pp. 1–12. [Google Scholar]
- Forouzesh, N. Binding Free Energy of the Novel Coronavirus Spike Protein and the Human ACE2 Receptor: An MMGB/SA Computational Study. In Proceedings of the 11th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, Gainesville, FL, USA, 21–24 September 2020; pp. 1–7. [Google Scholar]
- Forouzesh, N.; Onufriev, A.V. MMGB/SA Consensus Estimate of the Binding Free Energy between the Novel Coronavirus Spike Protein to the Human ACE2 Receptor. BioRxiv 2020. [Google Scholar] [CrossRef]
- Callaway, E. Making sense of coronavirus mutations. Nature 2020, 585, 174–177. [Google Scholar] [CrossRef]
- Wang, R.; Hozumi, Y.; Yin, C.; Wei, G.W. Mutations on COVID-19 diagnostic targets. Genomics 2020, 112, 5204–5213. [Google Scholar] [CrossRef]
- Chen, J.; Wang, R.; Wang, M.; Wei, G.W. Mutations strengthened SARS-CoV-2 infectivity. J. Mol. Biol. 2020, 432, 5212–5226. [Google Scholar] [CrossRef]
- Kollman, P.A.; Massova, I.; Reyes, C.; Kuhn, B.; Huo, S.; Chong, L.; Lee, M.; Lee, T.; Duan, Y.; Wang, W.; et al. Calculating structures and free energies of complex molecules: Combining molecular mechanics and continuum models. Accounts Chem. Res. 2000, 33, 889–897. [Google Scholar] [CrossRef]
- Homeyer, N.; Gohlke, H. Free energy calculations by the molecular mechanics Poisson- Boltzmann surface area method. Mol. Inform. 2012, 31, 114–122. [Google Scholar] [CrossRef]
- Miller III, B.R.; McGee Jr, T.D.; Swails, J.M.; Homeyer, N.; Gohlke, H.; Roitberg, A.E. MMPBSA. py: An efficient program for end-state free energy calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. [Google Scholar] [CrossRef]
- Onufriev, A.V.; Case, D.A. Generalized Born implicit solvent models for biomolecules. Annu. Rev. Biophys. 2019, 48, 275–296. [Google Scholar] [CrossRef]
- Onufriev, A.; Bashford, D.; Case, D.A. Modification of the generalized Born model suitable for macromolecules. J. Phys. Chem. B 2000, 104, 3712–3720. [Google Scholar] [CrossRef]
- Forouzesh, N.; Izadi, S.; Onufriev, A.V. Grid-based Surface Generalized Born Model for Calculation of Electrostatic Binding Free Energies. J. Chem. Inf. Model. 2017, 57, 2505–2513. [Google Scholar] [CrossRef]
- Izadi, S.; Harris, R.C.; Fenley, M.O.; Onufriev, A.V. Accuracy Comparison of Generalized Born Models in the Calculation of Electrostatic Binding Free Energies. J. Chem. Theory Comput. 2018, 14, 1656–1670. [Google Scholar] [CrossRef]
- Sigalov, G.; Scheffel, P.; Onufriev, A. Incorporating Variable Dielectric Environments Into the Generalized Born Model. J. Chem. Phys. 2005, 122, 094511. [Google Scholar] [CrossRef]
- Sigalov, G.; Fenley, A.; Onufriev, A. Analytical Electrostatics for Biomolecules: Beyond the Generalized Born Approximation. J. Chem. Phys. 2006, 124, 124902. [Google Scholar] [CrossRef]
- Still, W.C.; Tempczyk, A.; Hawley, R.C.; Hendrickson, T. Semianalytical Treatment of Solvation for Molecular Mechanics and Dynamics. J. Am. Chem. Soc. 1990, 112, 6127–6129. [Google Scholar] [CrossRef]
- Aguilar, B.; Shadrach, R.; Onufriev, A.V. Reducing the Secondary Structure Bias in the Generalized Born Model via R6 Effective radii. J. Chem. Theory Comput. 2010, 6, 3613–3630. [Google Scholar] [CrossRef]
- Aguilar, B.; Onufriev, A.V. Efficient Computation of the Total Solvation Energy of Small Molecules via the R6 Generalized Born Model. J. Chem. Theory Comput. 2012, 8, 2404–2411. [Google Scholar] [CrossRef] [PubMed]
- Mongan, J.; Svrcek-Seiler, W.A.; Onufriev, A. Analysis of Integral Expressions for Effective Born Radii. J. Chem. Phys. 2007, 127, 11B608. [Google Scholar] [CrossRef] [PubMed]
- Gallicchio, E.; Levy, R.M. AGBNP: An analytic implicit solvent model suitable for molecular dynamics simulations and high-resolution modeling. J. Comput. Chem. 2004, 25, 479–499. [Google Scholar] [CrossRef] [PubMed]
- Su, P.C.; Tsai, C.C.; Mehboob, S.; Hevener, K.E.; Johnson, M.E. Comparison of radii sets, entropy, QM methods, and sampling on MM-PBSA, MM-GBSA, and QM/MM-GBSA ligand binding energies of F. tularensis enoyl-ACP reductase (F abI). J. Comput. Chem. 2015, 36, 1859–1873. [Google Scholar] [CrossRef] [PubMed]
- Poma, A.B.; Li, M.S.; Theodorakis, P.E. Generalization of the elastic network model for the study of large conformational changes in biomolecules. Phys. Chem. Chem. Phys. 2018, 20, 17020–17028. [Google Scholar] [CrossRef]
- Bondi, A. Van der Waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Mantina, M.; Chamberlin, A.C.; Valero, R.; Cramer, C.J.; Truhlar, D.G. Consistent van der Waals radii for the whole main group. J. Phys. Chem. A 2009, 113, 5806–5812. [Google Scholar] [CrossRef]
- Onufriev, A.V.; Aguilar, B. Accuracy of continuum electrostatic calculations based on three common dielectric boundary definitions. J. Theor. Comput. Chem. 2014, 13, 1440006. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Anandakrishnan, R.; Aguilar, B.; Onufriev, A.V. H++ 3.0: Automating p K prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulations. Nucleic Acids Res. 2012, 40, W537–W541. [Google Scholar] [CrossRef]
- Izadi, S.; Anandakrishnan, R.; Onufriev, A.V. Building water models: A different approach. J. Phys. Chem. Lett. 2014, 5, 3863–3871. [Google Scholar] [CrossRef]
- Rudolph, M.G.; Linnemann, T.; Grünewald, P.; Wittinghofer, A.; Vetter, I.R.; Herrmann, C. Thermodynamics of Ras/effector and Cdc42/effector interactions probed by isothermal titration calorimetry. J. Biol. Chem. 2001, 276, 23914–23921. [Google Scholar] [CrossRef]
- Wrapp, D.; Wang, N.; Corbett, K.S.; Goldsmith, J.A.; Hsieh, C.L.; Abiona, O.; Graham, B.S.; McLellan, J.S. Cryo-EM structure of the 2019-nCoV spike in the prefusion conformation. Science 2020, 367, 1260–1263. [Google Scholar] [CrossRef]
| Bondi | 1.70 | 1.20 | 1.55 | 1.52 | 1.80 | 1.47 | 1.75 | 1.98 |
| OPT1 | 1.40 | 1.55 | 2.35 | 1.28 | 1.80 | 1.47 | 1.75 | 1.98 |
| Truncated Structure | Full Structure | Exp. | |||
|---|---|---|---|---|---|
| Bondi | OPT1 | Bondi | OPT1 | ||
| −453.76 ± 0.87 | −453.76 ± 0.87 | −614.29 ± 0.91 | −614.29 ± 0.91 | ||
| −14.71 ± 0.02 | −16.35 ± 0.02 | −14.32 ± 0.01 | −16.42 ± 0.02 | ||
| 401.55 ± 0.81 | 413.72 ± 0.87 | 566.49 ± 0.84 | 582.43 ± 0.87 | ||
| −66.93 ± 0.29 | −56.39 ± 0.37 | −62.12 ± 0.31 | −48.28 ± 0.44 | ||
| −T | 52.28 ± 1.49 | 52.28 ± 1.49 | 52.28 ± 1.49 | 52.28 ± 1.49 | |
| −14.65 ± 1.52 | −4.11 ± 1.54 | −9.84 ± 1.52 | 4 ± 1.55 | −10.6 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forouzesh, N.; Mishra, N. An Effective MM/GBSA Protocol for Absolute Binding Free Energy Calculations: A Case Study on SARS-CoV-2 Spike Protein and the Human ACE2 Receptor. Molecules 2021, 26, 2383. https://doi.org/10.3390/molecules26082383
Forouzesh N, Mishra N. An Effective MM/GBSA Protocol for Absolute Binding Free Energy Calculations: A Case Study on SARS-CoV-2 Spike Protein and the Human ACE2 Receptor. Molecules. 2021; 26(8):2383. https://doi.org/10.3390/molecules26082383
Chicago/Turabian StyleForouzesh, Negin, and Nikita Mishra. 2021. "An Effective MM/GBSA Protocol for Absolute Binding Free Energy Calculations: A Case Study on SARS-CoV-2 Spike Protein and the Human ACE2 Receptor" Molecules 26, no. 8: 2383. https://doi.org/10.3390/molecules26082383
APA StyleForouzesh, N., & Mishra, N. (2021). An Effective MM/GBSA Protocol for Absolute Binding Free Energy Calculations: A Case Study on SARS-CoV-2 Spike Protein and the Human ACE2 Receptor. Molecules, 26(8), 2383. https://doi.org/10.3390/molecules26082383







