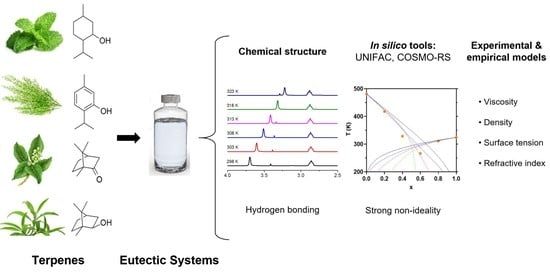
Physicochemical Characterization and Simulation of the Solid–Liquid Equilibrium Phase Diagram of Terpene-Based Eutectic Solvent Systems
Abstract
1. Introduction
2. Results and Discussion
2.1. Physical Properties of the Eutectic Systems
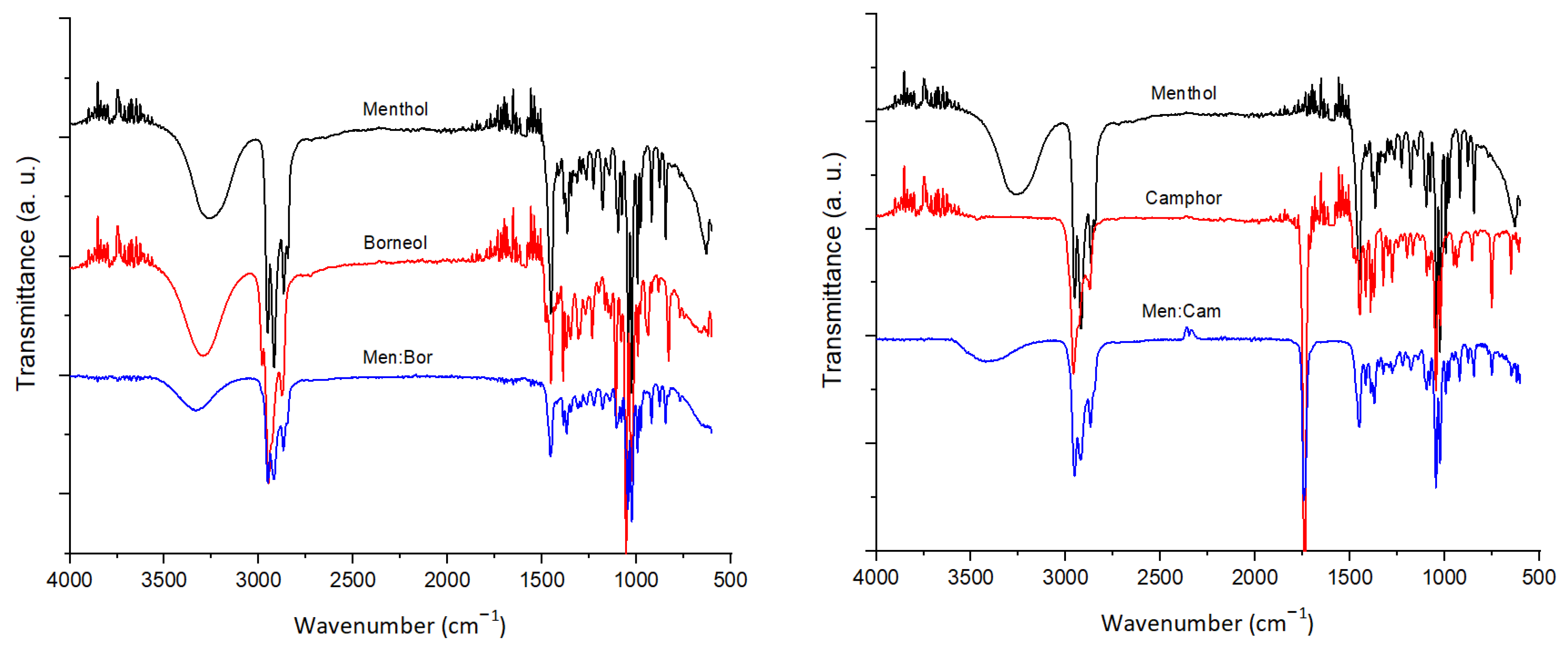
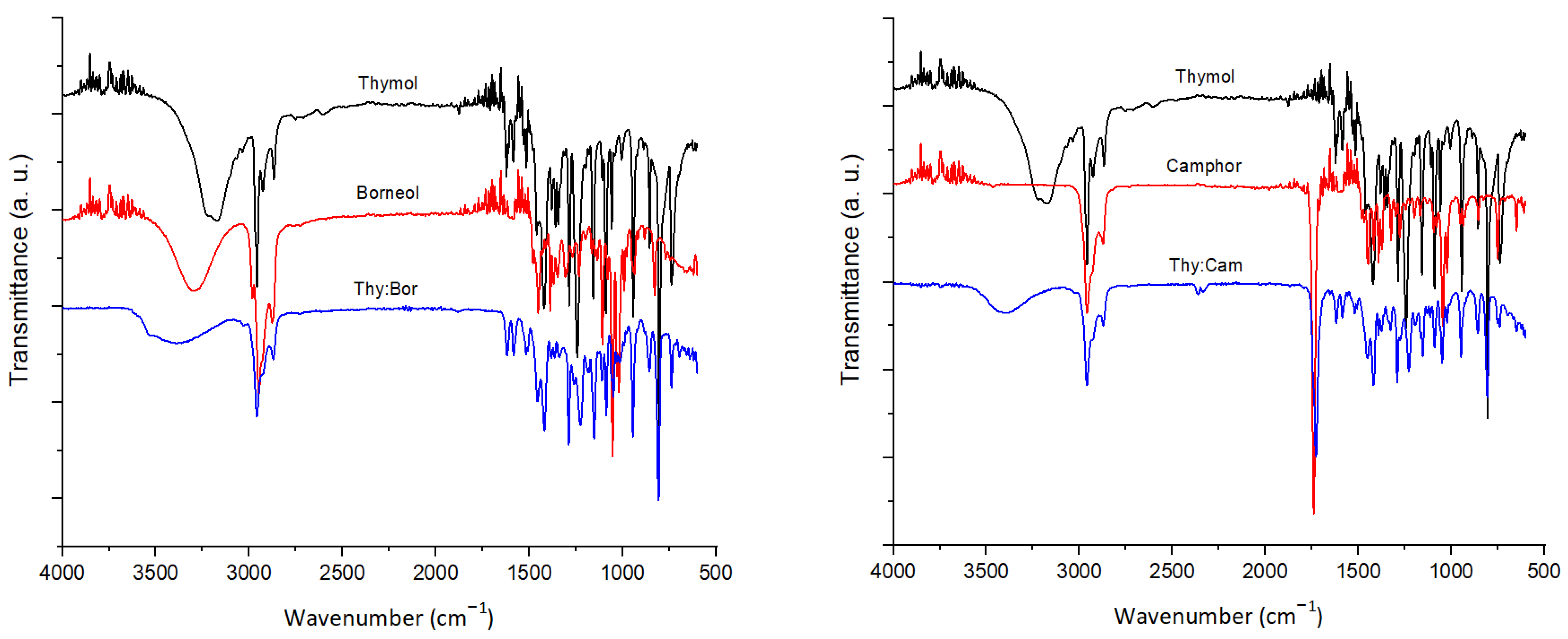
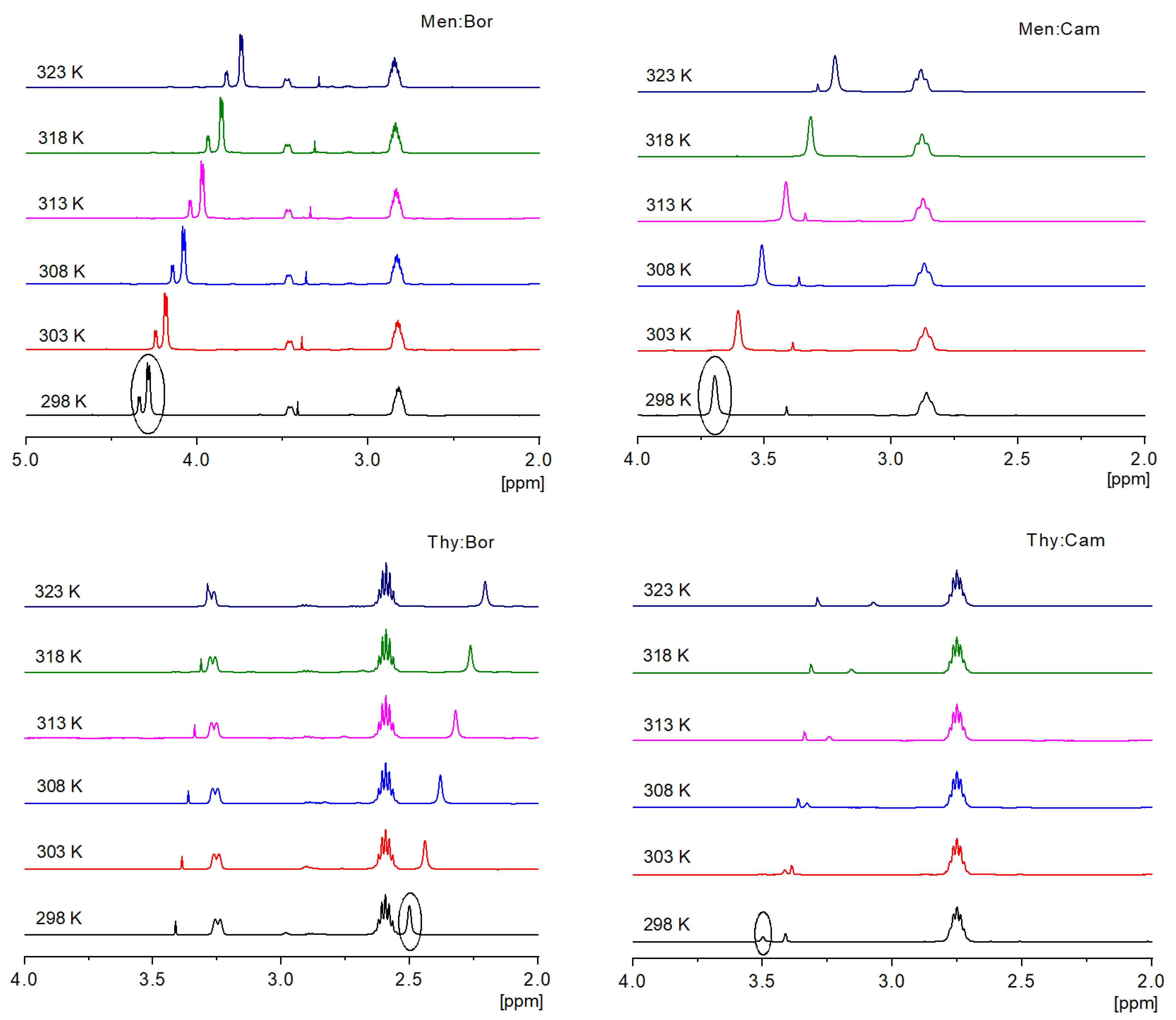
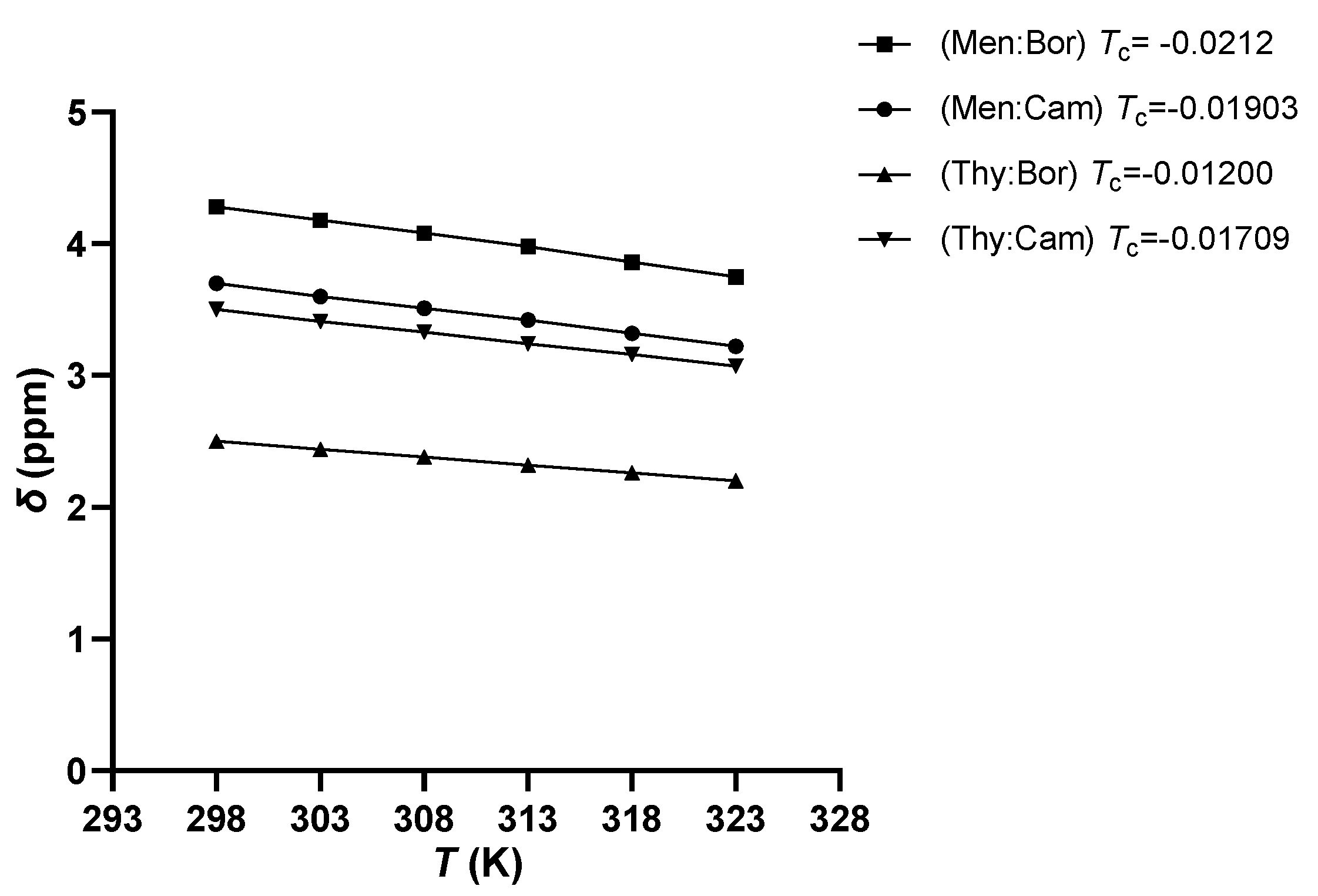
2.2. FTIR and 1H NMR Analysis
2.3. TGA and DSC Analysis
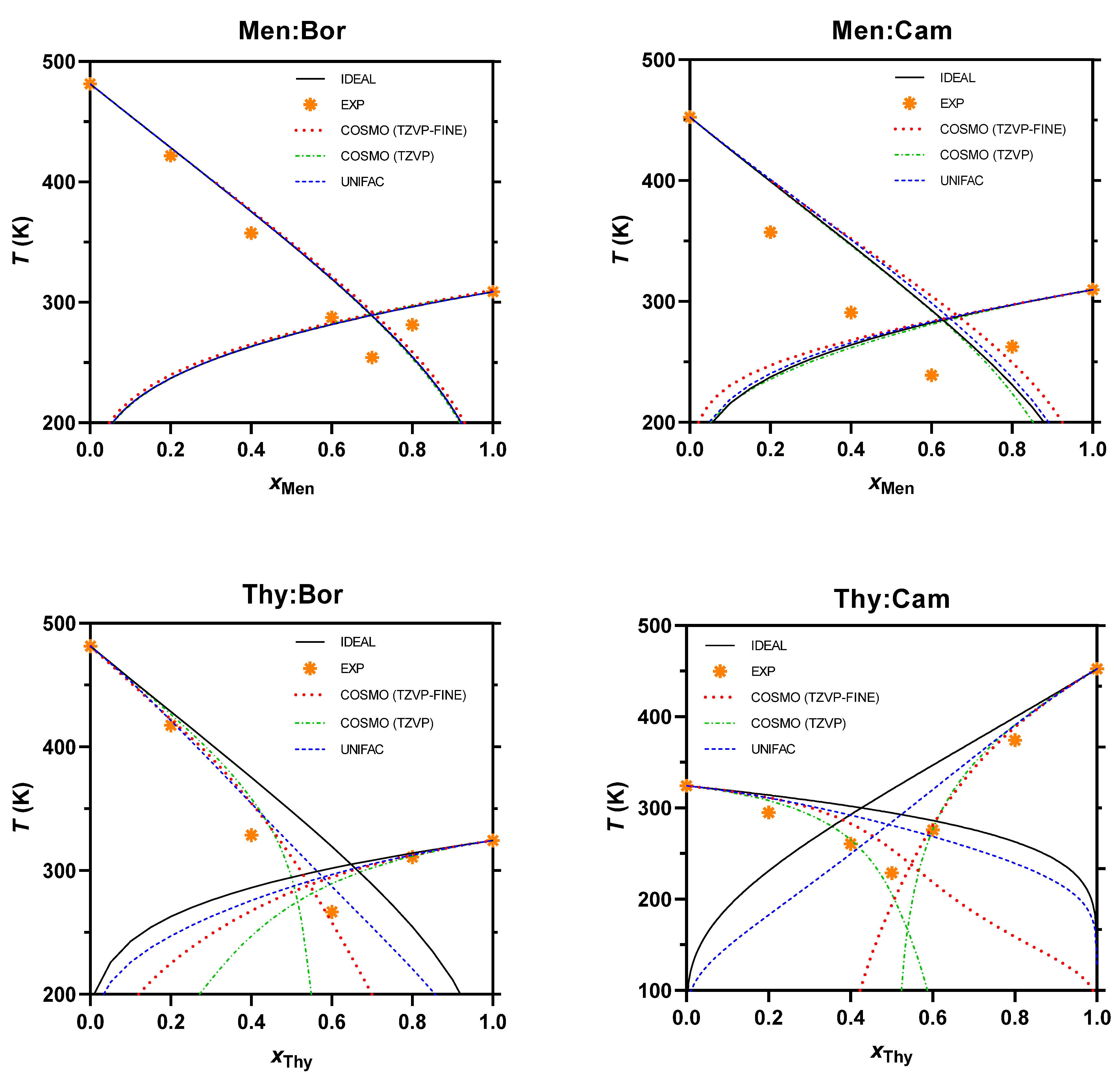
2.4. SLE Phase Diagram Simulation
3. Materials and Methods
3.1. Materials
3.2. Eutectic Mixtures Preparation
3.3. Analysis of the Physical Properties
3.4. Fourier-Transform Infrared Spectroscopy Analysis
3.5. 1H-NMR Analysis
3.6. TGA and DSC Analysis
3.7. SLE Phase Diagram Calculation
3.7.1. UNIFAC Function Computations
3.7.2. COSMO-RS Simulation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations
| Bor | Borneol |
| Cam | Camphor |
| COSMO-RS | Conductor-like Screening Model for Real Solvents |
| DES | Deep eutectic solvent |
| DMSO | Deuterated dimethyl sulfoxide |
| DSC | Differential scanning calorimetry |
| FTIR | Fourier-transform infrared spectroscopy |
| Men | Menthol |
| NMR | Nuclear Magnetic Resonance |
| SLE | Solid–liquid equilibrium |
| TGA | Thermogravimetric analysis |
| Thy | Thymol |
| UNIFAC | UNIversal Functional Activity Coefficient |
| Symbols | |
| A1–A9 | Optimized parameters for the proposed models |
| er | Percentage relative error |
| Mw | Molecular weight |
| n | Refractive index |
| P | Pressure |
| T | Temperature |
| V | Volume |
| x | Molar ratio |
| γ | Activity coefficient |
| ΔH | Enthalphy |
| η | Viscosity |
| ρ | Density |
| σ | Surface tension |
| σ1–σ6 | Optimized parameters for the proposed models |
| ω | Acentric factor |
| Subscripts | |
| c | Critical |
| coeff | Coefficient |
| cr | Crystallization |
| D | Degradation |
| E | Eutectic |
| exp | Experimental |
| g | Glass |
| i | Compounds i |
| L | Computed using models |
| m | Melting/fusion |
| ref | reference |
| Superscripts | |
| R | Residual |
| L | Computed using models |
| C | Combinatorial |
References
- Zdanowicz, M.; Wilpiszewska, K.; Spychaj, T. Deep eutectic solvents for polysaccharides processing. A review. Carbohydr. Polym. 2018, 200, 361–380. [Google Scholar] [CrossRef]
- Abbott, A.P.; Boothby, D.; Capper, G.; Davies, D.L.; Rasheed, R.K. Deep Eutectic Solvents formed between choline chloride and carboxylic acids: Versatile alternatives to ionic liquids. J. Am. Chem. Soc. 2004, 126, 9142–9147. [Google Scholar] [CrossRef]
- García, G.; Aparicio, S.; Ullah, R.; Atilhan, M. Deep eutectic solvents: Physicochemical properties and gas separation applications. Energy Fuels 2015, 29, 2616–2644. [Google Scholar] [CrossRef]
- Smith, E.L.; Abbott, A.P.; Ryder, K.S. Deep Eutectic Solvents (DESs) and Their Applications. Chem. Rev. 2014, 114, 11060–11082. [Google Scholar] [CrossRef] [PubMed]
- González De Castilla, A.; Bittner, J.P.; Müller, S.; Jakobtorweihen, S.; Smirnova, I. Thermodynamic and Transport Properties Modeling of Deep Eutectic Solvents: A Review on gE-Models, Equations of State, and Molecular Dynamics. J. Chem. Eng. Data 2020, 65, 943–967. [Google Scholar] [CrossRef]
- Calogirou, A.; Larsen, B.R.; Kotzias, D. Gas-phase terpene oxidation products: A review. Atmos. Environ. 1999, 33, 1423–1439. [Google Scholar] [CrossRef]
- Gonzalez-Burgos, E.; Gomez-Serranillos, M.P. Terpene Compounds in Nature: A Review of Their Potential Antioxidant Activity. Curr. Med. Chem. 2012, 19, 5319–5341. [Google Scholar] [CrossRef] [PubMed]
- De Cássia da Silveira e Sá, R.; Andrade, L.N.; De Sousa, D.P. A review on anti-inflammatory activity of monoterpenes. Molecules 2013, 18, 1227–1254. [Google Scholar] [CrossRef] [PubMed]
- Arita, R.; Morishige, N.; Sakamoto, I.; Imai, N.; Shimada, Y.; Igaki, M.; Suzuki, A.; Itoh, K.; Tsubota, K. Effects of a warm compress containing menthol on the tear film in healthy subjects and dry eye patients. Sci. Rep. 2017, 7, 1–6. [Google Scholar] [CrossRef]
- Huang, L.; Bai, J.; Yang, H.; Liu, J.; Cui, H. Combined use of borneol or menthol with labrasol promotes penetration of baicalin through rabbit cornea in vitro. Pak. J. Pharm. Sci. 2015, 28, 1–7. [Google Scholar]
- Liu, J.; Fu, S.; Wei, N.; Hou, Y.; Zhang, X.; Cui, H. The effects of combined menthol and borneol on fluconazole permeation through the cornea ex vivo. Eur. J. Pharmacol. 2012, 688, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Qi, H.P.; Gao, X.C.; Zhang, L.Q.; Wei, S.Q.; Bi, S.; Yang, Z.C.; Cui, H. In vitro evaluation of enhancing effect of borneol on transcorneal permeation of compounds with different hydrophilicities and molecular sizes. Eur. J. Pharmacol. 2013, 705, 20–25. [Google Scholar] [CrossRef]
- Mohammadi-Samani, S.; Yousefi, G.; Mohammadi, F.; Ahmadi, F. Meloxicam transdermal delivery: Effect of eutectic point on the rate and extent of skin permeation. Iran. J. Basic Med. Sci. 2014, 17, 112–118. [Google Scholar]
- Stott, P.W.; Williams, A.C.; Barry, B.W. Transdermal delivery from eutectic systems: Enhanced permeation of a model drug, ibuprofen. J. Control. Release 1998, 50, 297–308. [Google Scholar] [CrossRef]
- Silva, L.P.; Fernández, L.; Conceição, J.H.F.; Martins, M.A.R.; Sosa, A.; Ortega, J.; Pinho, S.P.; Coutinho, J.A.P. Design and characterization of sugar-based deep eutectic solvents using COSMO-RS. ACS Sustain. Chem. Eng. 2018, 6, 10724–10734. [Google Scholar] [CrossRef]
- Martins, M.A.R.; Pinho, S.P.; Coutinho, J.A.P. Insights into the Nature of Eutectic and Deep Eutectic Mixtures. J. Solut. Chem. 2019, 48, 962–982. [Google Scholar] [CrossRef]
- Kalhor, P.; Ghandi, K. Deep eutectic solvents for pretreatment, extraction, and catalysis of biomass and food waste. Molecules 2019, 24, 4012. [Google Scholar] [CrossRef]
- Taherzadeh, M.; Haghbakhsh, R.; Duarte, A.R.C.; Raeissi, S. Generalized Model to Estimate the Refractive Indices of Deep Eutectic Solvents. J. Chem. Eng. Data 2020, 65, 3965–3976. [Google Scholar] [CrossRef]
- Haghbakhsh, R.; Taherzadeh, M.; Duarte, A.R.C.; Raeissi, S. A general model for the surface tensions of deep eutectic solvents. J. Mol. Liq. 2020, 307, 112972. [Google Scholar] [CrossRef]
- Fredenslund, A.; Jones, R.L.; Prausnitz, J.M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures. AIChE J. 1975, 21, 1086–1099. [Google Scholar] [CrossRef]
- Klamt, A. Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena. J. Phys. Chem. 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Klamt, A.; Jonas, V.; Bürger, T.; Lohrenz, J.C.W. Refinement and parametrization of COSMO-RS. J. Phys. Chem. A 1998, 102, 5074–5085. [Google Scholar] [CrossRef]
- Bakhtyari, A.; Haghbakhsh, R.; Duarte, A.R.C.; Raeissi, S. A simple model for the viscosities of deep eutectic solvents. Fluid Phase Equilibria 2020, 521, 112662. [Google Scholar] [CrossRef]
- Leron, R.B.; Soriano, A.N.; Li, M.H. Densities and refractive indices of the deep eutectic solvents (choline chloride+ethylene glycol or glycerol) and their aqueous mixtures at the temperature ranging from 298.15 to 333.15K. J. Taiwan Inst. Chem. Eng. 2012, 43, 551–557. [Google Scholar] [CrossRef]
- Haghbakhsh, R.; Bardool, R.; Bakhtyari, A.; Duarte, A.R.C.; Raeissi, S. Simple and global correlation for the densities of deep eutectic solvents. J. Mol. Liq. 2019, 296, 111830. [Google Scholar] [CrossRef]
- Ghaedi, H.; Ayoub, M.; Sufian, S.; Shariff, A.M.; Lal, B. The study on temperature dependence of viscosity and surface tension of several Phosphonium-based deep eutectic solvents. J. Mol. Liq. 2017, 241, 500–510. [Google Scholar] [CrossRef]
- Wang, X.; Lu, X.; Zhou, Q.; Zhao, Y.; Li, X.; Zhang, S. Database and new models based on a group contribution method to predict the refractive index of ionic liquids. Phys. Chem. Chem. Phys. 2017, 19, 19967–19974. [Google Scholar] [CrossRef] [PubMed]
- Shahbaz, K.; Bagh, F.S.G.; Mjalli, F.S.; AlNashef, I.M.; Hashim, M.A. Prediction of refractive index and density of deep eutectic solvents using atomic contributions. Fluid Phase Equilibria 2013, 354, 304–311. [Google Scholar] [CrossRef]
- Piñaro, Á.; Brocos, P.; Amigo, A.; Pintos, M.; Bravo, R. Surface tensions and refractive indices of (tetrahydrofuran + n-alkanes) at T = 298.15 K. J. Chem. Thermodyn. 1999, 31, 931–942. [Google Scholar] [CrossRef]
- Popescu, C.M.; Popescu, M.C.; Vasile, C. Structural analysis of photodegraded lime wood by means of FT-IR and 2D IR correlation spectroscopy. Int. J. Biol. Macromol. 2011, 48, 667–675. [Google Scholar] [CrossRef]
- Charisiadis, P.; Kontogianni, V.G.; Tsiafoulis, C.G.; Tzakos, A.G.; Siskos, M.; Gerothanassis, I.P. 1H-NMR as a structural and analytical tool of intra- and intermolecular hydrogen bonds of phenol-containing natural products and model compounds. Molecules 2014, 19, 13643–13682. [Google Scholar] [CrossRef]
- Duarte, A.R.C.; Ferreira, A.S.D.; Barreiros, S.; Cabrita, E.; Reis, R.L.; Paiva, A. A comparison between pure active pharmaceutical ingredients and therapeutic deep eutectic solvents: Solubility and permeability studies. Eur. J. Pharm. Biopharm. 2017, 114, 296–304. [Google Scholar] [CrossRef]
- Rodrigues, L.A.; Pereira, C.V.; Leonardo, I.C.; Fernández, N.; Gaspar, F.B.; Silva, J.M.; Reis, R.L.; Duarte, A.R.C.; Paiva, A.; Matias, A.A. Terpene-Based Natural Deep Eutectic Systems as Efficient Solvents to Recover Astaxanthin from Brown Crab Shell Residues. ACS Sustain. Chem. Eng. 2020, 8, 2246–2259. [Google Scholar] [CrossRef]
- Li, Y.; Jia, Y.; Wang, Z.; Li, X.; Feng, W.; Deng, P.; Yuan, L. An insight into the extraction of transition metal ions by picolinamides associated with intramolecular hydrogen bonding and rotational isomerization. RSC Adv. 2014, 4, 29702–29714. [Google Scholar] [CrossRef]
- Alhadid, A.; Mokrushina, L.; Minceva, M. Formation of glassy phases and polymorphism in deep eutectic solvents. J. Mol. Liq. 2020, 314, 113667. [Google Scholar] [CrossRef]
- Kollau, L.J.B.M.; Vis, M.; Van Den Bruinhorst, A.; De With, G.; Tuinier, R. Activity modelling of the solid-liquid equilibrium of deep eutectic solvents. Pure Appl. Chem. 2019, 91, 1341–1349. [Google Scholar] [CrossRef]
- Bezold, F.; Minceva, M. Liquid-liquid equilibria of n-heptane, methanol and deep eutectic solvents composed of carboxylic acid and monocyclic terpenes. Fluid Phase Equilibria 2018, 477, 98–106. [Google Scholar] [CrossRef]
- Rycerz, L. Practical remarks concerning phase diagrams determination on the basis of differential scanning calorimetry measurements. J. Therm. Anal. Calorim. 2013, 113, 231–238. [Google Scholar] [CrossRef]
- Chemat, F.; Anjum, H.; Shariff, A.M.; Kumar, P.; Murugesan, T. Thermal and physical properties of (Choline chloride + urea + l-arginine) deep eutectic solvents. J. Mol. Liq. 2016, 218, 301–308. [Google Scholar] [CrossRef]
- Martins, M.A.R.; Crespo, E.A.; Pontes, P.V.A.; Silva, L.P.; Bülow, M.; Maximo, G.J.; Batista, E.A.C.; Held, C.; Pinho, S.P.; Coutinho, J.A.P. Tunable Hydrophobic Eutectic Solvents Based on Terpenes and Monocarboxylic Acids. ACS Sustain. Chem. Eng. 2018, 6, 8836–8846. [Google Scholar] [CrossRef]
- Valderrama, J.O.; Sanga, W.W.; Lazzús, J.A. Critical properties, normal boiling temperature, and acentric factor of another 200 ionic liquids. Ind. Eng. Chem. Res. 2008, 47, 1318–1330. [Google Scholar] [CrossRef]
- Mirza, N.R.; Nicholas, N.J.; Wu, Y.; Kentish, S.; Stevens, G.W. Estimation of Normal Boiling Temperatures, Critical Properties, and Acentric Factors of Deep Eutectic Solvents. J. Chem. Eng. Data 2015, 60, 1844–1854. [Google Scholar] [CrossRef]
- Prausnitz, J.M.; Lichtenthaler, R.N.; de Azevedo, E.G. Molecular Thermodynamics of Fluid-Phase Equilibria; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1999; ISBN 9780139777455. [Google Scholar]
- Okuniewski, M.; Paduszy, K.; Domanska, U.M. Phase Diagrams in Representative Terpenoid Systems—Measurements and Calculations with Leading Thermodynamic Models. Ind. Eng. Chem. Res. 2017, 56, 9753–9761. [Google Scholar] [CrossRef]
- Hansen, K. Evaluation of UNIFAC Group Interaction Parameters Using Properties Based on Quantum Mechanical Calculations. Master’s Thesis, New Jersey’s Science & Technology University, Newark, NJ, USA, 2005. [Google Scholar]
- Tiegs, D.; Gmehling, J.; Rasmussen, P.; Fredenslund, A. Vapor—Liquid Equilibria by UNIFAC Group Contribution. 4. Revision and Extension. Ind. Eng. Chem. Res. 1987, 26, 159–161. [Google Scholar] [CrossRef]
- Magnussen, T.; Rasmussen, P.; Fredenslund, A. Unifac Parameter Table for Prediction of Liquid-Liquid Equilibria. Ind. Eng. Chem. Process Des. Dev. 1981, 20, 331–339. [Google Scholar] [CrossRef]
- Jain, M.; Attarde, D.; Gupta, S.K. Estimation of unknown UNIFAC interaction parameters between thiophene and olefin, and thiol and olefin functional groups. Fluid Phase Equilibria 2017, 442, 81–86. [Google Scholar] [CrossRef]
- Voutsas, E.C.; Tassios, D.P. Analysis of the UNIFAC-Type Group-Contribution Models at the Highly Dilute Region. 1. Limitations of the Combinatorial and Residual Expressions. Ind. Eng. Chem. Res. 1997, 36, 4965–4972. [Google Scholar] [CrossRef]
- Oracz, P.; Góral, M.; Wilczek-Vera, G.; Warycha, S. Vapour-liquid equilibria. X. The ternary system cyclohexane-methanol-acetone at 293.15 and 303.15 K. Fluid Phase Equilibria 1996, 126, 71–92. [Google Scholar] [CrossRef]
- Hansen, H.K.; Rasmussen, P.; Fredenslund, A.; Schiller, M.; Gmehling, J. Vapor-Liquid Equilibria by UNIFAC Group Contribution. 5. Revision and Extension. Ind. Eng. Chem. Res. 1991, 30, 2352–2355. [Google Scholar] [CrossRef]
- Gmehling, J.; Li, J.; Schiller, M. A Modified UNIFAC Model. 2. Present Parameter Matrix and Results for Different Thermodynamic Properties. Ind. Eng. Chem. Res. 1993, 32, 178–193. [Google Scholar] [CrossRef]
- Eckert, F.; Klamt, A. Fast Solvent Screening via Quantum Chemistry: COSMO-RS Approach. AIChE J. 2002, 48, 369–385. [Google Scholar] [CrossRef]
- Klamt, A. COSMO-RS: From Quantum Chemistry to Fluid Phase Thermodynamics and Drug Design; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2005. [Google Scholar]
| Compound | Chemical Structure |
|---|---|
| Menthol | 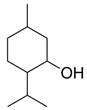 |
| Thymol | 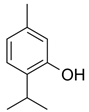 |
| Borneol |  |
| Camphor |  |
| Eutectic Systems | |||||
|---|---|---|---|---|---|
| Men:Bor (7:3) | Men:Cam (3:2) | Thy:Bor (7:3) | Thy:Cam (1:1) | ||
| MW (g/mol) | 155.66 | 154.65 | 151.43 | 151.23 | |
| Experimental | Viscosity ηexp (mPa/s) | 128.07 ± 0.24 | 19.23 ± 0.01 | 45.63 ± 0.20 | 21.10 ± 0.02 |
| Density ρexp (g/mL) | 0.9152 ± 0.0005 | 0.9178 ± 0.0001 | 0.9716 ± 0.0001 | 0.9675 ± 0.0001 | |
| Surface tension σexp (mN/m) | 29.04 ± 0.03 | 29.41 ± 0.08 | 31.75 ± 0.01 | 30.35 ± 0.06 | |
| Refractive index nexp | 1.4670 ± 0.0005 | 1.4635 ± 0.0008 | 1.5105 ± 0.0002 | 1.4970 ± 0.0003 | |
| Theoretical | Density ρL (g/mL) | 1.1116 | 1.1063 | 1.1500 | 1.1350 |
| Surface tension σL (mN/m) | 25.37 | 23.25 | 29.19 | 32.25 | |
| Refractive index n | 1.4708 | 1.4671 | 1.4795 | 1.4731 | |
| Men:Bor | Men:Cam | Thy:Bor | Thy:Cam | |
|---|---|---|---|---|
| Density ρ | 21.5 | 20.5 | 18.4 | 17.3 |
| Surface tension σ | −12.7 | −21.0 | −8.1 | 6.3 |
| Refractive index n | 0.26 | 0.25 | −2.05 | −1.59 |
| Component | Tfus (K) | ΔHfus (J/mol) |
|---|---|---|
| Menthol | 309.72 | 13.62 |
| Thymol | 324.31 | 18.54 |
| Borneol | 481.33 | 7.23 |
| Camphor | 452.41 | 6.32 |
| Eutectic System | Td (K) | Tcr (K) | ΔHcr (J/g) | Tg (K) |
|---|---|---|---|---|
| Men:Bor (7:3) | 366.02 | 254.08 | 21.17 | 223.03 |
| Men:Cam (3:2) | 358.29 | 239.92 | 28.60 | 196.98 |
| Thy:Bor (7:3) | 355.04 | 284.64 | 0.098 | 215.17 |
| Thy:Cam (1:1) | 370.74 | 260.69 | 0.077 | 194.23 |
| Eutectic Systems | |||||
|---|---|---|---|---|---|
| Men:Bor | Men:Cam | Thy:Bor | Thy:Cam | ||
| Ideal | TE, ideal (K) | 289.8 | 284.7 | 309.6 | 300.1 |
| xE, ideal | 0.696 | 0.628 | 0.722 | 0.457 | |
| UNIFAC | TE, UNIFAC (K) | 290.0 | 286.5 | 300.8 | 281.7 |
| xE, UNIFAC | 0.697 | 0.642 | 0.645 | 0.514 | |
| COSMO-RS (TZVP) | TE, TZVP (K) | 289.7 | 283.4 | 274.7 | 166.2 |
| xE, TZVP | 0.695 | 0.630 | 0.515 | 0.538 | |
| COSMO-RS (TZVP-FINE) | TE, TZVPD-FINE (K) | 290.7 | 288.1 | 293.2 | 237.9 |
| xE, TZVPD-FINE | 0.704 | 0.664 | 0.583 | 0.547 | |
| Parameter | Value | Units |
|---|---|---|
| σ1 | 393.4 | mN/m |
| σ2 | −5.3 × 10−5 | mN/m |
| σ3 | −3.72 × 10−2 | mN/m |
| σ4 | −50.3 | mN/m |
| σ5 | 1.132 | mN/m |
| σ6 | 108.9 | mN/m |
| A1 | 1 | mol⋅mL/g2 |
| A2 | 1 | mL⋅m/mol⋅mN |
| A3 | 1 | bar⋅mol/g⋅K0.5 |
| A4 | 1 | mol⋅K0.5/g |
| A5 | 5.17 × 10−2 | Dimensionless |
| A6 | −11.625 | mol/g |
| A7 | 2.27 × 10−3 | bar−1 |
| A8 | 1.3668 | Dimensionless |
| A9 | 25.89 | K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdallah, M.M.; Müller, S.; González de Castilla, A.; Gurikov, P.; Matias, A.A.; Bronze, M.d.R.; Fernández, N. Physicochemical Characterization and Simulation of the Solid–Liquid Equilibrium Phase Diagram of Terpene-Based Eutectic Solvent Systems. Molecules 2021, 26, 1801. https://doi.org/10.3390/molecules26061801
Abdallah MM, Müller S, González de Castilla A, Gurikov P, Matias AA, Bronze MdR, Fernández N. Physicochemical Characterization and Simulation of the Solid–Liquid Equilibrium Phase Diagram of Terpene-Based Eutectic Solvent Systems. Molecules. 2021; 26(6):1801. https://doi.org/10.3390/molecules26061801
Chicago/Turabian StyleAbdallah, Maha M., Simon Müller, Andrés González de Castilla, Pavel Gurikov, Ana A. Matias, Maria do Rosário Bronze, and Naiara Fernández. 2021. "Physicochemical Characterization and Simulation of the Solid–Liquid Equilibrium Phase Diagram of Terpene-Based Eutectic Solvent Systems" Molecules 26, no. 6: 1801. https://doi.org/10.3390/molecules26061801
APA StyleAbdallah, M. M., Müller, S., González de Castilla, A., Gurikov, P., Matias, A. A., Bronze, M. d. R., & Fernández, N. (2021). Physicochemical Characterization and Simulation of the Solid–Liquid Equilibrium Phase Diagram of Terpene-Based Eutectic Solvent Systems. Molecules, 26(6), 1801. https://doi.org/10.3390/molecules26061801