The Different Story of π Bonds
Abstract
:1. Introduction
2. Methods
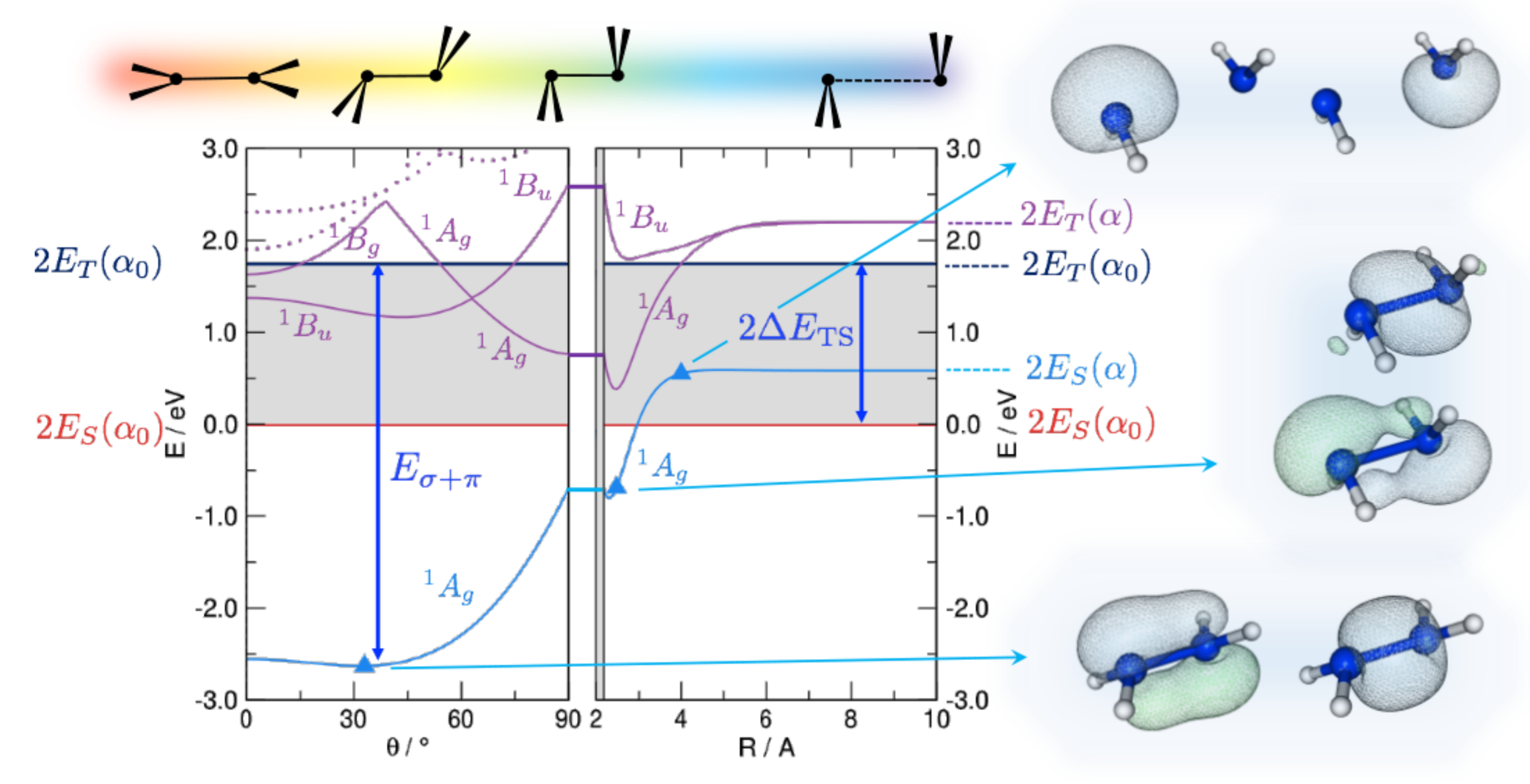
3. Trans-Bending
4. Bond-Length Alternation
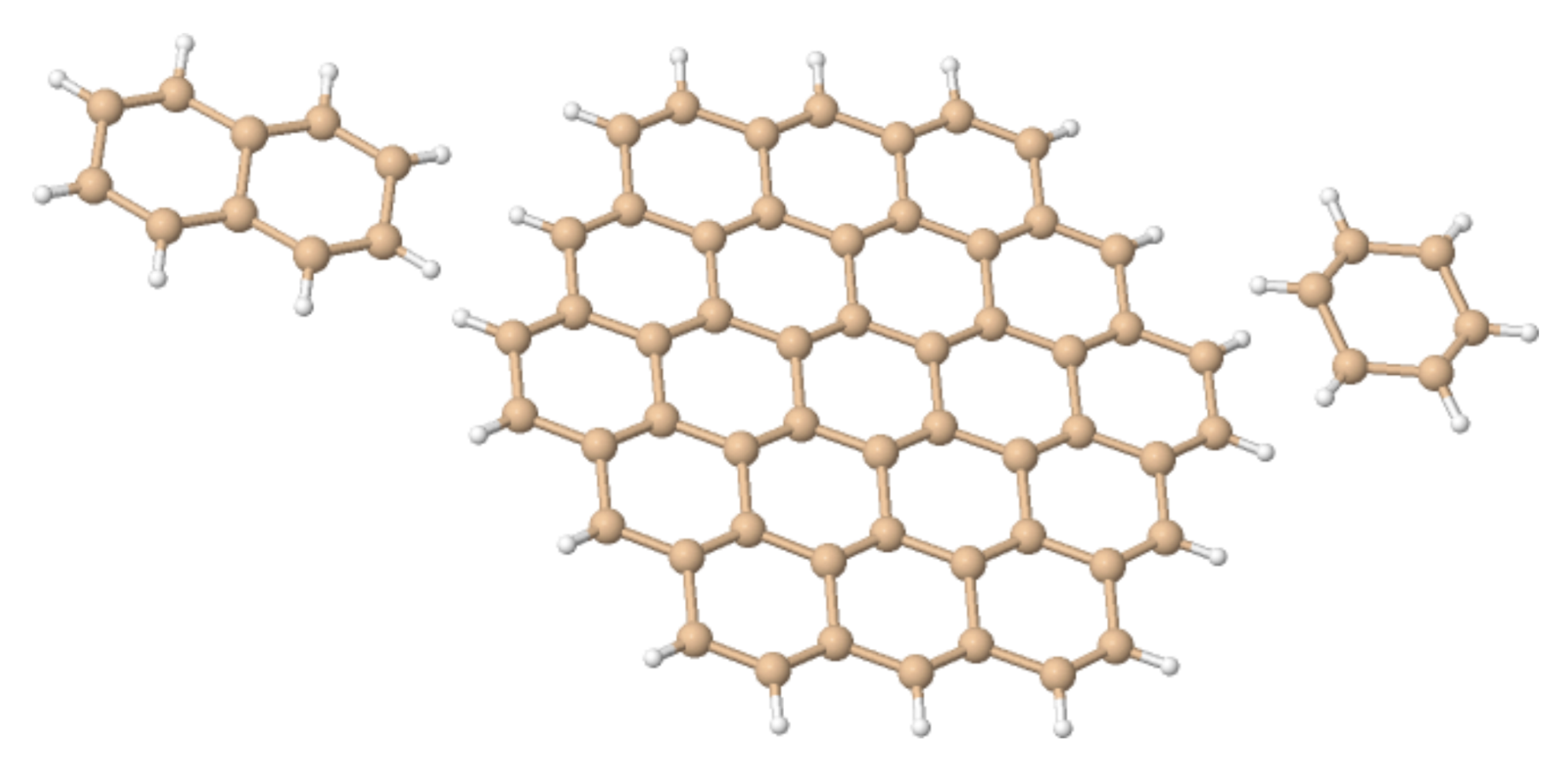
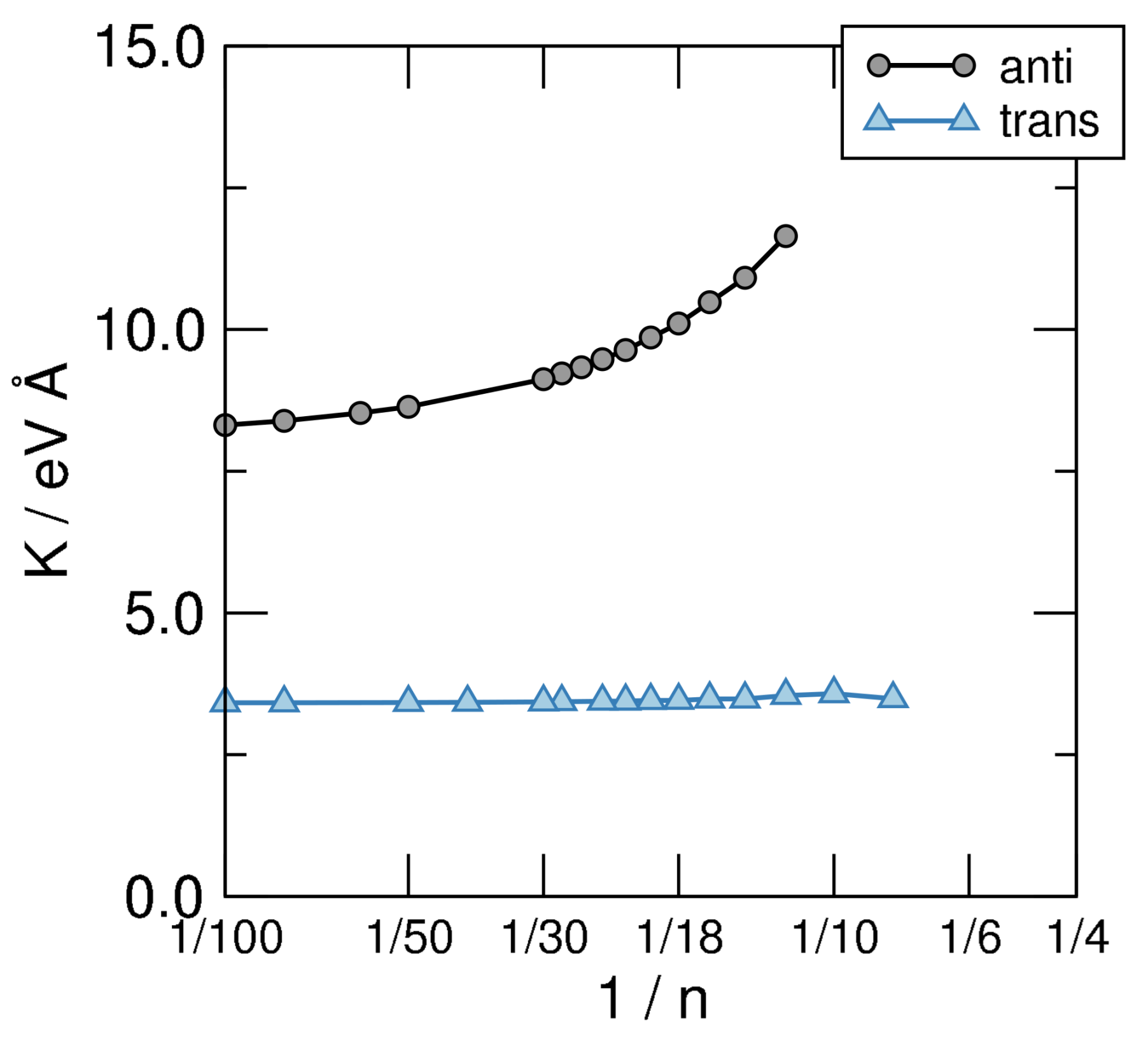
4.1. n-Annulenes
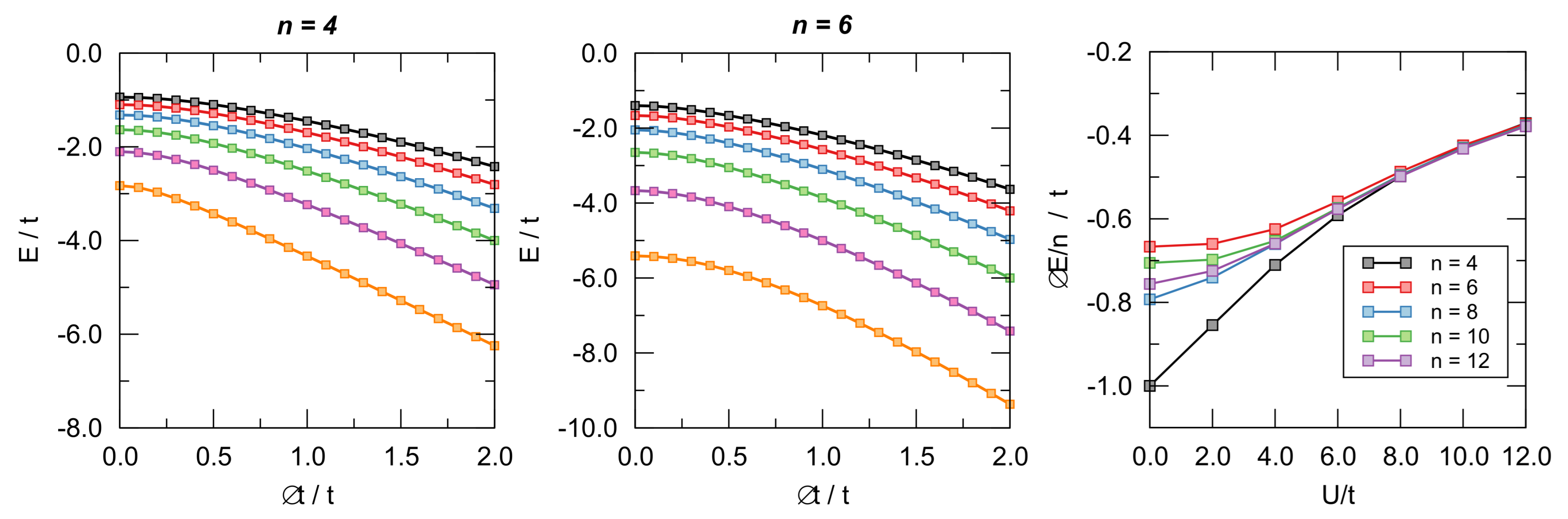
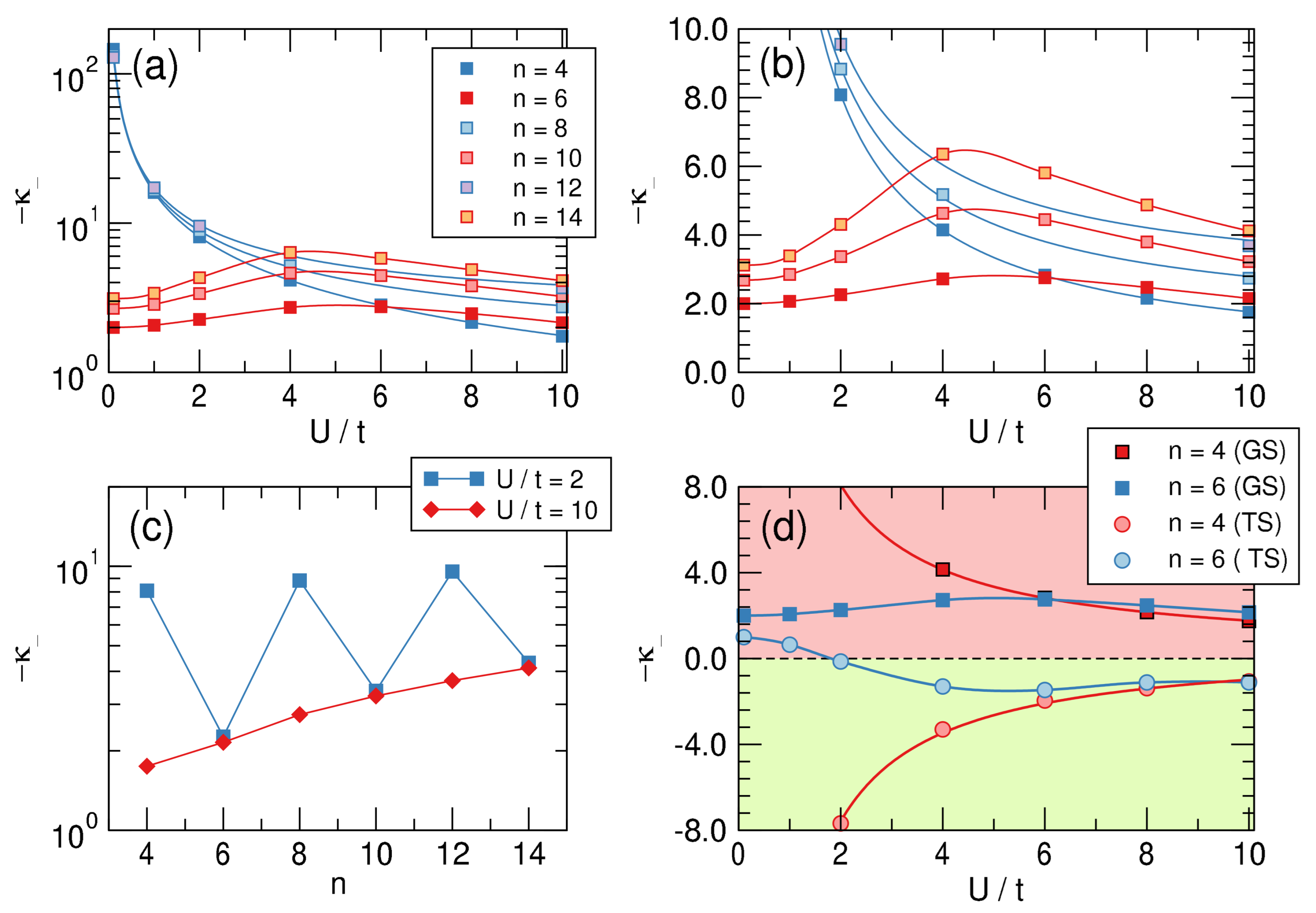
4.2. -Distortivity from Hubbard Calculations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
Abbreviations
| DFT | Density Functional Theory |
| AO | Atomic Orbital |
| MO | Molecular Orbital |
| NBO | Natural Bond Orbital |
| BLA | Bond Length Alternation |
| AE | Atomization Energy |
References
- Anthony, T.R.; Banholzer, W.F.; Fleischer, J.F.; Wei, L.; Kuo, P.K.; Thomas, R.L.; Pryor, R.W. Thermal diffusivity of isotopically enriched 12C diamond. Phys. Rev. B 1990, 42, 1104–1111. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K. The rise of graphene. In Nanoscience and Technology; World Scientific: Singapore, 2009; pp. 11–19. [Google Scholar] [CrossRef]
- Rudnick, R.; Gao, S. 3.01—Composition of the Continental Crust. In Treatise on Geochemistry; Holland, H.D., Turekian, K.K., Eds.; Pergamon: Oxford, UK, 2003; pp. 1–64. [Google Scholar] [CrossRef]
- Petkowski, J.J.; Bains, W.; Seager, S. On the potential of silicon as a building block for life. Life 2020, 10, 84. [Google Scholar] [CrossRef]
- Wen, X.; Cahill, T.; Hoffmann, R. Exploring Group 14 Structures: 1D to 2D to 3D. Chem. Eur. J. 2010, 16, 6555–6566. [Google Scholar] [CrossRef] [PubMed]
- Trinquier, G.; Barthelat, J.C. Structures of X2F4, from carbon to lead. Unsaturation through fluorine bridges in Group 14. J. Am. Chem. Soc. 1990, 112, 9121–9130. [Google Scholar] [CrossRef]
- Carter, E.A.; Goddard, W.A. Relation between singlet-triplet gaps and bond energies. J. Phys. Chem. 1986, 90, 998–1001. [Google Scholar] [CrossRef]
- Davidson, P.J.; Lappert, M.F. Stabilisation of metals in a low co-ordinative environment using the bis(trimethylsilyl)methyl ligand; coloured Sn II and Pb II alkyls, M[CH(SiMe3)2]2. J. Chem. Soc. Chem. Commun. 1973, 317a. [Google Scholar] [CrossRef]
- West, R.; Fink, M.J.; Michl, J. Tetramesityldisilene, a stable compound containing a silicon-silicon double bond. Science 1981, 214, 1343–1344. [Google Scholar] [CrossRef]
- Sekiguchi, A.; Kinjo, R.; Ichinohe, M. A stable compound containing a silicon-silicon triple bond. Science 2004, 305, 1755–1757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sekiguchi, A.; Ichinohe, M.; Kinjo, R. The Chemistry of Disilyne with a Genuine Si-Si Triple Bond: Synthesis, Structure, and Reactivity. Bull. Chem. Soc. Jpn. 2006, 79, 825–832. [Google Scholar] [CrossRef] [Green Version]
- Ishida, S.; Iwamoto, T.; Kabuto, C.; Kira, M. A stable silicon-based allene analogue with a formally sp-hybridized silicon atom. Nature 2003, 421, 725–727. [Google Scholar] [CrossRef] [PubMed]
- Abersfelder, K.; White, A.J.P.; Rzepa, H.S.; Scheschkewitz, D. A Tricyclic Aromatic Isomer of Hexasilabenzene. Science 2010, 327, 564–566. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, K.; Matsuo, T.; Hashizume, D.; Fueno, H.; Tanaka, K.; Tamao, K. A planar rhombic charge-separated tetrasilacyclobutadiene. Science 2011, 331, 1306–1309. [Google Scholar] [CrossRef]
- Power, P.P. π-Bonding and the Lone Pair Effect in Multiple Bonds between Heavier Main Group Elements. Chem. Rev. 1999, 99, 3463–3504. [Google Scholar] [CrossRef]
- Fischer, R.C.; Power, P.P. π-Bonding and the lone pair effect in multiple bonds involving heavier main group elements: Developments in the new millennium. Chem. Rev. 2010, 110, 3877–3923. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xie, Y.; Wei, P.; King, R.B.; Schaefer, H.F.; Schleyer, P.V.R.; Robinson, G.H. A stable silicon(0) compound with a Si=Si double bond. Science 2008, 321, 1069–1071. [Google Scholar] [CrossRef] [PubMed]
- Matsuo, T.; Hayakawa, N. π-Electron systems containing Si=Si double bonds. Sci. Technol. Adv. Mater. 2018, 19, 108–129. [Google Scholar] [CrossRef] [PubMed]
- De Crescenzi, M.; Berbezier, I.; Scarselli, M.; Castrucci, P.; Abbarchi, M.; Ronda, A.; Jardali, F.; Park, J.; Vach, H. Formation of Silicene Nanosheets on Graphite. ACS Nano 2016, 10, 11163–11171. [Google Scholar] [CrossRef]
- Meyer, J.C.; Geim, A.K.; Katsnelson, M.I.; Novoselov, K.S.; Booth, T.J.; Roth, S. The structure of suspended graphene sheets. Nature 2007, 446, 60–63. [Google Scholar] [CrossRef] [PubMed]
- de Heer, W.A.; Berger, C.; Ruan, M.; Sprinkle, M.; Li, X.; Hu, Y.; Zhang, B.; Hankinson, J.; Conrad, E. Large area and structured epitaxial graphene produced by confinement controlled sublimation of silicon carbide. Proc. Natl. Acad. Sci. USA 2011, 108, 16900–16905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Varykhalov, A.; Sánchez-Barriga, J.; Shikin, A.M.; Biswas, C.; Vescovo, E.; Rybkin, A.; Marchenko, D.; Rader, O. Electronic and Magnetic Properties of Quasifreestanding Graphene on Ni. Phys. Rev. Lett. 2008, 101, 157601. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Luican, A.; Andrei, E.Y. Scanning Tunneling Spectroscopy of Graphene on Graphite. Phys. Rev. Lett. 2009, 102, 176804. [Google Scholar] [CrossRef] [Green Version]
- Bansil, A.; Lin, H.; Das, T. Colloquium: Topological band theory. Rev. Mod. Phys. 2016, 88, 021004. [Google Scholar] [CrossRef] [Green Version]
- Vogt, P.; De Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M.C.; Resta, A.; Ealet, B.; Le Lay, G. Silicene: Compelling Experimental Evidence for Graphenelike Two-Dimensional silicon. Phys. Rev. Lett. 2012, 108, 155501. [Google Scholar] [CrossRef] [PubMed]
- Davila, M.E.; Xian, L.; Cahangirov, S.; Rubio, A.; Le Lay, G. Germanene: A novel two-dimensional germanium allotrope akin to graphene and silicene. New J. Phys. 2014, 16, 095002. [Google Scholar] [CrossRef]
- Trinquier, G.; Malrieu, J.P. Nonclassical distortions at multiple bonds. J. Am. Chem. Soc. 1987, 109, 5303–5315. [Google Scholar] [CrossRef]
- Malrieu, J.P.; Trinquier, G. Trans-bending at double bonds. Occurrence and extent. J. Am. Chem. Soc. 1989, 111, 5916–5921. [Google Scholar] [CrossRef]
- Trinquier, G.; Malrieu, J.P. Trans bending at double bonds: Scrutiny of various rationales through valence-bond analysis. J. Phys. Chem. 1990, 94, 6184–6196. [Google Scholar] [CrossRef]
- Jacobsen, H.; Ziegler, T. Nonclassical double bonds in ethylene analogs: Influence of Pauli repulsion on trans bending and. pi.-bond strength. A density functional study. J. Am. Chem. Soc. 1994, 116, 3667–3679. [Google Scholar] [CrossRef]
- Karni, M.; Apeloig, Y.; Kapp, J.; Schleyer, P.v.R. Theoretical Aspects of Compounds Containing Si, Ge, Sn and Pb. In The Chemistry of Organic silicon Compounds. Volume 3 PATAI’S Chemistry of Functional Groups; John Wiley & Sons, Ltd.: Chichester, UK, 2009. [Google Scholar] [CrossRef]
- Zhang, R.; Lee, S.; Law, C.K.; Li, W.K.; Teo, B.K. Silicon nanotubes: Why not? Chem. Phys. Lett. 2002, 364, 251–258. [Google Scholar] [CrossRef]
- Jose, D.; Datta, A. Understanding of the Buckling Distortions in Silicene. J. Phys. Chem. C 2012, 116, 24639–24648. [Google Scholar] [CrossRef]
- Molina, B.; Soto, J.; Castro, J. Pseudo Jahn?Teller effect in the decasilanaphthalene molecule: Towards the origin of the buckling in silicene. Chem. Phys. 2015, 460, 97–100. [Google Scholar] [CrossRef]
- Pizzochero, M.; Bonfanti, M.; Martinazzo, R. To bend or not to bend, the dilemma of multiple bonds. Phys. Chem. Chem. Phys. 2019, 21, 26342–26350. [Google Scholar] [CrossRef] [PubMed]
- Pyykkö, P. On the interpretation of “secondary periodicity” in the periodic system. J. Chem. Res. Synop. 1979, 11, 380–381. [Google Scholar]
- Kutzelnigg, W. Chemical Bonding in Higher Main Group Elements. Angew. Chem. Int. Ed. Engl. 1984, 23, 272–295. [Google Scholar] [CrossRef]
- Danovich, D.; Ogliaro, F.; Karni, M.; Apeloig, Y.; Cooper, D.L.; Shaik, S. Silynes (RCSiR’) and Disilynes (RSiSiR’): Why Are Less Bonds Worth Energetically More? Angew. Chem. Int. Ed. 2002, 40, 4023. [Google Scholar] [CrossRef]
- Ploshnik, E.; Danovich, D.; Hiberty, P.C.; Shaik, S. The Nature of the Idealized Triple Bonds Between Principal Elements and the σ Origins of Trans-Bent Geometries—A Valence Bond Study. J. Chem. Theory Comput. 2011, 7, 955–968. [Google Scholar] [CrossRef]
- Shaik, S.; Shurki, A.; Danovich, D.; Hiberty, P.C. A Different Story of pi-DelocalizationThe Distortivity of pi-Electrons and Its Chemical Manifestations. Chem. Rev. 2001, 101, 1501. [Google Scholar] [CrossRef]
- Longuet-Higgins, H.C.; Salem, L. The alternation of bond lengths in long conjugated chain molecules. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1959, 251, 172–185. [Google Scholar] [CrossRef]
- Shaik, S.; Bar, R. How important is resonance in organic species? Nouv. J. Chim. 1984, 8, 411–420. [Google Scholar]
- Hiberty, P.C.; Shaik, S.S.; Lefour, J.M.; Ohanessian, G. Is the Delocalized π-System of Benzene a Stable Electronic System? J. Org. Chem. 1985, 50, 4657–4659. [Google Scholar] [CrossRef]
- Shaik, S.S.; Hiberty, P.C.; Lefour, J.M.; Ohanessian, G. Is Delocalization a Driving Force in Chemistry? Benzene, Allyl Radical, Cyclobutadiene, and Their Isoelectronic Species. J. Am. Chem. Soc. 1987, 109, 363–374. [Google Scholar] [CrossRef]
- Peierls, R.E. Quantum Theory of Solids; Oxford University Press: Oxford, UK, 1955. [Google Scholar]
- Casari, C.S.; Milani, A. Carbyne: From the elusive allotrope to stable carbon atom wires. MRS Commun. 2018, 8, 207–219. [Google Scholar] [CrossRef]
- Banhart, F. Elemental carbon in the sp 1 hybridization. ChemTexts 2020, 6, 3. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian16 Revision A.03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Weinhold, F.; Landis, C.R. Natural Bond Orbitals and extensions of localized bonding concepts. Chem. Educ. Res. Pract. 2001, 2, 91–104. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R. Discovering Chemistry with Natural Bond Orbitals; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Clauss, A.D.; Nelsen, S.F.; Ayoub, M.; Moore, J.W.; Landis, C.R.; Weinhold, F. Rabbit-ears hybrids, VSEPR sterics, and other orbital anachronisms. Chem. Educ. Res. Pract. 2014, 15, 417–434. [Google Scholar] [CrossRef]
- Slater, J.C.; Koster, G.F. Simplified LCAO Method for the Periodic Potential Problem. Phys. Rev. 1954, 94, 1498–1524. [Google Scholar] [CrossRef]
- Porezag, D.; Frauenheim, T.; Köhler, T.; Seifert, G.; Kaschner, R. Construction of tight-binding-like potentials on the basis of density-functional theory: Application to carbon. Phys. Rev. B 1995, 51, 12947–12957. [Google Scholar] [CrossRef]
- Frauenheim, T.; Weich, F.; Köhler, T.; Uhlmann, S.; Porezag, D.; Seifert, G. Density-functional-based construction of transferable nonorthogonal tight-binding potentials for Si and SiH. Phys. Rev. B 1995, 52, 11492–11501. [Google Scholar] [CrossRef]
- Wehling, T.O.; Siasoglu, E.; Friedrich, C.; Lichtenstein, A.I.; Katsnelson, M.I.; Blugel, S. Strength of Effective Coulomb Interactions in Graphene and Graphite. Phys. Rev. Lett. 2011, 106, 236805. [Google Scholar] [CrossRef]
- Kawamura, M.; Yoshimi, K.; Misawa, T.; Yamaji, Y.; Todo, S.; Kawashima, N. Quantum lattice model solver HΦ. Comput. Phys. Commun. 2017, 217, 180–192. [Google Scholar] [CrossRef]
- Kami, M.; Apeloig, Y. Substituent Effects on the Geometries and Energies of the SiSi Double Bond. J. Am. Chem. Soc. 1990, 112, 8589–8590. [Google Scholar] [CrossRef]
- Andrew Taton, T.; Chen, P. A Stable Tetraazafulvalene. Angew. Chem. (Int. Ed. Engl.) 1996, 35, 1011–1013. [Google Scholar] [CrossRef]
- Karni, M.; Apeloig, Y.; Kapp, J.; von Rague Schleyer, P. Theoretical Aspects of Compounds Containing Si, Ge, Sn and Pb; John Wiley & Sons, Ltd.: New York, NY, USA, 2003; Volume 34. [Google Scholar] [CrossRef]
- Liu, M.; Artyukhov, V.I.; Lee, H.; Xu, F.; Yakobson, B.I. Carbyne from first principles: Chain of c atoms, a nanorod or a nanorope. ACS Nano 2013, 7, 10075–10082. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haas, Y.; Zilberg, S. The V14(b2u) Mode of Benzene in S0 and S1 and the Distortive Nature of the πElectron System: Theory and Experiment. J. Am. Chem. Soc. 1995, 117, 5387–5388. [Google Scholar] [CrossRef]
- Shaik, S.; Shurki, A.; Danovich, D.; Hiberty, P.C. Origins of the Exalted b 2u Frequency in the First Excited State of Benzene. J. Am. Chem. Soc. 1996, 118, 666–671. [Google Scholar] [CrossRef]
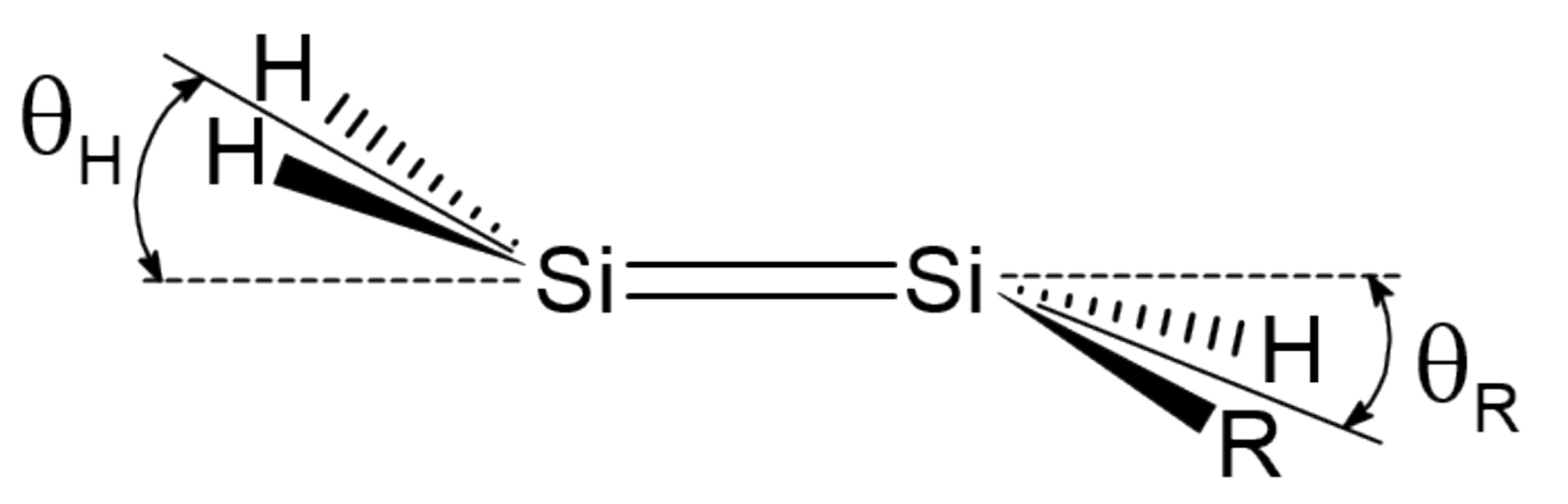


| h/Å | SiH | SiH | SiH |
|---|---|---|---|
| HF | 0.18 | 0.17 | 0.18 |
| PBE | 0.45 | 0.44 | 0.46 |
| B3LYP | 0.43 | 0.41 | 0.42 |
| M06L | 0.40 | 0.38 | 0.38 |
| M06 | 0.48 | 0.49 | 0.51 |
| M062X | 0.37 | 0.40 | 0.42 |
| M06HF | 0.33 | 0.43 | 0.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cappelletti, M.; Leccese, M.; Cococcioni, M.; Proserpio, D.M.; Martinazzo, R. The Different Story of π Bonds. Molecules 2021, 26, 3805. https://doi.org/10.3390/molecules26133805
Cappelletti M, Leccese M, Cococcioni M, Proserpio DM, Martinazzo R. The Different Story of π Bonds. Molecules. 2021; 26(13):3805. https://doi.org/10.3390/molecules26133805
Chicago/Turabian StyleCappelletti, Marco, Mirko Leccese, Matteo Cococcioni, Davide M. Proserpio, and Rocco Martinazzo. 2021. "The Different Story of π Bonds" Molecules 26, no. 13: 3805. https://doi.org/10.3390/molecules26133805
APA StyleCappelletti, M., Leccese, M., Cococcioni, M., Proserpio, D. M., & Martinazzo, R. (2021). The Different Story of π Bonds. Molecules, 26(13), 3805. https://doi.org/10.3390/molecules26133805