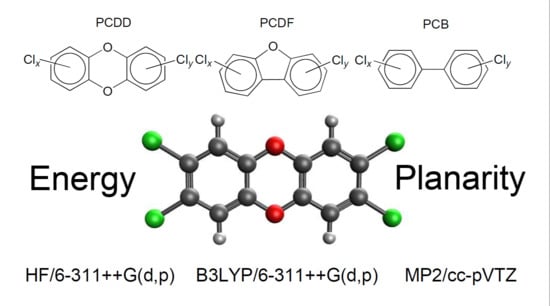
Quantum Chemical Investigation of Polychlorinated Dibenzodioxins, Dibenzofurans and Biphenyls: Relative Stability and Planarity Analysis
Abstract
1. Introduction
2. Results
2.1. Relative Stability
2.2. Isomer Distribution
2.3. Planarity
| PCDD | PCDF | PCB | |||
| Ca,Cc,Cd,Ch Cb,Cd,Cc,Cg Ca,Ce,Cf,Ch Cb,Cf,Ce,Cg | Ca,Cd,Cf,Cg Cb,Cc,Ce,Ch | Ci,Ck,Cl,Cp Cj,Cl,Ck,Co Ci,Cm,Cn,Cp Ci,Cn,Cm,Co | Ci,Cl,Cn,Co Cj,Ck,Cm,Cp | Cq,Cs,Ct,Cu Cq,Cs,Ct,Cv Cr,Cs,Ct,Cu Cr,Cs,Ct,Cv | |
2.4. Toxicity
- The twelve known dioxin-like PCBs with TEF values are among the ones with relatively small dihedral angles or are closer to being planar.
- According to the B3LYP and MP2 results, there are three non-coplanar PCDDs (PCDDs-46, 65, and 71) from both methods, and two additional (PCDDs-42 and 45) from B3LYP only. All of these are not substituted at all four lateral positions (2,3,7,8), which are the substitution positions of PCDDs known to be toxic [2]. One of these, PCDD-46, is substituted at positions exactly opposite to that of 2,3,7,8-tetrachlorodibenzodioxin (TCDD), the most toxic dioxin-like compound [2].
3. Discussion, Conclusions and Future Work
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations. Treaties and International Agreements Registered or Filed and Recorded with the Secretariat of the United Nations; United Nations: New York, NY, USA, 2006. [Google Scholar]
- Van den Berg, M.; Birnbaum, L.S.; Denison, M.; De Vito, M.; Farland, W.; Feeley, M.; Fiedler, H.; Hakansson, H.; Hanberg, A.; Haws, L.; et al. The 2005 World Health Organization reevaluation of human and mammalian toxic equivalency factors for dioxins and dioxin-like compounds. Toxicol. Sci. 2006, 93, 223–241. [Google Scholar] [CrossRef]
- European Commission. Commission Regulation (EC) No 1881/2006 of 19 December 2006 setting maximum levels for certain contaminants in foodstuffs. Off. J. Eur. Union 2006, 364, 5–24. [Google Scholar]
- Arulmozhiraja, S.; Fujii, T.; Tokiwa, H. Electron affinity for the most toxic 2,3,7,8-tetrachlorodibenzo-p-dioxin (TCDD): A density functional theory study. J. Phys. Chem. A 2000, 104, 7068–7072. [Google Scholar] [CrossRef]
- Dorofeeva, O.V.; Moiseeva, N.F.; Yungman, V.S.; Novikov, V.P. Ideal gas thermodynamic properties of biphenyl. Thermochim. Acta 2001, 374, 7–11. [Google Scholar] [CrossRef]
- Iino, F.; Tsuchiya, K.; Imagawa, T.; Gullett, B.K. An isomer prediction model for PCNs, PCDD/Fs, and PCBs from municipal waste incinerators. Environ. Sci. Technol. 2001, 35, 3175–3181. [Google Scholar] [CrossRef]
- Arulmozhiraja, S.; Fujii, T.; Morita, M. Density functional theory studies on radical ions of selected polychlorinated biphenyls. J. Phys. Chem. A 2002, 106, 10590–10595. [Google Scholar] [CrossRef]
- Chana, A.; Concejero, M.A.; de Frutos, M.; González, M.J.; Herradón, B. Computational studies on biphenyl derivatives. Analysis of the conformational mobility, molecular electrostatic potential, and dipole moment of chlorinated biphenyl: Searching for the rationalization of the selective toxicity of polychlorinated biphenyls (PCBs). Chem. Res. Toxicol. 2002, 15, 1514–1526. [Google Scholar] [CrossRef]
- León, L.A.; Notario, R.; Quijano, J.; Sánchez, C. Structures and enthalpies of formation in the gas phase of the most toxic polychlorinated dibenzo-p-dioxins. A DFT study. J. Phys. Chem. A 2002, 106, 6618–6627. [Google Scholar] [CrossRef]
- Dorofeeva, O.V.; Yungman, V.S. Enthalpies of formation of dibenzo-p-dioxin and polychlorinated dibenzo-p-dioxins calculated by density functional theory. J. Phys. Chem. A 2003, 107, 2848–2854. [Google Scholar] [CrossRef]
- Lee, J.-E.; Choi, W. DFT calculation on the electron affinity of polychlorinated dibenzo-p-dioxins. Bull. Korean Chem. Soc. 2003, 24, 792–796. [Google Scholar] [CrossRef][Green Version]
- Lee, J.E.; Choi, W.; Mhin, B.J. DFT calculation on the thermodynamic properties of polychlorinated dibenzo-p-dioxins: intramolecular Cl−Cl repulsion effects and their thermochemical implications. J. Phys. Chem. A 2003, 107, 2693–2699. [Google Scholar] [CrossRef]
- Arulmozhiraja, S.; Morita, M. Electron affinities and reductive dechlorination of toxic polychlorinated dibenzofurans: A density functional theory study. J. Phys. Chem. A 2004, 108, 3499–3508. [Google Scholar] [CrossRef]
- Dorofeeva, O.V.; Moiseeva, N.F.; Yungman, V.S. Thermodynamic properties of polychlorinated biphenyls in the gas phase. J. Phys. Chem. A 2004, 108, 8324–8332. [Google Scholar] [CrossRef]
- Ryu, J.-Y.; Mulholland, J.A.; Dunn, J.E.; Iino, F.; Gullett, B.K. Potential role of chlorination pathways in PCDD/F formation in a municipal waste incinerator. Environ. Sci. Technol. 2004, 38, 5112–5119. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Zhai, Z.-C.; Wang, L.-S.; Chen, J.-L.; Kikuchi, O.; Watanabe, T. Prediction of gas phase thermodynamic function of polychlorinated dibenzo-p-dioxins using DFT. J. Mol. Struc. Theochem 2004, 672, 97–104. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Zhai, Z.-C.; Wang, L.-S. Prediction of gas phase thermodynamic properties of polychlorinated dibenzo-furans by DFT. J. Mol. Struc. Theochem 2005, 725, 55–62. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Han, X.Y.; Zhai, Z.C.; Wang, L.S. Study on the thermodynamic property and relative stability of a series of polychlorinated biphenyls by density functional theory. Acta Chim. Sinica 2005, 63, 964–972. [Google Scholar]
- Zhai, Z.-C.; Wang, Z.-Y.; Chen, X.-H.; Wang, L.-S. DFT calculation on 204 polychlorinated biphenyls: Their thermodynamic function and implication of Cl substitute position. J. Mol. Struc. Theochem 2005, 714, 123–131. [Google Scholar] [CrossRef]
- Dorofeeva, O.V.; Vishnevskiy, Y.V.; Moiseeva, N.F. Assessment of Gaussian-3X theory for chlorinated organic molecules. Enthalpies of formation of chlorobenzenes and predictions for polychlorinated aromatic compounds. Struct. Chem. 2006, 17, 383–392. [Google Scholar] [CrossRef]
- Thompson, D.; Ewan, B.C.R. A group additivity algorithm for polychlorinated dibenzofurans derived from selected DFT analyses. J. Phys. Chem. A 2007, 111, 5043–5047. [Google Scholar] [CrossRef]
- Wang, L.; Heard, D.E.; Pilling, M.J.; Seakins, P. A Gaussian-3X prediction on the enthalpies of formation of chlorinated phenols and dibenzo-p-dioxins. J. Phys. Chem. A 2008, 112, 1832–1840. [Google Scholar] [CrossRef] [PubMed]
- Jansson, S.; Antti, H.; Marklund, S.; Tysklind, M. Multivariate relationships between molecular descriptors and isomer distribution patterns of PCDD/Fs formed during MSW combustion. Environ. Sci. Technol. 2009, 43, 7032–7038. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; He, Y.-L. The enthalpies of formation for polychlorinated dibenzofurans with use of G3XMP2 model chemistry and density functional theory. J. Phys. Chem. A 2009, 113, 238–245. [Google Scholar] [CrossRef] [PubMed]
- Ewan, B.C.R.; Thompson, D. Predicted specific heat behaviour of the polychlorinated dibenzofuran family from DFT analysis. Thermochim. Acta 2013, 558, 46–52. [Google Scholar] [CrossRef]
- Jansson, S.; Grabic, R. Multivariate relationships between molecular descriptors and isomer distribution patterns of PCBs formed during household waste incineration. Environ. Sci. Pollut. Res. 2014, 21, 3082–3090. [Google Scholar] [CrossRef]
- Zhou, Q.; Su, X.; Yong, Y.; Ju, W.; Fu, Z.; Li, X. Adsorption of 2, 3, 7, 8-tetrachlorodibenzao-p-dioxin (TCDD) on graphane decorated with Ni and Cu: A DFT study. Vacuum 2018, 149, 53–59. [Google Scholar] [CrossRef]
- Abronin, I.A.; Volkova, L.V. On the relationship between the energy characteristics of the isodesmic reactions of polychlorinated dioxins and their toxicity. Russ. Chem. Bull. 2019, 68, 867–869. [Google Scholar] [CrossRef]
- Bai, N.; Wang, W.; Zhao, Y.; Feng, W.; Li, P. Theoretical insights into the reaction mechanism between 2,3,7,8-tetrachlorodibenzofuran and hydrogen peroxide: A DFT study. ACS Omega 2019, 4, 358–367. [Google Scholar] [CrossRef]
- Hou, S.; Altarawneh, M.; Kennedy, E.M.; Mackie, J.C.; Weber, R.; Dlugogorski, B.Z. Formation of polychlorinated dibenzo-p-dioxins and dibenzofurans (PCDD/F) from oxidation of 4,4′-dichlorobiphenyl (4,4′-DCB). Proc. Combust. Inst. 2019, 37, 1075–1082. [Google Scholar] [CrossRef]
- Behjatmanesh-Ardakani, R.; Heydari, A. Molecular and dissociative adsorption of tetrachlorodibenzodioxin on M-doped graphenes (M = B, Al, N, P): Pure DFT and DFT + VdW calculations. J. Mol. Model. 2020, 26, 164. [Google Scholar] [CrossRef]
- Diao, J.; Li, Y.; Shi, S.; Sun, Y.; Sun, Y. QSAR models for predicting toxicity of polychlorinated dibenzo-p-dioxins and dibenzofurans using quantum chemical descriptors. Bull. Environ. Contam. Toxicol. 2010, 85, 109–115. [Google Scholar] [CrossRef]
- Larsson, M.; Kumar Mishra, B.; Tysklind, M.; Linusson, A.; Andersson, P.L. On the use of electronic descriptors for QSAR modelling of PCDDs, PCDFs and dioxin-like PCBs. SAR QSAR Environ. Res. 2013, 24, 461–479. [Google Scholar] [CrossRef]
- Hirano, M.; Hwang, J.-H.; Park, H.-J.; Bak, S.-M.; Iwata, H.; Kim, E.-Y. In silico analysis of the interaction of avian aryl hydrocarbon receptors and dioxins to decipher isoform-, ligand-, and species-specific activations. Environ. Sci. Technol. 2015, 49, 3795–3804. [Google Scholar] [CrossRef]
- Larsson, M.; Fraccalvieri, D.; Andersson, C.D.; Bonati, L.; Linusson, A.; Andersson, P.L. Identification of potential aryl hydrocarbon receptor ligands by virtual screening of industrial chemicals. Environ. Sci. Pollut. Res. 2018, 25, 2436–2449. [Google Scholar] [CrossRef]
- Zeinali, N.; Oluwoye, I.; Altarawneh, M.; Dlugogorski, B.Z. Destruction of dioxin and furan pollutants via electrophilic attack of singlet oxygen. Ecotoxicol. Environ. Saf. 2019, 184, 109605. [Google Scholar] [CrossRef]
- Ballschmiter, K.; Buchert, H.; Niemczyk, R.; Munder, A.; Swerev, M. Automobile exhausts versus municipal-waste incineration as sources of the polychloro-dibenzodioxins (PCDD) and -furans (PCDF) found in the environment. Chemosphere 1986, 15, 901–915. [Google Scholar] [CrossRef]
- Agudo, A.; Aronson, K.J.; Bonefeld-Jorgensen, E.C.; Cocco, P.; Cogliano, V.; Cravedi, J.-P.; Esch, H.; Fiedler, H.; Glauert, H.P.; Guo, Y.-L.L. Polychlorinated Biphenyls and Polybrominated Biphenyls; International Agency for Research on Cancer: Lyon, France, 2016. [Google Scholar]
- Ballschmiter, K.; Zell, M. Analysis of polychlorinated biphenyls (PCB) by glass capillary gas chromatography. Fresenius Z. Anal. Chem. 1980, 302, 20–31. [Google Scholar] [CrossRef]
- Dickson, L.C.; Lenoir, D.; Hutzinger, O. Quantitative comparison of de novo and precursor formation of polychlorinated dibenzo-p-dioxins under simulated municipal solid waste incinerator postcombustion conditions. Environ. Sci. Technol. 1992, 26, 1822–1828. [Google Scholar] [CrossRef]
- Tiernan, T.O.; Taylor, M.L.; Garrett, J.H.; VanNess, G.F.; Solch, J.G.; Deis, D.A.; Wagel, D.J. Chlorodibenzodioxins, chlorodibenzofurans and related compounds in the effluents from combustion processes. Chemosphere 1983, 12, 595–606. [Google Scholar] [CrossRef]
- Schwartz, T.R.; Campbell, R.D.; Stalling, D.L.; Little, R.L.; Petty, J.D.; Hogan, J.W.; Kaiser, E.M. Laboratory data base for isomer-specific determination of polychlorinated biphenyls. Anal. Chem. 1984, 56, 1303–1308. [Google Scholar] [CrossRef]
- Ballschmiter, K.; Swerev, M. Reaction pathways for the formation of polychlorodibenzodioxins (PCDD) and -furans (PCDF) in combustion processes I. Fresenius Z. Anal. Chem. 1987, 328, 125–127. [Google Scholar] [CrossRef]
- Yasuhara, A.; Ito, H.; Morita, M. Isomer-Specific Determination of polychlorinated dibenzo-p-dioxins and dibenzofurans in incinerator-related environmental samples. Environ. Sci. Technol. 1987, 21, 971–979. [Google Scholar] [CrossRef]
- Faroon, O.M.; Samuel Keith, L.; Smith-Simon, C.; De Rosa, C.T. Polychlorinated Biphenyls: Human Health Aspects; World Health Organization: Geneva, Switzerland, 2003. [Google Scholar]
- Hanari, N.; Horii, Y.; Okazawa, T.; Falandysz, J.; Bochentin, I.; Orlikowska, A.; Puzyn, T.; Wyrzykowska, B.; Yamashita, N. Dioxin-like compounds in pine needles around Tokyo Bay, Japan in 1999. J. Environ. Monit. 2004, 6, 305–312. [Google Scholar] [CrossRef]
- Kim, K.S.; Hirai, Y.; Kato, M.; Urano, K.; Masunaga, S. Detailed PCB congener patterns in incinerator flue gas and commercial PCB formulations (Kanechlor). Chemosphere 2004, 55, 539–553. [Google Scholar] [CrossRef]
- Haws, L.C.; Su, S.H.; Harris, M.; DeVito, M.J.; Walker, N.J.; Farland, W.H.; Finley, B.; Birnbaum, L.S. Development of a refined database of mammalian relative potency estimates for dioxin-like compounds. Toxicol. Sci. 2006, 89, 4–30. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Noma, Y.; Yamamoto, T.; Mori, Y.; Sakai, S.-i. PCB decomposition and formation in thermal treatment plant equipment. Chemosphere 2007, 67, 1383–1393. [Google Scholar] [CrossRef]
- Srogi, K. Levels and congener distributions of PCDDs, PCDFs and dioxin-like PCBs in environmental and human samples: A review. Environ. Chem. Lett. 2008, 6, 1–28. [Google Scholar] [CrossRef]
- Sundqvist, K.L.; Tysklind, M.; Geladi, P.; Hopke, P.K.; Wiberg, K. PCDD/F source apportionment in the Baltic sea using positive matrix factorization. Environ. Sci. Technol. 2010, 44, 1690–1697. [Google Scholar] [CrossRef]
- Jansson, S.; Lundin, L.; Grabic, R. Characterisation and fingerprinting of PCBs in flue gas and ash from waste incineration and in technical mixtures. Chemosphere 2011, 85, 509–515. [Google Scholar] [CrossRef]
- Barahona-Urbina, C.; Nunez-Gonzalez, S.; Gomez-Jeria, J.S. Model-based quantum-chemical study of the uptake of some polychlorinated pollutant compounds by zucchini subspecies. J. Chil. Chem. Soc. 2012, 57, 1497–1503. [Google Scholar] [CrossRef][Green Version]
- Hinwood, A.L.; Callan, A.C.; Heyworth, J.; Rogic, D.; de Araujo, J.; Crough, R.; Mamahit, G.; Piro, N.; Yates, A.; Stevenson, G.; et al. Polychlorinated biphenyl (PCB) and dioxin concentrations in residential dust of pregnant women. Environ. Sci. Process. Impacts 2014, 16, 2758–2763. [Google Scholar] [CrossRef]
- Thompson, D.; Ooi, T.C.; Anderson, D.R.; Fisher, R.; Ewan, B.C.R. The polychlorinated dibenzofuran fingerprint of iron ore sinter plant: Its persistence with suppressant and alternative fuel addition. Chemosphere 2016, 154, 138–147. [Google Scholar] [CrossRef]
- Huang, R.; Wang, P.; Zhang, J.; Chen, S.; Zhu, P.; Huo, W.; Jiang, Y.; Chen, Z.; Peng, J. The human body burden of polychlorinated dibenzo-p-dioxins/furans (PCDD/Fs) and dioxin-like polychlorinated biphenyls (DL-PCBs) in residents’ human milk from Guangdong Province, China. Toxicol. Res. 2019, 8, 552–559. [Google Scholar] [CrossRef]
- The Eightieth Meeting of the Joint FAO/WHO Expert Committee on Food Additives (JECFA). Safety Evaluation of Certain Food Additives and Contaminants, Supplement 1: Non-Dioxin-Like Polychlorinated Biphenyls; World Health Organization: Geneva, Switzerland, 2016. [Google Scholar]
- Datta, S.; Limpanuparb, T. Geometric and energetic data from quantum chemical calculations of halobenzenes and xylenes. Data Brief 2020, 30, 105386. [Google Scholar] [CrossRef]
- Limpanuparb, T.; Datta, S.; Chinsukserm, K.; Teeraniramitr, P. In silico geometric and energetic data of all possible simple rotamers made of non-metal elements. Data Brief 2020, 30, 105442. [Google Scholar] [CrossRef]
- Chinsukserm, K.; Lorpaiboon, W.; Teeraniramitr, P.; Limpanuparb, T. Geometric and energetic data from ab initio calculations of haloethene, haloimine, halomethylenephosphine, haloiminophosphine, halodiazene, halodiphosphene and halocyclopropane. Data Brief 2019, 27, 104738. [Google Scholar] [CrossRef]
- Riley, K.E.; Hobza, P. Assessment of the MP2 method, along with several basis sets, for the computation of interaction energies of biologically relevant hydrogen bonded and dispersion bound complexes. J. Phys. Chem. A 2007, 111, 8257–8263. [Google Scholar] [CrossRef]
- Shao, Y.; Gan, Z.; Epifanovsky, E.; Gilbert, A.T.; Wormit, M.; Kussmann, J.; Lange, A.W.; Behn, A.; Deng, J.; Feng, X. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015, 113, 184–215. [Google Scholar] [CrossRef]
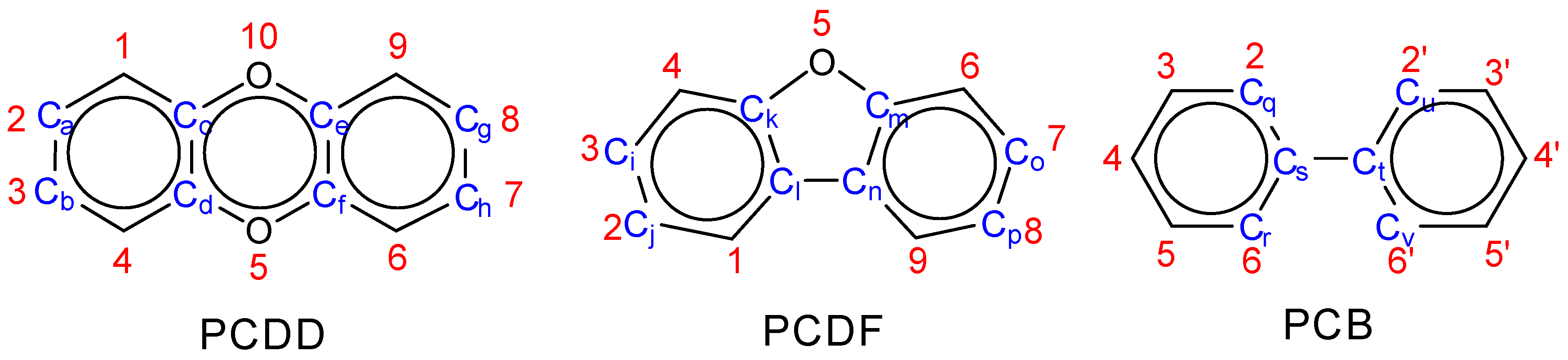
| Substitution Positions | Substituent Pair | PCDD | PCDF | PCB |
|---|---|---|---|---|
| Intra-Ring Interactions | ||||
| o- | Cl-Cl | 0–6 1 | 0–6 | 0–8 |
| Cl-O | 0–4 | 0–2 | N/A | |
| Cl-C | N/A | 0–2 | 0–4 | |
| Total | 0–10 | 0–10 | 0–12 | |
| m- | Cl-Cl | 0–4 | 0–4 | 0–8 |
| Cl-O | 0–8 | 0–4 | N/A | |
| Cl-C | N/A | 0–4 | 0–4 | |
| Total | 0–12 | 0–12 | 0–12 | |
| p- | Cl-Cl | 0–2 | 0–2 | 0–4 |
| Cl-O | 0–4 | 0–2 | N/A | |
| Cl-C | N/A | 0–2 | 0–2 | |
| Total | 0–6 | 0–6 | 0–6 | |
| Cross-ring interactions | ||||
| Over O-bridge | Cl-Cl | 0–2 2 | 0–1 3 | N/A |
| Over C-C bond | N/A | 0–1 3 | 0–4 4 | |
| PCDD | HF | B3LYP | MP2 | |||
|---|---|---|---|---|---|---|
| Parameters | CR- | O | CR- | O | CR- | O |
| p- | Cl-Cl | p- | Cl-Cl | p- | Cl-Cl | |
| m- | Cl-Cl | m- | Cl-Cl | m- | Cl-Cl | |
| o- | Cl-Cl | o- | Cl-Cl | o- | Cl-Cl | |
| o- | total | o- | total | o- | total | |
| total H | total H | total H | ||||
| ρ | 0.9998 | 0.9997 | 0.9996 | |||
| PCDF | HF | B3LYP | MP2 | |||
| Parameters | p- | Cl-O | m- | Cl-Cl | m- | Cl-Cl |
| m- | Cl-Cl | p- | Cl-O | p- | Cl-Cl | |
| o- | Cl-O | o- | Cl-O | p- | Cl-O | |
| o- | Cl-Cl | o- | Cl-Cl | o- | Cl-O | |
| CR- | C | CR- | C | o- | Cl-Cl | |
| total H | o- | total | CR- | C | ||
| total H | total H | |||||
| ρ | 0.9997 | 0.9962 | 0.9978 | |||
| PCB | HF | B3LYP | MP2 | |||
| Parameters | p- | total | m- | total | p- | total |
| m- | total | o- | Cl-Cl | m- | total | |
| o- | Cl-Cl | o- | total | o- | Cl-Cl | |
| o- | total | total H | total H | |||
| total H | ||||||
| ρ | 0.9993 | 0.9990 | 0.9978 | |||
| Coefficients | R | ρ | |||||
|---|---|---|---|---|---|---|---|
| C0 | C1 | C2 | C3 | C4 | |||
| HF | 50.858 | 20.325 | −10.751 | 0.724 | N/A | 0.9354 | 0.8735 |
| B3LYP | 37.926 | 24.996 | −11.419 | 0.529 | N/A | 0.9552 | 0.9599 |
| MP2 | 33.308 | 24.202 | −9.499 | 0.668 | −0.529 | 0.9800 | 0.9560 |
Sample Availability: Samples of the compounds are not available from the authors. | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Datta, S.; Limpanuparb, T. Quantum Chemical Investigation of Polychlorinated Dibenzodioxins, Dibenzofurans and Biphenyls: Relative Stability and Planarity Analysis. Molecules 2020, 25, 5697. https://doi.org/10.3390/molecules25235697
Datta S, Limpanuparb T. Quantum Chemical Investigation of Polychlorinated Dibenzodioxins, Dibenzofurans and Biphenyls: Relative Stability and Planarity Analysis. Molecules. 2020; 25(23):5697. https://doi.org/10.3390/molecules25235697
Chicago/Turabian StyleDatta, Sopanant, and Taweetham Limpanuparb. 2020. "Quantum Chemical Investigation of Polychlorinated Dibenzodioxins, Dibenzofurans and Biphenyls: Relative Stability and Planarity Analysis" Molecules 25, no. 23: 5697. https://doi.org/10.3390/molecules25235697
APA StyleDatta, S., & Limpanuparb, T. (2020). Quantum Chemical Investigation of Polychlorinated Dibenzodioxins, Dibenzofurans and Biphenyls: Relative Stability and Planarity Analysis. Molecules, 25(23), 5697. https://doi.org/10.3390/molecules25235697