Thermoelectric Properties of InA Nanowires from Full-Band Atomistic Simulations
Abstract
1. Introduction
2. Theoretical and Computational Method
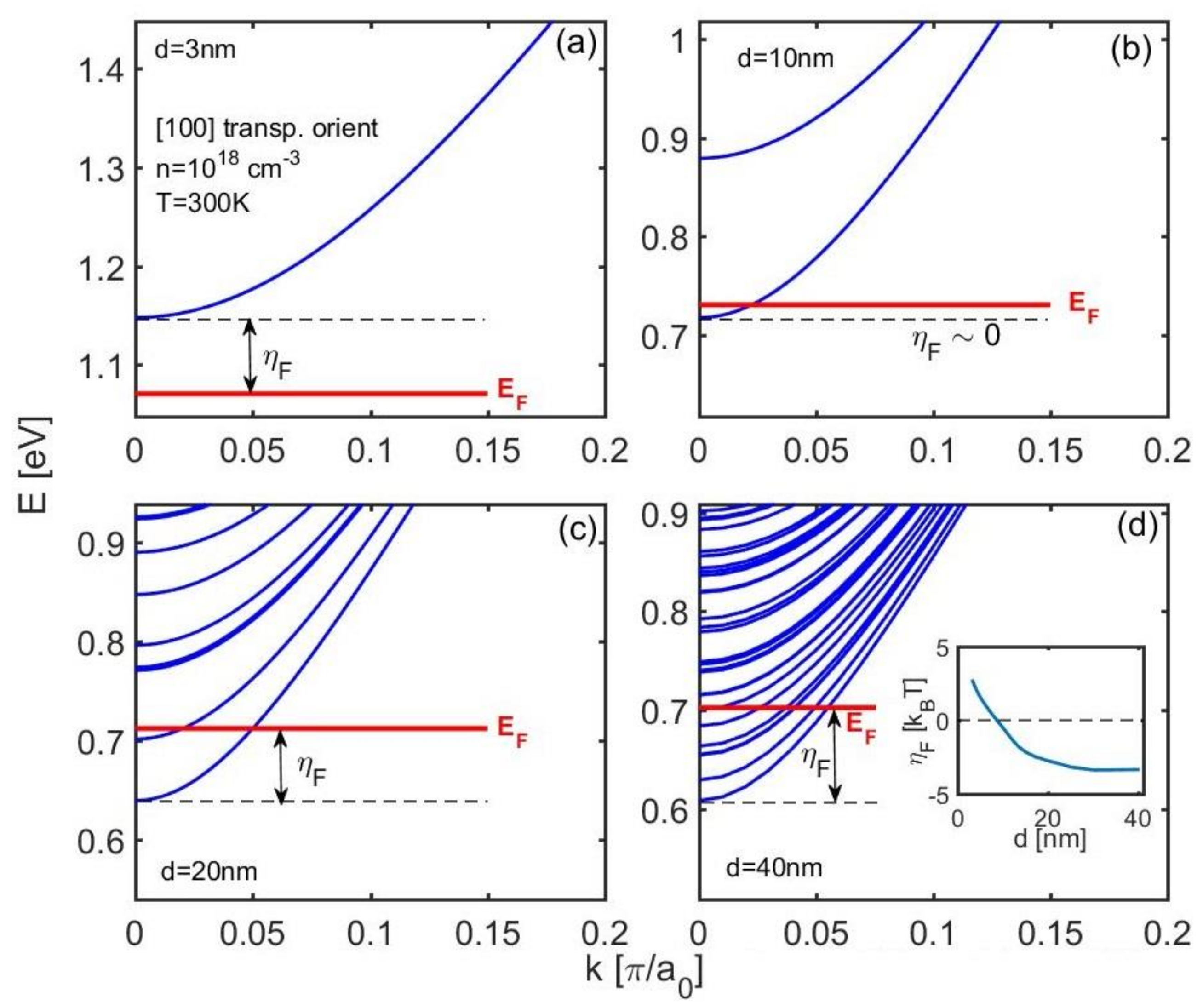
2.1. Bandstructure Features under Confinement
2.2. Transport Theory–Linearized BTE Formalism
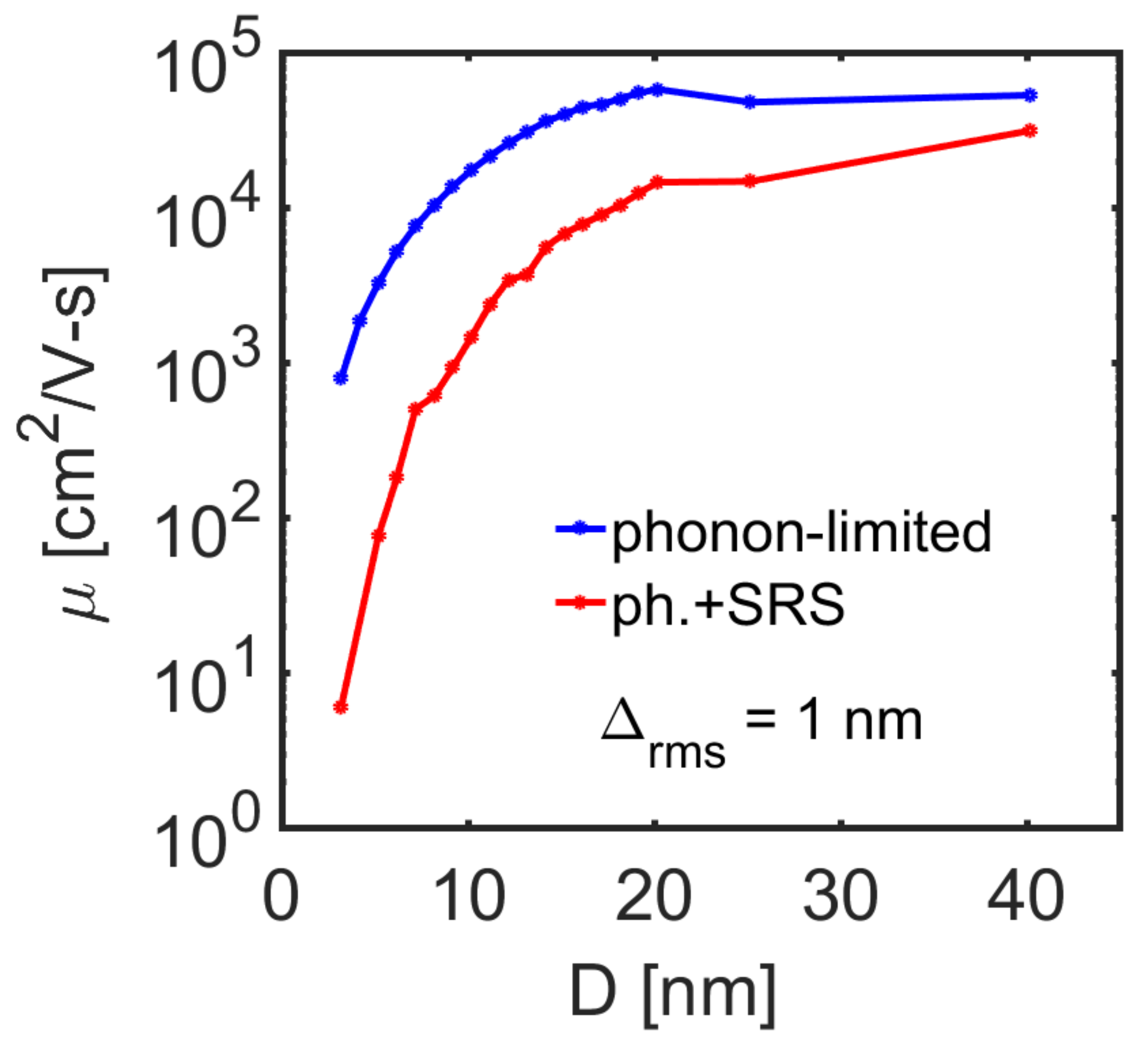
2.3. Calibration to Bulk Mobility
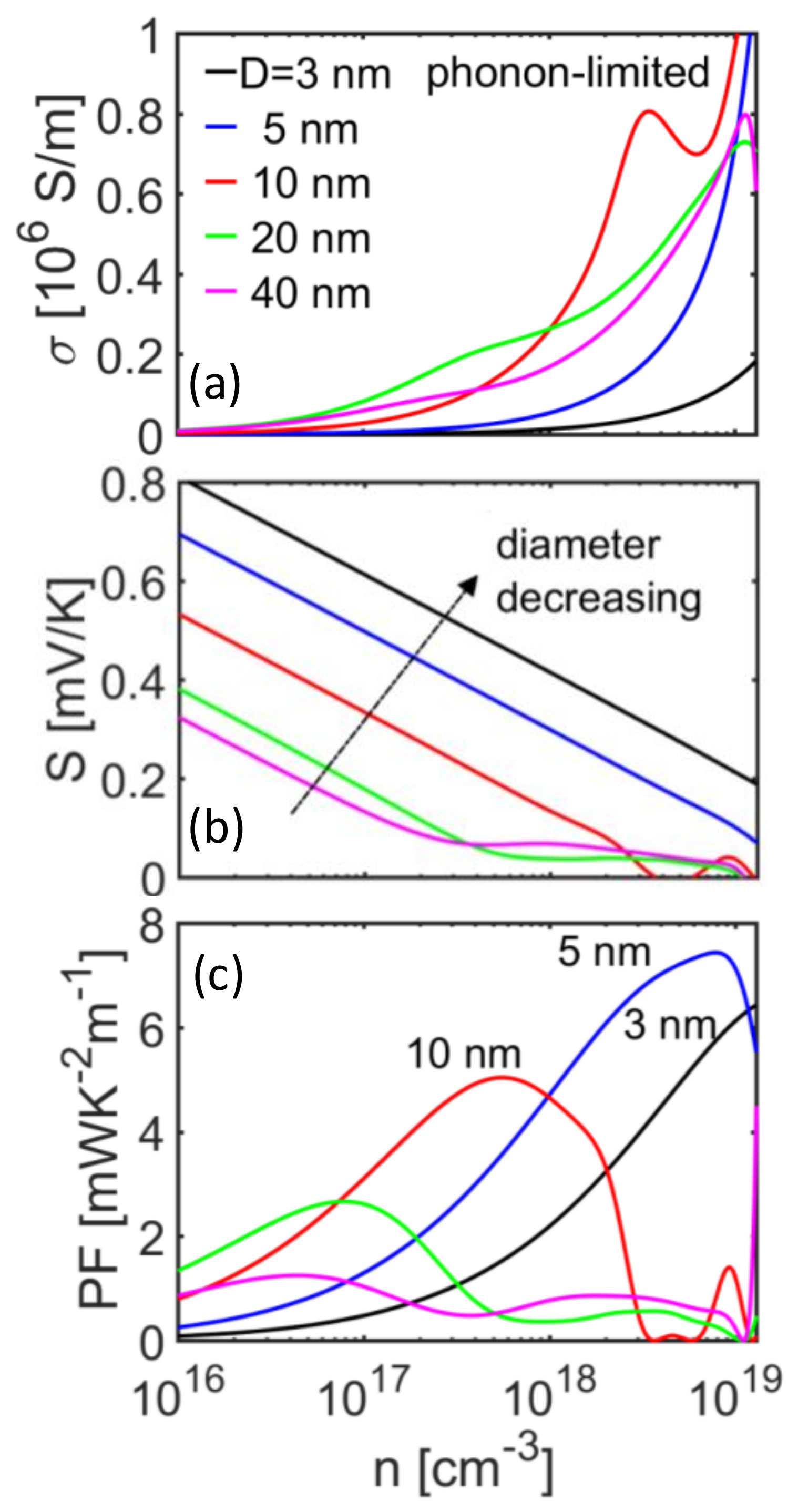
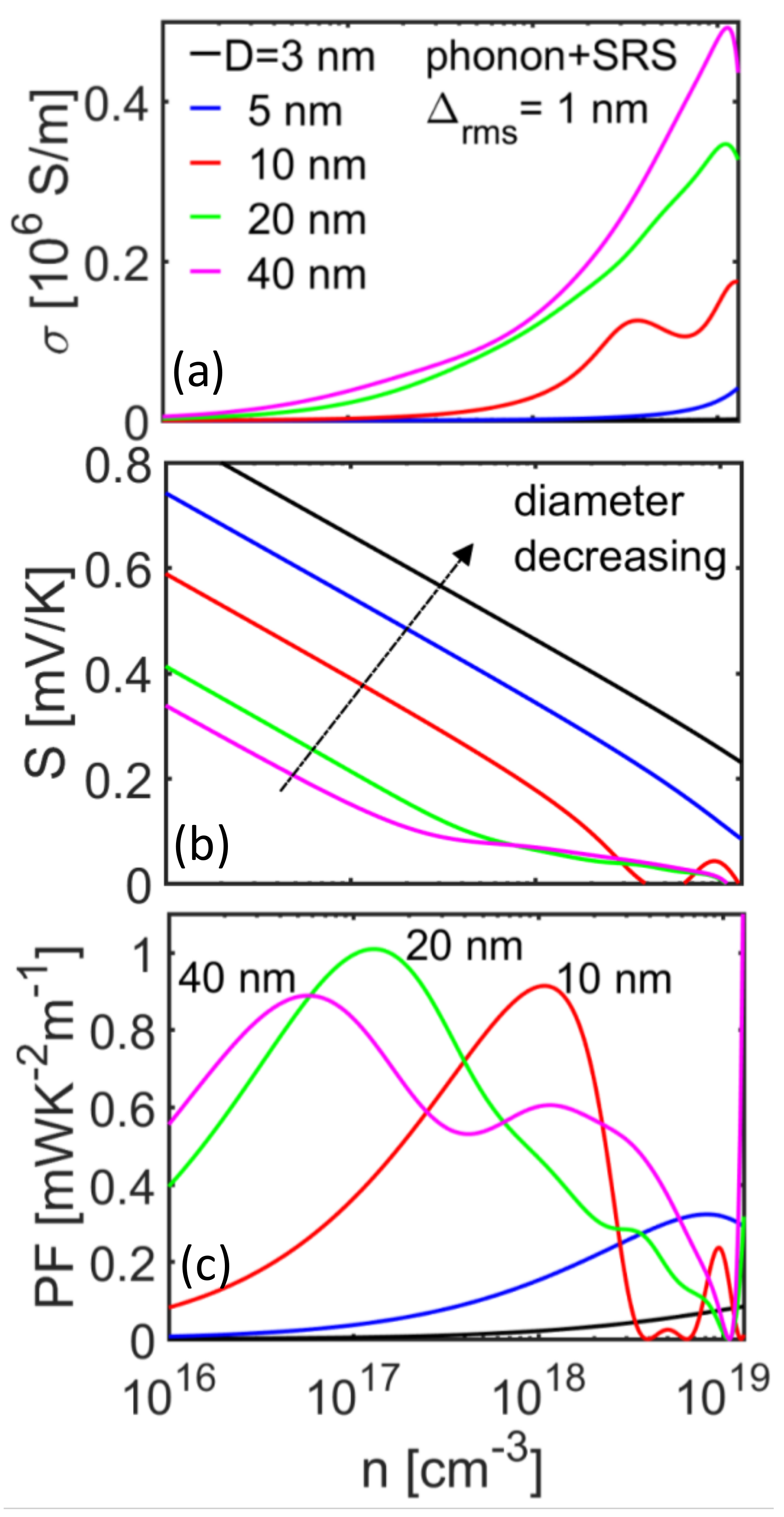
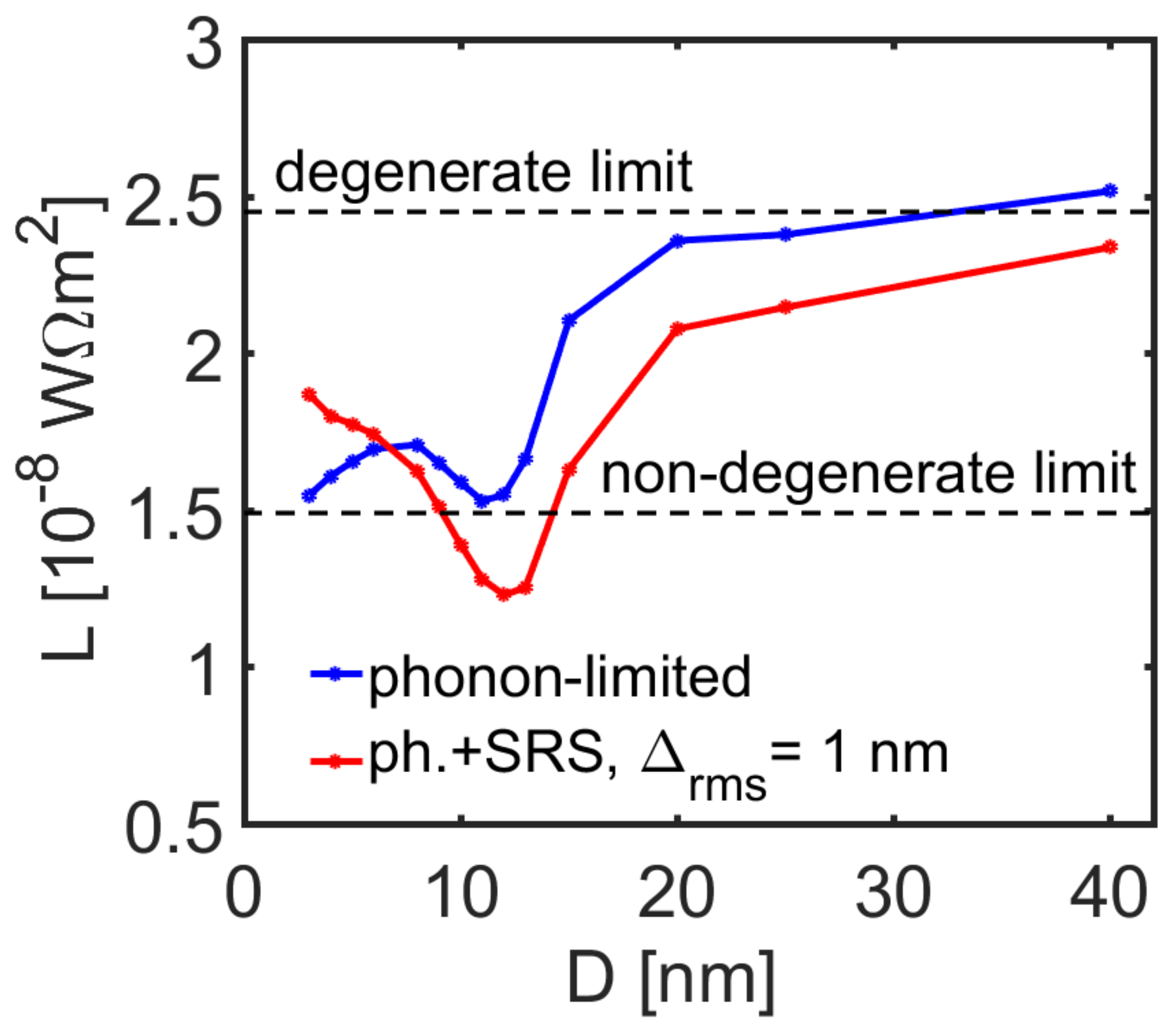
3. Results and Discussion
Thermoelectric Performance of InAs Nanowires
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Derivation of Equation (19)
Derivation of Equation (20) for ADP Scattering:
Derivation of Equation (24) for ODP Scattering:
Derivation of Equation (28) for POP Scattering:
References
- Beretta, D.; Neophytou, N.; Hodges, J.M.; Kanatzidis, M.G.; Narducci, D.; Martin-Gonzalez, M.; Beekman, M.; Balke, B.; Cerretti, G.; Tremel, W.; et al. Thermoelectrics: From history, a window to the future. Mater. Sci. Eng. R Rep. 2019, 138, 210–255. [Google Scholar] [CrossRef]
- Gelbstein, Y.; Davidow, J.; Leshem, E.; Pinshow, O.; Moisa, S. Significant lattice thermal conductivity reduction following phase separation of the highly efficient GexPb1-xTe thermoelectric alloys. Phys. Status Solidi B Basic Res. 2014, 251, 1431–1437. [Google Scholar] [CrossRef]
- Ayoun, D.B.; Sadia, Y.; Gelbstein, Y.J. High temperature thermoelectric properties evolution of Pb1-xSnxTe based alloys. J. Alloys Compd. 2017, 722, 33–38. [Google Scholar] [CrossRef]
- Xing, Y.; Xing, Y.; Liu, R.; Liao, J.; Zhang, Q.; Xia, X.; Wang, C.; Huang, H.; Chu, J.; Gu, M.; et al. High-efficiency half-Heusler thermoelectric modules enabled by self-propagating synthesis and topologic structure optimization. Energy Environ. Sci. 2019, 12, 3390. [Google Scholar] [CrossRef]
- Bravo, M.R.; Moure, A.; Fernández, J.F.; González, M.M. Skutterudites as thermoelectric materials: Revisited. RSC Adv. 2015, 5, 41653. [Google Scholar] [CrossRef]
- Boukai, A.I.; Bunimovich, Y.; Kheli, J.T.; Yu, Y.K.; Goddard Iii, W.A., III; Heath, J.R. Silicon nanowires as efficient thermoelectric materials. Nature 2008, 451, 168–171. [Google Scholar] [CrossRef]
- Hochbaum, A.I.; Chen, R.; Delgado, R.D.; Liang, W.; Garnett, E.C.; Najarian, M.; Majumdar, A.; Yang, P. Enhanced thermoelectric performance of rough silicon nanowires. Nature 2008, 451, 163–168. [Google Scholar] [CrossRef]
- Chen, R.; Lee, J.; Lee, W.; Li, D. Thermoelectrics of Nanowires. Chem. Rev. 2019, 119, 9260–9302. [Google Scholar] [CrossRef]
- Domínguez-Adame, F.; Gonzále, M.M.; Sánchez, D.; Cantarero, A. Nanowires: A route to efficient thermoelectric devices. Physica E Low Dimens. Syst. Nanostruct. 2019, 113, 213–225. [Google Scholar] [CrossRef]
- Manzano, C.V.; Gonzalez, M.M. Electrodeposition of V-VI Nanowires and Their Thermoelectric Properties. Front. Chem. 2019, 7, 516. [Google Scholar] [CrossRef]
- Ali, A.; Chen, Y.; Vasiraju, V.; Vaddiraju, S. Nanowire-based Thermoelectrics. Nanotechnology 2017, 28, 282001. [Google Scholar] [CrossRef] [PubMed]
- Calero, O.C.; González, M.M. Thermoelectric nanowires: A brief prospective. Scr. Mater 2016, 111, 54–56. [Google Scholar] [CrossRef]
- Pennelli, G.; Beilstein, J. Review of nanostructured devices for thermoelectric applications. Nanotechnology 2014, 5, 1268–1284. [Google Scholar]
- Ishibe, T.; Tomeda, A.; Watanabe, K.; Kamakura, Y.; Mori, N.; Naruse, N.; Mera, Y.; Yamashita, Y.; Nakamura, Y. Methodology of Thermoelectric Power Factor Enhancement by Controlling Nanowire Interface. ACS Appl. Mater. Interfaces 2018, 10, 37709–37716. [Google Scholar] [CrossRef] [PubMed]
- Hernandez, J.A.; Ruiz, A.; Fonseca, L.F.; Pettes, M.T.; Yacaman, M.J.; Benitez, A. Thermoelectric properties of SnSe nanowires with different diameters. Sci. Rep. 2018, 8, 11966. [Google Scholar] [CrossRef]
- Marchal, N.; Gomes, T.D.C.S.C.; Araujo, F.A.; Piraux, L. Large Spin-Dependent Thermoelectric Effects in NiFe-based Interconnected Nanowire Networks. Nanoscale Res. Lett. 2020, 15, 137. [Google Scholar] [CrossRef]
- Hicks, L.D.; Dresselhaus, M.S. Thermoelectric figure of merit of a one-dimensional conductor. Phys. Rev. Lett. 1993, 47, 16631. [Google Scholar] [CrossRef]
- Dresselhaus, M.; Chen, G.; Tang, M.Y.; Yang, R.; Lee, H.; Wang, D.; Ren, Z.; Fleurial, J.P.; Gogna, P. New Directions for Low-Dimensional Thermoelectric Materials. Adv. Mater. 2007, 19, 1043–1053. [Google Scholar] [CrossRef]
- Neophytou, N.; Kosina, H. On the interplay between electrical conductivity and Seebeck coefficient in ultra-narrow silicon nanowires. J. Electron. Mater 2012, 41, 1305–1311. [Google Scholar] [CrossRef]
- Kim, R.; Datta, S.; Lundstrom, M.S. Influence of dimensionality on thermoelectric device performance. J. Appl. Phys. 2009, 105, 034506. [Google Scholar] [CrossRef]
- Cornett, J.E.; Rabin, O. Effect of the energy dependence of the carrier scattering time on the thermoelectric power factor of quantum wells and nanowires. Appl. Phys. Lett. 2011, 98, 182104. [Google Scholar] [CrossRef]
- Vasylenko, A.; Marks, S.; Wynn, J.M.; Medeiros, P.V.C.; Ramasse, Q.M.; Morris, A.J.; Sloan, J.; Quigley, D. Electronic Structure Control of Sub-nanometer 1D SnTe via Nanostructuring within Single Walled Carbon Nanotubes. ACS Nano 2018, 12, 6023–6031. [Google Scholar] [CrossRef] [PubMed]
- Neophytou, N.; Kosina, H. Effects of confinement and orientation on the thermoelectric power factor of silicon nanowires. Phys. Rev. B 2011, 83, 245305. [Google Scholar] [CrossRef]
- Ramayya, E.B.; Maurer, L.N.; Davoody, A.H.; Knezevic, I. Thermoelectric properties of ultrathin silicon nanowires. Phys. Rev. B 2011, 86, 115328. [Google Scholar] [CrossRef]
- Kim, J.; Shim, W.; Lee, W. Bismuth nanowire thermoelectrics. J. Mater. Chem. C 2015, 3, 11999. [Google Scholar] [CrossRef]
- Lin, Y.M.; Sun, X.Z.; Dresselhaus, M.S. Theoretical investigation of thermoelectric transport properties of cylindrical Bi nanowires. Phys. Rev. B Condens. Matter 2000, 62, 4610–4623. [Google Scholar] [CrossRef]
- Chen, I.J.; Burke, A.; Svilans, A.; Linke, H.; Thelander, C. Thermoelectric Power Factor Limit of a 1D Nanowire. Phys. Rev. Lett. 2018, 120, 177703. [Google Scholar] [CrossRef]
- Wu, P.M.; Gooth, J.; Zianni, X.; Svensson, S.F.; Gluschke, J.G.; Dick, K.A.; Thelander, C.; Nielsch, K.; Linke, H. Large Thermoelectric Power Factor Enhancement Observed in InAs Nanowires. Nano Lett. 2013, 13, 4080–4086. [Google Scholar] [CrossRef]
- Prete, D.; Erdman, P.A.; Demontis, V.; Zannier, V.; Ercolani, D.; Sorba, L.; Beltram, F.; Rossella, F.; Taddei, F.; Roddaro, S.; et al. Thermoelectric Conversion at 30 K in InAs/InP Nanowire Quantum Dots. Nano Lett. 2019, 19, 3033–3039. [Google Scholar] [CrossRef]
- Jeon, S.G.; Park, D.W.; Shin, H.S.; Park, H.M.; Choi, S.Y.; Lee, S.J.; Yu, J.; Song, J.Y. Effects of doping and planar defects on the thermoelectric properties of InAs nanowires. RSC Adv. 2016, 6, 7791–7797. [Google Scholar] [CrossRef]
- Mensch, P.; Karga, S.; Schmidt, V.; Gotsmann, B.; Schmid, H.; Riel, H. One-dimensional behavior and high thermoelectric power factor in thin indium arsenide nanowires. Appl. Phys. Lett. 2015, 106, 093101. [Google Scholar] [CrossRef]
- Tian, Y.; Sakr, M.R.; Kinder, J.M.; Liang, D.; Macdonald, M.J.; Qiu, R.L.J.; Gao, H.-J.; Gao, X.P.A. One-dimensional quantum confinement effect modulated thermoelectric properties in InAs nanowires. Nano Lett. 2012, 12, 6492–6497. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, C.G.; Vasconcellos, A.R.; Luzzi, R. Mesoscopic hydro-thermodynamics of phonons in semiconductors: Heat transport in III-nitrides. Eur. Phys. J. B 2013, 86, 200. [Google Scholar] [CrossRef]
- Boykin, T.B.; Klimeck, G.; Bowen, R.C.; Oyafuso, F. Diagonal parameter shifts due to nearest-neighbor displacements in empirical tight-binding theory. Phys. Rev. B 2002, 125207. [Google Scholar] [CrossRef]
- Neophytou, N.; Paul, A.; Lundstrom, M.S.; Klimeck, G. Bandstructure effects in silicon nanowire electron transport. IEEE Trans Electron. Devices 2008, 55, 1286–1297. [Google Scholar] [CrossRef]
- Neophytou, N.; Paul, A.; Klimeck, G. Bandstructure effects in silicon nanowire hole transport. IEEE Trans Nanotechnol. 2008, 7, 710–719. [Google Scholar] [CrossRef][Green Version]
- Liu, Y.; Neophytou, N.; Low, T.; Klimeck, G.; Lundstrom, M.S. A Tight-binding Study of the Ballistic Injection Velocity for Ultra-thin body SOI MOSFETs. IEEE Trans Electron. Devices 2008, 55, 866. [Google Scholar] [CrossRef]
- Luisier, M.; Klimeck, G. Atomistic full-band simulations of silicon nanowire transistors: Effects of electron-phonon scattering. Phys. Rev. B 2009, 80, 155430. [Google Scholar] [CrossRef]
- Neophytou, N.; Kosina, H. Large enhancement in hole velocity and mobility in p-type [110] and [111] silicon nanowires by cross section scaling: An atomistic analysis. Nano Lett. 2010, 10, 4913. [Google Scholar] [CrossRef]
- Neophytou, N.; Wagner, M.; Kosina, H.; Selberherr, S. Analysis of Thermoelectric Properties of Scaled Silicon Nanowires Using an Atomistic Tight-Binding Model. J. Electron Mater 2010, 39, 1902. [Google Scholar] [CrossRef]
- Niquet, Y.M.; Delerue, C.; Allan, G.; Lannoo, M. Method for tight-binding parametrization: Application to silicon nanostructures. Phys. Rev. B 2000, 62, 5109. [Google Scholar] [CrossRef]
- Neophytou, N.; Kosina, H. Atomistic simulations of low-field mobility in Si nanowires: Influence of confinement and orientation. Phys. Rev. B 2011, 84, 085313. [Google Scholar] [CrossRef]
- Kim, J.; Kim, D.; Chang, T.; Lee, W. Quantum size effect on Shubnikov-de Haas oscillations in 100 nm diameter single-crystalline bismuth nanowire. Appl. Phys. Lett. 2014, 105, 123107. [Google Scholar] [CrossRef]
- Neophytou, N.; Kosina, H. Numerical study of the thermoelectric power factor in ultra-thin Si nanowires. J. Comput. Electr. 2012, 11, 29–44. [Google Scholar] [CrossRef][Green Version]
- Sofo, J.O.; Mahan, G.D. Thermoelectric figure of merit of superlattices. Appl. Phys. Lett. 1994, 65, 2690. [Google Scholar] [CrossRef]
- Neophytou, N. Theory and Simulation Methods for Electronic and Phononic Transport in Thermoelectric Materials; Springer Briefs in Physics: Cham, Switzerland, 2020. [Google Scholar]
- Graziosi, P.; Kumarasinghe, C.; Neophytou, N. Impact of the scattering physics on the power factor of complex thermoelectric materials. J. Appl. Phys. 2019, 126, 155701. [Google Scholar] [CrossRef]
- Lundstrom, M. Fundamentals of Carrier Transport; Cambridge University Press (CUP): Cambridge, UK, 2000; Volume 13. [Google Scholar]
- InAs—Indium Arsenide, Basic Parameters at 300 K. Available online: http://www.ioffe.ru/SVA/NSM/Semicond/InAs/basic.html (accessed on 10 September 2020).
- Yu, P.; Cardona, M. Fundamentals of Semiconductors; Springer: Berlin, Germany, 2010. [Google Scholar]
- Ahn, D. Theory of polar-optical-phonon scattering in a semiconductor quantum wire. J. Appl. Phys. 1991, 69, 3596. [Google Scholar] [CrossRef]
- Rode, D.L. Electron Transport in InSb, InAs, and InP. Phys. Rev. B 1971, 3, 3287. [Google Scholar] [CrossRef]
- Adachi, S. III-V Ternary and Quaternary Compounds. In Springer Handbook of Electronic and Photonic Materials; Springer Handbooks; Kasap, S., Capper, P., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Fischetti, M.V. Monte Carlo simulation of transport in technologically significant semiconductors of the diamond and zinc-blende structures. I. Homogeneous transport. IEEE Trans Electron. Devices 1991, 38, 634. [Google Scholar] [CrossRef]
- Harrison, J.W.; Hauser, J.R. Alloy scattering in ternary III-V compounds. Phys. Rev. B 1976, 13, 5347. [Google Scholar] [CrossRef]
- Potz, W.; Vogl, P. Theory of optical-phonon deformation potentials in tetrahedral semiconductors. Phys. Rev. B 1981, 24, 2025. [Google Scholar] [CrossRef]
- Sakaki, H.; Noda, T.; Hirakawa, K.; Tanaka, M.; Matsusue, T. Interface roughness scattering in GaAs/AlAs quantum wells. Appl. Phys. Lett. 1987, 51, 1934. [Google Scholar] [CrossRef]
- Uchida, K.; Takagi, S. Carrier scattering induced by thickness fluctuation of silicon-on-insulator film in ultrathin-body metal–oxide–semiconductor field-effect transistors. Appl. Phys. Lett. 2003, 82, 2916–2918. [Google Scholar] [CrossRef]
- Wang, F.; Yip, S.P.; Han, N.; Fok, K.W.; Lin, H.; Hou, J.J.; Dong, G.; Hung, T.F.; Chan, K.S.; Ho, J.C.; et al. Surface roughness induced electron mobility degradation in InAs nanowires. J. Nanotechnol. 2013, 24, 375202. [Google Scholar] [CrossRef]
- Ford, A.C.; Ho, J.C.; Chueh, Y.-L.; Tseng, Y.-C.; Fan, Z.; Guo, J.; Bokor, J.; Javey, A. Diameter-Dependent Electron Mobility of InAs Nanowires. Nano Lett. 2009, 9, 360. [Google Scholar] [CrossRef]
- Thesberg, M.; Kosina, H.; Neophytou, N. On the Lorenz number of multiband materials. Phys. Rev. B 2017, 95, 125206. [Google Scholar] [CrossRef]
- Prange, R.E.; Nee, T.W. Quantum Spectroscopy of the Low-Field Oscillations in the Surface Impedance. Phys. Rev. 1968, 168, 779. [Google Scholar] [CrossRef]


Sample Availability: Samples of the compounds are not available from the authors. | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Archetti, D.; Neophytou, N. Thermoelectric Properties of InA Nanowires from Full-Band Atomistic Simulations. Molecules 2020, 25, 5350. https://doi.org/10.3390/molecules25225350
Archetti D, Neophytou N. Thermoelectric Properties of InA Nanowires from Full-Band Atomistic Simulations. Molecules. 2020; 25(22):5350. https://doi.org/10.3390/molecules25225350
Chicago/Turabian StyleArchetti, Damiano, and Neophytos Neophytou. 2020. "Thermoelectric Properties of InA Nanowires from Full-Band Atomistic Simulations" Molecules 25, no. 22: 5350. https://doi.org/10.3390/molecules25225350
APA StyleArchetti, D., & Neophytou, N. (2020). Thermoelectric Properties of InA Nanowires from Full-Band Atomistic Simulations. Molecules, 25(22), 5350. https://doi.org/10.3390/molecules25225350





