Next Article in Journal
Gigantol has Protective Effects against High Glucose-Evoked Nephrotoxicity in Mouse Glomerulus Mesangial Cells by Suppressing ROS/MAPK/NF-κB Signaling Pathways
Next Article in Special Issue
Identification of the Tetrel Bonds between Halide Anions and Carbon Atom of Methyl Groups Using Electronic Criterion
Previous Article in Journal
Reactive Cobalt–Oxo Complexes of Tetrapyrrolic Macrocycles and N-based Ligand in Oxidative Transformation Reactions
Previous Article in Special Issue
Crystallographic and Computational Characterization of Methyl Tetrel Bonding in S-Adenosylmethionine-Dependent Methyltransferases
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 24
Issue 1
10.3390/molecules24010079
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Calculation of VS,max and Its Use as a Descriptor for the Theoretical Calculation of pKa Values for Carboxylic Acids

by
Guillermo Caballero-García
,
Gustavo Mondragón-Solórzano
,
Raúl Torres-Cadena
,
Marco Díaz-García
,
Jacinto Sandoval-Lira
and
Joaquín Barroso-Flores
*
Centro Conjunto de Investigación en Química Sustentable UAEM-UNAM, Unidad San Cayetano, Carretera Toluca–Atlacomulco km 14.5, Personal de la UNAM, Toluca 50200, Mexico
*
Author to whom correspondence should be addressed.
Molecules 2019, 24(1), 79; https://doi.org/10.3390/molecules24010079
Submission received: 16 October 2018 / Revised: 21 December 2018 / Accepted: 25 December 2018 / Published: 26 December 2018
(This article belongs to the Special Issue Tetrel Bonds)
Browse Figures
Versions Notes

Abstract

:
The theoretical calculation of pKa values for Brønsted acids is a challenging task that involves sophisticated and time-consuming methods. Therefore, heuristic approaches are efficient and appealing methodologies to approximate these values. Herein, we used the maximum surface electrostatic potential (VS,max) on the acidic hydrogen atoms of carboxylic acids to describe the H-bond interaction with water (the same descriptor that is used to characterize σ-bonded complexes) and correlate the results with experimental pKa values to obtain a predictive model for other carboxylic acids. We benchmarked six different methods, all including an implicit solvation model (water): Five density functionals and the Møller–Plesset second order perturbation theory in combination with six different basis sets for a total of thirty-six levels of theory. The ωB97X-D/cc-pVDZ level of theory stood out as the best one for consistently reproducing the reported pKa values, with a predictive power of 98% correlation in a test set of ten other carboxylic acids.

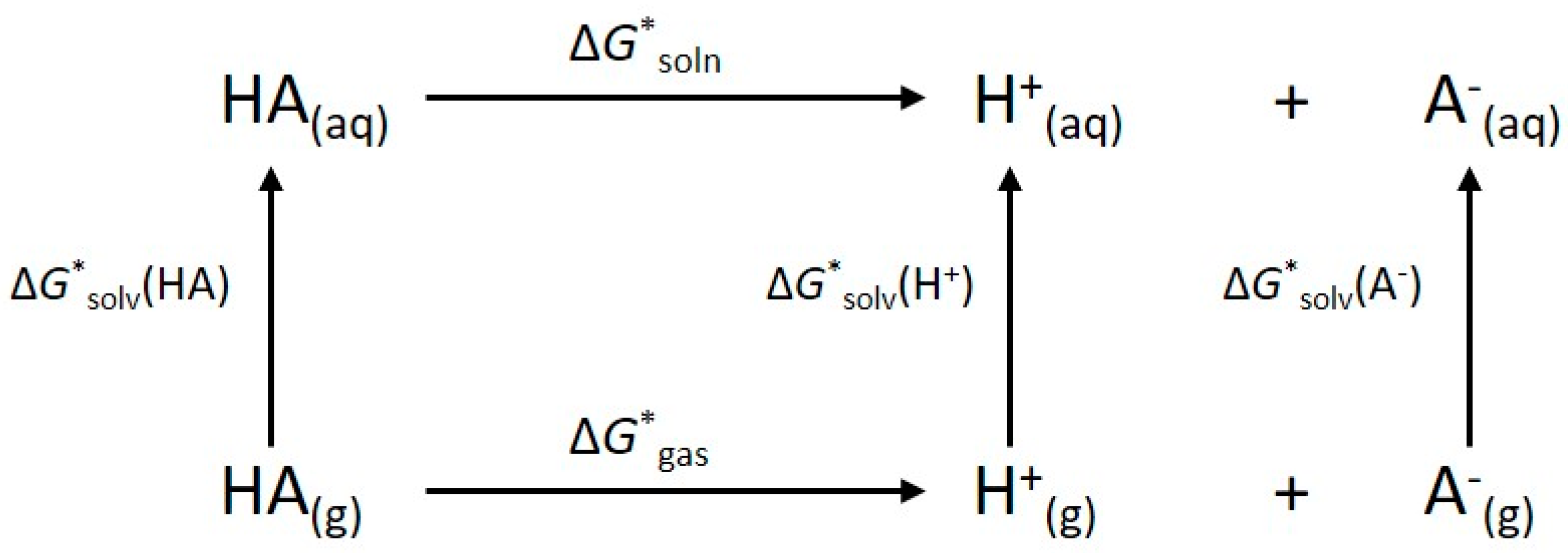
1. Introduction

The hydrogen bond is a strong, directional, non-covalent interaction responsible for a large number of chemical phenomena spanning from chemistry to biochemistry [1,2,3], which has become a paradigm amongst the toolbox of chemical concepts [4,5]. Hydrogen bonding is also a major driving force of chemical reactivity. For instance, the deprotonation of Brønsted acids in aqueous media, where the reaction constant, Ka, and its associated logarithmic quantity, pKa = −logKa, are an intrinsic characteristic of each acid. This process occurs through the abstraction of the acidic hydrogen atom using a water molecule (Equation 1). It is commonly regarded that the deprotonation reaction is mainly promoted by electrostatic interactions, given the partial positive charge on the acid hydrogen. Characterization of a protic acid through the pKa values is of practical importance and usefulness in various steps of the chemical design rationale, and therefore, it is an important quantity.
HA + H2O → H3O+ + A−
The accurate prediction of pKa values for carboxylic acids by means of computational methods covers a wide range of potential applications from chemical design and biochemistry research to drug development [6,7,8]. However, calculating the equilibrium constant for the deprotonation reaction of a Brønsted acid implies the calculation of the Gibbs Free Energy change, (−ΔG), which in turn entails the calculation of extremely accurate solvation energies for all species involved (Scheme 1). Calculation of accurate solvation free energies remains challenging, since it requires the use of sophisticated and computationally intensive methods, such as G3MP2 or CBS-QB3 [9], mostly due to a poor description of the solute–solvent interactions [10]. This method is highly sensitive to even slight deviations, since an error of only 1.36 kcal/mol—Barely above chemical accuracy—Leads to a unit error in the pKa, making it impractical for large molecules.
Since the interaction of water molecules with the acidic hydrogen atom is not isotropic, some parallels between hydrogen and σ–hole bonded systems arise. The formation of these directional interactions implies the presence of an electrostatic potential maximum located on the opposite side of the O–H σ–bond, which can be quantified by the maximum surface electrostatic potential, VS,max. By assuming that the deprotonation of a carboxylic acid begins with the formation of a hydrogen bond with a water molecule, RCOOH···H2O, we propose the use of VS,max as a suitable descriptor for the strength of this interaction, which in turn correlates with the corresponding pKa values, in a similar fashion to how a σ-hole-based interaction is quantified in halogen or tetrel bonds. Previously, the nucleophilicities and electrophilicities of Lewis acids and bases, respectively, have been derived from the interpolation of the mutual dissociation energies [11].
Previous efforts for deriving suitable pKa descriptors from ab initio or DFT descriptors have been successfully published, in some cases mixing implicit and explicit solvation models [12]. Electrostatic properties, such as the total molecular electrostatic potential (MEP) on the acidic hydrogen, combined with the sum of the valence Natural Atomic Orbital (NAO) energies on the acidic atom and the leaving proton for amino acids and nucleotides exhibits a correlation coefficient R2 = 0.91 [13] with the experimental pKa values. Monard and Jensen used various kinds of atomic charges of the conjugated phenolates, alkoxides, or thiolates, with the best correlations being observed for the atomic electrostatic charges from a Natural Population Analysis (NPA) calculated at the B3LYP/3-21G (R2 = 0.995) and M06-2X/6-311G (R2 = 0.986) levels of theory for alcohols and thiols, in implicit solvent, respectively. Other efforts include correlations on the excited states of photoacids [14] using Time Dependent DFT at the ωB97X-D/6-31G(d) level of theory for a family of hydroxyl-substituted aromatic compounds. QSPR models have yielded, for instance, a three parameters model which uses the MEP maxima, the number of carboxylic acid and amine groups for phenols, at the HF/6-31G(d,p) and B3LYP/6-31G(d,p) levels of theory (R2 = 0.96) [15]. It involves a four parameters linear equation comprising the highest normal mode vibrational frequency, the partial positive and negative charges divided by the total surface area and a reactivity index, defined in terms of a population analysis on the frontier orbital HOMO (R2 ca. 0.95 sic.) [16] for N-Base ligands at the semi empirical AM1 level of theory, as well as a Principal Components Analysis (PCA) for organic and inorganic acids (RMSE = 0.0195) [17]. Moreover, genetic algorithms (GA) and neural networks (NN) have employed frontier orbital energies for a chemical space of sixty commercial drugs [18] (GA, R2 = 0.703; NN, R2 = 0.929). Thus far, the only major commercial program capable of including the effects of molecular conformations on the estimation of pKa values is ‘Jaguar pKa′ [19,20]. For more thorough reviews on the development of pKa descriptors, please refer to References [21,22,23].
Non-covalent interactions like tetrel [24], pnicogen [25], chalcogen [26,27], carbon [28], and halogen [29,30,31] bonds offer some resemblances to H-bonded systems, both in structural and reactivity terms. All these forms of bonding correspond to directional, intermolecular non-covalent interactions of an electrostatic nature involving elements in groups 14 through 17, respectively. These atoms behave as electrophiles through the interaction with either n or π electrons from Lewis bases [32,33]. The formation of these non-covalent interactions stems from a similar origin, via the presence of σ–holes [34,35,36], a localized region of positive electrostatic potential on the surface of the bridge atom (prominently present in atoms of group 17), and opposite to the internuclear axis of one of the covalent σ bonds, hence the σ–holes. A stretch of this label has been applied to hydrogen bonding, despite the absence of p electrons on hydrogen atoms and the high polarizability of the hydrogen bonds [37,38,39].
Energetically, the strength of these interactions increases as the bridging atom increases its atomic number, the electronegativity of the atom bonded opposite to the non-covalent bond, and the number of electron-withdrawing groups bonded to the bridging atom. Tetrel bonds, for instance, are stabilizing interactions in nature [40,41] that form cooperative networks [26,42,43,44,45,46], a feature that is used as a powerful tool for the design of crystal structures [47,48,49]. The stabilization arising from these interactions ranges from 1 kcal/mol to 50 kcal/mol [50]. Therefore, the formation and strength of these interactions closely depends on the polarization of the electron density surrounding the bridging atom. In the particular case of tetrel bonds, these factors have been extensively investigated by Scheiner, who has further assessed the electronic [50,51] and steric [52] contributions.
Several computational studies on the nature of tetrel bonds have been published so far, from their strict quantum treatment [53] to their charge transfer dynamics in the attoseconds regime [54], and the tunneling bond-breaking processes promoted by σ-holes [55].
Thus, the importance of the study of non-covalent interactions has large implications for crystal engineering [56], biochemistry, and the understanding of chemical reactivity [57,58,59]. In our research group, we have reported the chemical reduction of a trichloromethyl group into a methyl group via the attack of σ–holes on chlorine atoms by thiophenolate anions, a reaction mechanism which is extensible to other trichloromethyl compounds [60].
Herein, we presented a benchmark of linear models which correlate the VS,max calculations with various DFT methods, and used MP2 as a reference (see methodology section), to the pKa values of carboxylic acids. Physically, the obtained value of VS,max on the acidic hydrogen atom reflects the attractive interaction between it and a water molecule, and thus in turn can be used to describe the deprotonation process in electrostatic terms.

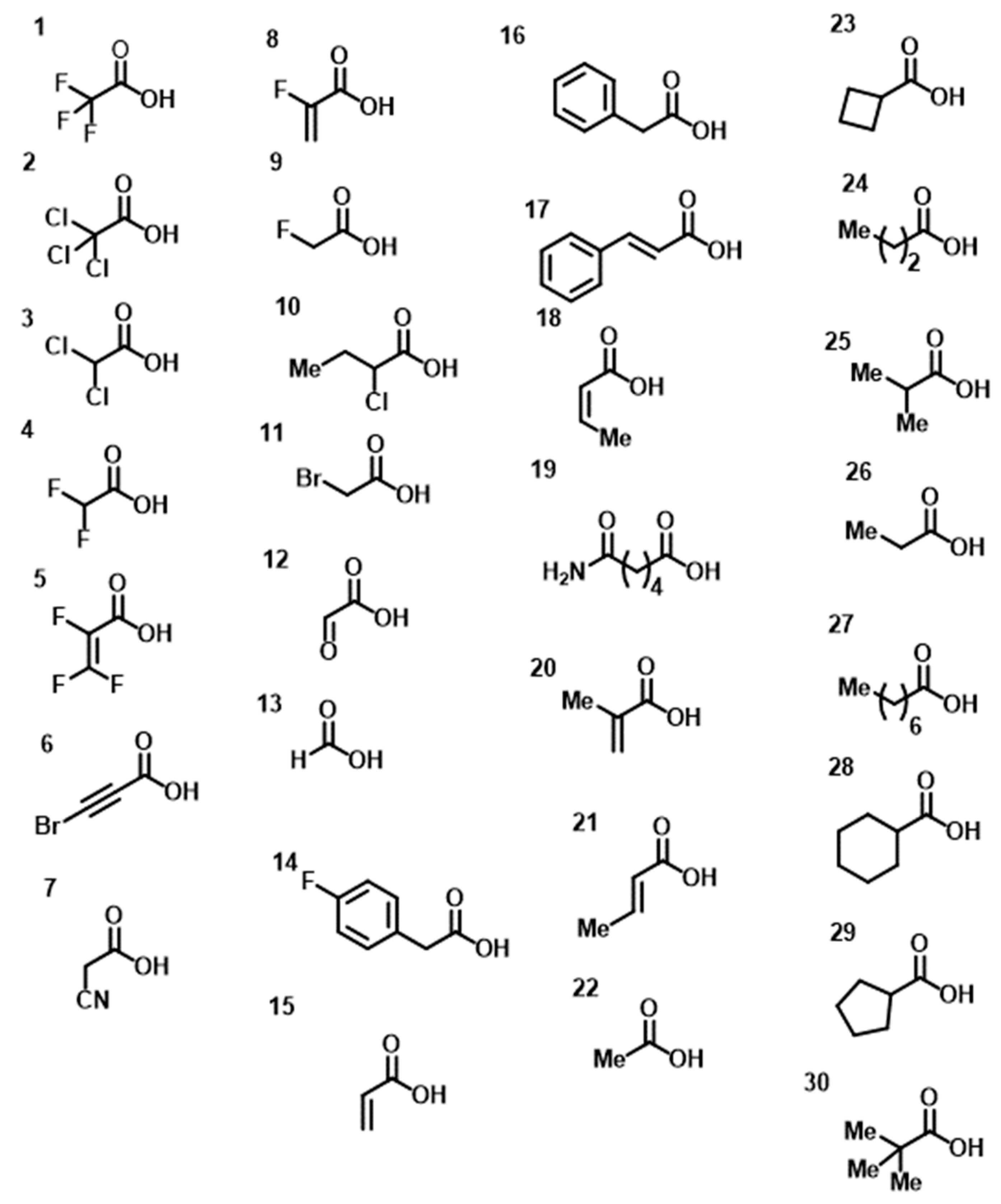
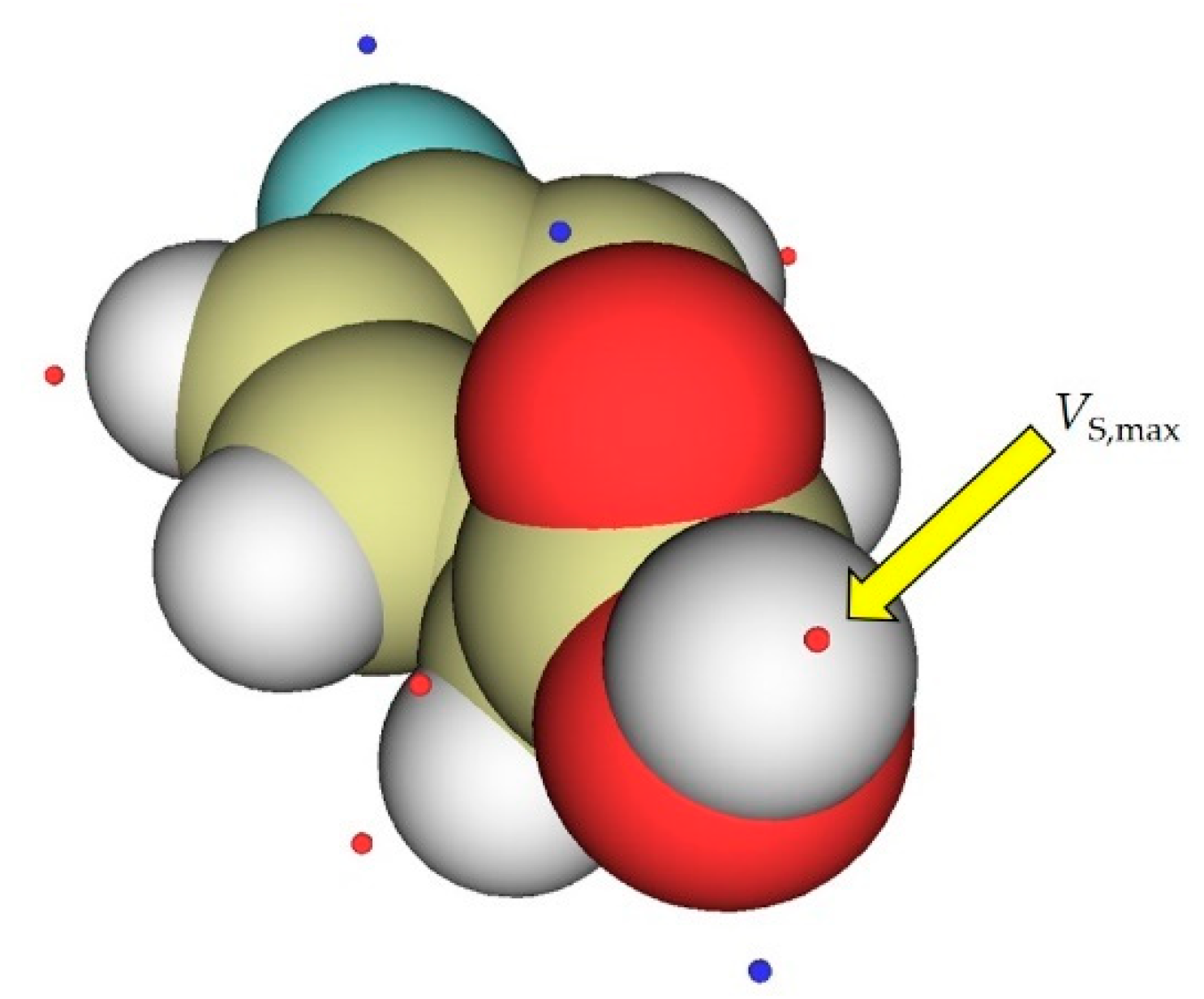
2. Results

Thirty (30) different carboxylic acids with reported pKa values were selected from Lange′s Handbook of Chemistry [61], and they were optimized and the surface electrostatic potential calculated (see methods section for full details). The structures of the acids are shown in Figure 1. The levels of theory used were obtained from the combination of the following functionals: ωB97X-D (A) [62], B3LYP (B) [63], LC-ωPBE (C) [64], M06-2X (D) [65] and PBE0 (E) [66], as well as the Møller-Plesset second-order perturbation theory, MP2 (F), and the following basis sets, 6-31+G(d,p) (1), 6-311++G(d,p) (2), cc-pVDZ (3), cc-pVTZ (4), aug-cc-pVTZ (5), and Def2-TZVP (6).
In total, thirty-six levels of theory were used to calculate the electronic structure of the thirty carboxylic acids, which comprised the chemical space under study for a total of 1080 different wave functions, upon which the maximum surface potential, VS,max, was calculated and plotted against the experimental pKaexp value. Our model was based on simple linear regressions to obtain the best fittings. The VS,max on each acidic hydrogen atom was used for the correlations, as an example, Figure 2 depicts the location of VS,max on the acid hydrogen atom for compound 14. This value was calculated on the isodensity surface ρ = 0.001 a.u., and it was used as a descriptor for the magnitude of the attractive interaction RCOOH···H2O.
All the correlation coefficients, slopes, and intercepts for all thirty-six levels of theory are collected in Table 1.
The obtained linear model is shown in Figure 3 for method (A) only, the plots with the rest of the methods (B)–(F) are presented in the Supporting Information section (Figures S3, S5, S7, S9 and S11).
A physical interpretation of the trends observed in Figure 3 can be rationalized in terms of the polarization of the O–H bond in the carboxylic acid motif. When the electron density of this bond was more polarized towards the oxygen atom, then the hydrogen atom possessed a more positive electrostatic potential, at the same time it was more labile and readily available for water to abstract it, thus having a lower pKa.
To further analyze the obtained models, a comparison between the experimental and calculated pKa values was made by calculating the ΔpKa = pKaexp − pKacal. Figure 4 shows these plots for the results obtained with the functional (A), where the corresponding ΔpKa plots for the other levels of theory are collected in the Supporting Information section (Figures S4, S6, S8, S10 and S12).
The set of models obtained for functionals (C) and (A) had the highest correlation values across the basis sets employed (see the discussion in Section 3 for further results analysis). Particularly, the A3 level of theory (ωB97X-D/cc-pVDZ) exhibited simultaneously, a high correlation (R2 = 0.9680) and the lowest ΔpKa values. Table S8 shows the pKa intervals for all levels of theory and it can be observed that all (C) models have a ΔpKa interval above 1.0 units, whereas all (A) models have ΔpKa intervals below 1.0 unit, which means an accuracy of ±0.5 pKa units. Considering these results and the calculation parameters supplied (isodensity and grid values), we proposed the following equation:
pKa = −0.2185 VS,max + 16.1879
To assess the predictive capabilities of our model, given by Equation (2), we built a test set with ten carboxylic acids (Figure 5), with pKa values that lay within the range covered by the original training set. The experimental pKa values were reported in Reference [61] and were reproduced in Table 2, together with the calculated values for the test set and the differences, which lay in the range of ΔpKa = ±0.3 units. Figure 6 shows the remarkable correlation between the experimental and calculated values with a correlation coefficient R2 = 0.9801.

3. Discussion

3.1. Computational Method: DFT or Ab Initio?

As a comparison standard, the Møller-Plesset second-order perturbation theory, MP2 (F), was included in the study, not only to assess its accuracy, but to compare the DFT and at least one wave function method as well. From all the tested levels of theory, the highest R2 correlation coefficients (Table 1) between VS,max and pKaexp values were obtained consistently with the ab initio MP2 method. Nevertheless, the DFT functional ωB97X-D functional (A), yielded comparably similar results at a fraction of the computational cost. The lowest correlation coefficients were obtained with the B3LYP functional (B), which, despite being one of the most popular ones to model organic molecules, could be describing the surface electrostatic potential inadequately. A similar performance to that of B3LYP was observed for the PBE0 functional (E), which in turn, was slightly improved when long range corrections were included in the case of LC-ωPBE (C). The latter functional was thought to yield much better results due to this long-range correlation term; however, that was not the case.
The M06-2X functional (D) also showed to be properly describing the surface electrostatic potentials, as shown in the high correlation coefficients. This was plausibly because of the dispersion terms included in its formulation. The ωB97X-D functional included an empirical dispersion term which was added a posteriori to correct the energy, but not the electron density [67].
Although the M06-2X functional is widely used and regarded as probably the best functional to model organic reactions [65], in this case, it yielded a larger discrepancy in the ΔpKa plots than the plots obtained with ωB97X-D (Figure 4 and Figure S8).
The fact that the MP2/cc-pVDZ and the ωB97X-D/cc-pVDZ yielded comparable results showed that for the case of modeling surface electrostatic potentials, a computationally expensive method may not always be preferred, as very similar or even better results can be obtained with a less demanding approach in just a fraction of the time.

3.2. Basis Set: Is Larger Better?

Most of the reported benchmarks to model organic molecules deal with the selection of the proper DFT functional methods [68,69,70]. However, little attention is paid to the basis set, or more precisely, to the proper functional/basis set combination (i.e., the level of theory). For further details, refer to Figures S13–S18, where the obtained models are organized by basis set.
Four out of the six methods yielded the strongest VS,max-pKa correlations when using the relatively medium size cc-pVDZ basis set. Surprisingly, the M06-2X functional presented the largest ΔpKa deviations when combined with the largest basis set aug-cc-pVTZ (Figures S7 and S8).
In the case of the MP2 calculations (Figure S12), increasing the so-called quality of the basis set may not be beneficial in all cases. When comparing the split-valence Pople’s basis sets, practically the same correlation was found with the double-ζ set and the corresponding triple-ζ quality one, 0.9613 versus 0.9625, respectively. On the other hand, the Dunning–Huzinaga basis showed a decrease in correlation when increasing the set size from cc-pVDZ to cc-pVTZ, 0.9702 and 0.9661, respectively. However, the ΔpKa deviations were practically consistent among the MP2 levels of theory.
In terms of the difference between the experimental and correlated pKa values, the A3 level of theory yielded the smallest ΔpKa deviations, with most of the differences kept under 0.5 pKa units, showing that, for this case, a larger basis set size may not always be better.

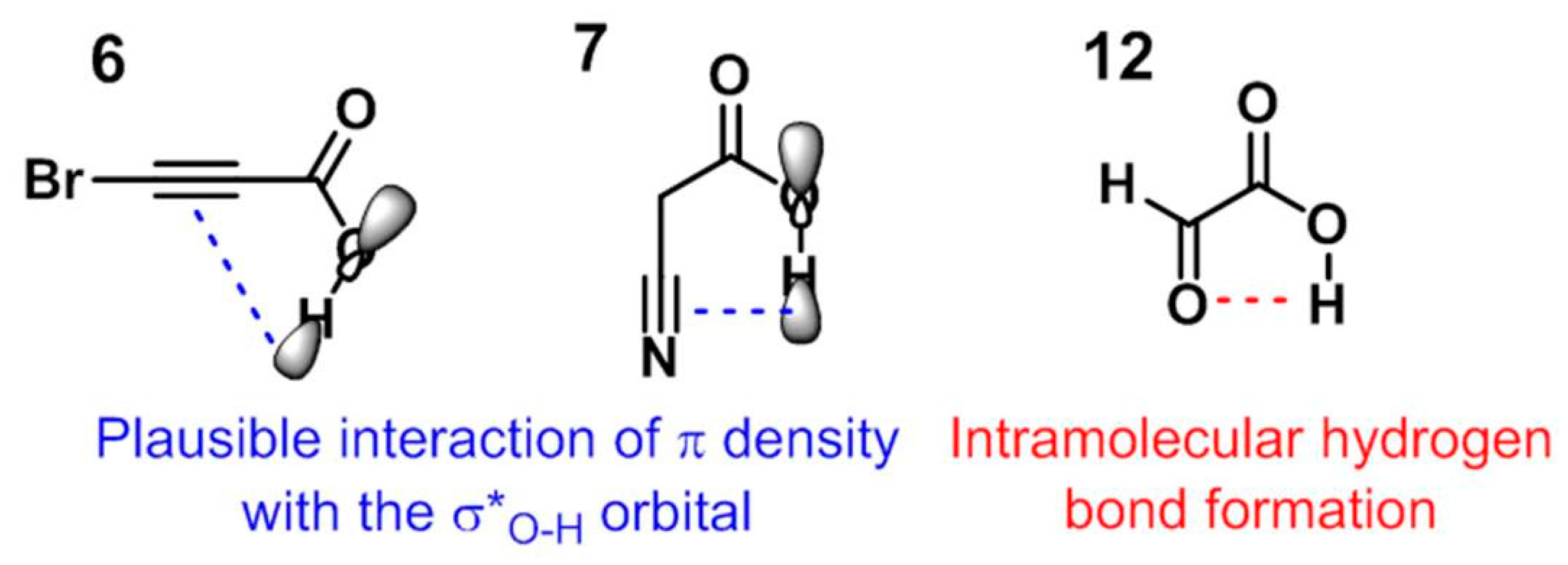
3.3. A Final Remark

In the thirty-six levels of theory tested in this study, the calculation of the VS,max of three compounds (6, 7, and 12) required an average of conformers, where the angle (D1 = O=C-O-H) was either 0.0° or 180.0°. The conformation D1 = 180.0° was stable due to strong delocalization effects from nearby п bonds to the σ*O-H orbital in the acidic hydrogen atom or intramolecular hydrogen bonding with Lewis basic motifs (Figure 7). For such kind of compounds, further improvements are required in the methodology for our linear models.
So far, the applicability domain of these regressions is limited by the pKa data used to construct the models (0.5 < pKa < 5.0). Caution must be taken when using the linear models presented herein for molecules outside this range.

4. Materials and Methods

Geometry optimizations and wave function printouts for the 30 carboxylic acids were performed using the Gaussian 09 rev. E01 suite of programs as in Reference [71], at each of the different levels of theory (see text). All calculations included the Conductor-like Polarizable Continuum Model (CPCM) implicit solvation model (water) as described in References [72,73]. The radii for cavity construction was the UFF default which takes the radii from the UFF (Universal Force Field) scaled by 1.1 with explicit spheres for hydrogen atoms. Frequency analyses were performed at the end of each geometry optimization at the same level of theory to verify that the found geometries corresponded to the energy minima. The ultrafine integration grid was used in all the calculations.
The maximum surface potential (VS,max) calculations were performed on the wave function files with the ‘MultiWFN’ program, version 3.3.8 as in Reference [74], using an isodensity value of 0.001 a.u. All the computed values were collected in the Supporting Information (Tables S1–S6).

5. Conclusions

VS,max is a scalar quantity that characterizes a σ-hole, and according to our calculations, it has also proven to be a suitable descriptor to be correlated with the pKa value of carboxylic acids, yielding differences in pKa of high accuracy. ΔpKa = ±0.30 when the ωB97X-D/cc-pVDZ level of theory was used to calculate the associated electron density upon which the VS,max value was obtained. By means of straightforward DFT calculations with a simple implicit solvation model (CPCM), the value of the VS,max could be calculated and Equation 2 obtained herein, could be used to estimate the pKa values without the need for a full thermodynamic cycle calculation; thus, avoiding long computations of solvation free energies and other costly quantities which require high accuracy methods.
The ωB97X-D/cc-pVDZ level of theory (A3) yielded the lowest ΔpKa values, standing as the best choice for estimating the pKa of any given acid through the calculation of the VS,max. Hence, we highly recommend this level of theory for geometry optimization and wave function file print. Care must be taken as the pKa value sought after should be between 0.5 and 5.0 pH units, for this is the applicability domain of our resulting equations, given the chemical space covered herein.
Further testing is needed for these regression models to become universal. However, it is important to stress that VS,max has turned out to be a powerful descriptor for predicting the pKa values of carboxylic acids as it is reflected by low, yet distinguishable differences across all methods studied herein. The presence of intramolecular non-covalent interactions, for example, hydrogen bonding, as well as highly electron-delocalizing groups within the chemical space, are key features to consider in the inclusion of an average of the VS,max for the most stable conformers. Our proposed descriptor is also dependent of the isodensity value for the definition of the surface upon which it is calculated, and it is highly recommended to keep the value suggested by Bader et al. [75] of ρ = 0.001 a.u. However, by taking these considerations into account as part of the parametrical requirements of Equation (2), then extremely accurate pKa results are obtained in a straightforward fashion.

Supplementary Materials

The following are available online, Tables S1–S6: Calculated VS,max values for carboxylic H atoms to the different levels of theory studied, Table S7: Reported pKa values for carboxylic acids studied. Figures S1, S3, S5, S7, S9 and S11: Correlation of pKaexp vs VS,max. Figures S2, S4, S6, S8, S10 and S12: Difference between the experimental and calculated pKa values (∆pKaexp−cal).

Author Contributions

Conceptualization, J.B.-F. and G.C.-G.; methodology, J.B.-F.; G.C.-G.; and J.S.-L.; validation, J.B.-F. and J.S.-L.; formal analysis, J.B.-F.; G.C.-G.; G.M.-S.; and J.S.-L.; data curation, G.C.-G.; G.M.-S.; R.T.-C.; and M.D.-G.; writing—original draft preparation, G.C.-G and G.M.-S.; writing—review and editing, J.B.-F.; G.C.-G.; and J.S.-L.; visualization, G.C.-G., J.S.-L.; and G.M.-S.; supervision, J.B.-F.; project administration, J.B.-F.

Funding

This research received no external funding.

Acknowledgments

We thank DGTIC-UNAM for granting us access to their supercomputing facilities known as ‘Miztli’. We also thank Citlalit Martínez for keeping our local computational facilities running properly. J.S.L. thanks DGAPA-UNAM for the postdoctoral scholarship. G.M.S. thanks CONACyT for the funding awarded (awardee number 771371).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Grabowski, S.J. What Is the Covalency of Hydrogen Bonding? Chem. Rev. 2011, 111, 2597–2625. [Google Scholar] [CrossRef] [PubMed]
  2. Zhao, G.J.; Han, K.L. Hydrogen bonding in the electronic excited state. Acc. Chem. Res. 2012, 45, 404–413. [Google Scholar] [CrossRef] [PubMed]
  3. Mejía, S.; Hernández-Pérez, J.M.; Sandoval-Lira, J.; Sartillo-Piscil, F. Looking inside the intramolecular C-H⋯O hydrogen bond in lactams derived from α-methylbenzylamine. Molecules 2017, 22, 361. [Google Scholar] [CrossRef] [PubMed]
  4. Yourdkhani, S.; Jabłoński, M. Revealing the physical nature and the strength of charge-inverted hydrogen bonds by SAPT(DFT), MP2, SCS-MP2, MP2C, and CCSD(T) methods. J. Comput. Chem. 2017, 38, 773–780. [Google Scholar] [CrossRef] [PubMed]
  5. Jabłoński, M. Binding of X–H to the lone-pair vacancy: Charge-inverted hydrogen bond. Chem. Phys. Lett. 2009, 477, 374–376. [Google Scholar] [CrossRef]
  6. Cruciani, G.; Milletti, F.; Storchi, L.; Sforna, G.; Goracci, L. In silico pKa prediction and ADME profiling. Chem. Biodivers. 2009, 6, 1812–1821. [Google Scholar] [CrossRef]
  7. Krieger, E.; Dunbrack, R.; Hooft, R.; Krieger, B. Computational Drug Discovery and Design. In Methods in Molecular Biology; Baron, R., Ed.; Springer: New York, NY, USA, 2012; Volume 819, ISBN 978-1-61779-464-3. [Google Scholar]
  8. Kim, M.O.; McCammon, J.A. Computation of pH-dependent binding free energies. Biopolymers 2016, 105, 43–49. [Google Scholar] [CrossRef]
  9. Liptak, M.D.; Gross, K.C.; Seybold, P.G.; Feldgus, S.; Shields, G.C. Absolute pKa Determinations for Substituted Phenols. J. Am. Chem. Soc. 2002, 124, 6421–6427. [Google Scholar] [CrossRef]
  10. Ho, J.; Coote, M.L. First-principles prediction of acidities in the gas and solution phase. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 649–660. [Google Scholar] [CrossRef]
  11. Alkorta, I.; Legon, A. Nucleophilicities of Lewis Bases B and Electrophilicities of Lewis Acids A Determined from the Dissociation Energies of Complexes B⋯A Involving Hydrogen Bonds, Tetrel Bonds, Pnictogen Bonds, Chalcogen Bonds and Halogen Bonds. Molecules 2017, 22, 1786. [Google Scholar] [CrossRef]
  12. Thapa, B.; Schlegel, H.B. Density Functional Theory Calculation of pKa’s of Thiols in Aqueous Solution Using Explicit Water Molecules and the Polarizable Continuum Model. J. Phys. Chem. A 2016, 120, 5726–5735. [Google Scholar] [CrossRef] [PubMed]
  13. Zhao, D.; Rong, C.; Yin, D.; Liu, S. Molecular Acidity of Building Blocks of Biological Systems: A Density Functional Reactivity Theory Study. J. Theor. Comput. Chem. 2013, 12, 1350034. [Google Scholar] [CrossRef]
  14. Wang, Y.F.; Cheng, Y.C. Molecular electrostatic potential on the proton-donating atom as a theoretical descriptor of excited state acidity. Phys. Chem. Chem. Phys. 2018, 20, 4351–4359. [Google Scholar] [CrossRef] [PubMed]
  15. Virant, M.; Drvarič Talian, S.; Podlipnik, Č.; Hribar-Lee, B. Modelling the Correlation Between Molecular Electrostatic Potential and pKa on Sets of Carboxylic Acids, Phenols and Anilines. Acta Chim. Slov. 2017, 560–563. [Google Scholar] [CrossRef]
  16. Palaz, S.; Türkkan, B.; Eroğlu, E. A QSPR Study for the Prediction of the pKa of N-Base Ligands and Formation Constant Kc of Bis(2,2′-bipyridine)Platinum(II)-N-Base Adducts Using Quantum Mechanically Derived Descriptors. ISRN Phys. Chem. 2012, 2012, 1–11. [Google Scholar] [CrossRef]
  17. Veyseh, S.; Hamzehali, H.; Niazi, A.; Ghasemi, J.B. Application of multivariate image analysis in QSPR study of pKa of various acids by principal components-least squares support vector machine. J. Chil. Chem. Soc. 2015, 60, 2985–2987. [Google Scholar] [CrossRef]
  18. Noorizadeh, H.; Farmany, A.; Noorizadeh, M. pKa modelling and prediction of drug molecules through GA-KPLS and L-M ANN. Drug Test. Anal. 2013, 5, 103–109. [Google Scholar] [CrossRef] [PubMed]
  19. Bochevarov, A.D.; Watson, M.A.; Greenwood, J.R.; Philipp, D.M. Multiconformation, Density Functional Theory-Based pKa Prediction in Application to Large, Flexible Organic Molecules with Diverse Functional Groups. J. Chem. Theory Comput. 2016, 12, 6001–6019. [Google Scholar] [CrossRef]
  20. Yu, H.S.; Watson, M.A.; Bochevarov, A.D. Weighted Averaging Scheme and Local Atomic Descriptor for pKa Prediction Based on Density Functional Theory. J. Chem. Inf. Model. 2018, 58, 271–286. [Google Scholar] [CrossRef]
  21. Seybold, P.G.; Shields, G.C. Computational estimation of pKa values. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 290–297. [Google Scholar] [CrossRef]
  22. Niu, Y.; Lee, J.K. pKa Prediction. In Applied Theoretical Organic Chemistry; Tantillo, D.J., Ed.; World Scientific: London, UK, 2018; pp. 6540–6544. ISBN 978-1-78634-408-3. [Google Scholar]
  23. Matta, C.F. Modeling biophysical and biological properties from the characteristics of the molecular electron density, electron localization and delocalization matrices, and the electrostatic potential. J. Comput. Chem. 2014, 35, 1165–1198. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-Bonding Interaction: Rediscovered Supramolecular Force? Angew. Chemie Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef] [PubMed]
  25. Gholipour, A. Mutual interplay between pnicogen–π and tetrel bond in PF3⊥X–Pyr…SiH3CN complexes: NMR, SAPT, AIM, NBO, and MEP analysis. Struct. Chem. 2018, 29, 1255–1263. [Google Scholar] [CrossRef]
  26. Guo, X.; Liu, Y.W.; Li, Q.Z.; Li, W.Z.; Cheng, J.B. Competition and cooperativity between tetrel bond and chalcogen bond in complexes involving F2CX (X = Se and Te). Chem. Phys. Lett. 2015, 620, 7–12. [Google Scholar] [CrossRef]
  27. Liu, M.; Li, Q.; Li, W.; Cheng, J.; McDowell, S.A.C. Comparison of hydrogen, halogen, and tetrel bonds in the complexes of HArF with YH3X (X = halogen, Y = C and Si). RSC Adv. 2016, 6, 19136–19143. [Google Scholar] [CrossRef]
  28. Mani, D.; Arunan, E. The X-C⋯Y (X = O/F, Y = O/S/F/Cl/Br/N/P) “carbon bond” and hydrophobic interactions. Phys. Chem. Chem. Phys. 2013, 15, 14377–14383. [Google Scholar] [CrossRef]
  29. Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The halogen bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef]
  30. Auffinger, P.; Hays, F.; Westhof, E.; Ho, P.S. Halogen bonds in biological molecules. Proc. Natl. Acad. Sci. USA. 2004, 101, 16789–16794. [Google Scholar] [CrossRef]
  31. Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef]
  32. Legon, A.C. Tetrel, pnictogen and chalcogen bonds identified in the gas phase before they had names: A systematic look at non-covalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 14884–14896. [Google Scholar] [CrossRef]
  33. Edwards, A.J.; Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. Intermolecular interactions in molecular crystals: What’s in a name? Faraday Discuss. 2017, 203, 93–112. [Google Scholar] [CrossRef] [PubMed]
  34. Liu, M.; Li, Q.; Scheiner, S. Comparison of tetrel bonds in neutral and protonated complexes of pyridine TF3 and furan TF3 (T = C, Si, and Ge) with NH3. Phys. Chem. Chem. Phys. 2017, 19, 5550–5559. [Google Scholar] [CrossRef] [PubMed]
  35. Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Comparison between tetrel bonded complexes stabilized by σ and π hole interactions. Molecules 2018, 23, 1416. [Google Scholar] [CrossRef] [PubMed]
  36. Kolář, M.H.; Hobza, P. Computer Modeling of Halogen Bonds and Other σ-Hole Interactions. Chem. Rev. 2016, 116, 5155–5187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  37. Shields, Z.P.; Murray, J.S.; Politzer, P. Directional tendencies of halogen and hydrogen bonds. Int. J. Quantum Chem. 2010, 110, 2823–2832. [Google Scholar] [CrossRef]
  38. Scheiner, S. Assembly of Effective Halide Receptors from Components. Comparing Hydrogen, Halogen, and Tetrel Bonds. J. Phys. Chem. A 2017, 121, 3606–3615. [Google Scholar] [CrossRef]
  39. Tang, Q.; Li, Q. Interplay between tetrel bonding and hydrogen bonding interactions in complexes involving F2XO (X = C and Si) and HCN. Comput. Theor. Chem. 2014, 1050, 51–57. [Google Scholar] [CrossRef]
  40. Del Bene, J.E.; Alkorta, I.; Elguero, J. Exploring the (H2C=PH2)+:N-Base Potential Surfaces: Complexes Stabilized by Pnicogen, Hydrogen, and Tetrel Bonds. J. Phys. Chem. A 2015, 119, 11701–11710. [Google Scholar] [CrossRef]
  41. Esrafili, M.D.; Vakili, M.; Javaheri, M.; Sobhi, H.R. Tuning of tetrel bonds interactions by substitution and cooperative effects in XH3Si···NCH···HM (X = H, F, Cl, Br; M = Li, Na, BeH and MgH) complexes. Mol. Phys. 2016, 114, 1974–1982. [Google Scholar] [CrossRef]
  42. Marín-Luna, M.; Alkorta, I.; Elguero, J. Cooperativity in Tetrel Bonds. J. Phys. Chem. A 2016, 120, 648–656. [Google Scholar] [CrossRef] [Green Version]
  43. Solimannejad, M.; Orojloo, M.; Amani, S. Effect of cooperativity in lithium bonding on the strength of halogen bonding and tetrel bonding: (LiCN)n···ClYF3 and (LiCN)n···YF3Cl (Y= C, Si and n = 1–5) complexes as a working model. J. Mol. Model. 2015, 21. [Google Scholar] [CrossRef] [PubMed]
  44. Mahmoudi, G.; Bauzá, A.; Frontera, A.; Garczarek, P.; Stilinović, V.; Kirillov, A.M.; Kennedy, A.; Ruiz-Pérez, C. Metal-organic and supramolecular lead(II) networks assembled from isomeric nicotinoylhydrazone blocks: The effects of ligand geometry and counter-ion on topology and supramolecular assembly. CrystEngComm 2016, 18, 5375–5385. [Google Scholar] [CrossRef]
  45. Wei, Y.; Cheng, J.; Li, W.; Li, Q. Regulation of coin metal substituents and cooperativity on the strength and nature of tetrel bonds. RSC Adv. 2017, 7, 46321–46328. [Google Scholar] [CrossRef] [Green Version]
  46. Esrafili, M.D.; Mohammadian-Sabet, F. Cooperativity of tetrel bonds tuned by infstituent effects. Mol. Phys. 2016, 114, 1528–1538. [Google Scholar] [CrossRef]
  47. George, J.; Dronskowski, R. Tetrel bonds in infinite molecular chains by electronic structure theory and their role for crystal stabilization. J. Phys. Chem. A 2017, 121, 1381–1387. [Google Scholar] [CrossRef] [PubMed]
  48. Mahmoudi, G.; Dey, L.; Chowdhury, H.; Bauzá, A.; Ghosh, B.K.; Kirillov, A.M.; Seth, S.K.; Gurbanov, A.V.; Frontera, A. Synthesis and crystal structures of three new lead(II) isonicotinoylhydrazone derivatives: Anion controlled nuclearity and dimensionality. Inorganica Chim. Acta 2017, 461, 192–205. [Google Scholar] [CrossRef]
  49. Mahmoudi, G.; Gurbanov, A.V.; Rodríguez-Hermida, S.; Carballo, R.; Amini, M.; Bacchi, A.; Mitoraj, M.P.; Sagan, F.; Kukulka, M.; Safin, D.A. Ligand-Driven Coordination Sphere-Induced Engineering of Hybride Materials Constructed from PbCl2 and Bis-Pyridyl Organic Linkers for Single-Component Light-Emitting Phosphors. Inorg. Chem. 2017, 56, 9698–9709. [Google Scholar] [CrossRef] [PubMed]
  50. Scheiner, S. Systematic Elucidation of Factors That Influence the Strength of Tetrel Bonds. J. Phys. Chem. A 2017, 121, 5561–5568. [Google Scholar] [CrossRef] [Green Version]
  51. Dong, W.; Li, Q.; Scheiner, S. Comparative strengths of tetrel, pnicogen, chalcogen, and halogen bonds and contributing factors. Molecules 2018, 23, 1681. [Google Scholar] [CrossRef]
  52. Scheiner, S. Steric Crowding in Tetrel Bonds. J. Phys. Chem. A 2018, 122, 2550–2562. [Google Scholar] [CrossRef]
  53. Laconsay, C.J.; Galbraith, J.M. A valence bond theory treatment of tetrel bonding interactions. Comput. Theor. Chem. 2017, 1116, 202–206. [Google Scholar] [CrossRef]
  54. Chandra, S.; Bhattacharya, A. Attochemistry of Ionized Halogen, Chalcogen, Pnicogen, and Tetrel Noncovalent Bonded Clusters. J. Phys. Chem. A 2016, 120, 10057–10071. [Google Scholar] [CrossRef] [PubMed]
  55. Kozuch, S.; Nandi, A.; Sucher, A. Ping-Pong Tunneling Reactions: Can Fluoride Jump at Absolute Zero? Chem.—A Eur. J. 2018. [Google Scholar] [CrossRef]
  56. Servati Gargari, M.; Stilinovic, V.; Bauzá, A.; Frontera, A.; McArdle, P.; Van Derveer, D.; Ng, S.W.; Mahmoudi, G. Design of Lead(II) Metal-Organic Frameworks Based on Covalent and Tetrel Bonding. Chem.—A Eur. J. 2015, 21, 17951–17958. [Google Scholar] [CrossRef]
  57. Grabowski, S.J. Tetrel bond-σ-hole bond as a preliminary stage of the SN2 reaction. Phys. Chem. Chem. Phys. 2014, 16, 1824–1834. [Google Scholar] [CrossRef]
  58. Szabó, I.; Császár, A.G.; Czakó, G. Dynamics of the F− + CH3Cl → Cl− + CH3F SN2 reaction on a chemically accurate potential energy surface. Chem. Sci. 2013, 4, 4362. [Google Scholar] [CrossRef]
  59. Stei, M.; Carrascosa, E.; Kainz, M.A.; Kelkar, A.H.; Meyer, J.; Szabó, I.; Czakó, G.; Wester, R. Influence of the leaving group on the dynamics of a gas-phase SN2 reaction. Nat. Chem. 2015, 8, 1–6. [Google Scholar] [CrossRef]
  60. Caballero-García, G.; Romero-Ortega, M.; Barroso-Flores, J. Reactivity of electrophilic chlorine atoms due to σ-holes: A mechanistic assessment of the chemical reduction of a trichloromethyl group by sulfur nucleophiles. Phys. Chem. Chem. Phys. 2016, 18, 27300–27307. [Google Scholar] [CrossRef]
  61. Lange, N.A.; Speight, J.G. Lange’s Handbook of Chemistry; McGraw-Hill: New York, NY, USA, 2005; ISBN 0071432205. [Google Scholar]
  62. Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef] [Green Version]
  63. Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
  64. Vydrov, O.A.; Scuseria, G.E.; Perdew, J.P. Tests of functionals for systems with fractional electron number. J. Chem. Phys. 2007, 126, 154109. [Google Scholar] [CrossRef] [PubMed]
  65. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
  66. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
  67. Risthaus, T.; Grimme, S. Benchmarking of London dispersion-accounting density functional theory methods on very large molecular complexes. J. Chem. Theory Comput. 2013, 9, 1580–1591. [Google Scholar] [CrossRef] [PubMed]
  68. Thanthiriwatte, K.S.; Hohenstein, E.G.; Burns, L.A.; Sherrill, C.D. Assessment of the Performance of DFT and DFT-D Methods for Describing Distance Dependence of Hydrogen-Bonded Interactions. J. Chem. Theory Comput. 2011, 7, 88–96. [Google Scholar] [CrossRef] [PubMed]
  69. Wolters, L.P.; Schyman, P.; Pavan, M.J.; Jorgensen, W.L.; Bickelhaupt, F.M.; Kozuch, S. The many faces of halogen bonding: A review of theoretical models and methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 523–540. [Google Scholar] [CrossRef]
  70. Jensen, F. Method Calibration or Data Fitting? J. Chem. Theory Comput. 2018, 14, 4651–4661. [Google Scholar] [CrossRef]
  71. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision D. 01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  72. Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef] [PubMed]
  73. Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
  74. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  75. Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
Sample Availability: Not available.
Molecules 24 00079 sch001 550
Scheme 1. Thermodynamic cycle for a protic acid deprotonation.
Scheme 1. Thermodynamic cycle for a protic acid deprotonation.
Molecules 24 00079 sch001
Molecules 24 00079 g001 550
Figure 1. Thirty carboxylic acids comprising the chemical space under study.
Figure 1. Thirty carboxylic acids comprising the chemical space under study.
Molecules 24 00079 g001
Molecules 24 00079 g002 550
Figure 2. Maximum surface electrostatic potential, VS,max, over the acidic hydrogen atom shown for compound 14 taking an isodensity value of 0.001 a.u. (isosurface not shown). Red dots represent positive VS,max values and the blue dots represent negative VS,max values.
Figure 2. Maximum surface electrostatic potential, VS,max, over the acidic hydrogen atom shown for compound 14 taking an isodensity value of 0.001 a.u. (isosurface not shown). Red dots represent positive VS,max values and the blue dots represent negative VS,max values.
Molecules 24 00079 g002
Molecules 24 00079 g003 550
Figure 3. Linear correlations between pKaexp against VS,max for DFT method (A), with the six basis sets (1) through (6).
Figure 3. Linear correlations between pKaexp against VS,max for DFT method (A), with the six basis sets (1) through (6).
Molecules 24 00079 g003
Molecules 24 00079 g004 550
Figure 4. ΔpKa = pKaexp – pKacal for DFT method (A) with the six basis sets (1) through (6).
Figure 4. ΔpKa = pKaexp – pKacal for DFT method (A) with the six basis sets (1) through (6).
Molecules 24 00079 g004
Molecules 24 00079 g005 550
Figure 5. Carboxylic acids used as a test set for Equation (2).
Figure 5. Carboxylic acids used as a test set for Equation (2).
Molecules 24 00079 g005
Molecules 24 00079 g006 550
Figure 6. Correlation between the experimental and calculated pKa values.
Figure 6. Correlation between the experimental and calculated pKa values.
Molecules 24 00079 g006
Molecules 24 00079 g007 550
Figure 7. Intramolecular interactions for compounds 6, 7, and 12, conformers at D1 = 180.0°.
Figure 7. Intramolecular interactions for compounds 6, 7, and 12, conformers at D1 = 180.0°.
Molecules 24 00079 g007
Table
Table 1. Linear regression parameters obtained for the pKa vs VS,max plots. Intercept units in kcal/mol.
Table 1. Linear regression parameters obtained for the pKa vs VS,max plots. Intercept units in kcal/mol.
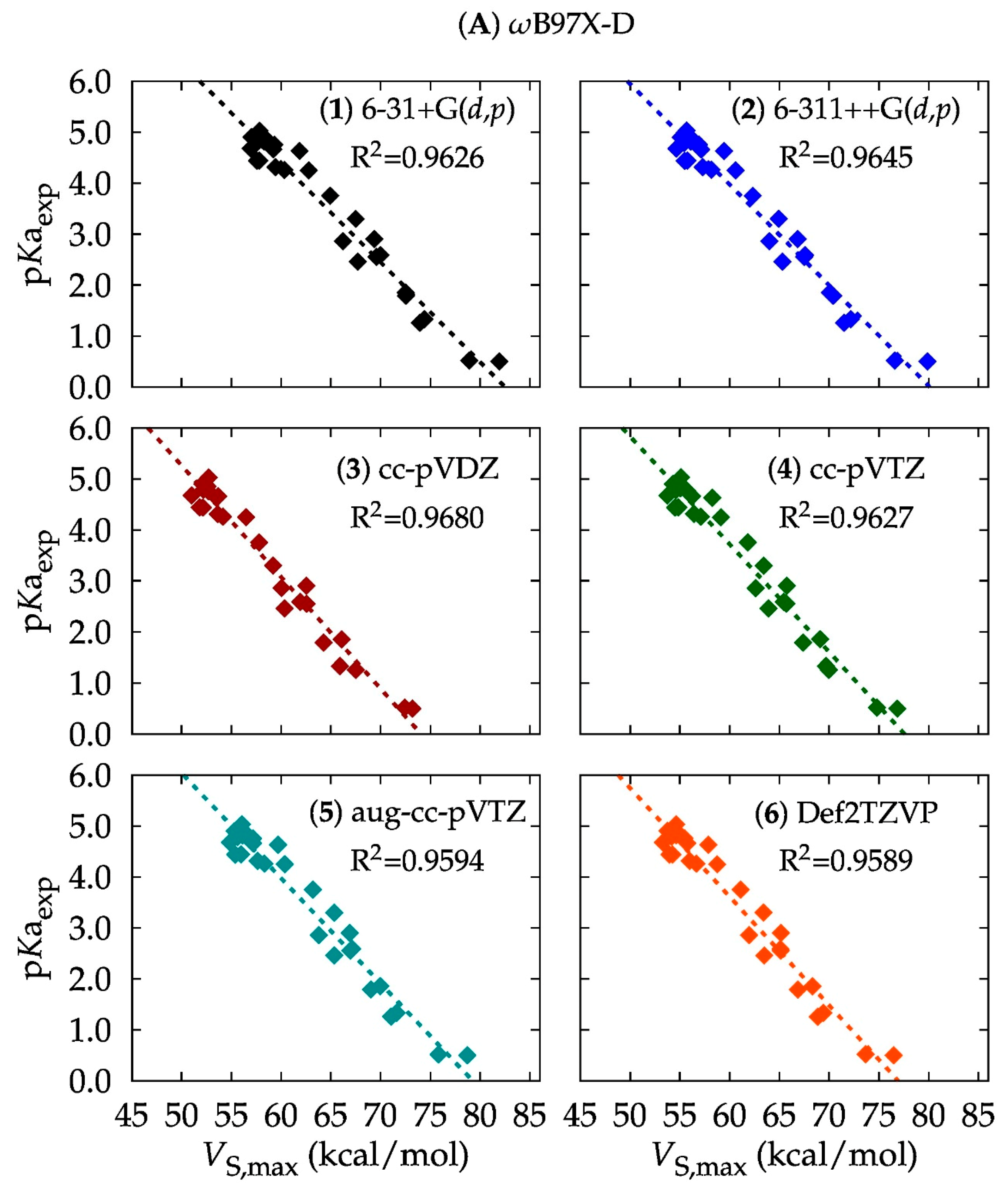
Level of TheorySlopeInterceptR2Level of TheorySlopeInterceptR2
A1−0.195416.12370.9626D1−0.198716.33520.9598
A2−0.197515.82130.9645D2−0.194715.50730.9598
A3−0.218516.18790.9680D3−0.220116.22120.9653
A4−0.211316.39580.9627D4−0.208216.24110.9577
A5−0.206316.35420.9594D5−0.202716.07800.9535
A6−0.213116.39670.9589D6−0.209515.99930.9534
B1−0.190215.18630.9494E1−0.195315.88400.9553
B2−0.190914.80190.9515E2−0.195315.38580.9511
B3−0.219115.51090.9570E3−0.216715.87990.9616
B4−0.207215.46140.9521E4−0.211816.12810.9536
B5−0.198315.15050.9457E5−0.203815.82320.9490
B6−0.203015.14490.9277E6−0.212515.97390.9485
C1−0.200116.43720.9654F1−0.199615.88140.9613
C2−0.199615.97000.9647F2−0.212315.91910.9625
C3−0.227216.64990.9682F3−0.228516.37780.9702
C4−0.216616.79450.9633F4−0.219816.32640.9661
C5−0.208516..47760.9597F5−0.209416.03990.9550
C6−0.216216.49720.9579F6−0.218716.16350.9616
Table
Table 2. VS,max calculated with the A3 model. Experimental and calculated pKa values for compounds a–j and the differences.
Table 2. VS,max calculated with the A3 model. Experimental and calculated pKa values for compounds a–j and the differences.
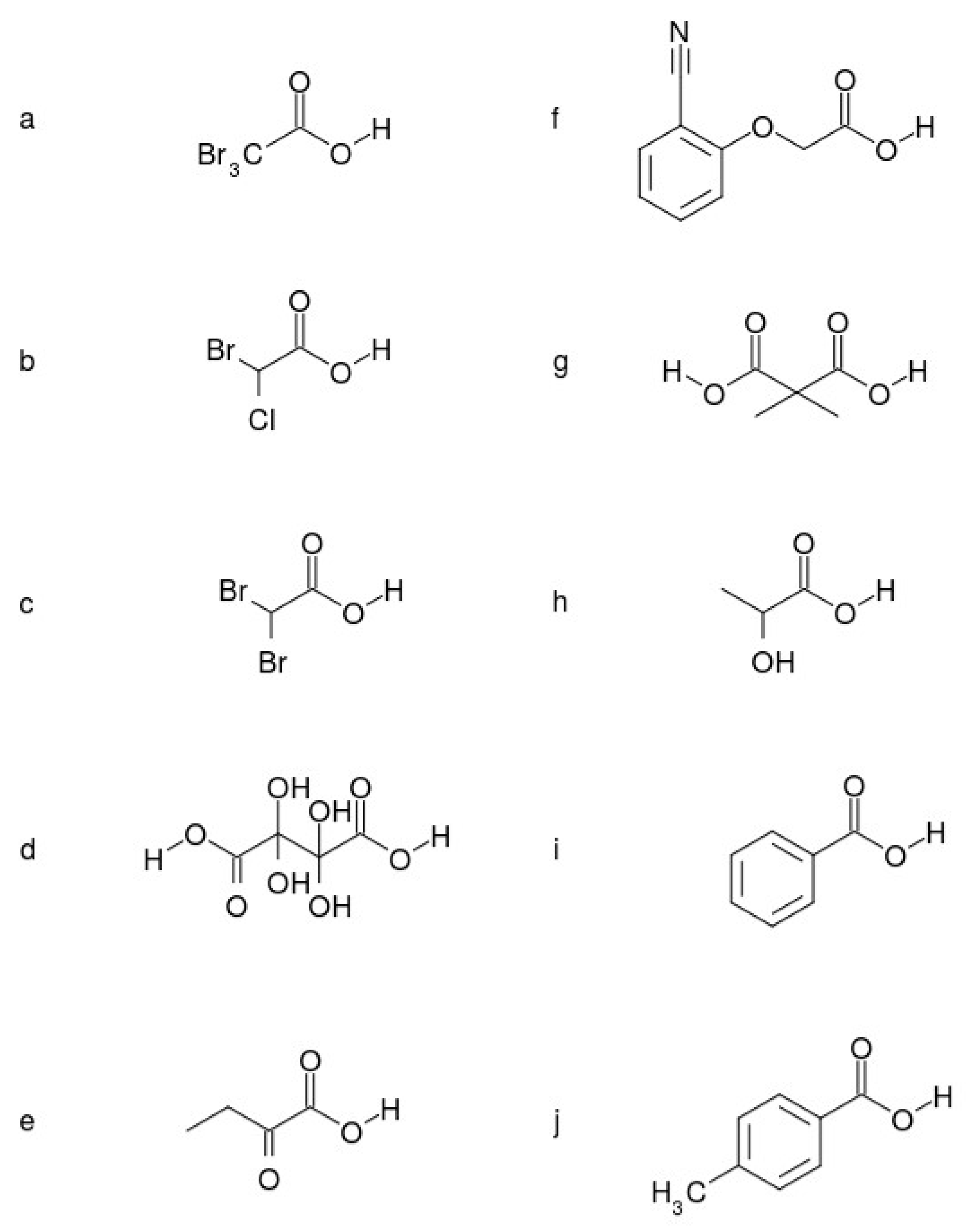
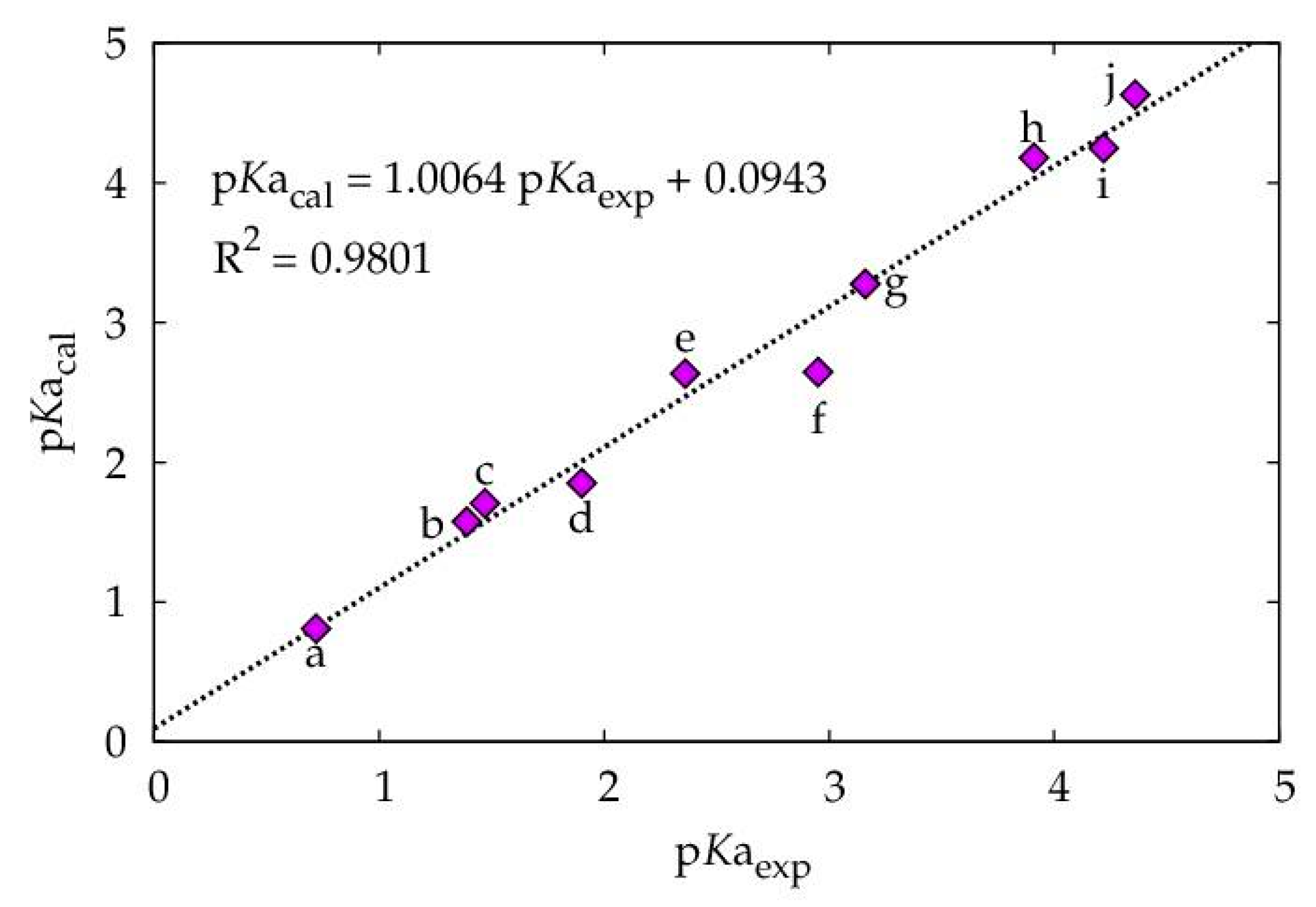
VS,maxpKaexp *pKacal **ΔpKaexp − cal
a70.37330.72000.8097−0.0897
b66.87451.39001.5743-0.1843
c66.27541.47001.7052−0.2352
d65.61121.90001.85030.0497
e62.02362.36002.6343−0.2743
f61.97192.95002.64560.3044
g59.09143.16003.2750−0.1150
h54.95613.91004.1787−0.2687
i54.63704.22004.24840.0284
j52.89254.36003.6296−0.2696
* See Reference [61]. ** Values obtained with Equation (2).

Share and Cite

MDPI and ACS Style

Caballero-García, G.; Mondragón-Solórzano, G.; Torres-Cadena, R.; Díaz-García, M.; Sandoval-Lira, J.; Barroso-Flores, J. Calculation of VS,max and Its Use as a Descriptor for the Theoretical Calculation of pKa Values for Carboxylic Acids. Molecules 2019, 24, 79. https://doi.org/10.3390/molecules24010079

AMA Style

Caballero-García G, Mondragón-Solórzano G, Torres-Cadena R, Díaz-García M, Sandoval-Lira J, Barroso-Flores J. Calculation of VS,max and Its Use as a Descriptor for the Theoretical Calculation of pKa Values for Carboxylic Acids. Molecules. 2019; 24(1):79. https://doi.org/10.3390/molecules24010079

Chicago/Turabian Style

Caballero-García, Guillermo, Gustavo Mondragón-Solórzano, Raúl Torres-Cadena, Marco Díaz-García, Jacinto Sandoval-Lira, and Joaquín Barroso-Flores. 2019. "Calculation of VS,max and Its Use as a Descriptor for the Theoretical Calculation of pKa Values for Carboxylic Acids" Molecules 24, no. 1: 79. https://doi.org/10.3390/molecules24010079

APA Style

Caballero-García, G., Mondragón-Solórzano, G., Torres-Cadena, R., Díaz-García, M., Sandoval-Lira, J., & Barroso-Flores, J. (2019). Calculation of VS,max and Its Use as a Descriptor for the Theoretical Calculation of pKa Values for Carboxylic Acids. Molecules, 24(1), 79. https://doi.org/10.3390/molecules24010079

Article Metrics

Back to TopTop