Determination of the Clean Air Delivery Rate (CADR) of Photocatalytic Oxidation (PCO) Purifiers for Indoor Air Pollutants Using a Closed-Loop Reactor. Part I: Theoretical Considerations
Abstract
:1. Introduction
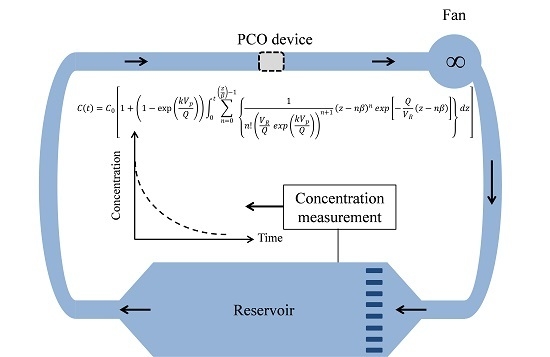
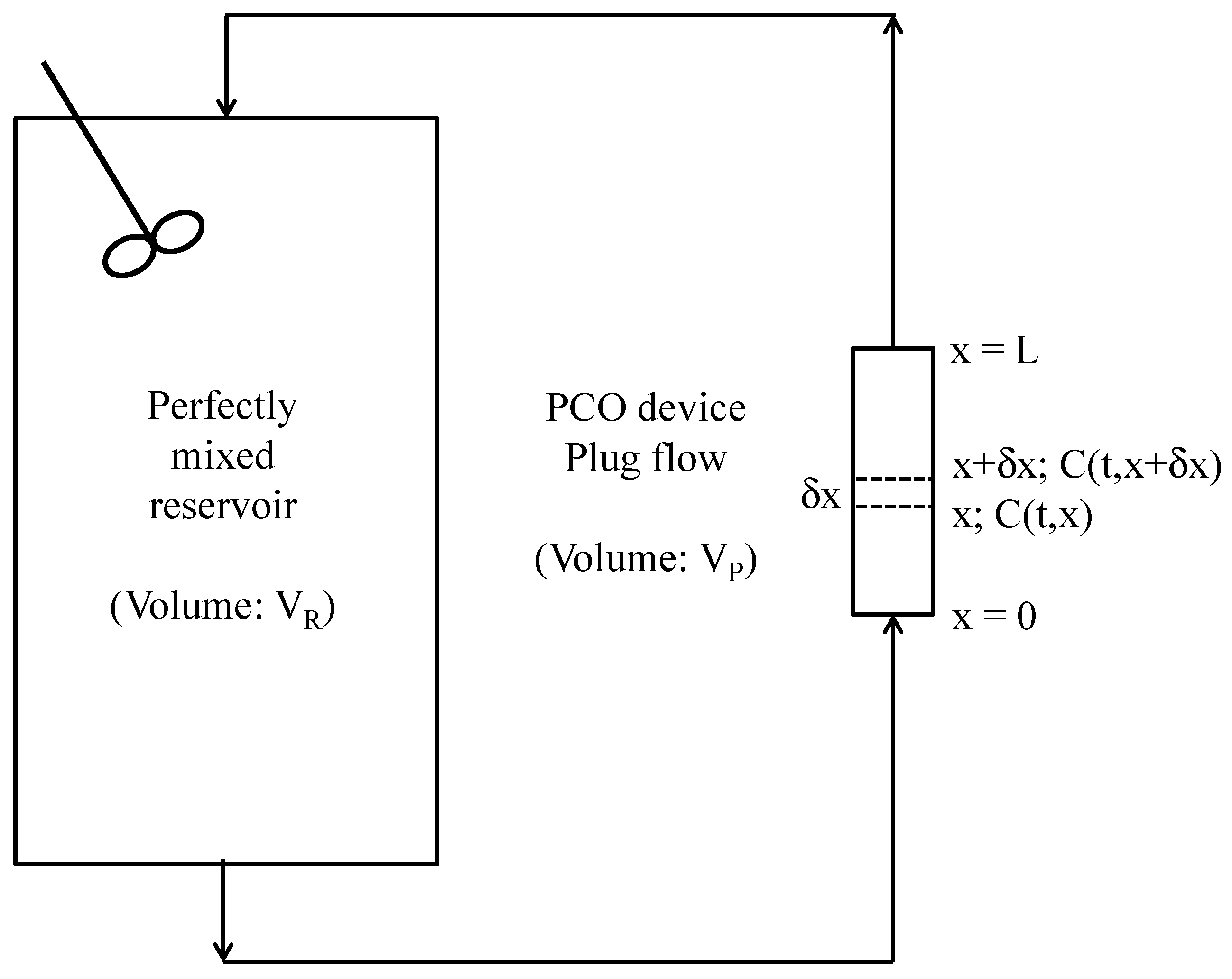
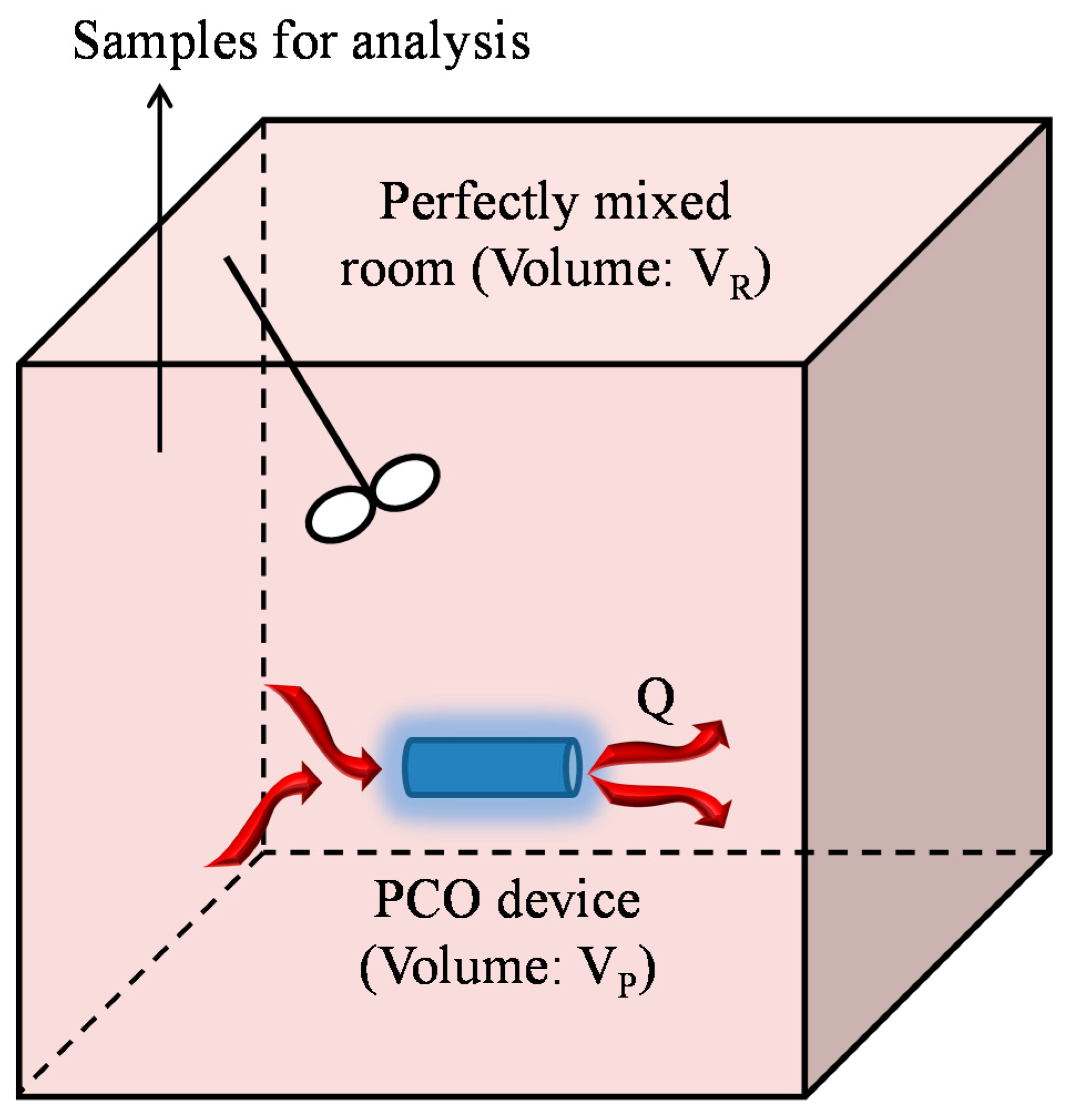
2. Model
- (i)
- Idealized plug flow occurs in the PCO device;
- (ii)
- The reservoir is a perfectly-mixed system;
- (iii)
- The mass transfer of pollutant occurs under convective-diffusion control;
- (iv)
- The kinetic constant does not change during the experiment;
- (v)
- The flow rate Q is constant with time and with position in the system;
- (vi)
- Temperature and thus the physical properties of air are constant both in space and time.
2.1. First Assumption
2.2. Second Assumption
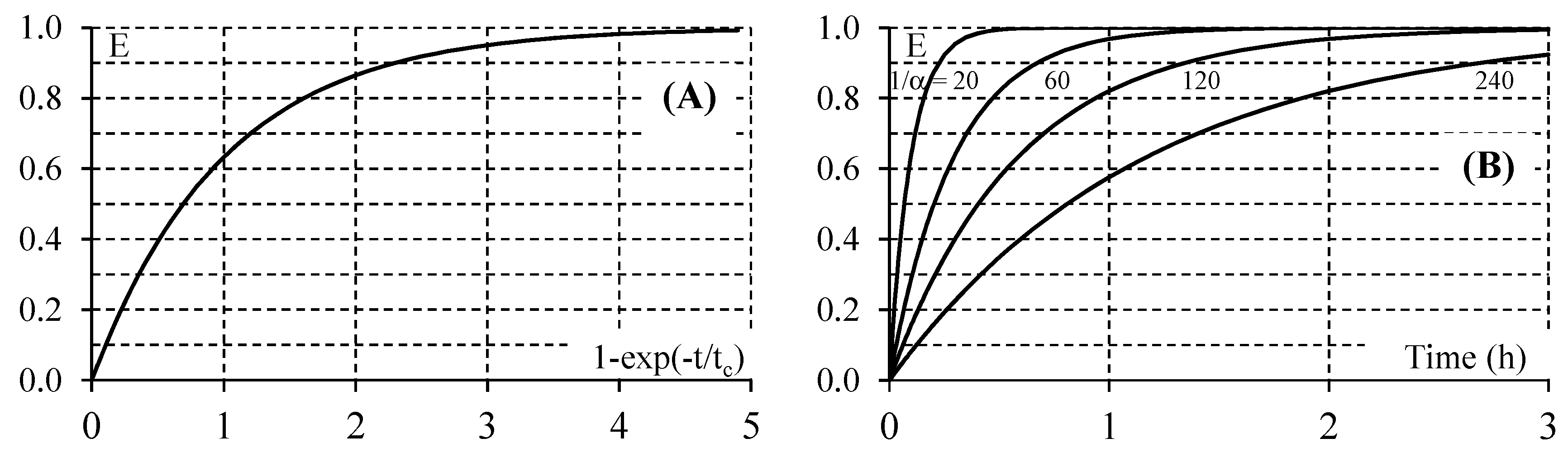
3. Discussion
Can the Model Be Used in a Large Closed Chamber?
4. Conclusions
Author Contributions
Conflicts of Interest
Appendix A. Nomenclature
- A: cross-sectional area of the PCO device (m2)
- C: pollutant concentration (mol∙m−3)
- CADR: Clean Air Delivery Rate (m3∙s−1)
- E: efficiency (dimensionless)
- k: overall degradation rate constant (s−1)
- ke: pollutant decay rate constant with the PCO device in operation (s−1)
- kn: natural decay rate constant (s−1)
- L: length of the PCO device (m)
- Q: flow rate (m3∙s−1)
- r: degradation rate (mol m−3∙s−1)
- t: time (s)
- tc: time constant of the closed-loop reactor (s)
- V: chamber volume (m3)
- VP: PCO device volume (m3)
- VR: reservoir volume (m3)
Appendix B. Greek letters
- τP: residence time in the PCO device (s)
- τR: residence time in the reservoir (s)
- α: fractional yield of the treated flow rate (dimensionless)
References
- Seppanen, O.A.; Fisk, W.J. Some quantitative relations between indoor environmental quality and work performance or health. Lawrence Berkeley Natl. Lab. 2006, 12, 957–973. [Google Scholar] [CrossRef]
- Zhong, L.; Haghighat, F. Photocatalytic air cleaners and materials technologies—Abilities and limitations. Build. Environ. 2015, 91, 191–203. [Google Scholar] [CrossRef]
- Destaillats, H.; Sleiman, M.; Sullivan, D.P.; Jacquiod, C.; Sablayrolles, J.; Molins, L. Key parameters influencing the performance of photocatalytic oxidation (PCO) air purification under realistic indoor conditions. Appl. Catal. B Environ. 2012, 128, 159–170. [Google Scholar] [CrossRef]
- Paz, Y. Application of TiO2 photocatalysis for air treatment: Patents’ overview. Appl. Catal. B Environ. 2010, 99, 448–460. [Google Scholar] [CrossRef]
- Costarramone, N.; Kartheuser, B.; Pecheyran, C.; Pigot, T.; Lacombe, S. Efficiency and harmfulness of air-purifying photocatalytic commercial devices: From standardized chamber tests to nanoparticles release. Catal. Today 2015, 252, 35–40. [Google Scholar] [CrossRef]
- Mills, A.; Hill, C.; Robertson, P. K.J. Overview of the current ISO tests for photocatalytic materials. J. Photochem. Photobiol. A Chem. 2012, 237, 7–23. [Google Scholar] [CrossRef]
- Kartheuser, B.; Costarramone, N.; Pigot, T.; Lacombe, S. NORMACAT project: Normalized closed chamber tests for evaluation of photocatalytic VOC treatment in indoor air and formaldehyde determination. Environ. Sci. Pollut. Res. 2012, 19, 3763–3771. [Google Scholar] [CrossRef] [PubMed]
- Disdier, J.; Pichat, P.; Mas, D. Measuring the effect of photocatalytic purifiers on indoor air hydrocarbons and carbonyl pollutants. J. Air Waste Manag. Assoc. 2005, 55, 88–96. [Google Scholar] [CrossRef] [PubMed]
- Batault, F.; Héquet, V.; Raillard, C.; Thévenet, F.; Locoge, N.; Le Coq, L. How chemical and physical mechanisms enable the influence of the operating conditions in a photocatalytic indoor air treatment device to be modeled. Chem. Eng. J. 2017, 307, 766–775. [Google Scholar] [CrossRef]
- Moulis, F.; Krýsa, J. Photocatalytic degradation of several VOCs (n-hexane, n-butyl acetate and toluene) on TiO2 layer in a closed-loop reactor. Catal. Today 2013, 209, 153–158. [Google Scholar] [CrossRef]
- Taranto, J.; Frochot, D.; Pichat, P. Photocatalytic air purification: Comparative efficacy and pressure drop of a TiO2-coated thin mesh and a honeycomb monolith at high air velocities using a 0.4 m3 close-loop reactor. Sep. Purif. Technol. 2009, 67, 187–193. [Google Scholar] [CrossRef]
- Suzuki, K. Photocatalytic Air Purification on TiO2 Coated Honeycomb Support, Proceedings of the First International Conférence on TiO2 Photocatalytic Purification and Treatment of Air and Water; Ollis, D.F., Al-Ekabi, H., Eds.; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1993; p. 421. [Google Scholar]
- Sauer, M.L.; Ollis, D.F. Photocatalyzed oxidation of ethanol and acetaldehyde in humidified air. J. Catal. 1996, 158, 570–582. [Google Scholar] [CrossRef]
- Nimlos, M.R.; Wolfrum, E.J.; Brewer, M.L.; Fennell, J.A.; Bintner, G. Gas-phase heterogeneous photocatalytic oxidation of ethanol: Pathways and kinetic modeling. Environ. Sci. Technol. 1996, 30, 3102–3110. [Google Scholar] [CrossRef]
- Li Puma, G.; Salvadó-Estivill, I.; Obee, T.N.; Hay, S.O. Kinetics rate model of the photocatalytic oxidation of trichloroethylene in air over TiO2 thin films. Sep. Purif. Technol. 2009, 67, 226–232. [Google Scholar] [CrossRef]
- Mo, J.; Zhang, Y.; Xu, Q.; Lamson, J.J.; Zhao, R. Photocatalytic purification of volatile organic compounds in indoor air: A literature review. Atmos. Environ. 2009, 43, 2229–2246. [Google Scholar] [CrossRef]
- Davis, A.P.; Hao, O.J. Reactor dynamics in the evaluation of photocatalytic oxidation kinetics. J. Catal. 1991, 131, 285–288. [Google Scholar] [CrossRef]
- Walker, A.T.S.; Wragg, A.A. The modelling of concentration-time relationships in recirculating electrochemical reactor systems. Electrochim. Acta 1977, 22, 1129–1134. [Google Scholar] [CrossRef]
- Davis, A.P.; Hao, O.J. Reply to comments on “reactor dynamics in the evaluation of photocatalytic oxidation kinetics”. J. Catal. 1992, 136, 629–630. [Google Scholar] [CrossRef]
- Wolfrum, E.J.; Turchi, C.S. Comments on “reactor dynamics in the evaluation of photocatalytic oxidation kinetics”. J. Catal. 1992, 136, 626–628. [Google Scholar] [CrossRef]
- Noh, K.-C.; Oh, M.-D. Variation of clean air delivery rate and effective air cleaning ratio of room air cleaning devices. Build. Environ. 2015, 84, 44–49. [Google Scholar] [CrossRef]
- Ginestet, A. Development and Evaluation of a New Test Method for Portable Air Cleaners—CR15_New Test Method for Portable Air Cleaners. Available online: http://www.aivc.org/sites/default/files/members_area/medias/pdf/CR/CR15_New%20test%20method%20for%20portable%20air%20cleaners.pdf (accessed on 17 September 2016).
- Zhang, Y.; Mo, J.; Li, Y.; Sundell, J.; Wargocki, P.; Zhang, J.; Little, J.C.; Corsi, R.; Deng, Q.; Leung, M.H.K.; et al. Can commonly-used fan-driven air cleaning technologies improve indoor air quality? A literature review. Atmos. Environ. 2011, 45, 4329–4343. [Google Scholar] [CrossRef]
- ANSI/AHAM (American National Standards Institute/Association of Home Appliance Manufacturers) AC-1-2006 Air Cleaners—Portable—CADR; AHAM: Washington, DC, USA, 2006.
- Kim, H.-J.; Han, B.; Kim, Y.-J.; Yoon, Y.-H.; Oda, T. Efficient test method for evaluating gas removal performance of room air cleaners using FTIR measurement and CADR calculation. Build. Environ. 2012, 47, 385–393. [Google Scholar] [CrossRef]
- Guieysse, B.; Hort, C.; Platel, V.; Munoz, R.; Ondarts, M.; Revah, S. Biological treatment of indoor air for VOC removal: Potential and challenges. Biotechnol. Adv. 2008, 26, 398–410. [Google Scholar] [CrossRef] [PubMed]
- Debono, O.; Thévenet, F.; Gravejat, P.; Héquet, V.; Raillard, C.; Le Coq, L.; Locoge, N. Gas phase photocatalytic oxidation of decane at ppb levels: Removal kinetics, reaction intermediates and carbon mass balance. J. Photochem. Photobiol. A Chem. 2013, 258, 17–29. [Google Scholar] [CrossRef]
- Debono, O.; Thevenet, F.; Gravejat, P.; Hequet, V.; Raillard, C.; Lecoq, L.; Locoge, N. Toluene photocatalytic oxidation at ppbv levels: Kinetic investigation and carbon balance determination. Appl. Catal. B Environ. 2011, 106, 600–608. [Google Scholar] [CrossRef]
- Ollis, D.F. Photocatalytic purification and remediation of contaminated air and water. Comptes Rendus de l’Académie des Sci. Series IIC Chem. 2000, 3, 405–411. [Google Scholar] [CrossRef]
- Peral, J.; Domènech, X.; Ollis, D.F. Heterogeneous photocatalysis for purification, decontamination and deodorization of air. J. Chem. Technol. Biotechnol. 1997, 70, 117–140. [Google Scholar] [CrossRef]
- AFNOR (Association Française de Normalisation) XP B44-013—Photocatalyse—Méthode d’essais et d’analyses pour la mesure d’efficacité de systèmes photocatalytiques pour l’élimination des composés organiques volatils/odeurs dans l’air intérieur en recirculation—Test en enceinte confinée. Available online: http://portailgroupe.afnor.fr/public_espacenormalisation/AFNORB44A/3%20pollutec-bk.pdf (accessed on 17 September 2016).
- Sample Availability: Not available.
| Time (s) | Time (h) | Difference (%) |
|---|---|---|
| 900 | 0.25 | 0.04 |
| 2700 | 0.75 | 0.16 |
| 5400 | 1.50 | 0.83 |
| 9000 | 2.50 | 3.00 |
| 10800 | 3.00 | 7.35 |
| 13500 | 3.75 | 23.72 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumont, É.; Héquet, V. Determination of the Clean Air Delivery Rate (CADR) of Photocatalytic Oxidation (PCO) Purifiers for Indoor Air Pollutants Using a Closed-Loop Reactor. Part I: Theoretical Considerations. Molecules 2017, 22, 407. https://doi.org/10.3390/molecules22030407
Dumont É, Héquet V. Determination of the Clean Air Delivery Rate (CADR) of Photocatalytic Oxidation (PCO) Purifiers for Indoor Air Pollutants Using a Closed-Loop Reactor. Part I: Theoretical Considerations. Molecules. 2017; 22(3):407. https://doi.org/10.3390/molecules22030407
Chicago/Turabian StyleDumont, Éric, and Valérie Héquet. 2017. "Determination of the Clean Air Delivery Rate (CADR) of Photocatalytic Oxidation (PCO) Purifiers for Indoor Air Pollutants Using a Closed-Loop Reactor. Part I: Theoretical Considerations" Molecules 22, no. 3: 407. https://doi.org/10.3390/molecules22030407
APA StyleDumont, É., & Héquet, V. (2017). Determination of the Clean Air Delivery Rate (CADR) of Photocatalytic Oxidation (PCO) Purifiers for Indoor Air Pollutants Using a Closed-Loop Reactor. Part I: Theoretical Considerations. Molecules, 22(3), 407. https://doi.org/10.3390/molecules22030407