Characterization at 25 °C of Sodium Hyaluronate in Aqueous Solutions Obtained by Transport Techniques
Abstract
:1. Introduction
2. Results and Discussion
2.1. Viscosity Data
| cNaHy [g·dm−3] | 1 | 0.7 | 0.5 | 0.25 | 0.1 |
| rel | 56.4 | 29.3 | 13.4 | 6.2 | 2.3 |
| ηspec | 55.4 | 28.3 | 12.4 | 5.2 | 1.3 |
| ηred [dm3·g−1] | 55.4 | 40.5 | 24.8 | 20.8 | 13.3 |
| [η] [dm3·g−1] | 7.27 | ||||
| kH | 0.88 | ||||
2.2. Concentration Dependence of Mutual Diffusion Coefficient, D, at Infinitesimal and Finite Concentrations
| c/(g·dm−3) | D ± SD (a)/(10−9 m2·s−1) |
|---|---|
| 1.000 2.000 3.000 4.000 5.000 | 1.232 ± 0.040 1.110 ± 0.030 1.008 ± 0.037 0.901 ± 0.038 0.786 ± 0.040 |
| D0 = 1.333 × 10−9 m2·s−1 (b) |
| c/(g·dm−3) | D ± SD(a)/(10−9 m2·s−1) |
|---|---|
| 0.010 0.025 0.050 0.100 0.250 1.000 | 0.780 ± 0.020 0.670 ± 0.018 0.602 ± 0.021 0.619 ± 0.010 0.560 ± 0.015 0.500 ± 0.018 |
2.3. Influence of the Kinetic and the Thermodynamic Factors on the Behaviour Diffusion of NaHy in Aqueous Solutions at Finite Concentrations
| C (g·dm−3) | Δ1/10−9 m2·s−1 M = 1.8 × 106 Da (a) | FM 10−9 m2·s−1 (b) | FT 10−9 m2·s−1 (c) | F’T 10−9 m2·s−1 (d) |
|---|---|---|---|---|
| 0.000 0.010 0.025 0.050 0.100 0.250 1.000 | 0 5.00 × 10−4 5.01 × 10−4 5.01 × 10−4 5.01 × 10−4 5.02 × 10−4 5.03 × 10−4 | 1.333 1.333 1.333 1.333 1.333 1.333 1.333 | 1.000 0.585 0.503 0.452 0.464 0.420 0.375 | 1.000 0.877 0.860 0.812 (f) 1.087 2.605 21.15 |
2.4. Influence of the Viscosity Factor on the Behaviour Diffusion of Hyaluronate in Aqueous Solutions at Finite Concentrations
| c/(g·dm−3) | DG (a)/(10−9 m2·s−1) | ΔD/D% (b) | DG’ (c)/(10−9 m2·s−1) | ΔD/D% (d) |
|---|---|---|---|---|
| 0.010 0.025 0.050 0.100 0.250 1.000 | 1.141 0.949 0.742 0.580 0.215 0.024 | −32 −29 −19 +8.6 +160 +1983 | 1.001 0.816 0.602 0.630 0.560 0.650 | −22 −18 0.0 −1.7 0.0 −0.4 |
2.5. Hydrodynamic Radius of the Unit of NaHy
| c/(g·dm−3) | Rh/nm |
|---|---|
| 0.000 0.010 0.025 0.050 0.100 0.250 1.000 | 0.184 0.269 0.261 0.266 0.172 0.071 (a) 0.009 (a) |
3. Experimental Section
3.1. Materials
3.2. Methods
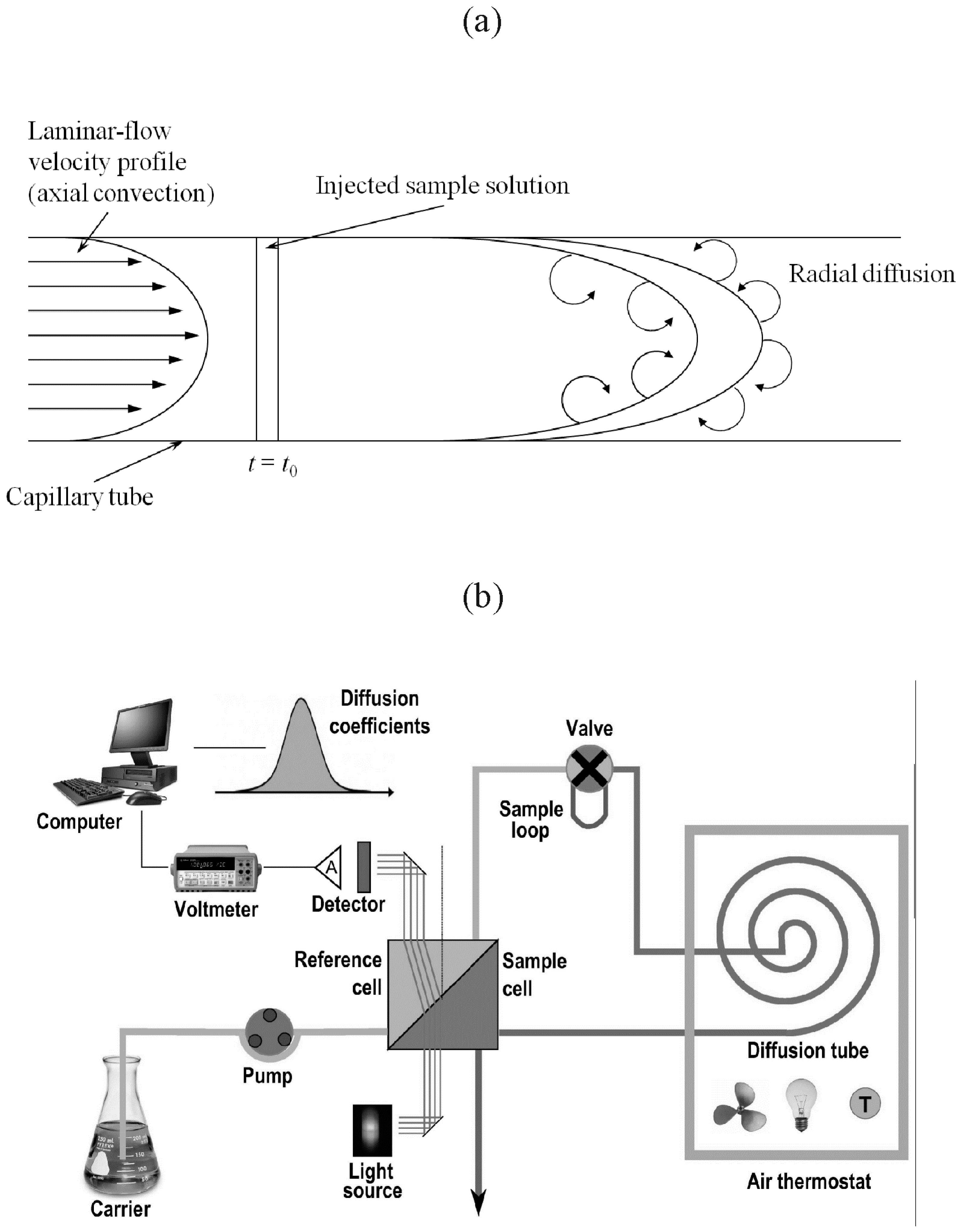
3.2.1. Mutual Diffusion Coefficients, D, Measurements from Taylor Technique
3.2.2. Viscosity, η, Measurements Obtained from Ubbelohde Viscometer
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Meyer, K.; Palmer, J.W. The polysaccharide of the vitreous humor. J. Biol. Chem. 1934, 107, 629–634. [Google Scholar]
- Garg, H.G.; Hales, Ch.A. Chemistry and Biology of Hyaluronan, 1st ed.; Elsevier: Oxford, UK, 2004. [Google Scholar]
- Gřundělová, L.; Mráček, A.; Kašpárková, V.; Minařík, A.; Smolka, P. The hyaluronan chain-chain interactions, conformations and coils size in solutions with quarternary salt. Carbohydr. Polym. 2013, 98, 1039–1044. [Google Scholar] [CrossRef] [PubMed]
- Verissimo, L.M.P.; Valada, T.I.C.; Sobral, A.J.F.N.; Azevedo, E.E.F.G.; Azevedo, M.L.G.; Ribeiro, A.C.F. Mutual diffusion of sodium hyaluranate in aqueous solutions. J. Chem. Thermodyn. 2014, 71, 14–18. [Google Scholar] [CrossRef]
- Scott, J.E. Supramolecular organisation of extracellular matrix glycosaminoglycans, in vitro and in the tissues. FASEB J. 1992, 6, 2639–2645. [Google Scholar] [PubMed]
- Scott, J.E.; Cummings, C.; Brass, A.; Chen, Y. Secondary and tertiary structures of hyaluronan in aqueous solution, investigated by rotary shadowing-electron microscopy and computer simulation. Hyaluronan is a very efficient network-forming polymer. Biochem. J. 1991, 274, 699–705. [Google Scholar]
- Heatley, F.; Scott, J.E. A water molecule participates in the secondary structure of hyaluronan. Biochem. J. 1988, 172, 489–493. [Google Scholar]
- Mráček, A.; Benešová, K.; Minařík, T.; Urban, P.; Lapčík, L. The diffusion process of Sodium Hyaluronate (Na-Ha) and Na-Ha-n-alkyl derivatives films swelling. J. Biomed. Mater. Res. 2007, 83A, 184–190. [Google Scholar] [CrossRef]
- Mráček, A.; Varhaníková, J.; Gřundělová, L.; Pokopcová, A.; Lehocký, M.; Velebný, V. The influence of Hofmeister series ions on Hyaluronan swelling and viscosity. Molecules 2008, 13, 1025–1034. [Google Scholar] [CrossRef] [PubMed]
- Mráček, A. The Measurement of Polymer Swelling Processes by an Interferometric Method and Evaluation of Diffusion Coefficients. Int. J. Mol. Sci. 2010, 11, 532–543. [Google Scholar] [CrossRef] [PubMed]
- Tyrrel, H.J.V. Diffusion and Heat Flow in Liquids, 1st ed.; Elsevier: London, UK, 1961. [Google Scholar]
- Loh, W. Taylor dispersion technique for investigation of diffusion in liquids and its applications. Quím. Nova 1997, 20, 541–545. [Google Scholar] [CrossRef]
- Barthel, J.; Gores, J.H.J.; Lohr, C.M.; Seidl, J.J. Taylor dispersion measurements at low electrolyte concentrations. I. Tetraalkylammonium perchlorate aqueous solutions. J. Solut. Chem. 1996, 25, 921–935. [Google Scholar]
- Callendar, R.; Leaist, D.G. Diffusion coefficients for binary, ternary, and polydisperse solutions from peak-width analysis of Taylor dispersion profiles. J. Solut. Chem. 2006, 35, 353–379. [Google Scholar] [CrossRef]
- Barros, M.C.F.; Ribeiro, A.C.F.; Esteso, M.A.; Lobo, V.M.M.; Leaist, D.G. Diffusion of levodopa in aqueous solutions of hydrochloric acid at 25 degrees. J. Chem. Thermodyn. 2014, 72, 44–47. [Google Scholar] [CrossRef]
- Barros, M.C.F.; Ribeiro, A.C.F.; Valente, A.J.M.; Lobo, V.M.M.; Cabral, A.M.T.D.P.V.; Veiga, F.J.B.; Teijeiro, C.; Esteso, M.A. Mass transport techniques as a tool for a better understanding of the structure of l-dopa aqueous solutions. Int. J. Pharm. 2013, 447, 293–297. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, A.C.F.; Rodrigo, M.M.; Barros, M.C.F.; Verissimo, L.M.P.; Romero, C.; Valente, A.J.M.; Esteso, M.A. Mutual diffusion coefficients of L-glutamic acid and monosodium L-glutamate in aqueous solutions at T = 298.15 K. J. Chem. Thermodyn. 2014, 74, 133–137. [Google Scholar] [CrossRef]
- Ribeiro, A.C.F.; Lobo, V.M.M.; Leaist, D.G.; Natividade, J.J.S.; Veríssimo, L.P.; Barros, M.C.F.; Cabral, A.M.T.D.P.V. Binary diffusion coefficients for aqueous solutions of lactic acid. J. Solut. Chem. 2005, 34, 1009–1016. [Google Scholar] [CrossRef]
- Ribeiro, A.C.F.; Valente, A.J.M.; Santos, C.I.A.V.; Prazeres, P.M.R.A.; Lobo, V.M.M.; Burrows, H.D.; Esteso, M.A.; Cabral, A.M.T.D.P.V.; Veiga, F.J.B.J. Binary mutual diffusion coefficients of aqueous solutions of α-cyclodextrin, 2-hydroxypropyl-α-cyclodextrin and 2-hydroxypropyl-β-cyclodextrin at temperatures from 298.15 K to 312.15 K. J. Chem. Eng. Data 2007, 52, 586–590. [Google Scholar] [CrossRef]
- Ribeiro, A.C.F.; Santos, C.I.A.V.A.; Valente, J.M.; Ascenso, O.S.; Lobo, V.M.M.; Burrows, H.D.; Cabral, A.M.T.D.P.V.; Veiga, F.J.B.; Teijeiro, C.; Esteso, M.A.J. Some transport properties of gamma-cyclodextrin aqueous solutions at 298.15 K and 310.15 K. J. Chem. Eng. Data 2008, 53, 755–759. [Google Scholar] [CrossRef]
- Ribeiro, A.C.F.; Fabela, I.; Sobral, A.J.F.N.; Verissimo, L.M.P.; Barros, M.C.F.; Melia Rodrigo, M.; Esteso, M.A. Diffusion of sodium alginate in aqueous solutions at T = 298.15 K. J. Chem. Thermodyn. 2014, 74, 263–268. [Google Scholar] [CrossRef]
- Rodrigo, M.M.; Valente, A.J.M.; Barros, M.C.F.; Verissimo, L.M.P.; Romero, C.; Esteso, M.A.; Ribeiro, A.C.F. Mutual diffusion coefficients of l-lysine in aqueous solution. J. Chem. Thermodyn. 2014, 74, 227–230. [Google Scholar] [CrossRef]
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions, 2nd ed.; Dover Publications Inc.: New York, NY, USA, 2002. [Google Scholar]
- Harned, H.S.; Owen, B.B. The Physical Chemistry of Electrolytic Solutions, 3rd ed.; Reinhold Publ. Corp.: New York, NY, USA, 1967. [Google Scholar]
- Bohdanecky, M.; Kovar, J. Viscosity of Polymer Solutions, 1st ed.; Jenkins, J.D., Ed.; Elsevier: Amsterdam, The Netherland, 1982; Volume 3. [Google Scholar]
- Scott, J.E.; Heatley, F. Hyaluronan forms specific stable tertiary structures in aqueous solution: A 13C NMR study. Biochemistry 1999, 96, 4850–4855. [Google Scholar]
- Šoltés, L.; Mendichi, R.; Lath, D.; Mach, M.; Bakoš, D. Molecular characteristics of some commercial high-molecular-weight hyaluronans. Biomed. Chromatogr. 2002, 16, 459–462. [Google Scholar] [CrossRef] [PubMed]
- Ruckmani, K.; Shaikh, S.Z.; Khalil, P.; Muneera, M.S.; Thusleem, O.A. Determination of sodium hyaluronate in pharmaceutical formulations by HPLC-UV. J. Pharm. Anal. 2013, 3, 324–329. [Google Scholar] [CrossRef]
- Caspersen, M.B.; Roubroeks, J.P.; Qun, L.; Shan, H.; Foght, J.; RuiDong, Z.; Tømmeraas, K. Thermal degradation and stability of sodium hyaluronate in solid state. Carbohydr. Polym. 2014, 107, 25–30. [Google Scholar] [CrossRef] [PubMed]
- Lowry, K.M.; Beavers, E.M. Thermal stability of sodium hyaluronate in aqueous solution. J. Biomed. Mater. Res. 1994, 28, 1239–1244. [Google Scholar] [CrossRef] [PubMed]
- Sample Availability: Samples of the compounds are available from the authors.
© 2015 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mráček, A.; Gřundělová, L.; Minařík, A.; Veríssimo, L.M.P.; Barros, M.C.F.; Ribeiro, A.C.F. Characterization at 25 °C of Sodium Hyaluronate in Aqueous Solutions Obtained by Transport Techniques. Molecules 2015, 20, 5812-5824. https://doi.org/10.3390/molecules20045812
Mráček A, Gřundělová L, Minařík A, Veríssimo LMP, Barros MCF, Ribeiro ACF. Characterization at 25 °C of Sodium Hyaluronate in Aqueous Solutions Obtained by Transport Techniques. Molecules. 2015; 20(4):5812-5824. https://doi.org/10.3390/molecules20045812
Chicago/Turabian StyleMráček, Aleš, Lenka Gřundělová, Antonín Minařík, Luís M. P. Veríssimo, Marisa C. F. Barros, and Ana C. F. Ribeiro. 2015. "Characterization at 25 °C of Sodium Hyaluronate in Aqueous Solutions Obtained by Transport Techniques" Molecules 20, no. 4: 5812-5824. https://doi.org/10.3390/molecules20045812
APA StyleMráček, A., Gřundělová, L., Minařík, A., Veríssimo, L. M. P., Barros, M. C. F., & Ribeiro, A. C. F. (2015). Characterization at 25 °C of Sodium Hyaluronate in Aqueous Solutions Obtained by Transport Techniques. Molecules, 20(4), 5812-5824. https://doi.org/10.3390/molecules20045812







