Theoretical Investigation on Nearsightedness of Finite Model and Molecular Systems Based on Linear Response Function Analysis
Abstract
:1. Introduction
2. Theoretical Background



 , because the number of electrons is conserved.
, because the number of electrons is conserved.
3. Results and Discussion
3.1. Model Systems
3.1.1. An Infinite Square Well Potential System








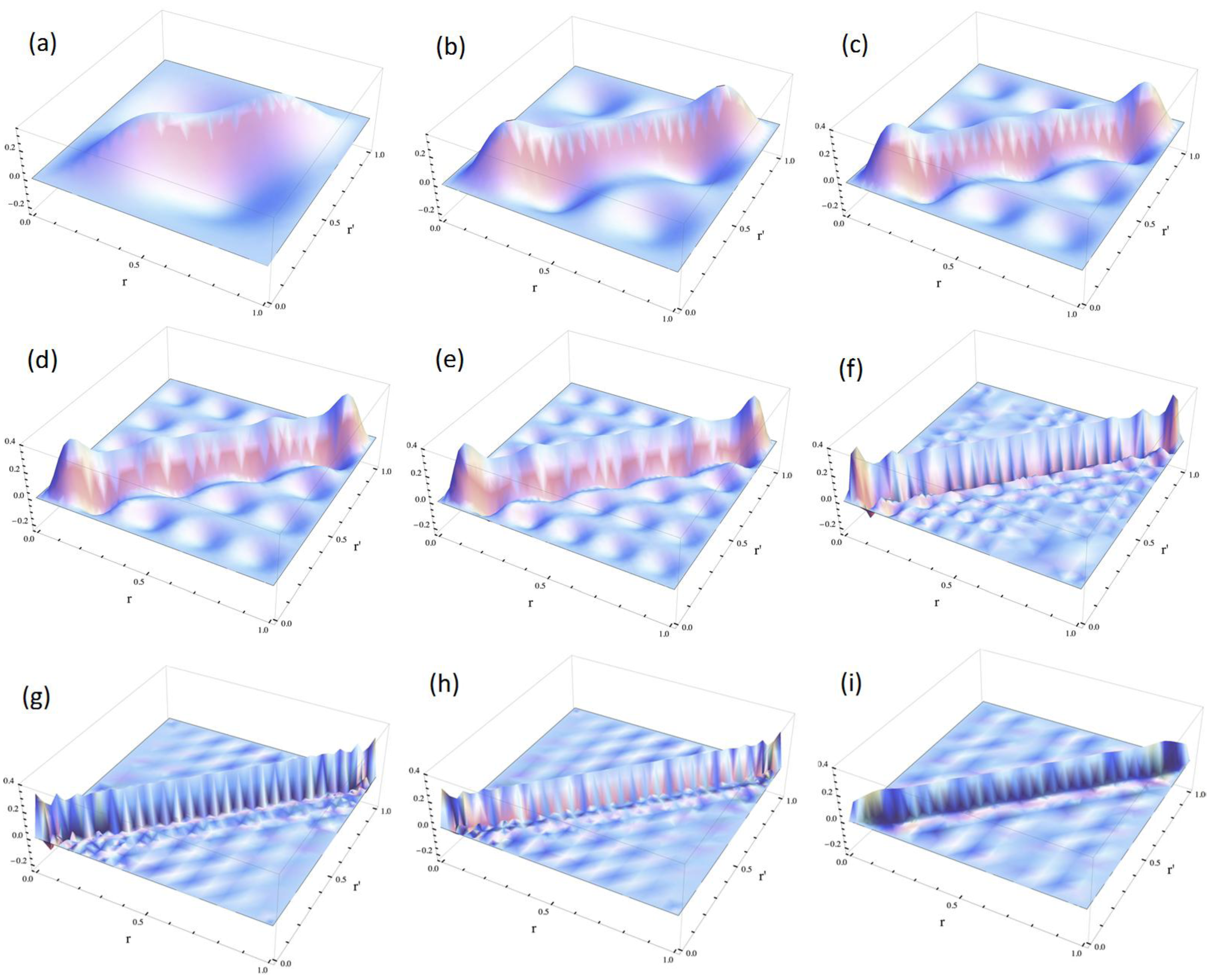
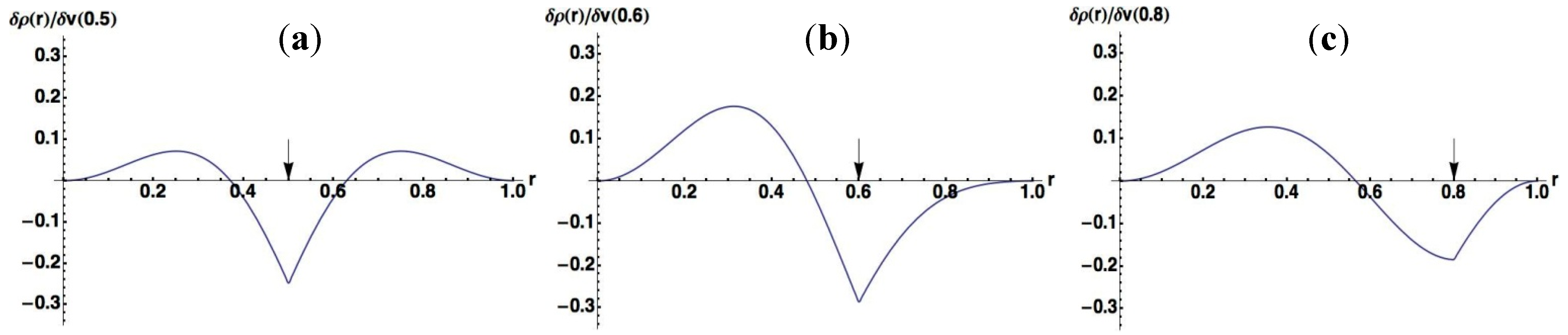
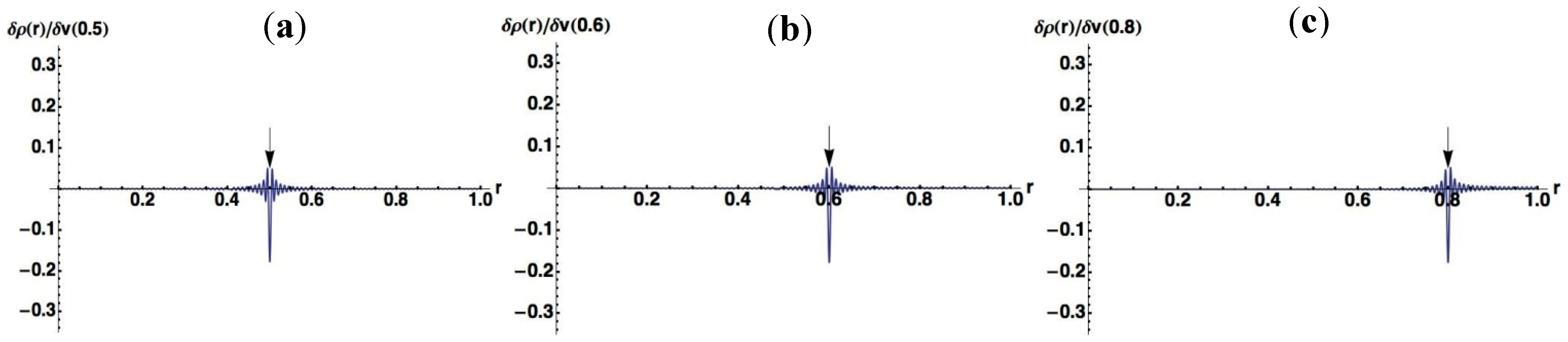
3.1.2. Double-well Potential Systems

 < V0, while the quasi-degeneracy is lifted for
< V0, while the quasi-degeneracy is lifted for  > V0:
> V0: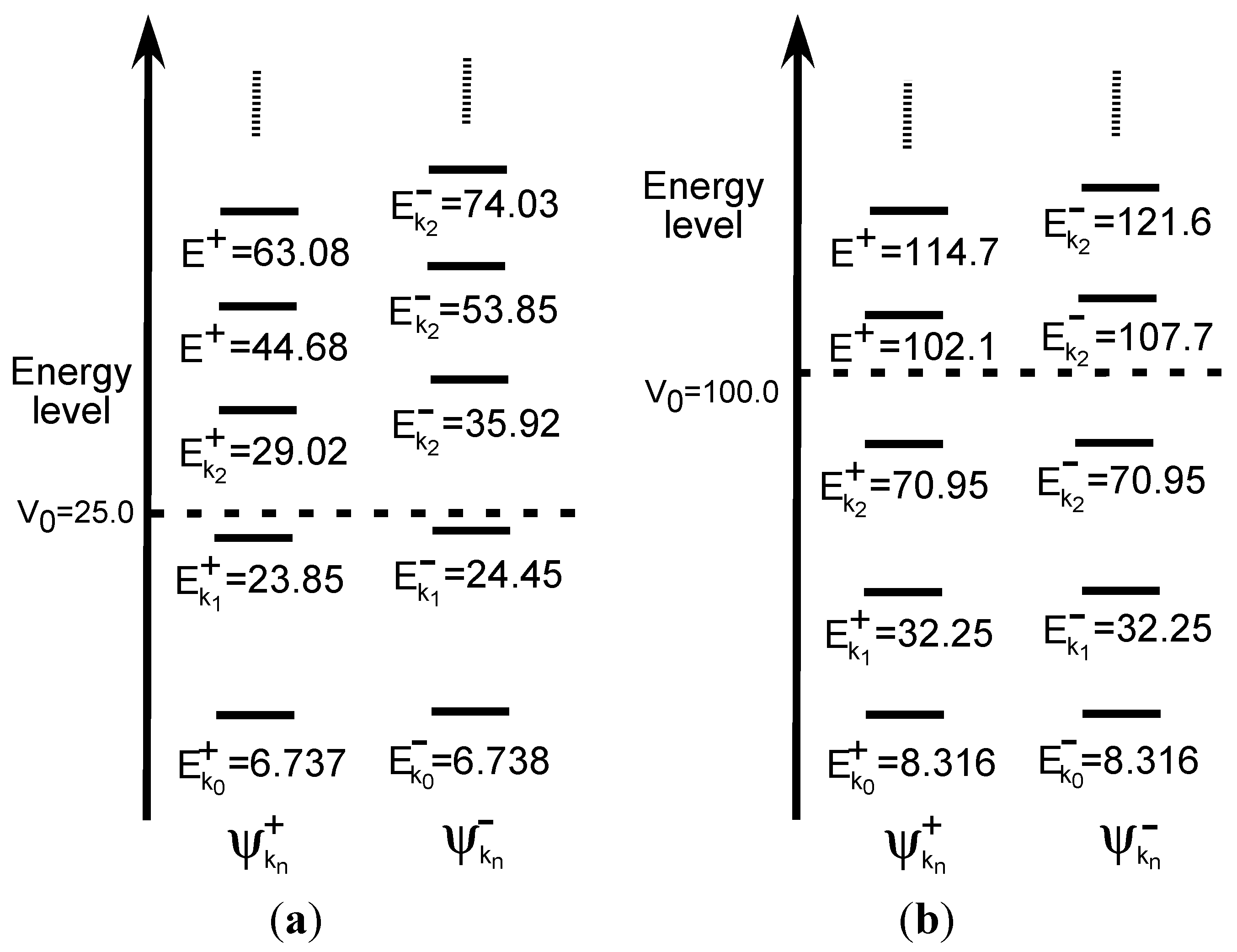
 < V0 are two and three for V0 = 25 and V0 = 100, respectively, as shown in Figure 4a,b. The exact eigenvalues are listed in the Section S2 in the Supplementary Materials. Now we performed the LRF analysis in a manner similar to that described in Section 3.1.1. We plotted LRFs for various numbers of Nocc for V0 = 25 in Figure 5 and V0 = 100 in Figure 6. For the plane of each plot, lines indicate the borders that divide the 1D space into three regions, −2 ≤ r(r′) ≤ −1, −1 ≤ r(r′) ≤ 1, and 1 ≤ r(r′) ≤ 2. For V0 = 25, there are four orbitals that have lower energies than the height of the barrier, V0. We can see from Figure 5a,b that there are significant nonlocal responses for Nocc = 1 and Nocc = 3 (Figure 5a,c), while there is no nonlocal responses for Nocc = 2 and Nocc = 4 (Figure 5b,d). For Nocc = 5 shown in Figure 5e, an amplitude appears in the central region, −1 ≤ r ≤ 1, that corresponds to the barrier region, because the electrons having energies higher than V0 = 25 exist. An interesting point is that the form of the amplitude within the central region, −1 ≤ r ≤ 1, in Figure 5e is similar to that in Figure 1a. This nonlocality of the central region reduces as Nocc increases as shown in Figure 5f–i. The LRF for Nocc = 50 shown in Figure 5i is similar to that of the single-well potential shown in Figure 1i, implying that NEM is a result of destructive interference among density amplitudes also in this case. A noteworthy point is that NEM seems to hold also for small numbers of electrons as shown in Figure 5b,d, which must be caused by a different mechanism. Similar results are observed in Figure 6. In particular, “NEM of small numbers of electrons” is also observed in Figure 6b–f, because there are three pairs of quasi-degenerate levels as shown in Figure 4b.
< V0 are two and three for V0 = 25 and V0 = 100, respectively, as shown in Figure 4a,b. The exact eigenvalues are listed in the Section S2 in the Supplementary Materials. Now we performed the LRF analysis in a manner similar to that described in Section 3.1.1. We plotted LRFs for various numbers of Nocc for V0 = 25 in Figure 5 and V0 = 100 in Figure 6. For the plane of each plot, lines indicate the borders that divide the 1D space into three regions, −2 ≤ r(r′) ≤ −1, −1 ≤ r(r′) ≤ 1, and 1 ≤ r(r′) ≤ 2. For V0 = 25, there are four orbitals that have lower energies than the height of the barrier, V0. We can see from Figure 5a,b that there are significant nonlocal responses for Nocc = 1 and Nocc = 3 (Figure 5a,c), while there is no nonlocal responses for Nocc = 2 and Nocc = 4 (Figure 5b,d). For Nocc = 5 shown in Figure 5e, an amplitude appears in the central region, −1 ≤ r ≤ 1, that corresponds to the barrier region, because the electrons having energies higher than V0 = 25 exist. An interesting point is that the form of the amplitude within the central region, −1 ≤ r ≤ 1, in Figure 5e is similar to that in Figure 1a. This nonlocality of the central region reduces as Nocc increases as shown in Figure 5f–i. The LRF for Nocc = 50 shown in Figure 5i is similar to that of the single-well potential shown in Figure 1i, implying that NEM is a result of destructive interference among density amplitudes also in this case. A noteworthy point is that NEM seems to hold also for small numbers of electrons as shown in Figure 5b,d, which must be caused by a different mechanism. Similar results are observed in Figure 6. In particular, “NEM of small numbers of electrons” is also observed in Figure 6b–f, because there are three pairs of quasi-degenerate levels as shown in Figure 4b. 
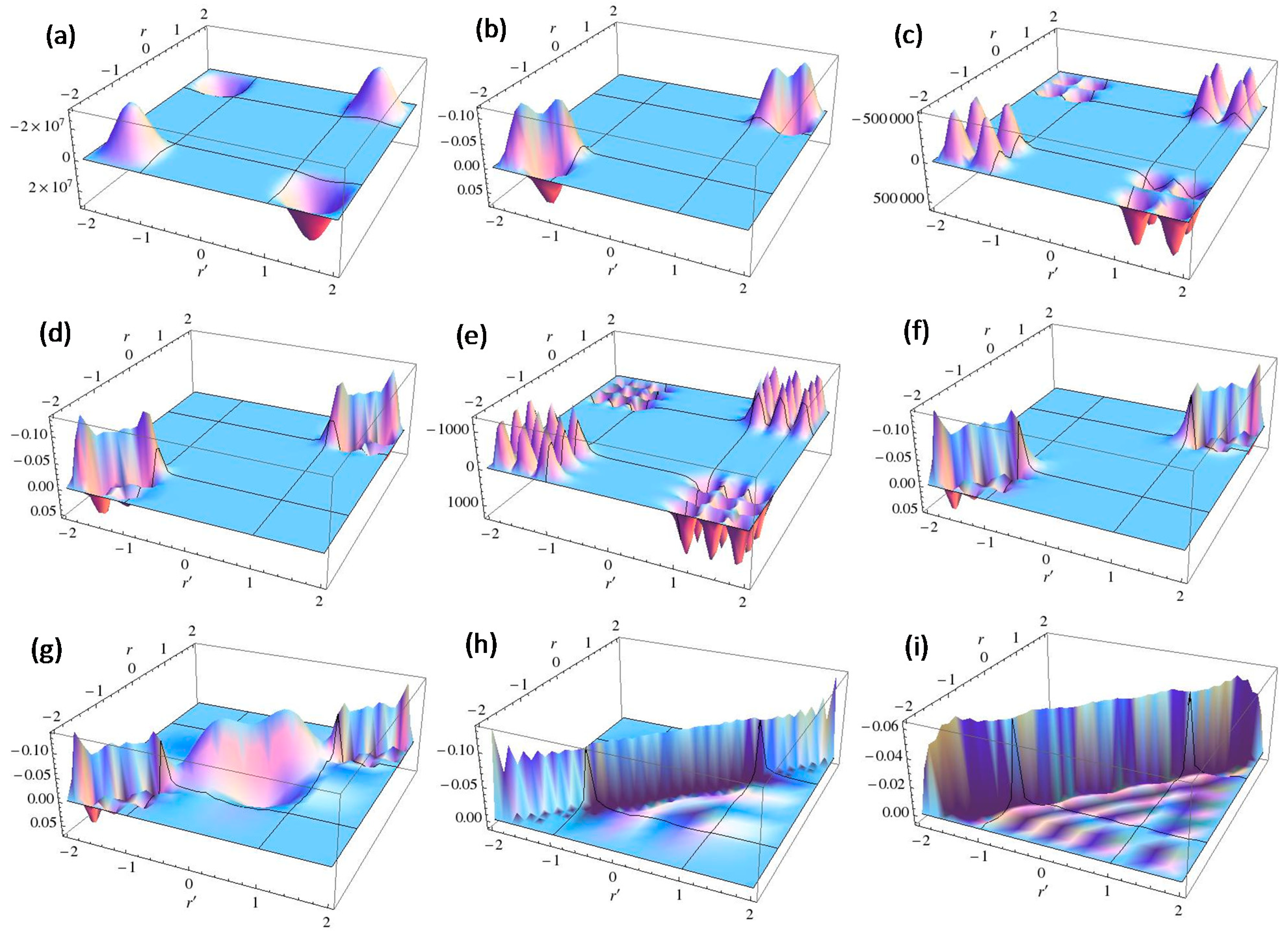
3.2. Molecular Systems
3.2.1. Molecular Systems’ Counterparts for the Model Systems



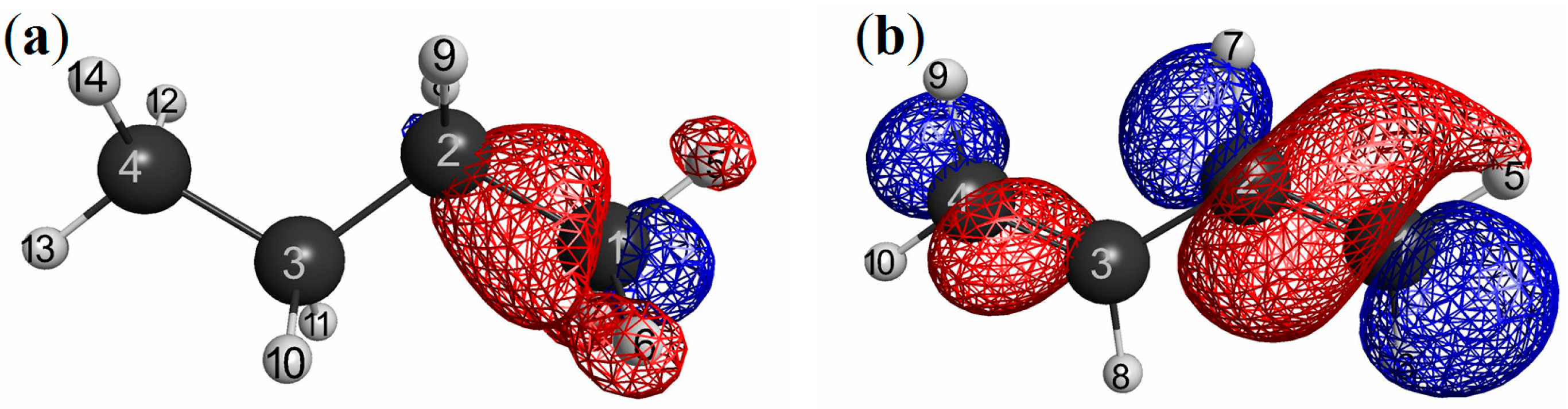
3.2.2. Dissociation of the Hydrogen Molecule: A Possible Mott-insulator Counterpart to NEM
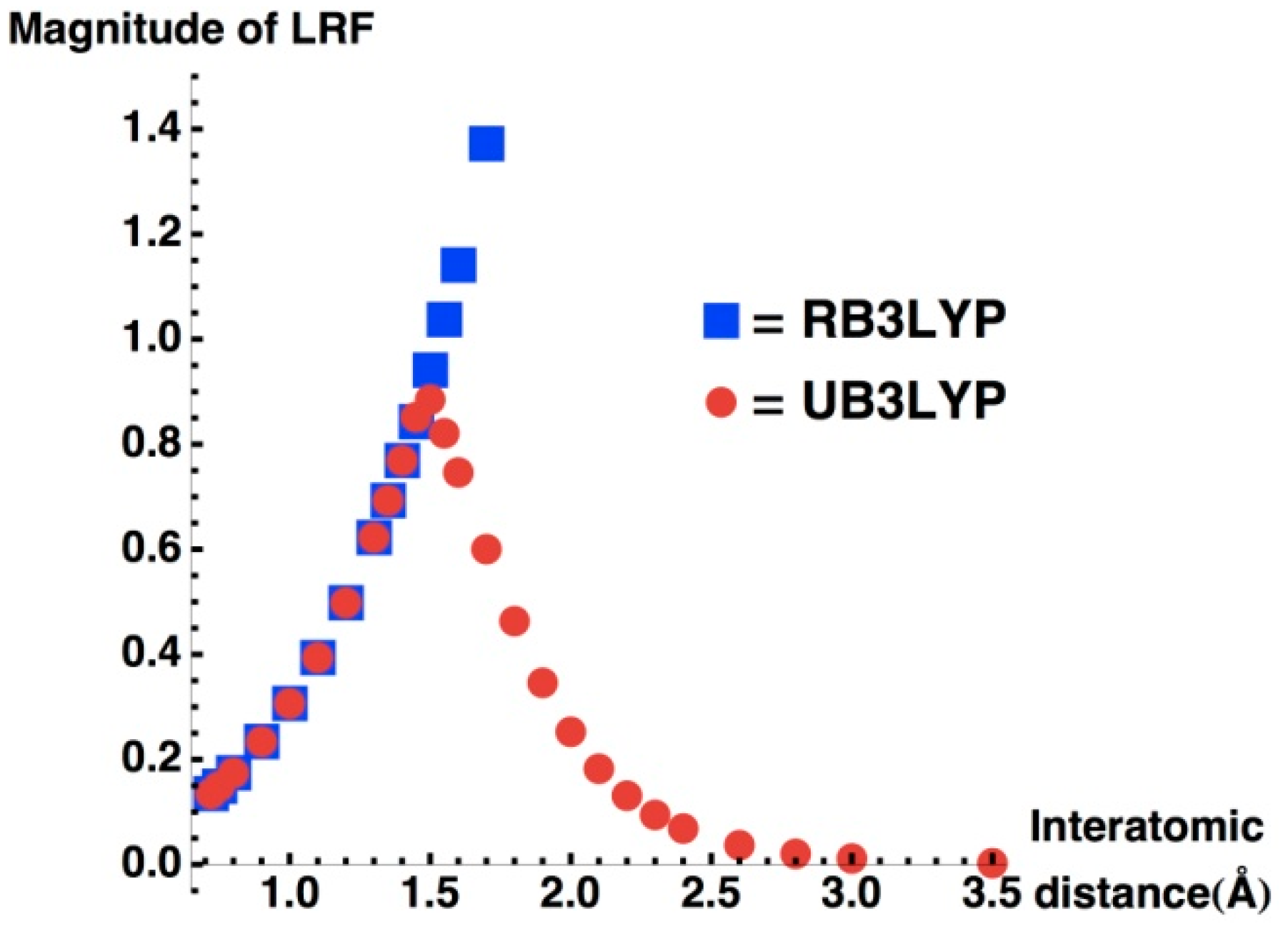
 with X being the right-atom as in the previous section, for the dissociation profile. We can see from this figure that the magnitude of LRF monotonically increases as the interatomic distance (R) increases for RB3LYP solutions. This is because the HOMO-LUMO gap in the denominator of the right-hand of Equation (15) decreases as the interatomic distance increases. For R < 1.5 Å, UB3LYP solutions are the same as the RB3LYP solutions. However, for R ≥ 1.5 Å, the magnitude of LRF decreases for UB3LYP solutions. This can be explained as follows. LRF of UB3LYP solutions is a sum of α and β parts:
with X being the right-atom as in the previous section, for the dissociation profile. We can see from this figure that the magnitude of LRF monotonically increases as the interatomic distance (R) increases for RB3LYP solutions. This is because the HOMO-LUMO gap in the denominator of the right-hand of Equation (15) decreases as the interatomic distance increases. For R < 1.5 Å, UB3LYP solutions are the same as the RB3LYP solutions. However, for R ≥ 1.5 Å, the magnitude of LRF decreases for UB3LYP solutions. This can be explained as follows. LRF of UB3LYP solutions is a sum of α and β parts:


 ).
).

3.2.3. Trialanine Peptide System: sp3 Junctions as a Possible Origin of NEM of Molecular Systems
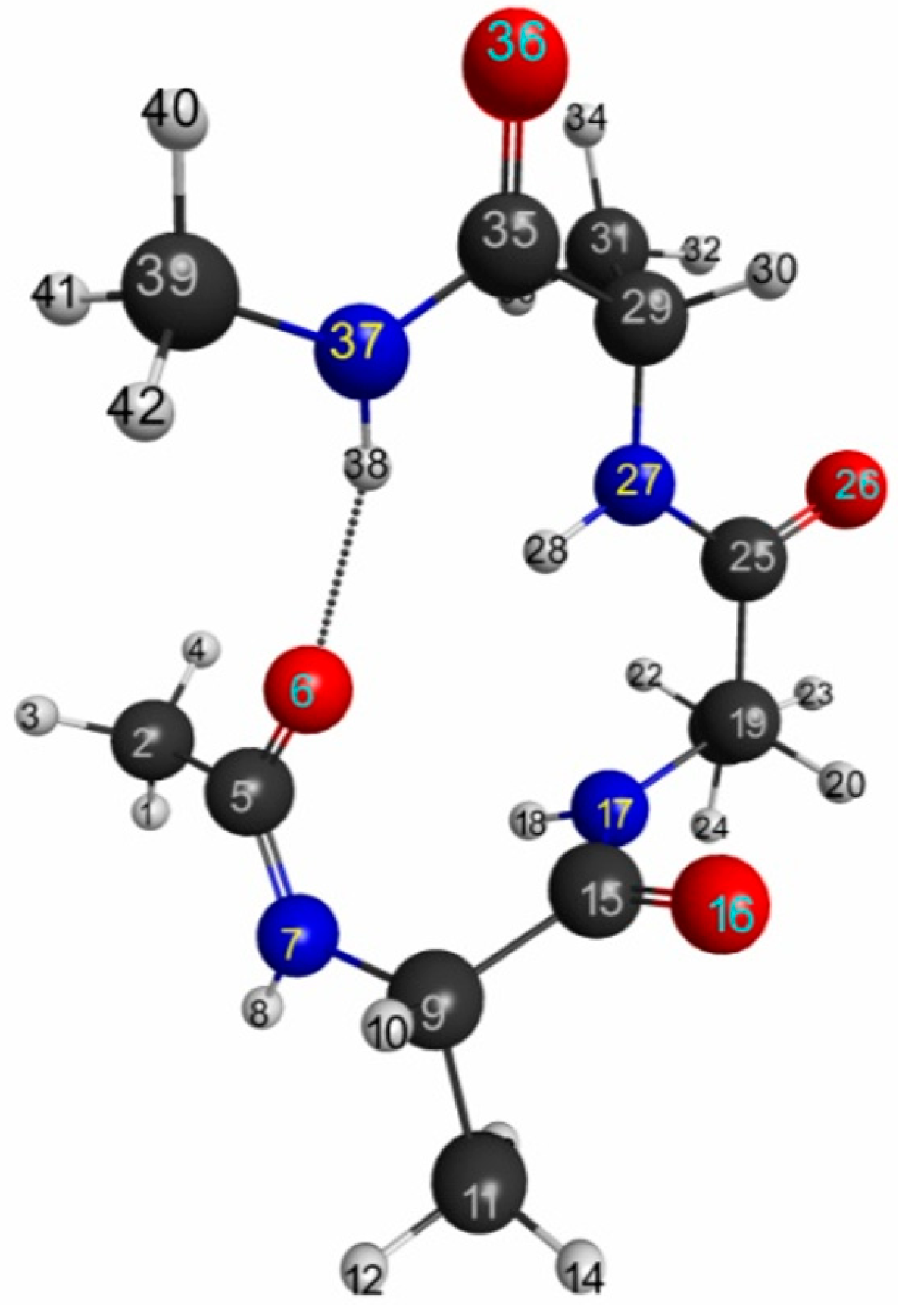
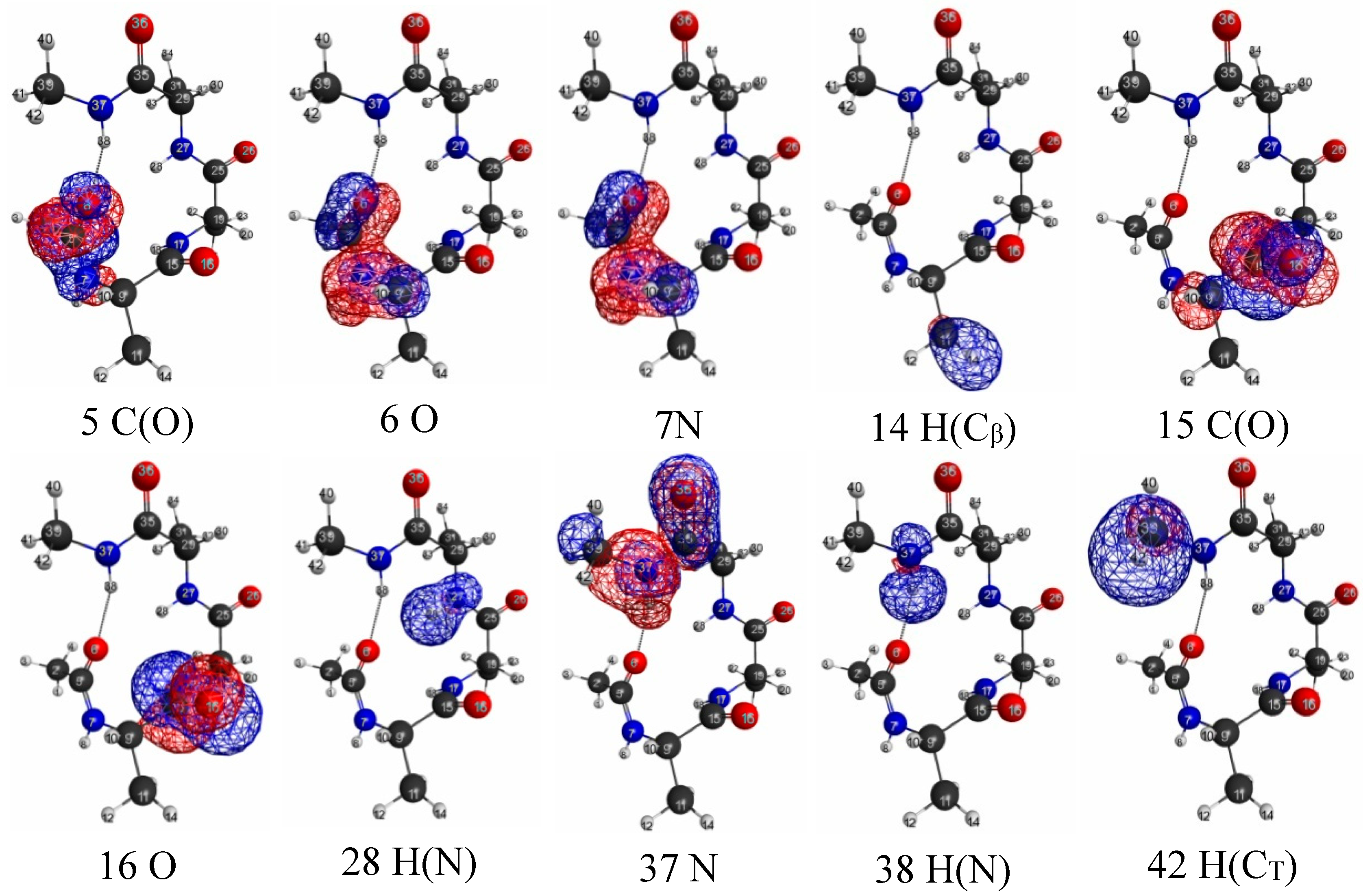
4. Conclusions
Supplementary Materials
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Warshel, A.; Karplus, M. Calculation of ground and excited state potential surfaces of conjugated molecules. I. Formulation and parametrization. J. Am. Chem. Soc. 1972, 94, 5612–5625. [Google Scholar]
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar]
- Kohn, W. Density functional and density matrix method scaling linearly with the number of atoms. Phys. Rev. Lett. 1996, 76, 3168–3171. [Google Scholar]
- Prodan, E.; Kohn, W. Nearsightedness of electronic matter. Proc. Natl. Acad. Sci. USA 2005, 112, 11635–11638. [Google Scholar]
- Kohn, W. Theory of insulating states. Phys. Rev. 1964, 133, A171–A181. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar]
- Kohn, W.; Sham, L.-J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar]
- Feynmann, R.P. Forces in molecules. Phys. Rev. 1939, 56, 340–343. [Google Scholar]
- Sukumar, M. A Matter of Density: Exploring the Electron Density Concept in the Chemical, Biological, and Materials Sciences; John-Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Friedel, J. The distribution of electrons round impurities in monovalent metals. Philos. Mag. 1952, 43, 153–189. [Google Scholar]
- Langer, J.S.; Vosko, S.H. The shielding of a fixed charge in a high-density electron gas. Philos. Mag. 1952, 43, 153–189. [Google Scholar]
- Kohn, W.; Vosko, S.H. Theory of nuclear resonance intensity in dilute alloys. Phys. Rev. 1960, 119, 912–918. [Google Scholar] [CrossRef]
- Ono, M.; Nishigata, Y.; Nishio, T.; Eguchi, T.; Hasegawa, Y. Electrostatic potential screened by a two-dimensional electron system: A real-space observation by scanning tunneling spectroscopy. Phys. Rev. Lett. 2006, 96, 016801:1–016801:4. [Google Scholar]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems, 3rd ed.; Dover Pubications: Mineola, NY, USA, 2003; pp. 171–183. [Google Scholar]
- Ayer, P.W.; Parr, R.G. Variational principles for describing chemical reactions. Reactivity indices based on the external potential. J. Am. Chem. Soc. 2001, 123, 2007–2015. [Google Scholar] [CrossRef]
- Geerlings, P.; Proft, F.D.; Langenaeker, W. Conceptual density functional theory. Chem. Rev. 2003, 103, 1793–1873. [Google Scholar]
- Berkowitz, M.; Parr, R.G. Molecular hardness and softness, local hardness and softness, hardness and softness kernels, and relations among these quantities. J. Chem. Phys. 1988, 88, 2554–2557. [Google Scholar] [CrossRef]
- Senet, P.J. Nonlinear electronic responses, Fukui functions and hardnesses as functionals of the groundstate electronic density. J. Chem. Phys. 1996, 105, 6471–6489. [Google Scholar]
- Sablon, N.; Proft, F.D.; Geerlings, P. The linear response kernel: Inductive and resonance effects quantified. J. Phys. Chem. Lett. 2010, 1, 1228–1234. [Google Scholar]
- Gonzalez-Suarez, M.; Aizman, A.; Contreras, R. Phenomenological chemical reactivity theory for mobile electrons. Theor. Chem. Acc. 2010, 126, 45–54. [Google Scholar]
- Mitito, E.; Putz, M.V. New Link between conceptual density functional theory and electron delocalization. J. Phys. Chem. A 2011, 115, 12459–12462. [Google Scholar] [CrossRef]
- Putz, M.V.; Chattaraj, P.K. Electrophilicity kernel and its hierarchy through softness in conceptual density functional theory. Int. J. Quantum Chem. 2013, 113, 2163–2171. [Google Scholar]
- Schiff, L.I. Quantum Mechanics, 3rd ed.; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Mathematica Ver. 9, Wolfram Research: Champaign, IL, USA. Available online: http://www.wolfram.com/mathematica (accessed on 25 August 2014).
- Yamanaka, S.; Yonezawa, Y.; Nakata, K.; Nishihara, S.; Okumura, M.; Takada, T.; Yamaguchi, K.; Nakamura, H. Locality and nonlocality of electronic structures of molecular systems: Toward QM/MM and QM/QM approaches. AIP Conf. Proc. 2012, 1504, 916–919. [Google Scholar]
- Ueda, K.; Yamanaka, S.; Nakata, K.; Ehara, M.; Okumura, M.; Yamaguchi, K.; Nakamura, H. Linear response function approach for the boundary problem of QM/MM methods. Int. J. Quantum Chem. 2013, 113, 336–341. [Google Scholar]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Jensen, F.; Dorigo, A.; Houk, K.N. A spin correction procedure for unrestricted Hartree-Fock and Moller-Plesset wavefunctions for singlet diradicals and polyradicals. Chem. Phys. Lett. 1988, 149, 537–542. [Google Scholar]
- Salomon-Ferrer, R.D.; Case, A.; Walker, R.C. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar]
- Kumar, S.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A.; Rosenberg, J.M. THE weighted histogram analysis method for free-energy calculations on biomolecules I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar]
- Sample Availability: Not available.
© 2014 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mitsuta, Y.; Yamanaka, S.; Yamaguchi, K.; Okumura, M.; Nakamura, H. Theoretical Investigation on Nearsightedness of Finite Model and Molecular Systems Based on Linear Response Function Analysis. Molecules 2014, 19, 13358-13373. https://doi.org/10.3390/molecules190913358
Mitsuta Y, Yamanaka S, Yamaguchi K, Okumura M, Nakamura H. Theoretical Investigation on Nearsightedness of Finite Model and Molecular Systems Based on Linear Response Function Analysis. Molecules. 2014; 19(9):13358-13373. https://doi.org/10.3390/molecules190913358
Chicago/Turabian StyleMitsuta, Yuki, Shusuke Yamanaka, Kizashi Yamaguchi, Mitsutaka Okumura, and Haruki Nakamura. 2014. "Theoretical Investigation on Nearsightedness of Finite Model and Molecular Systems Based on Linear Response Function Analysis" Molecules 19, no. 9: 13358-13373. https://doi.org/10.3390/molecules190913358
APA StyleMitsuta, Y., Yamanaka, S., Yamaguchi, K., Okumura, M., & Nakamura, H. (2014). Theoretical Investigation on Nearsightedness of Finite Model and Molecular Systems Based on Linear Response Function Analysis. Molecules, 19(9), 13358-13373. https://doi.org/10.3390/molecules190913358



