On Optimization of a Non-Endorreversible Curzon-Ahlborn Cycle

Abstract

A non-endoreversible Curzon and Ahlborn cycle is analyzed by introducing a factor of non-endoreversibility. The form of power output and ecological function, and the role of this factor is discussed. The Gutkowics-Krusin, Procaccia and Ross method to build a general expression for both the power output and the ecological function for this cycle is used. A numerical analysis of these expresions is made and the results are compared with other kind of approaches found in the literature of finite time thermodynamics.

1. Introduction

As it is known the Curzon and Ahlborn cycle [1] is a model of an endoreversible engine, shown in Figure 1. The efficiency of this cycle is a bound of real engines and it is written as

$${\eta }_{CA}=1-\sqrt{\frac{T_C}{T_H}},$$

(1)

where $T_C$ is the cold reservoir temperature and $T_H$ is the hot reservoir temperature. This endoreversible cycle is an engine in which entropy production during the exchange of heat between the system and its reservoirs of heat is only taken into account.

Equation (1) has been recovered by some procedures [2,3,4,5,6,7,8,9]. Particularly in reference [3] the optimal configuration of heat engines was studied. More recently this subject had been also studied by other authors [10,11,12,13,14]. On other hand, Gutkowics-Krusin, et al [9] introduced a procedure in which the power output of this cycle is took as a function of the compression ratio by using the parameter $\lambda$~${\left[\ln V_{\max }-\ln V_{\min }\right]}^{-1}$, where $V_{\max }$ and $V_{\min }$ are the maximun and the minimum volumes spanned in the cycle, respectively. Recently, with this method Ladino-Luna and de la Selva [15] by using Newton heat transfer law for ideal gas as working substance, and Ladino-Luna [16,17] for a van der Waals gas as working substance and by using Dulong and Petit heat transfer law, found the form of the function introduced by Angulo-Brown, named ecological function,

$$E=P-T_C\sigma ,$$

(2)

where P is the power output, $T_C$ is the temperature of cold reservoir and $\sigma$ is the total entropy production. They shown that ecological function has a similar property as power output when the compression ratio is taking into account, e. g. ecological efficiency obtained at maximum ecological function, with the definition $\epsilon =\frac{T_C}{T_H}$,

$${\eta }_E=1-\sqrt{\frac{{\epsilon }^2+\epsilon }{2}},$$

(3)

is a bound for efficiencies when the Curzon and Ahlborn model is performing at maximum ecological function, and when it is taking into account the time of all the processes in the cycle.

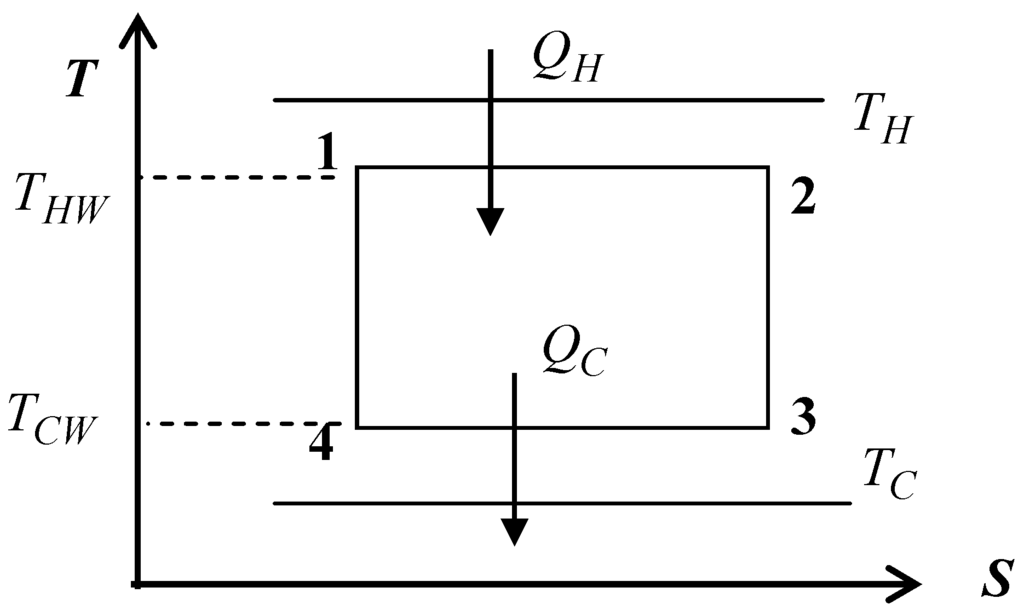
Figure 1. Curzon and Ahlborn cycle in the entropy, S, vs temperature, T, plane. $T_{HW}$ and $T_{CW}$ are the hot and cool temperatures of the isothermic processes of the cycle.

Figure 1. Curzon and Ahlborn cycle in the entropy, S, vs temperature, T, plane. $T_{HW}$ and $T_{CW}$ are the hot and cool temperatures of the isothermic processes of the cycle.

Angulo-Brown proposed an ecological criterion for finite-time Carnot heat engines, Equation (3), that represents a compromise between the high power output P and a loss power $T_C\sigma$. However Yan [18] showed that it might be more reasonable to use $E_0=P-T_0\sigma$ if the cold reservoir temperature $T_C$ is not equal to the enviroment temperature $T_0$ because in the definition of E two diferent quantities, exergy output a non-exergy $T_C\sigma$, were compared together. The criterion function $E_0$ could be more reasonable than Angulo-Brown criterion. Nevertheless, since $E_0\to E$ when $T_0\to T_C$ for the goal of this paper it can be used the optimization of E.

It is important to remark that Curzon and Ahlborn efficiency is an adequate approximation for conventional power plants, and ecological efficiency is the adequate approximation for modern power plants (nuclear and others) [19].

On other hand, except in reference [19], all of above authors consider an endoreversible Curzon and Ahlborn cycle; but in nature there is not any endoreversible engine. Thus other authors had analized the non-endoreversible Curzon and Ahlborn cycle [20,21,22,23,24,25,26].

Firstly Wu and Kiang [20] introduced a non-endoreversibility parameter, later Chen [21] analyzed the effect of thermal resistances, heat leakage and internal irreversibility by this non-endoreversibility parameter,

$$I_S\equiv \frac{\Delta S_C}{\Delta S_H},$$

(4)

where $\Delta S_C$ is the change of entropy obtained during the exchange of heat from the engine to cold reservoir, and $\Delta S_H$ is the change of entropy obtained during the exchange of heat from the hot reservoir to engine. Chen et al [22,23] carried out the ecological optimization for generalized irreversible Carnot engine with heat resistance, heat leakage and internal irreversibility for Newton heat transfer law, and linear phenomenological heat transfer law. Zhu et al [24,25] generalized convective heat transfer law $Q\propto {(\Delta T)}^n$, and generalized radiative heat transfer law $Q\propto \Delta (T^n)$. More recently the ecological optimization for generalized irreversible universal heat engine, including Diesel, Otto, Bryton Atkinson, Dual and Miller cycles, with heat resistance, heat leakage and internal irreversibility was carried out for newton heat transfer law [26]. The efficiency obtained by introducing this parameter, Equation (4), at maximum power output is [21],

$${\eta }_m=1-\sqrt{I_S\epsilon },I_S>1$$

(5)

Angulo-Brown et al [19] shown that a general property of endoreversible Curzon and Ahlborn cycle previously demostrated [27] can be extended for a non-endoreversible Curzon and Ahlborn cycle. Velasco et al [28] follow the idea in references [21], and they found expressions to measure possible reductions of undesired effects in heat engines operation. They pointed out that I_S is not depending of $\epsilon$ and rewrote equation (5) as,

$${\eta }_m=1-\sqrt{\frac{\epsilon }{I}},I\equiv \frac{1}{I_S},0<I<1.$$

(6)

Even more, Angulo-Brown et al [29] applied variational calcuclus to show that both the saving function [28] and a modified ecological criteria are equivalent.

In present work it is shown that the internal irreversibilities can be taken into account by replacing the ratio in the square root for ecological efficiency, Equation (3), by $\frac{{\epsilon }^2+\epsilon }{2I}$ in case of a non endoreversible Curzon and Ahlborn cycle and with instantaneous adiabats. More general expressions for non-instantaneous adiabats are presented also by using compression ratio. The Gutkowics-Krusin, Procaccia and Ross method [9] is combined with the Chen cyclic model [21] by taking into account the parameter of non-endoreversibility $I_S$ to obtain the form of power output function and of ecological function. Results are compared with others found in the literature of finite time thermodynamics.

2. Power output and ecological function for instantaneous adiabats

Consider the non-endoreversible Curzon and Ahlborn cycle model shown in Figure 2.

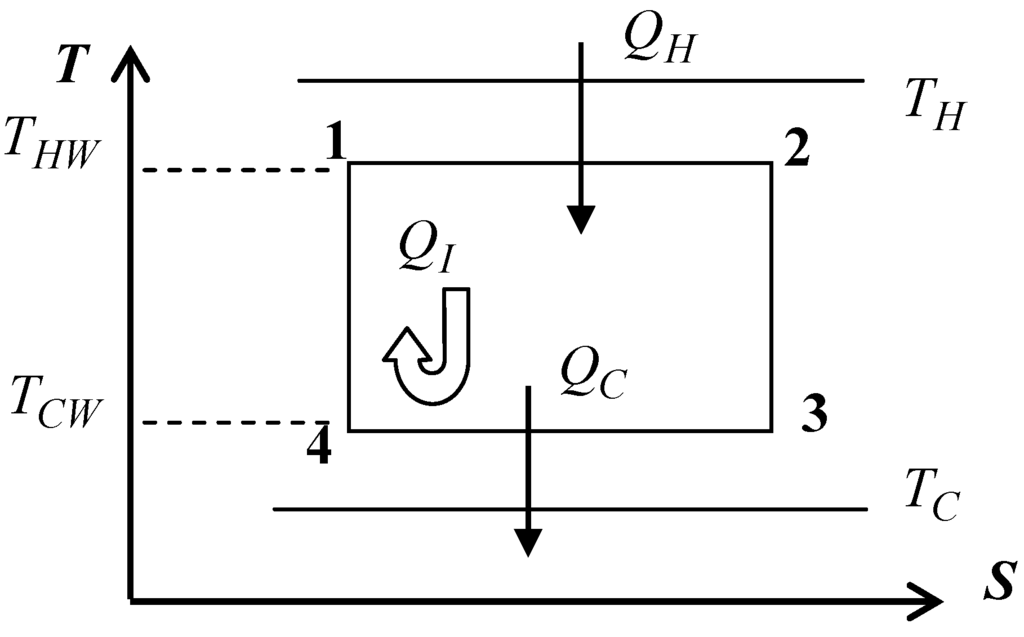
Figure 2. Curzon and Ahlborn cycle in the S-T plane. $Q_I$ is a heat generated by internal phenomena.

Figure 2. Curzon and Ahlborn cycle in the S-T plane. $Q_I$ is a heat generated by internal phenomena.

From the second law of thermodynamics the Clausius inequality can be written as,

$$\frac{Q_H}{T_H}-\frac{Q_C}{T_C}<0,$$

(7)

and by introducing the non-endoreversibility parameter $I_S$, Equation (7) becomes,

$$I_S\frac{Q_H}{T_H}-\frac{Q_C}{T_C}=0,$$

(8)

so that it is possible to write,

$$Q_C=\frac{T_C}{T_H}{I}_S{Q}_H.$$

(9)

Let it suppose one mol of ideal gas as working substance in the engine. Thus heat exchange can be written for each one of the isothermic branches in Figure 2 as,

$$Q_H=R{T}_{HW}\ln \frac{V_2}{V_1} \mathrm{and} Q_C=\frac{T_C}{T_H}{I}_{S}R{T}_{HW}\ln \frac{V_2}{V_1},$$

(10)

where $V_1,V_2,$ are the volumes obtained on the first isothermic process in the Curzon and Ahlborn cycle shown in Figure 1 and Figure 2, and R is the universal constant of ideal gases. It is obtained the work from the engine by using Equation (9) as,

$$W_I=R{T}_{HW}\left(1-I_S\frac{T_{CW}}{T_{HW}}\right)\ln \frac{V_2}{V_1}.$$

(11)

On other hand, there are some possibilities to write the total time of cycle. The simplest of them is considering this time like in references [9,15,16] with instantaneous adiabats. Assuming the exchange of heat obtained by Newton heat transfer law between two environments at temperatures, $T_i$ and $T_f$, $T_i>T_f$, with rapidity of heat exchange $\frac{dQ}{dt}$, and with $\alpha$ the heat conductance, one has

$$\frac{dQ}{dt}=\alpha (T_f-T_i).$$

(12)

Each of processes in the cycle occur with a different heat conductance. So, for simplicity let assume the same heat conductance in the processes of heat transfer in the Curzon and Ahlborn cycle. By ussing Equation (9) the total time of performing of cycle can be written now as,

$$t_{TOT}=\frac{R{T}_{HW}}{\alpha }\left[\frac{1}{T_H-T_{HW}}+\frac{I_S}{T_{CW}-T_C}\cdot \frac{T_{CW}}{T_{HW}}\right]\ln \frac{V_2}{V_1},$$

(13)

and as a consequence the power output is now,

$$P_I=\frac{W_I}{t_{TOT}}=\frac{\alpha \left(1-I_S\frac{T_{CW}}{T_{HW}}\right)}{\frac{1}{T_H-T_{HW}}+\frac{I_S}{T_{CW}-T_C}\cdot \frac{T_{CW}}{T_{HW}}}.$$

(14)

Equation (14) can be simplified with the definitions,

$$Z_I=I_S\frac{T_{CW}}{T_{HW}} \mathrm{and} u=\frac{T_{HW}}{T_H},$$

(15)

and by using the parameter $\epsilon$ definite since Equation (5). One has the new simplified expression for power output as,

$$P_I=\frac{\alpha T_H(1-Z_I)}{\frac{1}{1-u}+\frac{I_S{Z}_I}{Z_{I}u-\epsilon I_S}}.$$

(16)

As well as it is made for the work obtained from the engine, the change of entropy in the cycle is,

$$\Delta S_I=-\frac{Q_H}{T_H}+\frac{Q_C}{T_C}=-R\frac{T_H}{T_C}(\epsilon -Z_I)\ln \frac{V_3}{V_1},$$

(17)

and the corresponding ecological function is now written as,

$$E_I=P_I-T_C{\sigma }_I=P_I-T_C\frac{\Delta S_I}{t_{TOT}},$$

or with the changes of variables taken previously in power output, one has,

$$E_I=\frac{\alpha T_H(1-2Z_I+\epsilon )}{\frac{1}{1-u}+\frac{I_S{Z}_I}{Z_{I}u-\epsilon I_S}}.$$

(18)

Notice the similar algebraic structure of both power output and ecological function compared with these obtained in references [9,15,16]. Function $Z_I$ depends on the parameters $\epsilon$ and $I_S$, as a consequence the efficiency will be a function of the same variables. Now, it has to obtain the efficiencies at maximum power output and at maximum ecological function from a general expression in a similar form as in references [9,15,16],

$${\eta }_I=1-Z_I(\epsilon ,I_S).$$

(19)

3. Curzon and Ahlborn efficiency and ecological efficiency

Function $Z_I$ could be obtained for both maximization of power output and maximization of ecological function. Taking the derivative of both power output and ecological function for u at $Z_I$ constant, ${\left(\frac{\partial P_I}{\partial u}\right)}_{Z_I=const.}=0$ and ${\left(\frac{\partial E_I}{\partial u}\right)}_{Z_I=const.}=0$, it is obtain $u=u(Z_I,I_S)$ as,

$$u=\frac{(Z_I+\epsilon \sqrt{I_S})\sqrt{I_S}}{Z_I(1+\sqrt{I_S})}.$$

(20)

Now, from the derivative of power output at $u=const.$, ${\left(\frac{\partial P_I}{\partial Z_I}\right)}_{u=const.}=0$, it is obtain,

$$-\left[(Z_{I}u-\epsilon I_S)+Z_I{I}_S(1-u)\right](Z_{I}u-\epsilon I_S)+\epsilon I_S^2(1-Z_I)(1-u)=0,$$

(21)

which relate the variables u and $Z_I$; and by substituting (20) into (21) it follows that,

$$Z_I=\sqrt{I_S\epsilon },$$

(22)

and it is obtain the efficiency at maximum power output, namely,

$${\eta }_m=1-\sqrt{I_S\epsilon },$$

whose is the result obtained in references [21].

Similarly, in case of ecological function, by taking the derivative ${\left(\frac{\partial E_I}{\partial Z_I}\right)}_{u=const.}=0$, one can find a relation between the variables $Z_I$ and u, that is the following one,

$$-2\left[(Z_{I}u-\epsilon I_S)+Z_I{I}_S(1-u)\right](Z_{I}u-\epsilon I_S)+\epsilon I_S^2(1-2Z_I+\epsilon )(1-u)=0,$$

(23)

and by substituting Equation (20) into (23) it is obtain the expression of $Z_I$,

$$Z_I=\sqrt{\frac{1}{2}{I}_S(\epsilon +{\epsilon }^2)},$$

(24)

and the efficiency at maximum ecological function, Equation (18), is,

$${\eta }_{EI}=1-\sqrt{\frac{1}{2}{I}_S(\epsilon +{\epsilon }^2)}.$$

(25)

As in the paper of Velasco et al [28], it is introduced the change $I\equiv \frac{1}{I_S},$ where $0<I<1$, for case of ideal gas as working substance, and because it is found that the parameter $I$ has values into the range [0.8,0.9] for real engines, Table 1 shows a comparison between values of efficiencies from reference [28] and efficiencies calculated by Equation (25) in the range [0.8,0.9] of parameter I. Furthermore, Figure 3 shows that Equation (25) improve the values of theoretical efficiencies respect to the values calculated in reference [28]. The parameter $I_S$ appears into (1.11,1.25).

The parameter I permits a more realistic evaluation of performance of power plants as it could be appreciate in Figure 4, in wich is compared the endoreversible ecological efficiency, Equation (3), vs the non-endoreversible ecological efficiency, Equation (25). For power output one obtains the same comparison. Also the parameter I is not depend of working substance, only it is necesary to take a fluid as it. In addition to, as it can be verified, in the limit $I\to 1$ it is recovered the endorreversible behavior of Curzon and Ahlborn cycle, so that ${\eta }_m\to {\eta }_{CAN}$ and ${\eta }_{EI}\to {\eta }_E$. Figure 4 also shows this assumption.

Table 1. Comparison of efficiencies obtained by Velasco et. al. [28] with efficiencies from Equation (25).

Power Plant	$T_2$ (K)	$T_1$ (K)	${\eta }_{opt}$, $0.8\le I\le 0.9$	${\eta }_{obs}$	${\eta }_{EI}$, $0.8\le I\le 0.9$
Doel 4 (Belgium), 1985.	283	566	0.297 to 0.357	0.35000	0.31535 to 0.3545
Almaraz II (nuclear pressurized water reactor) Spain	290	600	0.315 to 0.373	0.34500	0.3306 to 0.36889
Sizewell B (nuclear pressurized water reactor) U. K.	288	581	0.302 to 0.361	0.36300	0.3198 to 0.35821
Cofrentes (nuclear boiling water reactor) Spain	289	562	0.282 to 0.343	0.34000	0.30238 to 0.34228
Heysham (nuclear advanced gas cooled reactor) U. K.	288	727	0.410 to 0.460	0.40000	0.41206 to 0.44568

Table 1. Comparison of efficiencies obtained by Velasco et. al. [28] with efficiencies from Equation (25).

Power Plant	$T_2$ (K)	$T_1$ (K)	${\eta }_{opt}$, $0.8\le I\le 0.9$	${\eta }_{obs}$	${\eta }_{EI}$, $0.8\le I\le 0.9$
Doel 4 (Belgium), 1985.	283	566	0.297 to 0.357	0.35000	0.31535 to 0.3545
Almaraz II (nuclear pressurized water reactor) Spain	290	600	0.315 to 0.373	0.34500	0.3306 to 0.36889
Sizewell B (nuclear pressurized water reactor) U. K.	288	581	0.302 to 0.361	0.36300	0.3198 to 0.35821
Cofrentes (nuclear boiling water reactor) Spain	289	562	0.282 to 0.343	0.34000	0.30238 to 0.34228
Heysham (nuclear advanced gas cooled reactor) U. K.	288	727	0.410 to 0.460	0.40000	0.41206 to 0.44568

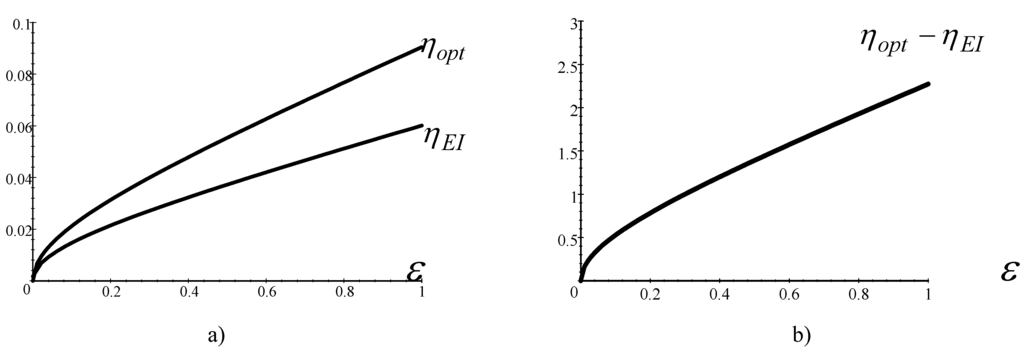
Figure 3. Comparative graphics between efficiencies ${\eta }_{opt}$ and ${\eta }_{EI}$. a) Difference of extreme values one by one for $0.8\le I\le 0.9$. b) Difference ${\eta }_{opt}-{\eta }_{EI}$, in the extreme of range of values for I.

Figure 3. Comparative graphics between efficiencies ${\eta }_{opt}$ and ${\eta }_{EI}$. a) Difference of extreme values one by one for $0.8\le I\le 0.9$. b) Difference ${\eta }_{opt}-{\eta }_{EI}$, in the extreme of range of values for I.

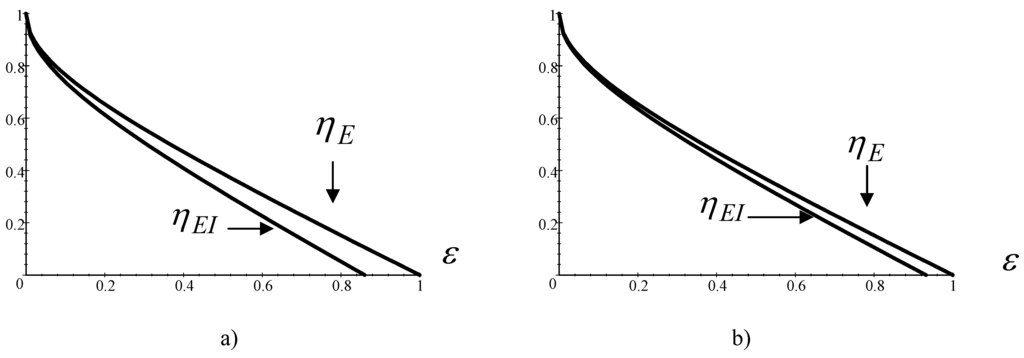
Figure 4. Comparison graphics between efficiencies ${\eta }_E$ and ${\eta }_{EI}$. a) For $I=0.8$. b) For $I=0.9$.

Figure 4. Comparison graphics between efficiencies ${\eta }_E$ and ${\eta }_{EI}$. a) For $I=0.8$. b) For $I=0.9$.

4. More general expressions for power output and for ecological function

To introduce the compression ratio it is neccesary to take into account the time of the adiabatic processes in the cycle. There is not a direct procedure to calculate this time, so that it is assume a similar procedure used in references [9,15,16]. Suppousing the adiabatic processes as multiple of the time of isothermic processes, the time of the first and the second adiabatic processes respectively are,

$$t_3=\frac{R{T}_{HW}}{\alpha (T_H-T_{HW})}\ln \frac{V_3}{V_4} \mathrm{and} t_4=-\frac{I_S\frac{T_{CW}}{T_{HW}}R{T}_{HW}}{\alpha (T_{CW}-T_C)}\ln \frac{V_1}{V_4}.$$

(26)

The negative sign in $t_4$ is introduced because the time has to be positive. Suppousing one mol of working substansce, now the total time of the cycle is,

$$t_{TOT}=\frac{R{T}_{HW}}{\alpha }\left[\frac{1}{T_H-T_{HW}}+\frac{I_s\frac{T_{CW}}{T_{HW}}}{T_{CW}-T_C}\right]\ln \frac{V_3}{V_1}.$$

(27)

The relation for volumes in adiabatic processes, $T{V}^{\gamma -1}=const.$, is used. So the power output of the cycle could be written by taking into account the changes of variables shown in Equation (15) as,

$$P_{I\lambda }=\frac{\alpha T_H(1-Z_I)(1+\lambda \ln Z_I-\lambda \ln I_S)}{\frac{1}{1-u}+\frac{Z_I{I}_S}{Z_{I}u-\epsilon I_S}},$$

(28)

and it could be verified that Equation (28) reduces to Equation (16) when $\lambda \to 0$. Similarly ecological function can be written as,

$$E_{I\lambda }=\alpha T_H\frac{(1-2Z_I+\epsilon )(1+\lambda \ln Z_I-\ln I_S)}{\frac{1}{1-u}+\frac{I_S{Z}_I}{Z_{I}u-\epsilon I_S}},$$

(29)

Similar results found in references [9,15] could be obtained now. On other hand, it is interesting to point out that power output and ecological function can be obtained for instantaneous adiabats and a non-linear heat transfer law, like $Q\propto {(\Delta T)}^k$, as

$$P_{Ik}=\frac{\alpha T_H^k(1-Z_I)}{\frac{1}{{(1-u)}^k}+\frac{Z_I{I}_S^k}{{(Z_{I}u-\epsilon I_S)}^k}} \mathrm{and} E_{Ik}=\frac{\alpha T_H^k(1-2Z_I+\epsilon )}{\frac{1}{{(1-u)}^k}+\frac{I_S^k{Z}_I}{{(Z_{I}u-\epsilon I_S)}^k}}.$$

5. Concluding remarks

A first interesting feature of the above results is that from the procedure to build power output and ecological function used in references [9,15,16], one can obtain similar expressions of the corresponding power output and ecological function for case of a non endoreversible Curzon and Ahlborn cycle. One has to introduce appropiate changes to obtain Equation (16) and Equation (18) in case of instantaneous adiabats. Numerical results obtained by other authors could be improve as it is shown in Table 1. Even more one has to hope a more improve if it is taking into account compression ratio by using a linear approximation of efficiencies obtained from maximization of Equation (28) and Equation (29). In case of a non ideal gas as working substance is important to point out that parameter $I_S$ appears by equation of state as was enphazised in reference [16] when the total heat is calculated. Also for case of non linear heat transfer law this parameter appears in a similar way. Notice that the Gutkowics-Krusin et al procedure [9] could be took as a methodology to take into account internal irreversibilities of the cycle. The relation of non-endoreversibilty parameter with physical quantities of power plants exceeds this paper, in which it is shown the plausibility of the propoused optimization method, and it deserves a special treatment in a further paper.