Distillation of a Complex Mixture. Part I: High Pressure Distillation Column Analysis: Modeling and Simulation
Abstract
:1. Introduction
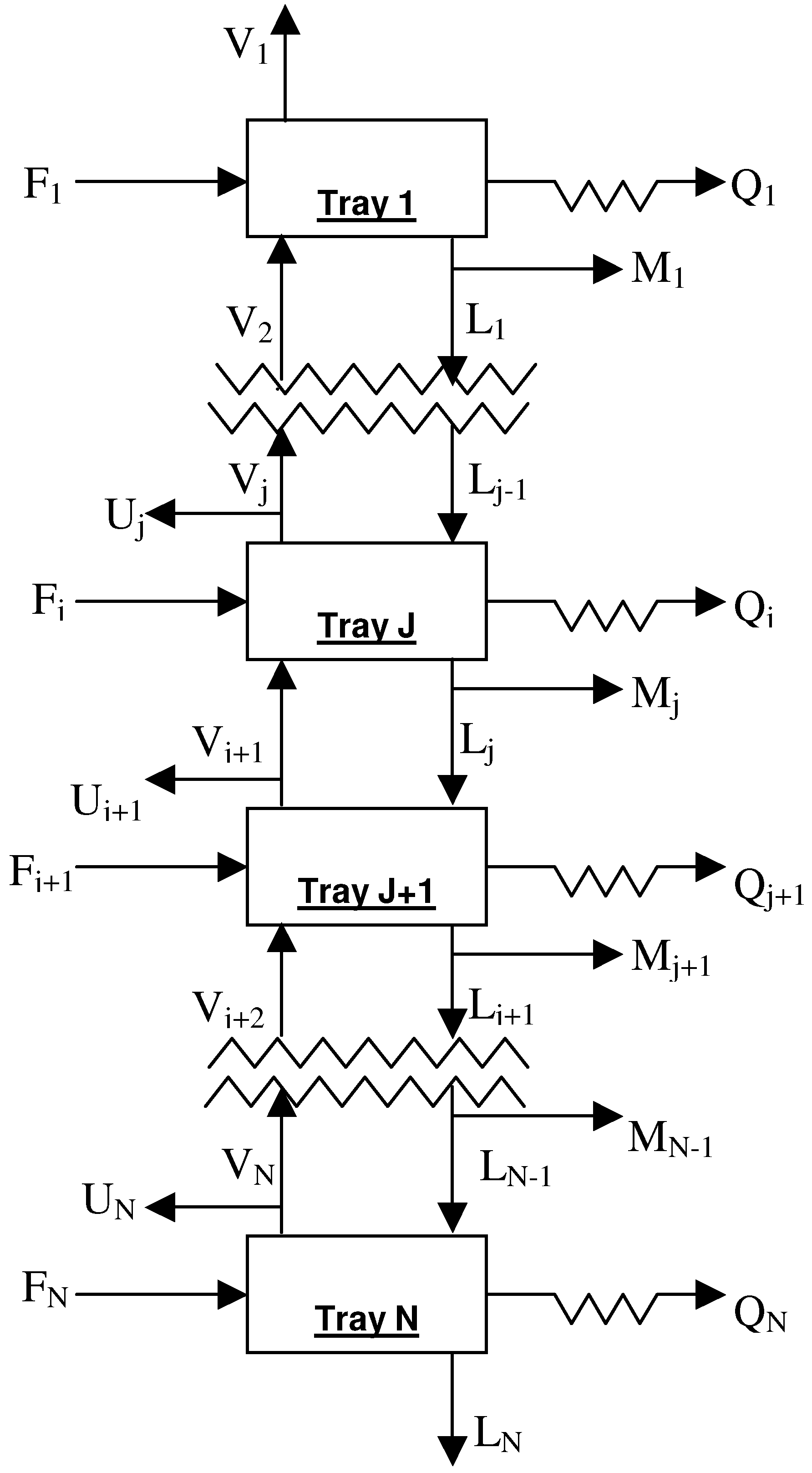
2. Column Modeling
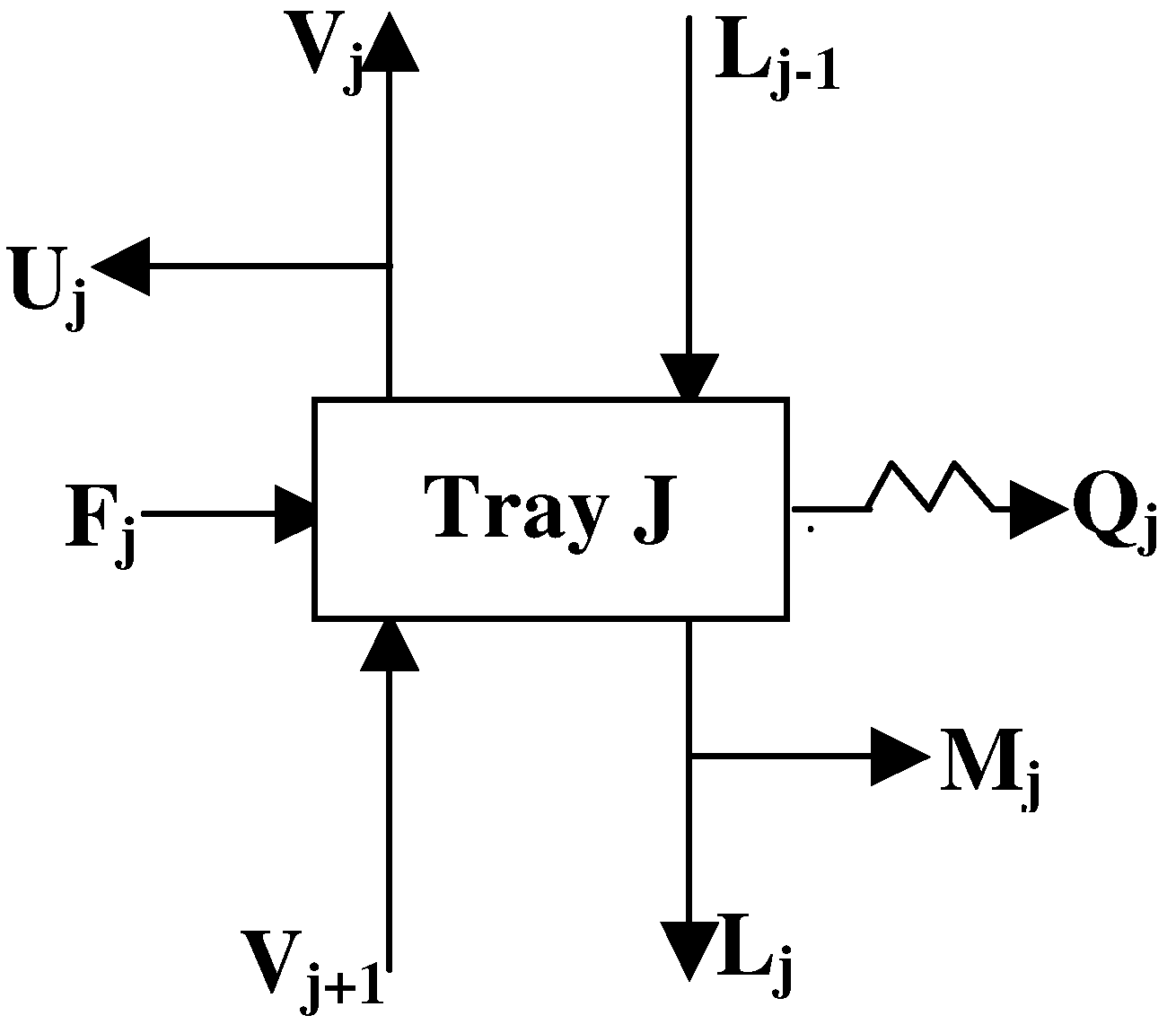
3. Analysis of Column Variance
| Specification | Number |
| 1 |
| C-1 |
| 1 |
| C-1 |
| 1 |
| C-1 |
| |
| 1 |
| 1 |
| 1 |
| 1 |
- -
- the total variables number of the unit as:
- -
- the number of independent relations as:
| Specification | Number |
| |
| (C+2) |
| (C+2) |
| N |
| N |
| N |
| N |
| 1 |
4. Simulation of the column
- Composition distribution of vapor and liquid phases in the whole column.
- Temperature of each tray.
- Flow rates of the phases in circulation between trays.
- Initiate values for Tj(0) and Vj (0) so that T0(1) corresponds to the dew point temperature and T0(N) to the bubble point temperature. For intermediate trays, the temperatures of initialization are supposed to vary linearly as:
- Evaluate the equilibrium coefficients Ki,j (ideal mixture)
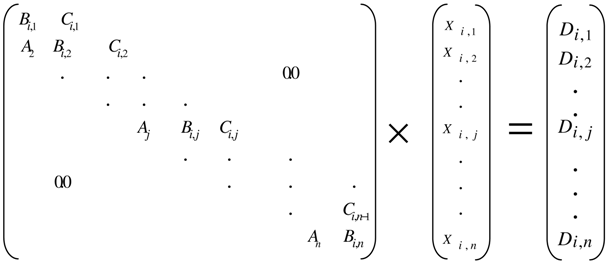
- Calculate all the compositions by solving the system of equations in the form of C tridiagonal matrix (Equation (10)) by using the Thomas’s method. [14]
- If all the equations of balances converge with Xi,j =1 for any tray, then it is imperative to standardize the values of Xi,j by taking:
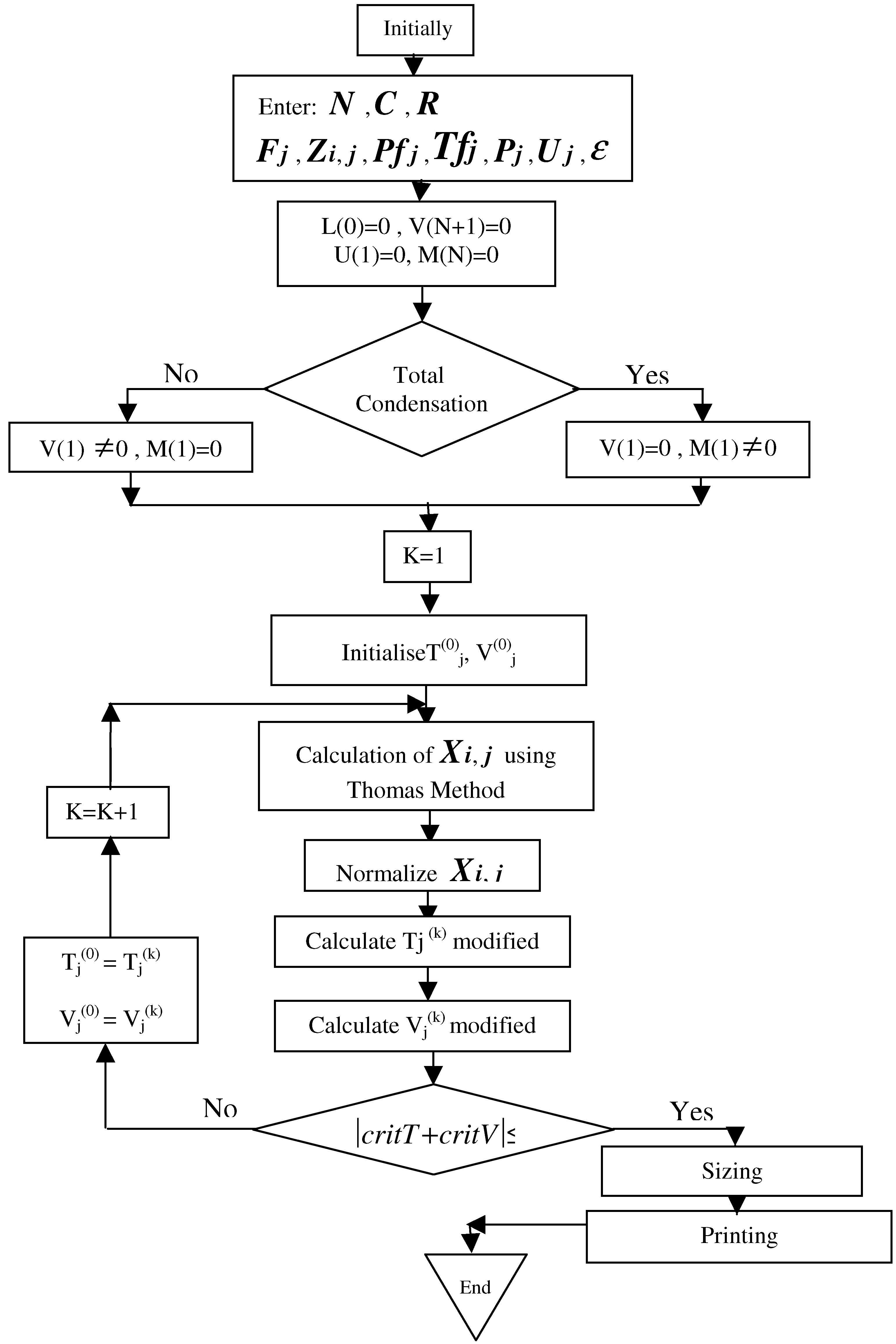
- Calculate the vapour concentrations:
- Calculate the vapour flow rate values Vj (from the heat balance):where Hlj and Hvj are respectively the enthalpies of liquid and vapour phases for tray j [15].
- Check if the calculated values Tj(k) and Vj(k) are of the same order of magnitude as the values Tj(k-1) and Vj(k-1) used for the preceding iteration. For this purpose, the following criterion of convergence is adopted:
- Otherwise, calculations are redone starting from step (2) based on values obtained in iteration K.
- Vapour and liquid enthalpies according to the temperature and the pressure whose expression is given in appendix.
- Density or are given by the Starling's equation [16]. It is interesting to notice that only the lowest value and the greatest value of have a physical significance, which correspond to and respectively.
- Equilibrium coefficients K at the tray temperature and pressure.
5. Operating mode
- Enriching section: Diam=4.1m
- Stripping section: Diam=5.5m
| Component | C1 | C2 | C3 | Iso-C4 | n-C4 | Iso-C5 | n-C5 | C6+ |
| Composition ( % mol.) | 0.26 | 1.97 | 60.06 | 14.22 | 23.39 | 0.08 | 0.02 | Traces |
6. Results and Discussion
6.1. Validation of the column simulation model
6.2. Variation of power exchanged with the column

| Component | Distillate composition ( molar fractions) | Residue composition ( molar fractions) | ||||
| Design | Simulation values | Deviation | Design | Simulation values | Deviation | |
| Methane | 0.0007 | 0.0041 | 0.0034 | 4.34 10-17 | 0.417 10-19 | 0.0000 |
| Ethane | 0.0147 | 0.0310 | 0.0163 | 0.1698 10-10 | 0.127 10-10 | 0.0000 |
| Propane | 0.9659 | 0.9530 | 0.0129 | 0.0100 | 0.0037 | 0.0063 |
| Iso-butane | 0.0160 | 0.0099 | 0.0061 | 0.3647 | 0.3665 | 0.0018 |
| N-butane | 0.0025 | 0.0019 | 0.0006 | 0.6226 | 0.6270 | 0.0044 |
| Iso-pentane | 5.95 10-9 | 8.3 10-9 | 0.0000 | 0.0021 | 0.0021 | 0.0000 |
| N-pentane | 2.36 10-10 | 2.88 10-10 | 0.0000 | 0.0005 | 0.0005 | 0.0000 |
| Temperature (°C) | 58.07 | 58.42 | 0.6% | 111.02 | 110.71 | 0.28% |
| Qc (kcal/hr) | 15.85 106 | 16.17 106 | 2% | |||
| Qr (kcal/hr) | 16.51 106 | 16.86 106 | 2% | |||
 |
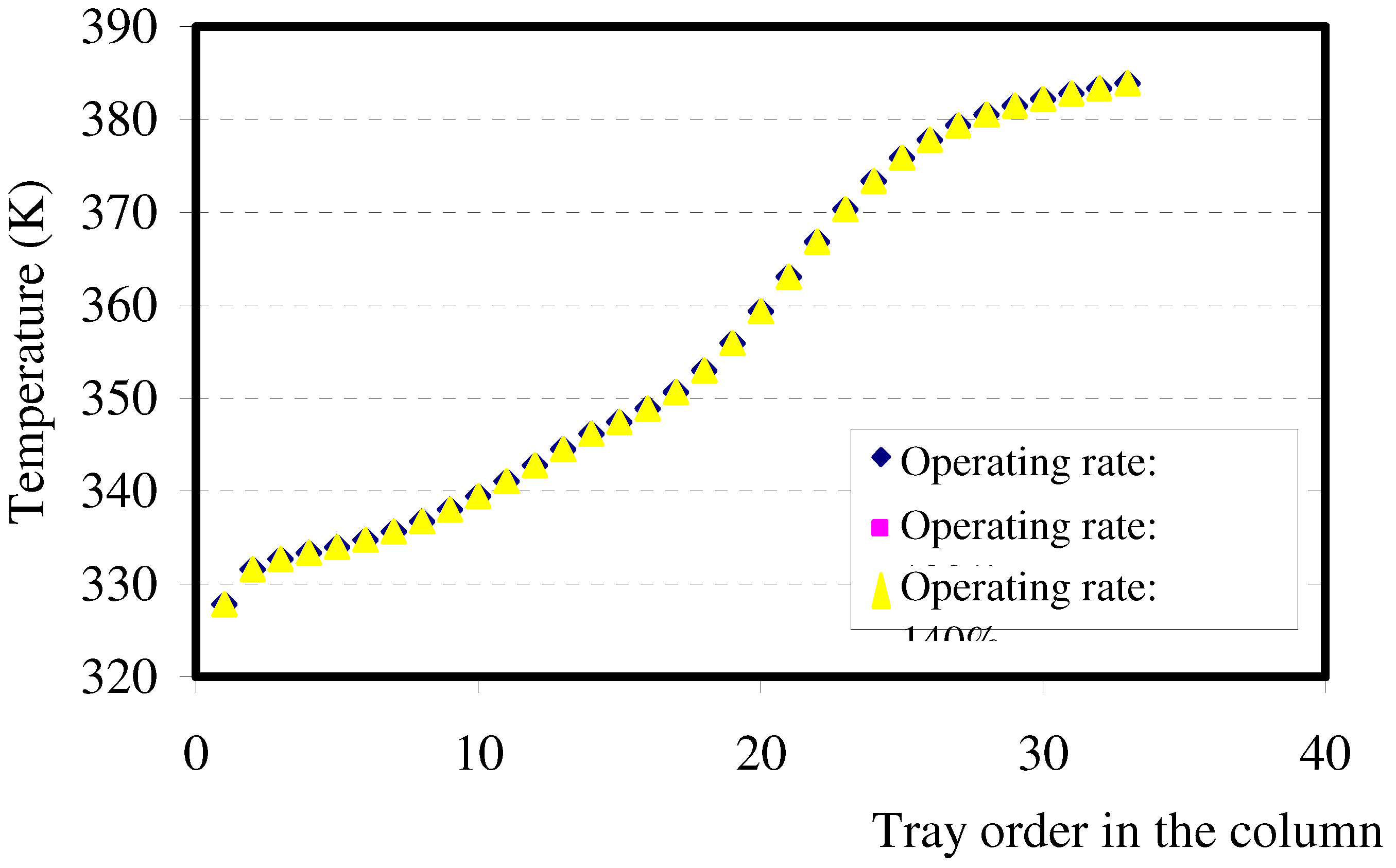
6.3. Temperature profile in the column:
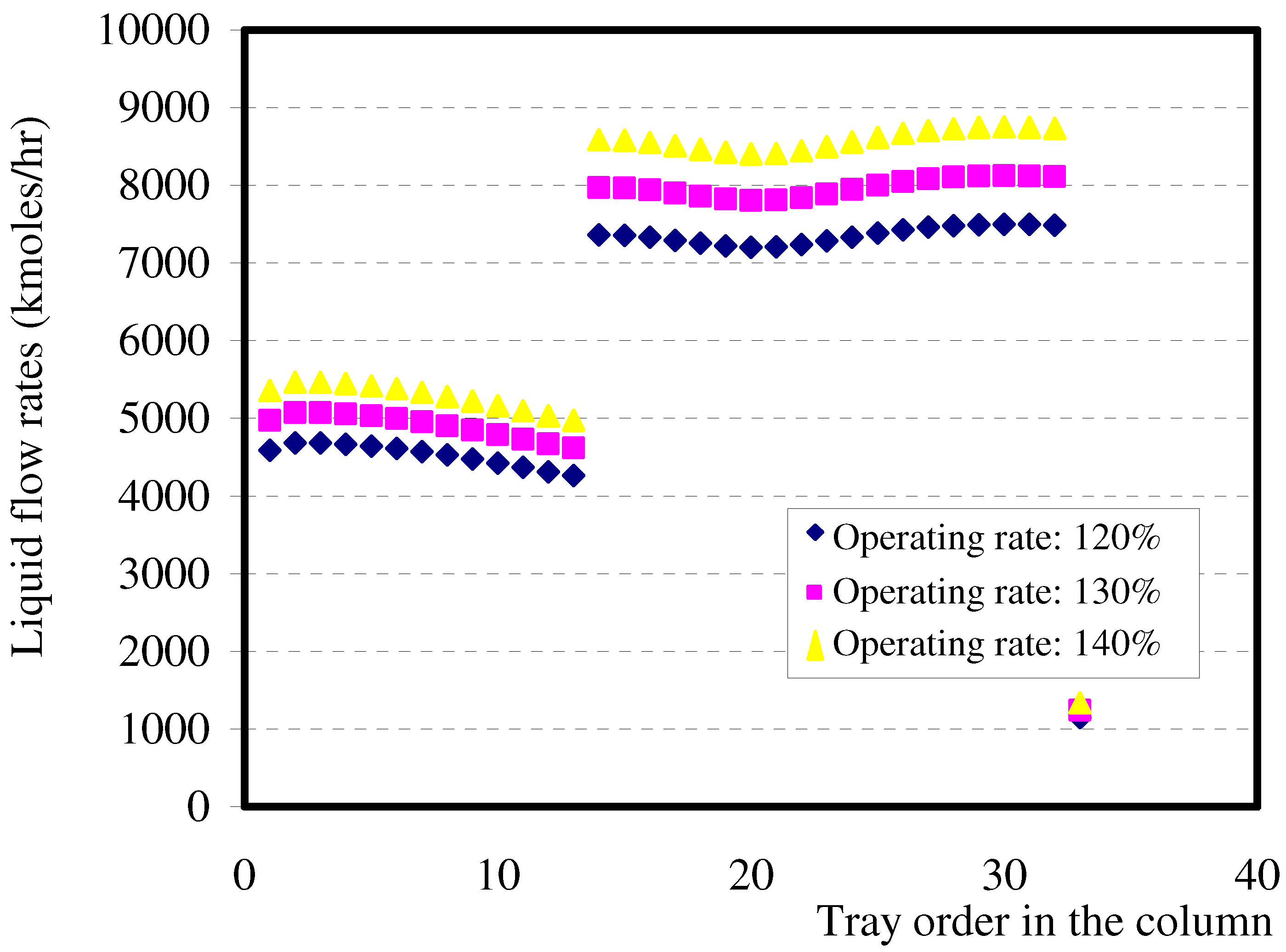
6.4. Distribution of the liquid flow rate in the column
- Zone I: corresponds to the liquid flow rate which varies slightly in the enriching section between tray 1 and tray 13.
- Zone II: refers especially to the feed tray where a sudden increase of the liquid flow rate occurs because the feed is introduced in the form of boiling liquid.
- Zone III: The liquid flow rate is fairly large in the stripping section, with a slight variation; but in the last trays, a decrease of the flow rate is noticed due to the high temperature which reigns at the bottom of columns. It should be noted that the shape of the second section would not be so sharp if the feed was a boiling liquid, a vapour or a biphasic mixture.
6.5. Distribution of the vapour flow rate in the column

Conclusion
Nomenclature
| C | Number of components of the mixture |
| D | Distillate flow rate (kmol/hr) |
| F | Feed flow rate (kmol/hr) |
| H | Enthalpy of a mass stream (kcal/kmol) |
| K | Vapour-liquid equilibrium coefficient (--) |
| L | Liquid stream flow rate (kmol/hr) |
| M | Liquid side stream flow rate (kmol/hr) |
| N | Number of trays in the column (--) |
| P | Operating pressure of the column (atm) |
| Qc | Calorific power exchanged with the condenser (kcal/hr) |
| Qr | Calorific power exchanged with the boiler (kcal/hr) |
| Tref | Reference temperature (273.15 K) |
| To | Temperature of the ambient conditions (298.15 K) |
| V | Vapour stream flow rate (kmol/hr) |
| U | Vapour side stream flow rate (kmol/hr) |
| X | Molar composition of the liquid phase |
| Y | Molar composition of the phase vapour |
| Z | Molar composition of the feed |
Indices
| f | Relating to the feed |
| I | Relating to the component in the mixture |
| J | Relating to the sequence number of the tray |
| C, c | Condenser (J=1) |
| R, r | Boiler (J=33) |
References
- Cicile, J.C. Distillation-Absorption, Techniques de l’Ingénieur; Ed. Technip: Paris, 1994; Sections J-2610, J-2611, J-2621, J-2622, J-2623. [Google Scholar]
- Claudel, B.; Andrieu, J.; Otterein, M. Bases de Génie Chimique; Techniques et Documentation: Paris, 1977; pp. 164–178. [Google Scholar]
- Walas, S.M. Textbook of Chemical Process Equipment-Selection and Design, 2nd Ed.; Butterworths Series in Chemical Engineering: USA, 1988; pp. 236–271. [Google Scholar]
- Wuithier, P. Raffinage et Génie chimique. 2nd Ed.; Ed. Technip: Paris, 1972; pp. 132–165. [Google Scholar]
- Chittur, K. ChE 448 Chemical Engineering Design, MultiComponent Distillation; K. Chittur: Huntsville, 1998. http://www.che.uah.edu/courseware/che448-Spring1998/multcomp/ (online courseware).
- Kwauk, M. A system for counting variables in separation processes. A. I. Ch. E. Journal 1956, 2, 240–248. [Google Scholar] [CrossRef]
- Koehler, J.; Poellmann, P.; Blass, E. A review on minimum energy calculations for ideal and nonideal distillations. Ind. Eng. Chem. Res. 1995, 34, 1003–1020. [Google Scholar] [CrossRef]
- Rong, B.G.; Kraslawski, A.; Nystrom, L. Design and synthesis of multicomponent thermally coupled distillation flow sheets. Comp. Chem. Eng. 2001, 25, 807–820. [Google Scholar] [CrossRef]
- Bausa, J.; Vonwatzdorf, R.; Marquardt, W. Minimum energy demand for nonideal multicomponent distillations in complex columns. Comput. Chem. Engng. 1996, 20, 55–60. [Google Scholar] [CrossRef]
- Agrawal, R.; Fidkowski, Z.T. Are thermally coupled distillation columns always thermodynamically more efficient for ternary distillations. Ind. Eng. Chem. Res. 1998, 37, 3444–3454. [Google Scholar] [CrossRef]
- Perry, R.H.; Green, D.W.; Maloney, J.O. Perry’s Chemical Engineer’s Handbook, 7th Ed.; McGraw-Hill: New York, 1997; pp. 1–54. [Google Scholar]
- Smith, F. Analysis of the Equilibrium Stage Separation Problem Formulation and Convergence. Am. Inst. Chem. Eng. J. 1964, 10, 698–711. [Google Scholar]
- Gilliland, E.R.; Reed, C.E. Degrees of freedom in multicomponent absorption and rectification columns. Ind. Eng. Chem. 1942, 34, 551–557. [Google Scholar] [CrossRef]
- Gourdin, A.; Boumahrat, M. Méthodes Numériques Appliquées; O.P.U: Algiers, 1993; pp. 147–202. [Google Scholar]
- Holland, C.; Pendon, G. Solve more Distillation Problems. Hydrocarbon Process. 1974, 53, 148–156. [Google Scholar]
- Starling, K.E.; Han, M.S. Thermo data refined for LPG. Pt. 15. Industrial applications. Hydrocarbon Process. 1972, 51, 107–115. [Google Scholar]
- Takamatsu, T.; Nakaiwa, M.; Huang, K.; Akiya, T.; Noda, H.; Nakanishi, T.; Aso, K. Simulation Oriented Development of a New Heat Integrated Distillation Column and its Characteristics for Energy Saving. Computers and Chemical Engineering 1997, 21, 243–247. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Malik, R.K.; Shenoy, U.V. Temperature-enthalpy curve for energy targeting of distillation columns. Computers and Chemical Engineering 1998, 22, 1733–1744. [Google Scholar] [CrossRef]
© 2007 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Mustapha, D.; Fatima, O.; Sabria, T. Distillation of a Complex Mixture. Part I: High Pressure Distillation Column Analysis: Modeling and Simulation. Entropy 2007, 9, 58-72. https://doi.org/10.3390/e9020058
Mustapha D, Fatima O, Sabria T. Distillation of a Complex Mixture. Part I: High Pressure Distillation Column Analysis: Modeling and Simulation. Entropy. 2007; 9(2):58-72. https://doi.org/10.3390/e9020058
Chicago/Turabian StyleMustapha, Douani, Ouadjenia Fatima, and Terkhi Sabria. 2007. "Distillation of a Complex Mixture. Part I: High Pressure Distillation Column Analysis: Modeling and Simulation" Entropy 9, no. 2: 58-72. https://doi.org/10.3390/e9020058
APA StyleMustapha, D., Fatima, O., & Sabria, T. (2007). Distillation of a Complex Mixture. Part I: High Pressure Distillation Column Analysis: Modeling and Simulation. Entropy, 9(2), 58-72. https://doi.org/10.3390/e9020058





